The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars
Abstract
1. Introduction
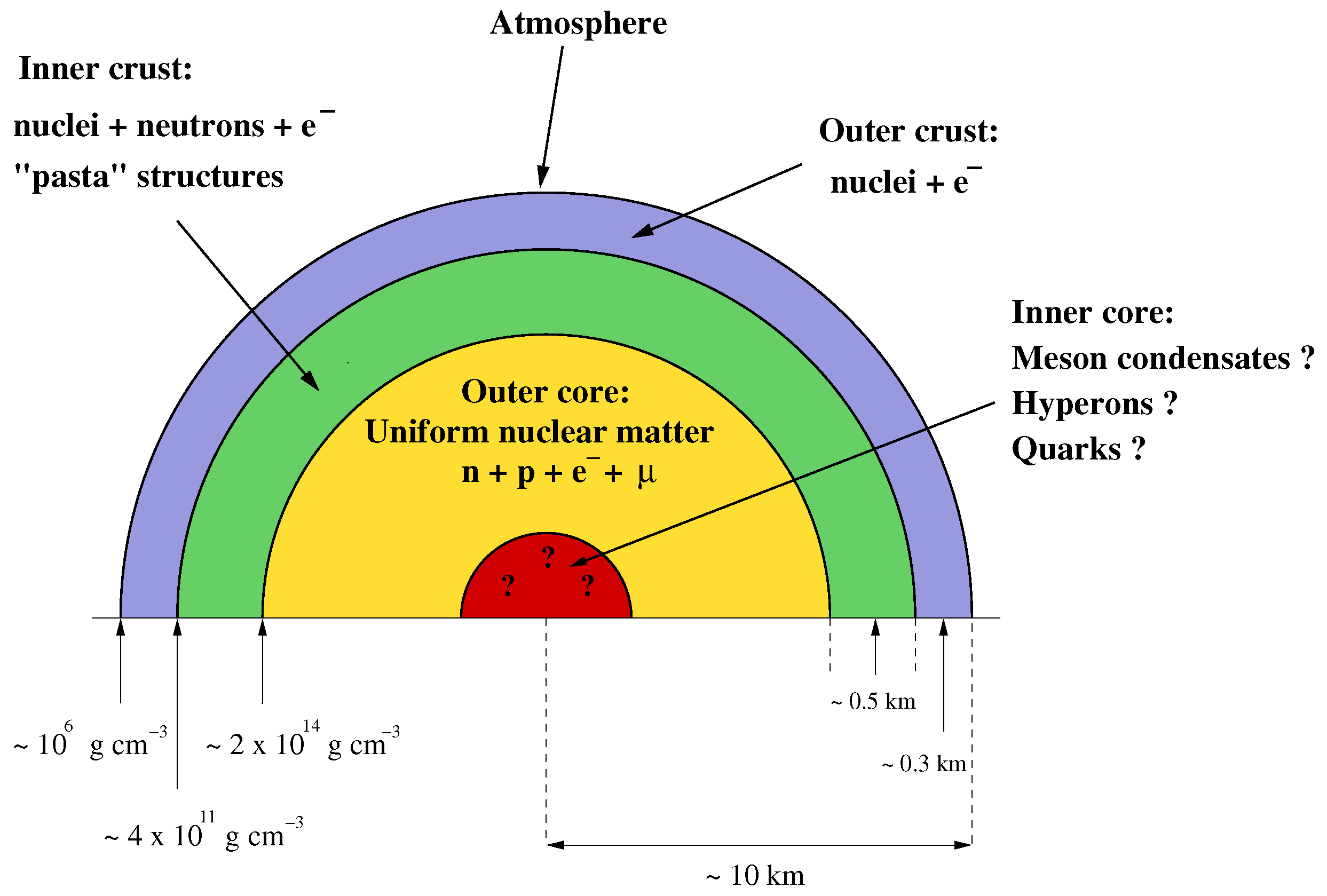
2. Neutron Stars in a Nutshell
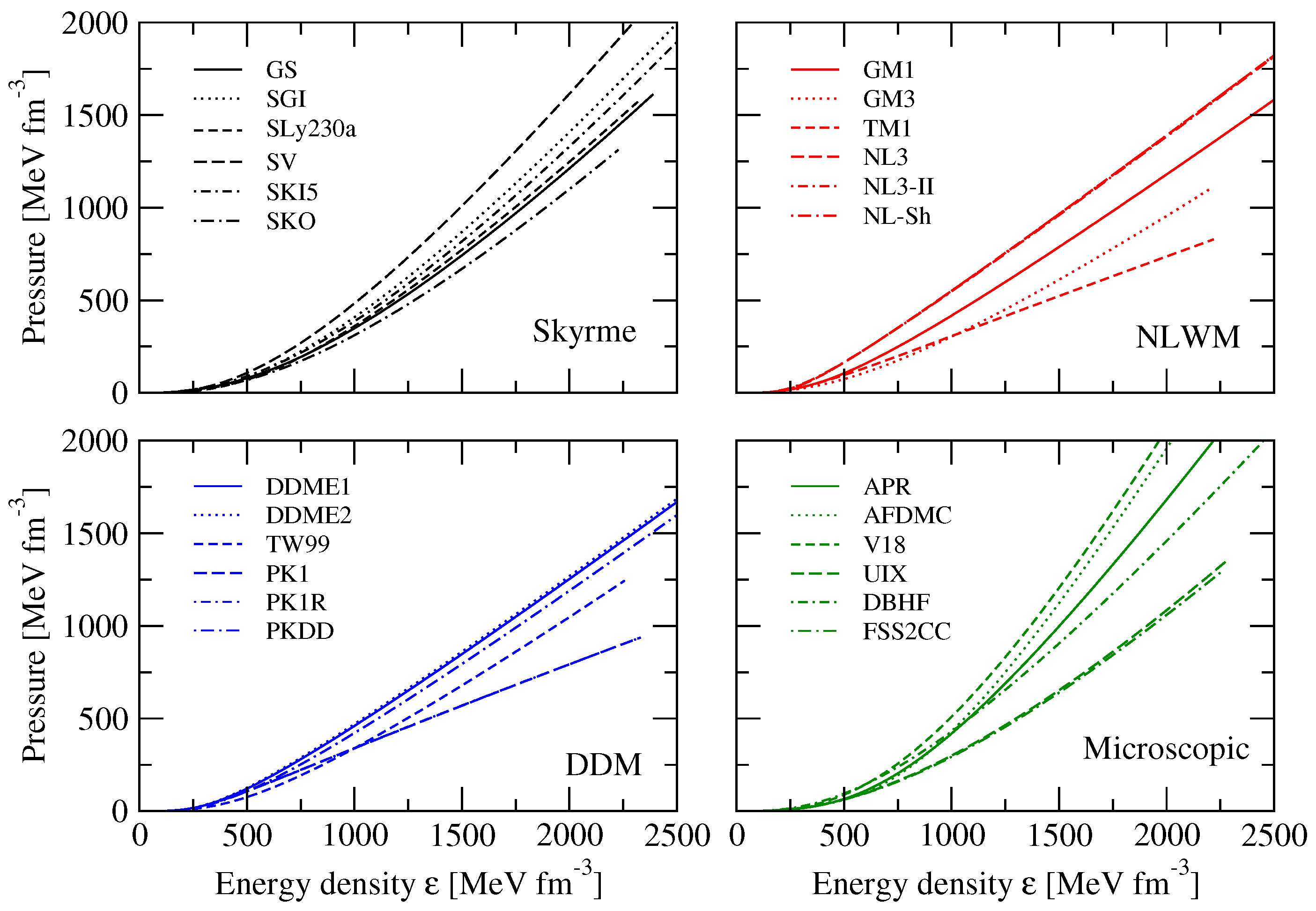
3. The Nuclear Equation of State
3.1. Laboratory Constraints on the Nuclear EoS
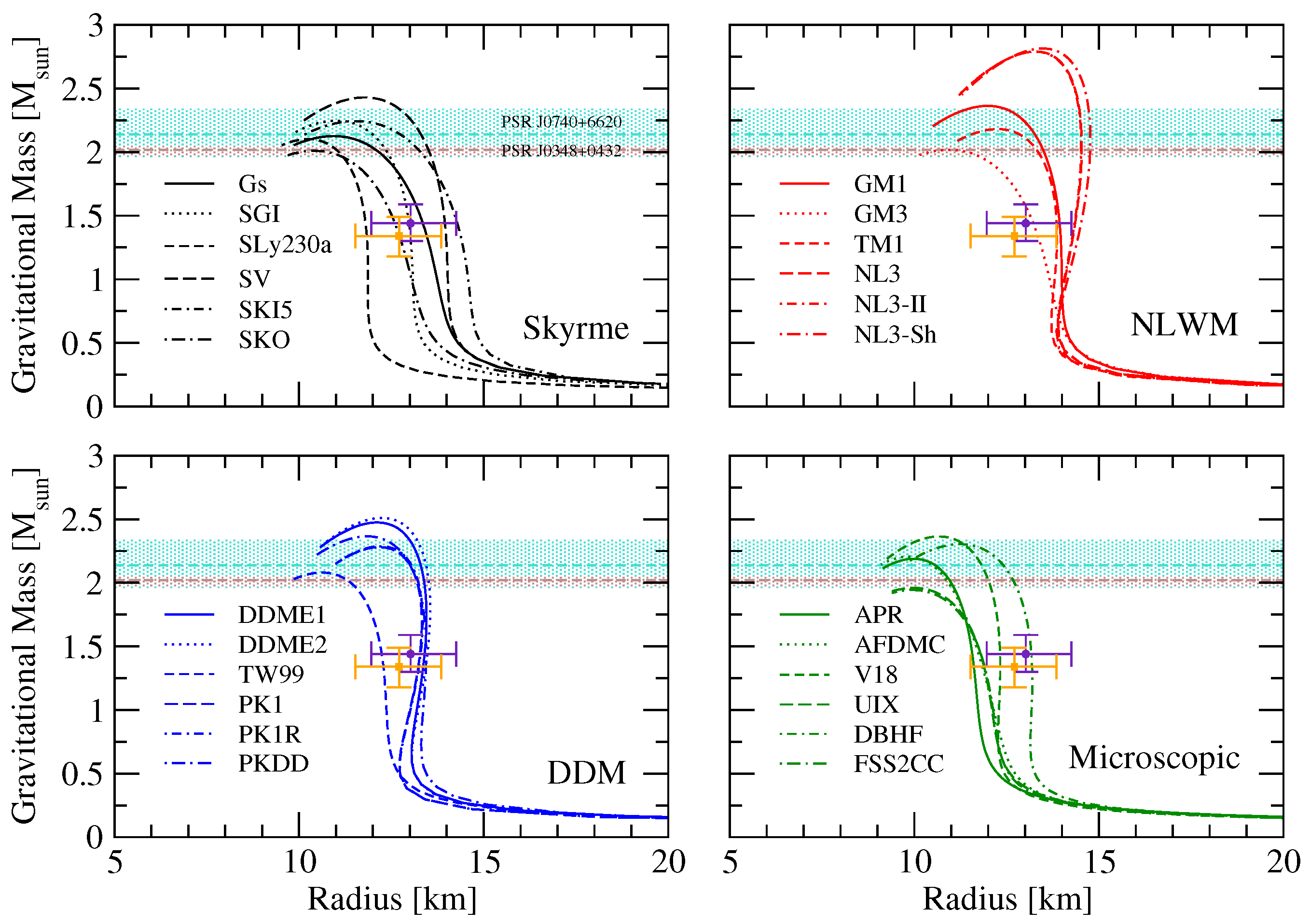
3.2. Astrophysical Constraints on the Nuclear EoS
4. EoS for -Stable Matter
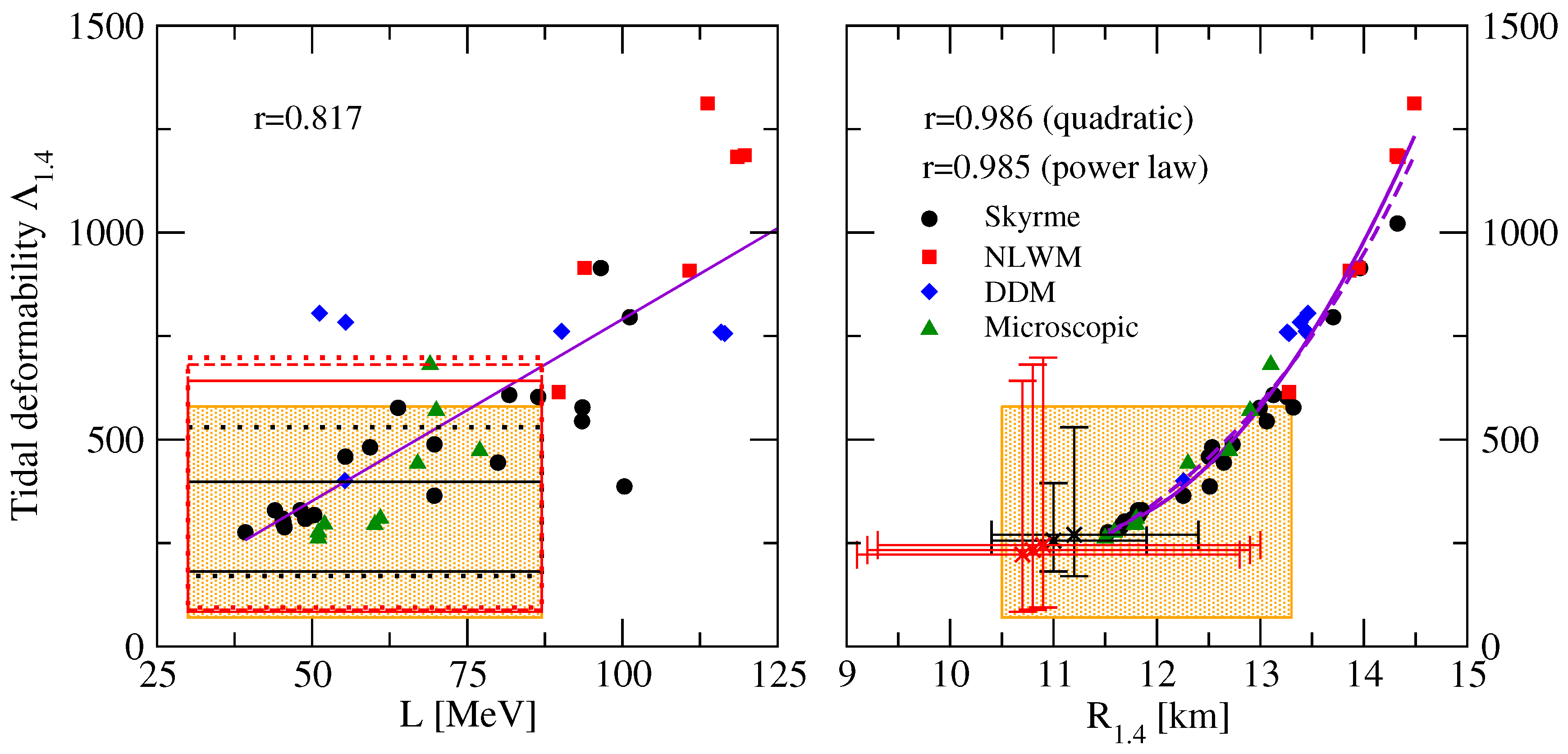
5. The Neutron Star Tidal Deformability
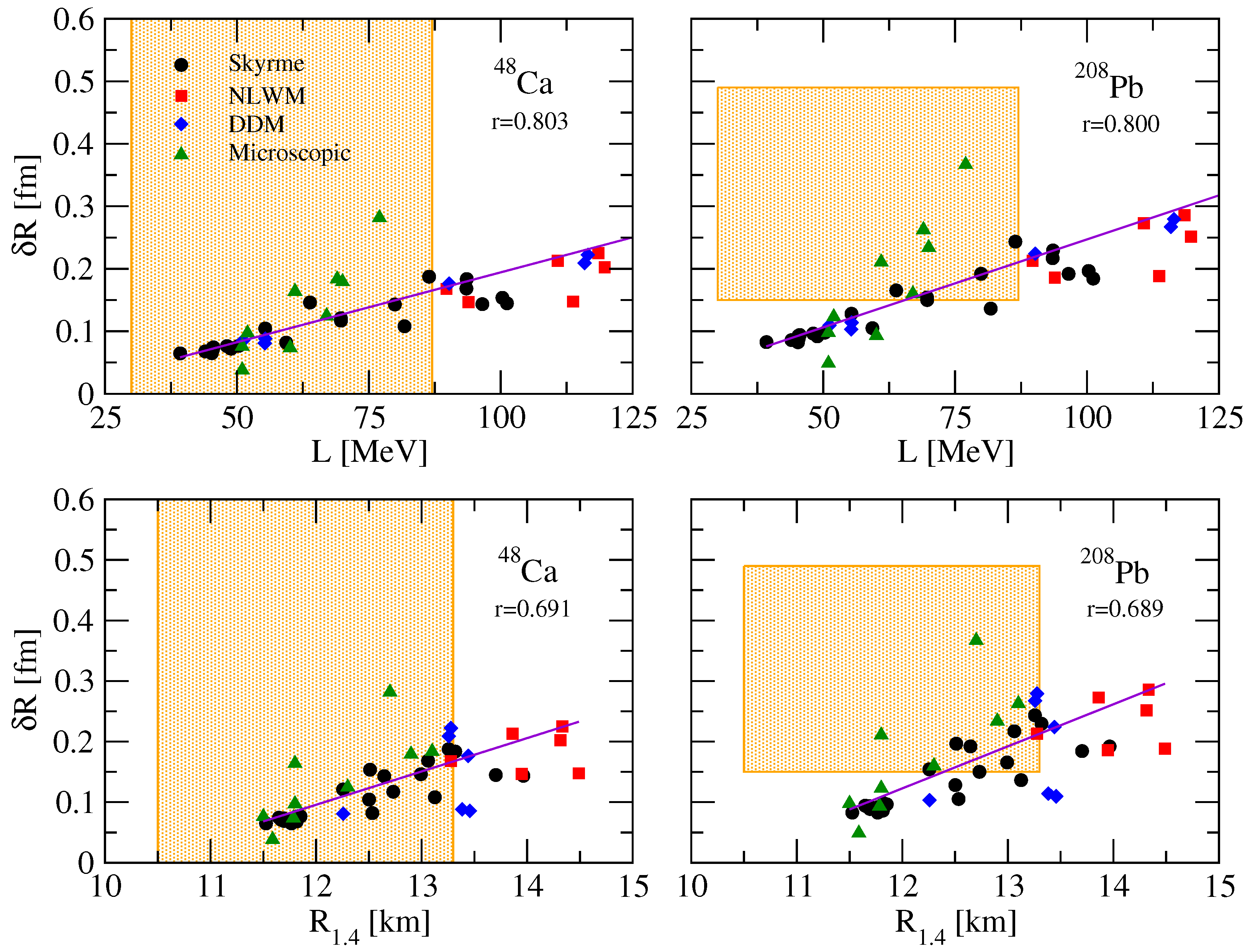
6. The Neutron-Skin Thickness
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Burgio, G.F.; Fantina, A.F. Nuclear Equation of state for Compact Stars and Supernovae. Astrophys. Space Sci. Libr. 2018, 457, 255. [Google Scholar]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Ann. Rev. Nucl. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.; Hessels, J.W. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Antoniadis, J. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Cromartie, H.T. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef]
- Guillot, S.; Servillat, M.; Webb, N.A.; Rutledge, R.E. Measurement of the Radius of Neutron Stars with High Signal-to-noise Quiescent Low-mass X-Ray Binaries in Globular Clusters. Astrophys. J. 2013, 772, 7. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Watts, A.L. Dense matter with eXTP. Sci. China Phys. Mech. Astron. 2019, 62, 29503. [Google Scholar] [CrossRef]
- Abbott, B. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly rotating relativistic stars. 1. Equations of structure. Astrophys. J. 1967, 150, 1005–1029. [Google Scholar] [CrossRef]
- Flanagan, E.E.; Hinderer, T. Constraining neutron star tidal Love numbers with gravitational wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef]
- Horowitz, C.J. Neutron rich matter in the laboratory and in the heavens after GW170817. Ann. Phys. 2019, 411, 167992. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J.; Wilson, J.R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066. [Google Scholar] [CrossRef]
- Blaschke, D.; Colpi, M.Y.; Horowitz, C.J.; Radice, D.E. First joint gravitational wave and electromagnetic observations: Implications for nuclear and particle physics. Eur. Phys. J. A 2019, 55. Available online: https://epja.epj.org/component/toc/?task=topic&id=1005 (accessed on 9 August 2020).
- Stone, J.R.; Reinhard, P.G. The Skyrme interaction in finite nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2007, 58, 587–657. [Google Scholar] [CrossRef]
- Vautherin, D.; Brink, D.M. Hartree-Fock Calculations with Skyrme’s Interaction. I. Spherical Nuclei. Phys. Rev. C 1972, 5, 626–647. [Google Scholar] [CrossRef]
- Quentin, P.; Flocard, H. Self-Consistent Calculations of Nuclear Properties with Phenomenological Effective Forces. Annu. Rev. Nucl. Part. Sci. 1978, 28, 523–594. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Friedrich, J.; Reinhard, P.G. Skyrme-force parametrization: Least-squares fit to nuclear ground-state properties. Phys. Rev. C 1986, 33, 335–351. [Google Scholar] [CrossRef]
- Giai, N.V.; Sagawa, H. Spin-isospin and pairing properties of modified Skyrme interactions. Phys. Lett. B 1981, 106, 379–382. [Google Scholar] [CrossRef]
- Chabanat, E. Report No. LYCENT 9501 (Unpublished). Ph.D. Thesis, Universitè Claude Bernard Lyon-1, Lyon, France, 1995. [Google Scholar]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densitiesPart II. Nuclei far from stabilities. Nucl. Phys. A 1998, 635, 231–256. [Google Scholar] [CrossRef]
- Beiner, M.; Flocard, H.; Van Giai, N.; Quentin, P. Nuclear ground-state properties and self-consistent calculations with the skyrme interaction (I). Spherical description. Nucl. Phys. A 1975, 238, 29–69. [Google Scholar] [CrossRef]
- Reinhard, P.G.; Flocard, H. Nuclear effective forces and isotope shifts. Nucl. Phys. A 1995, 584, 467–488. [Google Scholar] [CrossRef]
- Nazarewicz, W.; Dobaczewski, J.; Werner, T.R.; Maruhn, J.A.; Reinhard, P.G.; Rutz, K.; Chinn, C.R.; Umar, A.S.; Strayer, M.R. Structure of proton drip-line nuclei around doubly magic 48Ni. Phys. Rev. C 1996, 53, 740–751. [Google Scholar] [CrossRef] [PubMed]
- Bennour, L.; Heenen, P.H.; Bonche, P.; Dobaczewski, J.; Flocard, H. Charge distributions of 208Pb, 206Pb, and 205Tl and the mean-field approximation. Phys. Rev. C 1989, 40, 2834–2839. [Google Scholar] [CrossRef] [PubMed]
- Reinhard, P.G.; Dean, D.J.; Nazarewicz, W.; Dobaczewski, J.; Maruhn, J.A.; Strayer, M.R. Shape coexistence and the effective nucleon-nucleon interaction. Phys. Rev. C 1999, 60, 014316. [Google Scholar] [CrossRef]
- Tondeur, F.; Brack, M.; Farine, M.; Pearson, J.M. Static nuclear properties and the parametrisation of Skyrme forces. Nucl. Phys. A 1984, 420, 297–319. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the Lambda in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414. [Google Scholar] [CrossRef]
- Sumiyoshi, K.; Kuwabara, H.; Toki, H. Relativistic mean-field theory with non-linear σ and ω terms for neutron stars and supernovae. Nucl. Phys. A 1995, 581, 725–746. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540–543. [Google Scholar] [CrossRef]
- Sharma, M.M.; Nagarajan, M.A.; Ring, P. Rho meson coupling in the relativistic mean field theory and description of exotic nuclei. Phys. Lett. B 1993, 312, 377–381. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Finelli, P.; Ring, P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys. Rev. C 2002, 66, 024306. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Long, W.; Meng, J.; Giai, N.V.; Zhou, S.G. New effective interactions in relativistic mean field theory with nonlinear terms and density-dependent meson-nucleon coupling. Phys. Rev. C 2004, 69, 034319. [Google Scholar] [CrossRef]
- Machleidt, R.; Holinde, K.; Elster, C. The Bonn Meson Exchange Model for the Nucleon Nucleon Interaction. Phys. Rep. 1987, 149, 1–89. [Google Scholar] [CrossRef]
- Nagels, M.M.; Rijken, T.A.; de Swart, J.J. Low-energy nucleon-nucleon potential from Regge-pole theory. Phys. Rev. D 1978, 17, 768–776. [Google Scholar] [CrossRef]
- Weinberg, S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nucl. Phys. B 1991, 363, 3–18. [Google Scholar] [CrossRef]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288–292. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003, 68, 041001. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meißner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773–1825. [Google Scholar] [CrossRef]
- Baldo, M. Nuclear Methods And The Nuclear Equation Of State. Int. Rev. Nucl. Phys. 1999, 8. [Google Scholar] [CrossRef]
- Day, B.D. Elements of the Brueckner-Goldstone Theory of Nuclear Matter. Rev. Mod. Phys. 1967, 39, 719–744. [Google Scholar] [CrossRef]
- Brockmann, R.; Machleidt, R. Relativistic nuclear structure. I. Nuclear matter. Phys. Rev. C 1990, 42, 1965–1980. [Google Scholar] [CrossRef] [PubMed]
- Li, G.Q.; Machleidt, R.; Brockmann, R. Properties of dense nuclear and neutron matter with relativistic nucleon-nucleon interactions. Phys. Rev. C 1992, 45, 2782–2794. [Google Scholar] [CrossRef] [PubMed]
- Gross-Boelting, T.; Fuchs, C.; Faessler, A. Covariant representations of the relativistic Brueckner T-matrix and the nuclear matter problem. Nucl. Phys. A 1999, 648, 105–137. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Fabrocini, A.; Fantoni, S. Correlated basis function results for the Argonne models of nuclear matter. Phys. Lett. B 1993, 298, 263–266. [Google Scholar] [CrossRef]
- Kadanoff, L.; Baym, G. Quantum Statistical Mechanics; W.A. Benjamin Inc.: New York, NY, USA, 1962. [Google Scholar]
- Dickhoff, W.; Van Neck, D. Many-Body Theory Exposed; World Scientific Publishing: Singapore, 2005; 752p. [Google Scholar]
- Bogner, S.K.; Furnstahl, R.J.; Schwenk, A. From low-momentum interactions to nuclear structure. Prog. Part. Nucl. Phys. 2010, 65, 94–147. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Pieper, S.C.; Carlson, J.; Pand haripande, V.R. Quantum Monte Carlo calculations of A=8 nuclei. Phys. Rev. C 2000, 62, 014001. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, A.Y.; Schmidt, K.E.; Pederiva, F.; Fantoni, S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys. Rev. C 2009, 79, 054005. [Google Scholar] [CrossRef]
- Machleidt, R. The Meson theory of nuclear forces and nuclear structure. Adv. Nucl. Phys. 1989, 19, 189–376. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high quality N N potential models. Phys. Rev. C 1994, 49, 2950–2962. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. An Accurate nucleon-nucleon potential with charge independence breaking. Phys. Rev. C 1995, 51, 38–51. [Google Scholar] [CrossRef] [PubMed]
- Grangé, P.; Lejeune, A.; Martzolff, M.; Mathiot, J.F. Consistent three-nucleon forces in the nuclear many-body problem. Phys. Rev. C 1989, 40, 1040–1060. [Google Scholar] [CrossRef] [PubMed]
- Baldo, M.; Bombaci, I.; Burgio, G.F. Microscopic nuclear equation of state with three-body forces and neutron star structure. Astron. Astrophys. 1997, 328, 274–282. [Google Scholar]
- Zuo, W.; Lejeune, A.; Lombardo, U.; Mathiot, J.F. Microscopic three-body force for asymmetric nuclear matter. Eur. Phys. J. A 2002, 14, 469–475. [Google Scholar] [CrossRef]
- Li, Z.H.; Lombardo, U.; Schulze, H.J.; Zuo, W. Consistent nucleon-nucleon potentials and three-body forces. Phys. Rev. C 2008, 77, 034316. [Google Scholar] [CrossRef]
- Li, Z.H.; Schulze, H.J. Neutron star structure with modern nucleonic three-body forces. Phys. Rev. C 2008, 78, 028801. [Google Scholar] [CrossRef]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Wiringa, R.B. Quantum Monte Carlo calculations of A <= 6 nuclei. Phys. Rev. Lett. 1995, 74, 4396–4399. [Google Scholar] [CrossRef]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Pieper, S.C.; Wiringa, R.B. Quantum Monte Carlo calculations of nuclei with A <= 7. Phys. Rev. C 1997, 56, 1720–1750. [Google Scholar] [CrossRef]
- Baldo, M.; Fukukawa, K. Nuclear Matter from Effective Quark-Quark Interaction. Phys. Rev. Lett. 2014, 113, 242501. [Google Scholar] [CrossRef]
- Fukukawa, K.; Baldo, M.; Burgio, G.F.; Lo Monaco, L.; Schulze, H.J. Nuclear matter equation of state from a quark-model nucleon-nucleon interaction. Phys. Rev. C 2015, 92, 065802. [Google Scholar] [CrossRef]
- Gandolfi, S.; Illarionov, A.Y.; Fantoni, S.; Miller, J.C.; Pederiva, F.; Schmidt, K.E. Microscopic calculation of the equation of state of nuclear matter and neutron star structure. Mon. Not. Roy. Astron. Soc. 2010, 404, L35–L39. [Google Scholar] [CrossRef]
- Negele, J.W.; Vautherin, D. Neutron star matter at subnuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground state of matter at high densities: Equation of state and stellar models. Astrophys. J. 1971, 170, 299–317. [Google Scholar] [CrossRef]
- Feynman, R.P.; Metropolis, N.; Teller, E. Equations of State of Elements Based on the Generalized Fermi-Thomas Theory. Phys. Rev. 1949, 75, 1561–1573. [Google Scholar] [CrossRef]
- Audi, G.; Wapstra, A.H.; Thibault, C. The AME2003 atomic mass evaluation. (II). Tables, graphs and references. Nucl. Phys. A 2003, 729, 337–676. [Google Scholar] [CrossRef]
- de Vries, H.; de Jager, C.W.; de Vries, C. Nuclear Charge-Density-Distribution Parameters from Electron Scattering. At. Data Nucl. Data Tables 1987, 36, 495. [Google Scholar] [CrossRef]
- Colò, G.; van Giai, N.; Meyer, J.; Bennaceur, K.; Bonche, P. Microscopic determination of the nuclear incompressibility within the nonrelativistic framework. Phys. Rev. C 2004, 70, 024307. [Google Scholar] [CrossRef]
- Piekarewicz, J. Unmasking the nuclear matter equation of state. Phys. Rev. C 2004, 69, 041301. [Google Scholar] [CrossRef]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.M. Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 1974–1977. [Google Scholar] [CrossRef]
- Garg, U.; Li, T.; Okumura, S.; Akimune, H.; Fujiwara, M.; Harakeh, M.N.; Hashimoto, H.; Itoh, M.; Iwao, Y.; Kawabata, T.; et al. The Giant Monopole Resonance in the Sn Isotopes: Why is Tin so “Fluffy”? Nucl. Phys. A 2007, 788, 36–43. [Google Scholar] [CrossRef]
- Klimkiewicz, A.; Paar, N.; Adrich, P.; Fallot, M.; Boretzky, K.; Aumann, T.; Cortina-Gil, D.; Pramanik, U.D.; Elze, T.W.; Emling, H.; et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys. Rev. C 2007, 76, 051603. [Google Scholar] [CrossRef]
- Carbone, A.; Colò, G.; Bracco, A.; Cao, L.G.; Bortignon, P.F.; Camera, F.; Wieland, O. Constraints on the symmetry energy and neutron skins from pygmy resonances in Ni68 and Sn132. Phys. Rev. C 2010, 81, 041301. [Google Scholar] [CrossRef]
- Chen, L.W.; Ko, C.M.; Li, B.A. Determination of the Stiffness of the Nuclear Symmetry Energy from Isospin Diffusion. Phys. Rev. Lett. 2005, 94, 032701. [Google Scholar] [CrossRef] [PubMed]
- Danielewicz, P.; Lee, J. Symmetry energy I: Semi-infinite matter. Nucl. Phys. A 2009, 818, 36–96. [Google Scholar] [CrossRef]
- Brown, B.A. Neutron Radii in Nuclei and the Neutron Equation of State. Phys. Rev. Lett. 2000, 85, 5296–5299. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Brown, B.A. Neutron radii and the neutron equation of state in relativistic models. Phys. Rev. C 2001, 64, 027302. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Pollock, S.J.; Souder, P.A.; Michaels, R. Parity violating measurements of neutron densities. Phys. Rev. C 2001, 63, 025501. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Centelles, M.; Viñas, X.; Warda, M. Neutron Skin of Pb208, Nuclear Symmetry Energy, and the Parity Radius Experiment. Phys. Rev. Lett. 2011, 106, 252501. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Origin of the neutron skin thickness of Pb208 in nuclear mean-field models. Phys. Rev. C 2010, 82, 054314. [Google Scholar] [CrossRef]
- Fuchs, C. pp i Kaon production in heavy ion reactions at intermediate energies [review article]. Prog. Part. Nucl. Phys. 2006, 56, 1–103. [Google Scholar] [CrossRef]
- Tews, I.; Lattimer, J.M.; Ohnishi, A.; Kolomeitsev, E.E. Symmetry Parameter Constraints from a Lower Bound on Neutron-matter Energy. Astrophys. J. 2017, 848, 105. [Google Scholar] [CrossRef]
- Zhang, N.B.; Cai, B.J.; Li, B.A.; Newton, W.G.; Xu, J. How tightly is nuclear symmetry energy constrained by unitary Fermi gas? Nucl. Sci. Tech. 2017, 28, 181. [Google Scholar] [CrossRef]
- Margueron, J.; Hoffmann Casali, R.; Gulminelli, F. Equation of state for dense nucleonic matter from metamodeling. I. Foundational aspects. Phys. Rev. C 2018, 97, 025805. [Google Scholar] [CrossRef]
- Shlomo, S.; Kolomietz, V.M.; Colò, G. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. EPJA 2006, 30, 23–30. [Google Scholar] [CrossRef]
- Piekarewicz, J. Do we understand the incompressibility of neutron-rich matter? J. Phys. Nucl. Phys. 2010, 37, 064038. [Google Scholar] [CrossRef]
- Li, B.A.; Han, X. Constraining the neutron-proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys. Lett. B 2013, 727, 276–281. [Google Scholar] [CrossRef]
- Taylor, J.H. Pulsar Timing and Relativistic Gravity. Philos. Trans. R. Soc. Lond. Ser. A 1992, 341, 117–134. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Neutron Star Masses and Radii from Quiescent Low-Mass X-ray Binaries. Astrophys. J. 2014, 784, 123. [Google Scholar] [CrossRef]
- Guillot, S.; Rutledge, R.E. Rejecting Proposed Dense Matter Equations of State with Quiescent Low-mass X-Ray Binaries. Astroph. J. Lett. 2014, 796, L3. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Baldo, M.; Burgio, G.F.; Schulze, H.J. Onset of hyperon formation in neutron star matter from Brueckner theory. Phys. Rev. C 1998, 58, 3688–3695. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F.; Schulze, H.J. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys. Rev. C 2000, 61, 055801. [Google Scholar] [CrossRef]
- Lejeune, A.; Grange, P.; Martzolff, M.; Cugnon, J. Hot nuclear matter in an extended Brueckner approach. Nucl. Phys. A 1986, 453, 189–219. [Google Scholar] [CrossRef]
- Zuo, W.; Bombaci, I.; Lombardo, U. Asymmetric nuclear matter from an extended Brueckner-Hartree-Fock approach. Phys. Rev. C 1999, 60, 024605. [Google Scholar] [CrossRef]
- Bombaci, I.; Lombardo, U. Asymmetric nuclear matter equation of state. Phys. Rev. C 1991, 44, 1892–1900. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars From Multi-Messenger Observations of GW170817. Astrophys. J. 2017, 850, L19. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. 2018, 852, L25. [Google Scholar] [CrossRef]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. D 2019, 100, 023015. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Hinderer, T. Erratum: “Tidal Love Numbers of Neutron Stars” (2008, ApJ, 677, 1216). Astrophys. J. 2009, 697, 964. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints. Phys. Rep. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- Lim, Y.; Holt, J.W. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys. Rev. Lett. 2018, 121, 062701. [Google Scholar] [CrossRef] [PubMed]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Burgio, G.F.; Drago, A.; Pagliara, G.; Schulze, H.J.; Wei, J.B. Are Small Radii of Compact Stars Ruled out by GW170817/AT2017gfo? Astrophys. J. 2018, 860, 139. [Google Scholar] [CrossRef]
- Radice, D.; Dai, L. Multimessenger parameter estimation of GW170817. EPJA 2019, 55, 50. [Google Scholar] [CrossRef]
- Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Revisiting the Lower Bound on Tidal Deformability Derived by AT 2017gfo. Astrophys. J. Lett. 2019, 876, L31. [Google Scholar] [CrossRef]
- Wei, J.B.; Figura, A.; Burgio, G.F.; Chen, H.; Schulze, H.J. Neutron star universal relations with microscopic equations of state. J. Phys. G Nucl. Part. Phys. 2019, 46, 034001. [Google Scholar] [CrossRef]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron. 2020, 4, 625. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.B.; Lu, J.J.; Burgio, G.F.; Li, Z.H.; Schulze, H.J. Are nuclear matter properties correlated to neutron star observables? Eur. Phys. J. A 2020, 56, 63. [Google Scholar] [CrossRef]
- Zhao, T.; Lattimer, J. Tidal deformabilities and neutron star mergers. Phys. Rev. D 2018, 98, 063020. [Google Scholar] [CrossRef]
- Tsang, C.Y.; Tsang, M.B.; Danielewicz, P.; Fattoyev, F.J.; Lynch, W.G. Insights on Skyrme parameters from GW170817. Phys. Lett. B 2019, 796, 1–5. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef] [PubMed]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of State and Neutron Star Properties Constrained by Nuclear Physics and Observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars [review article]. Phys. Rep. 2005, 411, 325–375. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Piekarewicz, J. Neutron Star Structure and the Neutron Radius of 208Pb. Phys. Rev. Lett. 2001, 86, 5647–5650. [Google Scholar] [CrossRef]
- Furnstahl, R.J. Neutron radii in mean-field models. Nucl. Phys. A 2002, 706, 85–110. [Google Scholar] [CrossRef]
- Vidaña, I.; Providência, C.; Polls, A.; Rios, A. Density dependence of the nuclear symmetry energy: A microscopic perspective. Phys. Rev. C 2009, 80, 045806. [Google Scholar] [CrossRef]
- Abrahamyan, S.; others. Measurement of the Neutron Radius of 208Pb Through Parity-Violation in Electron Scattering. Phys. Rev. Lett. 2012, 108, 112502. [Google Scholar] [CrossRef] [PubMed]
- PREX/CREX Collaboration. CREX Run Plan. Available online: https://hallaweb.jlab.org/parity/prex/CREXrunPlan_2019Oct6_mcnulty.pdf (accessed on 7 August 2020).
- MREX Collaboration. Available online: https://indico.mitp.uni-mainz.de/event/47/contributions/1634/attachments/1355/1426/MREX.pdf (accessed on 7 August 2020).
| Model Class | EoS | [MeV] | [MeV] | [MeV] | L[MeV] | |
|---|---|---|---|---|---|---|
| Skyrme | ||||||
| Gs | 0.158 | 14.68 | 239.34 | 39.55 | 93.55 | |
| Rs | 0.158 | 14.01 | 248.33 | 38.45 | 86.41 | |
| SGI | 0.155 | 14.67 | 265.35 | 34.32 | 63.85 | |
| SLy0 | 0.16 | 15.28 | 226.42 | 34.82 | 45.37 | |
| SLy1 | 0.161 | 15.23 | 233.25 | 36.21 | 48.88 | |
| SLy2 | 0.161 | 15.16 | 234.54 | 36.01 | 48.84 | |
| SLy3 | 0.161 | 15.22 | 232.85 | 35.45 | 45.56 | |
| SLy4 | 0.16 | 15.18 | 232.19 | 35.26 | 45.38 | |
| SLy5 | 0.161 | 15.25 | 232.03 | 36.44 | 50.34 | |
| SLy6 | 0.159 | 15.10 | 230.09 | 34.74 | 45.21 | |
| SLy7 | 0.159 | 15.05 | 233.10 | 36.18 | 48.11 | |
| SLy8 | 0.161 | 15.22 | 233.34 | 34.84 | 45.36 | |
| SLy9 | 0.151 | 14.53 | 228.95 | 37.72 | 55.37 | |
| SLy10 | 0.156 | 14.92 | 231.75 | 35.32 | 39.24 | |
| SLy230a | 0.16 | 15.22 | 229.98 | 35.26 | 43.99 | |
| SV | 0.155 | 14.65 | 304.99 | 42.42 | 96.51 | |
| SkI1 | 0.161 | 15.59 | 233.87 | 51.24 | 160.46 | |
| SkI2 | 0.158 | 14.78 | 245.14 | 43.38 | 105.72 | |
| SkI3 | 0.158 | 14.99 | 259.44 | 44.32 | 101.16 | |
| SkI4 | 0.16 | 15.42 | 238.92 | 34.21 | 59.34 | |
| SkI5 | 0.156 | 14.73 | 257.41 | 49.44 | 129.29 | |
| SkI6 | 0.158 | 14.98 | 243.93 | 41.62 | 81.76 | |
| SkMP | 0.157 | 14.66 | 230.16 | 35.88 | 69.7 | |
| SkO | 0.161 | 15.04 | 228.10 | 38.52 | 79.92 | |
| SkO’ | 0.16 | 14.99 | 222.28 | 37.66 | 69.68 | |
| SkT4 | 0.159 | 15.12 | 235.48 | 43.19 | 93.48 | |
| SkT5 | 0.164 | 15.48 | 201.66 | 44.88 | 100.32 | |
| NLWM | ||||||
| GM1 | 0.153 | 16.34 | 300.28 | 32.49 | 93.92 | |
| GM3 | 0.153 | 16.36 | 240.53 | 32.54 | 89.83 | |
| TM1 | 0.145 | 16.26 | 281.16 | 36.89 | 110.79 | |
| NL3 | 0.148 | 16.24 | 271.54 | 37.4 | 118.53 | |
| NL3-II | 0.149 | 16.26 | 271.74 | 37.70 | 119.71 | |
| NL-Sh | 0.146 | 16.36 | 355.65 | 36.13 | 113.68 | |
| DDM | ||||||
| DDME1 | 0.152 | 16.2 | 244.72 | 33.067 | 55.46 | |
| DDME2 | 0.152 | 16.14 | 250.9 | 32.3 | 51.26 | |
| TW99 | 0.153 | 16.25 | 240.26 | 32.766 | 55.31 | |
| PK1 | 0.148 | 16.27 | 282.7 | 37.64 | 115.88 | |
| PK1R | 0.148 | 16.27 | 283.68 | 37.83 | 116.5 | |
| PKDD | 0.149 | 16.27 | 262.19 | 36.79 | 90.21 | |
| Microscopic | ||||||
| BOB | 0.170 | 15.4 | 238 | 33.7 | 70 | |
| V18 | 0.178 | 13.9 | 207 | 32.3 | 67 | |
| N93 | 0.185 | 16.1 | 229 | 36.5 | 77 | |
| UIX | 0.171 | 14.9 | 171 | 33.5 | 61 | |
| FSS2CC | 0.157 | 16.3 | 219 | 31.8 | 52 | |
| FSS2GC | 0.170 | 15.6 | 185 | 31.0 | 51 | |
| DBHF | 0.181 | 16.2 | 218 | 34.4 | 69 | |
| APR | 0.159 | 15.9 | 233 | 33.4 | 51 | |
| AFDMC | 0.160 | 16.0 | 239 | 31.3 | 60 | |
| Exp. | ∼ 0.14–0.17 | ∼ 15–17 | 220–260 | 28.5–34.9 | 30–87 | |
| Ref. | [96] | [96] | [97,98] | [1,99] | [1,99] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burgio, G.F.; Vidaña, I. The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe 2020, 6, 119. https://doi.org/10.3390/universe6080119
Burgio GF, Vidaña I. The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe. 2020; 6(8):119. https://doi.org/10.3390/universe6080119
Chicago/Turabian StyleBurgio, G. Fiorella, and Isaac Vidaña. 2020. "The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars" Universe 6, no. 8: 119. https://doi.org/10.3390/universe6080119
APA StyleBurgio, G. F., & Vidaña, I. (2020). The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe, 6(8), 119. https://doi.org/10.3390/universe6080119





