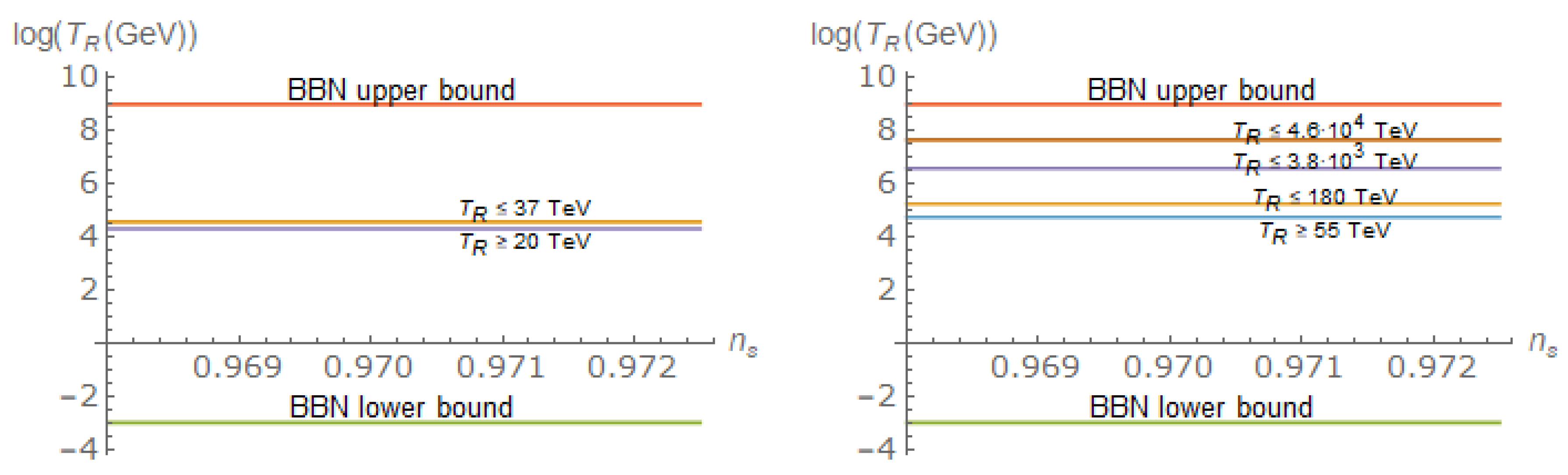The Spectrum of Gravitational Waves, Their Overproduction in Quintessential Inflation and Its Influence in the Reheating Temperature
Abstract
1. Introduction
2. Initial Conditions for Inflation and the Application of the WKB Approximation
3. The Peebles-Vilenkin Model
3.1. The Dynamics of the Model
3.1.1. Analytic Results
- After the end of kination.
- Before the end of kination.
3.1.2. Numerical Results
3.2. Compatibility of the Model with the Cosmological Perturbations
4. Reheating in Quintessential Inflation
4.1. Gravitational Production of Light Particles
4.2. Gravitational Production of Superheavy Particles
4.3. Instant Preheating
5. BBN Constraints Coming from the Production of Gravitational Waves
5.1. BBN Constraints from the Logarithmic Spectrum of Gws
- When the produced particles are very light and its energy density decays as . In this case, as was shown in [66], one will havewhere is once again the heating efficiency introduced previously. Thus, the constraint (57) eventually leads toTaking into account that when the reheating is due to the creation of very light particles during the phase transition the reheating temperature is (see Section 4.1)one has the following lower bound,Finally, note that we showed that when reheating is due to the gravitational production of light particles the reheating temperature is TeV, which means that the reheating via the gravitational production of light particles satisfies the bound (55).
- When the reheating is due to the production of superheavy particles which decay after the end of kination, as we showed in Section 4.2, we have that and and, thus,Therefore, the constraint (57) leads toNow, since in Section 4.2 we obtained the following value of the heating efficiency,we deduce that in the conformally coupled case the mass of the -field has to satisfy GeV, which is incompatible with our assumption GeV. This shows that the gravitational production of superheavy particles conformally coupled to gravity is not viable. On the contrary, when the -field is not conformally coupled to gravity, one gets the bound GeV, which means that the viability of our model requires its mass to be GeV when reheating is due to the gravitational production of superheavy particles noncoformally coupled to gravity.
- When the decay happens before the end of kination, as the case of instant reheating, a simple calculation leads toand, consequently, the constraint (57) becomeswhich applied to our model finally leads to another lower bound of the reheating temperature, which is obtained via instant preheating (see Section 4.3),where we used that in the case of instant preheating one has .Now, since the reheating temperature has to be less than TeV, one gets the bound , which is less restrictive than the one obtained in Section 4.3, meaning that when reheating is due to the production of particles via instant preheating, the bound (55) is clearly overpassed.
5.2. BBN Bounds from the Overproduction of Gws
6. Abundance of Dark Matter
6.1. Reheating Via Production of Superheavy Nonconformally Coupled to Gravity
6.2. Reheating via Instant Preheating
7. Other Kind of Potentials
8. Concluding Remarks
- Reheating via graviational particle production of superheavy particles not conformally coupled to gravity.
- Reheating via instant preheating.
| Reheating VIA | |||||||
|---|---|---|---|---|---|---|---|
| Gravitational Production of | Instant Preheating | ||||||
| Light Particles | Superheavy Particles Decaying | ||||||
| after Kination Ends | before Kination Ends | ||||||
| c.c. | n.c. | c.c. | n.c. | ||||
| (TeV) | ― | ― | ― | ― | |||
| (GeV) | ― | ― | ― | ||||
| (GeV) | ― | ― | – | ― | ― | ||
| (TeV) | ― | ||||||
| (GeV) | – | – | |||||
| (GeV) | ― | ― | ― | ― | |||
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The WKB Approximation in Cosmology
Appendix B. Calculation of the β-Bogoliubov Coefficient
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spokoiny, B. Deflationary Universe Scenario. Phys. Lett. 1993, 315, 40. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. 1999, 59, 063505. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. Cosmology with a time-variable cosmological “constant”. Astrophys. J. Lett. 1988, 352, L17. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Grav. 2013, 30, 214003. [Google Scholar] [CrossRef]
- Guth, A. The inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. 1981, 23, 347. [Google Scholar] [CrossRef]
- Linde, A. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. 1982, 108, 389. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, 91, 99. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- de Haro, J.; Amorós, J.; Pan, S. Simple inflationary quintessential model. Phys. Rev. D 2016, 93, 084018. [Google Scholar] [CrossRef]
- de Haro, J.; Amorós, J.; Pan, S. Simple inflationary quintessential model II: Power law potentials. Phys. Rev. 2016, 94, 064060. [Google Scholar] [CrossRef]
- de Haro, J.; Elizalde, E. Inflation and late-time acceleration from a double-well potential with cosmological constant. Gen. Rel. Grav. 2016, 48, 77. [Google Scholar] [CrossRef]
- de Haro, J. On the viability of quintessential inflation models from observational data. Gen. Rel. Grav. 2017, 49, 6. [Google Scholar] [CrossRef][Green Version]
- Haro, J.D.; Saló, L.A. Reheating constraints in quintessential inflation. Phys. Rev. D 2017, 95, 123501. [Google Scholar] [CrossRef]
- Geng, C.Q.; Lee, C.C.; Sami, M.; Saridakis, E.N.; Starobinsky, A.A. Observational constraints on successful model of quintessential Inflation. JCAP 2017, 1706, 11. [Google Scholar] [CrossRef]
- Aresté Saló, L.; de Haro, J. Quintessential inflation at low reheating temperatures. Eur. Phys. J. C 2017, 77, 798. [Google Scholar]
- Haro, J.; Pan, S. Bulk viscous quintessential inflation. Int. J. Mod. Phys. D 2018, 27, 1850052. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. A class of quintessential inflation models with parameter space consistent with BICEP2. Phys. Rev. 2014, 89, 123513. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Quintessential inflation with canonical and noncanonical scalar fields and Planck 2015 results. Phys. Rev. 2015, 92, 023522. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Unification of inflation and dark energy à la quintessential inflation. Int. J. Mod. Phys. 2015, 24, 1530014. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Evading Lyth bound in models of quintessential inflation. Phys. Lett. 2014, 737, 191–195. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Herrera, R.; Labrana, P.; Nissimov, E.; Pacheva, S. Cosmology, Inflation and Dark Energy. Gen. Rel. Grav. 2015, 47, 10. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.; Starobinsky, A. Reheating after Inflation. Phys. Rev. Lett. 1994, 73, 3195. [Google Scholar] [CrossRef] [PubMed]
- Kofman, L.; Linde, A.; Starobinsky, A. Towards the Theory of Reheating After Inflation. Phys. Rev. 1997, 56, 3258. [Google Scholar] [CrossRef]
- Greene, P.; Kofman, L.; Linde, A.; Starobinsky, A. Structure of Resonance in Preheating after Inflation. Phys. Rev. 1997, 56, 6175. [Google Scholar] [CrossRef]
- Shtanov, Y.; Traschen, J.; Brandenberger, R. Universe Reheating after Inflation. Phys. Rev. 1995, 51, 5438. [Google Scholar] [CrossRef]
- Bassett, B.A.; Liberati, S. Geometric Reheating after Inflation. Phys. Rev. 1998, 58, 021302. [Google Scholar] [CrossRef]
- Parker, L. Particle Creation in Expanding Universes. Phys. Rev. Lett. 1968, 21, 562. [Google Scholar] [CrossRef]
- Parker, L. Quantized Fields and Particle Creation in Expanding Universes. I. Phys. Rev. 1969, 183, 1057. [Google Scholar] [CrossRef]
- Parker, L. Quantized Fields and Particle Creation in Expanding Universes. II. Phys. Rev. 1970, 3, 346. [Google Scholar]
- Folov, V.M.; Mamayev, S.G.; Mostepanenko, V.M. On the difference in creation of particles with spin 0 and 1/2 in isotropic cosmologies. Phys. Lett. 1976, 55, 7. [Google Scholar]
- Grib, A.A.; Levitskii, B.A.; Mostepanenko, V.M. Particle creation from vacuum by a non-stationary gravitational field in the canonical formalism. Theor. Mat. Fiz. 1974, 19, 59. [Google Scholar]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Particle creation from vacuum in homogeneous isotropic models of the Universe. Gen. Rel. Grav. 1976, 7, 535. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. The creation of particles from a vacuum in a non-steady isotropic universe. Sov. Phys. J. 1974, 17, 1700. [Google Scholar] [CrossRef]
- Ford, L.H. Gravitational particle creation and inflation. Phys. Rev. D 1987, 35, 2955. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Massive particle production in anisotropic space-times. J. Phys. A Math. Gen. 1980, 13, 2109. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Starobinsky, A.A. Rate of particle production in gravitational fields. JETP Lett. 1977, 26, 252. [Google Scholar]
- Dimopoulos, K.; Owen, C. Quintessential Inflation with α-attractors. J. Cosmol. Astropart. Phys. 2017, 1706, 027. [Google Scholar] [CrossRef]
- Hashiba, S.; Yokoyama, J. Gravitational reheating through conformally coupled superheavy scalar particles. arXiv 2018, arXiv:1809.05410. [Google Scholar] [CrossRef]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. Dark energy, α-attractors, and large-scale structure surveys. J. Cosmol. Astropart. Phys. 2018, 1806, 041. [Google Scholar] [CrossRef]
- Felder, G.; Kofman, L.; Linde, A. Instant Preheating. Phys. Rev. D 1999, 59, 123523. [Google Scholar] [CrossRef]
- Felder, G.; Kofman, L.; Linde, A. Inflation and Preheating in NO models. Phys. Rev. D 1999, 60, 103505. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Wood, L.D.; Owen, C. Instant Preheating in Quintessential Inflation with α-Attractors. Phys. Rev. D 2018, 97, 063525. [Google Scholar] [CrossRef]
- Haro, J. Different reheating mechanisms in quintessence inflation. Phys. Rev. D 2019, 99, 043510. [Google Scholar] [CrossRef]
- Sami, M.; Sahni, V. Quintessential inflation on the brane and the relic gravity wave background. Phys. Rev. D 2004, 70, 083513. [Google Scholar] [CrossRef]
- Figueroa, D.G.; Tanin, E.H. Inconsistency of an inflationary sector coupled only to Einstein gravity. J. Cosmol. Astropart. Phys. 2019, 10, 050. [Google Scholar] [CrossRef]
- Giudice, G.F.; Kolb, E.W.; Riotto, A. Largest temperature of the radiation era and its cosmological implications. Phys. Rev. D 2001, 64, 023508. [Google Scholar] [CrossRef]
- Hasegawa, T.; Hiroshima, N.; Kohri, K.; Hansen, R.S.L.; Tram, T.; Hannestad, S. MeV-scale reheating temperature and thermalization of oscillating neutrinos by radiative and hadronic decays of massive particles. J. Cosmol. Astropart. Phys. 2019, 12, 012. [Google Scholar] [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Sarkar, S. The cosmology of decaying gravitinos. Nuc. Phys. B 1985, 259, 175. [Google Scholar] [CrossRef]
- Ellis, J.; Linde, A.; Nanopoulos, D. Inflation can save the gravitino. Phys. Lett. B 1982, 118, 59. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Wave Experiments and Early Universe Cosmology. Phys. Rept. 2000, 331, 283. [Google Scholar] [CrossRef]
- Haro, J. Gravitational production of dark matter in the Peebles-Vilenkin model. EPJC 2020, 20, 257. [Google Scholar] [CrossRef]
- Haro, J.; Saló, L.A. Gravitational production of superheavy baryonic and dark matter in quintessential inflation: Nonconformally coupled case. Phys. Rev. D 2019, 100, 043519. [Google Scholar] [CrossRef]
- Winitzki, S. Cosmological particle production and the precision of the WKB approximation. Phys. Rev. D 2005, 72, 104011. [Google Scholar] [CrossRef]
- Haro, J. Gravitational particle production: A mathematical treatment. J. Phys. A Mat. Theor. 2011, 44, 205401. [Google Scholar] [CrossRef]
- Rehagen, T.; Gelmini, G.B. Low reheating temperatures in monomial and binomial inflationary potentials. J. Cosmol. Astropart. Phys. 2015, 6, 039. [Google Scholar] [CrossRef]
- Linde, A. Particle Physics and Inflationary Cosmology. Contemp. Concepts Phys. 2005, 5, 1–362. [Google Scholar]
- Kaya, A.; Tarman, M. Stress-Energy Tensor of Adiabatic Vacuum in Friedmann-Robertson-Walker Spacetimes. J. Cosmol. Astropart. Phys. 2011, 1104, 040. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation Dynamics and Reheating. Rev. Mod. Phys. 2006, 78, 537. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Inflation for Large Scale Structure. In Large Scale Structure: Tracks and Traces, Proceedings of the 12th Potsdam Cosmology Workshop, Potsdam, Germany, 15–20 September 1997; Muller, V., Gottlober, S., Mucket, J.P., Wambsganss, J., Eds.; World Scientific: Singapore, 1998; pp. 375–380. [Google Scholar]
- Joy, M.; Sahni, V.; Starobinsky, A.A. New Universal Local Feature in the Inflationary Perturbation Spectrum. Phys. Rev. D 2008, 77, 023514. [Google Scholar] [CrossRef]
- Linde, A. Hybrid Inflation. Phys. Rev. D 1994, 49, 748. [Google Scholar] [CrossRef] [PubMed]
- Rubio, J.; Wetterich, C. Emergent scale symmetry: Connecting inflation and dark energy. Phys. Rev. D 2017, 96, 063509. [Google Scholar] [CrossRef]
- Haro, J.; Amorós, J.; Pan, S. The Peebles-Vilenkin quintessential inflation model revisited. Eur. Phys. J. C 2019, 79, 505. [Google Scholar] [CrossRef]
- Liddle, A.R.; Leach, S.M. How long before the end of inflation were observable perturbations produced? Phys. Rev. D 2003, 68, 103503. [Google Scholar] [CrossRef]
- Giovannini, M. Production and detection of relic gravitons in quintessential inflationary models. Phys. Rev. D 1999, 60, 123511. [Google Scholar] [CrossRef]
- Damour, T.; Vilenkin, A. String Theory and Inflation. Phys. Rev. D 1995, 53, 2981. [Google Scholar] [CrossRef]
- Bunch, T.S. Adiabatic regularisation for scalar fields with arbitrary coupling to the scalar curvature. J. Phys. A Math. Gen. 1980, 13, 1297. [Google Scholar] [CrossRef]
- Popov, V.S. Pair production in a variable external field (Quasiclassical Aproximation). Sov. Phys. JETP 1972, 34, 709. [Google Scholar]
- Marinov, S.M.; Popov, V.S. Electron-positron pair creation from vacuum induced by variable electric field. Fortschr. Phys. 1977, 25, 373. [Google Scholar] [CrossRef]
- Nikishov, A.I. Barrier scattering in field theory removal of Klein paradox. Nuc. Phys. B 1970, 21, 346. [Google Scholar] [CrossRef]
- Haro, J. Pair production in an uniform electric field. Int. Jour. Theor. Phys. 2003, 42, 531. [Google Scholar] [CrossRef]
- Giovannini, M. Gravitational waves constraints on post-inflationary phases stiffer than radiation. Phys. Rev. D 1998, 58, 083504. [Google Scholar] [CrossRef]
- Giovannini, M. Thermal history of the plasma and high-frequency gravitons. Class. Quant. Grav. 2009, 26, 045004. [Google Scholar] [CrossRef]
- Giovannini, M. Stochastic backgrounds of relic gravitons, TΛCDM paradigm and the stiff ages. Phys. Lett. B 2008, 668, 44. [Google Scholar] [CrossRef]
- Giovannini, M. The first observations of wide-band interferometers and the spectra of relic gravitons. Phys. Lett. B 2016, 759, 528. [Google Scholar] [CrossRef]
- Domcke, V.; Pieroni, M.; Binétruy, P. Primordial gravitational waves for universality classes of pseudoscalar inflation. J. Cosmol. Astropart. Phys. 2016, 6, 031. [Google Scholar] [CrossRef]
- Hashiba, S.; Yokoyama, J. Gravitational particle creation for dark matter and reheating. Phys. Rev. D 2019, 99, 043008. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Crotty, P.; Kolb, E.W.; Riotto, A. On the gravitational production of superheavy dark matter. Phys. Rev. D 2001, 64, 043503. [Google Scholar] [CrossRef]
- Ema, Y.; Nakayama, K.; Tang, Y. Production of Purely Gravitational Dark Matter. J. High Energy Phys. 2018, 9, 135. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Long, A.J. Gravitational production of super-Hubble-mass particles: An analytic approach. J. High Energy Phys. 2019, 1, 189. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Riotto, A.; Senatore, L. Isocurvature constraints on gravitationally produced superheavy dark matter. Phys. Rev. D 2005, 72, 023511. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Proceedings of the Second Seminar “Quantum Theory of Gravity”; INR Press: Moscow, Russia, 1982; pp. 58–72. [Google Scholar]
- Vilenkin, A. Classical and quantum cosmology of the Starobinsky inflationary model. Phys. Rev. D 1985, 32, 2511. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haro Cases, J.; Aresté Saló, L. The Spectrum of Gravitational Waves, Their Overproduction in Quintessential Inflation and Its Influence in the Reheating Temperature. Universe 2020, 6, 87. https://doi.org/10.3390/universe6060087
Haro Cases J, Aresté Saló L. The Spectrum of Gravitational Waves, Their Overproduction in Quintessential Inflation and Its Influence in the Reheating Temperature. Universe. 2020; 6(6):87. https://doi.org/10.3390/universe6060087
Chicago/Turabian StyleHaro Cases, Jaume, and Llibert Aresté Saló. 2020. "The Spectrum of Gravitational Waves, Their Overproduction in Quintessential Inflation and Its Influence in the Reheating Temperature" Universe 6, no. 6: 87. https://doi.org/10.3390/universe6060087
APA StyleHaro Cases, J., & Aresté Saló, L. (2020). The Spectrum of Gravitational Waves, Their Overproduction in Quintessential Inflation and Its Influence in the Reheating Temperature. Universe, 6(6), 87. https://doi.org/10.3390/universe6060087