Foundations of Finsler Spacetimes from the Observers’ Viewpoint
Abstract
:1. Introduction
1.1. Approach from the Foundations Viewpoint
- (1)
- there are inertial frames of reference (IFR) in which changes of coordinates are linear, and
- (2)
- the symmetries in the change of the time-like coordinate (and, independently, in the three spacelike ones) between two IFR’s are encoded in that linear structure.
1.2. Critical Revision of EPS Axiomatics
- An artificial requirement of smoothability of some combination of radar coordinates, which would forbid null cone structures incompatible with Lorentzian metrics. This was recently pointed out by Lammërzhal and Perlick’s [11], and it is developed here in detail (see Section 5.2.1).
- A deduction of the existence of a projective structure starting at a general version of the law of inertia. This would exclude the time-like pregeodesics for a Lorentz–Finsler metric (except those of Berwald-type), but again, the proof crucially relies on an argument of -differentiability, which is related to nontrivial issues on Finslerian metrics (see Section 5.2.2).
1.3. Precise Geometric Framework
- (1)
- Causal cone domain (Section 4). The physically meaningful domain for L is only the causal cone of a cone structure .Indeed, even in the classical relativistic case, only the future-directed causal directions for a cone determined by the metric g contains the elements physically measurable for any (true or gedanken) experiment. In relativity, the Lorentzian scalar product at each event p is determined by its value on the cone (or on its time-like directions); therefore, a Lorentz metric g can be determined on the whole even if, actually, only its value on can be measured. However, this is not by any means true for a Lorentz–Finsler metric L, where there is a huge freedom to extend the Lorentz–Finsler metric away from .Therefore, our Lorentz–Finsler metrics will be defined only on a (causal) cone structure2.
- (2)
- Smoothness, i.e., differentiability up to some appropriate order. Usually, such a requirement is regarded as a harmless macroscopic approximation to the structure of the spacetime. However, the discussion on EPS above shows that this is not so trivial in the Finslerian case. Furthermore, other issues appear in the literature:
- •
- The possibility that the cone is smooth, and the Lorentz–Finsler metric is smooth only on the time-like directions but cannot be smoothly extended to the cone, which happens in metrics such as Bogoslovski in very special relativity [21] and others [22]; see Section 6.1.
- •
- The lack of differentiability outside the zero section of Finsler product spacetimes, which may lead to definitions of Finsler static spacetimes which are not smooth in the static direction [2], a fact which can be overcome with our approach to the space of observers; see Section 4.2 (item 5 (b)).
- (3)
- Anisotropic speed of light. Finsler spacetimes permit different possibilities for a speed of light which may vary not only with the point (an issue already considered even for relativistic spacetimes, Section 3.3) but also with the direction (Section 6.2).
1.4. Importance of the Space of Observers
2. The Doubly Linearized Models
2.1. Postulates
2.2. Groups
- if , ,
- if , .
- (1)
- If the matrix also satisfies the property in Equation (4), then .
- (2)
- If , then there exists such that A is k-congruent, and either k is unique or it can be arbitrarily chosen in .
- (3)
- Let be - and -congruent, respectively. If is univocally determined and (resp. ) is k-congruent for some , then (resp. ) is -congruent.
- (1)
- Conservation of the IFR volume: , for any transition matrix A.
- (2)
- Transitivity: if A is the transition matrix from a first IFR, , to a second IFR, , then there exists an IFR, , such that the transition matrix A from to is equal to A.
- (3)
- Action by a group: the set of transition matrices A between elements of (as in Equation (5)) is a subgroup G of .
- (4)
- Apparent temporality: any transition matrix A between elements of satisfies (with as in Exercise 1; recall also the discussion at Section 2.4).
2.3. Linear Models of Spacetimes
- (1)
- Case . By the definition of , V is naturally endowed with a Lorentzian scalar product . Indeed, if is any IFR, then the unique such that B is an orthornormal basis for it, up to the normalization of its first vectorbecomes independent of the chosen R. Furthermore, for , the group is the Lorentz group; otherwise, is conjugate to the Lorentz group. Indeed, putting with , , the inverse of is andAnyway, the spacetime of special relativity is obtained.
- (2)
- Case . The group becomes the (non-orthochronous) Galilean groupThus, the dual basis of each IFR contains the same first element , up to a sign. When a choice in is carried out, naming it , then is called the absolute time. The kernel E of is endowed with a scalar product (being the elements of B an orthonormal basis of for each IFR). Then, E endowed with this scalar product is called the absolute space.Summing up, the spacetime of Galilei–Newton is recovered now.
- (3)
- In this case, the basis of each IFR contains the same first element up to a sign. Choosing a sign, this vector defines the absolute rest observer. Thus, the kernel (annihilator) of in the dual space (that is, the subspace Span of for each IFR) is also independent of the IFR. It is naturally endowed with a scalar product so that, for each IFR, the set becomes an orthonormal basis.Summing up, an a priori aphysical dual of Galilei–Newton spacetime (with a completely analogous geometric structure) is obtained.
- (4)
- Case . For , the group is the Euclidean orthonormal group6; otherwise, is conjugate to this group. Indeed, reasoning as in the case , V is naturally endowed with an Euclidean scalar product and any basis B of an IFR is orthornormal for up to the normalization of its first vector.Summing up, one obtains the a priori aphysical case when the full spacetime is endowed with a Euclidean scalar product, which is mathematically analogous to the Lorentzian one.
- (5)
- Case nonunique. In this case, the group is and, thus, the basis B and its dual for any IFR satisfy all the properties in the previous cases. In particular, choosing a sign, one has an absolute time T, an absolute rest observer (with ), and an absolute space of which the dual space can be identified with defined in the case .This case should be regarded as aphysical too7, and being obtained as a “degenerate” case of the previous ones, it will not be taken into account anymore.
2.4. Temporal Models and Interpretation of
- (a)
- The temporal models are time-oriented.
- (b)
- All the elements in are assumed to lie in the chosen time-orientation.
- (c)
- is assumed to be maximal for property (b). Thus, depending on the value of k, the orthochronous subgroup of the Lorentz (or conjugate to Lorentz), Galilean, or dual Galilean groups will act freely and transitively on .
- (d)
- When there is no possibility of confusion, is regarded as equal to in (c).
3. First Non-Linearization
3.1. General Case and Signature Change
3.2. Space of Observers
- (i)
- In the region , contains all the unit vectors for g and each is a sphere.
- (ii)
- In the region , contains all the future-directed time-like unit vectors for g and each is a hyperboloid.
- (iii)
- In the region , is equal to and each is an affine hyperplane not containing 0.
- (iv)
- In the region , is equal to the absolute rest vector field W (so, each is a subset containing a single nonzero tangent vector).
3.3. Pointwise Variation of Speed of Light
3.4. Relativistic vs. Leibnizian Structures
4. Second Non-Linearization
4.1. Background: Norms, Cones, and Lorentz–Finsler Metrics
- (i)
- positiveness: , with equality if and only if ,
- (ii)
- positive homogeneity: for all ,
- (iii)
- strongly convex indicatrix: is smooth away from 0, and the fundamental tensor field g defined as the Hessian of is positive definite on .
- (1)
- Positive homogeneity. This requirement only for enhances the applications of Finsler Geometry16, and it will be enough for our purposes. Positive homogeneity implies that is univocallly determined by its indicatrix (unit sphere) . In particular, the full homogeneity of becomes equivalent to the symmetry of with respect to the origin.
- (2)
- Smoothness. The standard definition of norm implies that they are only continuous. We assume smoothness (say, , pointing out the cases when lower regularity becomes relevant) away from 0. Using (ii), this is clearly equivalent to the smoothness of .
- (3)
- Role of triangle inequality. It is not imposed directly, however,
- (a)
- Triangle inequality becomes equivalent (for any 1-homogeneous function smooth away from 0) to the convexity of (i.e., its inner-pointing second fundamental form σ is positive semidefinite). Moreover, it is also equivalent to the convexity of the open unit ball (all the segments connecting points are included in ).
- (b)
- The strict triangle inequality becomes equivalent to the strict convexity of (the hyperplane tangent to at each point p only intersects at p). Moreover, it is also equivalent to the strict convexity of the closed unit ball (segments connecting points are included in the open ball up to the endpoints ).
- (c)
- Assuming (i) and (ii), hypothesis (iii) becomes equivalent to the strong convexity of (σ is positive definite), which is more restrictive than its strict convexity.
- (4)
- Conic Minkowski norms. These norms are as in Definition 5 just by allowing the map to be defined only on a cone domain (see Definition 7 below) of V. All the previous considerations on the triangle inequality extend trivially to such conic Minkowski norms.
- (5)
- Scalar products. Norms coming from (Euclidean) scalar products are Minkowski. Conversely, a Minkowski norm comes from a scalar product under one (and then both) of the following properties:
- (a)
- The classical parallelogram identity holds.
- (b)
- is -smooth at zero [48] (Proposition 4.1).
Recall also that, clearly, any norm coming from a (Euclidean or Lorentzian) scalar product is determined by its value on a cone domain.
- (1)
- 2-homogeneity. Taking instead of F, Finsler metrics can be defined alternatively as positive 2-homogeneous functions (this will be convenient for their Lorentzian extensions). Furthermore, the -smoothability of at 0 would imply that it comes from a Riemannian metric (recall Remark 4 (5)).
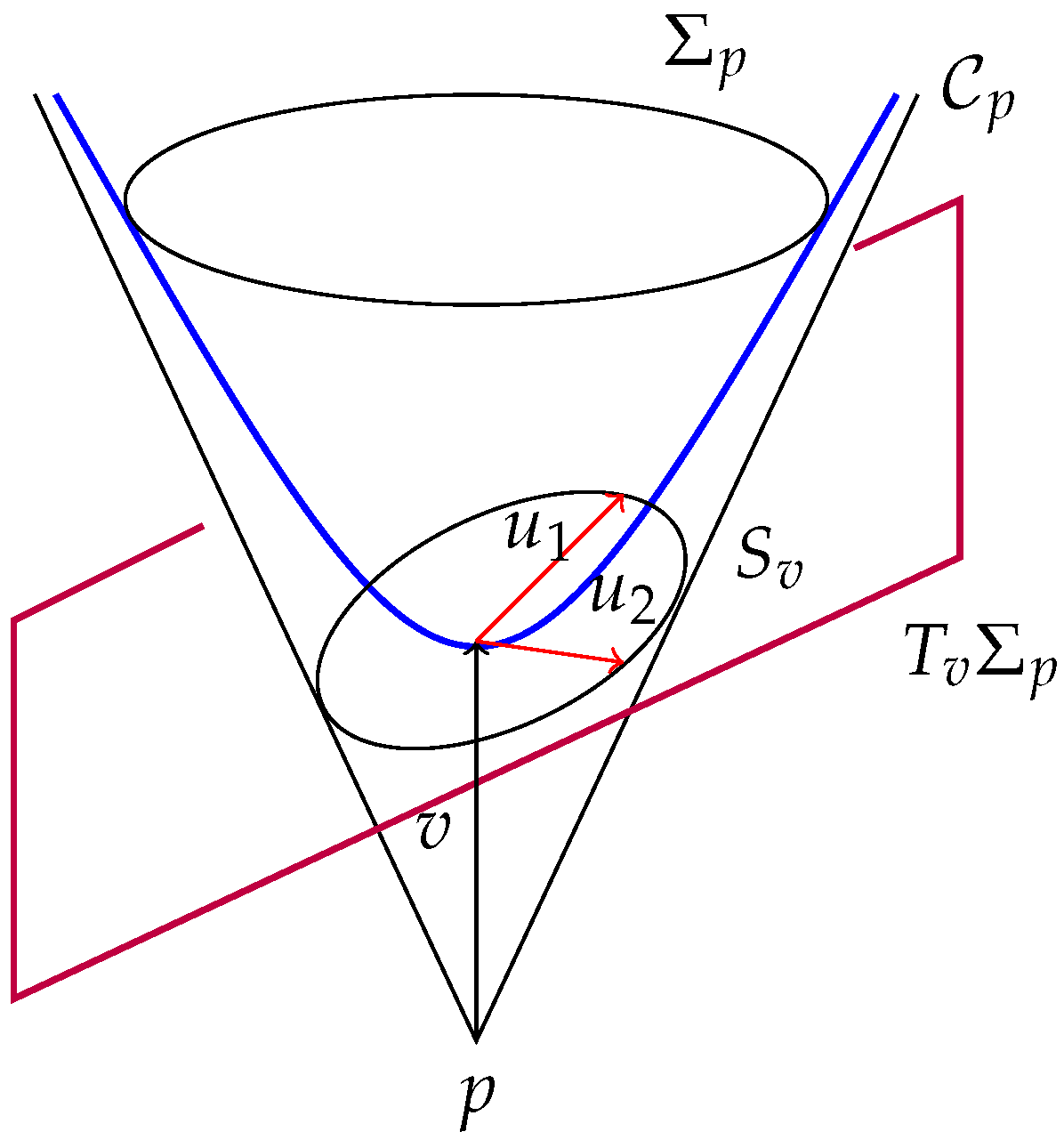
- (2)
- Role of the indicatrix. As F is determined by its indicatrix , a Finsler metric can be defined alternatively as a smooth hypersurface Σ embedded in satisfying appropriate conditions, namely, (a) Σ intersects transversely17 each and (b) this intersection is a strongly convex compact connected embedded hypersurface whose inner domain (such that , where ∂ denotes the boundary in V)18 contains the zero vector .
- (3)
- Fundamental tensor on a vector bundle. Each defines a fundamental tensor field on and, so, a 2-covariant tensor on each fiber of the (slit) tangent bundle . We will use the letter g to denote such a tensor field, so that, for each , will be a tensor on , being . Clearly, the definition of Finsler metric and fundamental tensor can be extended to any vector bundle, not necessarily the tangent one.
- (1)
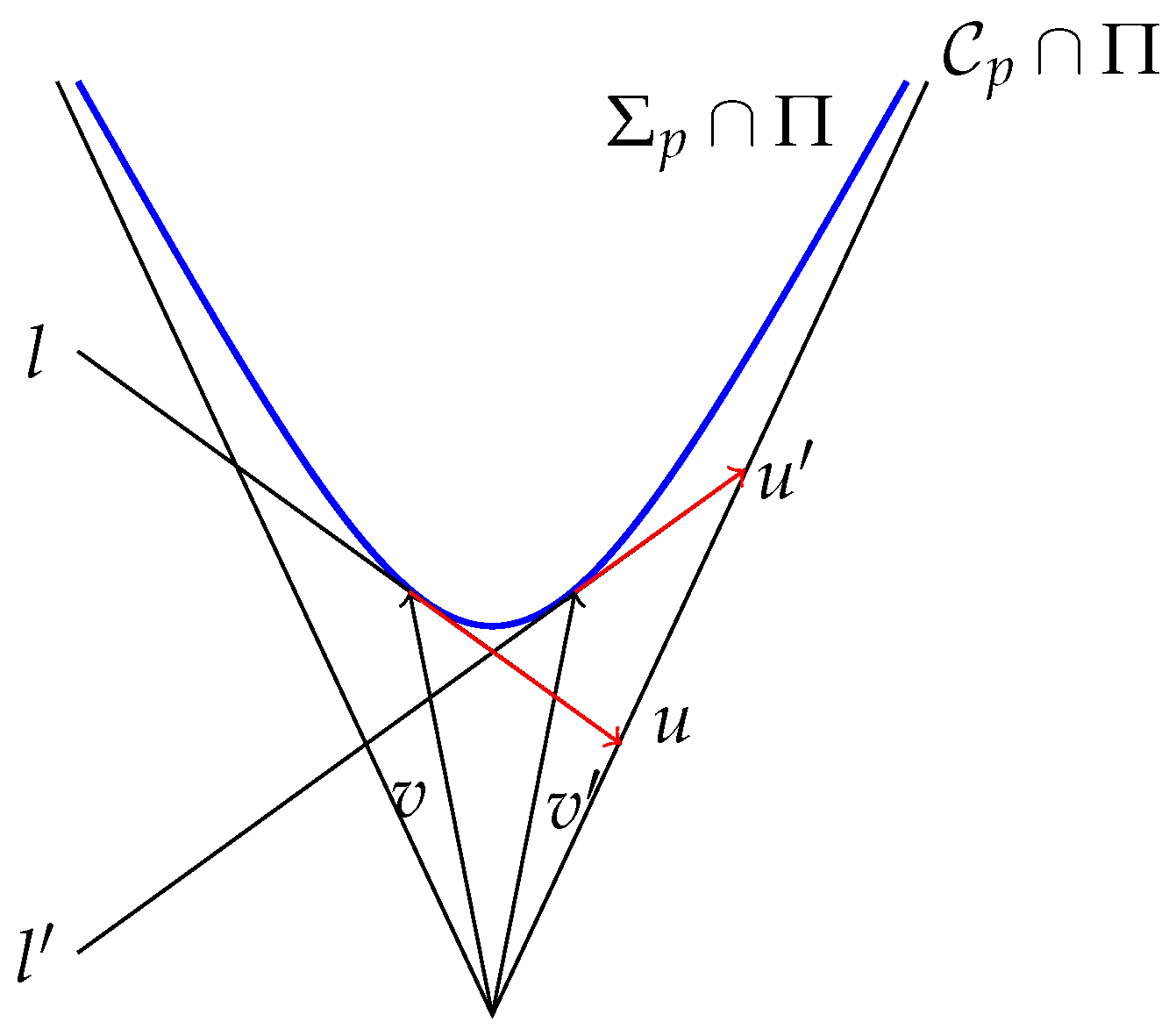
- Smoothness and transversality. Intuitively, a cone structure is just to smoothly put a cone at each , . From the formal viewpoint, however, this cannot be deduced only from the smoothness of , making necessary assumption (a) (recall Remark 5 (2) and footnote 17 or the discussion around Reference [49] Figure 2).
- (2)
- Cone triples. Any cone structure can be determined (in a highly nonunique way) by means of a cone triple , where Ω is any time-like 1-form on M (i.e., for all causal v), T is any time-like vector field with and F is the unique Finsler metric on ker such that for any ker [10] (Section 2.4). Conversely, any with and F Finsler on ker is the cone triple of some cone structure .
- (3)
- Extended classical Causality. allows one to extend basic elements of causality of spacetimes such as the chronological ≪, strict causal <, causal ≤, and horismotic → relations ( when and ) and, thus, the chronological/causal futures and pasts of a point, /. In particular, cone geodesics are defined as locally horismotic curves and they generalize the future-directed lightlike pregeodesics associated with the conformal structure of any Lorentz metric.
- (i)
- with equality if and only if .
- (ii)
- is positive 2-homogeneous: for all and .
- (iii)
- The fundamental tensor g obtained as the Hessian of has Lorentzian signature on .
- (1)
- A less redundant definition for (as well as for the Lorentz–Finsler metric L below) can be carried out without prescribing the cone ; see Reference [10] Def. 3.1 and 3.5.
- (2)
- Two homogeneities for are preferred to 1-homogeneity because of the general equality . Notice also that the Lorentzian signature is changed with respect to previous sections, and consistently, if is smoothly extended around any , then must become negative away from .
- (3)
- is determined by its indicatrix , which is now strongly concave and asymptotic to . Indeed, a Lorentz–Finsler metric could be defined alternatively as a strongly concave hypersurface in which is asymptotic to some cone structure under the mild technical condition that the map such that extends smoothly to with nondegenerate19g.
- (4)
- All the properties related to the triangle inequality in the positive definite case (which were associated with the convexity of the indicatrix and held for conic Minkowski norms; Remark 4 (3) is automatically translated now as reverse triangle inequalities in the Lorentz–Finsler case (associated with the concaveness of ).
- (5)
- Even though , can be continuously extended to 0 (). However, the smoothness of this extension20 depends on whether comes from a Lorentzian scalar product, as in the positive definite case.
- (6)
- It is possible to smoothly extend L (preserving the 2-homogeneity) to an open conic subset which contains (recall that ). This extension is far from unique, but the fundamental tensor in the boundary is well determined.
- (1)
- Any Lorentz–Finsler metric can be extended to as a smooth 2-homogeneous function with fundamental tensor g of Lorentzian signature; see [12]. However, such an extension is highly nonunique and, as we will see, it is not justified by direct measures of observers.
- (2)
- Given L, time-like and light-like geodesics are naturally defined, and they satisfy local maximizing properties which extend those of relativistic spacetimes (recall Remark 7(4) and Reference [10] Prop. 6.5). In particular, the light-like pregeodesics of L coincide with the cone geodesics of [10] (Section 6.2).
- (3)
- Thus, all the Lorentz–Finsler metrics with the same cone structure have the same light-like pregeodesics. Two such metrics, and , are called anisotropically equivalent, and they satisfy for some 0-homogeneous function on [10] (Section 3.3).
- (4)
- Any cone structure is associated with a Lorentz–Finsler metric L (and, then, with its anisotropically equivalent class). Indeed, if is determined by a cone triple , one can construct such an L starting at the mapwhere is the natural projection. G satisfies all the required properties of L except the differentiability on Span, the latter because of the lack of differentiability of at 0 when it is not Riemannian. Indeed, the indicatrix is not smooth precisely on T, that is, only at the point on each p. However, standard techniques of smoothability for convex functions allow one to smoothen G around T obtaining the required L [10] (Section 5.2).
- (5)
- The lack of differentiability of G above is analogous to the well-known lack of differentibility of any product of (non-Riemannian) Finsler manifolds. Indeed, if ) is a Finsler manifold, then is not smooth as Finsler or Lorentz–Finsler metrics on along the direction . This problem prevents the extension to the Lorentz–Finsler case of the trivial procedure to construct a relativistic product spacetime starting at a Riemannian manifold.
- (6)
- Given a Lorentz–Finsler metric, there exists a univocally determined A-anisotropic connection which is torsion-free and parallel. Moreover, when we consider a properly Lorentz–Finsler metric, this A-anisotropic connection can be extended to an open subset which contains . As the extension away from is highly nonunique, we will speak about -anisotropic connections. When , we will just say anisotropic connection21.
4.2. Physical Intuitions for Finsler Spacetimes
- (1)
- The fact that L is defined only on a cone domain A and that it is extended continuously to comes from the nature of the space of observers.Recall that, then, one has time-like geodesics (Remark 8 (2)) and, thus, freely falling observers. At least from a trivial mathematical viewpoint, this is enough to determine L and, then, the fundamental tensor g on the cone domain A.Notice that, given an observer , the tensor is then also obtained on the directions of . In principle, (which can be obtained just from ) could be measured, as it comprises properties of neighboring observers.
- (2)
- The smooth extensibility of both L and the fundamental tensor g (as a nondegenerate one) to the cone structure appears as a natural approximation (in principle, one would expect to remain close to the situation in a relativistic spacetime) which mathematically ensures that is truly a cone (with in Definition 7 satisfying strong convexity). Moreover, then L also determines light-like geodesics which, up to reparametrization, are inherent to the cone structure. The improper case of Finsler spacetimes satisfying the properties (i) and (ii) in Note 2 would also satisfy all these properties about geodesics and cones.Then, as a consequence, the behaviour of lightlike geodesics becomes completely analogous to the classical relativistic case. Indeed, Lorentz–Finsler metrics with the same cone structure are also related by an “anisotropic conformal factor ” (Remark 8(3)) and the cone structure also allows one to mimic the relativistic behaviour of causality (Remark 6(3)).
- (3)
- The physical considerations in the two previous items are also assumed in standard relativity. Namely, observers are always expected to measure only massive or massless particles, that is, elements with velocities in a causal cone. In seneral relativity, this is apparent from the EPS formulation, where radar coordinates are systematically used with this aim (see the next section). Certainly, the metric tensor g is assumed to be defined on all the directions in the relativistic case but the underlying reason is that g is fully determined by its value along the causal vectors (Remark 4(5)). This is not by any means true in the Lorentz–Finsler case, even if L can be extended to the whole (recall Remark 8(1)).
- (4)
- When a space-like separation in a direction l is going to be measured by an observer v, it seems natural to consider ; therefore, it would be irrelevant whether L is not defined outside the cone.Indeed, from a purely geometric viewpoint, would be naturally regarded as the rest space of the observer v at p and that would be the unique metric available there, even though the physical process to measure it might not be obvious. It is worth pointing out here Ishikawa’s claim in Reference [8] that can be measured, assuming that the physical light rays are those of . Indeed, this author criticizes Beem’s definition of light rays, which was constructed by using the light-like vectors on the cone . Anyway, in our opinion, Ishikawa’s claim needs further physical support.
- (5)
- It is worth emphasizing that no issue on smoothability occurs with , which can be assumed smooth (as in Remark 4(2)) in most interesting cases.(a) The Lorentz–Finsler metric L cannot be -extended to 0 in agreement with the behavior of norms in both the positive definite case and the Lorentz–Finsler one (Remark 4(5)). However, no physical or mathematical reason seems to require the smoothability of L at 0 (compare with the EPS approach in Section 5.2.1 below).(b) Product metrics or, with more generality, the rough Lorentz–Finsler version of static spacetimes , with natural coordinates at are never smooth at whenever F is Finsler but not Riemannian. Consequently, some authors have included the possible existence of non-smooth directions as a fundamental ingredient of Lorentz–Finsler metrics (see for example References [2,3,54]). Nevertheless, as explained in Remark 8, parts (4) and (5), general smoothing procedures can be applied. Furthermore, a natural definition of (smooth) static spacetimes as well as an explicit procedure to construct locally all of them are available in Reference [10] (Section 4.2).(c) Other issues of non-smoothness appear when modelling some specific physical situations (very special relativity and birefringence) and will be considered in Section 6.1.
5. Comparison with Ehlers–Pirani–Schild Approach
5.1. Summary of the Approach
- (1)
- Spacetime becomes a differential manifold M endowed with a cone structure. Essentially, this is obtained by means of axioms on light propagation which involve messages and echoes between particles.Indeed, these axioms allow one to find radar coordinates with respect to (freely falling, massive) particles, the latter represented by a class of unparametrized curves, which provide the structure of differentiable manifold, see EPS axioms —. Then, the cone structure is obtained by using two axioms, , on the local character of light propagation around each event e. Indeed, states that, given any particle P with some parameter t which passes through e, it follows that any event p ( P) can be connected with the particle by exactly two light rays23, while distinguishes two connected components for light rays. Moreover, also states that, if these two rays cross the curve at the events , then is required to be smooth in a small neighborhood of e. EPS claims that, then, will come from the conformal structure of some Lorentz metric (a particular case of our Definition 8) and, so, we can speak about -time-like directions.
- (2)
- Spacetime is endowed with a projective structure . This is achieved by means of two axioms, and , which model the free fall of particles.The first one states only the existence of a unique particle, represented by means of an (unparametrized) curve, for each event e and -time-like direction at e. The second axiom states that, around each event e, one can find coordinates such that any particle through e admits a parametrization satisfyingThis equality is regarded as an infinitesimal law of inertiA (consistently with Trautman [57]). By using Equation (10), EPS argues that a projective structure, which is claimed to be compatible with some affine connection , must appear. As a consequence, not only the original particles would be recovered as pregeodesics of but also one would obtain pregeodesics at any direction, time-like or not.
- (3)
- Spacetime is a Weyl space , where is an affine connection compatible with the cone structure , in the sense that the light-like -pregeodesics are also -pregeodesics. This is carried out by means of their axiom C, which matches particles and light rays.Specifically, this axiom assumes that, around each event e, any point in the -chronological future of e lies on a particle through e. This will imply that the light-like -pregeodesics of the conformal structure (namely, the -cone geodesics; see Remark 8(2)) are also pregeodesics for the projective structure in step (2). Then, EPS claims that such a compatibility selects a unique affine connection compatible with the projective structure.
- (4)
- Spacetime is endowed with a (time-oriented) Lorentzian metric g, up to an overall (constant) scalar factor. This is obtained by means of a Riemannian axiom, which takes into acccount that has its own parallel transport and its curvature tensor; the axiom imposes the compatibility of (one of) these two elements with g.Indeed, they state that the Riemannian compatibility of is equivalent to any of the following conditions: (a) the vectors obtained by -parallel transport of a single one v at along two curves with the same endpoint q have the same norm at q (computed with any of the homothetic scalar products compatible with ), or (b) using Jacobi fields to construct arbitrarily close particles, the proper times of two of such particles are linearly related at first order, that is, the regular ticking of a clock for the first particle implies the regular ticking for the second one.
5.2. Keys of Compatibility with Finslerian Spacetimes
5.2.1. EPS Step (1)
- (a)
- There are norms with an analytic indicatrix (thus, analytic away from 0) which do not come from a scalar product. For example, on , when the indicatrix is equal to the curve in polar coordinates for small (so that it is strongly convex).
- (b)
- Euclidean scalar products are very particular cases of analytic norms.
5.2.2. EPS Step (2)
5.2.3. EPS Step (3)
5.2.4. EPS Step (4)
5.2.5. Finslerian Examples Strictly Compatible with EPS
5.3. Constructive EPS Approach vs. Observer’s Approach
- (1)
- the impossibility to construct the metric from the behavior of the clocks alone,
- (2)
- the inclusion by hand of the hypothesis that metric geodesics will correspond with free motion, and then,
- (3)
- the expectation that the clocks constructed by means of freely falling particles and light rays will agree with the metric clocks.
6. Lorentz Symmetry Breaking
6.1. Modified Special Relativity
6.1.1. VSR and GVSR
6.1.2. Smoothability at the Cone and Birefringence
6.2. Anisotropic Speed of Light
the speed of light measured by at the direction is bigger (resp. smaller) than the speed of light in the directions close to u when (resp. ).
is compatible with a Lorentz scalar product if and only if is an ellipsoid,
6.3. Matter as Anisotropy and Quantum Physics
The existence of an anisotropy does not mean necessarily a “preexisting spacelike anisotropy of empty space”. Indeed, the existence of matter induces anisotropies in causal directions, and this might be reflected in the indicatrix of L.
- (1)
- individual particles;
- (2)
- description as a kinetic gas, by using a 1-particle distribution function (1PDF), which retains information about velocities; and
- (3)
- description as a fluid, where velocities at each point are also averaged.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aazami, A.B.; Javaloyes, M.A. Penrose’s singularity theorem in a Finsler spacetime. Class. Quantum Gravity 2016, 33, 025003. [Google Scholar] [CrossRef] [Green Version]
- Caponio, E.; Stancarone, G. Standard static Finsler spacetimes. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650040. [Google Scholar] [CrossRef] [Green Version]
- Caponio, E.; Stancarone, G. On Finsler spacetimes with a time-like Killing vector field. Class. Quantum Gravity 2018, 35, 085007. [Google Scholar] [CrossRef] [Green Version]
- Fuster, A.; Pabst, C. Finsler pp-waves. Phys. Rev. D 2016, 94, 104072. [Google Scholar] [CrossRef] [Green Version]
- Fuster, A.; Pabst, C.; Pfeifer, C. Berwald spacetimes and very special relativity. Phys. Rev. D 2018, 98, 084062. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, G.W.; Gomis, J.; Pope, C.N. General very special relativity is Finsler geometry. Phys. Rev. D 2007, 76, 081701. [Google Scholar] [CrossRef] [Green Version]
- Hohmann, M.; Pfeifer, C.; Voicu, N. Finsler gravity action from variational completion. Phys. Rev. D 2019, 100, 064035. [Google Scholar] [CrossRef] [Green Version]
- Ishikawa, H. Note on Finslerian relativity. J. Math. Phys. 1981, 22, 995–1004. [Google Scholar] [CrossRef]
- Javaloyes, M.A.; Sánchez, M. Finsler metrics and relativistic spacetimes. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1460032. [Google Scholar] [CrossRef] [Green Version]
- Javaloyes, M.A.; Sánchez, M. On the definition and examples of cones and Finsler spacetimes. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 2020, 114, 30. [Google Scholar] [CrossRef] [Green Version]
- Lammërzahl, C.; Perlick, V. Finsler geometry as a model for relativistic gravity. Int. J. Geom. Methods Mod. Phys. 2018, 15 (Supp. 1), 1850166. [Google Scholar] [CrossRef] [Green Version]
- Minguzzi, E. An equivalence of Finslerian relativistic theories. Rep. Math. Phys. 2016, 77, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V. Fermat Principle in Finsler Spacetimes. Gen. Relativ. Gravit. 2006, 38, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Pfeifer, C. Finsler spacetime geometry in Physics. Int. J. Geom. Methods Mod. Phys. 2019, 16 (Suppl. 2), 1941004. [Google Scholar] [CrossRef] [Green Version]
- Tavakol, R.; Van Den Bergh, N. Finsler spaces and the underlying geometry of space-time. Phys. Lett. A 1985, 112, 23–25. [Google Scholar] [CrossRef]
- Bernal, A.N.; López, M.P.; Sánchez, M. Fundamental Units of Length and Time. Found. Phys. 2002, 32, 77–108. [Google Scholar] [CrossRef] [Green Version]
- Ignatowsky, W.V. Einige allgemeine Bemerkungen über das Relativitätsprinzip. Phys. Z. 1910, 11, 972–976. Available online: https://de.wikisource.org/wiki/Einige_allgemeine_Bemerkungen_%C3%BCber_das_Relativit%C3%A4tsprinzip (accessed on 15 April 2020).
- Ignatowsky, W.V. Das Relativitätsprinzip. Arch. Math. Phys. Band 1910, 17, 1–24, Band 1911, 18, 17–40. Available online: https://de.wikisource.org/wiki/Das_Relativit%C3%A4tsprinzip_(Ignatowski) (accessed on 15 April 2020).
- Ehlers, J.; Pirani, F.A.E.; Schild, A. Republication of: The geometry of free fall and light propagation. Gen. Relativ. Gravit. 2012, 44, 1587–1609. [Google Scholar] [CrossRef]
- Ehlers, J.; Pirani, F.A.E.; Schild, A. Republication of: The geometry of free fall and light propagation. In General Relativity; Synge, J.L., O’Reifeartaigh, L., Eds.; Clarendon Press: Oxford, UK, 1972; pp. 63–84. [Google Scholar]
- Bogoslovsky, G. A special-relativistic theory of the locally anisotropic space-time. Il Nuovo Cimento B Ser. 1977, 40, 99–115. [Google Scholar] [CrossRef]
- Pfeifer, C.; Wohlfarth, M. Causal structure and electrodynamics on Finsler space-times. Phys. Rev. D 2011, 84, 044039. [Google Scholar] [CrossRef] [Green Version]
- Gielen, S.; Wise, D.K. Lifting general relativity to observer space. J. Math. Phys. 2013, 54, 052501. [Google Scholar] [CrossRef] [Green Version]
- Hohmann, M. Spacetime and observer space symmetries in the language of Cartan geometry. J. Math. Phys. 2016, 57, 082502. [Google Scholar] [CrossRef] [Green Version]
- Bernal, A.N.; Sánchez, M. Un paseo por las geometrías del espaciotiempo en el centenario de la Relatividad General. Gaceta RSME 2015, 18, 521–542. [Google Scholar]
- Lévy Leblond, J.-M. Une nouvelle limite non-relativiste du groupe de Poincaré. Ann. Inst. H. Poincaré Sect. A 1965, 3, 1–12. [Google Scholar]
- Duval, C.; Gibbons, G.W.; Horvathy, P.A.; Zhang, P.M. Carroll versus Newton and Galilei: Two dual non-Einsteinian concepts of time. Class. Quantum Gravity 2014, 31, 085016. [Google Scholar] [CrossRef]
- Figueroa-O-Farrill, J.; Grassie, R.; Prohazka, S. Geometry and BMS Lie algebras of spatially isotropic homogeneous spacetimes. J. High Energy Phys. 2019, 8, 119. [Google Scholar] [CrossRef] [Green Version]
- Geroch, R.P. Faster than light? In Advances in Lorentzian Geometry; Plaue, M., Rendall, A., Scherfner, M., Eds.; AMS/IP Studies in Advanced Mathematics, 49; International Press: Somerville, MA, USA, 2011. [Google Scholar]
- LIGO Scientific Collaboration and Virgo Collaboration; Fermi Gamma-ray Burst Monitor; INTEGRAL. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Bernal, A.N.; Sánchez, M. Leibnizian, Galilean and Newtonian structures of spacetime. J. Math. Phys. 2003, 44, 1129–1149. [Google Scholar] [CrossRef] [Green Version]
- Künzle, H.P. Galilei and Lorentz structures on space-time: comparison of the corresponding geometry and physics. Ann. Inst. H. Poincaré Sect. A 1972, 17, 337–362. [Google Scholar]
- Hartle, J.B.; Hawking, S.W. Wave function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Dray, T.; Ellis, G.; Hellaby, C.; Manogue, C.A. Gravity and signature change. Gen. Relativ. Gravit. 1997, 29, 591–597. [Google Scholar] [CrossRef] [Green Version]
- White, A.; Weinfurtner, S.; Visser, M. Signature change events: a challenge for quantum gravity? Class. Quantum Gravity 2010, 27, 045007. [Google Scholar] [CrossRef] [Green Version]
- Kossowski, M.; Kriele, M. Signature type change and absolute time in general relativity. Class. Quantum Gravity 1993, 10, 1157. [Google Scholar] [CrossRef]
- Vakilia, B.; Jalalzadehb, S. Signature transition in Einstein-Cartan cosmology. Phys. Lett. B 2013, 726, 28–32. [Google Scholar] [CrossRef] [Green Version]
- Albrecht, A.; Magueijo, J. A time varying speed of light as a solution to cosmological puzzles. Phys. Rev. D 1999, 59, 043516. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D. Cosmologies with varying light speed. Phys. Rev. D 1999, 59, 043515. [Google Scholar] [CrossRef] [Green Version]
- Moffat, J. Superluminary Universe: A Possible Solution to the Initial Value Problem in Cosmology. Int. J. Mod. Phys. D 1993, 2, 351–366. [Google Scholar] [CrossRef] [Green Version]
- Petit, J.P. An interpretation of cosmological model with variable light velocity. Mod. Phys. Lett. A 1998, 3, 1527–1532. [Google Scholar] [CrossRef] [Green Version]
- Ellis, G.F.R. Note on Varying Speed of Light Cosmologies. Gen. Relativ. Gravit. 2007, 39, 511–520. [Google Scholar] [CrossRef] [Green Version]
- Uzan, J.-P. Fundamental constants and their variation: Observational status and theoretical motivations. Rev. Mod. Phys. 2003, 75, 403–455. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D.; Magueijo, J. Varying-α theories and solutions to the Cosmological Problems. Phys. Lett. B 1998, 443, 104–110. [Google Scholar] [CrossRef]
- Sancho de Salas, J.B. Characterization of Levi-Civita and Newton-Cartan connections in dimension 2. Differ. Geom. Appl. 2020, 68, 101583. [Google Scholar] [CrossRef]
- Javaloyes, M.A.; Sánchez, M. On the definition and examples of Finsler metrics. Ann. Scuola Norm. Super. Pisa Cl. Sci. (5) 2014, 13, 813–858. [Google Scholar]
- Flores, J.L.; Herrera, J.; Sánchez, M. Gromov, Cauchy and Causal Boundaries for Riemannian, Finslerian and Lorentzian Manifolds. Mem. Am. Math. Soc. 2013, 226, 76. [Google Scholar] [CrossRef]
- Warner, F.W. The conjugate locus of a Riemannian manifold. Am. J. Math. 1965, 87, 575–604. [Google Scholar] [CrossRef]
- Caponio, E.; Javaloyes, M.A.; Sánchez, M. Wind Finslerian structures: From Zermelo’s navigation to the causality of spacetimes. arXiv 2014, arXiv:1407.5494. [Google Scholar]
- Javaloyes, M.A. Anisotropic tensor calculus. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1941001. [Google Scholar] [CrossRef] [Green Version]
- Javaloyes, M.A. Curvature computations in Finsler Geometry using a distinguished class of anisotropic connections. arXiv 2020, arXiv:1904.07178. [Google Scholar]
- Martínez, E.; Cariñena, J.F.; Sarlet, W. Derivations of differential forms along the tangent bundle projection. Differ. Geom. Appl. 1992, 2, 17–43. [Google Scholar] [CrossRef] [Green Version]
- Martínez, E.; Cariñena, J.F.; Sarlet, W. Derivations of differential forms along the tangent bundle projection. Part II. Differ. Geom. Appl. 1993, 3, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Lammërzahl, C.; Perlick, V.; Hasse, W. Observable effects in a class of spherically symmetric static Finsler spacetimes. Phys. Rev. D 2012, 86, 104042. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A. Riemann-Finsler geometry and Lorentz-violating kinematics. Phys. Lett. B 2011, 701, 137–143. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Russell, N.; Tso, R. Bipartite Riemann-Finsler geometry and Lorentz violation. Phys. Lett. B 2012, 716, 470–474. [Google Scholar] [CrossRef] [Green Version]
- Trautman, A. The general theory of relativity. Usp. Fiz. Nauk 1966, 89, 3–37, English translation: Sov. Phys. Usp. 1966, 9, 319–339. [Google Scholar] [CrossRef]
- Stachel, J. Conformal and projective structures in general relativity. Gen. Relativ. Gravit. 2011, 43, 3399–3409. [Google Scholar] [CrossRef]
- Szilasi, J.; Lovas, R.L.; Kertész, D.C. Ten ways to Berwald manifolds—And some steps beyond. arXiv 2011, arXiv:1106.2223. [Google Scholar]
- Akbar-Zadeh, H. Sur les espaces de Finsler à courbures sectionelles constantes. Acad. R. Belg. Bull. Cl. Sci. (5) 1988, 74, 281–322. [Google Scholar]
- Bao, D.; Chern, S.-S.; Shen, Z. An Introduction to Riemann-Finsler Geometry; Graduate Texts in Mathematics, 200; Springer: New York, NY, USA, 2000. [Google Scholar]
- Trautman, A. Editorial note to: J. Ehlers, F. A. E. Pirani and A. Schild, The geometry of free fall and light propagation. Gen. Relativ. Gravit. 2012, 44, 1581–1586. [Google Scholar] [CrossRef] [Green Version]
- Matveev, V.; Trautman, A. A criterion for compatibility of conformal and projective structures. Commun. Math. Phys. 2014, 329, 821–825. [Google Scholar] [CrossRef] [Green Version]
- Folland, G. Weyl structures. J. Differ. Geom. 1970, 4, 145–153. [Google Scholar] [CrossRef]
- Fatibene, L.; Francaviglia, M. Weyl Geometries and Timelike Geodesics. Int. J. Geom. Meth. Mod. Phys. 2012, 9, 1220006. [Google Scholar] [CrossRef]
- Matveev, V.; Scholz, A. Light cone and Weyl compatibility of conformal and projective structures. arXiv 2020, arXiv:2001.0149. [Google Scholar]
- Beem, J.K.; Ehrlich, P.E.; Easley, K.L. Global Lorentzian Geometry, 2nd ed.; Monographs and Textbooks in Pure and Applied Mathematics; Marcel Dekker Inc.: New York, NY, USA, 1996; Volume 202. [Google Scholar]
- Szabó, A. Positive definite Berwald spaces. Tensor 1981, 35, 25–39. [Google Scholar]
- Fuster, A.; Heefer, S.; Pfeifer, C.; Voicu, N. On the non metrizability of Berwald Finsler spacetimes. arXiv 2020, arXiv:2003.02300v1. [Google Scholar]
- Hohmann, M.; Pfeifer, C.; Voicu, N. Cosmological Berwald Spacetimes. arXiv 2020, arXiv:2003.02299v1. [Google Scholar]
- Synge, J.L. Relativity: The Special Theory; North Holland: Amsterdam, The Netherlands, 1960. [Google Scholar]
- Synge, J.L. Relativity: The General Theory; North Holland: Amsterdam, The Netherlands, 1964. [Google Scholar]
- Liberati, S. Tests of Lorentz invariance: A 2013 update. Class. Quantum Gravity 2013, 30, 133001. [Google Scholar] [CrossRef]
- Cohen, A.G.; Glashow, S.L. Very special relativity. Phys. Rev. Lett. 2006, 97, 021601. [Google Scholar] [CrossRef] [Green Version]
- Bogoslovsky, G. The rest momentum as an additional property of a massive particle in Finsler space-time. J. Phys. Conf. Ser. 2018, 1051, 012007. [Google Scholar] [CrossRef]
- Lammërzahl, C.; Hehl, F.W. Riemannian light cone from vanishing birefringence in premetric vacuum electrodynamics. Phys. Rev. D 2004, 70, 105022. [Google Scholar] [CrossRef] [Green Version]
- Sachs, R.K.; Wu, H.H. General Relativity for Mathematicians; Springer: New York, NY, USA, 1977. [Google Scholar]
- Mo, X.; Huang, L. On characterizations of Randers norms in a Minkowski space. Int. J. Math. 2010, 21, 523–535. [Google Scholar] [CrossRef]
- Javaloyes, M.A.; Vitório, H. Some properties of Zermelo navigation in pseudo-Finsler metrics under an arbitrary wind. Houst. J. Math. 2018, 44, 1147–1179. [Google Scholar]
- Nomizu, K.; Sasaki, T. Affine Differential Geometry; Cambridge Tracts in Mathematics; Cambridge University Press: Cambridge, UK, 1994; Volume 111. [Google Scholar]
- Finster, F.; Kleiner, J. Causal Fermion Systems as a Candidate for a Unified Physical Theory. J. Phys. Conf. Ser. 2015, 626, 012020. [Google Scholar] [CrossRef] [Green Version]
- Hohmann, M.; Pfeifer, C.; Voicu, N. Relativistic kinetic gases as direct sources of gravity. Phys. Rev. D 2020, 101, 024062. [Google Scholar] [CrossRef] [Green Version]
- Barceló, C.; Liberati, S.; Visser, M. Analogue Gravity. Living Rev. Relativ. 2011, 14, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caponio, E.; Javaloyes, M.A.; Sánchez, M. On the interplay between Lorentzian causality and Finsler metrics of Randers type. Rev. Mat. Iberoam. 2011, 27, 919–952. [Google Scholar] [CrossRef] [Green Version]
- Javaloyes, M.A.; Sánchez, M. Some criteria for wind Riemannian completeness and existence of Cauchy hypersurfaces. In Lorentzian Geometry and Related Topics; Springer Proc. Math. Stat., 211; Springer: Cham, Switzerland, 2017; pp. 117–151. [Google Scholar]
- Gibbons, G.W. A Spacetime Geometry picture of Forest Fire Spreading and of Quantum Navigation. arXiv 2017, arXiv:1708.02777. [Google Scholar]
- Javaloyes, M.A.; Sánchez, M. Wind Riemannian spaceforms and Randers-Kropina metrics of constant flag curvature. Eur. J. Math. 2017, 3, 1225–1244. [Google Scholar] [CrossRef] [Green Version]
- Markvorsen, S. A Finsler geodesic spray paradigm for wildfire spread modelling. Nonlinear Anal. Real World Appl. 2016, 28, 208–228. [Google Scholar] [CrossRef] [Green Version]
| 1. | The reason relies on a classical result for any Finsler metric F: its square is at the zero section if and only if F comes from a Riemannian metric (see Remark 5 (1) and Section 5.2). |
| 2. | |
| 3. | It is worth pointing out that [16] focuses on the viewpoint of general relativity. Therefore, the first postulate there is different to the one here. Our viewpoint was pointed in Reference [25] (written for a general audience in Spanish), and it is developed further here by introducing concepts such as apparent temporality (Theorem 1) or arguments as those on the varying of the speed of light. |
| 4. | The reader can consider the simple case (as in Equation (2)), when , (). The solutions of this case yield all the relevant possibilities. They follow easily by noticing that, from the algorithm, to compute the inverse matrix,
In particular, ⇔ and, then, . Therefore, this equality would follow by assuming additionally (i.e., in Equation (3)), which will correspond with the condition of apparent temporality in Theorem 1. |
| 5. | |
| 6. | It is worth pointing out that, in this case, not only the independent symmetries between time and spatial coordinates in Equation (3) hold but also the crossed symmetries and appear now. |
| 7. | Anyway, it would represent the model of space and time which goes back to Aristoteles. Recall that, in that model, one would assume not only the existence of the absolute space and time but also that, for any , there exists a physical observer at P at absolute rest. This would determine the affine line , which would be regarded as a “space point at any time”. |
| 8. | That is, a choice of one of the two time-like cones when and one of the two choices of absolute time or absolute rest observer when , resp. |
| 9. | However, recent measurements of gravitational waves show that the speed of propagation of light and gravitation are equal with an extraordinary accuracy [30]. |
| 10. | contains all the (ordered) linear bases of for all . |
| 11. | Such a structure is equivalent to having the 1-form and a positive semidefinite 2-contravariant tensor T of rank 3 with , studied in Reference [32]. Indeed, such a T induces a Riemannian metric in the dual of ker and, then, in ker. Conversely, the Leibnizian structure yields a Riemannian metric on ker and then in its dual; this yields the tensor T by imposing that its radical is Span. |
| 12. | Recall that models of signature changing metrics have been studied at least since the influential “no boundary” proposal by Hartle and Hawking [33]; see for example [34,35]. Moreover, the existence of an “absolute time” in the transition region has also been pointed out by several authors [36] (Section 2; see also Reference [37]). |
| 13. | In the more speculative case of a signature changing metric, the speed of light would change necessarily in the regions . Therefore, the possibility to measure a varying speed of light when would imply that the collapse of the lightcones (to a line or a hyperplane) could be measured gradually when approaching those regions. |
| 14. | Such a formula can be extended to include nonsymmetric connections by adding as a third datum a suitable component of the torsion; see Reference [31] Th. 27. |
| 15. | |
| 16. | Including those for relativistic stationary spacetimes; see Reference [47] and references therein. |
| 17. | |
| 18. | Such a exists by Jordan–Brower theorem. |
| 19. | These conditions would be satisfied by hypersurfaces suitably -close to the space of observers of any relativistic spacetime (notice that some issues appear involving the extendability of L to the cone and whether the cone is prescribed or not), and they can be constructed for any cone (recall Remark 8(4) below). |
| 20. | Recall that, for any function on (with a cone domain), the elementary definition of existence of a differential map at 0 makes sense because 0 is an accumulation point of the domain of and its uniqueness is guaranteed because contains n independent directions converging to 0. |
| 21. | Essentially, this is a connection where, formally, the Christoffel symbols of a chart depend also on the direction and, so, they are functions on , which are positive homogeneous of degree zero. The name and a thorough study of A-anisotropic connections were given in References [50,51]; see also Reference [52,53] for a study of connections on fiber bundles from a more general viewpoint. |
| 22. | Even though we focus on the relativistic case (disregarding the Leibnizian case and the other possibilities), one could also consider a Leibniz–Finsler structure on a manifold M, where h would be now a Finsler metric on instead of a Riemannian one, according to Table 1. |
| 23. | Along the events P, all the light rays from would trivially cross P at ; therefore, the function g below would be trivially extended as . However, the points on P would be excluded in order to define the differentiable structure of the manifold by using radar coordinates (recall the example in Footnote 24 below). |
| 24. | For example, let P be the t-axis and Q. A message from Q to P would yield the map if and if (see Example 1 below) which is not smooth at 0, in contradiction with (recall also Footnote 23). |
| 25. | Of course, one could introduce a spurious differential structure on so that becomes smooth for a non-Euclidean , but this would not be natural by any means. |
| 26. | In principle, the normal coordinates can be defined when the anisotropic connection is defined for all the vectors in , but it is always possible to extend the -anisotropic connection to all directions locally (see Reference [10] Remark 6.3, where the Lorentz–Finsler case is considered in detail). These coordinates are obtained using the exponential map in a neighborhood as in Reference [10] Lemma 6.2. |
| 27. | This means that its Chern–Rund connection defines an affine connection on the underlying manifold; see Reference [59] for quite a few of characterizations. |
| 28. | In modern language, a Weyl geometry on M is a conformal structure endowed with a connection on the -principle bundle , where the fiber of P at each is the class of homothetic Lorentzian scalar products compatible with (see for example Reference [64]); such a notion was considered in references on EPS such as Reference [65]. |
| 29. | Compare with EPS claim (1) in Section 5.3 below. |
| 30. | See for example Reference [67] Section 2.3. |
| 31. | would correspond with the direction of propagation of the wave, b would correspond with a parameter for a conformal transformation of which preserves the wave equation, and would correspond with a Finsler metric invariant by this transformation; see also Reference [75] for further information. |
| 32. | From a mathematical viewpoint, the property that lightcones are affinely diffeomorphic is a Berwald-type property. Recall that one of the characterizations of Berwald manifolds in the class of the Finsler ones is the existence of a torsion-free derivative operator such that the parallel translations with respect to it preserve the Finsler norms of tangent vectors [59] (Prop. 6); in particular, the norms at different points are isometric. |
| 33. | Equally, the rest space and the sky could be regarded as the hyperplane parallel to through the origin and the projection of along the direction into , respectively. This is a usual identification in general relativity [77]. |
| 34. | Observe that the cubic form coincides with the Matsumoto tensor of the pseudo-Minkowski norm having the affine hypersurface as indicatrix up to multiplication by a function (see for example Reference [78] or Reference [79]). The Matsumoto tensor is zero when the pseudo-Finsler metric comes from a scalar product. |
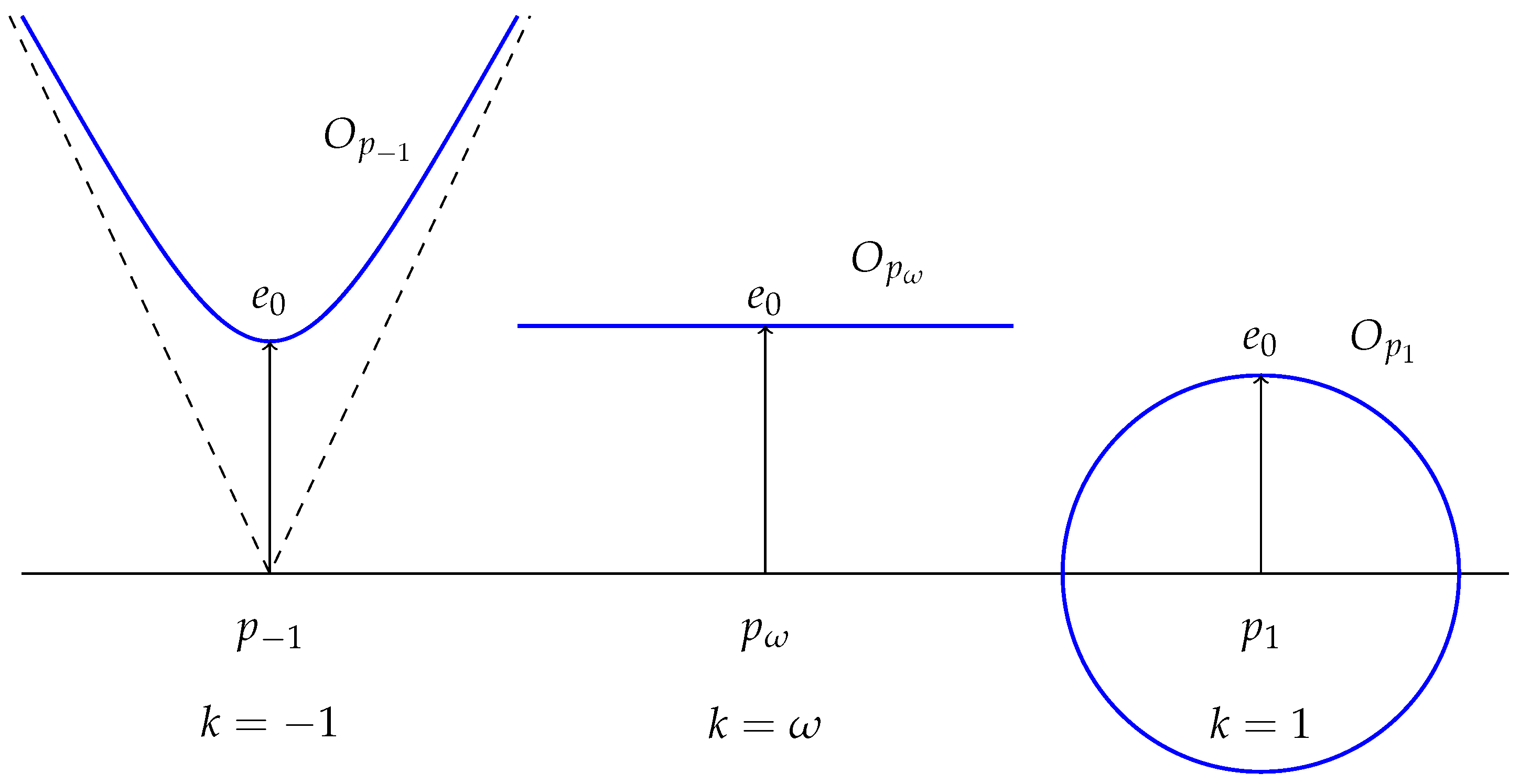
| Model | Linear space: affine Aff with vector V (translation-invariant elements) Geodesics ≡ straight lines | Smooth connected manifold M (pointwise dependent elements) | ||
| Quadratic forms (doubly linear) | No quadratic restriction | First nonlinearizat.: pointwise quadratic | Second nonlinearizat.: no quadratic restriction | |
| Space | Euclidean scalar product on | Minkowski norm | Riemannian metric | Finsler metric |
| Symmetry | (drop parallelogram identity + reversibility) | Unit sphere bundle = pointwise ellipsoid. Levi–Civita natural mathematical choice. | Indicatrix = pointwise strongly convex hypers. Cartan connection | |
| Space + time Classic | Galilei–Newton | Non-quadratic Galilei–Newton | Leibnizian structure: | Leibniz–Finsler str. |
| - absolute time (on V): Nonzero linear form | -Replace in Galilei–Newton by a norm. | Non-vanishing 1-form (eventually, ) with a Riemannian metric on the bundle . | -Replace the Riemannian metric on by a Finslerian one. | |
| - absolute space: Eucl. scalar product on . | Not developed (as far as we know) | Required to choose a linear connection parallelizing and ) | Not developed (as far as we know) | |
| Symmetry: orthochr. Galilean group | ||||
| Space − time Relat. | Special Relat. | Modified Special Relat. | General Relat. : | Finsler spacetime (with a cone str. ) |
| - Lorentzian scalar product | - cone | Pointwise smooth Lorentzian scalar product continuously time-oriented | Pointwise smooth Lorentz–Minkowski norm. | |
| -C time-orientation (choice of one between 2 cones) | - Lorentz-norm on causal vectors (eventually determined from ) | Levi–Civita connection: free fall, ligthlike pregeodesics, gravitational force | Geodesics determined by Cartan (and Chern etc.) connection. | |
| Symmetry: orthochr. Lorentz group | No symmetry but includes the case VSR (with proper a subgroup of ) | pregeodesics independent of L | ||
| Anisotropy with causal directions (possibly due to matter/energy) | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernal, A.N.; Javaloyes, M.A.; Sánchez, M. Foundations of Finsler Spacetimes from the Observers’ Viewpoint. Universe 2020, 6, 55. https://doi.org/10.3390/universe6040055
Bernal AN, Javaloyes MA, Sánchez M. Foundations of Finsler Spacetimes from the Observers’ Viewpoint. Universe. 2020; 6(4):55. https://doi.org/10.3390/universe6040055
Chicago/Turabian StyleBernal, Antonio N., Miguel A. Javaloyes, and Miguel Sánchez. 2020. "Foundations of Finsler Spacetimes from the Observers’ Viewpoint" Universe 6, no. 4: 55. https://doi.org/10.3390/universe6040055
APA StyleBernal, A. N., Javaloyes, M. A., & Sánchez, M. (2020). Foundations of Finsler Spacetimes from the Observers’ Viewpoint. Universe, 6(4), 55. https://doi.org/10.3390/universe6040055







