Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements
Abstract
1. Introduction
2. The Point Particle Case
2.1. The Direct Pericenter Precession Due to the 2PN Acceleration
2.2. The Indirect Pericenter Precession due to the 1PN Acceleration
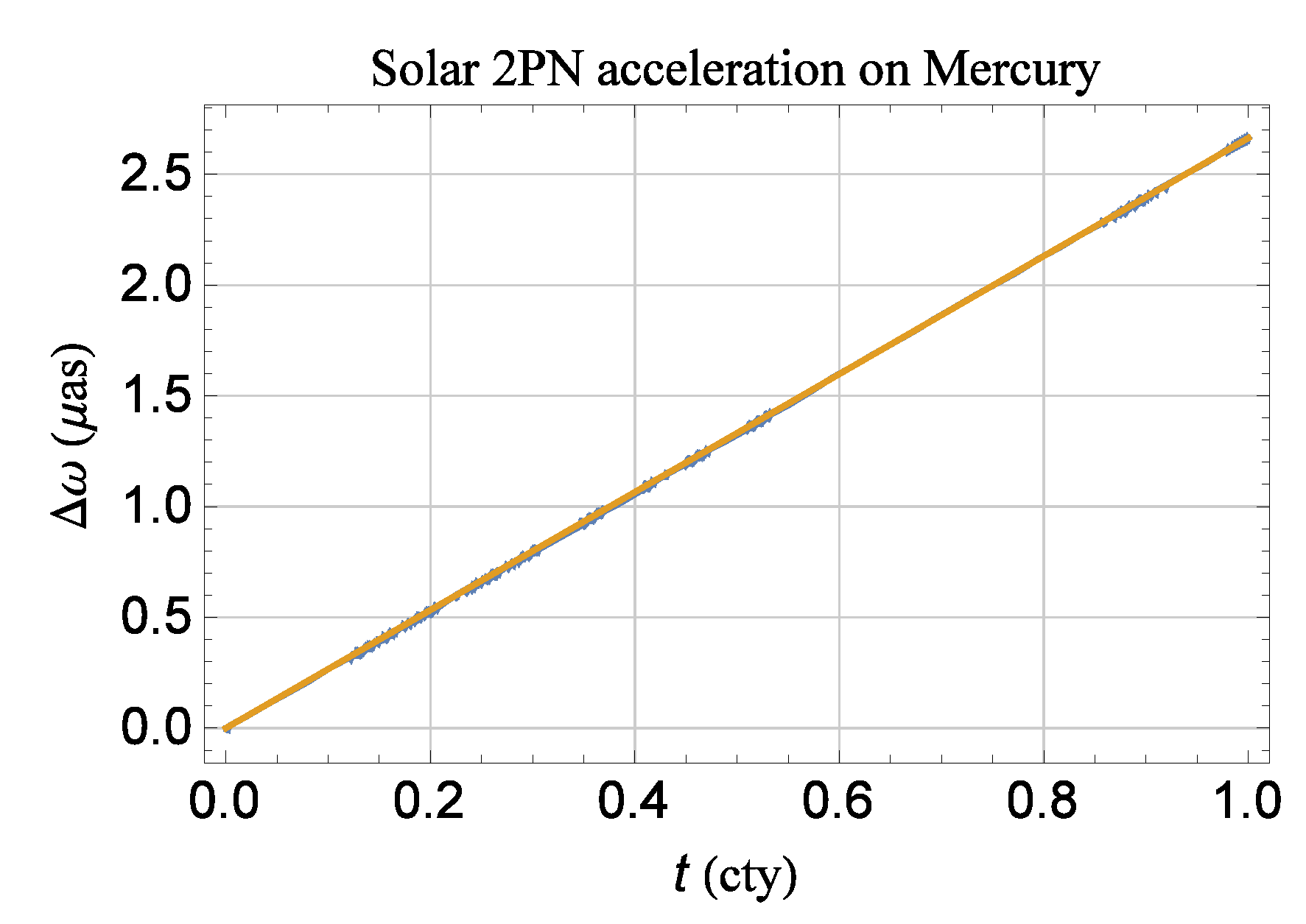
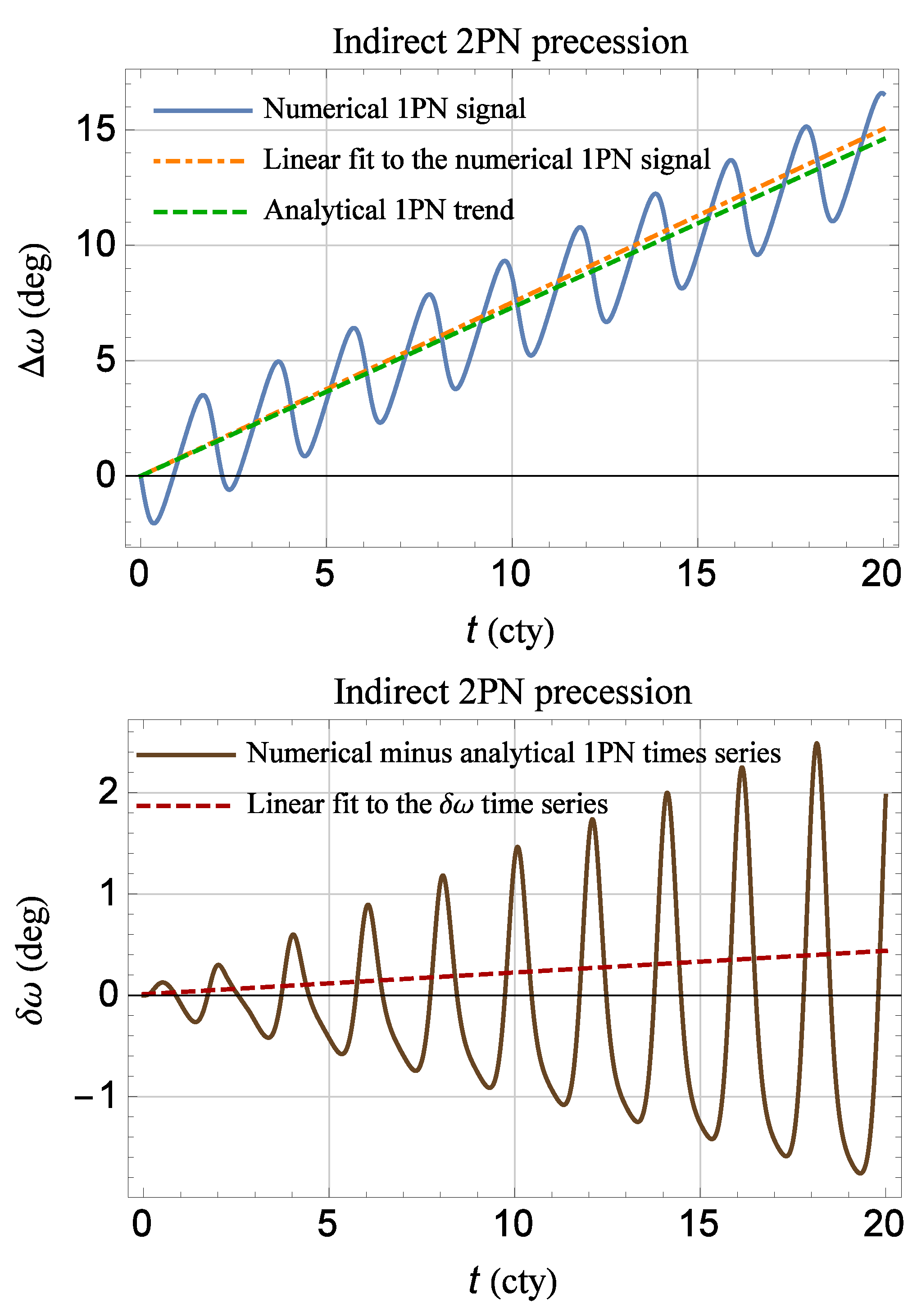
2.3. A Numerical Confirmation of the Direct and Indirect 2PN Pericenter Precessions
3. The Case of a Two-Body System
3.1. The Direct Pericenter Precession due to the 2PN Acceleration
3.2. The Indirect Pericenter Precession Due to the 1PN Acceleration
4. A Comparison with Other Works
5. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Debono, I.; Smoot, G.F. General relativity and cosmology: Unsolved questions and future directions. Universe 2016, 2, 23. [Google Scholar] [CrossRef]
- Bagchi, M. Periastron advance in neutron star–black hole binaries. Mon. Not. R. Astron. Soc. 2013, 428, 1201. [Google Scholar] [CrossRef][Green Version]
- Blanchet, L. Gravitational radiation from post-Newtonian sources and inspiralling compact binaries. Living Rev. Relat. 2014, 17, 2. [Google Scholar] [CrossRef] [PubMed]
- Damour, T.; Schaefer, G. Le problème des deux corps en relativité générale. CR Acad. Sci. Sér. II 1987, 305, 839. [Google Scholar]
- Damour, T.; Schafer, G. Higher-order relativistic periastron advances and binary pulsars. Nuovo Cimento B 1988, 101, 127. [Google Scholar] [CrossRef]
- D’Eliseo, M.M. Higher-order corrections to the relativistic perihelion advance and the mass of binary pulsars. Astrophys. Space Sci. 2011, 332, 121. [Google Scholar] [CrossRef]
- Do-Nhat, T. Full asymptotic expansion of the relativistic orbit of a test particle under the exact Schwarzschild metric. Phys. Lett. A 1998, 238, 328. [Google Scholar] [CrossRef]
- Gergely, L.A.; Keresztes, Z. Spinning compact binary dynamics and chameleon orbits. Phys. Rev. D 2015, 91, 024012. [Google Scholar] [CrossRef]
- Heng, F.; Zhao, F. Exact analytical solution to equations of perihelion advance in general relativity. Int. J. Theor. Phys. 2009, 48, 2198–2204. [Google Scholar]
- Hoenselaers, C. On Quadrupole Effects on Planetary Orbits Prog. Theor. Phys. 1976, 56, 324. [Google Scholar] [CrossRef][Green Version]
- Königsdörffer, C.; Gopakumar, A. Post-Newtonian accurate parametric solution to the dynamics of spinning compact binaries in eccentric orbits: The leading order spin-orbit interaction. Phys. Rev. D 2005, 71, 024039. [Google Scholar] [CrossRef]
- Kopeikin, S.M.; Potapov, V.A. Relativistic shift of the periastron of a double pulsar in the post-post-Newtonian approximation of General Relativity. Astron. Rep. 1994, 38, 104. [Google Scholar]
- Mak, M.K.; Leung, C.S.; Harko, T. Computation of the General Relativistic Perihelion Precession and of Light Deflection via the Laplace-Adomian Decomposition Method. Adv. High Energy Phys. 2018, 2018, 7093592. [Google Scholar] [CrossRef]
- Marín, C.; Poveda, J. Perihelion precession in binary systems: Higher order corrections. Astrophys. Space Sci. 2018, 363, 245. [Google Scholar] [CrossRef]
- Memmesheimer, R.-M.; Gopakumar, A.; Schäfer, G. Third post-Newtonian accurate generalized quasi-Keplerian parametrization for compact binaries in eccentric orbits. Phys. Rev. D 2004, 70, 104011. [Google Scholar] [CrossRef]
- Ohta, T.; Kimura, T. Launch window study for the highly eccentric orbit satellite HEOS-1. Prog. Theor. Phys. 1989, 81, 679. [Google Scholar] [CrossRef]
- Schäfer, G.; Wex, N. Second post-Newtonian motion of compact binaries. Phys. Lett. A 1993, 174, 196. [Google Scholar] [CrossRef]
- Schäfer, G.; Wex, N. Errata: Second post-Newtonian motion of compact binaries. Phys. Lett. A 1993, 177, 461. [Google Scholar] [CrossRef]
- Tucker, A.; Will, C.M. Pericenter advance in general relativity: Comparison of approaches at high post-Newtonian orders. Class. Quantum Gravity 2019, 36, 115001. [Google Scholar] [CrossRef]
- Walters, S.J. A simple exact series representation for relativistic perihelion advance. Mon. Not. R. Astron. Soc. 2018, 480, 3747. [Google Scholar] [CrossRef]
- Wex, N. The second post-Newtonian motion of compact binary-star systems with spin. Class. Quantum Gravity 1995, 12, 983. [Google Scholar] [CrossRef]
- Will, C.M. New general relativistic contribution to mercury’s perihelion advance. Phys. Rev. Lett. 2018, 120, 191101. [Google Scholar] [CrossRef] [PubMed]
- Will, C.M.; Maitra, M. Relativistic orbits around spinning supermassive black holes: Secular evolution to 4.5 post-Newtonian order. Phys. Rev. D 2017, 95, 064003. [Google Scholar] [CrossRef]
- Klioner, S.A.; Kopeikin, S.M. The post-Keplerian orbital representations of the relativistic two-body problem. Astrophys. J. 1994, 427, 951. [Google Scholar] [CrossRef]
- Bertotti, B.; Farinella, P.; Vokrouhlický, D. Physics of the Solar System; Springer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Brouwer, D.; Clemence, G.M. Methods of Celestial Mechanics; Academic Press: New York, NY, USA, 1961. [Google Scholar]
- Brumberg, V.A. Essential Relativistic Celestial Mechanics; Adam Hilger: Bristol, UK, 1991. [Google Scholar]
- Danby, J.M.A. Fundamentals of Celestial Mechanics; The Macmillan Company: New York, NY, USA, 1962. [Google Scholar]
- Kopeikin, S.; Efroimsky, M.; Kaplan, G. Relativistic Celestial Mechanics of the Solar System; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
- Murray, C.D.; Dermott, S.F. Solar System Dynamics; Cambridge Univ. Press: Cambridge, UK, 2000. [Google Scholar]
- Plummer, H.C. An Introductory Treatise in Dynamical Astronomy; Dover Publications, Inc.: New York, NY, USA, 1960. [Google Scholar]
- Poisson, E.; Will, C.M. Gravity; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Roy, A.E. Orbital Motion; Institute of Physics Publishing: Bristol, UK, 2005. [Google Scholar]
- Soffel, M.H. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer: Heidelberg, Gremany, 1989. [Google Scholar]
- Soffel, M.H.; Han, W.-B. Applied General Relativity; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Tisserand, F. Traité de Mécanique Céleste; Gauthier-Villars: Paris, France, 1989. [Google Scholar]
- Dey, L.; Gopakumar, A.; Valtonen, M.; Zola, S.; Susobhanan, A.; Hudec, R.; Pihajoki, P.; Pursimo, T.; Berdyugin, A.; Piirola, V.; et al. The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine. Universe 2019, 5, 108. [Google Scholar] [CrossRef]
- Dey, L.; Valtonen, M.J.; Gopakumar, A.; Zola, S.; Hudec, R.; Pihajoki, P.; Ciprini, S.; Matsumoto, K.; Sadakane, K.; Kidger, M.; et al. Authenticating the presence of a relativistic massive black hole binary in OJ 287 using its general relativity centenary flare: Improved orbital parameters. Astrophys. J. 2018, 866, 11. [Google Scholar] [CrossRef]
- Frutos-Alfaro, F.; Soffel, M. On relativistic multipole moments of stationary space–times. R. Soc. Open Sci. 2018, 5, 180640. [Google Scholar] [CrossRef]
- Heimberger, J.; Soffel, M.; Ruder, H. Relativistic effects in the motion of artificial satellites: The oblateness of the central body II. Celest. Mech. Dyn. Astron. 1990, 47, 205. [Google Scholar] [CrossRef]
- Meichsner, J.; Soffel, M.H. Effects on satellite orbits in the gravitational field of an axisymmetric central body with a mass monopole and arbitrary spin multipole moments. Celest. Mech. Dyn. Astron. 2015, 123, 1. [Google Scholar] [CrossRef][Green Version]
- Panhans, M.; Soffel, M.H. Gravito-magnetism of an extended celestial body. Class. Quantum Gravity 2014, 31, 245012. [Google Scholar] [CrossRef]
- Schanner, M.; Soffel, M. Relativistic satellite orbits: Central body with higher zonal harmonics. Celest. Mech. Dyn. Astron. 2018, 130, 40. [Google Scholar] [CrossRef]
- Soffel, M.; Wirrer, R.; Schastok, J.; Ruder, H.; Schneider, M. Relativistic effects in the motion of artificial satellites: The oblateness of the central body I. Celest. Mech. Dyn. Astron. 1987, 42, 81. [Google Scholar] [CrossRef]
- Iorio, L. Post-Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 2015, 24, 1550067. [Google Scholar] [CrossRef]
- Fienga, A.; Deram, P.; Viswanathan, V.; Di Ruscio, A.; Bernus, L.; Durante, D.; Gastineau, M.; Laskar, J. INPOP19a Planetary Ephemerides. Available online: https://hal.archives-ouvertes.fr/hal-02470929/document (accessed on 11 April 2020).
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The planetary and lunar ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 42, 1. [Google Scholar]
- Pitjeva, E.V.; Pitjev, N.P. Masses of the Main Asteroid Belt and the Kuiper Belt from the Motions of Planets and Spacecraft. Astron. Lett. 2018, 44, 554. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1875, 195, L51. [Google Scholar] [CrossRef]
- Burgay, M.; D’Amico, N.; Possenti, A.; Manchester, R.N.; Lyne, A.G.; Joshi, B.C.; McLaughlin, M.A.; Kramer, M.; Sarkissian, J.M.; Camilo, F. et al. An increased estimate of the merger rate of double neutron stars from observations of a highly relativistic system. Nature 2003, 426, 531. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, B.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A double-pulsar system: A rare laboratory for relativistic gravity and plasma physics. Science 2004, 303, 1153. [Google Scholar] [CrossRef]
- Egorov, V.A. Definition of the True Anomaly in Perturbed Motion. Sov. Astron. 1958, 2, 147. [Google Scholar]
- Mioc, V.; Radu, E. Perturbations in the Anomalistic Period of Artificial Satellites Caused by the Direct Solar Radiation Pressure Centre for Astronomy and Space Sciences, Satellite Tracking Station No. 1132. Astron. Nachr. 1979, 300, 313. [Google Scholar] [CrossRef]
- Roth, E.A. Launch window study for the highly eccentric orbit satellite HEOS-1. Celest. Mech. 1970, 2, 369. [Google Scholar] [CrossRef]
- Taratynova, G.P. Über die Bewegung von künstlichen Satelliten im nicht-zentralen Schwerefeld der Erde unter Berücksichtigung des Luftwiderstandes. Fortschr. Phys. 1959, 7, 55. [Google Scholar] [CrossRef]
- Will, C.M. Incorporating post-Newtonian effects in N-body dynamics. Phys. Rev. D 2014, 89, 044043. [Google Scholar] [CrossRef]
- Will, C.M. Erratum: Incorporating post-Newtonian effects in N-body dynamics. Phys. Rev. D 2015, 91, 029902. [Google Scholar] [CrossRef]
- Iorio, L. Calculation of the Uncertainties in the Planetary Precessions with the Recent EPM2017 Ephemerides and their Use in Fundamental Physics and Beyond. Astrophys. J. 2019, 157, 220. [Google Scholar] [CrossRef]
- Kidder, L.E. Coalescing binary systems of compact objects to (post)5/2–Newtonian order. V. Spin effects. Phys. Rev. D 1995, 52, 821. [Google Scholar] [CrossRef] [PubMed]
- Gergely, L.A. Spinning compact binary inspiral. II. Conservative angular dynamics. Phys. Rev. D 2010, 82, 104031. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of general relativity from timing the double pulsar. Science 2006, 314, 97. [Google Scholar] [CrossRef]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future measurements of the Lense-Thirring effect in the Double Pulsar. In Proceedings of the Fourteenth Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, Rome, Italy, 12–18 July 2015; Bianchi, M., Jansen, R.T., Ruffini, R., Eds.; World Scientific: Singapore, 2017; Volume 4, pp. 1860–1865. [Google Scholar]
- Weisberg, J.M.; Nice, D.J.; Taylor, J.H. Timing measurements of the relativistic binary pulsar PSR B1913+ 16. Astrophys. J. 2010, 722, 1030. [Google Scholar] [CrossRef]
- Schödel, R.; Ott, T.; Genzel, R.; Hofmann, R.; Lehnert, M.; Eckart, A.; Mouawad, N.; Alexander, T.; Reid, M.J.; Lenzen, R.; et al. A star in a 15.2-year orbit around the supermassive black hole at the centre of the Milky Way. Nature 2002, 419, 694. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1971. [Google Scholar]
- Arnowitt, R.; Deser, S.; Misner, C.W. Gravitational-electromagnetic coupling and the classical self-energy problem. Phys. Rev. 1960, 120, 313. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N. General relativistic celestial mechanics of binary systems. I. The post-Newtonian motion. Ann. Inst. Henri Poincaré Phys. Théor. 1985, 43, 107. [Google Scholar]
| 1. | For the sake of simplicity, we will omit the brackets denoting the average over one orbital revolution here and throughout the paper. |
| 2. | It is one of the possible names which can be attributed to the pericenter when black holes are involved [64]. It comes from the Latin word “niger”, meaning “black”. |
| 3. | In Kopeikin & Potapov [12], it is . |
| 4. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iorio, L. Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements. Universe 2020, 6, 53. https://doi.org/10.3390/universe6040053
Iorio L. Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements. Universe. 2020; 6(4):53. https://doi.org/10.3390/universe6040053
Chicago/Turabian StyleIorio, Lorenzo. 2020. "Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements" Universe 6, no. 4: 53. https://doi.org/10.3390/universe6040053
APA StyleIorio, L. (2020). Revisiting the 2PN Pericenter Precession in View of Possible Future Measurements. Universe, 6(4), 53. https://doi.org/10.3390/universe6040053




