Neutrino Telescopes and High-Energy Cosmic Neutrinos
Abstract
1. Introduction
1.1. Historical Notes
1.2. Plan of This Review
2. High-Energy Neutrinos in the Cosmos
2.1. The Cosmic Ray Connection
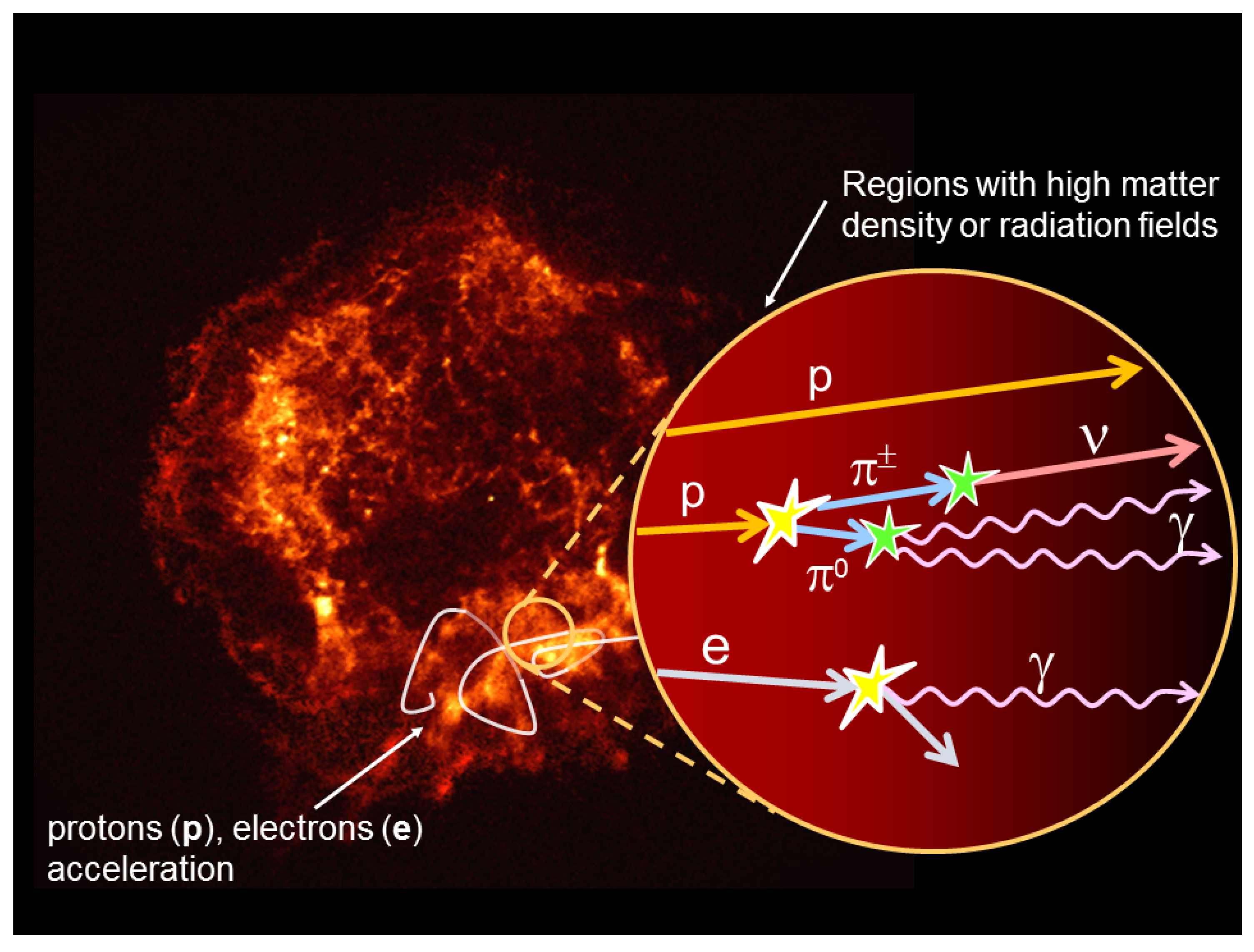
2.2. The and Mechanisms of Neutrino Production
- The -mechanism is a process with a defined threshold. For example, suppose having a photon target between the UV and X bands, say with energies of keV. For the production of a -resonance, kinematics dictates:which, according to (4), corresponds to neutrinos with minimal energy of TeV (see also Reference [16]). In this production mechanism, the resulting neutrino (and very high-energy -ray) spectra will reflect the energy distribution of the target photons. If the interaction region moves at relativistic speeds with Lorentz factor toward us, the observed neutrino energies are larger by a factor , see e.g., [16] and [31].
- The -mechanism is featured by a very important property of the hadronic interactions, namely the hypothesis of limiting fragmentation [32], to which we refer in the following as scaling. A detailed description of scaling variables, their definition, and the application on cosmic ray physics can be found in Reference [25]. According to the scaling, the secondary particle spectra corresponds quite strictly to the primary distribution. Consequently, if the cosmic rays are power-law distributed, also the neutrinos and the very high-energy -rays will be power law distributed, with (almost) the same slope. One commonly says that, in this case, the neutrino and gamma-ray spectra reflect the primary (cosmic ray) spectra. In particular, if some variant of Fermi acceleration mechanism applies, we would have
2.3. Connection of Neutrino and Gamma-Ray Astronomies
- -rays can be produced also in the leptonic mechanisms in which only electrons are usually involved;
- -rays can be absorbed if the target is thick;
- when the -rays propagate for long distances, they are subject to absorption over background photons due to pair production
3. From Cosmic Neutrino Sources to the Earth
3.1. Effects of Neutrino Propagation
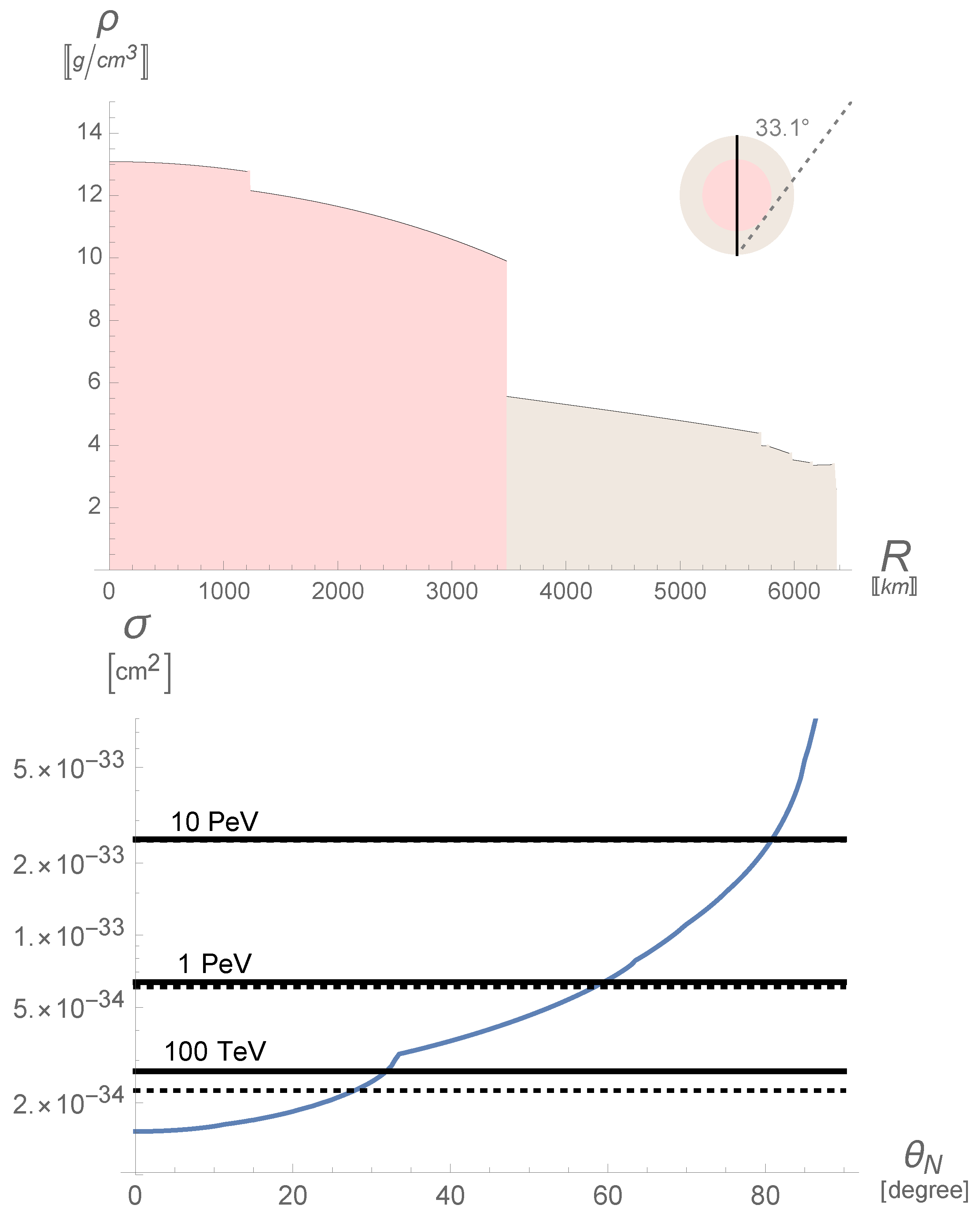
3.2. Neutrino Interactions in the Earth
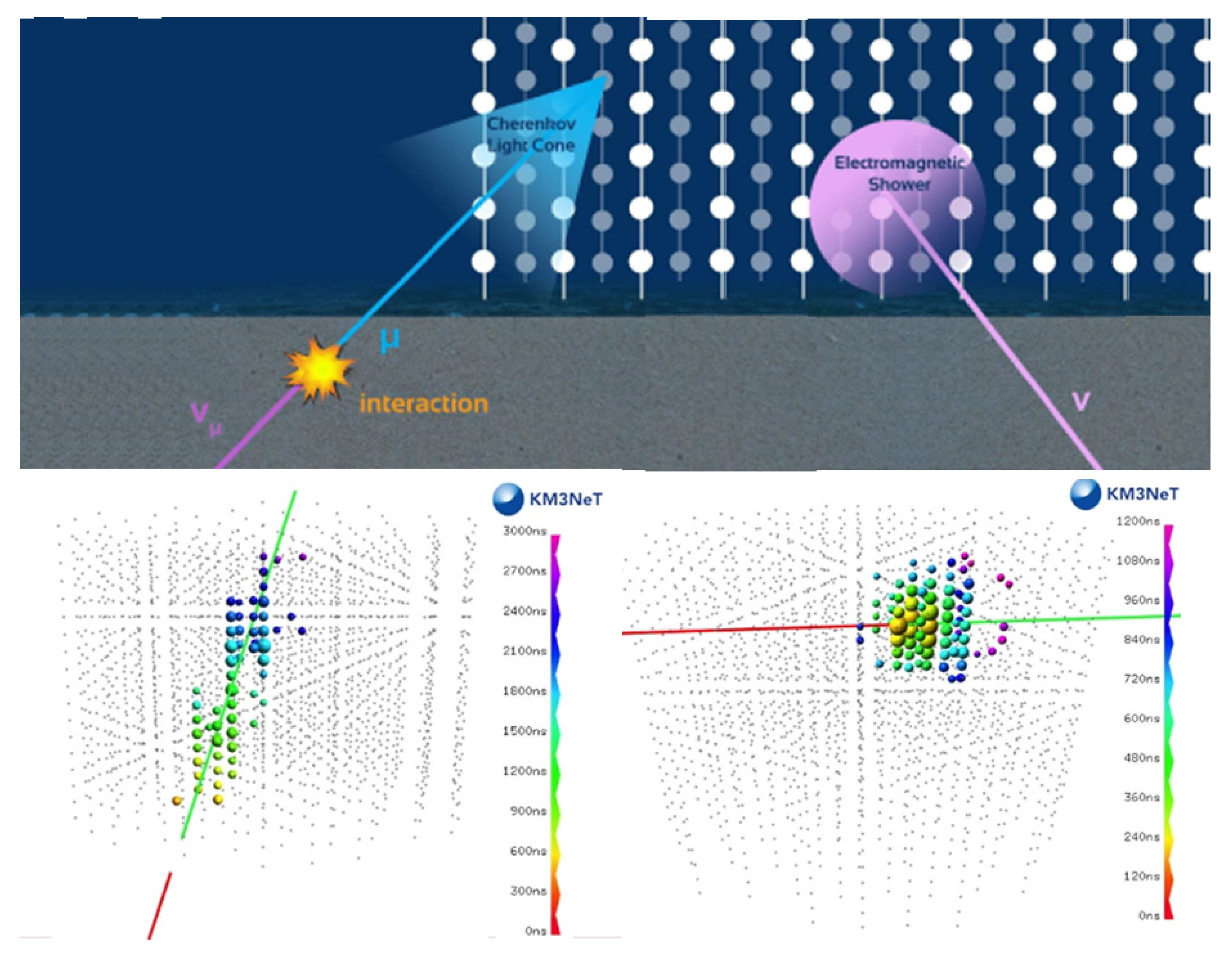
4. High Energy Neutrino Telescopes
4.1. Operating Principles
- offers a large volume of target nucleons for neutrino interactions;
- provides shielding against secondary particles produced by cosmic rays;
- allows the propagation of Cherenkov photons emitted by relativistic charged particles produced by the neutrino interaction.
4.2. Detectors All around the World
4.2.1. IceCube
4.2.2. ANTARES
4.2.3. KM3NeT
4.2.4. GVD
5. Topologies of the Events
5.1. Passing-Events
5.2. Contained Events
5.3. Double Core Events
5.4. Glashow Resonance
5.5. Effective Areas
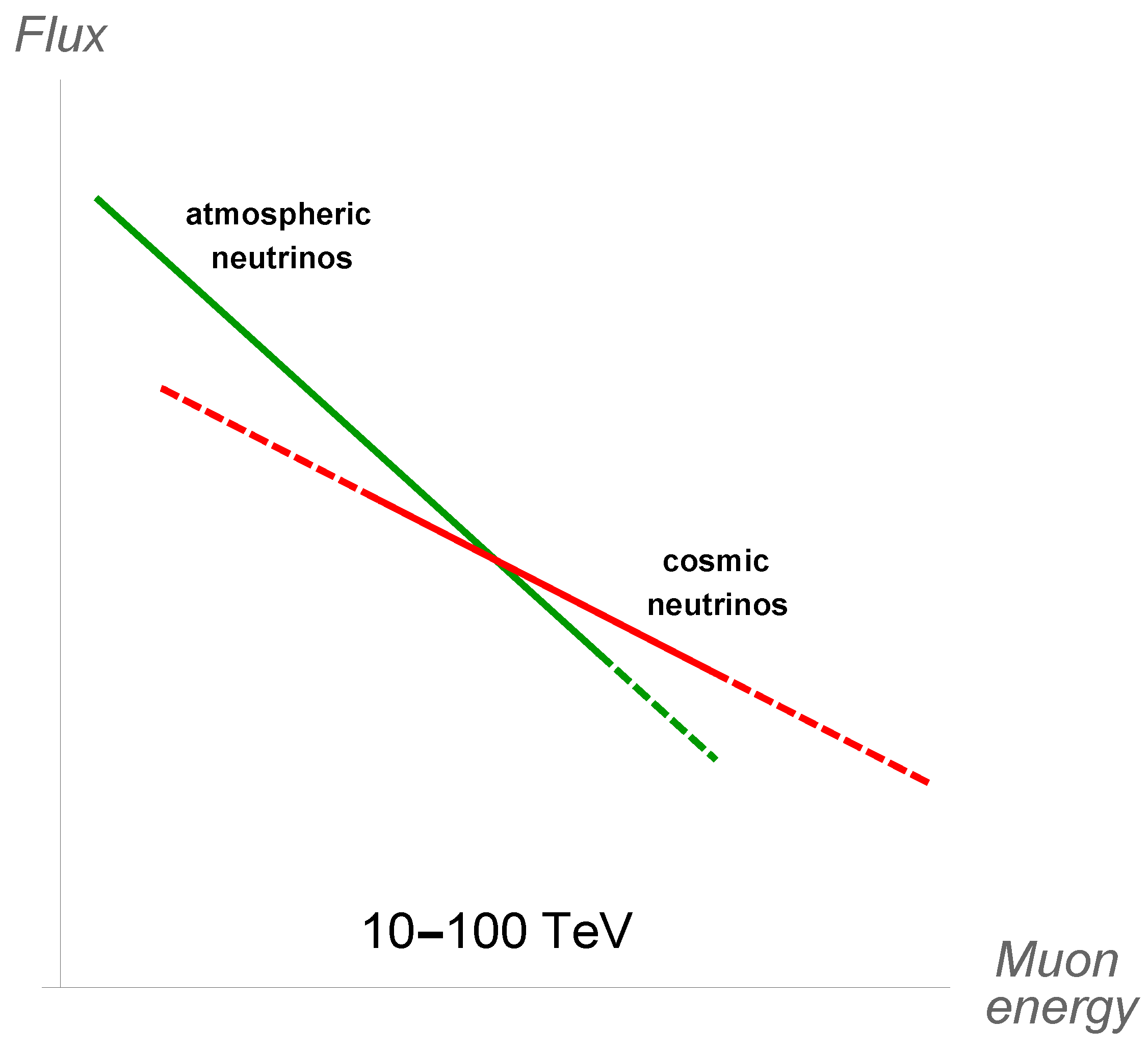
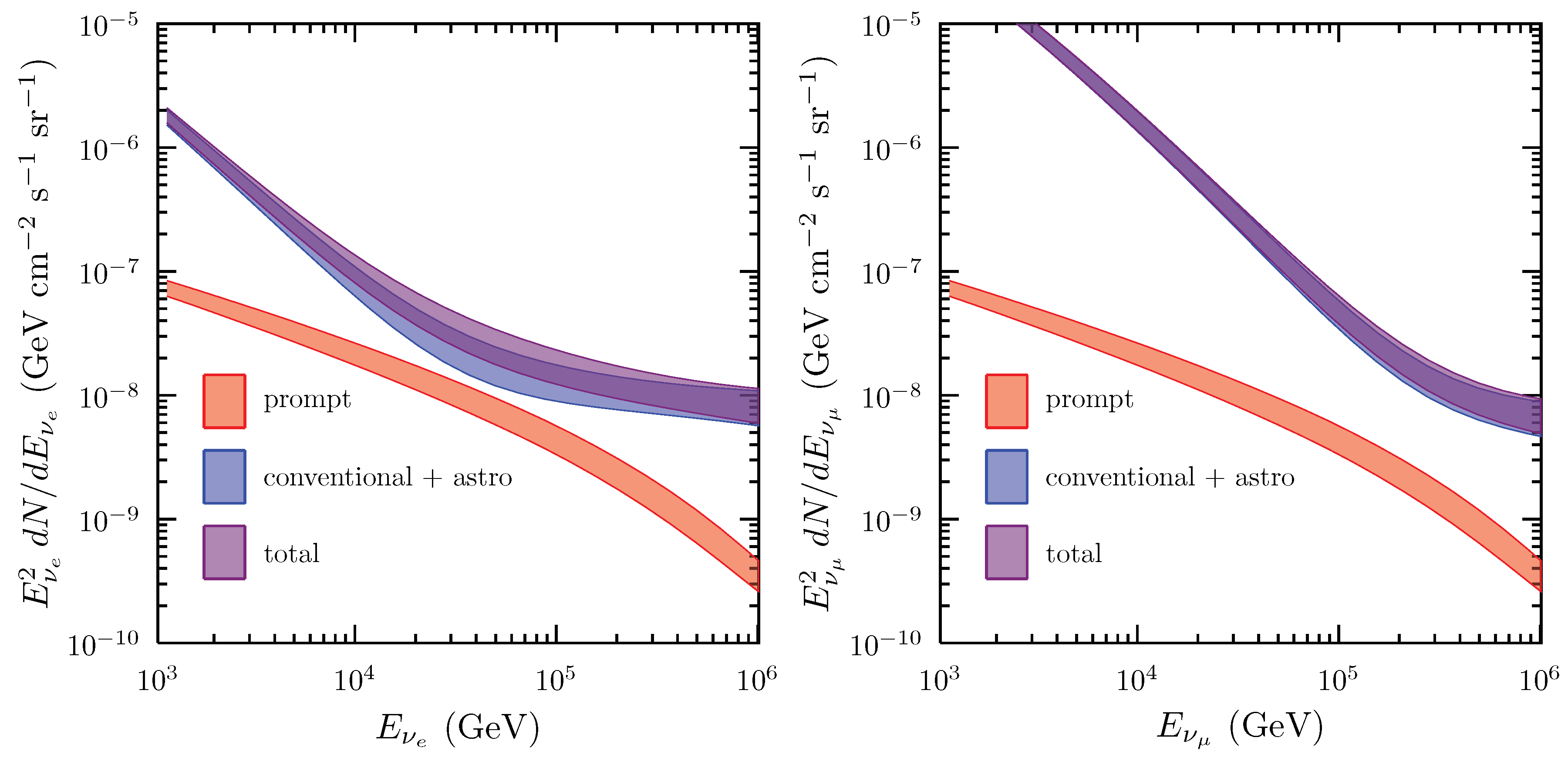
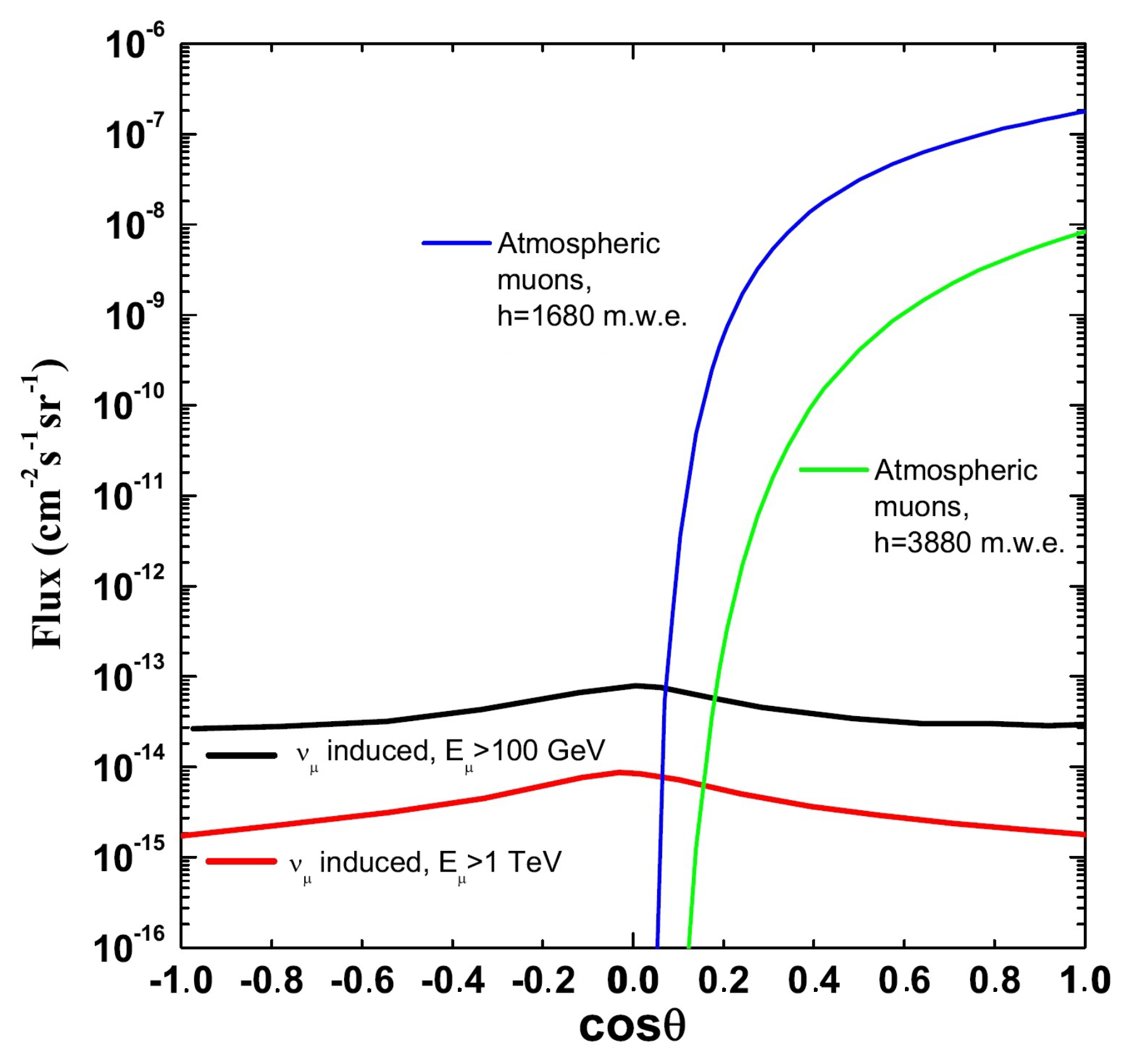
6. Background Processes
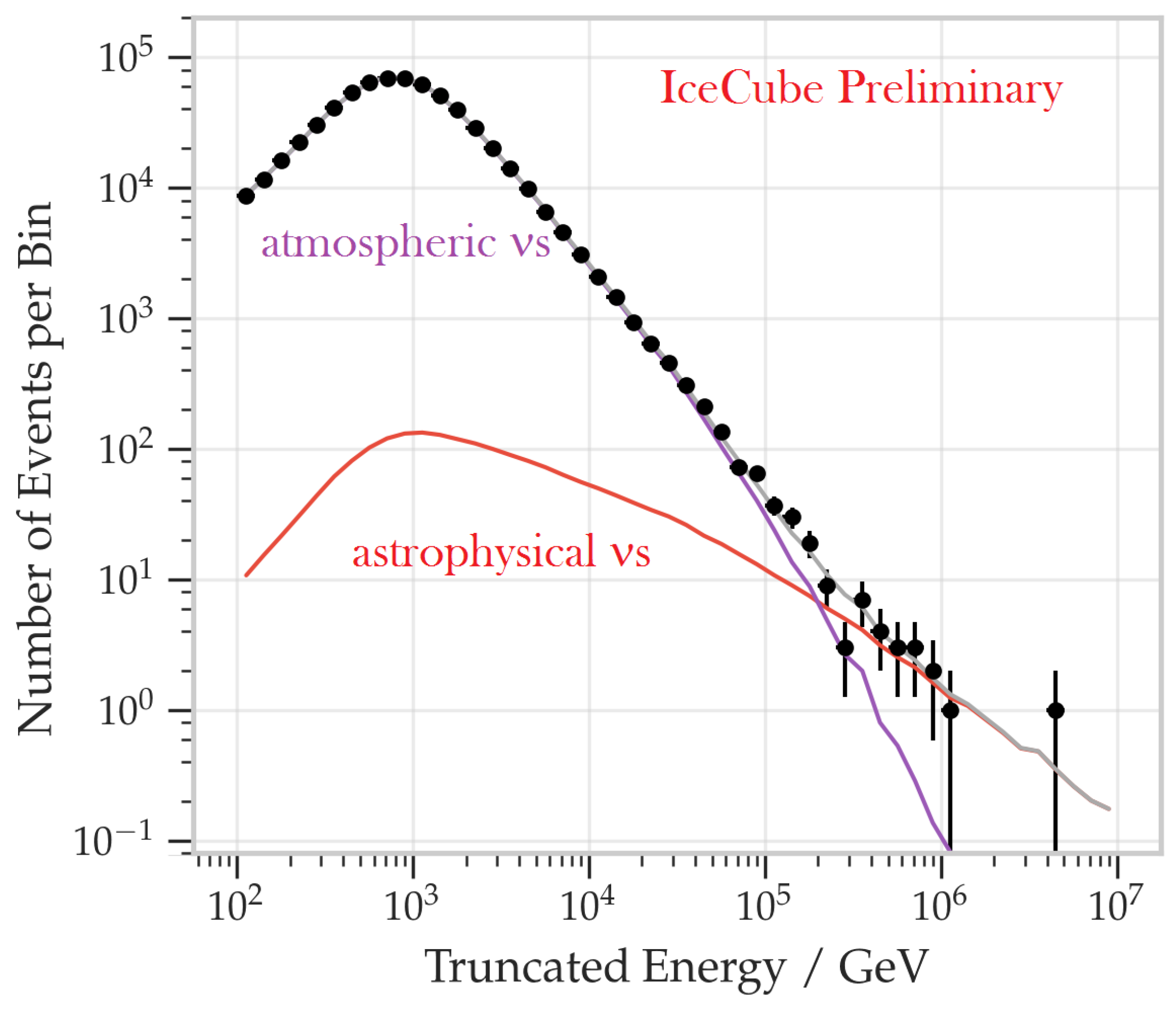
6.1. Atmospheric Neutrinos
6.2. Atmospheric Muons
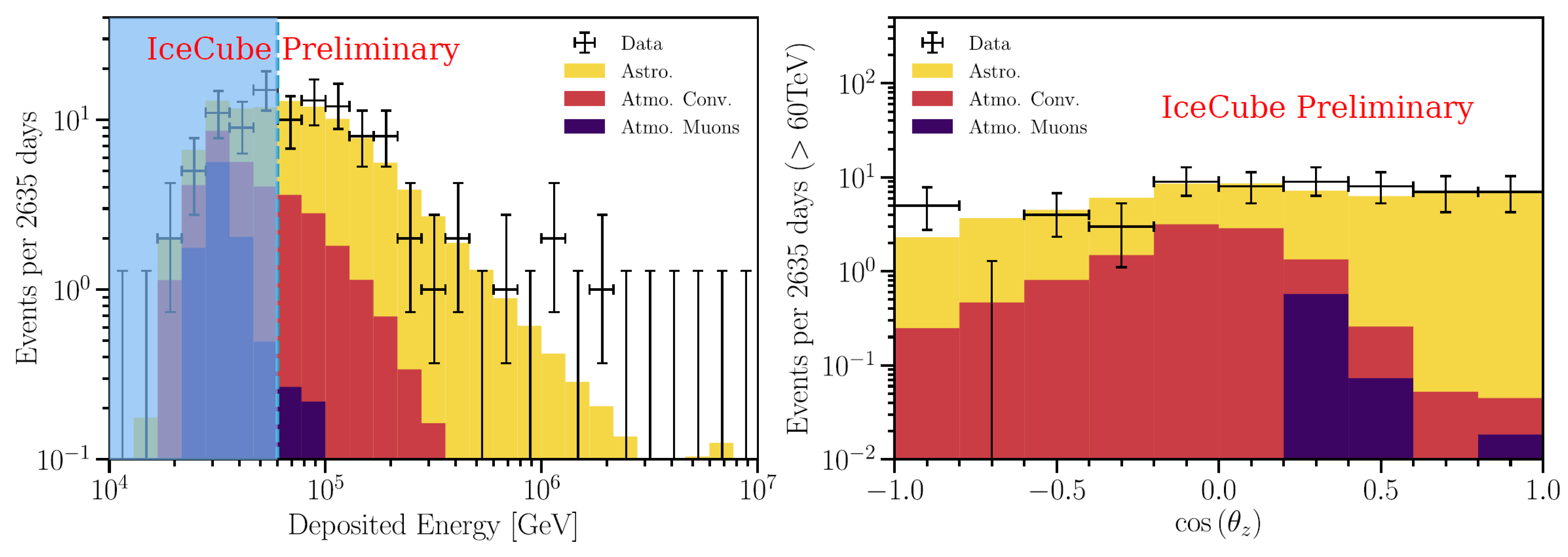
7. The Observational Status of High-Energy Neutrinos Astronomy
7.1. Contained Events
7.2. The Passing Muons
7.3. The Observation from TXS 0506 + 056
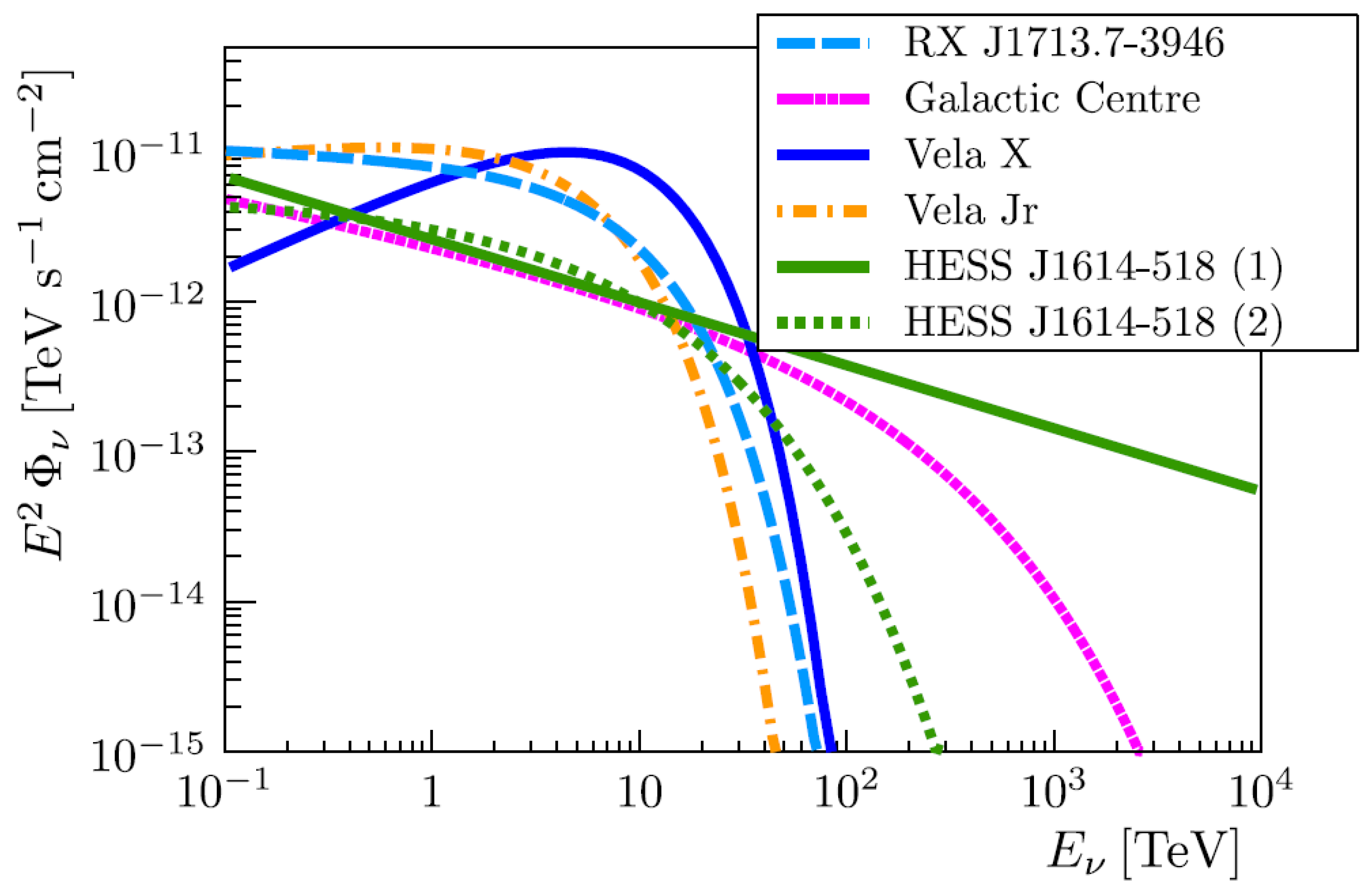
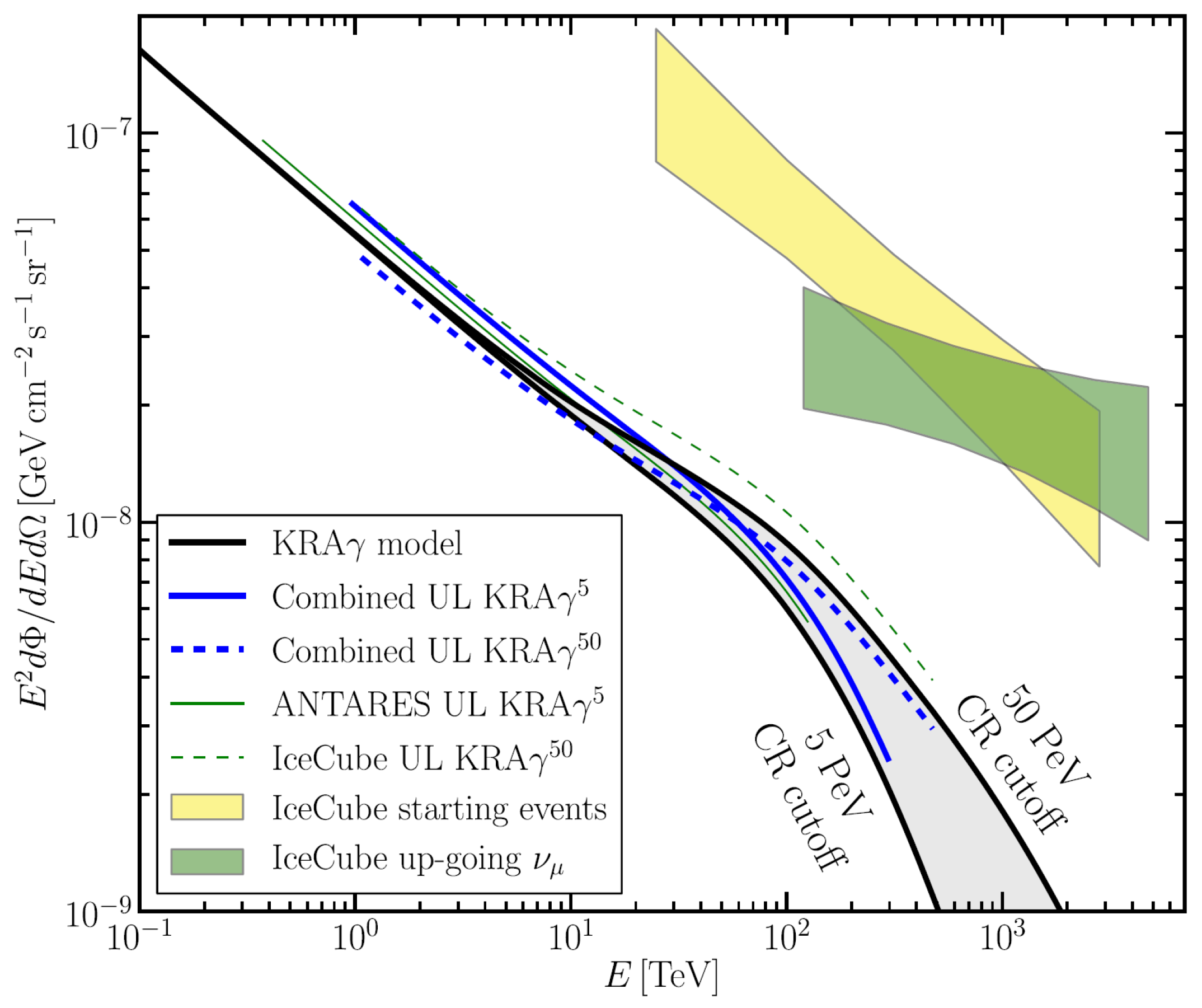
7.4. Studies of the Galactic Region
8. What Are the Main Sources of Cosmic Neutrinos?
8.1. Cosmic Rays and Cosmic Neutrinos
8.2. Extragalactic Sources
8.2.1. Active Galactic Nuclei
8.2.2. Blazars
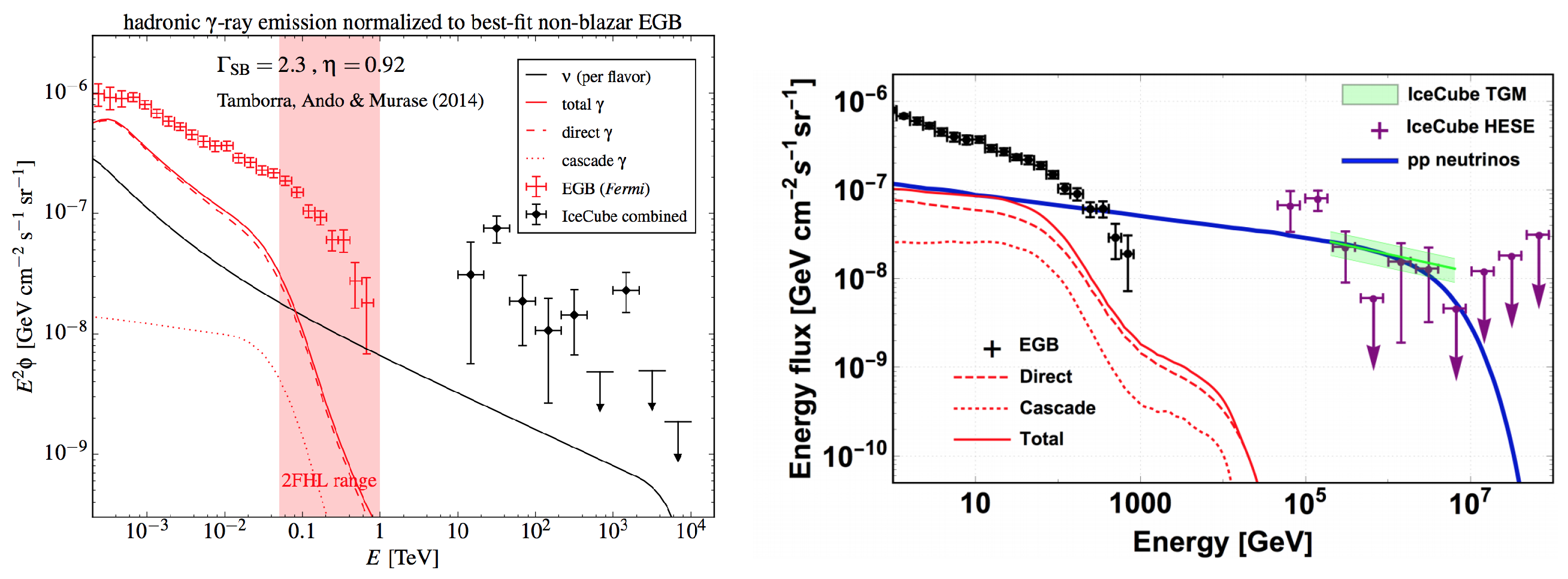
8.2.3. Starburst Galaxy
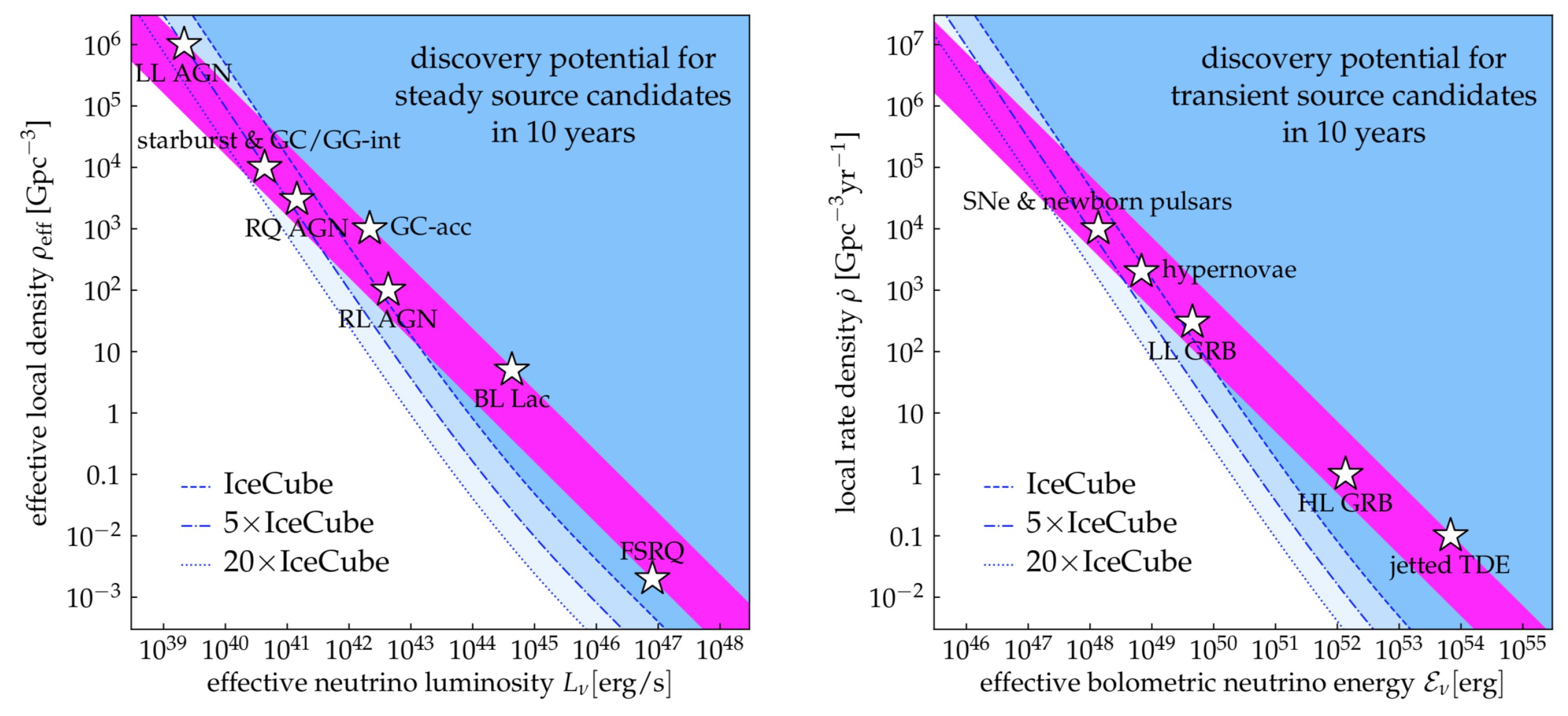
9. Discussion and Prospects
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. How to Estimate Neutrinos from Gamma-Rays
References
- Greisen, K. Cosmic ray showers. Ann. Rev. Nucl. Part Sci. 1960, 10, 63. [Google Scholar] [CrossRef]
- Markov, M.A.; Zheleznykh, I.M. On high energy neutrino physics in cosmic rays. Nucl. Phys. 1961, 27, 385. [Google Scholar] [CrossRef]
- Zheleznykh, I. Early years of high-energy neutrino physics in cosmic rays and neutrino astronomy (1957–1962). Int. J. Mod. Phys. A 2006, 21, 1. [Google Scholar] [CrossRef]
- Morrison, P. On Gamma-Ray Astronomy. Il Nuovo Cimento Vol VII 1958, 6, 858. [Google Scholar] [CrossRef]
- Reines, F.; Kropp, W.R.; Sobel, H.W.; Gurr, H.S.; Lathrop, J.; Crouch, M.F.; Sellschop, J.P.F.; Meyer, B.S. Muons produced by atmospheric neutrinos: Experiment. Phys. Rev. D 1971, 4, 80. [Google Scholar] [CrossRef]
- Chen, H.H.; Kropp, W.R.; Sobel, H.W.; Reines, F. Muons produced by atmospheric neutrinos: Analysis. Phys. Rev. D 1971, 4, 99. [Google Scholar] [CrossRef]
- Krishnaswamy, M.R.; Menon, M.G.K.; Narasimham, V.S.; Hinotani, K.; Ito, N.; Miyake, S.; Osborne, J.L.; Parsons, A.J.; Wolfendale, A.W. The Kolar Gold Fields Neutrino Experiment. 1. the Interactions of Cosmic Ray Neutrinos. Proc. R. Soc. Lond. A 1971, 323, 489. [Google Scholar]
- Aartsen, M.G.; et al.; [IceCube Collaboration] First observation of PeV-energy neutrinos with IceCube. Phys. Rev. Lett. 2013, 111, 021103. [Google Scholar] [CrossRef]
- Suzuki, A.; Koshiba, M. History of neutrino telescope/astronomy. Exper. Astron. 2009, 25, 209. [Google Scholar] [CrossRef]
- Spiering, C. Towards High-Energy Neutrino Astronomy. A Historical Review. Eur. Phys. J. H 2012, 37, 515. [Google Scholar] [CrossRef]
- Proceedings of the International Conference on History of the Neutrino: 1930–2018. Available online: Http://inspirehep.net/record/1760351 (accessed on 8 February 2020).
- Pontecorvo, B. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. Sov. Phys. JETP 1968, 26, 984. [Google Scholar]
- The Nobel Prize in Physics 2015. Available online: https://www.nobelprize.org/prizes/physics/2015/ (accessed on 30 December 2019).
- Spurio, M. Probes of Multimessenger Astrophysics - Charged Cosmic Rays, Neutrinos, γ-Rays and Gravitational Waves; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Capone, A.; Lipari, P.; Vissani, F. Neutrino Astronomy. In Multiple Messengers and Challenges in Astroparticle Physics; Aloisio, R., Coccia, E., Vissani, F., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Halzen, F.; Hooper, D. High-energy neutrino astronomy: The Cosmic ray connection. Rept. Prog. Phys. 2002, 65, 1025. [Google Scholar] [CrossRef]
- Lipari, P. Proton and Neutrino Extragalactic Astronomy. Phys. Rev. D 2008, 78, 083011. [Google Scholar] [CrossRef]
- Chiarusi, T.; Spurio, M. High-Energy Astrophysics with Neutrino Telescopes. Eur. Phys. J. C 2010, 65, 649. [Google Scholar] [CrossRef]
- Waxman, E. Neutrino astrophysics: A new tool for exploring the universe. Science 2007, 315, 63. [Google Scholar] [CrossRef][Green Version]
- DeYoung, T. Neutrino Astronomy with IceCube. Mod. Phys. Lett. 2009, A24, 1543. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Montaruli, T. In Search for Extraterrestrial High Energy Neutrinos. Ann. Rev. Nucl. Part Sci. 2010, 60, 129. [Google Scholar] [CrossRef]
- Katz, U.F.; Spiering, C. High-Energy Neutrino Astrophysics: Status and Perspectives. Prog. Part. Nucl. Phys. 2012, 67, 651. [Google Scholar] [CrossRef][Green Version]
- Gallo Rosso, A.; Mascaretti, C.; Palladino, A.; Vissani, F. Introduction to neutrino astronomy. Eur. Phys. J. Plus 2018, 133, 267. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Bulanov, S.V.; Ginzburg, V.L.; Dogiel, V.A.; Ptuskin, V.S. Astrophysics of Cosmic Rays; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Gaisser, T.K.; Engel, R.; Resconi, E. Cosmic Rays and Particle Physics; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Stecker, F.W. Cosmic Physics: The High Energy Frontier. J. Phys. G 2003, 29, R47. [Google Scholar] [CrossRef]
- Matthiae, G. The cosmic ray energy spectrum as measured using the Pierre Auger Observatory. New J. Phys. 2010, 12, 075009. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Volynsky, V.V. Generation Function Of High-energy Cosmic Neutrinos. I. PP-Neutrino. Available online: Http://adsabs.harvard.edu/full/1979ICRC...10..326B (accessed on 6 February 2020).
- Kelner, S.K.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma-rays, electrons and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Volkova, L.V. Energy Spectra and Angular Distributions of Atmospheric Neutrinos. Sov. J. Nucl. Phys. 1980, 31, 784. [Google Scholar]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley-VCH Pub.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Yen, E. New scaling variable and early scaling in single-particle inclusive distributions for hadron-hadron collisions. Phys. Rev. D 1974, 10, 836. [Google Scholar] [CrossRef]
- Allard, D. Extragalactic propagation of ultrahigh energy cosmic-rays. Astropart. Phys. 2012, 33, 39–40. [Google Scholar] [CrossRef]
- Celli, S.; Palladino, A.; Vissani, F. Neutrinos and γ-rays from the Galactic Center Region after H.E.S.S. multi-TeV measurements. Eur. Phys. J. C 2017, 77, 66. [Google Scholar] [CrossRef]
- Simple Quantum Integro Differential Solver (SQiIDS). Available online: http://www.lns.mit.edu/~caad/software.html (accessed on 30 December 2019).
- Aharonian, F.; O’Drury, L.; Volk, H.J. GeV/TeV gamma-ray emission from dense molecular clouds overtaken by supernova shells. Astron. Astroph. 1994, 285, 645. [Google Scholar]
- Drury, L.O.; Aharonian, F.A.; Volk, H.J. The Gamma-ray visibility of supernova remnants: A Test of cosmic ray origin. Astron. Astrophys. 1994, 287, 959. [Google Scholar]
- Naito, T.; Takahara, F. High-energy gamma-ray emission from supernova remnants. J. Phys. G 1994, 20, 477. [Google Scholar] [CrossRef]
- Alvarez-Muniz, J.; Halzen, F. Possible high-energy neutrinos from the cosmic accelerator RX J1713.7-3946. Astrophys. J. 2002, 576, L33. [Google Scholar] [CrossRef]
- Villante, F.L.; Vissani, F. How precisely neutrino emission from supernova remnants can be constrained by gamma ray observations? Phys. Rev. D 2008, 78, 103007. [Google Scholar] [CrossRef]
- Vissani, F.; Aharonian, F.; Sahakyan, N. On the Detectability of High-Energy Galactic Neutrino Sources. Astropart. Phys. 2011, 34, 778. [Google Scholar] [CrossRef][Green Version]
- Aiello, S.; et al.; [The KM3NeT collaboration] Sensitivity of the KM3NeT/ARCA neutrino telescope to point-like neutrino sources. Astropart. Phys. 2019, 111, 100–110. [Google Scholar] [CrossRef]
- Gribov, V.N.; Pontecorvo, B. Neutrino astronomy and lepton charge. Phys. Lett. B 1969, 28, 493. [Google Scholar] [CrossRef]
- Berezinsky, V.S.; Gazizov, A.Z. Cosmic neutrino and the possibility of Searching for W bosons with masses 30-100 GeV in underwater experiments. JETP Lett. 1977, 25, 254. [Google Scholar]
- Bilenky, S.M.; Pontecorvo, B. Lepton Mixing and Neutrino Oscillations. Phys. Rept. 1978, 41, 225. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Hernandez-Cabezudo, A.; Maltoni, M.; Schwetz, T. Global analysis of three-flavour neutrino oscillations: Synergies and tensions in the determination of θ23, δCP, and the mass ordering. J. High Energy Phys. 2019, 1901, 106. [Google Scholar] [CrossRef]
- Palladino, A.; Vissani, F. The natural parameterization of cosmic neutrino oscillations. Eur. Phys. J. C 2015, 75, 433. [Google Scholar] [CrossRef]
- Mascaretti, C.; Vissani, F. On the relevance of prompt neutrinos for the interpretation of the IceCube signals. J. Cosmol. Astropart. Phys. 2019, 1908, 004. [Google Scholar] [CrossRef]
- Palladino, A.; Mascaretti, C.; Vissani, F. The importance of observing astrophysical tau neutrinos. J. Cosmol. Astropart. Phys. 2018, 1808, 004. [Google Scholar] [CrossRef]
- Bugaev, E.; Montaruli, T.; Shlepin, Y.; Sokalski, I. Propagation of tau neutrinos and tau leptons through the Earth and their detection in underwater/ice neutrino telescopes. Astropart. Phys. 2004, 21, 491–509. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Murase, K.; Bartos, I. High-Energy Multimessenger Transient Astrophysics. Ann. Rev. Nucl. Part. Sci. 2019, 69, 477. [Google Scholar] [CrossRef]
- Halzen, F.; Kheirandish, A. Multimessenger Search for the Sources of Cosmic Rays Using Cosmic Neutrinos. Front. Astron. Space Sci. 2019, 6, 32. [Google Scholar] [CrossRef]
- Achterberg, A.; et al.; [IceCube Collaboration] First Year Performance of The IceCube Neutrino Telescope. Astropart. Phys. 2006, 26, 155–173. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] The Design and Performance of IceCube DeepCore. Astropart. Phys. 2012, 35, 615. [Google Scholar]
- Aartsen, M.G.; et al.; [IceCube Collaboration] The IceCube Neutrino Observatory: Instrumentation and Online Systems. J. Instrum. 2017, 12, P03012. [Google Scholar] [CrossRef]
- Ageron, M.; et al.; [ANTARES Collaboration] ANTARES: The first undersea neutrino telescope. Nucl. Instrum. Meth. 2011, A656, 11. [Google Scholar] [CrossRef]
- Albert, A.; et al.; [ANTARES Collaboration] Long-term monitoring of the ANTARES optical module efficiencies using 40K decays in sea water. Eur. Phys. J. C 2018, 78, 669. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G Nucl. Part. Phys. 2016, 43, 084001. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; et al.; [The KM3NeT collaboration] Intrinsic limits on resolutions in muon- and electron-neutrino charged-current events in the KM3NeT/ORCA detector. J. High Energy Phys. 2017, 5, 8. [Google Scholar]
- Aynutdinov, V.; Avrorin, V.A.; Aynutdinov, V.M.; Bannasch, R.; Belolaptikov, I.A.; Bogorodsky, D.Y.; Brudanin, V.B.; Budnev, N.M.; Danilchenko, I.A.; Domogatsky, G.V.; et al. The prototyping/early construction phase of the BAIKAL-GVD project. Nucl. Instrum. Methods Phys. Res. Sect. A 2014, 742, 82–88. [Google Scholar]
- Avrorin, A.D.; et al.; [Baikal-GVD Collaboration] Search for cascade events with Baikal-GVD. Available online: Https://arxiv.org/abs/1908.05430 (accessed on 6 February 2020).
- Learned, J.G.; Pakvasa, S. Detecting Nutau Oscillations as PeV Energies. Astropart. Phys. 1995, 3, 267. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Search for high-energy neutrinos from gravitational wave event GW151226 and candidate LVT151012 with ANTARES and IceCube. Phys. Rev. D 2016, 93, 022001. [Google Scholar] [CrossRef]
- Glashow, S.L. Resonant Scattering of Antineutrinos. Phys. Rev. 1960, 118, 316. [Google Scholar] [CrossRef]
- Palladino, A.; Pagliaroli, G.; Villante, F.L.; Vissani, F. Double pulses and cascades above 2 PeV in IceCube. Eur. Phys. J. C 2016, 76, 52. [Google Scholar] [CrossRef]
- Gandhi, R.; Quigg, C.; Reno, M.H.; Sarcevic, I. Ultrahigh-energy neutrino interactions. Astropart. Phys. 1996, 5, 81. [Google Scholar] [CrossRef]
- Abbasi, R.; et al.; [IceCube Collaboration] Measurement of the atmospheric neutrino energy spectrum from 100 GeV to 400 TeV with IceCube. Phys. Rev. D 2011, 83, 012001. [Google Scholar] [CrossRef]
- Adrian-Martinez, S.; et al.; [ANTARES Collaboration] Measurement of the atmospheric νμ energy spectrum from 100 GeV to 200 TeV with the ANTARES telescope. Eur. Phys. J. C 2013, 73, 2606. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Measurement of the Atmospheric νe Spectrum with IceCube. Phys. Rev. D 2015, 91, 122004. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Characterization of the Atmospheric Muon Flux in IceCube. Astropart. Phys. 2016, 78, 1. [Google Scholar] [CrossRef]
- Aiello, S.; et al.; [NEMO Collaboration] Measurement of the atmospheric muon depth intensity relation with the NEMO Phase-2 tower. Astropart. Phys. 2015, 66, 1. [Google Scholar] [CrossRef]
- Aguilar, J.A.; et al.; [ANTARES Collaboration] Zenith distribution and flux of atmospheric muons measured with the 5-line ANTARES detector. Astropart. Phys. 2010, 34, 179. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; et al.; [ANTARES Collaboration] Time calibration with atmospheric muon tracks in the ANTARES neutrino telescope. Astropart. Phys. 2016, 78, 43. [Google Scholar]
- Becherini, Y.; Margiotta, A.; Sioli, M.; Spurio, M. A Parameterisation of single and multiple muons in the deep water or ice. Astropart. Phys. 2006, 25, 1–13. [Google Scholar] [CrossRef]
- Schönert, S.; Gaisser, T.K.; Resconi, E.; Schulz, O. Vetoing atmospheric neutrinos in a high energy neutrino telescope. Phys. Rev. D 2009, 79, 043009. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Palomares-Ruiz, S.; Schneider, A.; Wille, L.; Yuan, T. Unified atmospheric neutrino passing fractions for large-scale neutrino telescopes. J. Cosmol. Astropart. Phys. 2018, 1807, 047. [Google Scholar]
- Gaisser, T.K.; Jero, K.; Karle, A.; van Santen, J. Generalized self-veto probability for atmospheric neutrinos. Phys. Rev. 2014, D90, 023009. [Google Scholar] [CrossRef]
- Halzen, F. IceCube: Opening a new window on the universe from the South Pole. Int. J. Mod. Phys. D 2018, 28, 1930007. [Google Scholar] [CrossRef]
- Ahlers, M.; Halzen, F. Opening a New Window onto the Universe with IceCube. Prog. Part Nucl. Phys. 2018, 102, 73. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Evidence for high-energy extraterrestrial neutrinos at the IceCube detector. Science 2013, 342, 1242856. [Google Scholar] [PubMed]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Flavor Ratio of Astrophysical Neutrinos above 35 TeV in IceCube. Phys. Rev. Lett. 2015, 114, 171102. [Google Scholar] [CrossRef] [PubMed]
- Schneider, A.; [The IceCube Collaboration]. Characterization of the Astrophysical Diffuse Neutrino Flux with IceCube High-Energy Starting Events. Available online: https://arxiv.org/abs/1907.11266 (accessed on 6 February 2020).
- Aartsen, M.G.; et al.; [IceCube Collaboration] Evidence for Astrophysical Muon Neutrinos from the Northern Sky with IceCube. Phys. Rev. Lett. 2015, 115, 081102. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Observation and Characterization of a Cosmic Muon Neutrino Flux from the Northern Hemisphere using six years of IceCube data. Astrophys. J. 2016, 833, 3. [Google Scholar] [CrossRef]
- Stettner, J.; [The IceCube Collaboration]. Measurement of the Diffuse Astrophysical Muon-Neutrino Spectrum with Ten Years of IceCube Data. Available online: https://arxiv.org/abs/1908.09551 (accessed on 6 February 2020).
- Paiano, S.; Falomo, R.; Treves, A.; Scarpa, R. The redshift of the BL Lac object TXS 0506+056. Astrop. J. 2018, 854, L32. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube and Fermi-LAT and MAGIC and AGILE and ASAS-SN and HAWC and H.E.S.S. and INTEGRAL and Kanata and Kiso and Kapteyn and Liverpool Telescope and Subaru and Swift NuSTAR and VERITAS and VLA/17B-403 Collaborations] Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, 6398. [Google Scholar]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147. [Google Scholar]
- Albert, A.; et al.; [ANTARES Collaboration] The Search for Neutrinos from TXS 0506+056 with the ANTARES Telescope. Astrophys. J. 2018, 863, L30. [Google Scholar] [CrossRef]
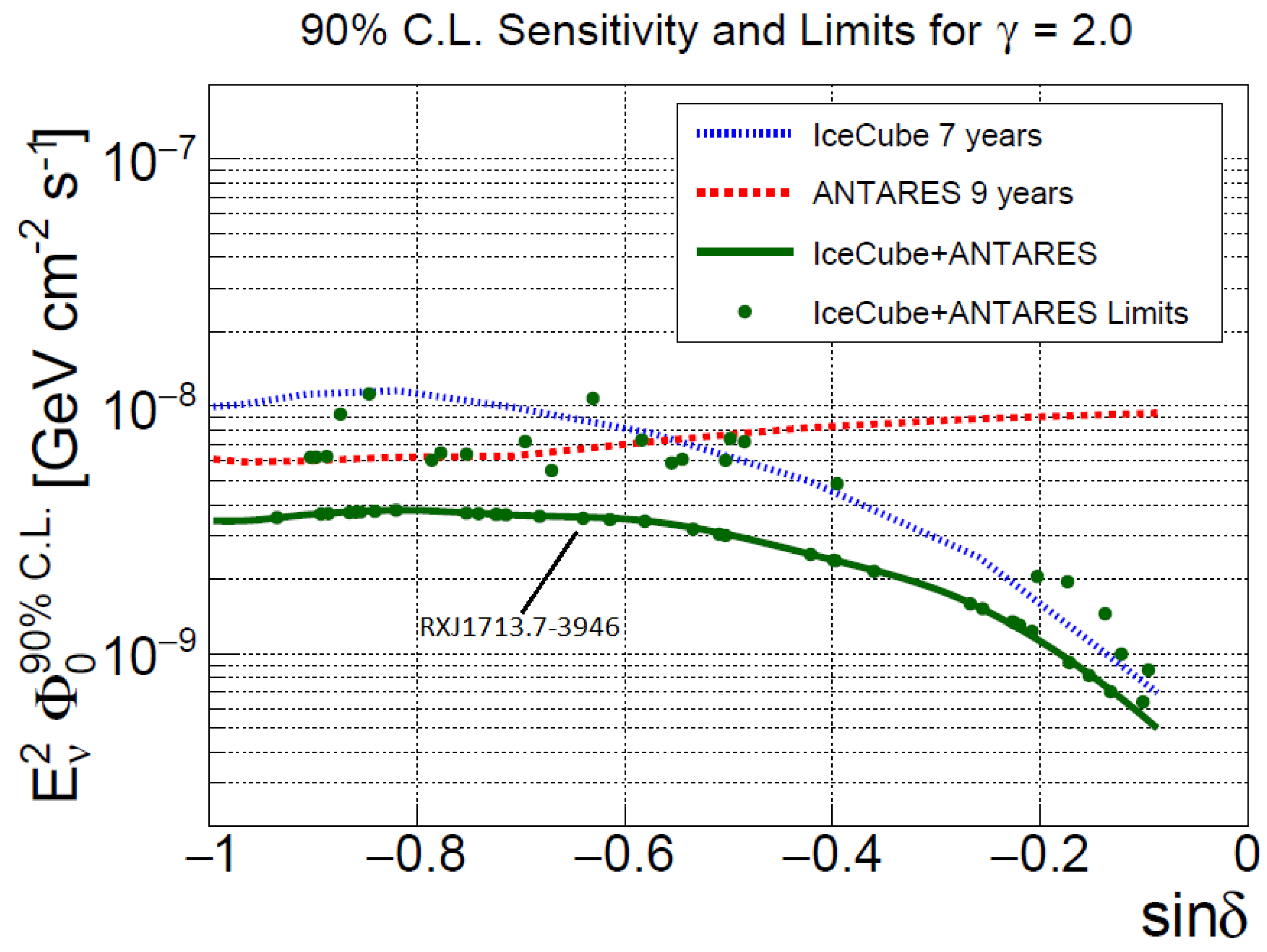
- Albert, A.; et al.; [ANTARES Collaboration] First all-flavor neutrino pointlike source search with the ANTARES neutrino telescope. Phys. Rev. D 2017, 96, 082001. [Google Scholar] [CrossRef]
- Albert, A.; et al.; [ANTARES and IceCube Collaborations] ANTARES and IceCube Combined Search for Neutrino Point-like and Extended Sources in the Southern Sky. arXiv 2020, arXiv:2001.04412. [Google Scholar]
- Albert, A.; et al.; [ANTARES and IceCube Collaborations] Joint Constraints on Galactic Diffuse Neutrino Emission from the ANTARES and IceCube Neutrino Telescopes. Astrophys. J. Lett. 2018, 86, L20. [Google Scholar] [CrossRef]
- Murase, K.; Waxman, E. Constraining High-Energy Cosmic Neutrino Sources: Implications and Prospects. Phys. Rev. D 2016, 94, 103006. [Google Scholar] [CrossRef]
- GCN: The Gamma-Ray Coordinates Network. Available online: https://gcn.gsfc.nasa.gov/ (accessed on 30 December 2019).
- Urry, C.M.; Padovani, P. Unified schemes for radio-loud active galactic nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Stecker, F.W.; Done, C.; Salamon, M.H.; Sommers, P. High-energy neutrinos from active galactic nuclei. Phys. Rev. Lett. 1991, 66, 2697. [Google Scholar] [CrossRef]
- Stecker, F.W. PeV neutrinos observed by IceCube from cores of active galactic nuclei. Phys. Rev. D 2013, 88, 047301. [Google Scholar] [CrossRef]
- Kalashev, O.; Semikoz, D.; Tkachev, I. Neutrinos in IceCube from active galactic nuclei. J. Exp. Theor. Phys. 2015, 120, 541. [Google Scholar] [CrossRef]
- Boettcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-Detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Ackermann, M.; et al.; [Fermi-LAT Collaboration] Resolving the Extragalactic γ-Ray Background above 50 GeV with the Fermi Large Area Telescope. Phys. Rev. Lett. 2016, 116, 151105. [Google Scholar] [CrossRef]
- Keivani, A.; Murase, K.; Petropoulou, M.; Fox, D.B.; Cenko, S.B.; Chaty, S.; Coleiro, A.; DeLaunay, J.J.; Dimitrakoudis, S.; Evans, P.A.; et al. A Multimessenger Picture of the Flaring Blazar TXS 0506+056: Implications for High-Energy Neutrino Emission and Cosmic Ray Acceleration. Astrophys. J. 2018, 864, 84. [Google Scholar] [CrossRef]
- Murase, K.; Oikonomou, F.; Petropoulou, M. Blazar Flares as an Origin of High-Energy Cosmic Neutrinos? Astrophys. J. 2018, 865, 124. [Google Scholar] [CrossRef]
- Palladino, A.; Rodrigues, X.; Gao, S.; Winter, W. Interpretation of the diffuse astrophysical neutrino flux in terms of the blazar sequenc. Astrophys. J. 2019, 871, 41. [Google Scholar] [CrossRef]
- Kadler, M.; Krauß, F.; Mannheim, K.; Ojha, R.; Müller, C.; Schulz, R.; Anton, G.; Baumgartner, W.; Beuchert, T.; Buson, S.; et al. Coincidence of a high-fluence blazar outburst with a PeV-energy neutrino event. Nat. Phys. 2016, 12, 807. [Google Scholar] [CrossRef]
- Murase, K.; Inoue, Y.; Dermer, C.D. Diffuse Neutrino Intensity from the Inner Jets of Active Galactic Nuclei: Impacts of External Photon Fields and the Blazar Sequence. Phys. Rev. D 2014, 90, 023007. [Google Scholar] [CrossRef]
- Padovani, P.; Resconi, E.; Giommi, P.; Arsioli, B.; Chang, Y.L. Extreme blazars as counterparts of IceCube astrophysical neutrinos. Mon. Not. R. Astron. Soc. 2016, 457, 3582. [Google Scholar] [CrossRef]
- Ackermann, M.; Ahlers, M.; Anchordoqui, L.; Bustamante, M.; Connolly, A.; Deaconu, C.; Grant, D.; Gorham, P.; Halzen, F.; Karle, A.; et al. Astrophysics Uniquely Enabled by Observations of High-Energy Cosmic Neutrinos. Bull. Am. Astron. Soc. 2019, 51, 185. [Google Scholar]
- Tamborra, I.; Ando, S.; Murase, K. Star-forming galaxies as the origin of diffuse high-energy backgrounds: Gamma-ray and neutrino connections, and implications for starburst history. J. Cosmol. Astropart. Phys. 2014, 1409, 043. [Google Scholar] [CrossRef]
- Chang, X.C.; Wang, X.Y. The diffuse gamma-ray flux associated with sub-PeV/PeV neutrinos from starburst galaxies. Astrophys. J. 2014, 793, 131. [Google Scholar] [CrossRef]
- Loeb, A.; Waxman, E. The Cumulative background of high energy neutrinos from starburst galaxies. J. Cosmol. Astropart. Phys. 2006, 0605, 003. [Google Scholar] [CrossRef]
- Bechtol, k.; Ahlers, M.; Di Mauro, M.; Ajello, M.; Vandenbroucke, J. Evidence against star-forming galaxies as the dominant source of IceCube neutrinos. Astrophys. J. 2017, 836, 47. [Google Scholar] [CrossRef]
- Palladino, A.; Fedynitch, A.; Rasmussen, R.W.; Taylor, A.M. IceCube Neutrinos from Hadronically Powered Gamma-Ray Galaxies. J. Cosmol. Astropart. Phys. 2019, 1909, 004. [Google Scholar] [CrossRef]
- Albert, A.; et al.; [ANTARES Collaborations] All-flavor Search for a Diffuse Flux of Cosmic Neutrinos with Nine Years of ANTARES Data. Astrophys. J. Lett. 2018, 853, L7. [Google Scholar] [CrossRef]
- Spurio, M. Constraints to a Galactic Component of the Ice Cube cosmic neutrino flux from ANTARES. Phys. Rev. D 2014, 90, 103004. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Bhupal Dev, P.S.; Soni, A. Two-component flux explanation for the high energy neutrino events at IceCube. Phys. Rev. D 2015, 92, 073001. [Google Scholar] [CrossRef]
- Palladino, A.; Vissani, F. Extragalactic plus Galactic model for IceCube neutrino events. Astrophys. J. 2016, 826, 185. [Google Scholar] [CrossRef]
- Vincent, A.C.; Palomares-Ruiz, S.; Mena, O. Analysis of the 4-year IceCube high-energy starting events. Phys. Rev. 2016, D94, 023009. [Google Scholar] [CrossRef]
- Aartsen, M.G.; et al.; [IceCube Collaboration] The contribution of Fermi-2LAC blazars to the diffuse TeV-PeV neutrino flux. Astrophys. J. 2017, 835, 45. [Google Scholar] [CrossRef]
- Palladino, A.; Vissani, F. Can BL Lacertae emission explain the neutrinos above 0.2 PeV? Astron. Astrophys. 2017, 604, A18. [Google Scholar] [CrossRef][Green Version]
- Abbasi, R.; et al.; [IceCube Collaboration] An absence of neutrinos associated with cosmic-ray acceleration in γ-ray bursts. Nature 2012, 484, 351. [Google Scholar]
- Aartsen, M.G.; et al.; [IceCube Collaboration] Search for Prompt Neutrino Emission from Gamma-Ray Bursts with IceCube. Astrophys. J. 2015, 805, L5. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Anton, G.; Ardid, M.; Aubert, J.-J.; Avgitas, T.; Baret, B.; Barrios-Martí, J.; Basa, S.; et al. Search for high-energy neutrinos from bright GRBs with ANTARES. Mon. Not. R. Astron. Soc. 2017, 469, 906. [Google Scholar] [CrossRef]
- Kappes, A.; Hinton, J.; Stegmann, C.; Aharonian, F.A. Potential Neutrino Signals from Galactic Gamma-Ray Sources. Astrophys. J. 2007, 656, 870. [Google Scholar] [CrossRef]
- Vissani, F. Neutrinos from galactic sources of cosmic rays with known γ-ray spectra. Astropart. Phys. 2006, 26, 310. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palladino, A.; Spurio, M.; Vissani, F. Neutrino Telescopes and High-Energy Cosmic Neutrinos. Universe 2020, 6, 30. https://doi.org/10.3390/universe6020030
Palladino A, Spurio M, Vissani F. Neutrino Telescopes and High-Energy Cosmic Neutrinos. Universe. 2020; 6(2):30. https://doi.org/10.3390/universe6020030
Chicago/Turabian StylePalladino, Andrea, Maurizio Spurio, and Francesco Vissani. 2020. "Neutrino Telescopes and High-Energy Cosmic Neutrinos" Universe 6, no. 2: 30. https://doi.org/10.3390/universe6020030
APA StylePalladino, A., Spurio, M., & Vissani, F. (2020). Neutrino Telescopes and High-Energy Cosmic Neutrinos. Universe, 6(2), 30. https://doi.org/10.3390/universe6020030




