Curvature Invariants for Charged and Rotating Black Holes
Abstract
1. Introduction
2. Preliminaries
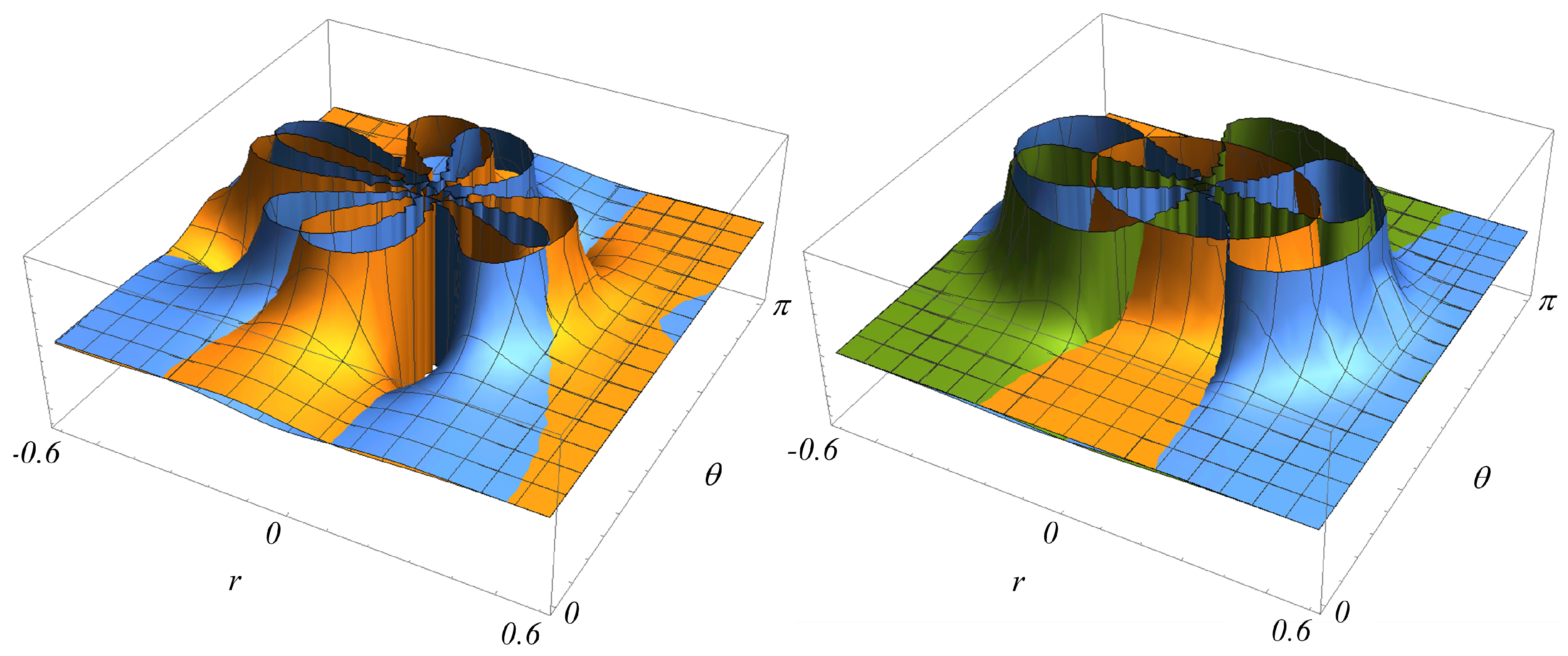
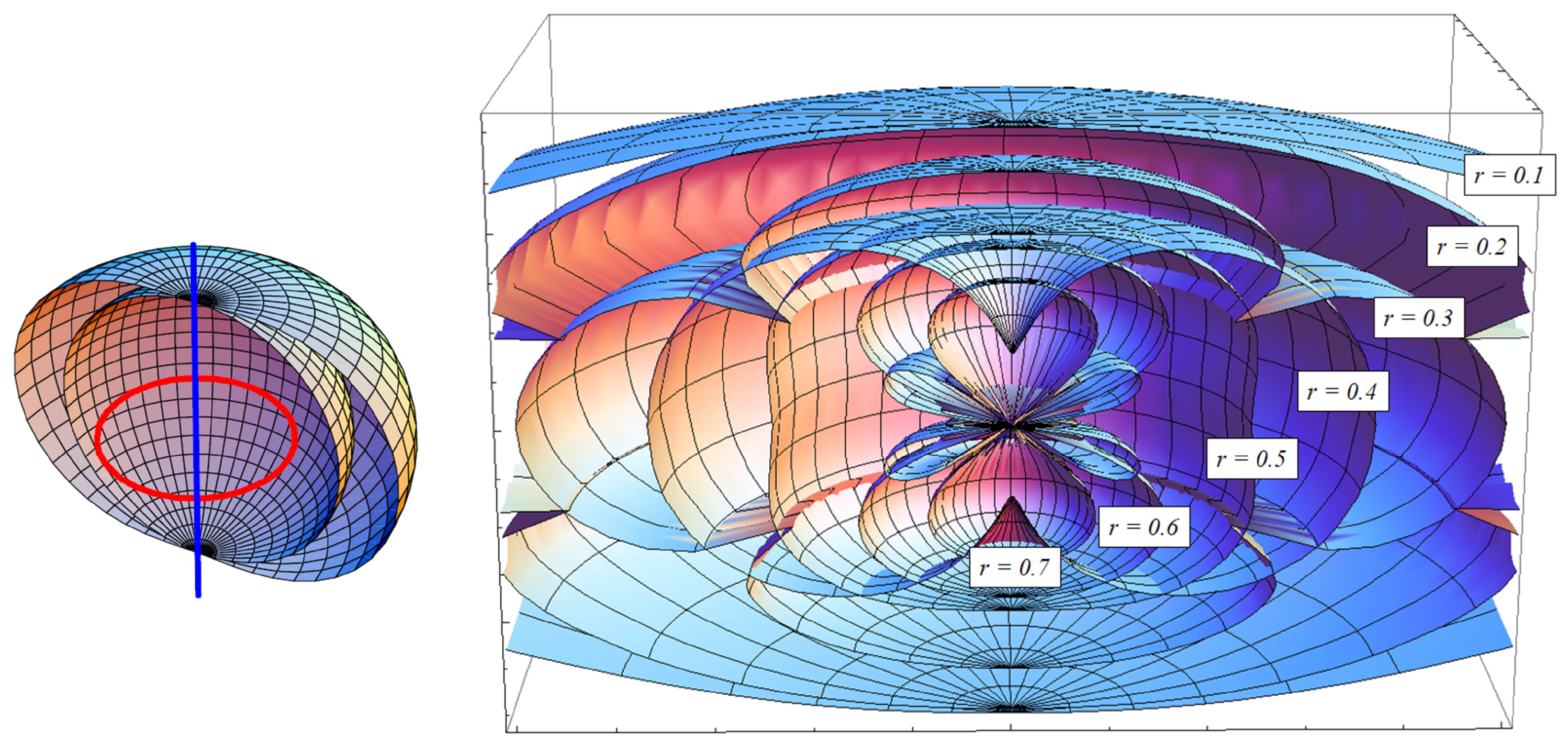
3. Results
- Weyl invariants:
- Ricci invariants:
- Mixed invariants:
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References and Note
- Pirani, F.A.E. Invariant formulation of gravitational radiation theory. Phys. Rev. 1957, 3, 1089. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Witten, L. Invariants of general relativity and the classification of spaces. Phys. Rev. 1959, 113, 357. [Google Scholar] [CrossRef]
- Petrov, A.Z. Einstein Spaces; Woodrow, J., Ed.; Kelleher, R.F., Translator; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Karlhede, A. A review of the geometrical equivalence of metrics in general relativity. Gen. Relativ. Gravit. 1980, 12, 693. [Google Scholar] [CrossRef]
- Coley, A.; Hervik, S.; Pelavas, N. Spacetimes characterized by their scalar curvature invariants. Class. Quantum Gravity 2009, 26, 025013. [Google Scholar] [CrossRef]
- Baker, J.; Campanelli, M. Making use of geometrical invariants in black hole collisions. Phys. Rev. D 2000, 62, 127501. [Google Scholar] [CrossRef]
- Cherubini, C.; Bini, D.; Capozziello, S.; Ruffini, R. Second order scalar invariants of the Riemann tensor: applications to black hole spacetimes. Int. J. Mod. Phys. D 2002, 11, 827. [Google Scholar] [CrossRef]
- Overduin, J.M. Spacetime, spin and Gravity Probe B. Class. Quantum Gravity 2015, 32, 224003. [Google Scholar] [CrossRef]
- Filipe Costa, L.; Wylleman, L.; Natário, J. Gravitomagnetism and the significance of the curvature scalar invariants. arXiv 2016, arXiv:1603.03143. [Google Scholar]
- Abdelqader, M.; Lake, K. Invariant characterization of the Kerr spacetime: Locating the horizon and measuring the mass and spin of rotating black holes using curvature invariants. Phys. Rev. D 2015, 91, 084017. [Google Scholar] [CrossRef]
- Page, D.N.; Shoom, A.A. Local invariants vanishing on stationary horizons: A diagnostic for locating black holes. Phys. Rev. Lett. 2015, 114, 141102. [Google Scholar] [CrossRef]
- McNutt, D.D.; Page, D.N. Scalar polynomial curvature invariant vanishing on the event horizon of any black hole metric conformal to a static spherical metric. Phys. Rev. D 2017, 95, 084044. [Google Scholar] [CrossRef]
- Coley, A.; McNutt, D. Identification of black hole horizons using scalar curvature invariants. Class. Quantum Gravity 2017, 35, 025013. [Google Scholar] [CrossRef]
- Aksteiner, S.; Bäckdahl, T. All local gauge invariants for perturbations of the Kerr spacetime. Phys. Rev. Lett. 2018, 121, 051104. [Google Scholar] [CrossRef] [PubMed]
- Mattingly, B.; Kar, A.; Julius, W.; Gorban, M.; Watson, C.; Ali, M.D.; Baas, A.; Elmore, C.; Shakerin, B.; Davis, E.; et al. Curvature invariants for Lorentzian traversable wormholes. Universe 2020, 6, 11. [Google Scholar] [CrossRef]
- Henry, R.C.; Overduin, J.M.; Wilcomb, K. A new way to see inside black holes. In Bridges Baltimore 2015: Mathematics, Music, Art, Architecture, Culture; Tessellations Publishing: Phoenix, AZ, USA, 2015; pp. 479–482. [Google Scholar]
- Carminati, J.; McLenaghan, R.G. Algebraic invariants of the Riemann tensor in a four-dimensional Riemannian space. J. Math. Phys. 1991, 32, 313. [Google Scholar] [CrossRef]
- Zakhary, E.; McIntosh, C.B.G. A complete set of Riemann invariants. Gen. Relativ. Gravit. 1997, 29, 539. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a rotating, charged mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Boyer, R.H.; Lindquist, R.W. Maximal analytic extension of the Kerr metric. J. Math. Phys. 1967, 8, 265. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman: New York, NY, USA, 1973; p. 877. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Addison Wesley: San Francisco, CA, USA, 2004. [Google Scholar]
- Adamo, T.; Newman, E.T. The Kerr-Newman metric: A review. arXiv 2016, arXiv:1603.03143. [Google Scholar]
- Henry, R.C. Kretschmann scalar for a Kerr-Newman black hole. Astrophys. J. 2000, 535, 350. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A brief introduction. In The Kerr Spacetime; Wiltshire, D.L., Visser, M., Scott, S.M., Eds.; Cambridge University Press: Cambridge, UK, 2009; p. 3. [Google Scholar]
- Mathematica, Version 12.0; Wolfram Research Inc.: Champaign, IL, USA, 2019. For the use of this package to calculate basic quantities in general relativity, such as the Riemann tensor and Ricci scalar, see Hartle, J.B. Gravity: An Introduction to Einstein’s General Relativity; Addison-Wesley: San Francisco, CA, USA, 2003; Appendix C. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Hamermesh, M., Translator; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Lake, K. Invariants of the Kerr vacuum. Gen. Relativ. Gravit. 2003, 35, 2271. [Google Scholar] [CrossRef][Green Version]
- Musgrave, P.; Lake, K. Scalar invariants of the radiating Kerr-Newman metric: A simple application of GRTensor. Comput. Phys. 1994, 8, 589. [Google Scholar] [CrossRef][Green Version]
- Martín-García, J.M.; Yllanes, D.; Portugal, R. The Invar tensor package: Differential invariants of Riemann. Comput. Phys. Commun. 2008, 179, 586. [Google Scholar] [CrossRef]
- MacCallum, M.A.H. Computer algebra in gravity research. Liv. Rev. Relativ. 2018, 1, 6. [Google Scholar] [CrossRef]
- Schmidt, H.-J. The square of the Weyl tensor can be negative. Gen. Relativ. Gravit. 2003, 35, 937. [Google Scholar] [CrossRef]
- Grøn, Ø.; Hervik, S. Einstein’s General Theory of Relativity; Springer: Berlin, Germany, 2010; p. 160. [Google Scholar]
- de Felice, F.; Bradley, M. Rotational anisotropy and repulsive effects in the Kerr metric. Class. Quantum Gravity 1988, 5, 1577. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Overduin, J.; Coplan, M.; Wilcomb, K.; Henry, R.C. Curvature Invariants for Charged and Rotating Black Holes. Universe 2020, 6, 22. https://doi.org/10.3390/universe6020022
Overduin J, Coplan M, Wilcomb K, Henry RC. Curvature Invariants for Charged and Rotating Black Holes. Universe. 2020; 6(2):22. https://doi.org/10.3390/universe6020022
Chicago/Turabian StyleOverduin, James, Max Coplan, Kielan Wilcomb, and Richard Conn Henry. 2020. "Curvature Invariants for Charged and Rotating Black Holes" Universe 6, no. 2: 22. https://doi.org/10.3390/universe6020022
APA StyleOverduin, J., Coplan, M., Wilcomb, K., & Henry, R. C. (2020). Curvature Invariants for Charged and Rotating Black Holes. Universe, 6(2), 22. https://doi.org/10.3390/universe6020022





