Black Hole Evaporation: A Perspective from Loop Quantum Gravity
Abstract
1. Introduction
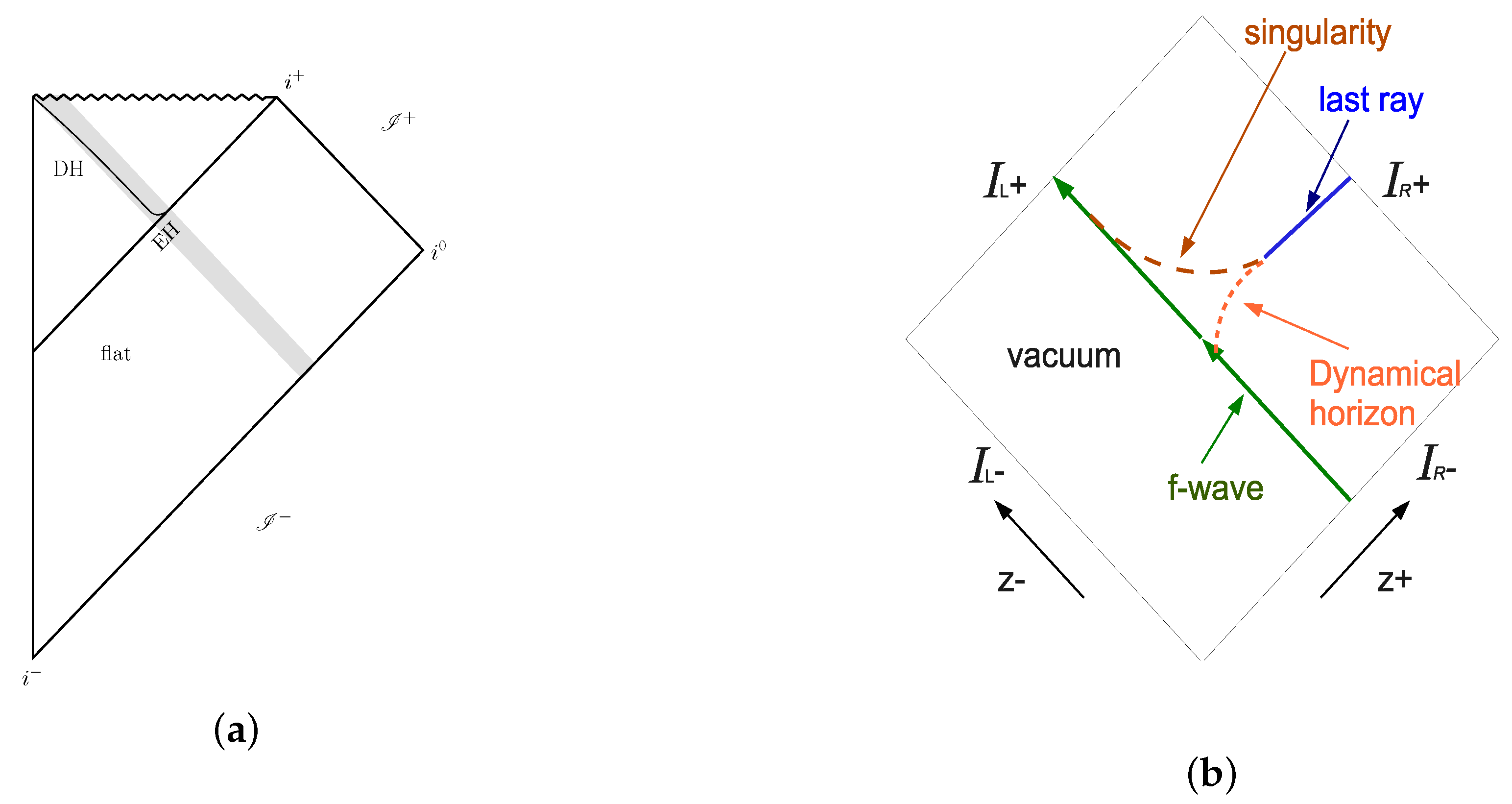
2. Black Hole Evaporation: Inclusion of Back-Reaction
2.1. Dynamical Horizons
2.2. No Violation of Semi-Classical Expectations
2.3. Singularity Resolution and the Quantum Region
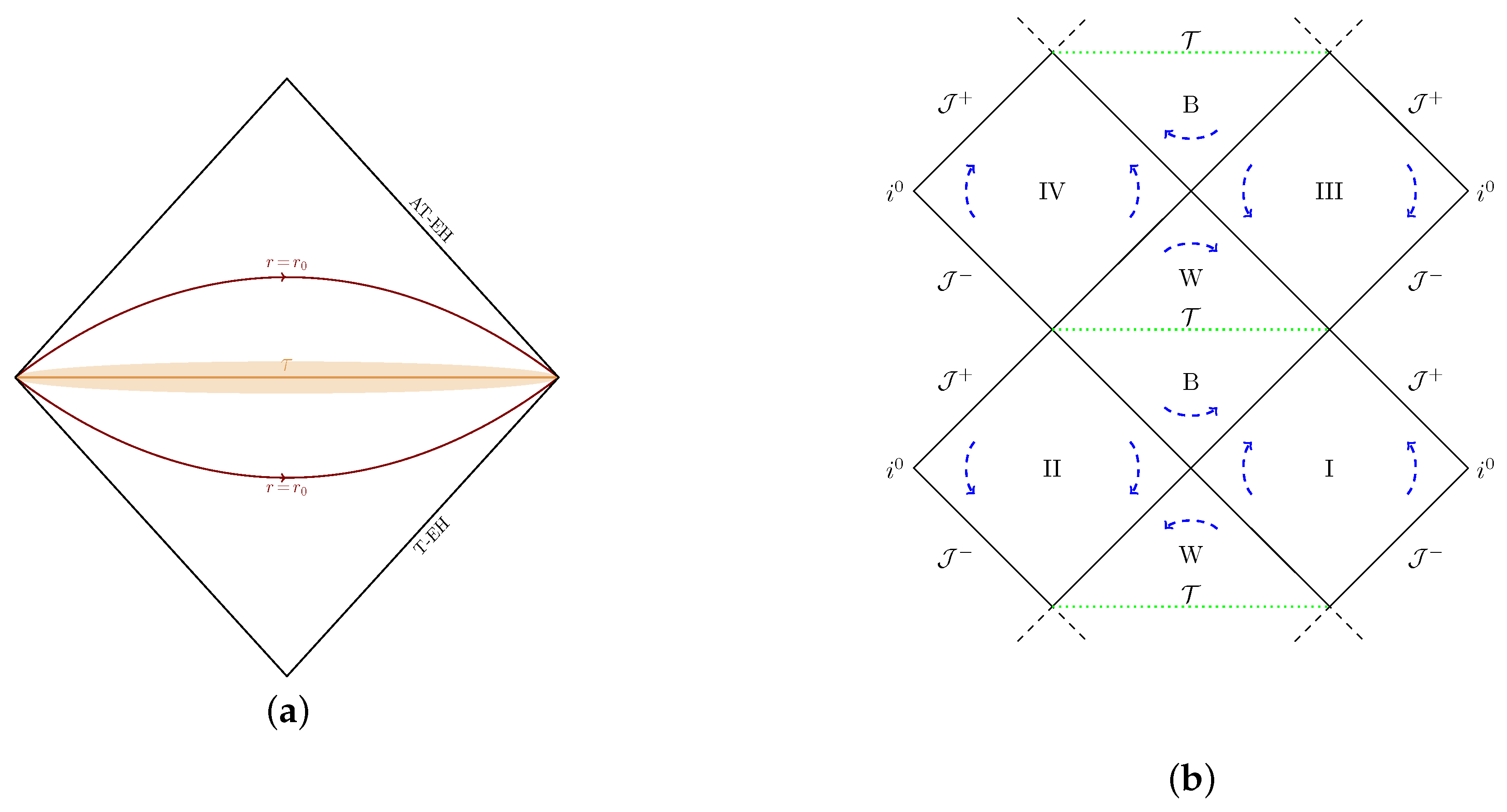
2.3.1. Kruskal Space–Time in Lqg
2.3.2. Beyond the Semi-Classical Region
- (i)
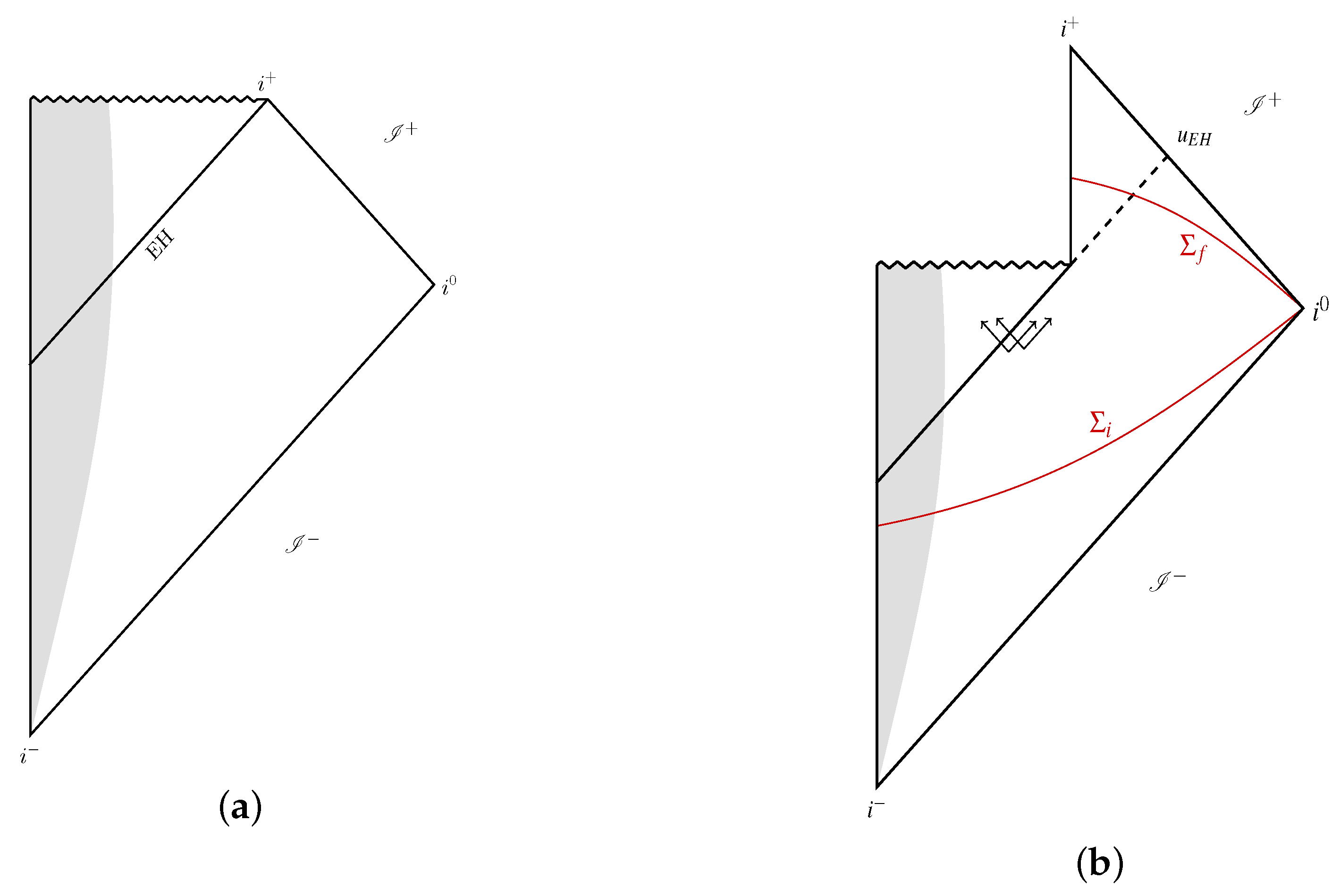
- A semi-classical phase which is expected to provide an excellent approximation to full quantum dynamics in the part of the trapped region that lies to past of the surface . This is the part of the trapped region to the past of the shaded (pink) portion in Figure 2b. During this phase dynamics would be well approximated by quantum field theory of the field on the Vaidya background. During this phase, space–time
- (ii)
- An adiabatic quantum gravity phase in which the space–time curvature is larger and enters the Planck regime but the evaporation process is adiabatic. This phase, depicted by the shaded pink region of Figure 2b, could be well-described by a dressed effective metric . The task is to calculate this and use it to describe the propagation of the field . This region is expected to constitute a neighborhood of the transition surface, , to the past of which we have a trapped region and to the future of which, an anti-trapped region, both defined using . The metric will incorporate two distinct sets of quantum effects. The first set is from LQG proper—such as negative effective energy density which is very large in the Planck domain and reduces the mass of the infalling scalar field enormously even at the left end, , of the shaded (pink) region, even though the influx of the Hawking partner modes is negligible there. As v increases, we slide to the right in this region, and then the negative energy density due to quantum geometry effects decreases but is compensated by the negative energy carried by more and more partner modes. The second set of quantum effects is precisely that from the dynamics of the scalar field. It includes both, the evolution of the incoming shell and the infalling partner modes. The actual calculation will incorporate both these types of effects in one go. But conceptually it is useful to separate the two contributions, since the first has been absent in most other approaches as they focus just on the partner modes and also ignore the quantum geometry effects. Finally, the Kruskal results depicted in Figure 4a suggest that the first set of effects will decay rapidly as we move away from Planck curvature into the semi-classical region. Therefore in the semi-classical region, will be well approximated by the semi-classical Vaidya metric used there.
- (iii)
- A full quantum gravity phase that is localized in the region depicted by a dark (red) blob at the right end of the shaded region in Figure 2b. This is the region in which not only is the curvature of Planck scale, but it is varying rapidly because of the evaporation process; dynamical nature of the back reaction is now significant. Therefore, description in terms of would now be inadequate. In this phase, one would have to use the LQG quantum state for the combined system, adapted to the spherical collapse under consideration. In terms of space–time geometry, the time-like piece of TDH continues to shrink in the semi-classical region and terminates in the full quantum region as depicted in Figure 2b.
2.4. Summary: The Global Picture
3. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Hawking, S.W.; Perry, M.J.; Strominger, A. Soft hair on black holes. Phys. Rev. Lett. 2016, 116, 231301. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G.; Wald, R.M. Information loss. Rep. Prog. Phys. 2017, 80, 092002. [Google Scholar] [CrossRef] [PubMed]
- Marolf, D. The black hole information problem: Past, present, and future. Rep. Prog. Phys. 2017, 80, 092001. [Google Scholar] [CrossRef] [PubMed]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or Firewalls? arXiv 2013, arXiv:1304.6483. [Google Scholar] [CrossRef]
- Giddings, S. Modulated Hawking radiation and a nonviolent channel for information release. arXiv 2014, arXiv:1401.5804. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Dynamical Horizons: Energy, Angular Momentum, Fluxes and Balance Laws. Phys. Rev. Lett. 2003, 89, 261101. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Dynamical Horizons and Their Properties. Phys. Rev. D 2003, 68, 104030. [Google Scholar] [CrossRef]
- Booth, I.; Brits, L.; Gonzalez, J.A.; Broeck, C.V.D. Marginally trapped tubes and dynamical horizons. Class. Quant. Grav. 2006, 23, 413–440. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and Dynamical Horizons and Their Properties. Livi. Rev. Rel. 2004, 7, 10. [Google Scholar] [CrossRef] [PubMed]
- Booth, I. Black hole boundaries. Can. J. Phys. 2005, 83, 1073–1099. [Google Scholar] [CrossRef]
- Ashtekar, A.; Ori, A. Unpublished calculations. 2014. [Google Scholar]
- Ashtekar, A. The Issue of Information Loss: The Current Status, ILQG Seminar of February 23rd, 2015. Available online: http://relativity.phys.lsu.edu/ilqgs/ashtekar022316.pdf (accessed on 9 December 2019).
- Page, D. Information in black hole radiation. Phys. Rev. Lett. 1993, 71, 3743–3746. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Agullo, I.; Singh, P. Loop quantum cosmology: A brief review. In Loop Quantum Gravity: The First 30 Years; Ashtekar, A., Pullin, J., Eds.; World Scientific: Singapore, 2017. [Google Scholar]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum transfiguration of Kruskal black holes. Phys. Rev. Lett. 2018, 121, 241301. [Google Scholar] [CrossRef]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum extension of the Kruskal space–time. Phys. Rev. D 2018, 98, 126003. [Google Scholar] [CrossRef]
- Ori, A. Personal communication.
- Ashtekar, A.; Bojowald, M. Black hole evaporation: A paradigm. Class. Quant. Grav. 2005, 22, 3349–3362. [Google Scholar] [CrossRef]
- Ori, A. Firewall or smooth horizon? Gen. Relativ. Gravit. 2016, 48, 9. [Google Scholar] [CrossRef][Green Version]
- Englehardt, N.; Horowitz, G.T. New insights into quantum gravity from gauge/gravity duality. Int. J. Mod. Phys. D 2016, 25, 1643002. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Frolov, V.P. Information loss problem and a ‘black hole’ model with a closed apparent horizon. JHEP 2014, 1405, 049. [Google Scholar] [CrossRef]
- Bardeen, J.M. Black hole evaporation without an event horizon. arXiv 2014, arXiv:1406.4098. [Google Scholar]
- Rovelli, C.; Vidotto, F. Planck stars. arXiv 2014, arXiv:1401.6562. [Google Scholar] [CrossRef]
- Bianchi, E.; Smerlak, M. Last gasp of a black hole: Unitary evaporation implies non-monotonic mass loss. Gen. Relativ. Gravit. 2014, 46, 1809. [Google Scholar] [CrossRef][Green Version]
- Bianchi, E.; Lorenzo, T.D.; Smerlak, M. Entanglement entropy production in gravitational collapse: Covariant regularization and solvable models. JHEP 2015, 6, 180. [Google Scholar] [CrossRef][Green Version]
- Haggard, H.M.; Rovelli, C. Black hole fireworks: Quantum-gravity effects outside the horizon spark black to white hole tunneling. Phys. Rev. D 2015, 92, 104020. [Google Scholar] [CrossRef]
- Bianchi, E.; Christodoulou, M.; D’Ambrosio, F.; Haggard, H.M.; Rovelli, C. White holes as remnants: A surprising scenario for the end of a black hole. arXiv 2018, arXiv:1802.04264. [Google Scholar] [CrossRef]
- Martin-Dessuad, P.; Rovelli, C. Evaporating black to white hole. arXiv 2019, arXiv:1905.0251v2. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pretorius, F.; Ramazanoglu, F. Surprises in the evaporation of two dimensional black holes. Phys. Rev. Lett. 2011, 106, 161303. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pretorius, F.; Ramazanoglu, F. Evaporation of two dimensional black holes. Phys. Rev. D 2011, 83, 044040. [Google Scholar] [CrossRef]
- Ori, A. Approximate solution to the CGHS field equations for two-dimensional evaporating black holes. Phys.Rev. D 2010, 82, 104009. [Google Scholar] [CrossRef]
- Levi, A.; Ori, A. Two-dimensional semiclassical static black holes: Finite-mass correction to the Hawking temperature and outflux. Phys. Rev. D 2013, 88, 024024. [Google Scholar] [CrossRef]
- Geroch, R.; Horowitz, G.T. Asymptotically Simple Does Not Imply Asymptotically Minkowskian. Phys. Rev. Lett. 1978, 40, 203–206, Errata: Phys. Rev. Lett. 1978, 40, 350; Phys. Rev. Lett. 1978, 40, 483. [Google Scholar] [CrossRef]
- Ashtekar, A.; Taveras, V.; Varadarajan, M. Information is Not Lost in the Evaporation of 2D Black Holes. Phys. Rev. Lett. 2008, 100, 211302. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W.; Stewart, J.M. Naked and thunderbolt singularities in black hole evaporation. Nucl. Phys. B 1993, 400, 393–415. [Google Scholar] [CrossRef][Green Version]
- Anderson, P.R.; Clark, R.D.; Fabbri, A.; Good, M.R.R. Late time approach to Hawking radiation: Terms beyond leading order. Phys. Rev. D 2019, 100, 061703. [Google Scholar] [CrossRef]
- Hayward, S. The disinformation problem for black holes (pop version). arXiv 2005, arXiv:gr-qc/0504038. [Google Scholar]
- Hayward, S. The disinformation problem for black holes (conference version). arXiv 2005, arXiv:gr-qc/0504037. [Google Scholar]
- Christodoulou, M.; Lorenzo, T.D. On the volume inside old black holes. Phys. Rev. D 2016, 94, 104002. [Google Scholar] [CrossRef]
- Christodoulou, M.; Rovelli, C. How big is a black hole? Phys. Rev. D 2015, 91, 064046. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum Geometry and the Schwarzschild singularity. Class. Quant. Grav. 2006, 23, 391–411. [Google Scholar] [CrossRef]
- Modesto, L. Loop quantum black hole. Class. Quant. Grav. 2006, 23, 5587–5602. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Vandersloot, K. Loop quantum dynamics of Schwarzschild interior. Phys. Rev. D 2007, 76, 1004030. [Google Scholar] [CrossRef]
- Chiou, D.W. Phenomenological loop quantum geometry of the Schwarzschild black hole. Phys. Rev. D 2008, 78, 064040. [Google Scholar] [CrossRef]
- Campiglia, M.; Gambini, R.; Pullin, J. Loop quantization of a spherically symmetric midi-superspaces: The interior problem. AIP Conf. Proc. 2008, 977, 52–63. [Google Scholar]
- Brannlund, J.; Kloster, S.; DeBenedictis, A. The Evolution of Λ Black Holes in the Mini-Superspace Approximation of Loop Quantum Gravity. Phys. Rev. D 2009, 79, 084023. [Google Scholar] [CrossRef]
- Corichi, A.; Singh, P. Loop quantum dynamics of Schwarzschild interior revisited. Class. Quant. Grav. 2016, 33, 055006. [Google Scholar] [CrossRef]
- Dadhich, N.; Joe, A.; Singh, P. Emergence of the product of constant curvature spaces in loop quantum cosmology. Class. Quant. Grav. 2015, 32, 185006. [Google Scholar] [CrossRef]
- Olmedo, J.; Saini, S.; Singh, P. From black holes to white holes: A quantum gravitational symmetric bounce. Class. Quant. Grav. 2017, 34, 225011. [Google Scholar] [CrossRef]
- Cortez, J.; Cuervo, W.; Morales-Técotl, H.A.; Ruelas, J.C. On effective loop quantum geometry of Schwarzschild interior. Phys. Rev. D 2017, 95, 064041. [Google Scholar] [CrossRef]
- Alesci, E.; Bahrami, S.; Pranzetti, D. Quantum gravity predictions for black hole interior geometry. Phys. Lett. B 2019, 797, 134908. [Google Scholar] [CrossRef]
- Bodendorfer, N.; Mele, F.M.; Mùnch, J. Effective quantum extended spacetime of polymer Schwarzschild black hole. Class. Quantum Grav. 2019, 36, 195015. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawlowski, T.; Singh, P.; Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum Nature of the Big Bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P.; Vandersloot, K. Loop quantum cosmology of k=1 FRW models. Phys. Rev. D 2007, 75, 024035. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. The pre-inflationary dynamics of loop quantum cosmology: Confronting quantum gravity with observations. Class. Quantum. Grav. 2013, 30, 085014. [Google Scholar] [CrossRef]
- Kaminski, W.; Kolanowski, M.; Lewandowski, J. Dressed metric predictions revisited. arXiv 2019, arXiv:1912.02556. [Google Scholar]
- Amadei, L.; Perez, A. Hawking’s information puzzle: A solution realized in loop quantum cosmology. arXiv 2019, arXiv:1911.00306. [Google Scholar]
- Levanony, D.; Ori, A. Interior design of a two-dimensional semiclassical black hole: Quantum transition across the singularity. Phys. Rev. D 2010, 81, 104036. [Google Scholar] [CrossRef]
| 1. | I would like to emphasize that there is neither a black hole nor a white hole, because both of them have singularities, while the quantum space–time has none. Therefore we will refer to these regions simply as trapped and anti-rapped. The past boundary of the trapped region is a dynamical horizon and its future boundary is the transition surface . The past boundary of the anti-trapped region is and the future boundary is another dynamical horizon. See Figure 2b. |
| 2. | |
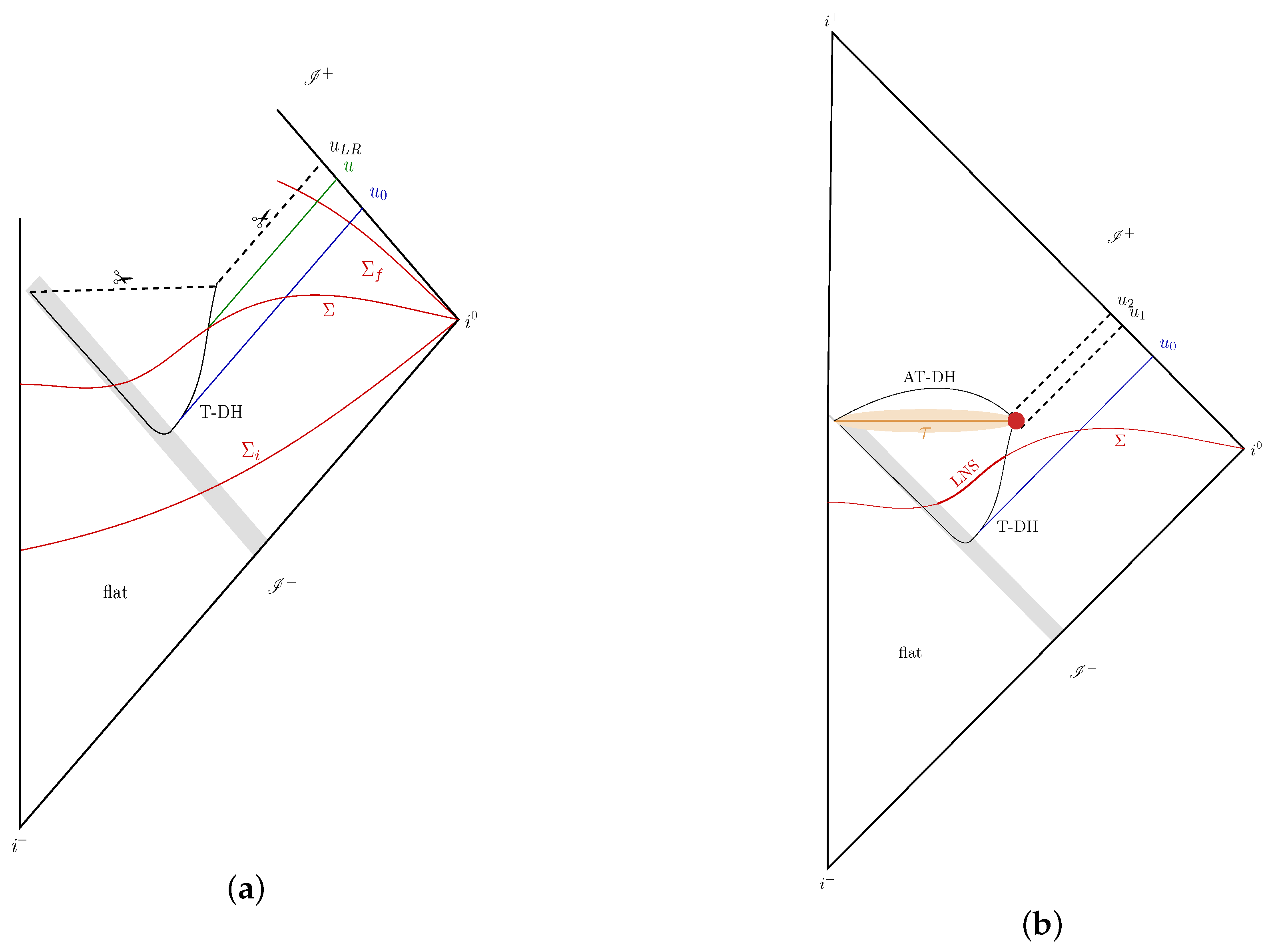
| 3. | In fact, in this specific case, space–time metric is completely regular across the last ray; there is no ‘thunderbolt’ suggested by Hawking and Stewart [39]. Therefore, in a more complete, quantum theory, one can expect space–time to extend further. If the singularity were to be resolved in full quantum gravity, then the quantum space–time would have a longer as suggested in Figure 3b. General conditions under which unitarity can be restored in this space–time are discussed in [38]. |
| 4. | Another geometrically natural family of 3-surfaces is defined by constancy of the trace of the extrinsic curvature is constant [43]. But they do not provide a foliation of the entire trapped region because if we start from the right end—the time-like piece of T-DH—the leaves ‘pile up’, all approaching the 2-sphere on the left end. But the main phenomenon of developing enormously long necks occurs also on these 3-surfaces. This foliation was motivated by a calculation of the growth of the volume of 3-surfaces inside the event horizon of a collapsing shell in classical GR [44]. |
| 5. | If the spatial topology is non-compact, the scale factor a does not have an invariant meaning. In this case, the spatial region with a fixed comoving volume has the minimum physical volume at the LC bounce. |
| 6. | Illustrative numbers: The expectation is that one can use the adiabatic approximation discussed below during the long process in which decreases from to, say, (when ), and the full quantum treatment would be necessary only at every end when decreases further. |
| 7. | |
| 8. | This and other open issues in this program (described below) are being analyzed in collaboration with Tommaso De Lorenzo. Several steps in narrowing down the a priori freedom in the program grew out of our discussions. |
| 9. | The second of these reasons—space–time geometry considerations—seem to apply also to the left end of , suggesting that one may have to use quantum geometry also in a blob near the left end. However, since the first and the third considerations do not apply there, in the main text I focused on the right end. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ashtekar, A. Black Hole Evaporation: A Perspective from Loop Quantum Gravity. Universe 2020, 6, 21. https://doi.org/10.3390/universe6020021
Ashtekar A. Black Hole Evaporation: A Perspective from Loop Quantum Gravity. Universe. 2020; 6(2):21. https://doi.org/10.3390/universe6020021
Chicago/Turabian StyleAshtekar, Abhay. 2020. "Black Hole Evaporation: A Perspective from Loop Quantum Gravity" Universe 6, no. 2: 21. https://doi.org/10.3390/universe6020021
APA StyleAshtekar, A. (2020). Black Hole Evaporation: A Perspective from Loop Quantum Gravity. Universe, 6(2), 21. https://doi.org/10.3390/universe6020021



