Abstract
Riemann curvature invariants are important in general relativity because they encode the geometrical properties of spacetime in a manifestly coordinate-invariant way. Fourteen such invariants are required to characterize four-dimensional spacetime in general, and Zakhary and McIntosh showed that as many as seventeen can be required in certain degenerate cases. We calculate explicit expressions for all seventeen of these Zakhary–McIntosh curvature invariants for the Kerr–Newman metric that describes spacetime around black holes of the most general kind (those with mass, charge, and spin), and confirm that they are related by eight algebraic conditions (dubbed syzygies by Zakhary and McIntosh), which serve as a useful check on our results. Plots of these invariants show richer structure than is suggested by traditional (coordinate-dependent) textbook depictions, and may repay further investigation.
PACS:
04.20.Jb; 04.70.Bw; 95.30.Sf
1. Introduction
Quantities whose value is manifestly independent of coordinates are particularly useful in general relativity [1]. Riemann or curvature invariants, formed from the Riemann tensor and derivatives of the metric, are one example. In principle, one can construct fourteen such quantities in four-dimensional spacetime, since the Riemann curvature tensor has twenty independent components subject to six conditions on the metric [2]. These quantities have proved useful in, for example, classifying metrics [3,4] and deciding whether or not they are equivalent [5,6]. They have been applied to speed up the estimation of gravitational-wave signatures from black-hole collisions [7], to distinguish between “gravito-electrically” versus “gravito-magnetically dominated” regions of spacetime [8,9,10], to measure the mass and spin and locate the horizons of black holes [11,12,13,14], and to study perturbations of the Kerr metric [15], Lorentzian wormholes [16], and others [17].
More than fourteen independent curvature invariants may be required to describe certain degenerate cases in the presence of matter [18]. Zakhary and McIntosh (ZM) reviewed this problem and offered the first complete list of seventeen independent real curvature invariants for all possible metric types (6 Petrov types and 15 Segre types, or 90 types in all) [19]. However, the ZM invariants are defined in terms of spinorial quantities whose physical meaning can be obscure. Here, we apply the ZM formalism to the Kerr–Newman metric to obtain for the first time explicit algebraic expressions for all seventeen invariants for black holes of the most general kind (those with mass, charge, and spin). Our results will be of most astrophysical interest in the case of nonzero spin and zero charge (because all real black holes rotate, but few possess significant charge due to the preferential infall of opposite-charged matter).
2. Preliminaries
Our starting point is the line element for Kerr–Newman spacetime [20] expressed in Boyer–Lindquist coordinates [21,22,23,24]
where
Here, m is the mass of the black hole as measured at infinity, is its Schwarzschild radius, and where J and q are angular momentum and electric charge.
Switching to natural units where and re-arranging terms, we re-express the metric in a form more amenable to symbolic computation [25]:
This metric reduces to the Kerr solution when , the Reissner–Nordström solution when , the Schwarzschild solution when , and Minkowski spacetime (in oblate spheroidal coordinates) when [23,26]. The angular coordinates are standard spherical polar angles ( is the angular displacement from the black hole’s spin axis) but the Boyer–Lindquist coordinate r is not conventional; it goes over to the usual radial distance far from the black hole, but goes to zero at the ring singularity and at the center of the geometry.
To calculate the curvature invariants for this metric, we used Mathematica [27] (For the convenience of readers, our code is included as Supplementary Material with this article). The Christoffel symbols and Riemann tensor are obtained as usual from and , where means and repeated indices are summed over (Einstein summation convention). Contracting gives the Ricci tensor and the Ricci (or curvature) scalar . Indices are lowered or raised with the metric, so that the Riemann tensor in fully covariant form, for example, is .
We need the Weyl (or conformal curvature) tensor, defined in dimensions by [2,23]
We also need the dual of the Weyl tensor, defined by [28]
where is the Levi–Civita tensor, defined by [23]
Here, g is the determinant of the metric so , and where is the Levi–Civita symbol (or tensor density). We note from a computer algebra point of view that there should be no overlap between the names of variables used for physical quantities and those reserved for tensor indices (here ).
3. Results
With the above quantities in hand, we are in a position to obtain for the first time explicit expressions for all seventeen ZM invariants for the most general possible black holes using the metric in Equation (3). Their definitions fall into three groups:
- Weyl invariants:
- Ricci invariants:
- Mixed invariants:
Note that and both vanish for the Kerr–Newman metric, which is of Petrov Type D and Segre type [(11)(1,1)] [19].
In principle, computer evaluation of Equations (7)–(9) is straightforward. In practice, the challenge is not so much computation as simplification: the resulting expressions may contain hundreds or even thousands of terms (for example, powers of , , , , etc.). These can be simplified in two ways. First, if working with the angular coordinate , one needs to specify its range (here, ) and define a “trig simplifier” that converts any symbolic expression into a function of a single desired trigonometric function (here ). Alternatively, one can re-express the metric in terms of a “rational polynomial” coordinate so that , and [26]. The second method proves significantly faster in most cases. We obtain the following results (each organized in the most compact available form, or by powers of q and when no simpler form is found):
These quantities represent a coordinate-invariant description of spacetime curvature around the most general possible black holes that is complete in the sense defined by Zakhary and McIntosh [19]. They do not seem to have been given before, apart from a derivation of the Kretschmann scalar [25] and a study of the Weyl invariants and [29]. Related expressions for an earlier set of invariants due to Carminati and McLenaghan [18] have been explored using GRTensor [30]. Other aspects of invariants have been discussed using specially designed software [31], and a general review of the application of symbolic computing to problems in general relativity was given by MacCallum [32].
The thirteen nonzero invariants in Equation (10) are not all algebraically independent, as the choice of a specific metric uses up additional degrees of freedom. In fact, the Kerr–Newman metric has enough symmetries that only five of the ZM invariants (apart from the Ricci scalar ) are actually independent [19]. A minimally independent set of ZM invariants for black holes with mass, charge, and spin can be formed by the Weyl invariants , the Ricci invariant , and the mixed invariants . (This number drops to two in the case of uncharged—i.e., astrophysical—black holes described by the Kerr metric, for which alone are sufficient.) All five quantities are plotted in Figure 1.
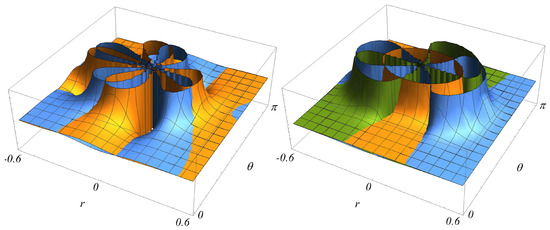
Figure 1.
(a) The Weyl invariants (yellow) and (blue); and (b) the Ricci invariant (yellow) and mixed invariants (blue) and (green), all plotted as a function the Boyer–Lindquist coordinates r and for a black hole of mass , angular momentum per unit mass and charge .
The ZM invariants for Kerr–Newman black holes are therefore related by independent algebraic equations, which we obtain explicitly below. A subset of ZM invariants can also be related to the Kretschmann scalar [25]. In four dimensions, this relationship reads [8]
This equation provides one check of our results.
More generally, proportionality relations between the curvature invariants have been dubbed “syzygies” by Zakhary and McIntosh, who defined the following needed quantities [19]:
(Note that here is not related to the Kretschmann invariant K.)
Using Equation (10), we are able to confirm the existence of syzygies similar to those proposed by Zakhary and McIntosh for metrics of Petrov Type D. However, our proportionality constants differ somewhat from theirs. Specifically, we find for the Kerr–Newman metric that
where an overbar denotes the complex conjugate, and where
We stress that the syzygies in Equation (13) provide a rigorous cross-check of the expressions we have obtained in Equation (10). That these equations provide exactly eight constraints can be seen by expanding and equating real and imaginary parts of Equation (13), whereupon
These equations may be readily used to check our main results in Equation (10).
4. Discussion
The plots in Figure 1 show that the geometry of spacetime inside charged and rotating black holes is far from simple. Curvature is particularly extreme near the ring singularity at , and is negative over significant regions of the phase space, as discussed by several workers [29,33]. This is interesting since the Weyl tensor encodes the degrees of freedom corresponding to a free gravitational field [34]. The fluctuations themselves have been attributed to conflicting contributions from the gravito-electric and gravito-magnetic components of this field, the latter generated by the black hole’s rotation [8,10,35].
Plots in the full phase space are rich in information, but can be hard to reconcile intuitively with more conventional representations of the interior structure of rotating black holes such as that shown in Figure 2a [22]. Here, the axis of rotation is marked with a vertical line. The ring is the singularity. The inner shell (located at ) is the horizon, while the outer shell is the static limit. This diagram, by contrast with the plots in Figure 1, suggests that spacetime curvature inside the black hole is constant and positive. Both inferences are incorrect.
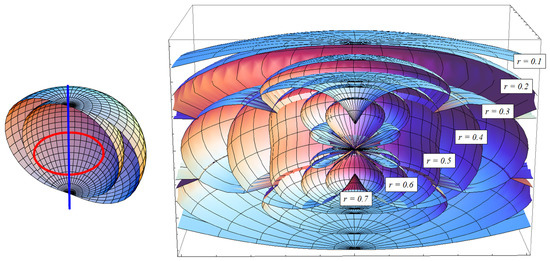
Figure 2.
(a) A typical textbook representation of the interior structure of a rotating black hole. We argue that such coordinate-dependent depictions can be misleading, and should be supplemented by illustrations involving invariants. (b) The magnitude of the Weyl invariant in ordinary spherical coordinates (), plotted for several values of the Boyer–Lindquist radial coordinate r.
In Figure 2b, we “unpack” one of the ZM invariants, , and plot the logarithm of its magnitude in standard spherical polar coordinates for several values of r. This figure is meant to be illustrative, as a contrast with Figure 2a, and does not cover the entire phase space (for example, only positive values of r are shown). Nevertheless, we feel it has considerable pedagogical value. The contours plotted here are surfaces of constant r. Thus, one can see at a glance, for example, that becomes extremely large near the equatorial plane close to the ring singularity (i.e., for small or ). As one gets farther from the singularity () the magnitude of is no longer so large near the equatorial plane, but its shape as a function of polar angle becomes increasingly complex. This behavior is in stark contrast to that suggested by the traditional textbook representation in Figure 2a. Both kinds of figures have their uses, but the one on the right conveys a truth that the one on the left cannot. The traditional view misleads because it is not based on invariant quantities; it is simply a figure drawn in a particular coordinate system (Boyer–Lindquist). It is wrong in precisely the same way that the size of Greenland is wrong on a Mercator projection map of the world. Just as it is impossible to draw a map of the Earth realistically on a flat sheet of paper, it is impossible to portray the interior of a black hole realistically—unless what is shown is invariant.
Black holes are fascinating objects, not just for their inherent geometrical properties but because they reverse the usual course of scientific discovery. Usually, we observe first, and use mathematics later on to organize and explain what we have observed. However, the interior of the black hole is, by definition, the one place we will never be able to observe. Here, we can explore only through mathematics. Visualization, and hopefully deeper physical understanding, will follow later. The expressions obtained here for the ZM invariants are perhaps a first step in this process.
Supplementary Materials
The following are available online at https://www.mdpi.com/2218-1997/6/2/22/s1.
Author Contributions
All the authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
These results are based in part upon work supported by the Fisher College of Science and Mathematics at Towson University and the Maryland Space Grant Consortium.
Conflicts of Interest
The authors declare no conflict of interest.
References and Note
- Pirani, F.A.E. Invariant formulation of gravitational radiation theory. Phys. Rev. 1957, 3, 1089. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Witten, L. Invariants of general relativity and the classification of spaces. Phys. Rev. 1959, 113, 357. [Google Scholar] [CrossRef]
- Petrov, A.Z. Einstein Spaces; Woodrow, J., Ed.; Kelleher, R.F., Translator; Pergamon Press: Oxford, UK, 1969. [Google Scholar]
- Karlhede, A. A review of the geometrical equivalence of metrics in general relativity. Gen. Relativ. Gravit. 1980, 12, 693. [Google Scholar] [CrossRef]
- Coley, A.; Hervik, S.; Pelavas, N. Spacetimes characterized by their scalar curvature invariants. Class. Quantum Gravity 2009, 26, 025013. [Google Scholar] [CrossRef]
- Baker, J.; Campanelli, M. Making use of geometrical invariants in black hole collisions. Phys. Rev. D 2000, 62, 127501. [Google Scholar] [CrossRef]
- Cherubini, C.; Bini, D.; Capozziello, S.; Ruffini, R. Second order scalar invariants of the Riemann tensor: applications to black hole spacetimes. Int. J. Mod. Phys. D 2002, 11, 827. [Google Scholar] [CrossRef]
- Overduin, J.M. Spacetime, spin and Gravity Probe B. Class. Quantum Gravity 2015, 32, 224003. [Google Scholar] [CrossRef]
- Filipe Costa, L.; Wylleman, L.; Natário, J. Gravitomagnetism and the significance of the curvature scalar invariants. arXiv 2016, arXiv:1603.03143. [Google Scholar]
- Abdelqader, M.; Lake, K. Invariant characterization of the Kerr spacetime: Locating the horizon and measuring the mass and spin of rotating black holes using curvature invariants. Phys. Rev. D 2015, 91, 084017. [Google Scholar] [CrossRef]
- Page, D.N.; Shoom, A.A. Local invariants vanishing on stationary horizons: A diagnostic for locating black holes. Phys. Rev. Lett. 2015, 114, 141102. [Google Scholar] [CrossRef]
- McNutt, D.D.; Page, D.N. Scalar polynomial curvature invariant vanishing on the event horizon of any black hole metric conformal to a static spherical metric. Phys. Rev. D 2017, 95, 084044. [Google Scholar] [CrossRef]
- Coley, A.; McNutt, D. Identification of black hole horizons using scalar curvature invariants. Class. Quantum Gravity 2017, 35, 025013. [Google Scholar] [CrossRef]
- Aksteiner, S.; Bäckdahl, T. All local gauge invariants for perturbations of the Kerr spacetime. Phys. Rev. Lett. 2018, 121, 051104. [Google Scholar] [CrossRef] [PubMed]
- Mattingly, B.; Kar, A.; Julius, W.; Gorban, M.; Watson, C.; Ali, M.D.; Baas, A.; Elmore, C.; Shakerin, B.; Davis, E.; et al. Curvature invariants for Lorentzian traversable wormholes. Universe 2020, 6, 11. [Google Scholar] [CrossRef]
- Henry, R.C.; Overduin, J.M.; Wilcomb, K. A new way to see inside black holes. In Bridges Baltimore 2015: Mathematics, Music, Art, Architecture, Culture; Tessellations Publishing: Phoenix, AZ, USA, 2015; pp. 479–482. [Google Scholar]
- Carminati, J.; McLenaghan, R.G. Algebraic invariants of the Riemann tensor in a four-dimensional Riemannian space. J. Math. Phys. 1991, 32, 313. [Google Scholar] [CrossRef]
- Zakhary, E.; McIntosh, C.B.G. A complete set of Riemann invariants. Gen. Relativ. Gravit. 1997, 29, 539. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a rotating, charged mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Boyer, R.H.; Lindquist, R.W. Maximal analytic extension of the Kerr metric. J. Math. Phys. 1967, 8, 265. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman: New York, NY, USA, 1973; p. 877. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry; Addison Wesley: San Francisco, CA, USA, 2004. [Google Scholar]
- Adamo, T.; Newman, E.T. The Kerr-Newman metric: A review. arXiv 2016, arXiv:1603.03143. [Google Scholar]
- Henry, R.C. Kretschmann scalar for a Kerr-Newman black hole. Astrophys. J. 2000, 535, 350. [Google Scholar] [CrossRef]
- Visser, M. The Kerr spacetime: A brief introduction. In The Kerr Spacetime; Wiltshire, D.L., Visser, M., Scott, S.M., Eds.; Cambridge University Press: Cambridge, UK, 2009; p. 3. [Google Scholar]
- Mathematica, Version 12.0; Wolfram Research Inc.: Champaign, IL, USA, 2019. For the use of this package to calculate basic quantities in general relativity, such as the Riemann tensor and Ricci scalar, see Hartle, J.B. Gravity: An Introduction to Einstein’s General Relativity; Addison-Wesley: San Francisco, CA, USA, 2003; Appendix C. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Hamermesh, M., Translator; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Lake, K. Invariants of the Kerr vacuum. Gen. Relativ. Gravit. 2003, 35, 2271. [Google Scholar] [CrossRef][Green Version]
- Musgrave, P.; Lake, K. Scalar invariants of the radiating Kerr-Newman metric: A simple application of GRTensor. Comput. Phys. 1994, 8, 589. [Google Scholar] [CrossRef][Green Version]
- Martín-García, J.M.; Yllanes, D.; Portugal, R. The Invar tensor package: Differential invariants of Riemann. Comput. Phys. Commun. 2008, 179, 586. [Google Scholar] [CrossRef]
- MacCallum, M.A.H. Computer algebra in gravity research. Liv. Rev. Relativ. 2018, 1, 6. [Google Scholar] [CrossRef]
- Schmidt, H.-J. The square of the Weyl tensor can be negative. Gen. Relativ. Gravit. 2003, 35, 937. [Google Scholar] [CrossRef]
- Grøn, Ø.; Hervik, S. Einstein’s General Theory of Relativity; Springer: Berlin, Germany, 2010; p. 160. [Google Scholar]
- de Felice, F.; Bradley, M. Rotational anisotropy and repulsive effects in the Kerr metric. Class. Quantum Gravity 1988, 5, 1577. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).