Abstract
This review is a pedagogical introduction to models of gravity and how they are constrained through cosmological observations. We focus on the Horndeski scalar-tensor theory and on the quantities that can be measured with a minimum of assumptions. Alternatives or extensions of general relativity have been proposed ever since its early years. Because of the Lovelock theorem, modifying gravity in four dimensions typically means adding new degrees of freedom. The simplest way is to include a scalar field coupled to the curvature tensor terms. The most general way of doing so without incurring in the Ostrogradski instability is the Horndeski Lagrangian and its extensions. Testing gravity means therefore, in its simplest term, testing the Horndeski Lagrangian. Since local gravity experiments can always be evaded by assuming some screening mechanism or that baryons are decoupled, or even that the effects of modified gravity are visible only at early times, we need to test gravity with cosmological observations in the late universe (large-scale structure) and in the early universe (cosmic microwave background). In this work, we review the basic tools to test gravity at cosmological scales, focusing on model-independent measurements.
1. Introduction
Gravity is the force that shapes the overall temporal and spatial structure of the universe. There is not much need then to explain why it is important to test its validity at all scales and regimes. The substantial progress in collecting cosmological data achieved in the last couple of decades has made it possible, for the first time, to test gravity and measure its properties at astrophysical and cosmological scales. To test a theory, one either has to build a set of alternatives against which to compare the standard model, or to parametrize the deviations from it in some meaningful and general way: both approaches are referred to as “modified gravity”.
Lovelock’s theorem [1] states that Einstein’s gravity is the unique local diffeomorphism invariant theory of a tensor field in 4D with second-order equations of motion. It is clear then that modifying gravity often implies adding new degrees of freedom, either scalars, vectors, or tensors. Adding a mass to the graviton, for instance, requires an additional tensor field; including more derivatives is also equivalent to adding more propagating degrees of freedom. Other options based on torsion, non-metricity, or non-locality can also be contemplated (see for instance the review [2]).
In this paper, we review the main properties of an important class of modified gravity based on a single scalar field, the so-called Horndeski Lagrangian (HL). This model is general enough to display most of the phenomenology of non-Einsteinian gravity: the generalized Poisson equation, Yukawa corrections to Newton’s potential, the presence of anisotropic stress, changes in the gravitational wave speed, instabilities, and ghosts. Still, the HL is relatively simple in that it contains a single propagating degree of freedom in addition to general relativity. Using the HL as a paradigm of modified gravity, we focus on its observability at various scales, from the local environment to galaxy clusters, with emphasis on cosmological observations. Although the recent measurement of the gravitational wave speed [3] severely constrains one of the phenomenological time-dependent parameters of the Horndeski model, as we will see, the other parameters are still mostly unconstrained and open to theoretical and observational investigation. A major topic of this review is the question of which properties of gravity can be measured as model-independently as possible.
We will not try to cover exhaustively the field of research in modified gravity; good reviews are already available [2,4]. Rather, we wish to discuss pedagogically some aspects or issues that are generic to the quest for traces of modified gravity.
We assume units such that and metric signature . An overdot denotes derivation with respect to cosmic time t, a prime with respect to . A comma will refer to a partial derivative, i.e., . Additionally, where is the covariant derivative. Greek indexes run over space and time coordinates, while Latin indexes run over space coordinates only.
2. Beyond Einstein
The re-discovery of the most general scalar-tensor theory that gives second-order equations of motion, Horndeski action [5], or covariant Galileons [6], and their extensions [7,8,9,10,11,12,13] provides a very general framework for such theories (see [14] for a recent review). The HL is defined as the sum of four terms to . Defining with the canonical kinetic term, the four terms are specified by two non-canonical kinetic functions and and by two coupling functions , all of them in principle arbitrary:
where is the action for matter fields—dark matter, baryons, and radiation—and
Note that and must have an X dependence; otherwise, they are total derivatives and could be rewritten—after integration by parts—as K and , respectively. (Notice that the number of these functions cannot be reduced by field redefinitions without going beyond Horndeski action [7,15]). As usual, each term in the HL has dimension . Often one chooses the scalar field to have dimensions of mass, but this is not necessary. As already mentioned, the Horndeski Lagrangian is the most general Lagrangian for a single scalar, which gives second-order equations of motion for both the scalar and the metric on an arbitrary background. This is a necessary, but not a sufficient, condition for the absence of instabilities, as we will see later on. The terms couple the field to the Ricci scalar R and the Einstein tensor . As a consequence, are the gravity-modifying coupling function. The background equations of motion of the HL are given for completeness in the appendix, although we do not need them in the following. It is enough to realize that the large freedom offered by the HL allows one to find a background evolution that satisfies all observational constraints.
Let us now briefly discuss some useful limits of the HL.
- If and (it is actually sufficient ), the HL reduces to the Einstein–Hilbert Lagrangian with a scalar field having a non-canonical kinetic sector given by . The canonical form is obtained for and ( is sufficient). CDM is recovered for .
- The “minimal” form of modified gravity within the HL is provided by and : this is then equivalent to a Brans–Dicke scalar-tensor model, again with a non-canonical kinetic sector.
- The original Brans–Dicke model is recovered assuming a kinetic sector, , and .
- If the kinetic sector vanishes, , then we reduce ourselves to an model [16], whose Lagrangian is . In fact, this model is equivalent to a scalar-tensor theory with and a potential where . This relation should then be inverted to obtain and used to replace R with in .
- If one sets , then the Lagrangian is invariant under the shift with . This shift-symmetric version of the HL is connected to the covariant Galileon when the functional dependence of the is fixed [6] and is able to produce the accelerated expansion without a potential that makes the field slow roll.
In general, the equations of motion for the scalar will couple it to the matter-energy density. The full set of equations of motion has been studied in several papers, for instance in [17,18]. Any modification of the HL, or addition of terms (except the so-called Beyond Horndeski terms), based on the same scalar field, will introduce higher-order equations of motion and associated instabilities, as a consequence of the Ostrogradsky theorem [19,20]. (See [21] for a discussion on how to exorcise Ostrogradski ghosts in non-degenerate theories.) Of course one can in principle add several scalar fields; however, on grounds of simplicity, this is rather unnatural. Notice that we do not demand that the drives the present-day accelerated expansion. It could be, after all, that the modification of gravity and the accelerated expansion are independent phenomena. It would be very interesting, though, to explain the latter in terms of the former.
3. Decomposition in Modes and Stability
Einstein’s gravity is carried by a massless spin-2 field, the metric. Being represented by a symmetric matrix, a metric in four dimensions has 10 degrees of freedom (DOFs). These DOFs can be collected according to how they behave under spatial rotations, i.e., as scalars, vectors and tensors. There are then four scalars (4 DOFs), two divergence-free vectors (4 DOFs), and one traceless, divergence-free tensor (2 DOFs). However, only the tensor DOFs propagate; that is, they are subject to linearized equations of motion that are second-order in the time derivatives. The other DOFs obey constraint equations, fully determined by the matter content. This should have been expected, since a massless tensor field, like the gravitational field, has only two independent degrees of freedom.
The two propagating degrees of freedom are associated with the two polarizations of the gravitational waves. To see that there are no other propagating DOFs, one can proceed by linearly expanding the metric around Minkowski
and keeping only scalar terms, i.e., functions that can be obtained from scalar or derivatives of scalars. The most general such metric is then
Inserting this metric into the Einstein–Hilbert Lagrangian without matter and developing it to a second order, one finds the second-order action in Minkowski space:
The linearly perturbed equations of motion can be obtained then by the Euler–Lagrange equations with respect to , but here we need only identify the degrees of freedom. When one varies the action with respect to B, one gets the constraint , which then shows that is not a propagating DOF. The same is true for , since there are no time derivatives for it. As we know, in fact, the potentials are determined by the matter distribution through two constraints, the Poisson equations, which do not involve time derivatives. Therefore, there are no scalar propagating DOFs in Einstein gravity without matter.
The same holds for the vector degrees of freedom. If one instead considers the tensor DOFs in
where, after imposing the traceless, divergence-less conditions, and considering a wave propagating in direction ,
one finds that the two modes obey in vacuum the same gravitational wave equation, , analogous to electromagnetic waves. GWs propagate therefore with speed equal to unity.
The same procedure can be applied to the HL. One finds then in the absence of matter fields [18,22]
where is the scalar mode perturbation, represents the two tensor modes, and represents their speed of propagation, respectively. As expected, HL has now three propagating DOFs, plus those belonging to the matter sector.
The four coefficients, , depend on the HL functions. Their expression will be given in Section 6. From the classical point of view, stability is guaranteed when (with ) have the same sign. In fact, in this case, the equations of motion are well-behaved wave equations with speed , whose amplitude is constant (or decaying in an expanding space), rather than growing exponentially as it would happen for (gradient instability). For the quantum stability, however, one must also require (or more exactly, the same sign of the kinetic energy of matter particles, assumed by convention to be positive), since otherwise the Hamiltonian is unbounded from below, which means particles can decay into lower and lower energy states, without limit, generating so-called ghosts. Therefore, for the overall stability of the theory, one requires .
4. The Quasi-Static Approximation
In what follows, we put ourselves in Fourier space. That is, we replace every perturbation variable with a plane wave parametrized by the comoving wavevector , . Since we deal only with linearized equations, this simply means replacing every perturbation variable or their time derivative with its corresponding Fourier coefficient or its time derivative , and every space derivative of order n with . We drop from now on the k subscripts. We then assume that the so-called quasi-static approximation(QSA) is valid for the evolution of perturbations. This implies that we are observing scales well inside the cosmological horizon, , where k is the comoving wavenumber, and inside the Jeans length of the scalar, such that the terms containing k (i.e., the spatial derivatives) dominate over the time-derivative terms. For the scalar field, this means we neglect its wavelike nature and convert its Klein–Gordon differential equation into a Poisson-like constraint equation. If , the scales at which the QSA is valid correspond to all sub-horizon scales, which are also the observed scales in the recent universe. For models with , the QSA might be valid only in a narrow range of scales, or even be completely lost in the non-linear regime.
Let us explain in more detail the QSA procedure by using standard gravity as an example. Let us write down the perturbation equations for a single pressureless matter fluid in CDM. From now on, we adopt the Friedmann–Lemaître–Robertson–Walker (FLRW) perturbed metric in the so-called longitudinal gauge, namely
If we use as a time variable, such that the coefficients of the perturbation variables become dimensionless, and we are left with [23]
where, instead of the matter density , we use ,
and where , and if is the peculiar velocity, such that . A glance at these equations tells us that, as an order of magnitude, . Moreover, we assume for every perturbation variable (unless there is an instability, see below) and, consequently, . Therefore, for , the equations become
and one can derive the well-known second-order growth equation with dimensionless coefficients
The same QSA procedure can be followed for more complicated systems. When a coupled scalar field is present, its perturbation is of the same order as the gravitational potentials, .
The QSA says nothing about the background behavior. Additional conditions might be imposed: for instance, that the background scalar field slow rolls are such that the kinetic terms, proportional to the derivatives , are negligible with respect to the potential ones. This is indeed expected in order to produce an accelerated regime not too dissimilar from CDM; however, first, one can have acceleration driven by purely kinetic terms, and second, acceleration can be produced even with a significant fraction of energy in the kinetic terms. Therefore, slow-roll approximation and QSA should be kept well distinguished. However, in some formulas below, we will explicitly make use of the slow-roll approximation on top of the QSA.
Let us emphasize that the QSA applies only for classically stable systems. Imagine a scalar field obeying a second-order equation in Fourier space
where from now on we use the physical wavenumber
instead of the comoving one, and where are the friction and the source, respectively, depending in general on the background solution and on other coupled fields. If , the solution will increase asymptotically as , and in this case will not be negligible with respect to as we assumed in the QSA.
For simplicity, from now on we assume that the space curvature has been found to be vanishing, so . Using Einstein’s field equations and a pressureless perfect fluid for matter, we can derive from the HL two generalized Poisson equations in Fourier space, one for and one for :
where z is the redshift, k the physical wavenumber, the matter density contrast, and and Y are two functions of scale and time that parametrize deviations from standard gravity (we remind the reader that, in our units, ). In some papers, the function Y is also called . Comparing with Equations (12) and (13), we see that in Einstein’s general relativity they reduce to . Clearly, the anisotropic stress , or gravitational slip, is defined as
(From now on, all the perturbation quantities are meant to be root-mean-squares of the corresponding random variables and are therefore positive definite; we can therefore define ratios such as .) A value of can be generated in standard general relativity only by off-diagonal spatial elements of the energy-momentum tensor. For a perturbed fluid, these elements are quadratic in the velocity, , and therefore vanish at first order for non-relativistic particles. Free-streaming relativistic particles can instead induce a deviation from : this is the case of neutrinos. However, they play a substantial role only during the radiation era and are negligible today [24]. Therefore, in the late universe means that gravity is modified, unless there is some hitherto unknown abundant form of hot dark matter.
In the QSA, one can show that for HL [17,25]
for suitably defined functions of time alone that depend only on . Their full form will be given in Section 6 along with another popular parametrization of the HL equations proposed in [22]. In general, the functions are proportional to , where is a mass scale. In the simplest cases, corresponds to the standard mass m, i.e., the second derivative of the scalar field potential, plus other terms proportional to or . These kinetic terms are expected to be subdominant if drives acceleration today or, more in general, during an evolution that is not strongly oscillating, so often we can assume that scale simply as . This approximation will be adopted in the explicit expression for and conformal coupling that are given below. If the scalar field drives the acceleration, one expects m to be very small, of order eV. In this case, at the observable sub-horizon scales, and . If instead this scale is of the order of the linear scales that can be directly observed (e.g., 100 Mpc), then one could observationally detect the k-dependence of and find that, at sufficiently large scale, such that , .
The same form of can be obtained also in other theories not based on scalars that produce second-order equations of motion, namely, in bimetric models [26] and in vector models [27].
It is worth stressing the fact that the time dependence of , expressed by the functions , is essentially arbitrary. Given observations at several epochs, one can always design an HL that exactly fits the data, no matter how precise they are. In contrast, the space dependence, which in Fourier space becomes the k dependence, is very simple and fixed. The reason is that the HL equations are by definition second-order, and therefore contain at most factors of . The k dependence is therefore potentially a more robust test for the validity of the HL than the time one. A model with two coupled scalar fields would instead generate for a ratio of polynomials of order (see, e.g., [28]). Clearly, one has to remember that all this is valid at linear scales: if the k dependence is important only at non-linear scales, e.g., for Mpc, then it might be completely lost.
Another equivalent form that we will employ often is
where
This form has a simple physical interpretation. is the modifier of the -Poisson equation, just as Y is the modifier of the -Poisson equation. The parameters are the strengths of the fifth-force mediated by the scalar field for (the metric time-time perturbed component) and for (the metric space-space perturbed component), respectively. Finally, m is the effective mass of the scalar field, and its spatial range. This interpretation will be discussed in the next section.
A particularly simple case is realized with the models, where is the function of the curvature R that is to be added to the Einstein–Hilbert Lagrangian. In this case in fact,
The derivative is often negligible at the present epoch, in order to reproduce a viable cosmology. In this case, and, for large k, and , regardless of the specific model.
Another simple case is conformal scalar-tensor theory, with , , and , where . In this form, the strength of the fifth force is . In this case, we have
where . When M is vanishingly small, and . Comparing with Equation (26), we see that, for , .
5. Potentials in Real Space
In real space, one can derive the modified Newtonian potential for a radial mass density distribution by inverse Fourier transformation. Let us start with Equation (24):
For a non-linear static structure (e.g., the Earth or a galaxy) the local density is much higher than the background average density, so , where is the background density, and
is the Fourier transform of . The Poisson Equation (21) becomes then
In real space and for a radial configuration, this reads
where
is the inverse Fourier transform of , and V is an arbitrary large volume that encompasses the structure (since we use the physical k, r now refers to the physical distance). Assuming that vanishes at infinity, Equation (31) has the general solution
where and where is the standard Newtonian potential, while is the Yukawa correction proportional to . This can be solved for any given radial density distribution . For (or , we are back to the Newtonian case.
Let us focus now on the modified gravity part. This can be analytically integrated in some simple cases. We write
where F has two parts
For a mass point at the origin, for instance, one has where is the Dirac delta function in 3D, defined for any regular function as ; therefore,
i.e., the so-called Yukawa correction. The total potential is then
where we reintroduced for a moment Newton’s constant . As anticipated, gives the strength of the Yukawa interaction, and its spatial range. The prefactor renormalizes the product , such that only the product is then observable (besides ). Sometimes is denoted because it can be seen as a renormalization of Newton’s constant.
A typical dark matter halo can be approximated by a Navarro–Frenk–White profile [29] with scale and density parameter ,
In this case, we have [30]
where is the ExpIntegral function,
Exactly the same procedure can be applied to the second potential , which obeys another Poisson equation
One has now
Notice that the mass m is the same for : there is only one boson, not two. The real-space expression for for a point-mass M is then identical to the one for with in place of and in place of ,
Finally, the so-called lensing potential is responsible for the gravitational lensing of source images in the linear regime. In this regime, given an elliptical source at distance characterized by semiaxes of angular extent , the image we see is distorted by intervening matter into a new set of semiaxes where the distortion matrix is proportional to
All observations of gravitational lensing lead therefore ultimately to an estimation of . What is observed in practice is the power spectrum of ellipticities, i.e., the correlation of ellipticities of galaxies in the sky due to a non-zero along the line of sight (see, e.g., [31], chap. 10).
From Equations (20) and (21), we see then that
In our formalism, the lensing potential in real space amounts then to
where
Since is in general different from unity, the mass one infers at infinity from the potential (often called dynamical mass) is different from the mass that one infers from the potential and from the lensing combination , i.e., (lensing mass). These masses of course coincide in standard gravity. As we will see below, one can indeed compare observationally the estimations and extract by taking suitable ratios.
6. The Parameters of the Yukawa Correction
In [22], it has been shown that the HL perturbation equations can be entirely written in terms of four functions of time only, , given as
This parametrization (collectively called ) is linked to the physical properties of the HL. Briefly, expresses the deviation of the GW speed from c, ; is connected to the field kinetic sector, and to the mixing (“braiding”) of the scalar and gravitational kinetic terms; is the time-dependent effective reduced Planck mass, and its running. They are designed such that for CDM. They do not vanish, in general, for standard gravity with a non- CDM background expansion, nor for non-standard gravity with a CDM expansion. Several observational limits on these parameters in specific models have already been obtained (see, e.g., [32]).
It is clear that cancellations can occur among terms belonging to different sectors. However, one should distinguish between dynamical cancellations, i.e., involving a particular background solution for , and algebraic cancellations, which only depend on a special choice for the functions . The former ones, if they exist at all and are not unstable, can be guaranteed only for some particular set of initial conditions, and might occur only for some period, unless the solution happens to be an attractor. The algebraic cancellations, however, are independent of the background evolution and therefore valid at all times. Therefore, usually only the second class is regarded as an interesting one.
We can now express the four coefficients introduced in Equation (8) that determine the stability of the HL as [22]
where
and where and (with this last relation one can get rid of everywhere). Here, “matter” represents all the components in addition to the scalar field, i.e., baryons, dark matter, neutrinos, and radiation. The matter equation of state is then an effective value for all the matter components. Note that in the standard minimally coupled scalar field case , and .
The relation between the “observable” parameters that enter the Yukawa correction and the “physical” parameters is
where
(With respect to the mass defined in [22], we have .)
Two remarks are in order. First, the quantity acts as an effective squared mass in the perturbation equation of motion for ; we need to assume therefore that it is non-negative to avoid instability below some finite value of k. Second, the expressions for and are completely general and do not assume the QSA. The QSA is needed only when we connect the theory to observations through .
Considering now only pressureless matter, from the background equations in the Appendix A, we see that,
where . In a CDM background, , and simplifies to . Notice that does not appear in the - relation: this means that the kinetic parameter is not an observable in the QSA linear regime. In Section 13, we will discuss which combinations of are model-independent (MI) observables in cosmology.
Assuming Einstein–Hilbert action for the gravitational sector and a canonical kinetic term for the scalar field, we have and , so and
Therefore, and
so that, as per construction, .
It is worth noticing that the stability conditions imply and therefore if one also requires . As we have seen, is the range of the fifth-force interaction, so it makes sense that it is positive definite for stable systems. In the standard Brans–Dicke model with a potential , for instance, and neglecting several subdominant kinetic terms, we have
where ; therefore, finally,
where (notice that in Brans–Dicke has dimensions mass, and is therefore dimensionless), so the fifth-force range is
Assuming a CDM expansion and , the conditions for stability during the matter era simplify to and
Generalizing, we have that for a background parametrized by a (possibly time-dependent) EOS and for matter with an effective , one has
To these stability conditions, arising from Equations (60) and (61), one should add the requirement that the friction term in the perturbation equations for , or equivalently, for the gravitational potentials , is positive. This condition is quite milder than those from Equations (60) and (61). While a negative , for instance, even for a short period, induces a unbounded growth for , a negative friction term typically leads to a power-law growth , which might be a problem only if it lasts for too long. However, in order to obtain the friction instability condition, one should carefully investigate the existence of growing modes also when the various coefficient are time-dependent and no simple criteria have been identified so far. Therefore, we just quote the condition for negative friction (i.e., stability) for the gravitational waves, best obtained by writing down the equation in conformal time, since in this case the term is time-independent (provided ). The condition is simply .
From the relations (64), we can derive the Yukawa strengths
The Yukawa strength is always positive, so the fifth force is attractive if . We also notice that if , then and the two strengths become equal, and . Therefore, , and, finally, , even if both potentials do actually have a non-vanishing Yukawa correction, such that . In order for the parameters to vanish, the gravity sector of the HL must be standard, , barring the case of accidental dynamical cancellation for some particular background evolution. Therefore, we conclude that implies, and is implied by, modified gravity, at least when matter is represented by a perfect fluid [33]. One cannot make a similar statement for Y. This is a crucial statement for what follows. Notice, however, that, as we show below, although modified gravity implies , a value does not necessarily imply standard gravity, but only scale-free gravity, at least at the quasi-static level. In [34], it has been shown that at all scales implies indeed standard gravity.
We can draw more conclusions from Equations (79).
- The two strengths are equal also if . In this case, and has no scale dependence.
- The limit of the modified gravity parameters (provided we are still in the linear regime) isThis coincides with Equation (4.9) of [22]. If , thenIt turns out that, if one imposes stability, , then Y is always larger than, or equal to, , such that matter perturbations in Horndeski with always grow faster, in the quasi-static regime, than any standard gravity model with the same and the same background. It also follows that the lensing combination that appears in Equation (52) amounts toSince the denominator has to be positive for stability, the sign of the effect on the gravitational lensing depends only on .
- The Yukawa corrections disappear completely if , i.e., forThis is therefore the general condition to have a scale-free gravity, corresponding to (we recently noticed that this relation was first provided in an unpublished draft by Mariele Motta in early 2016). If we also assume and consequently (conformal coupling) in the HL, as required by the GW speed constraints we discuss in Section 8, it follows that [35,36] (note that in [35] is defined as our ), and thatwhich gives an algebraic cancellation for and . In this particular model, the local gravity experiments would not detect a Yukawa correction, even if gravity actually couples to the scalar field. Gravity then becomes scale free. The Planck mass would still vary with time, however. Therefore, in this model, even if gravity is actually modified. Assuming a CDM background, for this model to be stable, implies the condition . For constant or slowly varying, the stability condition amounts to , so ; therefore, Y, or the effective Newton’s constant, will decrease with time. A larger Y in the past means faster perturbation growth for the same . Once again, however, since is not an MI observable quantity, whether this means that perturbations grow faster than in CDM or not is a model-dependent statement.
- From Equation (52), we find also that the lensing potential lacks a Yukawa term whenever , defined in (54), i.e., , which amounts toWe then see that , not only when but also for . Again imposing the GW speed constraint, this becomes . On the HL functions, this implieswhich actually means that the sector, after an integration by parts, can be absorbed in . Therefore, for the conformal coupling and when the term is absent or does not depend on X, the lensing potential becomes simply twice the standard Newtonian potentialThis means that radiation, being conformally invariant (the electromagnetic Lagrangian does not change for ), does not feel the modification of gravity, except for the overall factor , which, if time-dependent, induces a time-dependent mass or Newton’s constant.
- In the same case as above, and , one haswhich becomeswhen the kinetic component is small. Similarly, . For , one obtains a Yukawa strength of for the potential. This case is exactly realized for the models.
- Finally, in the uncoupled case , in which only the kinetic sector of the scalar field is modified, one has that , such that there is a Yukawa correction, but at all quasi-static scales.
7. Local Tests of Gravity
Gravity has been tested for a long time in the laboratory and within the solar system (see, e.g., [37]). The generic outcome of these experiments is that Einsteinian gravity works well at all of the scales that have been probed so far. In many experiments one assumes the existence of the same type of “fifth-force” Yukawa correction to the static Newtonian potential predicted by the HL model,
(Here we drop the subscript from since we need to consider only ; moreover, any overall parameter can be absorbed in .) Current limits on and have been obtained in a range of scales from micrometers to astronomical units. The constraints on the strength obviously weakens for very small . To give an idea, at the smallest scales probed in the laboratory, one has [38] at m and at m (Casimir-force experiments probe even shorter scales, but the constraints on become correspondingly weaker). At planetary scales, one has for m (Earth–Moon distance), and at m (planetary orbits). Beyond this distance, the constraints from direct tests of the Newtonian potential weaken again.
However, the scalar field responsible for the Yukawa term induces also two post-Newtonian corrections to the Minkowski metric. For a mass distribution with velocity field and density distribution , we define U as the potential that solves the standard Poisson equation for non-relativistic particles, i.e., [37]
and as a velocity-weighted potential
We can then write the parametrized post-Newtonian metric as follows:
(The full post-Newtonian metric includes several other terms that are not excited by a conformally coupled scalar field, see, e.g., [2]). Clearly, produces the standard weak-field metric. Taking the extreme case of , one has
where . The parameter can be seen as the local-gravity analogue of the anisotropic stress , both being the ratio of at a linear level.
Local tests of gravity can, therefore, measure the Yukawa correction for both , i.e., and , and the ratio , in a model-independent way. The parameter , for instance, is constrained to be less than [39], inducing a similar constraint on at large scales. A similar constraint applies also to . With such a small strength, there would hardly be any interesting effect in cosmology.
However, all these tests are performed within a limited range of scales, both spatial and temporal. Moreover, the tests are performed with (some of) the standard matter particles and not with, say, dark matter. Therefore, they are completely escaped if standard model particles do not feel modified gravity, for instance, because the scalar field that carries the modification of gravity does not couple to them or because of screening effects, as we discuss next.
So far we have considered only linear scales. At strongly non-linear scales, e.g., in the galaxy or in the solar system, the effects of modified gravity depend on the actual configuration of the scalar field. If such a configuration is static and homogeneous within a scale , then the effects of modified gravity can be screened within , since they are proportional to the variation of . This is the so-called chameleon effect [40,41]. On the other hand, screening can occur also because of non-linearities in the kinetic part of the Klein–Gordon equation: this is the Vainshtein effect [42,43]. Finally, a third mechanism appears if the coupling sets on a vanishing value in structures (high density regions), via a symmetry restoration, while being different from zero at the background (low density) [44,45,46,47]. In all cases, the strong deviation from standard gravity that we might see in cosmology are no longer visible by local experiments. In this sense, one can always build models that escape the local gravity constraints. This can be achieved also by assuming that the baryons are completely decoupled from the scalar field.
In light of these arguments, let us consider for instance in more detail the constraint on associated with the big bang nucleosynthesis (BBN), sometimes quoted as one of the most stringent cosmological bound. The yields of light elements during the primordial expansion depends on both the baryon-to-photon constant ratio and the cosmic expansion rate during nucleosynthesis, which in turn depend on at that time and on various standard model parameters. Fixing the standard model parameters and estimating by CMB measurements, one can find constraints on [48] by comparing the predicted abundances with the observed ones, for instance deuterium in quasar absorption systems. This means that at nucleosynthesis was close to on Earth today. The easiest explanation, which is that did not vary at all or at least in any way less than 0.2 throughout the expansion, implies (equal to in CDM), where is the cosmic age. However, in the solar system might be screened, as we have mentioned, and therefore equal to the “bare” of standard gravity. Therefore, any model which is standard general relativity in the early universe, like essentially all models built to explain present day’s acceleration, will automatically pass the BBN constraint. Moreover, one should notice that this constraint depends on an estimate of from CMB that assumes CDM. Additionally, is, in fact, degenerate with the number of relativistic degrees of freedom at nucleosynthesis, such that the bound applies to rather than to alone. Finally, a simultaneous change in the other standard-model parameters might considerably weaken the constraint (see [49,50]).
8. The Impact of Gravitational Waves
The Horndeski model predict an anomalous propagation speed for gravitational waves (or rather, ), since the scalar field is coupled in a non-conformal way. As already mentioned, one has [25,51],
The almost simultaneous detection of GWs and the electromagnetic counterparts tells us that, within 40 Mpc (at ) from us, GWs propagate essentially at the speed of light [3]. Since the signals arrived within a 1s difference and since the light took s to reach us, we have that . Such a tight constraint immediately ruled out most of the scalar-tensor theories containing derivative couplings to gravity or at least those models which show this effect in the nearby universe (in cosmological scales) [35,52,53,54,55,56]. That is, we need to have and . In other words, the surviving Lagrangian has an arbitrary but a vanishing and an X-independent . This kind of Lagrangian is just a form of Brans–Dicke gravity (plus a scalar field potential and a non-canonical kinetic term). It is also equivalent to standard gravity with matter conformally coupled to a scalar field, i.e., coupled to a metric . A dynamical cancellation among the terms depending on and appears extremely fine-tuned. A possible way out is to design a model with an attractor on which the conformal coupling holds, as proposed in [57]. In this case, after the attractor is reached, we measure , but this does not have to be true in the past. Deviations from the speed of light in the past could be detected in B-mode CMB polarization [58].
The constraints on also affect directly . From Equation (65), one has in fact
Hence, the GW constraint implies that should also be equal to unity for sufficiently large scales (small k) [59]; i.e., it should recover its general relativity value. The obvious exception are theories without a mass scale in addition to the Planck mass [60], in which case at all scales. On the other hand, no obvious GW constraint affects Y.
Gravitational waves might in principle measure another HL parameter: the running of the Planck mass, . In fact, as it has been shown, for instance, in [33], the GW amplitude h obeys the equation
Assuming , this equation in the sub-horizon limit is solved by [61]
where the prefactor is the ratio of the Planck mass values at emission and at observation, and is the standard amplitude expression that, for merging binaries, can be approximated as (see, e.g., [62], Equation (4.189))
Here, is the luminosity distance, the so-called chirp mass, and the GW frequency measured by the observer.
GWs in standard gravity can measure the luminosity distance because the chirp mass and the frequency can be independently measured by the interferometric signal. In modified gravity, what is really measured is therefore a GW distance [61,63,64]
Comparing this with an optical determination of leads to a direct measurement of at various epochs, and therefore of .
It is, however, likely that both the emission and the observation occur in heavily screened environments. In this case, is the same at both ends, and no deviation from would be observed. If emission occurs in a partially unscreened environment, then one should see instead some deviation, although not necessarily connected to the cosmological, unscreened, value of .
9. Model Dependence
The standard model of cosmology, CDM, is amazingly simple. It consists of a flat, homogeneous, and isotropic background space with perturbations that, at scales above some Megaparsec, have been evolving linearly until recently. The initial conditions for perturbations are set by the inflationary mechanism and provide an initially linear and scale-invariant spectrum of scalar, vector, and tensor perturbations, i.e., power-law spectra , where x stands for the three types of perturbations that can be excited in general relativity. These are encoded in a spin-2 massless field that mediates gravitational interactions via Einstein’s equations. The energy content is shared among relativistic particles (photons) as well as quasi-relativistic particles, neutrinos, pressureless “cold” dark matter particles, standard model particles (“baryons”), and a cosmological constant. The density of photons can be directly measured via the CMB temperature: it amounts to ; the density of neutrinos depends on their mass and is known to be less than 1% of the total content today. Therefore, today, only the last three components are important. The density of baryons can be fixed by the primordial BBN [65]. Since the space curvature has been measured (although so far only in a model-dependent way) to be negligible, only a single parameter is left free: the present fraction of the total energy density in pressureless matter, . The fraction in the cosmological constant is then .
With this one free parameter, the fraction of energy in the cosmological constant, , CDM fits all the current cosmological data: the cosmic microwave background (CMB), the weak lensing data, the redshift distortion data (RSD), and the distance indicators (supernovae Ia, SNIa; baryon acoustic oscillations, BAOs; cosmic chronometers, CCH; gravitational waves, GW).
There are indeed a few discrepancies. In particular, two seem to be more robust. The first is the value of obtained through local measurements, in particular through Cepheids, km/s/Mpc [66], independent of cosmology, which deviates from the Planck [67] value obtained through extrapolation from the last scattering epoch performed assuming CDM, km/s/Mpc [67]. The second one is the level of linear matter clustering embodied in the normalization parameter : here again, the value from CMB ( [67] differs from the late-universe value delivered by weak lensing, [68] and by RSD data [69], .
Another source of discrepancies is related to the dark matter clustering [70]. Dark-matter-only simulations fail at reproducing some of the observed properties of the DM distribution. Although the inclusion of baryon physics may solve this, so far there is no conclusive statement, and some of these issues may in fact be due to a modification of gravity.
These conflicting results already display a basic problem of cosmological parameter estimation, namely the fact that it is very often model-dependent. The Planck satellite estimates of the cosmological parameters, from to h, from the equation of state of dark energy to the clustering amplitude , can be obtained only by assuming, among others, a particular model of initial conditions (inflation) and of later evolution ( CDM). For instance, if we assume instead of the cosmological constant value , one obtains km/sec/Mpc ([67], Figure 27), outside the error range given above.
Another example of model-dependency comes from distance indicators and the dark energy equation of state. Cosmological distance indicators, whether based on SNIa, BAOs, or otherwise, basically measure the comoving distance
where is the present amount of spatial curvature k expressed as a fraction of total energy density. We see that depends only on and . However, since distance indicators depend on the assumption of a standard candle or ruler or clock, whose absolute value we do not know, the absolute scale of , i.e., , cannot be measured (except for “standard sirens”, i.e., gravitational waves [71]). Assuming for simplicity that , the only direct observable is . If we also neglect radiation (a very good approximation for observations at redshift less than a few) and assume that, besides pressureless matter, we have a dark energy component with EOS , we have
where
We can then invert the Relation (107) and obtain
where means differentiation with respect to redshift. It appears then that, in order to reconstruct , one needs to know , in addition to . For instance, if the true cosmology were CDM with and we assumed erroneously that , we would infer and , which is much different from the true value .
The problem is that is not a model-independent observable. Whenever an estimate of is given, e.g., from CMB or lensing or SNIa, it always depends on assuming a model. The reason is that there is no way, with phenomena based on gravity alone (clustering and velocity of galaxies, lensing, integrated Sachs–Wolfe, etc.), to distinguish between various components of matter, since matter responds universally to gravity, unless one breaks the equivalence principle (see the “dark degeneracy” of [72]). Therefore, to measure , one has to assume a model, i.e., a parametrization, with extremely precise measurements. For instance, if , then we reduce the complexity to just two parameters, and a measurement of at at least three different redshifts can simultaneously fix . Without a parametrization, cannot be reconstructed. With a parametrization, the result depends on the parametrization itself.
On the other hand, it is clear that we can always perform null tests on , as for most other cosmological parameters. That is, we can assume a specific , e.g., , and test whether it is consistent with the data. In this case, in flat space, one needs just three distance measurements at three different redshifts, since there are only two parameters, and . If the system of three equations in two parameters has no solution, the CDM model is falsified. While it is relatively easy to test, i.e., falsify, a model of gravity, it is much more complicated to measure the properties of gravity in a way that does not demand too many assumptions. This explains why the title of this paper mentions “measuring”, and not “testing”, gravity.
The rest of the paper will discuss what kind of model-independent measurements we can perform in cosmology, with emphasis on parameters of modified gravity. As is obvious, one cannot claim absolute model independence. The point is rather to clearly isolate the assumptions, and see how far can one reach with a minimum amount of them. In the following, we will assume. the following:
(a) the universe is well-described by a homogeneous and isotropic geometry with small (linear) perturbations;
(b) gravity is universal;
(c) standard model particles behave from inflation onwards in the same way as we test them in our laboratories;
(d) dark matter is “cold”.
One can replace the last statement with the assumption that we know the equation of state and sound speed of dark matter, provided it is not relativistic and that the fluid remains barotropic, i.e., , as we will show later on. Unless otherwise specified, however, for the rest of this work, we assume pressureless, cold dark matter.
Notice that we are not assuming any particular form of gravity, standard or otherwise: in fact, we refer to “gravity” as to one or more forces that act universally and without screening, at least beyond a certain scale. Therefore, we include in our treatment gravity plus at least one scalar, vector, and tensor field. Later on, we will use the Horndeski generalized scalar-tensor model for a specific example, but the methods discussed here are not restricted to this case.
10. Model-Independent Determination of the Homogeneous and Isotropic Geometry
What we observe in cosmology are redshifts and angular positions of sources. However, we need to build models for and test distances. Can we convert redshifts and angles into distances in an MI way? If this turns out not to be possible, then there is no reason to continue our investigation to the perturbation level. Fortunately, it appears we can.
The FLRW metric of a homogeneous and isotropic universe in spherical coordinates is
where is the scale factor normalized at present time to . If we measure in units of the natural scale length , the metric can be rewritten as
The value of has been estimated by Planck to be extremely small, ([67], Table 5, last column), but, again, this is a model-dependent estimate, and for now we consider it as a free parameter. We see that, up to an overall scale, the FLRW metric depends only on and on , from which is obtained by inverting
where again t is in units of .
BAOs are the remnant of primordial pressure waves propagating through the plasma of baryons and photons before their decoupling. By assumption (, we assume their interaction at all times is the same as in our laboratories. Therefore, we can predict that the comoving scale of the BAO today is a constant R independent of the redshift at which it is observed. For instance, in CDM, R (in units of ) is equal to
where the indexes refer to radiation, baryons, and dark matter, respectively; moreover, , is the redshifts of the drag epoch (see the numerical formula given in [73]), and is the redshift at equivalence. The value R can be used as a standard ruler: as for SNIa, we do not need to know R; we need only to assume that it is constant. Therefore, we can search in the clustering of galaxies for such a scale, in particular by identifying a peak in the correlation function. The angle under which we observe R gives us the “transverse BAO”. In turn, this angle gives us the dimensionless angular diameter distance
The correlation function, however, depends both on the angle between sources and on their redshift difference. That is, one can observe also a “longitudinal BAO” scale, which, for a small redshift separation , amounts to
This means that BAOs can estimate at every redshift two combinations involving and and therefore determine both in an MI way. Therefore, the FLRW metric can in principle be reconstructed within the range covered by BAO observations, without assumptions in addition to (a). Clearly, SNIa and other distance indicators can contribute to the statistics, but do not offer information on alternative combinations of cosmological parameters. Once we have the FLRW metric, the redshifts and angles can be converted to distance by solving . Given two sources at redshifts separated by an angle , their relative distance is [74]
where the comoving distance is defined in (106). The background geometry is then recoverable in an MI way. However, this is not a test of gravity.
We move then to the next layer: perturbations.
11. Measuring Gravity: The Anisotropic Stress
We have seen that the gravitational slip is defined as the ratio between the two gravitational potentials
The lensing potential is the combination that exerts a force on the relativistic particles (i.e., for our purposes, light), while exerts a force on non-relativistic particles (i.e., for our purposes, galaxies). The explicit form of the equation of motion for a generic particle moving with velocity and relativistic factor in a weak-field Minkowski metric is in fact [75]
For small velocities, only the last term on the rhs survives; for relativistic velocities, only the square bracket term. This means that, in order to test gravity at cosmological scales, we need to combine observations of lensing and of the clustering and velocity of galaxies.
The linear gravitational perturbation theory provides the growth of the matter density contrast at any redshift z and any wavenumber k, given a background cosmology and a gravity model. It is convenient to also define the growth function
and the growth rate
where, as usual, the prime stands for derivative with respect to .
However, what we observe is the galaxy number density contrast in redshift space, usually expressed in terms of the galaxy power spectrum as a function of wavenumber k and redshift, . Since galaxies are expected to be a biased tracer of mass, we need to introduce a bias function
that, in general, depends on time and space (that is, on ). If , then the number density of galaxies in a given place is proportional to the amount of underlying total matter, . If (), then galaxies are more (or less) clustered than matter. Moreover, since we observe in redshift space, which means we observe a sum of cosmic expansion and the radial component of the local peculiar velocity, to convert to real space, we need the Kaiser transformation [76], which induces a correction factor that depends on the cosine of the angle between the line of sight and the wavevector .
This means that the relation between what we observe, namely the galaxy power spectrum in redshift space, and what we need to test gravity, namely , can be written as [77]
where
where is the root-mean-square matter density contrast today. ( are mnemonics for amplitude and redshift, respectively.) With this definition, is normalized as
where is the window function for an 8 Mpc sphere, and . Sometimes one defines , which is then normalized to unity. can be referred to as the shape of the present power spectrum. Equation (122) shows that are the only two observables one can derive from linear galaxy clustering. This dataset is often collectively called redshift distortion (RSD).
There is then a third observable that one can obtain from weak lensing. From Equation (52), we see that by estimating the shear distortion, one can measure the quantity
Since can be estimated independently, we define another observable, to be denoted L [25], as follows:
Together with , the quantities are the only cosmological information one can directly gather at the linear level (as we have seen, is also a direct observable, but for simplicity, we have assumed that is negligible at all relevant epochs). Other observations, like the integrated Sachs–Wolfe or velocity fields, only give combinations of , rather than new information. A direct measurement of the peculiar velocity field and its time derivative, for instance, would produce through the Euler Equation (10) an estimation of the combination ; however, this is equivalent to . At least at the linear level, one could add more statistics, but will always end up with these four quantities rather than, say, a direct estimate of or Y. A preliminary non-linear analysis [78] shows that, employing higher-order statistics, we can obtain more MI information, but we will not consider this here.
We can now write the lensing equation in Fourier space in the following way (see [79]):
where . The linearized matter conservation equations, i.e., the continuity equation and the Euler equation, can be combined in a single second-order equation,
which depends only on the pressureless assumption (d) and not on the gravitational model. In terms of our observational variables and for slowly varying potentials, this becomes
These equations show clearly that lensing and matter growth can measure some combination of and their derivatives, as will be seen explicitly below. For now, let us just rewrite Equation (129), employing also Equation (21) as
We see then that Y is not, unfortunately, an MI quantity. Even if we have precise information on , we would still need, at any , the combination , which is not an observable. Only a null test of standard gravity plus a specific cosmological model, say CDM, is possible: in this case in fact, , and are known, and we have that is uniquely measured by a combination of . Any two measures at different k or z values must then give the same . We show below that , in contrast to Y, is an MI quantity.
Although might be interesting statistics on their own, our goal here is to test gravity. Now, the bias function depends on complicated, possibly non-linear and hydrodynamical processes; thus, even if b depends on gravity, we do not know how. Additionally, the shape of the power spectrum depends on initial conditions (inflation) and, possibly, on processes that distorted the initial spectrum during the cosmic evolution. In fact, even if we could exactly measure the power spectrum shape from CMB without a parametrization such as or its “running”, nothing precludes the possibility that an unknown process, for instance the presence of early dark energy or early modified gravity, has distorted the spectrum at some intermediate redshift between the last scattering and today. Therefore, in order to obtain model-independent measures, we should eliminate both b and . It was shown in [25,79] that one can obtain only three statistics where the effects of the shape of the primordial power spectrum is canceled out, namely
In the last equation, we introduced the often-employed quantity
Notice that we are not defining as an integral over the power spectrum at z, as in Equation (124), because we are interested in the k-dependence. These quantities depend in general on in an arbitrary way. Every other ratio of or their derivatives can be obtained through or their derivatives.
Let us discuss the three statistics in turn. The first quantity, , often called in the literature, contains the bias function. Since we do not know how to extract gravitational information, if any, from the bias, we do not consider it any longer.
Concerning , we notice that, although related, what is observed is R and not . In order to determine the latter from the observable R, one has to assume a value of (typically chosen to be given by CDM), such that it is not a model-independent observable. One could imagine that alone is instead a direct test of gravity, since it depends only on f. However, to predict the theoretical value of R (or f) as a function of the gravity parameter Y from Equation (130), one needs to choose a value of and the initial condition at some epoch for every k. In almost all the papers on this topic since [80], this initial condition is assumed to be given by a purely matter-dominated universe at some high redshift (this is, for instance, how the well-known approximated formula is obtained). However, in models of early dark energy or early modified gravity, this assumption is broken. Therefore, once again, alone cannot provide an MI measurement of gravity. Exactly as we have seen for the dark energy EOS , if one parametrizes with a sufficiently small number of free parameters, then the RSD data alone, which provide , can fix both and .
We can also see that is trivially related to the statistics, whose expected value at a scale k is (see [81] and references therein)
In CDM and with Planck 2015 parameters, its present value is . With our definitions, the relation with is given by
The statistics has been used several times as a test of modified gravity [81,82,83,84]. However, it is not per se a model-independent test. In fact, the theoretical value of depends on and on f. As already stressed, is not an observable quantity. Moreover, the growth rate f is estimated by solving the differential equation of the perturbation growth, and this requires initial conditions and Y. As a consequence of this, when we compare to the predicted value (131), we can never know whether any discrepancy is due to a different value of , to different initial conditions, or to non-standard modified gravity parameters . As previously shown, one can employ only to perform a null test of standard gravity plus CDM, or other specific models. This is, of course, a task of primary importance, but is different from measuring the properties of gravity in a model-independent way.
In contrast, we can define MI statistics to measure gravity, in particular the parameter by combining the equation for the growth of structure formation, Equation (129), with the lensing Equation (127) and with Equations (14) and (21). We see then that the gravitational slip as a function of model-independent observables is given by
In order to distinguish the observables from the theoretical expectations, we denoted the combination on the lhs of this equation as . The statistics is model-independent because it estimates directly without any need to assume a model for the bias, nor to guess or , nor to assume initial conditions for f. Therefore, if observationally one finds 1, then CDM and all of the models in standard gravity and in which dark energy is a perfect fluid are ruled out. As a consequence, cautionary remarks such as those in [85], namely, that their results about cannot be employed until the tension between in different observational dataset is resolved, do not apply to . The price to pay is that Equation (137) depends on derivatives of E and, through , of . Derivatives of random variables are notoriously very noisy. In the next sections, we will compare several methods to extract the signal.
If we abandon the linear regime then, of course, new observables can be devised, see e.g., [78]. One interesting case is provided by relaxed galaxy clusters, for which we can reasonably expect that the virial theorem is at least approximately respected. In this case, we can directly measure the potential by the Jeans equation, i.e., the equilibrium equation between the motion of the member galaxies and the gravitational force (note that the potential remains linear for galaxies and clusters, even for a non-linear distribution of matter). The lensing potential can instead be mapped through weak and strong lensing of background galaxies. In this case, one can gather much more information on the modified gravity parameters than in the linear regime [30]. However, the validity of this approach relies entirely on two important assumptions. First, we must assume the validity of the virial theorem, which can be more or less reasonable, but cannot be proved independently. Second, since we have access only to the radial component of the member galaxy velocities, we must assume a model for the velocity anisotropy, i.e., how the other components are distributed within the cluster.
Concluding this section, we recap and emphasize the main points. are the only independent linear observables in cosmology. The ratios are independent of the initial conditions (i.e., of the power spectrum shape). are also independent of the galaxy bias. The combination is, therefore, a model-independent test of gravity: it does not depend on the bias, on initial conditions, nor on other unobservable quantities such as and . If , gravity is not Einsteinian; if does not have the same dependence as the Horndeski’s theory, the entire Horndeski model is rejected. All this, of course, assumes that our conditions (a)–(d) are verified.
12. General Perfect Fluid
What happens if we remove condition (d), namely, that matter is pressureless? If matter is a perfect fluid and we know or hypothesize a different equation of state and sound speed, then Equation (128) is modified since the continuity and Euler equations, which come directly from the conservation of the energy-momentum tensor, now read
where the sound speed is , and is the matter anisotropic stress. Here we are assuming that represents the density contrast of matter, both baryons and dark matter, whose microphysical properties are described with some effective parameters . Assuming a zero anisotropic stress, since we are dealing with non-relativistic matter, and for small and constant w and , we obtain the following second-order differential equation:
which reduces to Equation (17) for cold dark matter, where . In the case of a constant w, the matter would not follow an behavior as a function of time, but it would scale with , such that the lensing Equation (127) would now read
Taking the appropriate ratios of the two equations above, we can obtain as we did for Equation (137), but this time, some extra term appear:
where and . Both and reduce to zero for standard cold dark matter, such that we recover Equation (137) exactly in that case. For a barotropic fluid such that , and . In this case, we have again an MI estimator for , provided we know . On the other hand, if , we see that this estimation of contains the growth rate f, which we argued is not a model-independent observable in the linear regime. However, an extension of this formalism to the quasilinear scales [78] has shown that f can indeed be recovered in a model-independent way, using observations of the bispectrum.
13. The Linear, Scalar, Quasi-Static, Model-Independent Horndeski Observables
For the previous sections, we can draw a remarkable conclusion. Since is the only linear, quasi-static, MI cosmological observable, we see that, among the HL parameters, only the time-dependent functions (see Equation (23)) share the same property. The GW speed constraint has already measured . Assuming this can be extended at all times, such that , and assuming H is also measured in an MI way, we see that what can still be measured at the linear perturbation level are the combinations
which correspond to the two scales one can measure in . If vanishes, , and , as in the standard case. As we have already seen, this happens only in two cases: for and for .
14. Data
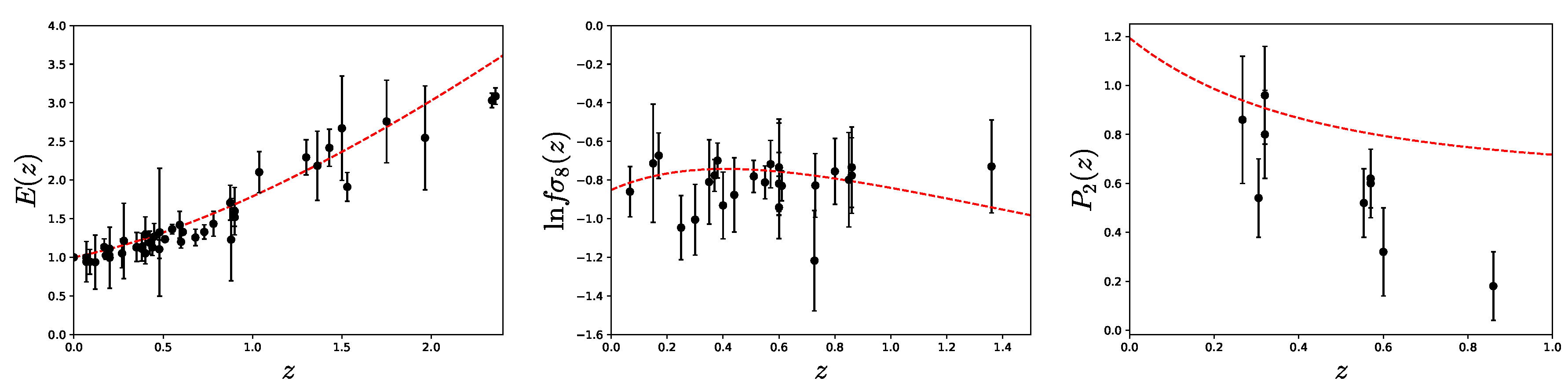
In the next sections, we obtain an estimate of using all the currently available data (This section and the next two are a summary of a published paper by A. M. Pinho, S. Casas, and L. Amendola, entitled Model-Independent Reconstruction of the Linear Anisotropic Stress , arXiv:1805.00025, JCAP11(2018)027). The first step is to reconstruct (and therefore ), , and using all the currently available relevant data, shown in Figure 1, where we also plot the CDM the curves of the different functions using the cosmological parameters from the TT+lowP+lensing Planck 2015 best-fits [67]. A similar analysis, with a much smaller dataset than is available, was carried out also in [86].
Figure 1.
Data sets used in this work (black dots with error bars), plotted with the corresponding theoretical CDM prediction as a function of redshift (solid red line), using a Planck 2015 cosmology. Left panel: data. We used the Planck 2015 value of to convert some of the data points from to (see main text). Central panel: Plot of the logarithm of the data points. Right panel: Data set for , obtained using data and the relation (136) that converts between different notations. For , we see a larger discrepancy between CDM and the data points, which was also noted in [85] and references therein.
For the Hubble parameter measurements, we have used the most recent compilation of data from [87], including the measurements from [88,89,90,91], the Baryon Oscillation Spectroscopic Survey (BOSS) [92,93,94], and the Sloan Digital Sky Survey (SDSS) [95,96]. In this compilation, the majority of the measurements were obtained using the cosmic chronometric technique. This method infers the expansion rate by taking the difference in redshift of a pair passively-evolving galaxies. The remaining measurements were obtained through the position of the BAO peaks in the power spectrum of a galaxy distribution for a given redshift. For this case, the measurements from [92] and [93] are obtained using the BAO signal in the Lyman- forest distribution alone or cross-correlated with quasi-stellar objects (QSOs) (for the details of the method, we refer the reader to the original papers). The reference [96] provides the covariance matrix of three measurements from the radial BAO galaxy distribution. To this compilation, we add the results from WiggleZ [97]. In addition to these, we use the recent results from [98] where a compilation of type Ia supernovae from CANDELS and CLASH Multi-cycle Treasury programs were analyzed, yielding a few tight measurements of the expansion rate .
The data include the results from KiDS+2dFLenS+GAMA [85], i.e., a joint analysis of weak gravitational lensing, galaxy clustering, and redshift space distortions. We also include image and spectroscopic measurements of the Red Cluster Sequence Lensing Survey (RCSLenS) [99], where the analysis combines the Canada–France–Hawaii Telescope Lensing Survey (CFHTLenS), the WiggleZ Dark Energy Survey, and the Baryon Oscillation Spectroscopic Survey (BOSS). The work of VIMOS Public Extragalactic Redshift Survey (VIPERS) [84] is also accounted for in our data. The latter reference uses redshift-space distortions and galaxy–galaxy lensing.
These sources provide measurements in real space within the scales h Mpc and in the linear regime, which is the one in which we are interested. They have been obtained over a relatively narrow range of scales , meaning that we can consider them relative to the -th Fourier component, as a first approximation. In any case, the discussion about the k-dependence of is beyond the scope of this work, so the final result can be seen as an average over the range of scales effectively employed in the observations. Moreover, in the estimation of , based on [81], one assumes that the redshift of the lens galaxies can be approximated by a single value. With these approximations, indeed is equivalent to ; otherwise, represents some sort of average value along the line of sight. We caution that these approximations can have a systematic effect both on the measurement of and on our derivation of . In future work, we will quantify the level of bias possibly introduced by these approximations in our estimate.
Finally, the quantity is connected to the parameter. Our data include measurements from the 6dF Galaxy Survey [100], the Subaru FMOS galaxy redshift survey (FastSound) [101], WiggleZ [97], the VIMOS-VLT Deep Survey (VVDS) [102], the VIMOS Public Extragalactic Redshift Survey (VIPERS) [84,103,104,105], and the Sloan Digital Sky Survey (SDSS) [96,106,107,108,109,110,111,112]. The values from [113,114] will not be considered since the value is not directly reported.
15. Reconstruction of Functions from Data
The only difficulty in obtaining is that we need to take the ratios at the same redshift, while we have data points at different redshifts, and that we need to take derivatives of and . This essentially means we need to have a reliable way to interpolate the data to reconstruct the underlying behavior.
There is no universally accepted method to interpolate data. Depending on how many assumptions one makes regarding the theoretical model, e.g., whether the reconstructed functions need just to be continuous, or smooth, depending on few or many parameters, etc., one obtains unavoidably different results, especially in the final errors. Here, we consider and compare three methods to obtain the value of : binning, the Gaussian process (GP), and generalized linear regression.
The first, and simplest, method assembles the data into bins. This consists of dividing the data into a particular redshift interval (bin), and for each of these intervals one calculates the average value of the subset of the data contained in that bin. The corresponding redshift and error of each bin are computed as weighted averages.
Another way to reconstruct a continuous function from a dataset is by using a Gaussian process algorithm as explained in [115]. This process can be regarded as the generalization of Gaussian distributions to function space since it provides a distribution over functions instead of a distribution of a random variable. Considering a dataset , where represents deterministic variables and random variables, the goal is to obtain a continuous function that best describes the dataset. A function f evaluated at a point x is a Gaussian random variable with mean and variance . The values depend on the function value evaluated at other points (particularly if they are close points). The relation between these can be given by a covariance function . The covariance function is in principle arbitrary. Since we are interested in reconstructing the derivatives of the data, a Gaussian covariance function expressed as
is the chosen function since it is the most common and has the least number of additional parameters. This function depends on the hyperparameters and ℓ, which allow us to set the strength of the covariance function. These hyperparameters can be regarded as the typical scale and change in the x and y direction. The full covariance function takes the data covariance matrix C into account by . The log likelihood is then
where is the determinant of . The distribution Equation (146) is usually sharply peaked and so we maximize the distribution to optimize the hyperparameters, although this is an approximation to the marginalization process and it may not be the best approach for all datasets. We employ the Python publicly available GaPP code from Seikel et al. (2012) [116].
As a third method, we use a generalized linear regression. Let us assume we have N data , one for each value of the independent variable and that
where are errors (random variables) which are assumed to be distributed as Gaussian variables. Here, represents theoretical functions that depend linearly on a number of parameters :
where are functions of the variable , chosen to be simple powers, and , such that represents polynomials of order n.
The order of the polynomial is in principle arbitrary, up to the number N of datapoints. However, it is clear that, with too many free parameters, the resulting will be very close to zero, i.e., statistically unlikely. At the same time, too many parameters also render the numerical Fisher matrix computationally unstable (producing, e.g., a non-positive definite matrix) and the polynomial wildly oscillating. On the other hand, too few parameters restrict the allowed family of functions. Therefore, we select the order of the polynomial function by choosing the degree for which the reduced chi-squared , is closest to unity and such that the Fisher matrix is positive definite.
16. Results
Let us now discuss the results of the final observable for each of these methods. The binning method contains fewer assumptions compared to the polynomial regression or Gaussian process methods. It is essentially a weighted average over the data points and the error bars at each redshift bin. Since we need to take derivatives in order to calculate and , and we have few data points, we opt to compute finite difference derivatives. This has the caveat that it introduces correlations among the errors of the function and its derivatives, that we cannot take into account with this simple method. Moreover, for the binning method, we do not take into account possible non-diagonal covariance matrices for the data, which we do for polynomial regression and the Gaussian process reconstruction.
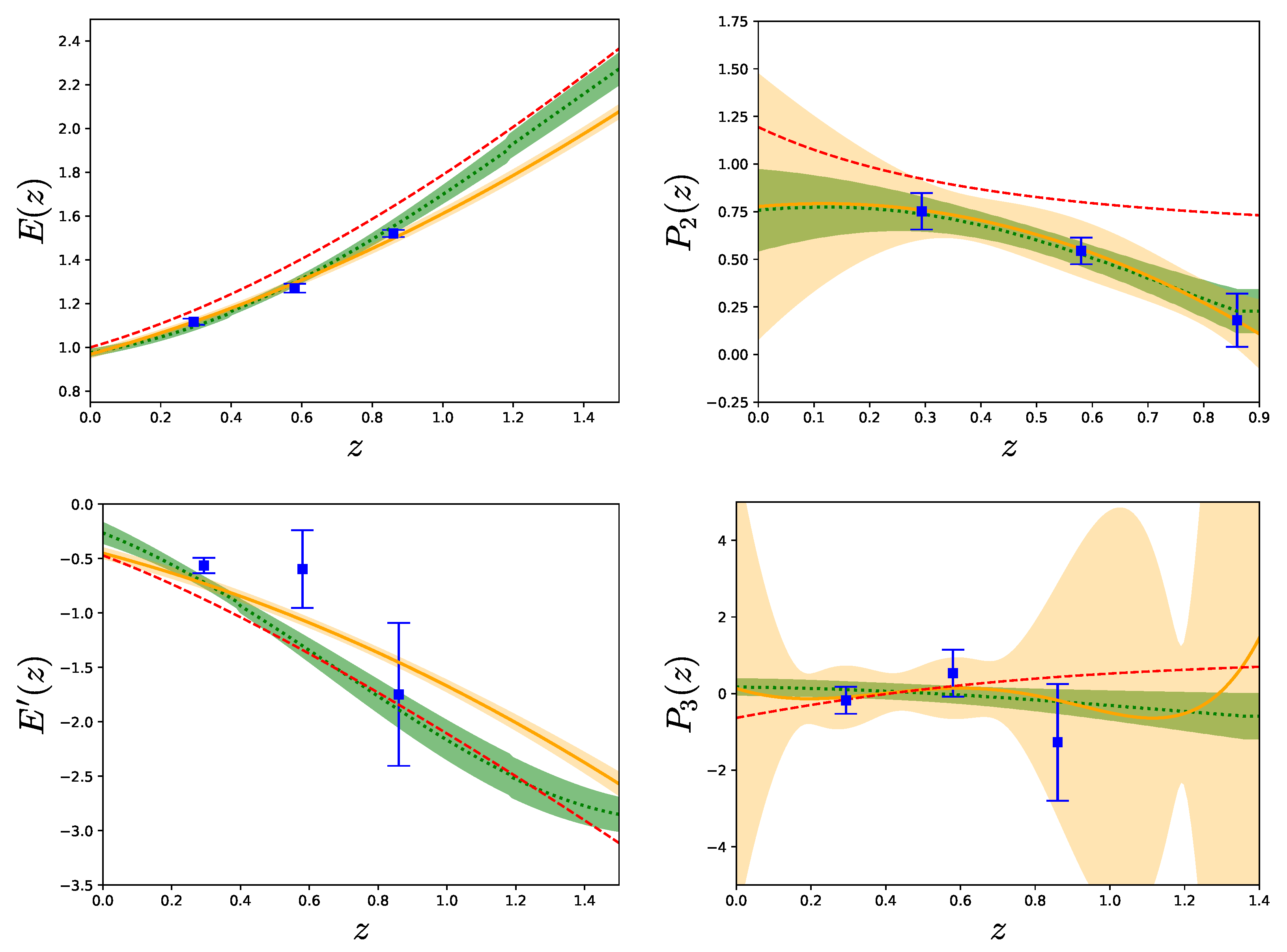
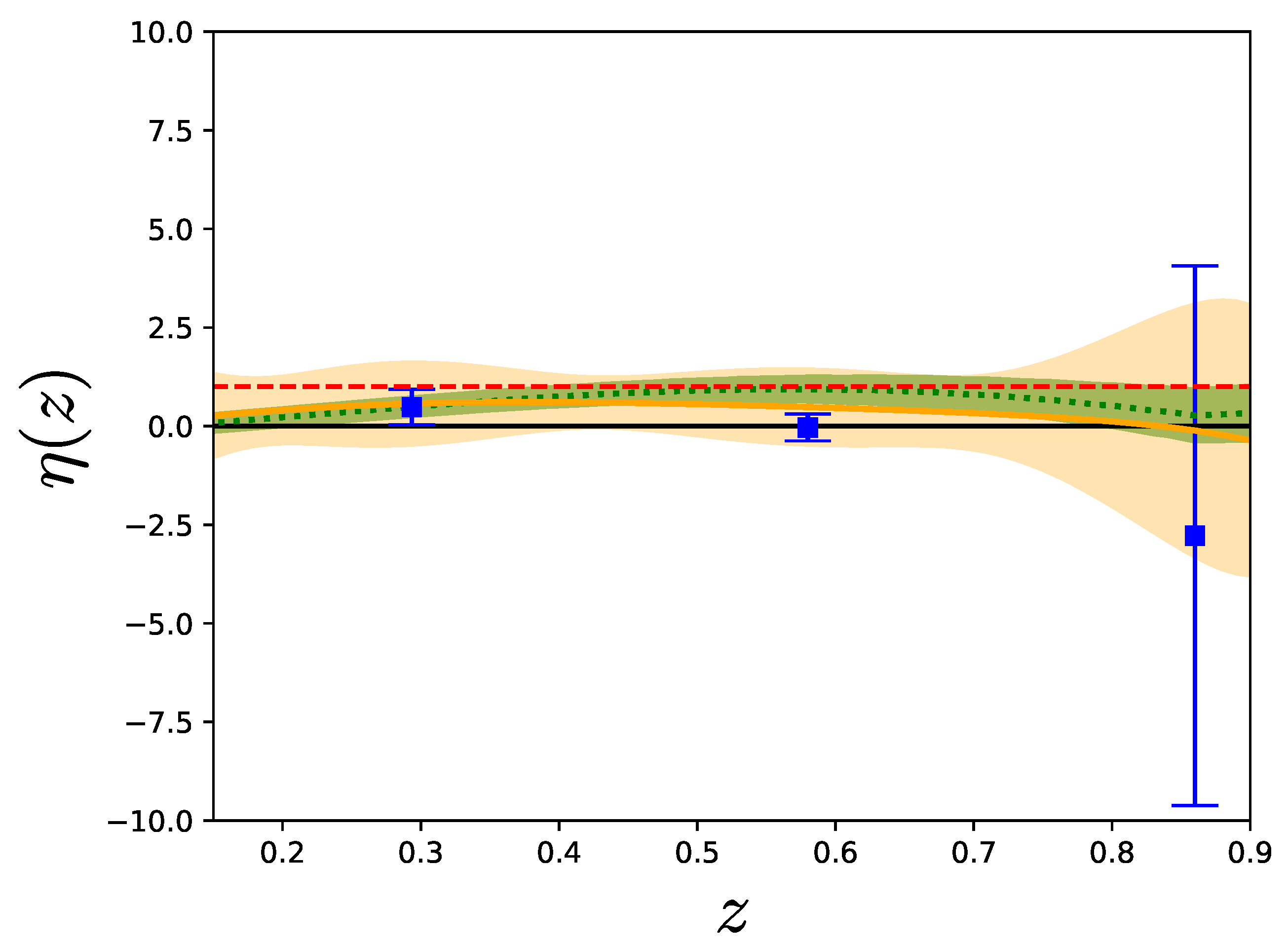
Figure 2 shows the reconstructed functions obtained by the binning method, the Gaussian process, and polynomial regression, alongside the theoretical prediction of the standard CDM model. In all cases, the error bars or the bands represent the uncertainty.
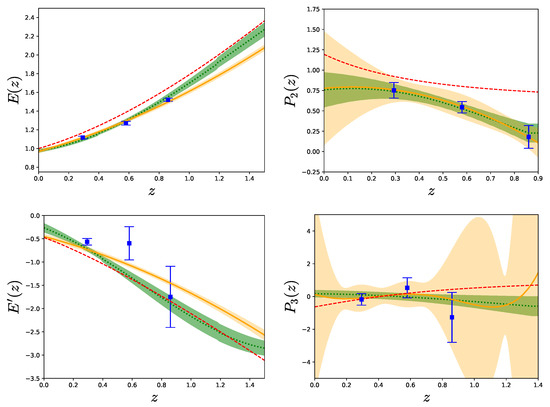
Figure 2.
Comparison of the three reconstruction methods for each of the model-independent variables. The binning method is shown in blue squares with error bars, the Gaussian process is shown as a green dotted line with green bands, and polynomial regression is shown as a solid yellow line with yellow bands. All of them depict the uncertainty. Left panel: Plot of the reconstructed function on the top and its derivative on the bottom. Right panel: Plot of the reconstructed function on the top and the reconstructed function on the bottom. For each case, we show the theoretical prediction of our reference CDM model as a red dashed curve.
With the binning method, the number of bins is limited by the maximum number of existing data redshifts from the smallest data set corresponding to one of our model-independent observables. In this case, this is the quantity , for which we have effectively only three redshift bins. There are nine data points, but most of them are very close to each other in redshift, due to being measured by different collaborations or at different scales in real space for the same z. As explained in the data section above, we only regard this data as an average over different scales, assuming that non-linear corrections have been correctly taken into account by the respective experimental collaboration. Since we do not have to take derivatives of , or equivalently , this leaves us with three possible redshift bins, centered at , , and , all of them with an approximate bin width of . At these redshifts, we obtain , , and . These values and the estimation of the intermediate model-independent quantities can be seen in Table A2.
Regarding the Gaussian process method, we computed the normalized Hubble function and its derivative, and , with the dgp module of the GaPP code. We reconstructed and for the redshift interval of the data using the Gaussian function as the covariance function and the initial values of the hyperparameters that were later estimated by the code. The same procedure was done for the data. We obtained, for the and functions, the hyperparameters and and, for the function, and .
For the observable, the hyperparameters obtained by the GaPP code led to a very flat and unrealistic reconstruction, so we took another approach for obtaining the optimal hyperparameters. We sampled the logarithm of the marginal likelihood on a grid of hyperparameters , from 0.01 to 2, setting thus a prior with the redshift range of the dataset, and 300 points equally separated in log-space for each dimension. We remind the reader that the hyperparameter constrains the typical scale on the independent variable z. Thus, as an additional prior, we impose that needs to be smaller than the redshift range of the data, which was not guaranteed by the default GaPP code. We then chose a pair of hyperparameters corresponding to the maximum of the log-marginal likelihood. Therefore, for the data, we obtained and . Its reconstructed derivative can be seen in the lower right panel of Figure 2. The function remains relatively flat, compared to the one given by other methods, but this approach has improved the determination of this observable.
Regarding the choice of the kernel function, several functions were compared, each of them with a different number of parameters, to see the impact on the output. We tested the Gaussian kernel with two parameters, (): the rational quadratic kernel with three parameters and the double Gaussian kernel with four parameters (see the original reference for the explicit implemented formula [116]). We performed tests using the data obtained with the cosmic chronometer technique and the data. Our tests show that the different choices shift the reconstructed function up to on its central value compared to the Gaussian kernel function. This happens for , but the effect is negligible for . Taking into account the above choices and procedure, we report that with the Gaussian process method we obtain , , and .
For the polynomial regression method, we find , , and . Note that we applied the criteria of a closest to one and a positive definite Fisher matrix to choose the order of the polynomial for each of the datasets. These criteria led to a choice of a polynomial of order 3 for the and data and order 6 for the data. These polynomials can be seen in Figure 2 as solid yellow lines, together with their uncertainty bands. The higher order of the polynomial of explains the “bumpiness” of the reconstruction of , leading to larger errors on this observable in comparison to the GP method.
In Figure 3, we show the reconstructed as a function of redshift with the three different methods, again with GP in a green dashed line, polynomial regression in a yellow solid line, and the binning method in blue squares with error bars. It is possible to conclude that the methods are consistent with each other, within their uncertainties, and that in most bins the results are consistent with the standard gravity scenario. We find that the error bars of the Gaussian process reconstruction are generally smaller than the other methods, such that at the lowest redshift, GP is not compatible with at nearly , while in the case of the binning method at the intermediate redshift, , the tension is nearly .
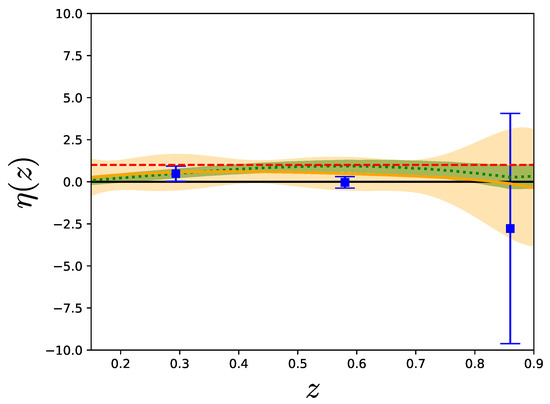
Figure 3.
Plot of the reconstructed as a function of redshift, using the binning method (blue squares), the Gaussian process (green dotted line), and linear regression (yellow solid line). The corresponding error bands (error bars for the binning method), represent the 1 estimated error on the reconstruction. As a reference, we show, in a dashed red line, the value in a standard gravity scenario.
Finally, we can combine the estimates at three redshifts of Table A2 into a single value. Assuming a constant in this entire observed range and performing a simple weighted average, we find (binning), (Gaussian process), and (polynomial regression). The Gaussian process method yields the smallest error and excludes standard gravity. However, despite being sometimes advertised as “model-independent”, we believe that this method actually makes a strong assumption, since it compresses the ignorance of the reconstruction into a kernel function that depends on two or a small number of parameters, which are often not even fully marginalized over, which was done in our case. Furthermore, the binning method taken at face value would rule out standard gravity. However, as already mentioned, we did not take into account the correlation induced by the finite differences, and this might have decreased the overall error. Overall, we think the polynomial regression method is the most satisfactory one, providing the best compromise between the least number of assumptions and the best estimation of the data derivative. Therefore, we consider it as our “fiducial” result.
17. Conclusions
Measuring the properties of gravity at large scales will be one of the main tasks of cosmology for the next few years. Several large observational campaigns that are underway, or will soon be [117,118,119,120,121], will collect enough data on galaxy clustering and lensing to render this task possible to a high level of accuracy.
In order to test gravity, one has to provide an alternative, either a full model or at least some parametrization, that goes beyond Einstein’s gravity. Here we chose to consider the Horndeski Lagrangian because, although it is based on a single scalar field, it displays most of the properties that make modified gravity models such a rich area of research. We connected a more theoretically oriented parameterization, the parameters of [22], with more phenomenologically oriented ones, the parameters. To gain a deeper physical understanding, we also discussed some interesting limiting cases: how the Newtonian potentials look in real space, and the impact of the constraints from gravitational wave speed.
The first practical goal in cosmology is to test and possibly rule out specific models of gravity and background expansion. For instance, one can rule out CDM in a number of ways, the simplest of which being measuring a deviation from the predicted behavior (which is not equivalent, as we have seen, to simply finding deviations from a equation of state). Models in which gravity is modified can often be designed to have a perfect CDM background, so it is necessary to test them at the perturbation level.
Here, however, a problem arises, namely that many more assumptions generally need to be made. Some of them, listed in Section 9, are in some sense of fundamental character, and we follow them in this work. However, most cosmological analyses that test gravity assume, in addition, one or more of the following assumptions: (1) that the initial conditions are given by a simple inflationary spectrum described by one or two parameters; (2) that the cosmological evolution at a z value larger than a few is given by a pure CDM-dominated universe living in standard gravity; (3) that the linear bias depends only on time and not on scale; and (4) that the value of some parameters, such as obtained from CMB analyses assuming CDM, can also be applied to different models.
We have shown that the statistics called can be measured without any of these four assumptions. These statistics can be used as an estimator of the anisotropic stress parameter , one of the two phenomenological functions of linearized, scalar, sub-horizon modified gravity. In this sense, we say that is (relatively) model-independent. If differs from unity, either gravity is modified, or at least one of the four “fundamental” assumptions of Section 9 are false.
We have provided a preliminary estimate of based on currently available data, in the redshift range . The full k- and z-dependence is still inaccessible with current data. According to [25], the Euclid mission will be able to measure to a few percent, which is thus almost two orders of magnitude better than current values, and will be able to begin placing interesting limits on the k- and z-dependence. As the philosopher of science Alexandre Koyré said concerning the emergence of modern science (Koyré, A. (1948). Du monde de l’à peu près à l’univers de la précision. In A. Koyré (Ed.), Etudes d’histoire de la pensée philosophique (pp. 341–362). Paris: Gallimard.), and with regard to measuring gravity at cosmological scales, we will finally move “from the world of approximation to the universe of precisi on.”
Acknowledgments
We acknowledge DFG for support through the TR33 project, “The Dark Universe.” We thank Alejandro Guarnizo Trilleras, Jiaming Zhao, Adrià Gómez, Guillem Domènech, Martin Kunz, Ippocratis Saltas, Mariele Motta, and Ignacy Sawicki for discussions and collaboration on these topics. We also wish to thank Jiaming Zhao for his valuable comments. D.B. acknowledges support from the Attraccíon del Talento Científico en Salamanca programme during the last stages of this work. A.M.P. gratefully acknowledges the support by the Landesgraduiertenförderung (LGF) grant of the Graduiertenakademie Universität Heidelberg. S.C. acknowledges support from CNES and CNRS grants.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A. Background Equations of Motion of the Horndeski Lagrangian
The equations of motion for a flat Friedmann–Lemaître–Robertson–Walker (FLRW) metric are [17,22]
Here, are the conserved background energy density and the pressure of matter, respectively; analogously and are the background energy density and pressure of the Horndeski field, defined as
where is defined in Equation (55), and in Equation (58). Since in the literature there are various definitions of the energy density associated with the scalar field, we report in Table A1 the relation between the one adopted in this work and others. (We thank Jiaming Zhao for pointing out potential issues related to this.) Following [22], we write the equation of motion of the scalar field as a (non-)conservation equation of the “shift-charge density” n,
with
and with the non-conservation term, driven by a violation of the shift symmetry , given by the derivative of :

Table A1.
Comparison table for the different definition of energy density and pressure of the scalar field.
Table A1.
Comparison table for the different definition of energy density and pressure of the scalar field.
| This Work | Ref. [122] | Ref. [22] | |
|---|---|---|---|
| Energy density | |||
| Pressure |

Table A2.
The reconstructed or measured model-independent variables at three different redshifts , together with their errors, for each of the reconstruction methods. The polynomial regression method is compatible with the CDM scenario, while the other two methods show some tension at lower redshifts.
Table A2.
The reconstructed or measured model-independent variables at three different redshifts , together with their errors, for each of the reconstruction methods. The polynomial regression method is compatible with the CDM scenario, while the other two methods show some tension at lower redshifts.
| Method | Parameter | Redshift Bins | Weighted Mean | ||
|---|---|---|---|---|---|
| Binning | |||||
| Gaussian Process | |||||
| Polynomial Regression | |||||
References
- Lovelock, D. The Four-Dimensionality of Space and the Einstein Tensor. J. Math. Phys. 1972, 13, 874–876. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Papantonopoulos, E. (Ed.) Modifications of Einstein’s Theory of Gravity at Large Distances; Lecture Notes in Physics; Springer: Berlin, Germany, 2015; Volume 892. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009, 79, 084003. [Google Scholar] [CrossRef]
- Zumalacárregui, M.; García-Bellido, J. Transforming gravity: From derivative couplings to matter to second-order scalar-tensor theories beyond the Horndeski Lagrangian. Phys. Rev. D 2014, 89, 064046. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Exploring gravitational theories beyond Horndeski. J. Cosmol. Astropart. Phys. 2015, 1502, 018. [Google Scholar] [CrossRef]
- Gleyzes, J.; Langlois, D.; Piazza, F.; Vernizzi, F. Healthy theories beyond Horndeski. Phys. Rev. Lett. 2015, 114, 211101. [Google Scholar] [CrossRef]
- Crisostomi, M.; Koyama, K.; Tasinato, G. Extended Scalar-Tensor Theories of Gravity. J. Cosmol. Astropart. Phys. 2016, 1604, 044. [Google Scholar] [CrossRef]
- Crisostomi, M.; Hull, M.; Koyama, K.; Tasinato, G. Horndeski: Beyond, or not beyond? J. Cosmol. Astropart. Phys. 2016, 1603, 038. [Google Scholar] [CrossRef]
- Ben Achour, J.; Langlois, D.; Noui, K. Degenerate higher order scalar-tensor theories beyond Horndeski and disformal transformations. Phys. Rev. D 2016, 93, 124005. [Google Scholar] [CrossRef]
- Langlois, D.; Noui, K. Degenerate higher derivative theories beyond Horndeski: Evading the Ostrogradski instability. J. Cosmol. Astropart. Phys. 2016, 1602, 034. [Google Scholar] [CrossRef]
- Kobayashi, T. Horndeski Theory and Beyond: A Review; IOP Publishing Ltd.: Bristol, UK, 2019. [Google Scholar]
- Bettoni, D.; Liberati, S. Disformal invariance of second order scalar-tensor theories: Framing the Horndeski action. Phys. Rev. D 2013, 88, 084020. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Kobayashi, T.; Tsujikawa, S. Effective gravitational couplings for cosmological perturbations in the most general scalar–tensor theories with second-order field equations. Phys. Lett. B 2011, 706, 123–133. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. Conditions for the cosmological viability of the most general scalar-tensor theories and their applications to extended Galileon dark energy models. J. Cosmol. Astropart. Phys. 2012, 1202, 007. [Google Scholar] [CrossRef]
- Ostrogradski, M. Mémoires sur les équations différentielles, relatives au problème des isopérimètres. Mem. Ac. St. Petersbourg 1850, VI, 385–517. [Google Scholar]
- Woodard, R.P. Ostrogradsky’s theorem on Hamiltonian instability. Scholarpedia 2015, 10, 32243. [Google Scholar] [CrossRef]
- Chen, T.j.; Fasiello, M.; Lim, E.A.; Tolley, A.J. Higher derivative theories with constraints: Exorcising Ostrogradski’s Ghost. J. Cosmol. Astropart. Phys. 2013, 1302, 042. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I. Maximal freedom at minimum cost: Linear large-scale structure in general modifications of gravity. J. Cosmol. Astropart. Phys. 2014, 7, 050. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Weinberg, S. Damping of tensor modes in cosmology. Phys. Rev. D 2004, 69, 023503. [Google Scholar] [CrossRef]
- Amendola, L.; Kunz, M.; Motta, M.; Saltas, I.D.; Sawicki, I. Observables and unobservables in dark energy cosmologies. Phys. Rev. D 2013, 87, 023501. [Google Scholar] [CrossRef]
- Könnig, F.; Amendola, L. Instability in a minimal bimetric gravity model. Phys. Rev. D 2014, 90, 044030. [Google Scholar] [CrossRef]
- De Felice, A.; Heisenberg, L.; Kase, R.; Mukohyama, S.; Tsujikawa, S.; Zhang, Y.l. Effective gravitational couplings for cosmological perturbations in generalized Proca theories. Phys. Rev. D 2016, 94, 044024. [Google Scholar] [CrossRef]
- Vardanyan, V.; Amendola, L. How can we tell whether dark energy is composed of multiple fields? Phys. Rev. D 2015, 92, 024009. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of cold dark matter halos. Astrophys. J. 1996, 462, 563–575. [Google Scholar] [CrossRef]
- Pizzuti, L.; Sartoris, B.; Amendola, L.; Borgani, S.; Biviano, A.; Umetsu, K.; Mercurio, A.; Rosati, P.; Balestra, I.; Caminha, G.B.; et al. CLASH-VLT: Constraints on f(R) gravity models with galaxy clusters using lensing and kinematic analyses. J. Cosmol. Astropart. Phys. 2017, 7, 023. [Google Scholar] [CrossRef]
- Dodelson, S. Modern Cosmology; Academic Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Kreisch, C.D.; Komatsu, E. Cosmological Constraints on Horndeski Gravity in Light of GW170817. J. Cosmol. Astropart. Phys. 2018, 1812, 030. [Google Scholar] [CrossRef]
- Saltas, I.D.; Sawicki, I.; Amendola, L.; Kunz, M. Anisotropic Stress as a Signature of Nonstandard Propagation of Gravitational Waves. Phys. Rev. Lett. 2014, 113, 191101. [Google Scholar] [CrossRef]
- Sawicki, I.; Saltas, I.D.; Motta, M.; Amendola, L.; Kunz, M. Nonstandard gravitational waves imply gravitational slip: On the difficulty of partially hiding new gravitational degrees of freedom. Phys. Rev. D 2017, 95, 083520. [Google Scholar] [CrossRef]
- Lombriser, L.; Lima, N.A. Challenges to self-acceleration in modified gravity from gravitational waves and large-scale structure. Phys. Lett. B 2017, 765, 382–385. [Google Scholar] [CrossRef]
- Linder, E.V. No slip gravity. J. Codmol. Astropart. Phys. 2018, 3, 005. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Adelberger, E.G.; Heckel, B.R.; Nelson, A.E. Tests of the Gravitational Inverse-Square Law. Annu. Rev. Nucl. Part. Sci. 2003, 53, 77–121. [Google Scholar] [CrossRef]
- Patrignani, C. Review of Particle Physics. Chin. Phys. 2016, C40, 100001. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef]
- Vainshtein, A.I. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C. An introduction to the Vainshtein mechanism. Class. Quant. Grav. 2013, 30, 184001. [Google Scholar] [CrossRef]
- Pietroni, M. Dark energy condensation. Phys. Rev. D 2005, 72, 043535. [Google Scholar] [CrossRef]
- Olive, K.A.; Pospelov, M. Environmental dependence of masses and coupling constants. Phys. Rev. D 2008, 77, 043524. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Symmetron Fields: Screening Long-Range Forces Through Local Symmetry Restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef] [PubMed]
- Hinterbichler, K.; Khoury, J.; Levy, A.; Matas, A. Symmetron Cosmology. Phys. Rev. D 2011, 84, 103521. [Google Scholar] [CrossRef]
- Copi, C.J.; Davis, A.N.; Krauss, L.M. New Nucleosynthesis Constraint on the Variation of G. Phys. Rev. Lett. 2004, 92, 171301. [Google Scholar] [CrossRef] [PubMed]
- Dent, T.; Stern, S.; Wetterich, C. Primordial nucleosynthesis as a probe of fundamental physics parameters. Phys. Rev. D 2007, 76, 063513. [Google Scholar] [CrossRef]
- Iocco, F.; Mangano, G.; Miele, G.; Pisanti, O.; Serpico, P.D. Primordial nucleosynthesis: From precision cosmology to fundamental physics. Phys. Rep. 2009, 472, 1–76. [Google Scholar] [CrossRef]
- Bettoni, D.; Ezquiaga, J.M.; Hinterbichler, K.; Zumalacárregui, M. Speed of Gravitational Waves and the Fate of Scalar-Tensor Gravity. Phys. Rev. D 2017, 95, 084029. [Google Scholar] [CrossRef]
- Lombriser, L.; Taylor, A. Breaking a Dark Degeneracy with Gravitational Waves. J. Cosmol. Astropart. Phys. 2016, 1603, 031. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef]
- Sakstein, J.; Jain, B. Implications of the Neutron Star Merger GW170817 for Cosmological Scalar-Tensor Theories. Phys. Rev. Lett. 2017, 119, 251303. [Google Scholar] [CrossRef]
- Amendola, L.; Bettoni, D.; Domènech, G.; Gomes, A.R. Doppelgänger dark energy: Modified gravity with non-universal couplings after GW170817. J. Cosmol. Astropart. Phys. 2018, 1806, 029. [Google Scholar] [CrossRef]
- Amendola, L.; Ballesteros, G.; Pettorino, V. Effects of modified gravity on B-mode polarization. Phys. Rev. D 2014, 90, 043009. [Google Scholar] [CrossRef]
- Amendola, L.; Kunz, M.; Saltas, I.D.; Sawicki, I. The fate of large-scale structure in modified gravity after GW170817 and GRB170817A. Phys. Rev. Lett. 2018, 120, 131101. [Google Scholar] [CrossRef]
- Nersisyan, H.; Lima, N.A.; Amendola, L. Gravitational wave speed: Implications for models without a mass scale. arXiv 2018, arXiv:1801.06683. [Google Scholar]
- Amendola, L.; Sawicki, I.; Kunz, M.; Saltas, I.D. Direct detection of gravitational waves can measure the time variation of the Planck mass. J. Cosmol. Astropart. Phys. 2018, 2018, 030. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves: Volume 1: Theory and Experiments; Gravitational Waves; OUP: Oxford, UK, 2008. [Google Scholar]
- Nishizawa, A. Generalized framework for testing gravity with gravitational-wave propagation. I. Formulation. Phys. Rev. D 2018, 97, 104037. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. The gravitational-wave luminosity distance in modified gravity theories Phys. Rev. D 2018, 97, 104066. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big Bang Nucleosynthesis: 2015. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galactic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. Astrophys J. 2018, 855, 136. [Google Scholar] [CrossRef]
- Planck Collaboration; Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Hildebrandt, H.; Viola, M.; Heymans, C.; Joudaki, S.; Kuijken, K.; Blake, C.; Erben, T.; Joachimi, B.; Klaes, D.; Miller, L.; et al. KiDS-450: Cosmological parameter constraints from tomographic weak gravitational lensing. Month. Not. R. Astron. Soc. 2017, 465, 1454–1498. [Google Scholar] [CrossRef]
- Barros, B.J.; Amendola, L.; Barreiro, T.; Nunes, N.J. Coupled quintessence with a ΛCDM background: Removing the σ8 tension. J. Cosmol. Astropart. Phys. 2019, 2019, 007. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Bullock, J.S.; Governato, F.; Kuzio de Naray, R.; Peter, A.H.G. Cold dark matter: Controversies on small scales. Proc. Natl. Acad. Sci. USA 2014, 112, 12249–12255. [Google Scholar] [CrossRef]
- Abbott, B.P.; The LIGO Scientific Collaboration and The Virgo Collaboration. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Kunz, M. Degeneracy between the dark components resulting from the fact that gravity only measures the total energy-momentum tensor. Phys. Rev. D 2009, 80, 123001. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Hu, W. Baryonic Features in the Matter Transfer Function. Astrophys J. 1998, 496, 605–614. [Google Scholar] [CrossRef]
- Liske, J. On the cosmological distance and redshift between any two objects. Month. Not. R. Astron. Soc. 2000, 319, 557–561. [Google Scholar] [CrossRef][Green Version]
- Baldi, M.; Pettorino, V.; Amendola, L.; Wetterich, C. Oscillating nonlinear large scale structure in growing neutrino quintessence. Mon. Not. R. Astron. Soc. 2011, 418, 214. [Google Scholar] [CrossRef]
- Kaiser, N. Clustering in real space and in redshift space. Mon. Not. R. Astron. Soc. 1987, 227, 1–21. [Google Scholar] [CrossRef]
- Seo, H.J.; Eisenstein, D.J. Probing Dark Energy with Baryonic Acoustic Oscillations from Future Large Galaxy Redshift Surveys. Asotrphys. J. 2003, 598, 720–740. [Google Scholar] [CrossRef]
- Rampf, C.; Villa, E.; Amendola, L. Quasilinear observables in dark energy cosmologies. Phys. Rev. D 2017, 95, 123516. [Google Scholar] [CrossRef]
- Motta, M.; Sawicki, I.; Saltas, I.D.; Amendola, L.; Kunz, M. Probing dark energy through scale dependence. Phys. Rev. D 2013, 88, 124035. [Google Scholar] [CrossRef]
- Lahav, O.; Lilje, P.B.; Primack, J.R.; Rees, M.J. Dynamical effects of the cosmological constant. Month. Not. R. Astron. Soc. 1991, 251, 128–136. [Google Scholar] [CrossRef]
- Leonard, C.D.; Ferreira, P.G.; Heymans, C. Testing gravity with EG: Mapping theory onto observations. J. Cosmol. Astropart. Phys. 2015. [Google Scholar] [CrossRef]
- Zhang, P.; Liguori, M.; Bean, R.; Dodelson, S. Probing Gravity at Cosmological Scales by Measurements which Test the Relationship between Gravitational Lensing and Matter Overdensity. Phys. Rev. Lett. 2007, 99, 141302. [Google Scholar] [CrossRef] [PubMed]
- Reyes, R.; Mandelbaum, R.; Seljak, U.; Baldauf, T.; Gunn, J.E.; Lombriser, L.; Smith, R.E. Confirmation of general relativity on large scales from weak lensing and galaxy velocities. Nature 2010, 464, 256–258. [Google Scholar] [CrossRef]
- De La Torre, S.; Jullo, E.; Giocoli, C.; Pezzotta, A.; Bel, J.; Granett, B.R.; Guzzo, L.; Garilli, B.; Scodeggio, M.; Bolzonella, M.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS). Gravity test from the combination of redshift-space distortions and galaxy-galaxy lensing at 0.5 < z < 1.2. Astron. Astrophys. 2017, 608, A44. [Google Scholar] [CrossRef]
- Amon, A.; Blake, C.; Heymans, C.; Leonard, C.D.; Asgari, M.; Bilicki, M.; Choi, A.; Erben, T.; Glazebrook, K.; Harnois-Déraps, J.; et al. KiDS+2dFLenS+GAMA: Testing the cosmological model with the Eg statistic. Mon. Not. R. Astron. Soc. 2018, 479, 3422–3437. [Google Scholar] [CrossRef]
- Trilleras, A.G. A Model-Independent Approach to Dark Energy Cosmologies: Current and Future Constraints. Ph.D. Thesis, Rupert-Karls-Universität, Heidelberg, Germany, 2015. [Google Scholar]
- Yu, H.; Ratra, B.; Wang, F.Y. Hubble Parameter and Baryon Acoustic Oscillation Measurement Constraints on the Hubble Constant, the Deviation from the Spatially-Flat Lambda cdm Model, The Deceleration-Acceleration Transition Redshift, and Spatial Curvature. Astrophys. J. 2018, 856, 3. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2004, 71. [Google Scholar] [CrossRef]
- Stern, D.; Jimenez, R.; Verde, L.; Stanford, S.A.; Kamionkowski, M. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. II. A Spectroscopic Catalog of Red Galaxies in Galaxy Clusters. Astrophys. J. Suppl. Ser. 2010, 188, 280. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z 1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 1208, 006. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.G.; Pieri, M.M.; Hamilton, J.C.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
- Font-Ribera, A.; Kirkby, D.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, É.; Bailey, S.; Bhardwaj, V.; Bautista, J.; et al. Quasar-Lyman α Forest Cross-Correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 1405, 027. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z0.45: Direct evidence of the epoch of cosmic re-acceleration. J. Cosmol. Astropart. Phys. 2016, 5, 014. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, H.; Yuan, S.; Liu, S.; Zhang, T.J.; Sun, Y.C. Four New Observational H(z) Data From Luminous Red Galaxies of Sloan Digital Sky Survey Data Release Seven. Res. Astron. Astrophys. 2014, 14, 1221. [Google Scholar] [CrossRef]
- Alam, S.; BOSS Collaboration. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2016, 470, 2617–2652. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z<1. Mon. Not. R. Astron. Soc. 2012, 425, 405–414. [Google Scholar] [CrossRef]
- Riess, A.G.; Rodney, S.A.; Scolnic, D.M.; Shafer, D.L.; Strolger, L.G.; Ferguson, H.C.; Postman, M.; Graur, O.; Maoz, D.; Jha, S.W.; et al. Type Ia Supernova Distances at z > 1.5 from the Hubble Space Telescope Multi-Cycle Treasury Programs: The Early Expansion Rate. Astrophys. J. 2018, 853, 126. [Google Scholar] [CrossRef]
- Blake, C.; Joudaki, S.; Heymans, C.; Choi, A.; Erben, T.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Nakajima, R.; van Waerbeke, L.; et al. RCSLenS: Testing gravitational physics through the cross-correlation of weak lensing and large-scale structure. Mon. Not. R. Astron. Soc. 2016, 456, 2806–2828. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Poole, G.B.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Z = 0 measurements of the growth rate and σ8. Mon. Not. R. Astron. Soc. 2012, 423, 3430–3444. [Google Scholar] [CrossRef]
- Okumura, T.; Hikage, C.; Totani, T.; Tonegawa, M.; Okada, H.; Glazebrook, K.; Blake, C.; Ferreira, P.G.; More, S.; Taruya, A.; et al. The Subaru FMOS galaxy redshift survey (FastSound). IV. New constraint on gravity theory from redshift space distortions at z = 1.4. Publ. Astron. Soc. Jpn. 2016, 68, 38. [Google Scholar] [CrossRef]
- Song, Y.S.; Percival, W.J. Reconstructing the history of structure formation using redshift distortions. J. Cosmol. Astropart. Phys. 2009, 2009, 004. [Google Scholar] [CrossRef]
- Hawken, A.J.; Granett, B.R.; Iovino, A.; Guzzo, L.; Peacock, J.A.; de la Torre, S.; Garilli, B.; Bolzonella, M.; Scodeggio, M.; Abbas, U.; et al. The VIMOS Public Extragalactic Redshift Survey: Measuring the growth rate of structure around cosmic voids. Astron. Astrophys. 2017, 607, A54. [Google Scholar] [CrossRef]
- De la Torre, S.; Guzzo, L.; Peacock, J.A.; Branchini, E.; Iovino, A.; Granett, N.R.; Abbas, U.; Adami, C.; Arnouts, C.; Bel, J.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS). Galaxy clustering and redshift-space distortions at z = 0.8 in the first data release. Astron. Astrophys. 2013, 557, A54. [Google Scholar] [CrossRef]
- Mohammad, F.G.; Granett, B.R.; Guzzo, L.; Bel, J.; Branchini, E.; de la Torre, S.; Moscardini, L.; Peacock, J.A.; Bolzonella, M.; Garilli, B.; et al. An unbiased estimate of the growth rate of structure at <z> = 0.85 using the clustering of luminous blue galaxies. Astron. Astrophys. 2018, 610, A59. [Google Scholar]
- Howlett, C.; Ross, A.J.; Samushia, L.; Percival, W.J.; Manera, M. The clustering of the SDSS main galaxy sample—II. Mock galaxy catalogues and a measurement of the growth of structure from redshift space distortions at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 848–866. [Google Scholar] [CrossRef]
- Samushia, L.; Percival, W.J.; Raccanelli, A. Interpreting large-scale redshift-space distortion measurements. Mon. Not. R. Astron. Soc. 2012, 420, 2102–2119. [Google Scholar] [CrossRef]
- Tojeiro, R.; Percival, W.J.; Brinkmann, J.; Brownstein, J.R.; Eisenstein, D.J.; Manera, M.; Maraston, C.; McBride, C.K.; Muna, D.; Reid, B.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Measuring structure growth using passive galaxies. Mon. Not. R. Astron. Soc. 2012, 424, 2339. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, Y. Modelling the anisotropic two-point galaxy correlation function on small scales and single-probe measurements of H(z), DA(z) and f(z)σ8(z) from the Sloan Digital Sky Survey DR7 luminous red galaxies. Mon. Not. R. Astron. Soc. 2013, 435, 255–262. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Percival, W.J.; Brownstein, J.R.; Chuang, C.H.; Grieb, J.K.; Ho, S.; Kitaura, F.S.; Maraston, C.; Prada, F.; Rodríguez-Torres, S.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: RSD measurement from the LOS-dependent power spectrum of DR12 BOSS galaxies. Mon. Not. R. Astron. Soc. 2016, 460, 4188–4209. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Percival, W.J.; Cuesta, A.J.; Brownstein, J.R.; Chuang, C.H.; Ho, S.; Kitaura, F.S.; Maraston, C.; Prada, F.; Rodríguez-Torres, S.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: BAO measurement from the LOS-dependent power spectrum of DR12 BOSS galaxies. Mon. Not. R. Astron. Soc. 2016, 460, 4210–4219. [Google Scholar] [CrossRef]
- Chuang, C.; Prada, F.; Pellejero-Ibanez, M.; Beutler, F.; Cuesta, A.J.; Eisenstein, D.J.; Escoffier, S.; Ho, S.; Kitaura, F.; Kneib, J.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements from CMASS anisotropic galaxy clustering. Mon. Not. R. Astron. Soc. 2016, 461, 3781–3793. [Google Scholar] [CrossRef]
- Cabré, A.; Gaztañaga, E. Clustering of luminous red galaxies—I. Large-scale redshift-space distortions. Mon. Not. R. Astron. Soc. 2009, 393, 1183–1208. [Google Scholar] [CrossRef]
- Guzzo, L.; Pierleoni, M.; Meneux, B.; Branchini, E.; Le Fèvre, O.; Marinoni, C.; Garilli, B.; Blaizot, J.; De Lucia, G.; Pollo, A.; et al. A test of the nature of cosmic acceleration using galaxy redshift distortions. Nature 2008, 451, 541–544. [Google Scholar] [CrossRef]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Seikel, M.; Clarkson, C.; Smith, M. Reconstruction of dark energy and expansion dynamics using Gaussian processes. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Auguères, J.-L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- Amendola, L.; Appleby, S.; Avgoustidis, A.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Rel. 2013, 16, 6. [Google Scholar] [CrossRef]
- Rawlings, S. Cosmology with the Square Kilometre Array. arXiv 2011, arXiv:1105.6333. [Google Scholar]
- LSST Science Collaboration; Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.J.; Axelrod, T.S.; et al. LSST Science Book, Version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Levi, M.; Bebek, C.; Beers, T.; Blum, R.; Cahn, R.; Eisenstein, D.; Flaugher, B.; Honscheid, K.; Kron, R.; Lahav, O.; et al. The DESI Experiment, a whitepaper for Snowmass 2013. arXiv 2013, arXiv:1308.0847. [Google Scholar]
- Zumalacarregui, M.; Bellini, E.; Sawicki, I.; Lesgourgues, J.; Ferreira, P.G. hiclass: Horndeski in the Cosmic Linear Anisotropy Solving System. J. Cosmol. Astropart. Phys. 2017, 1708, 019. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).