Abstract
Neutrinoless double beta () decay searches are currently among the major foci of experimental physics. The observation of such a decay will have important implications in our understanding of the intrinsic nature of neutrinos and shed light on the limitations of the Standard Model. The rate of this process depends on both the unknown neutrino effective mass and the nuclear matrix element () associated with the given transition. The latter can only be provided by theoretical calculations, hence the need of accurate theoretical predictions of for the success of the experimental programs. This need drives the theoretical nuclear physics community to provide the most reliable calculations of . Among the various computational models adopted to solve the many-body nuclear problem, the shell model is widely considered as the basic framework of the microscopic description of the nucleus. Here, we review the most recent and advanced shell-model calculations of considering the light-neutrino-exchange channel for nuclei of experimental interest. We report the sensitivity of the theoretical calculations with respect to variations in the model spaces and the shell-model nuclear Hamiltonians.
1. Introduction
Neutrinoless double beta () decay is a process in which two neutrons inside the nucleus transform into two protons with the emission of two electrons and no neutrinos. With only two electrons in the final state, lepton number conservation needs to be violated by two units for the process to occur. The observation of decay would imply that neutrinos are Majorana particles—that is, they are their own antiparticles [1]—and give insight into leptogenesis scenarios for the generation of the observed matter-antimatter asymmetry in the universe [2]. In fact, decay is the most promising laboratory probe of lepton number violation and it is, in fact, the subject of intense experimental activities [3,4,5,6,7,8,9,10,11,12,13,14]. The current reported half-lives of Ge, Te, and Xe are larger than year [13], year [14], and year [7], respectively, with next generation ton scale experiments expecting a two orders of magnitude improvement in the half life sensitivity.
Since decay measurements use atomic nuclei as a laboratory to test the extent of the Standard Model, nuclear theory plays a crucial role in correctly interpreting the experimental data and disentangling nuclear physics effects from unknown lepton number violating mechanisms. The half-life of the decays is given by
where is a phase-space (or kinematic) factor [15,16], is the nuclear matrix element (NME), and is a function of the neutrino masses and their mixing matrix elements that accounts for beyond-standard-model physics. Within the light-neutrino exchange mechanisms, has the following expression:
where is the axial coupling constant, is the electron mass, and is the effective neutrino mass. It is then clear that access to unknown neutrino properties is granted only if is calculated with great accuracy.
Currently, the calculated matrix elements for nuclei of experimental interest are characterized by large uncertainties. For nuclear systems with medium masses and beyond, the many-body nuclear problem cannot be solved exactly with the available computational resources. For these systems, one is inevitably forced to truncate the model spaces and reduce or neglect the effects of many-body correlations and electroweak currents. As a result, different computational methods provide calculated swhich differ by a factor of two [17]. On the above grounds, it is clear that reliable calculations of sare a prime goal of nuclear many-body investigations.
The ab initio framework for nuclei allows retaining the complexity of many-body correlations and currents. Within this approach nuclei are described as systems made of nucleons interacting via two- and three-body forces. Interactions with external probes, such as electrons, neutrinos, and photons, are described using many-body current operators. One- and two-body current operators describe external probes interacting with individual nucleons and pairs of correlated nucleons, respectively. This scheme has been implemented successfully to study light to intermediate mass nuclei within several many-body computational approaches. Due to their prohibitive computational cost, ab initio methods have been used to study transitions in light nuclei instead. While transitions in light nuclei do not have a direct experimental interest, these studies provide us with an important benchmark to test other many-body methods that can be used to calculate transition matrix elements for heavy-mass nuclei of experimental interest. Further, they allow us to size the importance of the different lepton number violating mechanisms leading to decay processes, and to quantify the effect of the various approximations used in the many-body methods for medium to large nuclear systems. Studies along this line have been carried out (e.g., [18,19,20]). Only very recently, the ab initio community is venturing calculations of decay matrix element of experimental relevance, as reported, for example, by Yao et al. [21], who calculated the of Ca—the lightest system where the Q-value is compatible with the decay—combining the in-medium similarity renormalization group with the generator-coordinate method [22].
Besides the exceptions mentioned above, the nuclear physics community has been primarily focused on employing approximated many-body methods to access heavy open-shell nuclei of experimental interest. These approximated methods generally invoke a truncation of the full Hilbert space of configurations. To account for missing dynamics and degrees of freedom in the nuclear wave functions, the nuclear Hamiltonian is then replaced by an effective or renormalized Hamiltonian, i.e., . This procedure is carried out, in general, by fitting parameters inherent the given nuclear model to spectroscopic properties of the nuclei under investigation. Nuclear models adopted to study decay of nuclei of experimental interest are: the interacting boson model [23,24,25], the quasiparticle random-phase approximation (QRPA) [26,27,28], the energy density functional methods [29], the covariant density-functional theory [30,31,32,33,34,35,36], and the shell model (SM) [37,38,39,40,41]. These models agree within a factor of two (see, for example, Figure 5 of Ref. [17] and references therein) when calculating decay matrix elements of A = 48–150 nuclei. The difference is mostly to be ascribed to the different renormalization procedures adopted by the different models.
In addition to renormalizing the nuclear Hamiltonian, in this scheme, one has to renormalize the free constants that appear in the definitions of the decay operators—e.g., proton and neutron electric charges, spin and orbital gyromagnetic factors, etc. For example, the axial coupling constant [42] needs to be quenched by a factor of q [43], because all the aforementioned models usually overestimate Gamow–Teller (GT) rates when compared to the experimental data [44]. The choice of q depends on the nuclear structure model, the dimensions of the reduced Hilbert space, and the mass of the nuclei under investigation [45]. The common procedure to handle the quenching of is to fit GT related data (e.g., single- decay strengths, two-neutrino double- decay rates, etc.), and some authors argue that the value of q required to reach agreement between theoretical and experimental values should be also employed to calculate (see, e.g. [45,46]). In passing, it is worth mentioning that within the ab initio framework one can utilize the free nucleonic charges, magnetic moments, and axial coupling constant without having to resort to quenching, provided that corrections from two-body currents and two-body correlations are accounted for [47,48,49,50,51,52,53,54]. In this work, we review the most recent and advanced SM results of for nuclei currently candidates for the detection of the decay in many laboratories around the world. We focus on the sensitivity of the calculations with respect to variations in the model spaces and the shell-model nuclear Hamiltonians, as well as to the variations in the “short-range correlations” which reveal the role of SM correlated wave functions.
The paper is organized as follows. In Section 2, we outline the basics theory of the nuclear SM and short-range correlations, and provide the analytical expressions of the nuclear matrix elements, for both neutrinoless and two-neutrino double beta decay. The latter are reported to assess the validity of the adopted nuclear wave functions. In fact, a comparison with experimental data is clearly possible for two-neutrino double beta decays. Section 3 is devoted to the results of the latest SM calculations for Ca → Ti, Ge → Se, Se → Kr, Te → Xe, and Xe → Ba and decays. Comparisons between experimental and calculated sare reported at the end of Section 3.2 with a discussion on the quenching. Our conclusions are given in Section 4.
2. Theoretical Overview
2.1. The Nuclear Shell Model
The nuclear shell model allows for a microscopic description of the structure of the nucleus [55,56], and it is the root of most current ab initio approaches (No-Core Shell Model, Coupled Cluster Method, and In-Medium Similarity Renormalization Group). It is based on the ansatz that each nucleon inside the nucleus moves independently in a spherically symmetric mean field generated by all other constituents. The mean field is usually described by a Woods–Saxon or a harmonic oscillator (HO) potential supplemented by a strong spin–orbit term.
This basic version of the shell model successfully explains the appearance of protons and/or neutrons “magic numbers”—characterizing nuclei bounded more tightly with respect to their neighbors—along with several nuclear properties [57], including angular momenta and parity for ground-states of odd-mass nuclei. Within this framework, nucleons arrange themselves in well defined and separated energy levels, i.e., the “shells”. It is worth emphasizing that shell-model wave functions do not include correlations induced by the strong short-range two-nucleon interaction. We come back to this point below when we discuss the “short-range correlations” (SRC).
The SM can be further improved, especially its description of low-energy nuclear structure, introducing the “interacting shell model” (ISM) picture. In the ISM, the complex nuclear many-body problem is reduced to a simplified one where only few valence nucleons interact in the reduced model space spanned by a single major shell above an inert core. The valence nucleons interact via a two-body “residual interaction”, that is the part of the interaction which is not already accounted for in the central potential. The inclusion of the residual interaction removes the degeneracy of the states belonging to the same configuration and produces a mixing of different configurations.
The SM Hamiltonian consists of one- and two-body components and associated parameters, namely the single-particle (SP) energies and the two-body matrix elements (TBMEs) of the residual interaction. These parameters account for the degrees of freedom that are not explicitly included in the truncated Hilbert space of configurations. As a matter of fact, SP energies and TBMEs should be determined to include, in an effective way, the excitations of both the core and the valence nucleons into the shells above the model space.
The construction of the effective SM Hamiltonian, , can be carried out into two distinct ways. In one approach, one starts from realistic two- and three-nucleon forces (see [58] and references therein for a review on realistic two- and three-nucleon potentials) and derives the effective Hamiltonian from them. The will then have eigenvalues that belong to the set of eigenvalues of the full nuclear Hamiltonian, defined in the whole Hilbert space. The alternative approach is phenomenological. In this case, the SM Hamiltonian one- and two-body components are adjusted to reproduce a selected set of experimental data. For the fitting procedure one could: (i) use adjustable parameters entering the analytical expressions of the residual interaction; (ii) directly consider the Hamiltonian matrix elements as free parameters (see, e.g., [59,60]); or (iii) fine tune the TBMEs of a realistic to reproduce the experimental results. The phenomenological approach has been widely utilized since its formulation in the 1950s, and it successfully reproduces a huge amount of data and describes some of the most fundamental properties of the structure of atomic nuclei [61].
The SM provides suitable and well tested nuclear wave functions for the initial and final states entering the calculation of associated with decays. SM results based on both the realistic and phenomenological are reported in Section 3.
2.2. Short-Range Correlations
Short-range correlations (SRCs) are required to account for physics that is missing in all models that expand nuclear wave functions in terms of a truncated non-correlated SP basis. In particular, two-body decay operators—such as those entering decays—acting on an unperturbed (uncorrelated) wave function yield results that are intrinsically different from those obtained acting the real (correlated) nuclear wave function [62,63]. Due to the highly repulsive nature of the short-range two-nucleon interaction, and in order to carry out nuclear structure calculations, one is forced to perform a consistent regularization of the two-nucleon potential, , and of any two-body transition operator [64].
In nuclear structure calculations based on realistic potentials, one has to deal with non-zero values of the non-correlated wave function, , at short distances. This can be appreciated in Figure 1. However, because of the repulsive nature of the interaction at small inter-particle distances (or, equivalently, the repulsive behavior at high-momentum) the correlated wave function, , has to approach zero as the inter-nucleon distance diminishes, and as fast as the core repulsion increases, see Figure 1.
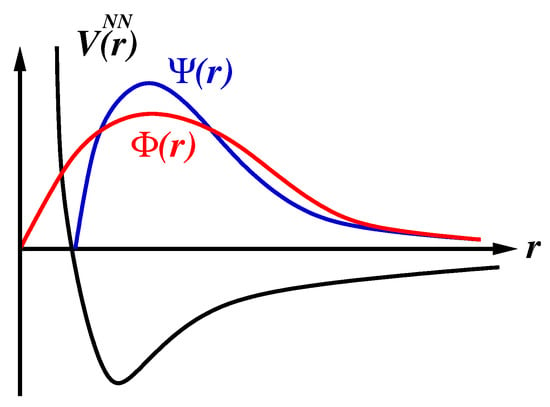
Figure 1.
Representation of a realistic potential , as a function of the inter-nucleon distance r (black line). The correlated, , and non-correlated, , wave functions are represented by the blue and red lines, respectively. See text for details.
To remedy to this shortcoming, one has to renormalize the short-range (high-momentum) components of the potential whenever a perturbative approach to the many-body problem is pursued. The most common way to soften the matrix elements of the decay operator is to include SRC given by Jastrow-type functions [65,66]. Recently, SRC have been modeled using the Unitary Correlation Operator Method (UCOM) [38,63]. This approach prevents the overlap between wave functions of a pair of nucleons [67].
Another approach was proposed by some of the present authors in [68,69], where the renormalization of the the two-body decay operator is carried out consistently with the procedure [70] adopted to renormalize the repulsive high-momentum components of the potential. In particular, the renormalization of occurs through a unitary transformation, , which decouples the full momentum space of the two-nucleon Hamiltonian, , into two subspaces; the first one is associated with the relative-momentum configurations below a cutoff and is specified by a projector operator P, while the second one is defined in terms of its complement [68]. Being a unitary transformation, preserves the physics of the original potential for the two-nucleon system, e.g., the calculated values of all nucleon–nucleon observables are the same as those reproduced by solving the Schrödinger equation for two nucleons interacting via .
The two-body operator, , is calculated in the momentum space and renormalized using . This ensure a consistency with the potential, whose high-momentum (short range) components are dumped by the introduction of the cutoff . The vertices appearing in the perturbative expansion of the box are substituted with the renormalized operator. The latter is defined as for relative momenta , and is set to zero for . The magnitude of the overall effect of this renormalization procedure is comparable to using the SRC modeled by the Unitary Correlation Operator Method [38], which is a lighter softening of than the one provided by Jastrow-type SRC [68].
2.3. The -Decay Operator for the Light-Neutrino Exchange
We now turn our attention to the vertices of the bare operator, , for the light-neutrino-exchange channel [17].
We recall that the formal expression of —where stands for Fermi (F), Gamow–Teller (GT), or tensor (T) decay channels—is written in terms of the one-body transition-density matrix elements between the daughter and parent nuclei (grand-daughter and daughter nuclei) (). Here, p and n denote proton and neutron states, and refer to the parent, daughter, and grand-daughter nuclei, respectively, while reads [71,72]:
where the tilde denotes a time-conjugated state, .
The operators given by [17]:
where are the neutrino potentials defined as:
In the equation above, fm, is the spherical Bessel function, for Fermi and Gamow–Teller components, while for the tensor component. For the sake of clarity, the explicit expressions [17] of neutrino form functions, , for light-neutrino exchange are reported below:
For the vector, , axial-vector, , and weak-magnetism, , form factors, we use the dipole approximation:
where , , , and the cutoff parameters MeV and MeV.
The total nuclear matrix element can be then written as
Equation (2) can be easily calculated within the QRPA computational approach, while all other models—including most of the SMs—have to resort to the closure approximation. This approximation is based on the observation that the relative momentum q of the neutrino, appearing in the propagator of Equation (6), is of the order of 100–200 MeV [17], while the excitation energies of the nuclei involved in the transition are of the order of 10 MeV [71]. It is then customary to replace the energies of the intermediate states, , appearing in Equation (6), by an average value . This allow us to simplify both Equations (2) and (6). In particular, can be re-written in terms of the two-body transition-density matrix elements as
and the neutrino potentials become
Most SM calculations adopt the closure approximation to define the operators given in Equations (3)–(5), and take the average energies from the evaluations of Haxton and Stephenson Jr. [73] and Tomoda [74]. It is important to point out that Sen’kov and Horoi [71] performed SM calculations of for Ca both within and beyond the closure approximation, and found that in the second case the results are ∼10% larger.
In most cases, short-range correlations are included when computing the radial matrix elements of the neutrino potentials . In particular, the HO wave functions and are corrected by a factor , which takes into account the short range correlations induced by the nuclear interaction
The functional form of the correlation function is usually written using a Jastrow-like parameterization as [66]
where a, b, and c are parameters whose values depend on the renormalization procedure adopted to renormalize the non-correlated HO wave functions, (e.g., Jastrow or UCOM schemes, see Section 2.2 for details). In Table 1, we report the values of the a, b, and c constants commonly employed in SM calculations. In addition to the values proposed by Miller and Spencer [65], we show those based on the modern nucleon–nucleon interactions CD-Bonn and AV18 and derived by Sim [26].

Table 1.
Values of the SRC parameters.
2.4. The -Decay Operator
As pointed out in the Introduction, because of the impossibility to compare the theoretical values of with the experiment, one has to find another way to check the reliability of the computed results. A viable route that is often considered in the literature is the calculation of the standard or ordinary two-neutrinos double beta decay transitions where one observes the emission of two electrons and two antineutrinos. Two-neutrino double beta decays are simply the occurrence of two single beta decay transitions inside a nucleus. They differ from decays in the characteristic value of momentum transfer, which is negligible in ordinary decays and of the order of hundreds of MeVs in decay. Here, we list the expressions of the GT and Fermi components of the two-neutrinos double beta decay matrix elements , namely
In the equation above, is the excitation energy of the intermediate state, and , with and the Q value of the transition and the mass difference of the initial and final nuclear states, respectively. The index n runs over all possible intermediate states induced by the given transition operator.
It should be pointed out that the Fermi component is zero in Hamiltonians that conserve the isospin, and most of the SM effective Hamiltonians do. It would play a marginal role only when isospin violation mechanisms are introduced, for example, to account for the effects of the Coulomb force acting between the valence protons [73,75]. In practice, in most calculations, the Fermi component is neglected altogether.
An efficient way to calculate is to resort to the Lanczos strength-function method [61], which allows including the intermediate states required to obtain a given accuracy for the calculated values.
The theoretical values are then compared with the experimental counterparts, which are extracted from the observed half life
One can base the evaluation of the on the closure approximation, commonly adopted to study -decay NMEs [73]. Within this approximation, one can avoid explicitly calculating the intermediate states. The drawback is that, in using the closure on the intermediate states, the two one-body transition operators become a two-body operator.
This approximation is more adapt to evaluate where the neutrino’s momentum is about one order of magnitude greater than the average excitation energy of the intermediate states. This allows safely neglecting intermediate-state-dependent energies from the energy denominator appearing in the neutrino potential (see discussion in Section 2.3). Conversely, the closure approximation has turned out to be unsatisfactory when used to calculate , and that is because the momentum transfer in process are much smaller. Theoretical calculations of are discussed in the next session.
3. Shell-Model Results
In this section, we report SM results for based on both the phenomenological and realistic s. All the calculations are based on the light-neutrino-exchange hypothesis, and the values of all the input parameters are the same as reported in Section 2.3. The only exception is the parameter, whose adopted value is equal to 1.254 in some reported calculations. It is worth pointing out, however, that, in [76], where a detailed analysis of the sensitivity of the results on the values of the input parameters can be found, it is shown that the effects of such a tiny difference in are negligible. We focus our attention on the Ca, Ge, Se, Te, Te, and Xe emitters. These results have been obtained performing a complete diagonalizations of . The latter has been defined in different valence spaces tailored for the specific decay under investigation. All the calculations based on phenomenological interactions are performed starting from Brueckner G-matrix elements “fine tuned” to reproduce some specific set of spectroscopic data.
3.1. Results from Phenomenological s
We test different phenomenological s. All these interactions have been derived modifying the matrix elements of a G-matrix so as to reproduce a chosen set of spectroscopic properties of some nuclei belonging to the mass region of interest. With this procedure one can end up with results that provide similar descriptions of the nuclei under consideration, nevertheless the phenomenological TBMEs are quite different each other.
It is worth stressing that the calculated s, reported in this section, are obtained using free value of the axial coupling constant without any quenching factor.
The double-magic nucleus Ca is the lightest emitter investigated in regular decay searches. The SM calculation for is obtained using the model space spanned by four neutron and proton single-particle orbitals 0f, 1p, 1p, and 0f. It is worth mentioning that the regular decay of Ca is a paradigm for shell-model calculations. Because within the model space all spin-orbit partners are present, the Ikeda sum rule is satisfied [77].
Several phenomenological SM effective interactions have been developed to describe -shell nuclei. Among these are the GXPF1 [78], GXPF1A [79], KB3 [80], KB3G [81], and FPD6 [82] interactions. In Table 2, we compare the most recent results for the of Ca obtained using the GXPF1A [71] and KB3G interactions [83].

Table 2.
of Ca. (a) and (b) denote AV18 and CD-Bonn SRC parameterizations, respectively. The results are taken from [71,83].
For the medium-mass emitters Ge and Se, the calculations adopt the valence space with the four neutron and proton single-particle orbitals 0f, 1p, 1p, and 0g outside doubly-magic Ni, as for instance in [83,84], where the effective interactions GCN2850 [38] and JUN45 [85] are employed. These results are given in Table 3 and Table 4.


Finally, in Table 5 and Table 6, we report and compare the calculated for Te and Xe. These are based on two different effective interactions, namely the SVD [86] and GCN5082 [38] defined in the valence space spanned by the neutron and proton orbitals 0g, 1d, 1d, 2s, and 0h. Results with the SVD and GCN5082 interactions are taken, respectively, from [40,83].


From the results shown above, it can be inferred that the effect associated with using different SRCs does not exceed 10%, while different effective interactions can provide results differing up to 50%. The results reported in this section are based on the closure approximation. As discussed above, Senkov and coworkers showed in a series of papers [71,84,87] that, in going beyond this approximation, the decay becomes about larger.
We recall that the results reported in Table 2, Table 3, Table 4, Table 5 and Table 6 are obtained without quenching the axial coupling constant. However, the calculations based on the empirical SM Hamiltonians so far considered need a quenching factor q different from 1 to reproduce the experimental values of the nuclear matrix elements of the corresponding -decays s. This can be appreciated in Table 7 where we list the scalculated with the empirical effective Hamiltonians GXPF1A, KB3G, JUN45, GCN2850 and GCN5082 and compare them with the experimental data. In these calculations, which are performed employing the Lanczos strength-function method [61], the unquenched value of (or equivalently a quenching factor ) has been used, and, as expected, the theory is systematically overpredicting the experimental data.

Table 7.
sfor Ca, Ge, Se, Te, and Xe -decay calculated with GXPF1A, KB3G, JUN45, GCN2850, and GCN5082 interactions and compared with data [88]; there are no published results based on the SVD interaction. These calculations use a quenching factor . The values of sare reported in MeV.
3.2. Results from Realistic s
In the realistic SM (RSM), is constructed from realistic potentials. This is achieved via a similarity transformation utilized to constrain both the SM Hamiltonian and the SM transition operators. More details on this procedure can be found in the papers by B. H. Brandow [91], T. T. S. Kuo and coworkers [92,93], and K. Suzuki and S. Y. Lee [94,95]. Perturbative and non-perturbative derivations of were most recently reviewed by Coraggio et al. [96] and Stroberg et al. [97], respectively. The derivation of effective SM decay operators carried out consistently with is discussed in [98,99]. Fundamental contributions to the field were made by I. S. Towner, who extensively investigated the role of many-body correlations induced by the truncation of the Hilbert space, especially for spin- and spin–isospin-dependent one-body decay operators [43,100].
The first calculations of starting from realistic potentials and associated effective SM decay operators, were made by Kuo and coworkers in the middle of 1980s for Ca [64]. In their work, and the associated transition operators were based on the Paris and the Reid potentials [101,102]. The short-range repulsive behavior was renormalized by calculating the corresponding Brueckner reaction matrices [103]. Many-body perturbation theory was then implemented to derive both the TBMEs of and the effective -decay operator. The effect of the SRC was embedded in the defect wave function [104], consistently with the renormalization procedure from the Paris and Reid potentials. Finally, the authors calculated the half lives of Ca -decay, for both light- and heavy-neutrino exchange, as a function of the neutrino effective mass.
More recently, J. D. Holt and J. Engel calculated effective SM operators sfrom modern chiral effective field theory potentials. In particular, they started from the chiral potential by Entem and Machleidt [105] and cured its perturbative behavior using the procedure [70]. The was expanded up to third order in perturbation theory and used to calculate for Ge, Se [106], and Ca [107]. The effects of SRC was included via an effective Jastrow function obtained from Brueckner theory calculations [26]. For Ge and Se decays, the authors employed the empirical GCN2850 [38] and JUN45 [85] SM interactions, respectively, and for the decay of Ca they used the GXPF1A [79]. The values obtained by Holt and Engel in the light-neutrino exchange channel are = 1.30 for Ca, = 3.77 for Ge, and = 3.62 for Se [106,107].
Holt and Engel [106] also calculated the Ge matrix element. The calculation used the closure approximation. However, as we discussed in Sessions Section 2.3 and Section 2.4, this approximation is not robust when applied to study processes where the values of momentum transfer are small. In fact, the authors obtain a result for Ge that is about two times larger than the one calculated with the Lanczos strength-function method [41,108], and about five times larger than the experimental value [88].
RSM calculations based on the high-precision CD-Bonn potential [109] were recently carried out by Coraggio et al. [69], where the repulsive high-momentum components have been integrated out through the technique with “hard cutoff” fm [70]. The shave been calculated within the SM using , and effective decay operators sup to the third order in perturbation theory. Two-body matrix elements entering the -decay operator have been renormalized consistently within the to account for short-range correlations (see Section 2.2 for more details) and Pauli-principle violations in the effective SM operator. It should be pointed out that calculations of systems with a number n of valence nucleons require the derivation of n-body effective operators, that take into account the evolution of the number of valence particle in the model space P. The correlation between P-space configurations and those belonging to Q space is affected by the filling of the model-space orbitals, and in a perturbative expansion of SM operators this is considered by way of n-body diagrams. This is called the “Pauli-blocking effect” and calculations in [69], where all SM parameters are consistently derived from the realistic potential without any empirical adjustments, take it into consideration by including the contribution of three-body correlation diagrams to derive .
The results for decay in the light-neutrino exchange channel of Ca, Ge, Se, Te, and Xe are reported in Table 8.

Table 8.
sof Ca, Ge, Se, Te, and Xe decays obtained with the realistic effective Hamiltonians and operators [69]. The tensor component has been neglected.
It is worth pointing out that this approach to SM calculations has been successfully tested on energy spectra, electromagnetic transition strengths, GT strength distributions, and nuclear matrix elements for the two-neutrino decay [110,111], without resorting to effective proton/neutron charges and gyromagnetic factors, or quenching of . In Table 9, we report the the calculated values of from [111] and compare them with experimental data [88].

Table 9.
Same as in Table 7, but the calculated values [111] are obtained employing effective Hamiltonians and decay operators derived starting from the CD-Bonn realistic potential (see text for details) and compared with experiment [88].
A few comments are now in order. As pointed out in the Introduction, SM calculations overestimate and Gamow–Teller transition strengths. To remedy to this deficiency, one introduces a quenching factor q that is multiplied to to reduce the values of the calculated matrix elements. This factor depends on: (i) the mass region of the nuclei involved in the decay process; and (ii) the dimension of the model space used in the calculation. The quenching factor has on average the empirical value [45]).
The quenching factor accounts for missing correlations and missing many-body effects in the transition operators. The truncation of the full Hilbert space to the reduced SM space has the effect of excluding all correlations between the model-space configurations and the configurations belonging to either the doubly-closed core or the shells placed in energies above the SM space. In addition, SM calculations are based on the single-nucleon paradigm for the transition operators. However, two-body electroweak currents [47,48,49,50,51,52,53,54,112,113,114,115,116,117,118,119,120] are found to play a role in several electroweak observables. These involve the exchange of mesons and nucleonic excitations.
I. S. Towner extensively studied how to construct effective -decay operators that account for the degrees of freedom that are not explicitly included in the model space (see [43]). This is more recently investigated in [110,111]. The results reported in Table 9 demonstrate a satisfactory agreement with the data can be obtained without resorting to quenching factors q if one employs effective GT operators within the SM.
Moreover, Coraggio et al. [69] showed that the renormalization procedure implemented to account for missing configurations plays a marginal role in the calculated s, while it is relevant in -decay induced by the one-body GT operator. This evidences that the mechanisms which underlies the renormalization of the one-body single- and the two-body decay operators are different.
In closing, we address the role of many-body electroweak currents in the redefinition of single--decay and -decay operators. Within the shell model, one can use nuclear potentials derived within chiral perturbation theory [121,122], and include also the contributions of chiral two-body electroweak currents. Studies along these lines have been recently carried out in [54,123,124], where the authors found significant contributions from two-body axial currents in -decay. Concurrently, the study reported in [125] argues that many-body electroweak currents should play a negligible role in standard GT transitions (namely, - and decays) due to the “chiral filter” mechanism [125]. The chiral filter mechanism may be no longer valid for decay since the transferred momentum is ∼100 MeV, which will require further investigations to fully understand the role of many-body currents in SM calculations of s.
3.3. Comparison between SM Calculations
In Figure 2, we group most of the SM results for Ca →Ti, Ge →Se, Se →Kr, Te → Xe, and Xe →Ba. We have chosen the results according to the following criteria:
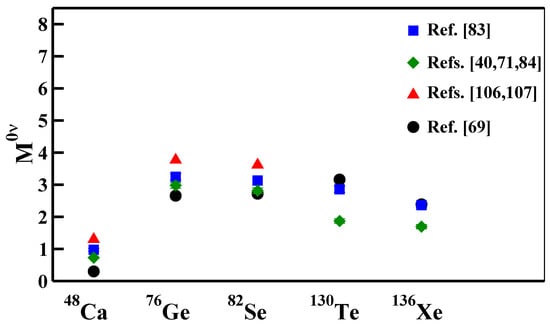
Figure 2.
scalculated using different and -decay operators. Blue squares represent the results based on the Strasbourg–Madrid s [83]. Green diamonds correspond to the calculations by Horoi and coworkers [40,71,84]. Results by Holt and Engel are indicated by the red triangles [106,107]. Black dots indicate results by some of the present authors reported in [69].
- (a)
- All the SM calculations for a given transition are based on the same model space.
- (b)
- All the calculations use the closure approximation.
- (c)
- Whenever the calculations use different choices of SRCs, the average value and associated error bar is reported.
The scale on the y-axis is consistent with the one employed in Figure 5 of [17]. We stress that our criteria rule out, for the sake of consistency, results from SM calculations where alternative approaches have been followed. For example, we recall that Horoi and coworkers have extensively performed calculations beyond the closure approximation [71,84,87]. In particular, as already mentioned several times, results for the of Ca calculated with and without the closure approximation differ by ∼10%. Likewise, we neglect the results of large-scale SM calculations, where model spaces larger than a single major shell are used. This is the case, for instance, of the work by Horoi and Brown [39] and by Iwata and coworkers [126]. In the former, the authors showed how the enlargement of the standard model space by the inclusion of the spin–orbit partners of g and h orbitals leads to a 10–30% reduction of the calculated for the Xe emitter. In the latter, the authors reported the results for the of Ca based on large-scale shell-model calculations including two harmonic oscillator shells ( and shells). They found that is enhanced by about 30% with respect to -shell calculations when excitations up to are explicitly included.
The spread among different results is rather narrow, except from the Te →Xe decay since the results in [40] are more than larger than those in [69,83]. We observe that the results from [69,83] are close each other, and the scalculated by Holt and Engel [106,107] are consistently larger than those from other SM calculations. The computational methods reported in the figure use substantially different SM effective Hamiltonians, yet they all lead to equally satisfactory results for a large amount of structure data. This leads us to argue that the SM approach is reliable for the study of decay.
Finally, comparing Figure 2 with the compilation of results reported in Figure 5 of [17], we confirm that also these more recent SM calculations provide values that are smaller than those obtained with other nuclear models such as the Interacting Boson Model, the QRPA, and Energy Density Functional methods. Since the advantage of the nuclear shell model with respect to other approaches is to include a larger number of nuclear correlations, one may argue that by enlarging the dimension of the Hilbert space of nuclear configurations it should be expected a reduction in magnitude of the predicted values of s, as found, e.g., in [39].
4. Conclusions
In this paper, we briefly review the present status of SM calculations of -decay nuclear matrix elements. More precisely, we focus our attention on the CaTi, GeSe, SeKr, TeXe, and XeBa decays. These transitions are relevant to the current and planned experimental programs. We consider calculations performed with phenomenological SM Hamiltonians, as well as studies where SP energies, two-body matrix elements, and effective decay operators have been derived from realistic potentials. For completeness, important aspects that characterize the calculation of , such as the role of short-range correlations and the closure approximation, are briefly discussed. These and other approximations, such as the size of the model space, may affect the results by ≲30%.
We show how different SM calculations, notwithstanding the diversity of the effective Hamiltonians that are employed to calculate the nuclear wave functions, exhibit a rather narrow spread among the predictions of the nuclear matrix elements, making the SM a solid and reliable framework for calculations.
Author Contributions
All authors have actively and equally contributed to the manuscript preparation and to the development of the ideas here presented. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schechter, J.; Valle, J.W.F. Neutrinoless Double beta Decay in SU(2) x U(1) Theories. Phys. Rev. D 1982, 25, 2951. [Google Scholar] [CrossRef]
- Davidson, S.; Nardi, E.; Nir, Y. Leptogenesis. Phys. Rept. 2008, 466, 105–177. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Hanakago, H.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Kato, R.; Koga, M.; Matsuda, S.; Mitsui, T.; et al. Limit on Neutrinoless ββ Decay of 136Xe from the First Phase of KamLAND-Zen and Comparison with the Positive Claim in 76Ge. Phys. Rev. Lett. 2013, 110, 062502. [Google Scholar] [CrossRef] [PubMed]
- Agostini, M.; Allardt, M.; Andreotti, E.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barnabé Heider, M.; Barros, N.; Baudis, L.; Bauer, C.; et al. Results on Neutrinoless Double-β Decay of 76Ge from Phase I of the GERDA Experiment. Phys. Rev. Lett. 2013, 111, 122503. [Google Scholar] [CrossRef]
- Albert, J.B.; Auty, D.J.; Barbeau, P.S.; Beauchamp, E.; Beck, D.; Belov, V.; Benitez-Medina, C.; Bonatt, J.; Breidenbach, M.; Brunner, T.; et al. Search for Majorana neutrinos with the first two years of EXO-200 data. Nature 2014, 510, 229–234. [Google Scholar]
- Andringa, S.; Arushanova, E.; Asahi, S.; Askins, M.; Auty, D.J.; Back, A.R.; Barnard, Z.; Barros, N.; Beier, E.W.; Bialek, A.; et al. Neutrino Masses and Oscillations 2015. Adv. High Energy Phys. 2016, 2016, 6194250. [Google Scholar]
- Gando, A.; Gando, Y.; Hachiya, T.; Hayashi, A.; Hayashida, S.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Karino, Y.; Koga, M.; et al. Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef]
- Elliott, S.R.; Abgrall, N.; Arnquist, I.J.; Avignone, F.T., III; Barabash, A.S.; Bertrand, F.E.; Bradley, A.W.; Brudanin, V.; Busch, M.; Buuck, M.; et al. Initial Results from the Majorana Demonstrator. J. Phys. Conf. Ser. 2017, 888, 012035. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Belyaev, S.T.; et al. Background-free search for neutrinoless double-β decay of 76Ge with GERDA. Nature 2017, 544, 47–52. [Google Scholar]
- Aalseth, C.E.; Abgrall, N.; Aguayo, E.; Alvis, S.I.; Amman, M.; Arnquist, I.J.; Avignone, F.T.; Back, H.O.; Barabash, A.S.; Barbeau, P.S.; et al. Search for Neutrinoless Double-β Decay in 76Ge with the Majorana Demonstrator. Phys. Rev. Lett. 2018, 120, 132502. [Google Scholar] [CrossRef] [PubMed]
- Albert, J.B.; Anton, G.; Badhrees, I.; Barbeau, P.S.; Bayerlein, R.; Beck, D.; Belov, V.; Breidenbach, M.; Brunner, T.; Cao, G.F.; et al. Search for Neutrinoless Double-Beta Decay with the Upgraded EXO-200 Detector. Phys. Rev. Lett. 2018, 120, 072701. [Google Scholar] [CrossRef] [PubMed]
- Alduino, C.; Alessandria, F.; Alfonso, K.; Andreotti, E.; Arnaboldi, C.; Avignone, F.T.; Azzolini, O.; Balata, M.; Bandac, I.; Banks, T.I.; et al. First Results from CUORE: A Search for Lepton Number Violation via 0νββ Decay of 130Te. Phys. Rev. Lett. 2018, 120, 132501. [Google Scholar] [CrossRef] [PubMed]
- Agostini, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; Bezrukov, L.; et al. Improved Limit on Neutrinoless Double-β Decay of 76Ge from GERDA Phase II. Phys. Rev. Lett. 2018, 120, 132503. [Google Scholar] [CrossRef] [PubMed]
- Azzolini, O.; Barrera, M.T.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Canonica, L.; Capelli, S.; et al. First Result on the Neutrinoless Double-β Decay of 82Se with CUPID-0. Phys. Rev. Lett. 2018, 120, 232502. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase-space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase space factors for β+β+ decay and competing modes of double-β decay. Phys. Rev. C 2013, 87, 024313. [Google Scholar] [CrossRef]
- Engel, J.; Menéndez, J. Status and Future of Nuclear Matrix Elements for Neutrinoless Double-Beta Decay: A Review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef]
- Pastore, S.; Carlson, J.; Cirigliano, V.; Dekens, W.; Mereghetti, E.; Wiringa, R.B. Neutrinoless double-β decay matrix elements in light nuclei. Phys. Rev. C 2018, 97, 014606. [Google Scholar] [CrossRef]
- Wang, X.; Hayes, A.; Carlson, J.; Dong, G.; Mereghetti, E.; Pastore, S.; Wiringa, R. Comparison between variational Monte Carlo and shell model calculations of neutrinoless double beta decay matrix elements in light nuclei. Phys. Lett. B 2019, 798, 134974. [Google Scholar] [CrossRef]
- Basili, R.; Yao, J.; Engel, J.; Hergert, H.; Lockner, M.; Maris, P.; Vary, J. Benchmark neutrinoless double-β decay matrix elements in a light nucleus. Phys. Rev. C 2020, 102, 014302. [Google Scholar] [CrossRef]
- Yao, J.M.; Bally, B.; Engel, J.; Wirth, R.; Rodríguez, T.R.; Hergert, H. Ab Initio Treatment of Collective Correlations and the Neutrinoless Double Beta Decay of 48Ca. Phys. Rev. Lett. 2020, 124, 232501. [Google Scholar] [CrossRef] [PubMed]
- Griffin, J.J.; Wheeler, J.A. Collective Motions in Nuclei by the Method of Generator Coordinates. Phys. Rev. 1957, 108, 311–327. [Google Scholar] [CrossRef]
- Barea, J.; Iachello, F. Neutrinoless double-β decay in the microscopic interacting boson model. Phys. Rev. C 2009, 79, 044301. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. Limits on neutrino masses from neutrinoless double-β decay. Phys. Rev. Lett. 2012, 109, 042501. [Google Scholar] [CrossRef]
- Barea, J.; Kotila, J.; Iachello, F. Nuclear matrix elements for double-β decay. Phys. Rev. C 2013, 87, 014315. [Google Scholar] [CrossRef]
- Šimkovic, F.; Faessler, A.; Müther, H.; Rodin, V.; Stauf, M. 0νββ-decay nuclear matrix elements with self-consistent short-range correlations. Phys. Rev. C 2009, 79, 055501. [Google Scholar] [CrossRef]
- Fang, D.L.; Faessler, A.; Rodin, V.; Šimkovic, F. Neutrinoless double-β decay of deformed nuclei within quasiparticle random-phase approximation with a realistic interaction. Phys. Rev. C 2011, 83, 034320. [Google Scholar] [CrossRef]
- Faessler, A.; Rodin, V.; Simkovic, F. Nuclear matrix elements for neutrinoless double-beta decay and double-electron capture. J. Phys. G 2012, 39, 124006. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Martínez-Pinedo, G. Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys. Rev. Lett. 2010, 105, 252503. [Google Scholar] [CrossRef]
- Song, L.S.; Yao, J.M.; Ring, P.; Meng, J. Relativistic description of nuclear matrix elements in neutrinoless double-β decay. Phys. Rev. C 2014, 90, 054309. [Google Scholar] [CrossRef]
- Yao, J.M.; Song, L.S.; Hagino, K.; Ring, P.; Meng, J. Systematic study of nuclear matrix elements in neutrinoless double-β decay with a beyond-mean-field covariant density functional theory. Phys. Rev. C 2015, 91, 024316. [Google Scholar] [CrossRef]
- Song, L.S.; Yao, J.M.; Ring, P.; Meng, J. Nuclear matrix element of neutrinoless double-β decay: Relativity and short-range correlations. Phys. Rev. C 2017, 95, 024305. [Google Scholar] [CrossRef]
- Jiao, C.F.; Engel, J.; Holt, J.D. Neutrinoless double-β decay matrix elements in large shell-model spaces with the generator-coordinate method. Phys. Rev. C 2017, 96, 054310. [Google Scholar] [CrossRef]
- Yao, J.M.; Engel, J.; Wang, L.J.; Jiao, C.F.; Hergert, H. Generator-coordinate reference states for spectra and 0νββ decay in the in-medium similarity renormalization group. Phys. Rev. C 2018, 98, 054311. [Google Scholar] [CrossRef]
- Jiao, C.F.; Horoi, M.; Neacsu, A. Neutrinoless double-β decay of 124Sn, 130Te, and 136Xe in the Hamiltonian-based generator-coordinate method. Phys. Rev. C 2018, 98, 064324. [Google Scholar] [CrossRef]
- Jiao, C.; Johnson, C.W. Union of rotational and vibrational modes in generator-coordinate-type calculations, with application to neutrinoless double-β decay. Phys. Rev. C 2019, 100, 031303. [Google Scholar] [CrossRef]
- Menéndez, J.; Poves, A.; Caurier, E.; Nowacki, F. Occupancies of individual orbits, and the nuclear matrix element of the 76Ge neutrinoless ββ decay. Phys. Rev. C 2009, 80, 048501. [Google Scholar] [CrossRef]
- Menéndez, J.; Poves, A.; Caurier, E.; Nowacki, F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl. Phys. A 2009, 818, 139. [Google Scholar] [CrossRef]
- Horoi, M.; Brown, B.A. Shell-Model Analysis of the 136Xe Double Beta Decay Nuclear Matrix Elements. Phys. Rev. Lett. 2013, 110, 222502. [Google Scholar] [CrossRef]
- Neacsu, A.; Horoi, M. Shell model studies of the 130Te neutrinoless double-β decay. Phys. Rev. C 2015, 91, 024309. [Google Scholar]
- Brown, B.A.; Fang, D.L.; Horoi, M. Evaluation of the theoretical nuclear matrix elements for ββ decay of 76Ge. Phys. Rev. C 2015, 92, 041301. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Towner, I.S. Quenching of spin matrix elements in nuclei. Phys. Rep. 1987, 155, 263–377. [Google Scholar] [CrossRef]
- Chou, W.T.; Warburton, E.K.; Brown, B.A. Gamow-Teller beta-decay rates for A ≤ 18 nuclei. Phys. Rev. C 1993, 47, 163–177. [Google Scholar] [CrossRef]
- Suhonen, J.T. Value of the Axial-Vector Coupling Strength in β and ββ Decays: A Review. Front. Phys. 2017, 5, 55. [Google Scholar] [CrossRef]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar] [CrossRef]
- Park, T.S.; Min, D.P.; Rho, M. Chiral dynamics and heavy-fermion formalism in nuclei: Exchange axial currents. Phys. Rep. 1993, 233, 341. [Google Scholar] [CrossRef][Green Version]
- Park, T.S.; Min, D.P.; Rho, M. Chiral Lagrangian approach to exchange vector currents in nuclei. Nucl. Phys. 1996, A596, 515–552. [Google Scholar] [CrossRef]
- Baroni, A.; Girlanda, L.; Pastore, S.; Schiavilla, R.; Viviani, M. Nuclear axial currents in chiral effective field theory. Phys. Rev. C 2016, 93, 015501. [Google Scholar] [CrossRef]
- Krebs, H.; Epelbaum, E.; Meißner, U.G. Nuclear axial current operators to fourth order in chiral effective field theory. Ann. Phys. 2017, 378, 317–395. [Google Scholar] [CrossRef]
- Krebs, H.; Epelbaum, E.; Meißner, U.G. Box diagram contribution to the axial two-nucleon current. Phys. Rev. C 2020, 101, 055502. [Google Scholar] [CrossRef]
- Pastore, S.; Baroni, A.; Carlson, J.; Gandolfi, S.; Pieper, S.C.; Schiavilla, R.; Wiringa, R. Quantum Monte Carlo calculations of weak transitions in A = 6–10 nuclei. Phys. Rev. C 2018, 97, 022501. [Google Scholar] [CrossRef]
- King, G.B.; Andreoli, L.; Pastore, S.; Piarulli, M.; Schiavilla, R.; Wiringa, R.B.; Carlson, J.; Gandolfi, S. Chiral effective field theory calculations of weak transitions in light nuclei. Phys. Rev. C 2020, 102, 025501. [Google Scholar] [CrossRef]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β-decay rates resolved from first principles. Nat. Phys. 2019, 15, 428. [Google Scholar] [CrossRef]
- Mayer, M.G. On Closed Shells in Nuclei. II. Phys. Rev. 1949, 75, 1969. [Google Scholar] [CrossRef]
- Haxel, O.; Jensen, J.H.D.; Suess, H.E. On the “Magic Numbers” in Nuclear Structure. Phys. Rev. 1949, 75, 1766. [Google Scholar] [CrossRef]
- Mayer, M.G.; Jensen, J.H.D. Elementary Theory of Nuclear Shell Structure; John Wiley: New York, NY, USA, 1955. [Google Scholar]
- Machleidt, R. Historical perspective and future prospects for nuclear interactions. Int. J. Mod. Phys. E 2017, 26, 1730005. [Google Scholar] [CrossRef]
- Elliott, J.P. Nuclear forces and the structure of nuclei. In Cargèse Lectures in Physics; Jean, M., Ed.; Gordon and Breach: New York, NY, USA, 1969; Volume 3, p. 337. [Google Scholar]
- Talmi, I. Fifty Years of the Shell Model — The Quest for the Effective Interaction. Adv. Nucl. Phys. 2003, 27, 1. [Google Scholar]
- Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef]
- Bethe, H.A. Theory of Nuclear Matter. Annu. Rev. Nucl. Sci. 1971, 21, 93. [Google Scholar] [CrossRef]
- Kortelainen, M.; Civitarese, O.; Suhonen, J.; Toivanen, J. Short-range correlations and neutrinoless double beta decay. Phys. Lett. B 2007, 647, 128. [Google Scholar] [CrossRef]
- Wu, H.F.; Song, H.Q.; Kuo, T.T.S.; Cheng, W.K.; Strottman, D. Majorana neutrino and Lepton-Number non-conservation in 48Ca nuclear double beta decay. Phys. Lett. B 1985, 162, 227. [Google Scholar] [CrossRef]
- Miller, G.A.; Spencer, J.E. A survey of pion charge-exchange reactions with nuclei. Ann. Phys. (N. Y.) 1976, 100, 562–606. [Google Scholar] [CrossRef]
- Neacsu, A.; Stoica, S.; Horoi, M. Fast, efficient calculations of the two-body matrix elements of the transition operators for neutrinoless double-β decay. Phys. Rev. C 2012, 86, 067304. [Google Scholar] [CrossRef]
- Feldmeier, H.; Neff, T.; Roth, R.; Schnack, J. A unitary correlation operator method. Nucl. Phys. A 1998, 632, 61–95. [Google Scholar] [CrossRef]
- Coraggio, L.; Itaco, N.; Mancino, R. Short-range correlations for neutrinoless double-beta decay and low-momentum NN potentials. arXiv 2019, arXiv:1910.04146. [Google Scholar]
- Coraggio, L.; Gargano, A.; Itaco, N.; Mancino, R.; Nowacki, F. Calculation of the neutrinoless double-β decay matrix element within the realistic shell model. Phys. Rev. C 2020, 101, 044315. [Google Scholar] [CrossRef]
- Bogner, S.; Kuo, T.T.S.; Coraggio, L.; Covello, A.; Itaco, N. Low momentum nucleon-nucleon potential and shell model effective interactions. Phys. Rev. C 2002, 65, 051301(R). [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M. Neutrinoless double-β decay of 48Ca in the shell model: Closure versus nonclosure approximation. Phys. Rev. C 2013, 88, 064312. [Google Scholar] [CrossRef]
- Šimkovic, F.; Faessler, A.; Rodin, V.; Vogel, P.; Engel, J. Anatomy of the 0νββ nuclear matrix elements. Phys. Rev. C 2008, 77, 045503. [Google Scholar] [CrossRef]
- Haxton, W.C.; Stephenson, G.J., Jr. Double beta decay. Prog. Part. Nucl. Phys. 1984, 12, 409. [Google Scholar] [CrossRef]
- Tomoda, T. Double beta decay. Rep. Prog. Phys. 1991, 54, 53. [Google Scholar] [CrossRef]
- Elliott, S.R.; Petr, V. Double beta decay. Annu. Rev. Nucl. Part. Sci. 2002, 52, 115–151. [Google Scholar] [CrossRef]
- Neacsu, A.; Stoica, S. Study of nuclear effects in the computation of the 0νββ decay matrix elements. J. Phys. G 2013, 41, 015201. [Google Scholar] [CrossRef]
- Ikeda, K. Collective excitation of unlike pair states in heavier nuclei. Prog. Theor. Phys. 1964, 31, 434. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys. Rev. C 2004, 69, 034335. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. Shell-model description of neutron-rich pf-shell nuclei with a new effective interaction GXPF 1. Eur. Phys. J. A 2005, 25, 499. [Google Scholar] [CrossRef]
- Poves, A.; Zuker, A. Theoretical spectroscopy and the fp shell. Phys. Rep. 1981, 70, 235–314. [Google Scholar] [CrossRef]
- Poves, A.; Sánchez-Solano, J.; Caurier, E.; Nowacki, F. Shell model study of the isobaric chains A = 50, A = 51 and A = 52. Nucl. Phys. A 2001, 694, 157. [Google Scholar] [CrossRef]
- Richter, W.A.; der Merwe, M.G.V.; Julies, R.E.; Brown, B.A. New effective interactions for the 0f1p shell. Nucl. Phys. A 1991, 523, 325. [Google Scholar] [CrossRef]
- Menendez, J. Neutrinoless ββ decay mediated by the exchange of light and heavy neutrinos: The role of nuclear structure correlations. J. Phys. G 2018, 45, 014003. [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M.; Brown, B.A. Neutrinoless double-β decay of 82Se in the shell model: Beyond the closure approximation. Phys. Rev. C 2014, 89, 054304. [Google Scholar] [CrossRef]
- Honma, M.; Otsuka, T.; Mizusaki, T.; Hjorth-Jensen, M. New effective interaction for f5pg9-shell nuclei. Phys. Rev. C 2009, 80, 064323. [Google Scholar] [CrossRef]
- Qi, C.; Xu, Z.X. Monopole-optimized effective interaction for tin isotopes. Phys. Rev. C 2012, 86, 044323. [Google Scholar] [CrossRef]
- Sen’kov, R.A.; Horoi, M. Shell-model calculation of neutrinoless double-β decay of 76Ge. Phys. Rev. C 2016, 93, 044334. [Google Scholar] [CrossRef]
- Alexander, B. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 Review. Universe 2020, 6, 159. [Google Scholar]
- Kostensalo, J.; Suhonen, J. Consistent large-scale shell-model analysis of the two-neutrino ββ and single β branchings in 48Ca and 96Zr. Phys. Lett. B 2020, 802, 135192. [Google Scholar] [CrossRef]
- Caurier, E.; Nowacki, F.; Poves, A. Shell Model description of the ββ decay of 136Xe. Phys. Lett. B 2012, 711, 62. [Google Scholar] [CrossRef]
- Brandow, B.H. Linked-Cluster Expansions for the Nuclear Many-Body Problem. Rev. Mod. Phys. 1967, 39, 771. [Google Scholar] [CrossRef]
- Kuo, T.T.S.; Lee, S.Y.; Ratcliff, K.F. A folded-diagram expansion of the model-space effective hamiltonian. Nucl. Phys. A 1971, 176, 65. [Google Scholar] [CrossRef]
- Krenciglowa, E.M.; Kuo, T.T.S. Convergence of effective hamiltonian expansion and partial summations of folded diagrams. Nucl. Phys. A 1974, 235, 171. [Google Scholar] [CrossRef]
- Lee, S.Y.; Suzuki, K. The effective interaction of two nucleons in the s-d shell S.Y. Lee, K. Suzuki. Phys. Lett. B 1980, 91, 173–176. [Google Scholar] [CrossRef]
- Suzuki, K.; Lee, S.Y. Convergent Theory for Effective Interaction in Nuclei. Prog. Theor. Phys. 1980, 64, 2091–2106. [Google Scholar] [CrossRef]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T.T.S. Effective shell-model hamiltonians from realistic nucleon–nucleon potentials within a perturbative approach. Ann. Phys. (N. Y.) 2012, 327, 2125–2151. [Google Scholar] [CrossRef][Green Version]
- Stroberg, S.R.; Hergert, H.; Bogner, S.K.; Holt, J.D. Nonempirical Interactions for the Nuclear Shell Model: An Update. Annu. Rev. Nucl. Part. Sci. 2019, 69, 307–362. [Google Scholar] [CrossRef]
- Ellis, P.J.; Osnes, E. An introductory guide to effective operators in nuclei. Rev. Mod. Phys. 1977, 49, 777. [Google Scholar] [CrossRef]
- Suzuki, K.; Okamoto, R. Effective Operators in Time-Independent Approach. Prog. Theor. Phys. 1995, 93, 905–917. [Google Scholar] [CrossRef]
- Towner, I.S.; Khanna, K.F.C. Corrections to the single-particle M1 and Gamow-Teller matrix elements. Nucl. Phys. A 1983, 399, 334–364. [Google Scholar] [CrossRef]
- Lacombe, M.; Loiseau, B.; Richard, J.M.; Mau, R.V.; Côtè, J.; Pirés, P.; Tourreil, R.D. Parametrization of the Paris N-N potential. Phys. Rev C 1980, 21, 861. [Google Scholar] [CrossRef]
- Reid, R.V. Local phenomenological nucleon-nucleon potentials. Ann. Phys. (N. Y.) 1968, 50, 411–448. [Google Scholar] [CrossRef]
- Krenciglowa, E.M.; Kung, C.L.; Kuo, T.T.S.; Osnes, E. The nuclear reaction matrix. Ann. Phys. 1976, 101, 154–194. [Google Scholar] [CrossRef]
- Kuo, T.T.S.; Brown, G.E. Structure of finite nuclei and the free nucleon-nucleon interaction: An application to 18O and 18F. Nucl. Phys. 1966, 85, 40–86. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Chiral 2π exchange at fourth order and peripheral NN scattering. Phys. Rev. C 2002, 66, 014002. [Google Scholar] [CrossRef]
- Holt, J.D.; Engel, J. Effective double-β-decay operator for 76Ge and 82Se. Phys. Rev. C 2013, 87, 064315. [Google Scholar] [CrossRef]
- Kwiatkowski, A.A.; Brunner, T.; Holt, J.D.; Chaudhuri, A.; Chowdhury, U.; Eibach, M.; Engel, J.; Gallant, A.T.; Grossheim, A.; Horoi, M.; et al. New determination of double-β-decay properties in 48Ca: High-precision Qββ-value measurement and improved nuclear matrix element calculations. Phys. Rev. C 2014, 89, 045502. [Google Scholar] [CrossRef]
- Horoi, M. Nuclear Structure for Reactions and Decays. J. Phys. Conf. Ser. 2013, 413, 012020. [Google Scholar] [CrossRef]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001, 63, 024001. [Google Scholar] [CrossRef]
- Coraggio, L.; De Angelis, L.; Fukui, T.; Gargano, A.; Itaco, N. Calculation of Gamow-Teller and two-neutrino double-β decay properties for 130Te and 136Xe with a realistic nucleon-nucleon potential. Phys. Rev. C 2017, 95, 064324. [Google Scholar] [CrossRef]
- Coraggio, L.; De Angelis, L.; Fukui, T.; Gargano, A.; Itaco, N.; Nowacki, F. Renormalization of the Gamow-Teller operator within the realistic shell model. Phys. Rev. C 2019, 100, 014316. [Google Scholar] [CrossRef]
- Pastore, S.; Schiavilla, R.; Goity, J.L. Electromagnetic two-body currents of one-and two-pion range. Phys. Rev. C 2008, 78, 064002. [Google Scholar] [CrossRef]
- Pastore, S.; Girlanda, L.; Schiavilla, R.; Viviani, M.; Wiringa, R.B. Electromagnetic currents and magnetic moments in chiral effective field theory (χ EFT). Phys. Rev. C 2009, 80, 034004. [Google Scholar] [CrossRef]
- Pastore, S.; Girlanda, L.; Schiavilla, R.; Viviani, M. Two-nucleon electromagnetic charge operator in chiral effective field theory (χ EFT) up to one loop. Phys. Rev. C 2011, 84, 024001. [Google Scholar] [CrossRef]
- Pastore, S.; Wiringa, R.B.; Pieper, S.C.; Schiavilla, R. Quantum Monte Carlo calculations of electromagnetic transitions in 8Be with meson-exchange currents derived from chiral effective field theory. Phys. Rev. C 2014, 90, 024321. [Google Scholar] [CrossRef]
- Pastore, S.; Pieper, S.C.; Schiavilla, R.; Wiringa, R.B. Quantum Monte Carlo calculations of electromagnetic moments and transitions in A≤9 nuclei with meson-exchange currents derived from chiral effective field theory. Phys. Rev. C 2013, 87, 035503. [Google Scholar] [CrossRef]
- Piarulli, M.; Girlanda, L.; Marcucci, L.E.; Pastore, S.; Schiavilla, R.; Viviani, M. Electromagnetic structure of A = 2 and 3 nuclei in chiral effective field theory. Phys. Rev. C 2013, 87, 014006. [Google Scholar] [CrossRef]
- Kolling, S.; Epelbaum, E.; Krebs, H.; Meissner, U.G. Two-pion exchange electromagnetic current in chiral effective field theory using the method of unitary transformation. Phys. Rev. C 2009, 80, 045502. [Google Scholar] [CrossRef]
- Kolling, S.; Epelbaum, E.; Krebs, H.; Meissner, U.G. Two-nucleon electromagnetic current in chiral effective field theory: One-pion exchange and short-range contributions. Phys. Rev. C 2011, 84, 054008. [Google Scholar] [CrossRef]
- Bacca, S.; Pastore, S. Electromagnetic reactions on light nuclei. J. Phys. G 2014, 41, 123002. [Google Scholar] [CrossRef]
- Fukui, T.; De Angelis, L.; Ma, Y.Z.; Coraggio, L.; Gargano, A.; Itaco, N.; Xu, F.R. Realistic shell-model calculations for p-shell nuclei including contributions of a chiral three-body force. Phys. Rev. C 2018, 98, 044305. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Coraggio, L.; De Angelis, L.; Fukui, T.; Gargano, A.; Itaco, N.; Xu, F.R. Contribution of chiral three-body forces to the monopole component of the effective shell-model Hamiltonian. Phys. Rev. C 2019, 100, 034324. [Google Scholar] [CrossRef]
- Menéndez, J.; Gazit, D.; Schwenk, A. Chiral two-body currents in nuclei: Gamow-Teller transitions and neutrinoless double-beta decay. Phys. Rev. Lett. 2011, 107, 062501. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.J.; Engel, J.; Yao, J.M. Quenching of nuclear matrix elements for 0νββ decay by chiral two-body currents. Phys. Rev. C 2018, 98, 031301. [Google Scholar] [CrossRef]
- Rho, M. A Solution to the Quenched gA Problem in Nuclei and Dense Baryonic Matter. arXiv 2019, arXiv:1903.09976. [Google Scholar]
- Iwata, Y.; Shimizu, N.; Otsuka, T.; Utsuno, Y.; Menéndez, J.; Honma, M.; Abe, T. Large-Scale Shell-Model Analysis of the Neutrinoless ββ Decay of 48Ca. Phys. Rev. Lett. 2016, 116, 112502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).