The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe
Abstract
1. Introduction
2. Lagrangian Density
3. The Derivation of the Field Equations and Its Consequences
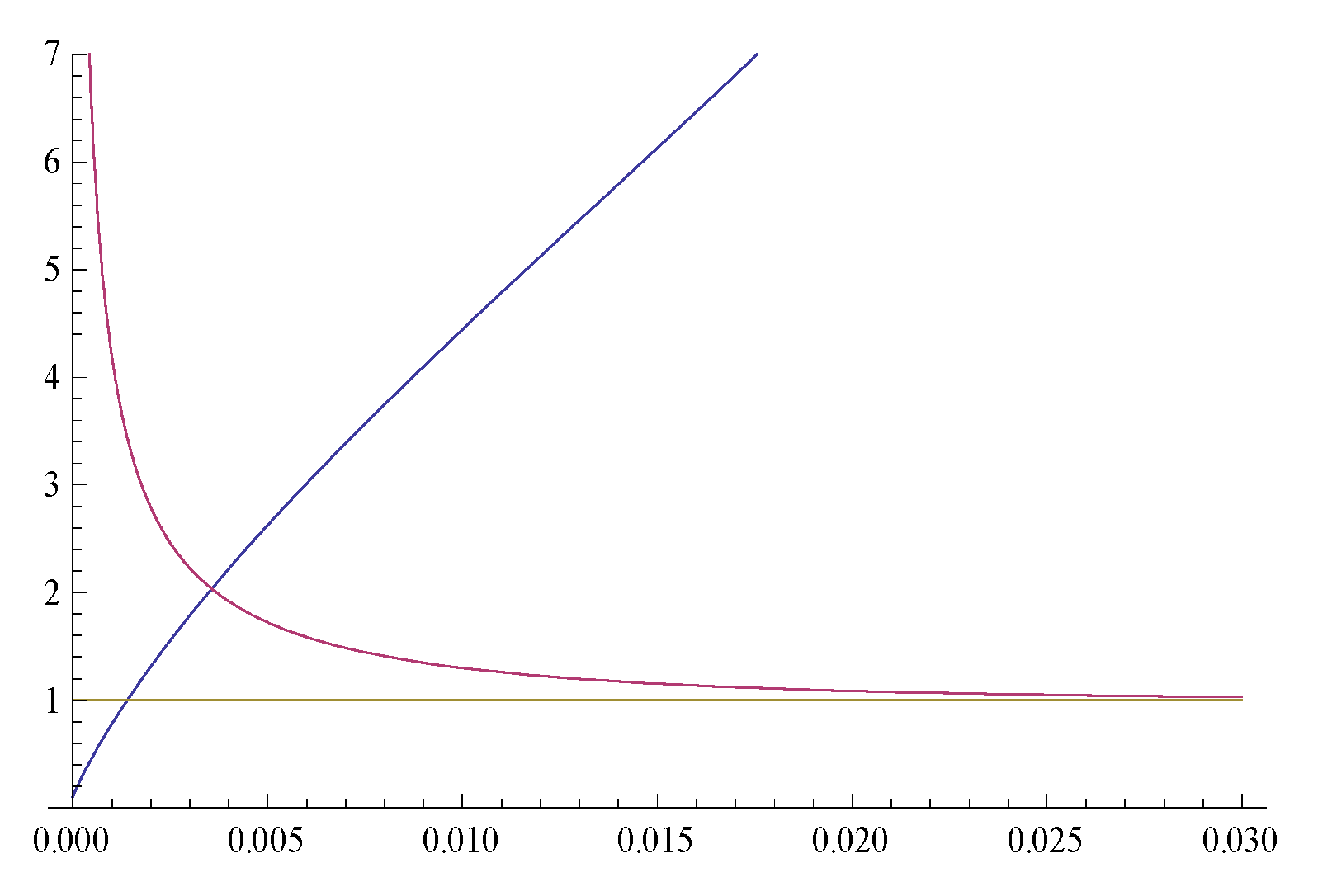
4. Cosmological Solution for the Primordial Universe
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kibble, T.W.B. Lorentz invariance and the gravitational field. J. Math. Phys. 1961, 2, 212–221. [Google Scholar] [CrossRef]
- Trautman, A. Recent advances in the Einstein–Cartan theory of gravity. Ann. N. Y. Acad. Sci. 1975, 262, 241–245. [Google Scholar] [CrossRef]
- Frolov, B.N. Principle of local invariance and Noether theorem. Vestn. Mosk. Univ. Ser. Fiz. Astron. 1963, 6, 48–58. (In Russian) [Google Scholar]
- Frolov, B.N. Principle of local invariance and Noether theorem. In Modern Problems of Gravitation/Proceedings of the 2nd Soviet Gravitation Conference; Publishing House of Tbilisi University: Tbilisi, Georgia, 1967; pp. 270–278. (In Russian) [Google Scholar]
- Frolov, B.N.; Sardanashvily, G.A. Gravitation and gauge fields. Sov. J. Phys. 1974, 17, 1228–1231. [Google Scholar] [CrossRef]
- Hayashi, K. Extended translational invariance and associated gauge fields. Progr. Theor. Phys. 1967, 38, 491–507. [Google Scholar] [CrossRef]
- Hayashi, K. Gauge theories of massive and massless tensor fields. Progr. Theor. Phys. 1968, 39, 495–515. [Google Scholar] [CrossRef]
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundtion and prospects. Revs. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Blagojevic, M. Gravitation and Gauge Symmetries; Institute Physics Publishing IOP Publishing Ltd.: Bristol, UK; Philadelphia, PA, USA, 2002. [Google Scholar]
- Frolov, B.N. Poincar’e–Gauge Theory of Gravity; Prometej Publishing House: Moscow, Russia, 2003. (In Russian) [Google Scholar]
- Frolov, B.N. On foundations of Poincar’e–gauge theory of gravity. Grav. Cosmol. 2004, 10, 116–120. [Google Scholar]
- Ponomarev, V.N.; Barvinsky, A.O.; Obukhov, Y.N. Gauge Approach and Quantization Methods in Gravity Theory; Nauka: Мoscow, Russia, 2017; p. 360. [Google Scholar]
- Charap, J.M.; Tait, W. A gauge theory of the Weyl group. Proc. R. Soc. 1974, A340, 249–262. [Google Scholar]
- Kasuya, M. Gauge theory in the Einstein–Cartan–Weyl space-time. Nuovo Cim. 1975, 28B, 127–137. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N.; Zhukovsky, V.C. Gauge Field Theory for Poincare–Weyl Group. Phys. Rev. 2006, 74, 064012. [Google Scholar] [CrossRef]
- Babourova, O.V.; Zhukovskii, V.C.; Frolov, B.N. A Weyl-Cartan space-time model based on the gauge principle. Theor. Math. Phys. 2008, 157, 1420–1432. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N.; Zhukovsky, V.C. Theory of Gravitation on the Basis of the Poincare–Weyl Gauge Group. Gravit. Cosmol. 2009, 15, 13–15. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Long range forces and broken symmetries. Proc. R. Soc. 1973, A333, 403–418. [Google Scholar]
- Babourova, O.V.; Frolov, B.N. Dark energy, Dirac’s scalar field and the cosmological constant problem. arXiv 2011, arXiv:1112.4449. [Google Scholar]
- Babourova, O.V.; Frolov, B.N. Mathematical Problems of the Modern Theory of Gravity; MPSU Press: Мoscow, Russia, 2012. (In Russian) [Google Scholar]
- Babourova, O.V.; Frolov, B.N.; Lipkin, K.N. Theory of gravitation with scalar Dirac field in exterior form formalism and the cosmological constant problem. Gravit. Cosmol. 2012, 18, 225–231. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N. Dark Energy as a Cosmological Consequence of Existence of the Dirac Scalar Field in Nature. Phys. Res. Intern. 2015, 2015, 952181. [Google Scholar] [CrossRef]
- Rubakov, V.A. Harrison–Zel’dovich spectrum from conformal invariance. arXiv 2009, arXiv:0906.3693. [Google Scholar]
- Sazhin, M.V. Anisotropy and polarization of cosmic microwave background: State of the art. Phys. Uspekhi. 2004, 47, 187–194. [Google Scholar] [CrossRef]
- Gliner, E.B. Algebraic properties of the energy–momentum tensor and vacuum–like states of matter. Sov. Phys. J. Exp. Theor. Phys. 1966, 22, 378–382. [Google Scholar]
- Gliner, E.B. Inflationary universe and the vacuumlike state of physical medium. Phys. Uspekhi. 2002, 45, 213–220. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N.; Klimova, E.A. Plane torsion waves in quadratic gravitational theories in Riemann–Cartan space. Class. Quantum Grav. 1999, 16, 1149–1162. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N.; Febres, E.V. Spherically symmetric solution of gravitation theory with a Dirac scalar field in the Cartan–Weyl space. Russ. Phys. J. 2015, 57, 1297–1299. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N.; Kudlaev, P.E.; Romanova, E.V. Spherically symmetric solution of the Weyl–Dirac theory of gravitation and possible influence of dark matter on the interplanetary spacecraft motion. arXiv 2016, arXiv:1610.09525. [Google Scholar]
- Babourova, O.V.; Frolov, B.N.; Kudlaev, P.E. Axially Symmetric Solution of the Weyl–Dirac Theory of Gravitation and the Problem of Rotation Curves of Galaxies. Gravit. Cosmol. 2018, 24, 118–121. [Google Scholar] [CrossRef]
- Babourova, O.V.; Frolov, B.N. Harrison-Zel’dovich scale invariance and the exponential decrease of the “cosmological constant” in the super-early Universe. arXiv 2020, arXiv:2001.05968. [Google Scholar]
- Weinberg, S. The Cosmological Constant Problems. arXiv 2000, arXiv:0005265v1. [Google Scholar]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Li, M.; Li, X.-D.; Wang, S.; Wang, Y. Dark Energy. Commun. Theor. Phys. 2011, 56, 525–604. [Google Scholar] [CrossRef]
- Gorbunov, D.S.; Rubakov, V.A. Introduction to the Theory of the Early Universe: Hot Big Bang Theory; World Scientific: Singapore, 2011. [Google Scholar]
- Martin, J. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). C. R. Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Speeding up the universe using dust with pressure. Phys. Rev. 2018, 98, 103520. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babourova, O.; Frolov, B. The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe. Universe 2020, 6, 230. https://doi.org/10.3390/universe6120230
Babourova O, Frolov B. The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe. Universe. 2020; 6(12):230. https://doi.org/10.3390/universe6120230
Chicago/Turabian StyleBabourova, Ol’ga, and Boris Frolov. 2020. "The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe" Universe 6, no. 12: 230. https://doi.org/10.3390/universe6120230
APA StyleBabourova, O., & Frolov, B. (2020). The Solution of the Cosmological Constant Problem: The Cosmological Constant Exponential Decrease in the Super-Early Universe. Universe, 6(12), 230. https://doi.org/10.3390/universe6120230



