Abstract
In the Einstein–Cartan gravitational theory with the chameleon field, while changing its mass independently of the density of its environment, we analyze the Friedmann–Einstein equations for the Universe’s evolution with the expansion parameter a being dependent on time only. We analyze the problem of an identification of the chameleon field with quintessence, i.e., a canonical scalar field responsible for dark energy dynamics, and for the acceleration of the Universe’s expansion. We show that since the cosmological constant related to the relic dark energy density is induced by torsion (Astrophys. J. 2016, 829, 47), the chameleon field may, in principle, possess some properties of quintessence, such as an influence on the dark energy dynamics and the acceleration of the Universe’s expansion, even in the late-time acceleration, but it cannot be identified with quintessence to the full extent in the classical Einstein–Cartan gravitational theory.
PACS:
03.50.-z; 04.25.-g; 04.25.Nx; 14.80.Va
1. Introduction
The chameleon field, changing its mass independently of a density of its environment [1,2], has been invented to avoid the problem of the equivalence principle violation [3]. Nowadays it is accepted that the chameleon field, identified with quintessence [4,5,6,7,8,9,10], i.e., a canonical scalar field, can be useful for an explanation of the late-time acceleration of the Universe’s expansion [11,12,13,14] and may shed light on the origins of dark energy and dark energy dynamics [15,16,17,18,19,20,21]. Since the relic dark energy density is closely related to the cosmological constant [15], in contrast to such a hypothesis that the chameleon field might originate the cosmological constant proportionally to the homogeneous static dark energy density, it has been shown at the model-independent level within the Einstein–Cartan gravitational theory [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] that the cosmological constant or the relic dark energy density has a geometrical origin caused by torsion [39]. In this case the chameleon field is able only to evolve above the relic background of the dark energy simulating its dynamics and, of course, to make a certain influence on the acceleration of the Universe’s expansion.
For the observation of torsion in the terrestrial laboratories there have been derived potentials of low-energy torsion–neutron interactions [40,41,42]. In terrestrial laboratories, the extreme smallness of absolute values of torsion was confirmed in different estimates of constraints on the contributions of torsion to observables of elementary particle interactions [43,44,45,46,47,48], including the qBounce experiments with ultracold neutrons (UCNs) [49,50,51,52,53,54,55] (see also [48]).
The chameleon–matter interactions were also intensively investigated in terrestrial laboratories [49,50,51,52,53,54,55,56,57] in experiments with ultracold and cold neutrons through some effective low-energy chameleon–neutron potentials [58,59,60,61] and by using cold atoms in the atom interferometry [62,63,64,65,66]. However, recently the importance of the chameleon field as quintessence in the late-time acceleration of the Universe has been questioned by Wang et al. [67] and Khoury [68] by pointing out that the conformal factor, relating Einstein’s and Jordan’s frames and defining the chameleon–matter interactions, is essentially constant over the last Hubble time. According to Wang et al. [67] and Khoury [68], this implies a negligible influence of the chameleon field on the late-time acceleration of the Universe’s expansion. To some extent, this should also imply that the chameleon field cannot possess such a property of quintessence as responsibility for the late-time acceleration of the Universe’s expansion [5,6,7].
Thus, the aim of this paper is to investigate the properties of the chameleon field in comparison to the properties of quintessence. We would like to remind readers that by definition, quintessence is a hypothetical state of dark energy described by a canonical scalar field for an explanation of the observable acceleration of the Universe’s expansion. We have to also emphasize that our analysis is restricted by the classical Einstein–Cartan gravitational theory. Below we show that the chameleon field has no relation to the origin of the cosmological constant, or the relic dark energy density, which is induced by torsion [39]. However, the chameleon field can still influence on the Universe’s expansion even in the late-time acceleration, caused by its evolution above the background of the relic dark energy [39]. By analyzing Einstein’s equations for the flat Universe in spacetime with the Friedmann metric, dependent on the expansion parameter a [69], we show that conservation of a total energy–momentum tensor of the system, including the chameleon field, radiation and matter (dark and baryon matter), demands the conformal factor to be equal to unity if and only if the dependencies of the radiation and matter densities on the expansion parameter a do not deviate from their standard forms, and respectively [69]. We obtain the same result by analyzing the first order differential Friedmann–Einstein equation, relating to the chameleon field, radiation and matter densities, and the second order differential Friedmann–Einstein equation, relating to the chameleon field, radiation and matter densities and their pressures, where and are the first and second time derivatives of the expansion parameter. Of course, the equality of the conformal factor to unity suppresses any coupling of the chameleon field to a matter density of its environment and makes such a scalar field unhelpful for avoiding the problem of the equivalence principle violation [3]. However, it does not prevent the chameleon field, evolving above the background of the relic dark energy, from a simulation of a dark energy dynamics and having an influence on the acceleration of the Universe’s expansion. Then, we show that the Friedmann–Einstein equation for is the first integral of the Friedmann–Einstein equation for if and only if the total energy–momentum of the system, including the chameleon field, radiation and matter, is locally conserved. As a result we infer that (i) if the radiation and matter densities obey their standard dependence on the expansion parameter and the conformal factor is equal to unity and the chameleon field loses the possibility to couple to an environment, and (ii) if the dependencies of the radiation and matter densities deviate from their standard behavior and , the conformal factor is not equal to unity and makes possible interactions of the chameleon field with its environment. In this case, usage of the chameleon field for the problem of equivalence principle violation becomes meaningful. In spite of the fact that the chameleon field does not possess the main property of quintessence in order to be a hypothetical form of dark energy [4], since the relic dark energy density or the cosmological constant has a geometrical origin related to torsion [39], the chameleon field, evolving above the relic dark energy and simulating a dark energy dynamics, might be responsible for an acceleration of the Universe’s expansion.
The paper is organized as follows. In Section 2 we derive Einstein’s equations in the Einstein–Cartan gravitational theory with torsion, chameleon and matter fields. Following [39] we show that the contribution of torsion to the Einstein–Hilbert action is presented in the form of the cosmological constant. Then, following Khoury and Weltman [1] we include the part of the integrand of the Einstein–Hilbert action proportional to the cosmological constant for the potential of the self-interaction of the chameleon field. This implies that the chameleon field has no relation to an origin of the cosmological constant or the relic dark energy density but can only evolve above such a relic background caused by torsion and simulate dark energy dynamics. In Section 3 in the flat Friedmann spacetime with the standard Friedmann metric , i.e., , and and , we show that the Einstein equations reduce themselves to the Friedmann–Einstein equations of the Universe’s evolution with the chameleon field, radiation and matter (dark and baryon) densities. Since the Einstein tensor , where and R are the Ricci tensor and scalar curvature, respectively, obey the Bianchi identity , where is the covariant divergence [69], the total energy–momentum tensor of the system, including the chameleon field, radiation and matter (dark and baryon), should be locally conserved. We find that local conservation of the total energy–momentum tensor imposes the evolution equations for the radiation and matter densities, where the dependence of them on the expansion parameter a is corrected by the conformal factor in comparison to the standard dependence and , respectively [69]. We show that the Friedmann–Einstein equation for is the first integral of the Friedmann–Einstein equation for if and only if the total energy momentum of the system, including the chameleon field, radiation and matter, is locally conserved. In case of the standard dependence of the radiation and matter densities on the expansion parameters and [69], local conservation of the total energy–momentum tensor of the chameleon field, radiation and matter demand the conformal factor to be equal to unity. This suppresses any interaction of the chameleon field with an ambient environment. In Section 4 we discuss experiments to probe torsion in the terrestrial laboratories through effective low-energy torsion-neutron interactions derived in [40,41,42]. In Section 5 we discuss the results obtained.
2. Einstein’s Equations in the Einstein–Cartan Gravitational Theory with Chameleon and Matter Fields
We take the Einstein–Hilbert action of the Einstein–Cartan gravitational theory without chameleon and matter fields in the standard form [27,37,69]:
where is the reduced Planck mass, is the Newtonian gravitational constant [70] and g is the determinant of the metric tensor . The scalar curvature is defined by [27,37]
where and are the Riemann and Ricci tensors in the Einstein–Cartan gravitational theory, respectively. Then, is the affine connection
where are the Christoffel symbols [69]
and is the contorsion tensor, related to torsion by and with the following properties: and [27,37]. The integrand of the Einstein–Hilbert action Equation (1) can be represented in the following form:
where we have denoted
and R is the Ricci scalar curvature of the Einstein gravitational theory, expressed in terms of the Christoffel symbols [69] only. When removing in Equation (5) the total derivatives and integrating by parts, we delete the third term and transcribe the fourth term into the form , where is the covariant derivative of the metric tensor , vanishing because of the metricity condition [69].
Derivation of Equation (5)
Let us show that can be presented in the form of Equation (5). Using Equation (3) we get an obvious relation
Having replaced the first term in the brackets by the total derivative and by adding the last term in the brackets, we arrive at the expression
Then, the first term in the brackets we rewrite as follows:
Since and are equal to [69] (see Equation (10.107) and Equation (9.56))
the fourth and fifth terms in the first line in Equation (9) and the second and third terms in the brackets are cancelled out in pairs. This reduces Equation (9) to Equation (5).
Now we may show that the contribution of the fourth term in Equation (5) to the Einstein–Hilbert action reduces to the contribution of the term . The contribution of the fourth term in Equation (5) to the Einstein–Hilbert action is defined by the integral
After the integration by parts in the first term we get
Having omitted the surface term and having renamed some indices in the second integral in Equation (12), we arrive at the expression
where we have used the property of the Christoffel symbols . The expression in the brackets is the covariant derivative of the metric tensor (see, for example, [27,69])
Thus, the contribution of the fourth term to the Einstein–Hilbert action is proportional to the integral
This confirms our assertion concerning a vanishing contribution of the fourth term in Equation (5) to the Einstein–Hilbert action in case of the metricity condition [69].
Since it has been shown in [39] that , where is the cosmological constant [69,71,72] (see also [15]) or the relic dark energy density, the Einstein–Hilbert action Equation (1) of the Einstein–Cartan gravitational theory with the scalar curvature Equation (2) can be represented in the following form [39]:
As has been shown in [39], the same result is valid for the Poincaré gauge gravitaitonal theory [73,74,75,76,77] (see also [31,32,33,34]). Using Equation (11) the action of the Einstein–Cartan gravitational theory with torsion, chameleon fields and matter fields we take in the form [39]
where is the Lagrangian of the chameleon field
and is the potential of the chameleon self-interaction. In Equation (17), following Khoury and Weltman [1], we have included additively the cosmological constant in the form of the relic dark energy density into the potential of the chameleon field self-interaction; i.e., . This implies that the chameleon field has no relation to the origin of the cosmological constant or the relic dark energy density. It can only evolve above the relic background of the dark energy, caused by torsion.
The matter fields and the radiation [78,79] are described by the Lagrangian . The interactions of the matter fields and radiation with the chameleon field are expressed in terms of the metric tensor in the Jordan frame [1,2,80], which is conformally related to Einstein’s frame metric tensor by (or ) and with , where is the chameleon–matter coupling constant [1,2]. The factor can be interpreted also as a conformal coupling to matter fields and radiation [80] (see also [1,2,81]). For simplicity we have set the chameleon–photon coupling constant [79] to be equal to the chameleon–matter coupling constant .
By varying the action of Equation (17) with respect to the metric tensor (see, for example, [69]), we arrive at Einstein’s equations, modified by the contribution of the chameleon field. We get
where is the Ricci tensor [69]; and are the matter (with radiation, which we treat as a radiative fluid [82,83,84,85,86]) and chameleon energy–momentum tensors, respectively, determined by
The factor appears in front of because of the relation
where we have used that
since [80] and . Then, the quantities , and in the Jordan frame are related to the quantities , p and in Einstein’s frame as [80]
This gives . By plugging Equation (20) with into Equation (19), we arrive at Einstein’s equations
where is the total energy–momentum tensor equal to
where the contribution of torsion [39] is included additively in the potential of the self-interactions of the chameleon field. Below we analyze the Einstein equations (Equation (24)) in the cold dark matter (CDM) model [70] in the Friedmann flat spacetime with the line element [69,70]
where and with . Then, is the expansion parameter of the Universe’s evolution [69]. The Christoffel symbols , the components of the Ricci tensor and the scalar curvature R are equal to [69]
where and and are first and second derivatives with respect to time.
3. Friedmann–Einstein Equations of the Universe’s Evolution
In Friedmann spacetime, Einstein’s equations (Equation (24)) define the equations of the Universe’s evolution, which are usually called Friedmann’s equations (or the Friedmann–Einstein equations) [69]. They are given by
and
where and are the radiation and matter densities. The scalar field couples to radiation and matter densities through the conformal factor . Then, the radiation density and pressure are related by the equation of state [69]. For the description of matter we use the cold dark matter (CDM) model with the pressureless dark and baryon matter [70]. The scalar field density and pressure are equal to
Varying the action Equation (17) with respect to the scalar field and its derivative one gets the equation of motion for the scalar field [81]. In Friedmann spacetime it reads
where is the effective potential given by
The contribution of the radiation density comes into the effective potential in the form . As for the equation of state , such a contribution vanishes. Thus, through the interaction with matter density the scalar field can acquire a non-vanishing mass if the effective potential obeys the constraints
i.e., the effective potential possesses a minimum at . An important role for a dependence of a chameleon field mass on a density of an environment is the conformal factor and its deviation from unity.
3.1. Bianchi Identity, Conservation of Total Energy–Momentum Tensor and Conformal Factor
By using Equation (27) and taking into account that in the Friedmann flat spacetime the non-vanishing components of the Einstein tensor are equal to
one may show that Einstein’s tensor obeys the Bianchi identity [69]
where is a covariant divergence and are the Christoffel symbols [69]. As a result, the covariant divergence of the total energy–momentum tensor should also vanish
Due to time-dependence only Equation (31) takes the form
where we have taken into account Equation (27). Using the non-vanishing components of the total energy momentum tensor
we transcribe Equation (32) into the form
Since Equation (31) can be rewritten as follows:
we may remove the contribution of the chameleon field in Equation (39). As result, we get
where we have used the equation of state [69]. Due to independence of radiation and matter densities, Equation (41) can be split into evolution equations of the radiation and matter densities:
For the standard dependence of the radiation and matter densities on the expansion parameter [69],
where , , and are the expansion parameter, the Hubble rate and the relative radiation and matter densities at our time [70], the equations for the radiation and matter densities Equation (42) are satisfied identically for .
Thus, if the radiation and matter densities depend on the expansion parameter a as and , local conservation of the total energy–momentum in the Universe can be fulfilled if and only if the conformal factor , relating Einstein’s and Jordan’s frames and defining the chameleon–matter coupling, is equal to unity; i.e., . However, in this case there is no influence of the chameleon field on the evolution of the radiation and matter densities and a dependence of the chameleon field mass on a density of its environment. In turn, for the evolution equations (Equation (37)) admit some exact solutions. It is convenient to search these solutions independently of the expansion parameter a. Treating the conformal factor as a function of the expansion parameter a, i.e., setting , the solutions to Equation (37) can be given by
where and are the radiation and matter densities at out time and , i.e., in the era of the late-time acceleration of the Universe’s expansion or the dark energy–dominated era. The integration constants of the first order differential equations (Equation (35)) are fixed by the conditions and , respectively [69,70]. According to the solutions (Equation (44)), the chameleon field has an influence on the evolution of the radiation and matter densities.
As an example of the conformal factor we may use [1,2], where is the chameleon field as a function of the expansion parameter a and the solution to Equation (31), i.e., . Keeping the linear order contributions in the expansion we get
Thus, the deviations of the radiation and matter densities from their standard behavior and are given by
Some observations of deviations of the radiation and matter densities in the Universe from their standard form might, in principle, evidence an existence of the chameleon field. Nevertheless, we have to emphasize that the contributions of the conformal factor to the radiation and matter densities at our time are not practically observable. It is seen from the solutions (Equation (44)) that the conformal factor affects the evolution of the radiation and matter densities during the radiation and matter-dominated eras only. Of course, an influence of the chameleon field evolution on the distribution of the radiation density might seem rather questionable, since the evolution equation (Equation (37)) defines an evolution of the product , where one may hardly separate from . By introducing an effective radiation density we obtain a canonical radiation density Equation (43), where the contribution of at is hidden very likely in .
3.2. The Friedmann–Einstein (Equation Equation (28)) as the First Integral of the Friedmann–Einstein Equation (Equation (29))
It is well–known that without the chameleon field and for the conformal factor the Friedmann–Einstein differential equation for is the first integral of the Friedmann–Einstein differential equation for [69]. However, such a property of Equation (28) with the chameleon field and the conformal factor to be the first integral of Equation (29) has not so far been investigated and proven in the literature. In order to prove that Equation (28) is the first integral of Equation (29) with the contributions of the chameleon field and the conformal factor , we rewrite Equation (28) as follows:
where is the chameleon field density, given by Equation (30) with the replacement (see Equation (32)). In order to find as a function of the expansion parameter a we use Equation (31) and transcribe it into the form
where we have denoted , assuming that is a function of a; i.e., . As a function of the expansion parameter a, the effective potential is given by
where with the additive contribution of the relic dark energy density, induced by torsion, and . The solution to Equation (48) is equal to
where the term corresponds to the contribution of the kinetic term of a scalar field [87]. The integration constant , we define as follows: , where is the integration constant, having the meaning of a relative density of a scalar field at time [70]. As a result, Equation (47) takes the form
where in the right-hand-side (r.h.s.) all densities and the conformal factor are functions of the expansion parameter a. Further, it is convenient to rewrite Equation (29) as follows:
where we have used Equation (51). Since the second derivative of the expansion parameter a with respect to time can be given by
one may transcribe Equation (47) into the form
The solution to Equation (54) amounts to
where C is the integration constant. Dividing both sides of Equation (55) by we arrive at the equation
where we have set . Thus, Equation (51) is the first integral of Equation (29). Making a replacement we arrive at the expression
Since the radiation and matter densities as functions of a obey the equations
and that (see Equation (44)), we transcribe the right–hand–side (r.h.s.) of Equation (57) into the form
This proves that Equation (28) is the first integral of Equation (29) if the total energy–momentum is locally conserved. The evolution of the chameleon field density independently of the expansion parameter a is defined by Equation (50), which we rewrite as follows:
where . and the third term in Equation (60) is the model-dependent part of the potential of the self-interaction of the chameleon field [4,10,16,88], taken as a function of the expansion parameter a, i.e., . Such a chameleon field density may affect the acceleration of the Universe’s expansion. Setting in Equation (60) we get
where the second and the last terms might still provide an acceleration of the Universe’s expansion additional to that caused by the first term , which is induced by torsion [39].
4. Torsion–Neutron Low-Energy Interactions
Our analysis carried out above may give an impression that after the absorption of torsion by the cosmological constant, the Einstein–Cartan gravitational theory reduces to Einstein’s gravitational theory [69]. Such an impression can be real only in case of the absence of fermions. As has been shown in [40,41,42], there is a huge variety of minimal and nonminimal low-energy torsion–neutron interactions. The torsion tensor field , being a tensor of the third rank and antisymmetric with respect to indices and , i.e., , is defined by 24 independent components: (i) four vectors , (ii) four axial vectors and (iii) 16 tensors [35,36,44] (see also [40,41,42]). The effective low-energy torsion–neutron potentials are presented in the form of expansion in powers of , where m is the neutron mass, and restricted by the terms of order , by using the Foldy–Wouthuysen (FW) canonical transformations [89]. The most interesting effective low-energy torsion–neutron interactions are induced in the rotating coordinate systems, which can be used for experimental probes of torsion in terrestrial laboratories [48,60]. It is important to emphasize that a part of these effective low-energy torsion–neutron interactions provide a violation of time-reversal invariance [42], which can be probed in the terrestrial laboratories.
According to [42], in the coordinate system rotating with an angular velocity the time component of the 4-vector of the torsion field induces the T–odd, i.e., violating time reversal symmetry, optical potential
where is the operator of the neutron spin and are Pauli matrices [90]. As has been shown in [47], because of the T–odd interaction (Equation (62)), the cross section for low-energy neutron–nucleus scattering, caused by the beam of polarized neutrons passing through a spinning cylinder, should acquire the correction [39]
where R and L are the radius and length of the spinning cylinder, and p is a neutron momentum (for a detailed discussion of the p-dependence of we refer to [47] below Equation (5)). The aim of the proposed experiment is a search for the -dependent part of the helicity-dependent part of the difference of the cross sections for neutron–nucleus scattering, caused by neutrons polarized parallel and antiparallel to the neutron beam axis coinciding with the axis of a spinning cylinder. For contemporary experimental abilities, such a T–odd correction allows one to probe the time component of the 4-vector part of the torsion field at the level of sensitivity of about . This is a few orders of magnitude better in comparison to the estimate obtained in [44].
Another part of the effective low-energy torsion–neutron potentials, which is not proportional to , can be used for probes of the components of the torsion field in the qBounce experiments dealing with ultracold neutrons (UCNs) bouncing in the gravitational field of the Earth [49,50,51,52,53,54,55] (see also [48]). As an example, we consider the effective low-energy potential of the time-component (pseudoscalar) of the 4-axial vector and the time-time-space-components of the tensor [42]
where and are the angular velocity and the radius vector of the Earth as they are shown in Figure 1. Then, is the radius–vector of the UCN in the laboratory.
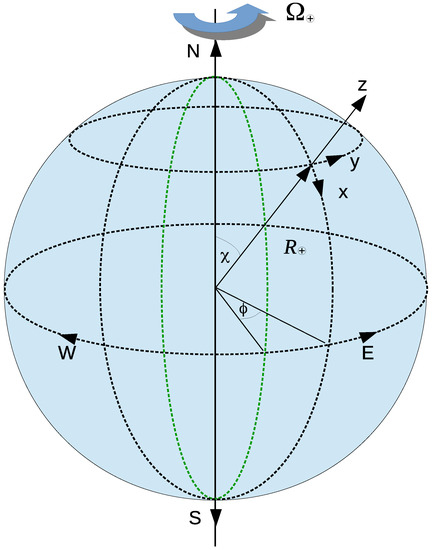
Figure 1.
The position of the ILL laboratory doing the qBounce experiments on the surface of the Earth.
The experiments with UCNs, bouncing in the gravitational field of the Earth, are being performed in the laboratory at Institut Laue Langevin (ILL) in Grenoble. The ILL laboratory is fixed to the surface of the Earth in the northern hemisphere. Following [91,92,93,94,95] we choose the ILL laboratory or the standard laboratory frame with coordinates , where the x, y and z axes point south, east and vertically upwards, respectively, with northern and southern poles on the axis of the Earth’s rotation with the Earth’s sidereal frequency . The position of the ILL laboratory on the surface of the Earth is determined by the angles and , where is the colatitude of the laboratory, defined in terms of the latitude , and is the longitude of the laboratory measured east of south with the values N and E [96], respectively. The beam of UCNs moves from south to north antiparallel to the x–direction and with energies of UCNs quantized in the z–direction.
In the qBounce experiments the contributions of interactions beyond the gravitational interaction of the Earth are measured in terms of the transition frequencies of the transitions between two gravitational states of UCNs and [49,50,51,52,53,54,55] (see also [59,60]). As of the small values of the components of the torsion field the contribution of the -dependent part of the effective torsion–neutron potential Equation (64), where the vector defines a location of the UCN in the coordinate system , to the transition frequencies between quantum gravitational states of UCNs can be neglected in comparison to the contributions of the terms independent of . Relative to the axes the vectors and are equal to and , respectively. This allows one to transcribe the effective low-energy torsion–neutron potential Equation (64) into the form
where are operators of the neutron spin –operator components. Thus, measuring the transition frequencies of spin-flip transitions between gravitational states one may measure the contributions of the pseudoscalar and tensor and components of the torsion field. A predictable power of the qBounce experiments we may demonstrate by example of the estimate of the contribution of the pseudoscalar component of the torsion field coupled to UCNs. Indeed, according to Lämmerzahl [43], the value of the pseudoscalar component of the torsion field is constrained by . Its contribution to the transition frequencies between quantum gravitational states of UCNs is of about . This value is at the level of current experimental sensitivity [55] and the sensitivity of a nearest future, which is of about and even [49,97]. The experiments discussed in this sections and and many others, which could be carried out by using effective low-energy potentials of torsion–neutron interactions derived in [40,41,42], might make reliable the geometrical origin of the cosmological constant or the relic dark energy, induced by torsion [39].
5. Discussion
We would like to emphasize that our analysis of the chameleon field as a candidate for quintessence is carried out within the classical Einstein–Cartan gravitational theory with the Einstein-Hilbert action linear in the Ricci scalar curvature. By definition [4], quintessence is a hypothetical form of dark energy described by a canonical scalar field for an explanation of the observable acceleration of the Universe’s expansion. The most important that quintessence should be a hypothetical form of dark energy. In this connection in the Einstein–Cartan gravitational theory, when the cosmological constant or the relic dark energy density has the geometrical origin, caused by torsion, the chameleon field possesses no chance to be a hypothetical form of dark energy. In other words having provided a geometrical origin for the cosmological constant or the relic dark energy torsion deprives the chameleon field to have a chance to be quintessence. As a result, the chameleon field is able only to evolve above the relic background of the dark energy, caused by torsion, but not to originate it. Then, as a consequence of conservation of the total energy–momentum of the system, the chameleon field can affect the dark energy dynamics and as well as the Universe’s expansion even also the late-time acceleration. We have shown that such an influence of the chameleon field on the acceleration of the Universe’s expansion retains also even if the conformal factor, relating Einstein’s and Jordan’s frames and defining the interaction of the chameleon field with its ambient matter, is equal to unity (see Equations (60) and (61). This result is closely related to our proof that for the system, including the chameleon field, radiation and matter (dark and baryon matter), the Friedmann–Einstein equation for is the first integral for the Friedmann–Einstein equation for .
We have found that local conservation of the total energy–momentum of the system, including the chameleon field, radiation and matter (dark and baryon matter), leads to the equations of the evolution of the radiation and matter densities, corrected by the conformal factor. Of course, since for radiation the evolution equation defines an evolution of the product , where the conformal factor is a function of the expansion parameter a, such a product does not deviate from the standard behavior . Since the radiation density enters to the Friedmann–Einstein equations only in the form of the product one may not probably separate the contribution of the conformal factor above the standard shape proportional to . In turn, for the matter density the contribution of the conformal factor leads to a deviation from the standard behavior [69]. However, such a deviation might be, in principle, noticeable only during the matter-dominated era. In the dark energy–dominated era that is in our time of the late-time acceleration of the Universe, where the expansion parameter is equal to for the Hubble time [69], the contributions of the conformal factor to the radiation and matter densities in comparison to the standard values and are practically unobservable. This agrees well with the constraints on the deviations of the radiation and matter densities from their values at our time to a few parts per million [98], which can be obtained from the constraints on the fifth force caused by the chameleon field in the Galaxy and the Solar system.
The cosmological constant , induced by torsion [39], we have included additively to the potential of the self-interaction of the chameleon field as a background of the relic dark energy: . In the chameleon field theory [1,2] the relic dark energy density is defined as follows: , where the scale is calculated for the relative dark energy density [70]. The -dependent part of the potential of the self-interaction of the chameleon field is arbitrary to some extent, i.e., model-dependent, and demands a special analysis similar to that carried out in [4,10,16,88]. However, such an analysis goes beyond the scope of our paper. We would like to emphasize that a specific analysis of a dynamics of the chameleon field such as different mechanisms of chameleon screening and a formation of a fifth force, for example, in the Galaxy and the Solar system is related also to a special choice of the potential of the self-interaction of the chameleon field [16,98]. Such an analysis has been carried out by Brax et al. [16] and Jain et al. [98]. The repetition of such an analysis goes beyond the scope of this paper.
As regards the assertion by Wang et al. [67] and Khoury [68] that since the conformal factor is practically constant during the Hubble time, so the chameleon field is not responsible for the late-time acceleration of the Universe, one may argue that the conformal factor might be, in principle, practically constant (or better to say unity), but such a behavior of the conformal factor does not prohibit the chameleon field, evolving above the relic dark energy background induced by torsion, to take a certain part in dark energy dynamics and, correspondingly, in the acceleration of the Universe’s expansion (see Equations (60) and (61)) and even so in the late-time acceleration of the Universe’s expansion.
As regards another canonical scalar fields which can be introduced for an explanation of an origin of dark energy and an influence on acceleration of the Universe’s expansion such as symmetron and dilaton, we may say the following. Since the dynamics of the symmetron field differs from the dynamics of the chameleon one only by the shape of the potential of self-interaction [99], our conclusion concerning an identification of the chameleon field with quintessence is fully applicable to the symmetron one. In other words the symmetron field cannot be quintessence to full extent. Moreover, we have to mention that an existence of the symmetron field and its importance for an evolution of the Universe might seem to be rather questionable after the qBounce experiments [55] on the transition frequencies between quantum gravitational states of UCNs, which have excluded the existence of the symmetron field.
Then, we have to confess that our analysis of an identification of a canonical scalar field with quintessence, carried out within the classical Einstein–Cartan gravitational theory, can say practically nothing concerning dilaton. Indeed, unlike the gravitational theories with the chameleon and symmetron fields the gravitational theories with dilaton are based on string theory in terms of the non-riemannian structure of space-time [100,101,102,103,104,105,106,107]. Of course, since an inclusion of dilaton as a canonical scalar field is closely related to a requirement of scale invariance of the action of the dynamical system under consideration, the classical Einstein–Cartan gravitational theory can be, in principle, modified by a requirement of scale invariance [108]. However, in such a modified Einstein–Cartan gravitational theory the problem of the geometrical origin of the cosmological constant or the relic dark energy caused by torsion demands a special analysis, which goes beyond the scope of this paper. Nevertheless, if in such a modified Einstein–Cartan gravitational theory torsion would be a geometrical origin of the cosmological constant or the relic dark energy density, our conclusion concerning an impossibility to identify dilation with quintessence might have been valid only within such a modified Einstein–Cartan gravitational theory.
Robust support fpr the geometrical origin of the cosmological constant or the relic dark energy could be experimental observations of torsion in terrestrial laboratories in terms of its contributions to observables of different physical processes. In Section 4 we have discussed two of these experiments, which can be carried out by using beams of polarized UCNs. We mean the contribution of the T–odd torsion–neutron low-energy interaction to the cross section for the scattering of the beam of polarized neutrons by nucleus in the end of spinning cylinder. This allows one to estimate the value of the time component of the 4-vector part of the torsion field at the level of about . Another experiment on the probe of torsion can be carried out at ILL by the French–Austrian qBounce Collaboration by using Gravity Resonance Spectroscopy (GRS), a new measuring technique combining quantum measurements and gravity experiments [49,50,51,52,53,54,55]. The qBounce experiments, measuring transition frequencies between quantum gravitational states of UCNs, allow one to probe torsion with a sensitivity of about and even [49,97]. This should improve the existing upper bound on the pseudoscalar component of the torsion field by a few orders of magnitude and give new constraints on the tensor components of the torsion field [44].
Author Contributions
A.N.I.: Conceptualization, Methodology, Data Curation, Investigation, Supervision, Writing—Original draft preparation. M.W.: Formal analysis, Investigation, Methodology, Software, Validation, Writing—Original draft preparation. All authors have read and agreed to the published version of the manuscript.
Funding
The work of A. N. Ivanov was supported by the Austrian “Fonds zur Förderung der Wissenschaftlichen Forschung” (FWF) under the contracts P31702-N27, P26636-N20 and P33279-N, and “Deutsche Förderungsgemeinschaft” (DFG) AB 128/5-2. The work of M. Wellenzohn was supported by the MA 23 (FH-Call 16) under the project “Photonik— Stiftungsprofessur für Lehre”.
Acknowledgments
We are grateful to Hartmut Abele for stimulating discussions and to Philippe Brax and Alkistis Pourtsidou for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Mota, D.F.; Shaw, D.J. Evading equivalence principle violations, cosmological, and other experimental constraints in scalar field theories with a strong coupling to matter. Phys. Rev. D 2007, 75, 063501. [Google Scholar] [CrossRef] [Green Version]
- Will, C.M. Theory and Experiment in Gravitational Physics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef] [PubMed]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef] [Green Version]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896. [Google Scholar] [CrossRef] [Green Version]
- Steinhardt, P.J. Quintessence and cosmic acceleration. NATO Sci. Ser. C 2001, 565, 143. [Google Scholar]
- Steinhardt, P.J. The quintessential Universe. AIP Conf. Proc. 2001, 586, 279. [Google Scholar]
- Steinhardt, P.J. A quintessential introduction to dark energy. Philos. Trans. R. Soc. Lond. A 2003, 361, 2497. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Quintessence: A review. Class. Quantum Gravity 2013, 30, 21400. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Deustua, S.; Fabbro, S.; Goldhaber, G.; Groom, D.E.; Kim, A.G.; Kim, M.Y.; Knop, R.A.; Nugent, P.; et al. Cosmology from type Ia supernovae. Bull. Am. Astron. Soc. 1997, 29, 1351. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astron. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Goobar, A.; Perlmutter, S.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Groom, D.E.; Hook, I.M.; et al. The acceleration of the universe: Measurements of cosmological parameters from type Ia supernovae. Phys. Scr. T 2000, 85, 47. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef] [Green Version]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Khoury, J.; Weltman, A. Detecting dark energy in orbit: The cosmological chameleon. Phys. Rev. D 2004, 70, 123518. [Google Scholar] [CrossRef] [Green Version]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef] [Green Version]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark energy and the accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385. [Google Scholar] [CrossRef] [Green Version]
- Jain, B.; Joyce, A.; Thompson, R.; Upadhye, A.; Battat, J.; Brax, P.; Davis, A.; de Rham, C.; Dodelson, S.; Erickcek, A.; et al. Novel probes of gravity and dark energy. arXiv 2013, arXiv:1309.5389. [Google Scholar]
- Brax, P.; Davis, A.-C. Casimir, gravitational, and neutron tests of dark energy. Phys. Rev. D 2015, 91, 063503. [Google Scholar] [CrossRef] [Green Version]
- Pignol, G. Probing dark energy models with neutrons. Int. J. Mod. Phys. A 2015, 30, 1530048. [Google Scholar] [CrossRef] [Green Version]
- Cartan, É. Sur une généralisation de la notion de courbure de Riemann et les espaces à torsion. C. R. Acad. Sci. 1922, 174, 593. [Google Scholar]
- Cartan, É. Sur les variétés à connexion affine et la relativité généralisée (prémière partie). Ann. Ec. Norm. 1923, 40, 325. [Google Scholar] [CrossRef]
- Cartan, É. Sur les variétés à connexion affine et la relativité généralisée (prémière partie). Ann. Ec. Norm. 1924, 41, 1. [Google Scholar] [CrossRef] [Green Version]
- Cartan, É. Sur les variétés à connexion affine et la relativité généralisée (deuxième partie). Ann. Ec. Norm. 1925, 42, 17. [Google Scholar] [CrossRef] [Green Version]
- Cartan, É.; Einstein, A. Letters of Absolute Parallelism; Princeton University Press: Princeton, NJ, USA, 1975. [Google Scholar]
- Schrödinger, E. Space-Time Structure; Cambridge at the University Press: Cambridge, UK, 1950. [Google Scholar]
- Hehl, F.W.; Kerlick, G.D.; van der Heyde, P. General relativity with spin and torsion and its deviations from Einstein’s theory. Phys. Rev. D 1974, 10, 1066–1069. [Google Scholar] [CrossRef]
- Hehl, F.W.; van der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef] [Green Version]
- Hehl, F.W.; Obukhov, Y.N. Elie Cartan’s torsion in geometry and in field theory, an essay. Ann. Fond. Louis Broglie 2007, 32, 157–194. [Google Scholar]
- Hehl, F.W. Gauge Theories of Gravity and Spacetime. arXiv 2012, arXiv:1204.3672v2. [Google Scholar]
- Blagojević, M.; Hehl, F.W. (Eds.) Gauge Theories of Gravitation: A Reader with Commentaries; Imperial College Press: London, UK, 2013. [Google Scholar]
- Hehl, F.W.; Obukhov, Y.N. Conservation of energy-momentum of matter as the basis for the gauge theory of gravitation. arXiv 2019, arXiv:1909.01791. [Google Scholar]
- Obukhov, Y.N.; Hehl, F.W. General relativity as a special case of Poincaré gauge gravity. Phys. Rev. D 2020, 102, 044058. [Google Scholar] [CrossRef]
- Shapiro, I.L. Physical aspects of the space-time torsion. Phys. Rep. 2002, 357, 113–213. [Google Scholar] [CrossRef] [Green Version]
- Hammond, R.T. Torsion gravity. Rep. Prog. Phys. 2002, 65, 599–649. [Google Scholar] [CrossRef]
- Kostelecký, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef] [Green Version]
- Ni, W.-T. Reports on Progress in Physics Searches for the role of spin and polarization in gravity. Rep. Prog. Phys. 2010, 73, 056901. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Wellenzohn, M. Einstein–Cartan gravity with torsion field serving as an origin for the cosmological constant or dark energy density. Astrophys. J. 2016, 829, 47. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Wellenzohn, M. Nonrelativistic approximation of the Dirac equation for slow fermions coupled to the chameleon and torsion fields in the gravitational field of the Earth. Phys. Rev. D 2015, 92, 065006. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Wellenzohn, M. Effective low-energy potential for slow Dirac fermions in Einstein-Cartan Gravity with torsion and chameleon field. Phys. Rev. D 2015, 92, 125004. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Wellenzohn, M. Spin precession of slow neutrons in Einstein-Cartan gravity with torsion, chameleon, and magnetic field. Phys. Rev. D 2016, 93, 045031. [Google Scholar] [CrossRef] [Green Version]
- Lämmerzahl, C. Constraints on space-time torsion from Hughes-Drever experiments. Phys. Lett. A 1997, 228, 223–231. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Russell, N.; Tasson, J.D. Constraints on torsion from bounds on Lorentz violation. Phys. Rev. Lett. 2008, 100, 111102. [Google Scholar] [CrossRef] [Green Version]
- Obukhov, Y.N.; Silenko, A.J.; Teryaev, O.V. Spin-torsion coupling and gravitational moments of Dirac fermions: Theory and experimental bounds. Phys. Rev. D 2014, 90, 124068. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, R.; Snow, W.M.; Yan, H. A first experimental limit on in-matter torsion from neutron spin rotation in liquid 4He4. Phys. Lett. B 2014, 730, 353–356, Erratum in 2015, 744, 415. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Snow, W.M. Parity-even and time-reversal-odd neutron optical potential in spinning matter induced by gravitational torsion. Phys. Lett. B 2017, 764, 186–189. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N. Presented at the Workshop Dark Energy in the Laboratory, Chicheley Hall, UK, 20–22 April 2016.
- Abele, H.; Jenke, T.; Leeb, H.; Schmiedmayer, J. Ramsey’s method of separated oscillating fields and its application to gravitationally induced quantum phase shifts. Phys. Rev. D 2010, 81, 065019. [Google Scholar] [CrossRef] [Green Version]
- Jenke, T.; Geltenbort, P.; Lemmel, H.; Abele, H. Realization of a gravity-resonance-spectroscopy technique. Nat. Phys. 2011, 7, 468–472. [Google Scholar] [CrossRef]
- Abele, H.; Jenke, T.; Stadler, D.; Geltenbort, P. QuBounce: The dynamics of ultra-cold neutrons falling in the gravity potential of the Earth. Nucl. Phys. A 2009, 827, 593c–595c. [Google Scholar] [CrossRef]
- Jenke, T.; Stadler, D.; Abele, H.; Geltenbort, P. Q-BOUNCE—Experiments with quantum bouncing ultracold neutrons. In Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment; Particle Physics with Slow Neutrons; Elsevier: Amsterdam, The Netherlands, 2009; Volume 611, pp. 318–321. [Google Scholar]
- Abele, H.; Leeb, H. Gravitation and quantum interference experiments with neutrons. New J. Phys. 2012, 14, 055010. [Google Scholar] [CrossRef]
- Jenke, T.; Cronenberg, G.; Bürgdorfer, J.; Chizhova, L.A.; Geltenbort, P.; Ivanov, A.N.; Lauer, T.; Lins, T.; Rotter, S.; Saul, H.; et al. Gravity resonance spectroscopy constrains dark energy and dark matter scenarios. Phys. Rev. Lett. 2014, 112, 151105. [Google Scholar] [CrossRef] [Green Version]
- Cronenberg, G.; Brax, P.; Filter, H.; Geltenbort, P.; Jenke, T.; Pignol, G.; Pitschmann, M.; Thalhammer, M.; Abele, H. Acoustic Rabi oscillations between gravitational quantum states and impact on symmetron dark energy. Nat. Phys. 2018, 14, 1022–1026. [Google Scholar] [CrossRef]
- Lemmel, H.; Brax, P.; Ivanov, A.N.; Jenke, T.; Pignol, G.; Pitschmann, M.; Potocar, T.; Wellenzohn, M.; Zawisky, M.; Abele, H. Neutron interferometry constrains dark energy chameleon fields. Phys. Lett. B 2015, 743, 310–314. [Google Scholar] [CrossRef]
- Li, K.; Arif, M.; Cory, D.G.; Haun, R.; Heacock, B.; Huber, M.G.; Nsofini, J.; Pushin, D.A.; Saggu, P.; Sarenac, D.; et al. Neutron limit on the strongly-coupled chameleon field. Phys. Rev. D 2016, 93, 062001. [Google Scholar] [CrossRef] [Green Version]
- Brax, P.; Pignol, G. Strongly coupled chameleons and the neutronic quantum bouncer. Phys. Rev. Lett. 2011, 107, 111301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanov, A.N.; Höllwieser, R.; Jenke, T.; Wellenzohn, M.; Abele, H. Influence of the chameleon field potential on transition frequencies of gravitationally bound quantum states of ultracold neutrons. Phys. Rev. D 2013, 87, 105013. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Cronenberg, G.; Höllwieser, R.; Jenke, T.; Pitschmann, M.; Wellenzohn, M.; Abele, H. Exact solution for chameleon field, self-coupled through the Ratra-Peebles potential with n = 1 and confined between two parallel plates. Phys. Rev. D 2016, 94, 085005. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, A.N.; Pitschmann, M. Nonrelativistic approximation of the Dirac equation for slow fermions in static metric spacetimes. Phys. Rev. D 2014, 90, 045040. [Google Scholar] [CrossRef] [Green Version]
- Burrage, C.; Copeland, E.J.; Hinds, E.A. Probing dark energy with atom interferometry. JCAP 2015, 2015, 42. [Google Scholar] [CrossRef]
- Burrage, C.; Copeland, E.J. Using atom interferometry to detect dark energy. Contemp. Phys. 2016, 57, 164–176. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, P.; Jaffe, M.; Haslinger, P.; Simmons, Q.; Müller, H.; Khoury, J. Atom-interferometry constraints on dark energy. Science 2015, 349, 849–851. [Google Scholar] [CrossRef] [Green Version]
- Elder, B.; Khoury, J.; Haslinger, P.; Jaffe, M.; Müller, H.; Hamilton, P. Chameleon dark energy and atom interferometry. Phys. Rev. D 2016, 94, 044051. [Google Scholar] [CrossRef] [Green Version]
- Burrage, C.; Sakstein, J. Tests of chameleon gravity. Living Rev. Relat. 2018, 21, 1. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Hui, L.; Khoury, J. No-go theorems for generalized chameleon field theories. Phys. Rev. Lett. 2012, 109, 241301. [Google Scholar] [CrossRef] [PubMed]
- Khoury, J. Chameleon field theories. Class. Quantum Gravity 2013, 30, 214004. [Google Scholar] [CrossRef] [Green Version]
- Rebhan, E. Theoretische Physik: Relativitätstheorie und Kosmologie; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Particle Data Group. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Evolution of the cosmological constant. Nature 1999, 398, 25. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Lorentz invariance and the gravitational field. J. Math. Phys. 1961, 2, 212. [Google Scholar] [CrossRef] [Green Version]
- Utiyama, R. Invariant theoretical interpretation of interaction. Phys. Rev. 1956, 101, 1597. [Google Scholar] [CrossRef]
- Sciama, D.W. On the interpretation of the Einstein-Schrodinger unified field theory. J. Math. Phys. 1961, 2, 472. [Google Scholar] [CrossRef]
- Sciama, D.W. The physical structure of general relativity. Rev. Mod. Phys. 1964, 36, 463–469. [Google Scholar] [CrossRef]
- Blagojević, M. Gravitation and Gauge Symmetries; Series in High–Energy Physics, Cosmology and Gravitation; Foster, B., Grishchuk, L., Kolb, E.W., MacCallum, M.A.H., Perkins, D.H., Schutz, B.F., Eds.; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 2001. [Google Scholar]
- Davis, A.-C.; Schelpe, C.A.O.; Shaw, D.J. Effect of a chameleon scalar field on the cosmic microwave background. Phys. Rev. D 2009, 80, 064016. [Google Scholar] [CrossRef] [Green Version]
- Baum, S.; Cantatore, G.; Hoffmann, D.H.H.; Karuza, M.; Semertzidis, Y.K.; Upadhye, A.; Zioutas, K. Detecting solar chameleons through radiation pressure. Phys. Lett. B 2014, 739, 167–173. [Google Scholar] [CrossRef]
- Dicke, R.H. Mach’s principle and invariance under transformation of units. Phys. Rev. 1962, 125, 2163. [Google Scholar] [CrossRef]
- Ivanov, A.N.; Wellenzohn, M. Standard electroweak interactions in gravitational theory with chameleon field and torsion. Phys. Rev. D 2015, 91, 085025. [Google Scholar] [CrossRef] [Green Version]
- Tomas, L.H. The radiation field in a fluid in motion. Q. J. Math. 1930, 1, 239. [Google Scholar] [CrossRef]
- Weinberg, S. Entropy generation and the survival of photo-galaxies in an expanding Universe. Astrophys. J. 1971, 168, 175. [Google Scholar] [CrossRef]
- Straumann, N. On radiative fluids. Helv. Phys. Acta 1976, 49, 269. [Google Scholar]
- Schweizer, M.A. Transient and transport coefficients for radiative fluids. Astrophys. J. 1982, 258, 798–811. [Google Scholar] [CrossRef]
- Schweizer, M.A. Relativistic radiative hydrodynamics. Ann. Phys. 1988, 183, 80. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Turok, N. Cosmic evolution in a cyclic universe. Phys. Rev. D 2002, 65, 126003. [Google Scholar] [CrossRef] [Green Version]
- Copeland, E.J.; Mizuno, S.; Shaeri, M. Dynamics of a scalar field in Robertson-Walker spacetimes. Phys. Rev. D 2009, 79, 103515. [Google Scholar] [CrossRef] [Green Version]
- Foldy, L.L.; Wouthuysen, S.A. On the Dirac theory of spin 1/2 particle and its nonrelativistic limit. Phys. Rev. 1950, 78, 29. [Google Scholar] [CrossRef]
- Itzykson, C.; Zuber, J.-B. Quantum Field Theory; McGraw-Hill Inc.: New York, NY, USA, 1980. [Google Scholar]
- Bluhm, R.; Kostelecký, V.A.; Lane, C.D.; Russell, N. Clock-comparison tests of Lorentz and CPT symmetry in space. Phys. Rev. Lett. 2002, 88, 090801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kostelecký, V.A.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef] [Green Version]
- Bluhm, R.; Kostelecký, V.A.; Lane, C.D.; Russell, N. Probing Lorentz and CPT violation with space-based experiments. Phys. Rev. D 2003, 68, 125008. [Google Scholar] [CrossRef] [Green Version]
- Kostelecký, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Kostelecký, V.A. Lorentz-violating spinor electrodynamics and Penning traps. Phys. Rev. D 2016, 94, 056008. [Google Scholar] [CrossRef] [Green Version]
- GPS Coordinates of Grenoble. Available online: https://latitude.to/map/fr/france/cities/grenoble (accessed on 26 November 2020).
- Ivanov, A.N.; Wellenzohn, M.; Abele, H. Probing of violation of Lorentz invariance by ultracold neutrons in the Standard Model Extension. Phys. Lett. B 2019, 797, 134819. [Google Scholar] [CrossRef]
- Jain, B.; Vikram, V.; Sakstein, J. Astrophysical tests of modified gravity: Constraints from distance indicators in the nearby Universe. Astrophys. J. 2013, 779, 39. [Google Scholar] [CrossRef] [Green Version]
- Hinterbichler, K.; Khoury, J. Symmetron fields: Screening Long-range forces through local symmetry restoration. Phys. Rev. Lett. 2010, 104, 231301. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Polyakov, A.M. The string dilation and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef] [Green Version]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a runaway dilaton. Phys. Rev. D 2001, 65, 023508. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Piazza, F.; Veneziano, G. Violations of the equivalence principle in a dilaton-runaway scenario. Phys. Rev. D 2002, 66, 046007. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Piazza, F.; Veneziano, G. Runaway dilaton and equivalence principle violations. Phys. Rev. Lett. 2002, 89, 081601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fujii, Y. Mass of the dilaton and the cosmological constant. Prog. Theor. Phys. 2003, 110, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Gasperini, M. Dilaton cosmology and phenomenology. Lect. Notes Phys. 2008, 737, 787–844. [Google Scholar]
- Guendelman, E.I.; Kaganovich, A.B. Absence of the fifth force problem in a model with spontaneously broken dilatation symmetry. Ann. Phys. 2008, 323, 866–882. [Google Scholar] [CrossRef] [Green Version]
- Brax, P.; van de Bruck, C.; Davis, A.-C. The dilaton and modified gravity. Phys. Rev. D 2010, 82, 063519. [Google Scholar] [CrossRef] [Green Version]
- Saa, A. Einstein-Cartan theory of gravity revisited. arXiv 1993, arXiv:9309027. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).