On the Discrete Version of the Schwarzschild Problem
Abstract
1. Introduction
2. The Method
3. Calculation
3.1. Equations in the Leading Order over Metric Variations
3.2. Discrete Version of the Lense–Thirring Metric
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Hamber, H.W. Quantum Gravity on the Lattice. Gen. Rel. Gravit. 2009, 41, 817. [Google Scholar] [CrossRef]
- Regge, T. General relativity theory without coordinates. Nuovo Cimento 1961, 19, 558. [Google Scholar] [CrossRef]
- Feinberg, G.; Friedberg, R.; Lee, T.D.; Ren, M.C. Lattice gravity near the continuum limit. Nucl. Phys. B 1984, 245, 343. [Google Scholar] [CrossRef]
- Cheeger, J.; Müller, W.; Shrader, R. On the curvature of the piecewise flat spaces. Commun. Math. Phys. 1984, 92, 405. [Google Scholar] [CrossRef]
- Hamber, H.W.; Williams, R.M. Newtonian Potential in Quantum Regge Gravity. Nucl. Phys. B 1995, 435, 361. [Google Scholar] [CrossRef]
- Hamber, H.W.; Williams, R.M. On the Measure in Simplicial Gravity. Phys. Rev. D 1999, 59, 064014. [Google Scholar] [CrossRef]
- Perez, A. The spin-foam approach to quantum gravity. Living Rev. Relativ. 2013, 16, 3. [Google Scholar] [CrossRef]
- Ponzano, G.; Regge, T. Semiclassical limit of Racah Coeficients. In Spectroscopy and Group Theoretical Methods in Physics: Racah Memorial Volume; Bloch, F., Cohen, S.G., de Shalit, A., Sambursky, S., Talmi, I., Eds.; Publishing House: North-Holland, Amsterdam, The Netherlands, 1968; pp. 1–58. [Google Scholar]
- Ambjorn, J.; Goerlich, A.; Jurkiewicz, J.; Loll, R. Nonperturbative Quantum Gravity. Phys. Rep. 2012, 519, 127. [Google Scholar] [CrossRef]
- Miković, A.; Vojinović, M. Quantum gravity for piecewise flat spacetimes. SFIN 2018, XXXI, 267. [Google Scholar]
- Wong, C.-Y. Application of Regge calculus to the Schwarzshild and Reissner-Nordstrøm geometries. J. Math. Phys. 1971, 12, 70. [Google Scholar] [CrossRef]
- Brewin, L. Einstein-Bianchi system for smooth lattice general relativity. I. The Schwarzschild spacetime. Phys. Rev. D 2012, 85, 124045. [Google Scholar] [CrossRef]
- Collins, P.A.; Williams, R.M. Dynamics of the Friedmann universe using Regge calculus. Phys. Rev. D 1973, 7, 965. [Google Scholar] [CrossRef]
- Gentle, A.P. A cosmological solution of Regge calculus. Class. Quantum Gravity 2013, 30, 085004. [Google Scholar] [CrossRef][Green Version]
- Brewin, L.C. A numerical study of the Regge calculus and Smooth Lattice methods on a Kasner cosmology. Class. Quantum Gravity 2015, 32, 195008. [Google Scholar] [CrossRef]
- Liu, R.G.; Williams, R.M. Regge calculus models of closed lattice universes. Phys. Rev. D 2016, 93, 023502. [Google Scholar] [CrossRef]
- Glaser, L.; Loll, R. CDT and cosmology. Comptes Rendus Physique 2017, 18, 265. [Google Scholar] [CrossRef]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum Transfiguration of Kruskal Black Holes. Phys. Rev. Lett. 2018, 121, 241301. [Google Scholar] [CrossRef]
- Ashtekar, A.; Olmedo, J.; Singh, P. Quantum extension of the Kruskal spacetime. Phys. Rev. D 2018, 98, 126003. [Google Scholar] [CrossRef]
- Dupuis, M.; Ryan, J.P.; Speziale, S. Discrete gravity models and Loop Quantum Gravity: A short review. SIGMA 2012, 8, 052. [Google Scholar] [CrossRef]
- Khatsymovsky, V.M. On the non-perturbative graviton propagator. Int. J. Mod. Phys. A 2018, 33, 1850220. [Google Scholar] [CrossRef]
- Khatsymovsky, V.M. On the discrete Christoffel symbols. Int. J. Mod. Phys. A 2019, 34, 1950186. [Google Scholar] [CrossRef]
- Khatsymovsky, V.M. On the discrete version of the black hole solution. Int. J. Mod. Phys. A 2020, 35, 2050058. [Google Scholar] [CrossRef]
- Khatsymovsky, V.M. Defining integrals over connections in the discretized gravitational functional integral. Mod. Phys. Lett. A 2010, 25, 1407. [Google Scholar] [CrossRef]
- Fröhlich, J. Regge calculus and discretized gravitational functional integrals. In Nonperturbative Quantum Field Theory: Mathematical Aspects and Applications, Selected Papers; Publishing House, World Scientific: Singapore, 1992; p. 523, IHES preprint 1981 (unpublished). [Google Scholar]
- Holst, S. Barbero’s Hamiltonian Derived from a Generalized Hilbert-Palatini Action. Phys. Rev. D 1996, 53, 5966. [Google Scholar] [CrossRef] [PubMed]
- Fatibene, L.; Francaviglia, M.; Rovelli, C. Spacetime Lagrangian Formulation of Barbero-Immirzi Gravity. Class. Quantum Gravity 2007, 24, 4207. [Google Scholar] [CrossRef]
- Barbero, J.F. Real Ashtekar Variables for Lorentzian Signature Space-times. Phys. Rev. D 1995, 51, 5507. [Google Scholar] [CrossRef] [PubMed]
- Immirzi, G. Quantum Gravity and Regge Calculus. Nucl. Phys. Proc. Suppl. 1997, 57, 65. [Google Scholar] [CrossRef]
- Khatsymovsky, V.M. Tetrad and self-dual formulations of Regge calculus. Class. Quantum Gravity 1989, 6, L249. [Google Scholar] [CrossRef]
- Arnowitt, R.; Deser, S.; Misner, C.W. The Dynamics of General Relativity. In Gravitation: An Introduction to Current Research; Witten, L., Ed.; Wiley: New York, NY, USA, 1962; Chapter 7; p. 227, (Preprint arXiv:gr-qc/0405109). [Google Scholar]
- DeWitt, B.S. Quantization of fields with infinite-dimensional invariance groups. III. Generalized Shwinger-Feynman theory. J. Math. Phys. 1962, 3, 1073. [Google Scholar] [CrossRef]
- Misner, C.W. Feynman quantization of general relativity. Rev. Mod. Phys. 1957, 29, 497. [Google Scholar] [CrossRef]
- Rocek, M.; Williams, R.M. The quantization of Regge calculus. Z. Phys. C 1984, 21, 371. [Google Scholar] [CrossRef]
- Lemaitre, G. L’univers en expansion. Ann. Soc. Sci. Brux. A 1933, 53, 51. [Google Scholar]
- Stanyukovich, K.P. On the question of the Schwarzschild metric in a synchronous reference frame. Rep. USSR Acad. Sci. 1969, 187, 75. [Google Scholar]
- Williams, R.M. Quantum Regge calculus model in the Lorentzian domain and its Hamiltonian formulation. Class. Quantum Gravity 1986, 3, 853. [Google Scholar] [CrossRef]
- Painlevé, P. La mécanique classique et la théorie de la relativité. C. R. Acad. Sci. (Paris) 1921, 173, 677. [Google Scholar]
- Gullstrand, A. Allgemeine Lösung des statischen Einkörperproblems inder Einsteinschen Gravitationstheorie. Arkiv. Mat. Astron. Fys. 1922, 16, 1. [Google Scholar]
- Thirring, H.; Lense, J. Über den Einfluss der Eigenrotation der Zentralkörperauf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 156–163. [Google Scholar]
- Baines, J.; Berry, T.; Simpson, A.; Visser, M. Painleve-Gullstrand form of the Lense-Thirring spacetime. arXiv 2020, arXiv:2006.14258. [Google Scholar]
- Sorkin, R. The electromagnetic field on a simplicial net. J. Math. Phys. 1975, 16, 2432. [Google Scholar] [CrossRef]
- Weingarten, D. Geometric formulation of electrodynamics and general relativity in discrete space-time. J. Math. Phys. 1977, 18, 165. [Google Scholar] [CrossRef]
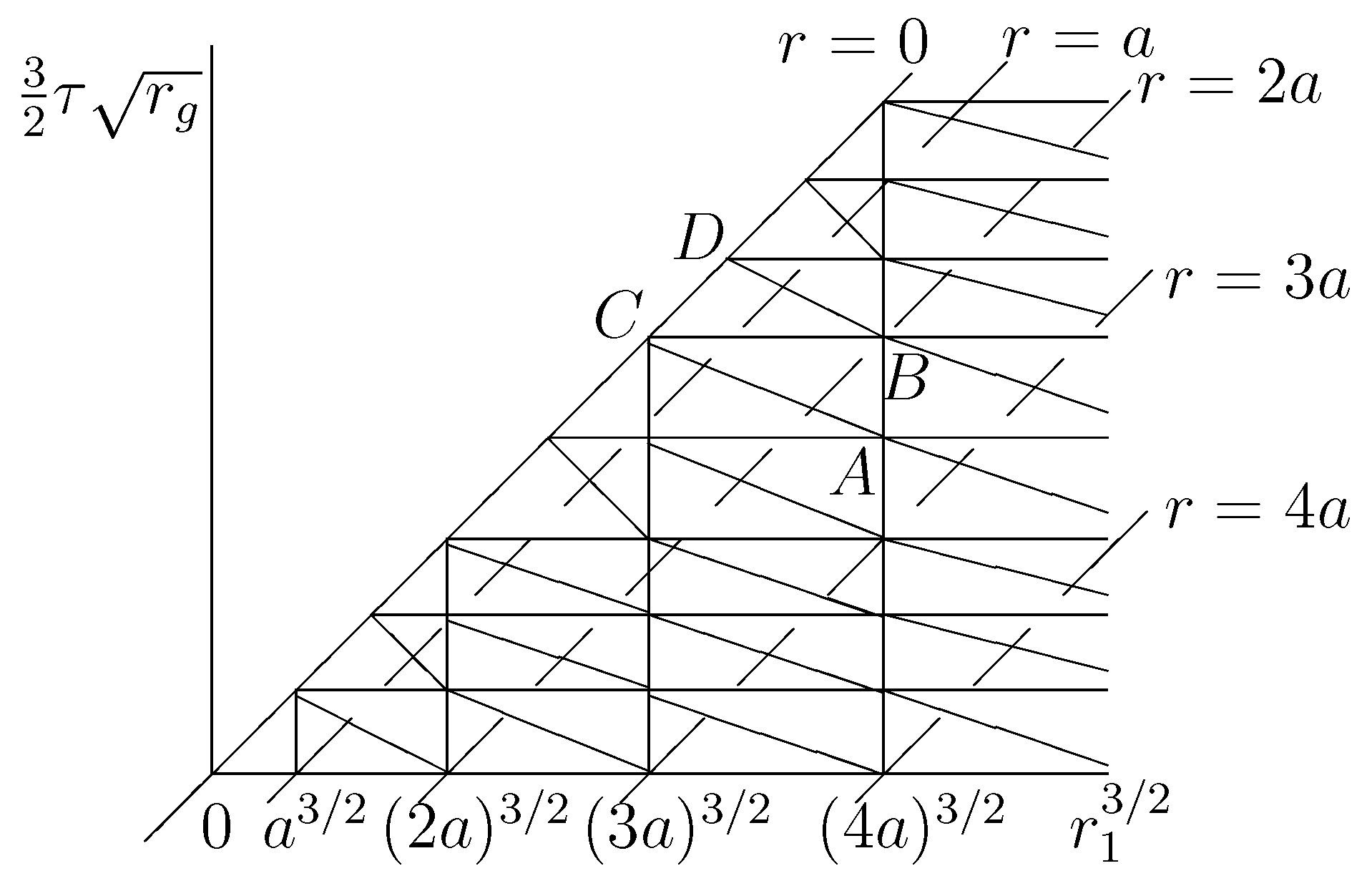
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatsymovsky, V. On the Discrete Version of the Schwarzschild Problem. Universe 2020, 6, 185. https://doi.org/10.3390/universe6100185
Khatsymovsky V. On the Discrete Version of the Schwarzschild Problem. Universe. 2020; 6(10):185. https://doi.org/10.3390/universe6100185
Chicago/Turabian StyleKhatsymovsky, Vladimir. 2020. "On the Discrete Version of the Schwarzschild Problem" Universe 6, no. 10: 185. https://doi.org/10.3390/universe6100185
APA StyleKhatsymovsky, V. (2020). On the Discrete Version of the Schwarzschild Problem. Universe, 6(10), 185. https://doi.org/10.3390/universe6100185




