Hybrid Metric-Palatini Gravity: Regular Stringlike Configurations
Abstract
1. Introduction
2. HMPG and Its Scalar-Tensor Representation
3. Cylindrical Symmetry: Equations and Boundary Conditions
3.1. Equations
3.2. Boundary Conditions
4. Stringlike Solutions: Analysis
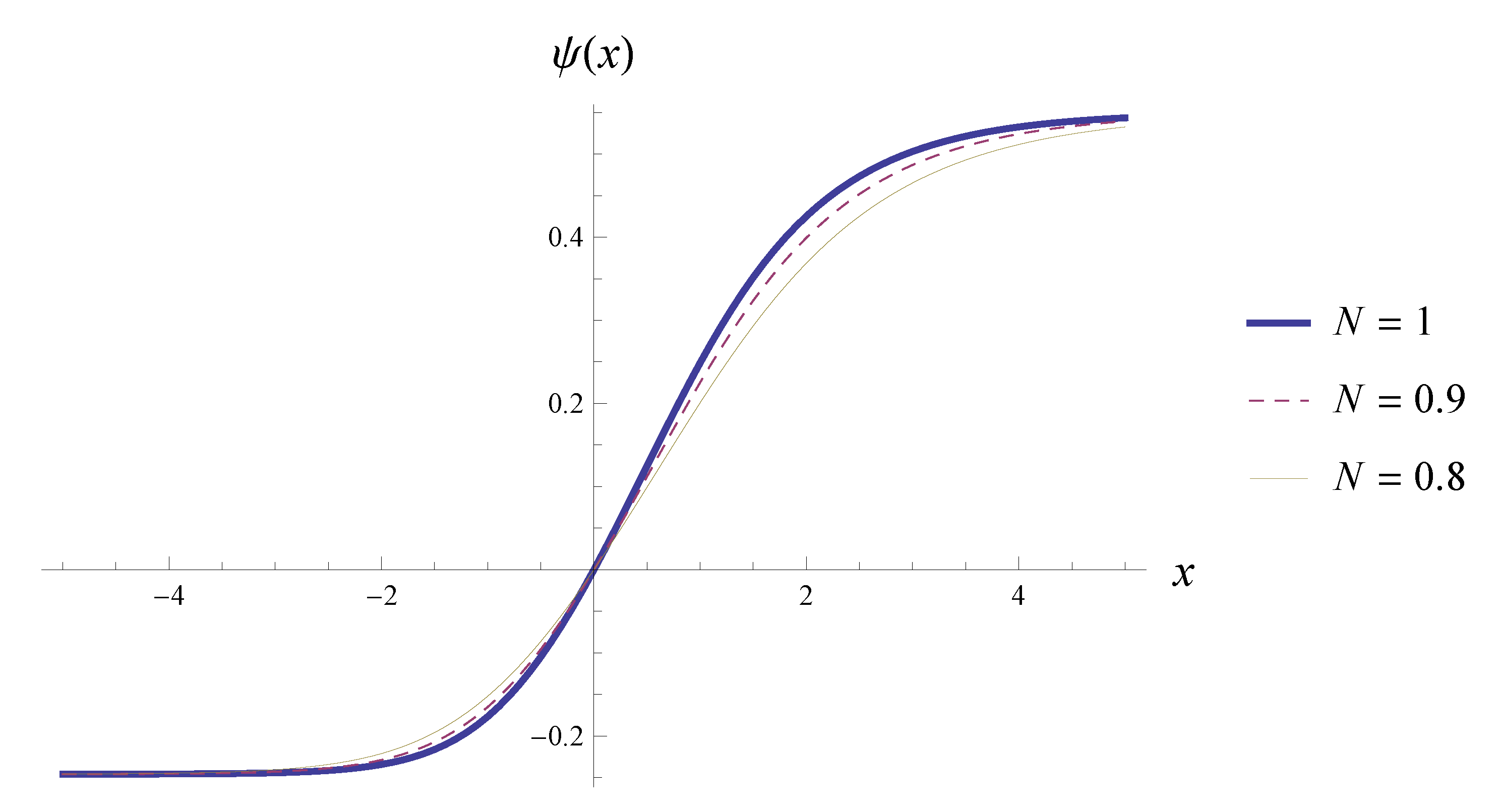
4.1. Solitons in the Einstein Frame
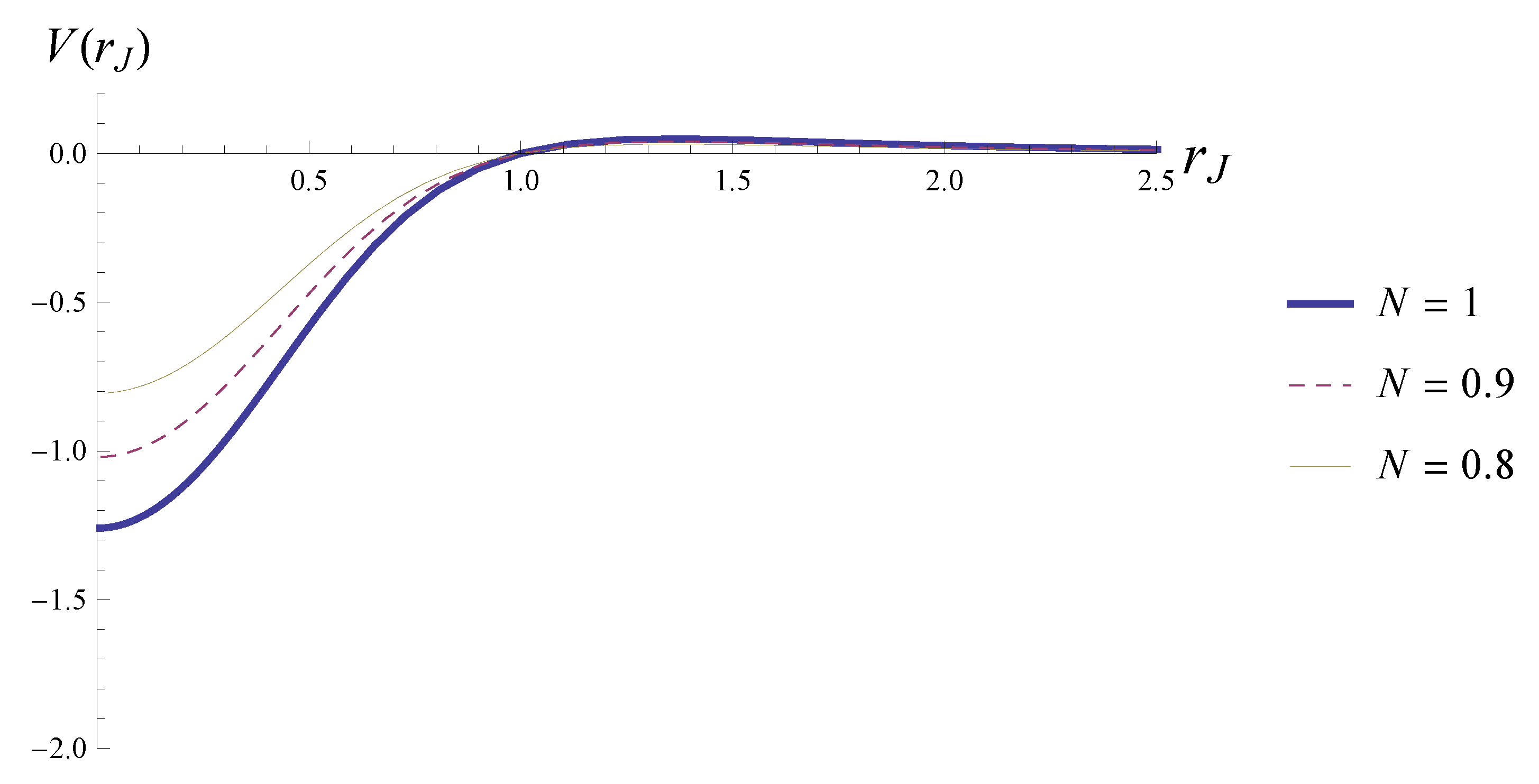
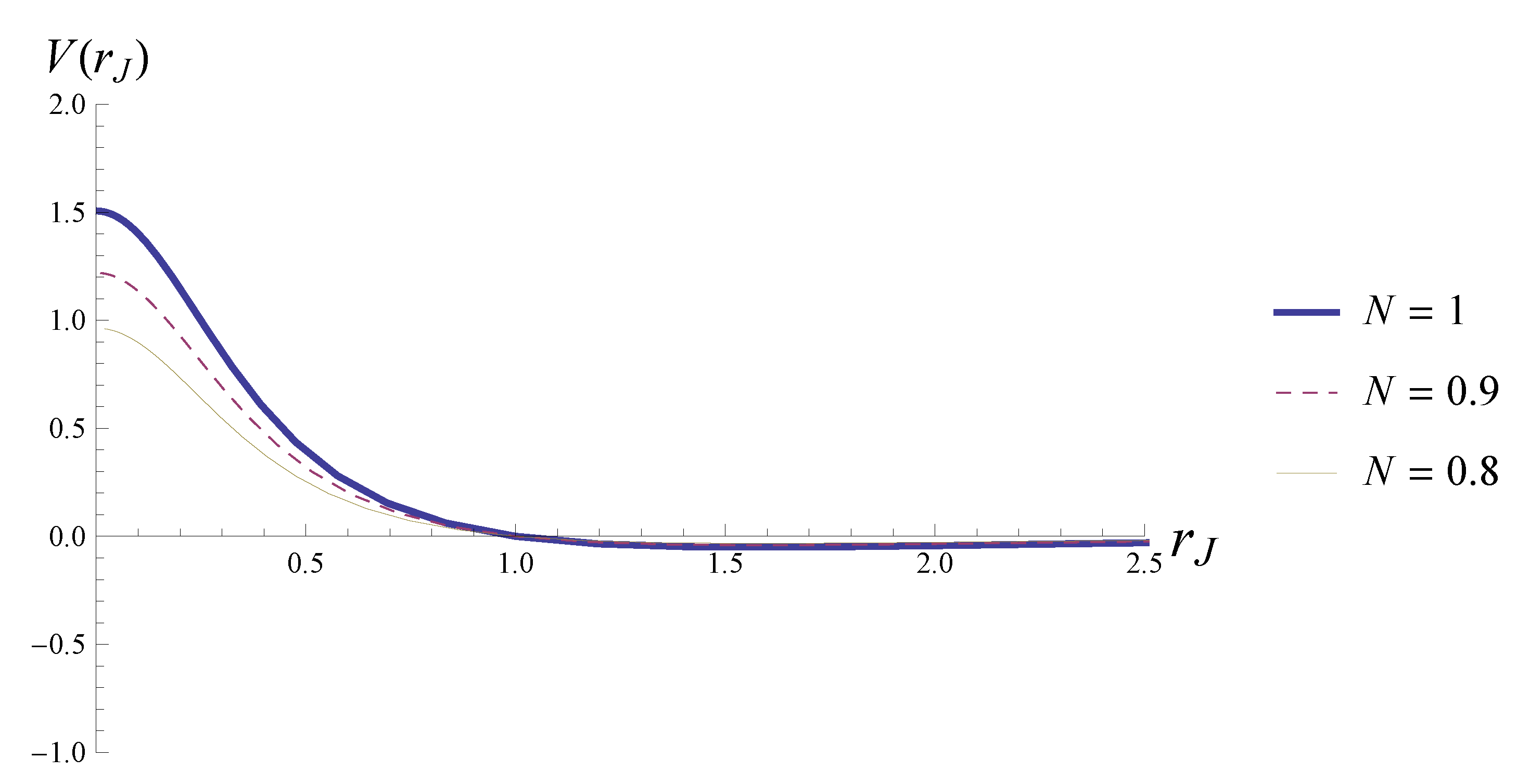
4.2. Solitons in the Jordan Frame
5. Examples
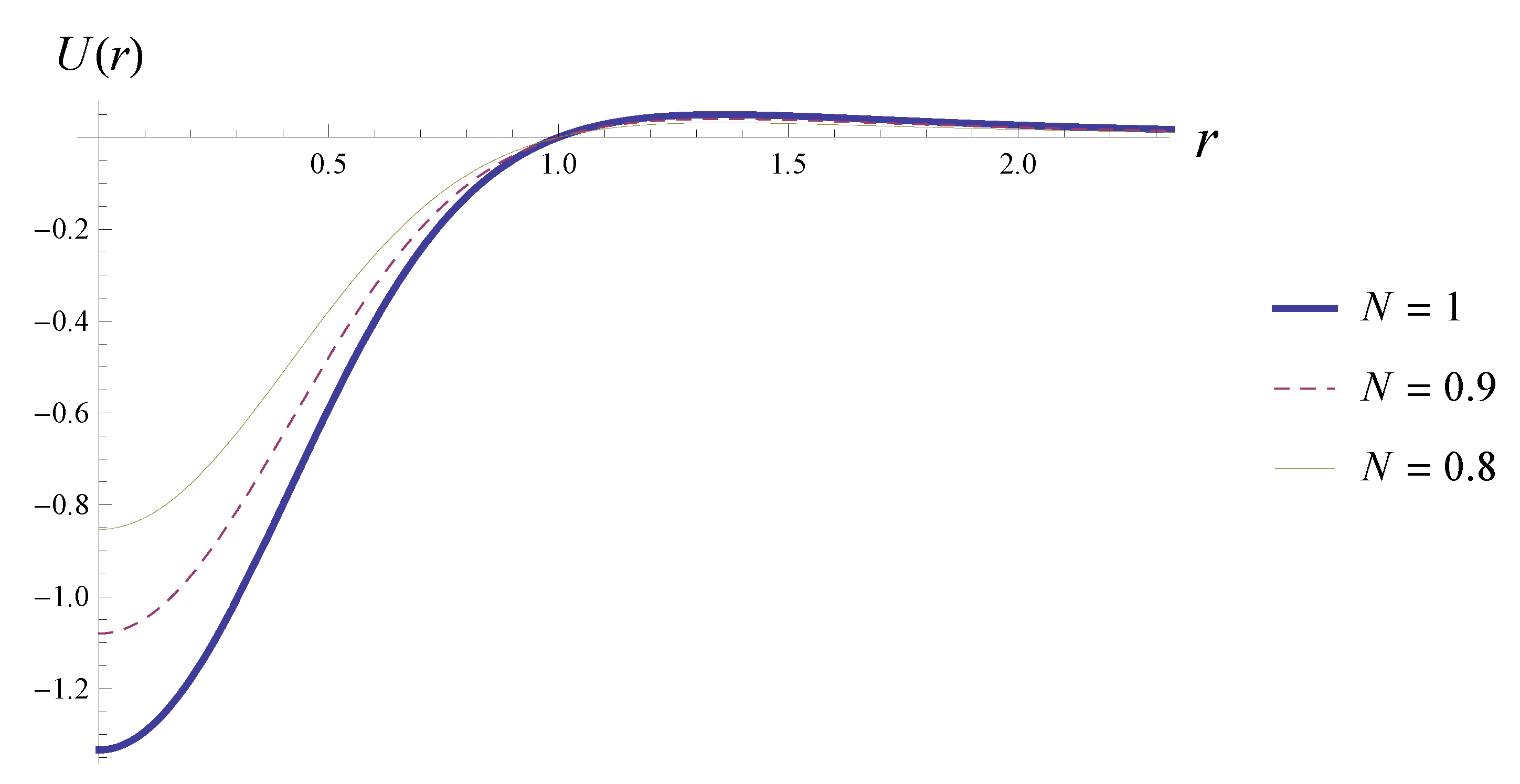
5.1. Example 1: Zero Potential
5.2. Example 2: Exponential Potential
5.3. Example 3: Solitons with Nonzero Potential on the Axis
5.3.1. The Canonical Sector,
5.3.2. The Phantom Sector,
6. Discussion
- Vacuum static cylindrically symmetric solutions with a regular asymptotic or a regular axis are necessarily boost-invariant in the subspace.
- If the conformal factor between and is regular in the whole range and finite in the limits , then solitonic solutions simultaneously exist in and in and they are characterized by the same deficit angle.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ishak, M. Testing general relativity in cosmology. Living Rev. Relativ. 2019, 22, 1. [Google Scholar] [CrossRef] [PubMed]
- Basak, S.; et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2018, 641, 6. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1835. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nojiri, S.-I.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Metric-Palatini gravity unifying local constraints and late-time cosmic acceleration. Phys. Rev. D 2012, 85, 084016. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Hybrid metric-Palatini gravity. Universe 2015, 1, 199. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N. Extensions of f(R) Gravity: Curvature-Matter Couplings and Hybrid Metric-Palatini Theory; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Harko, T.; Lobo, F.S.N. Beyond Einstein’s General Relativity: Hybrid metric-Palatini gravity and curvature-matter couplings. Int. J. Mod. Phys. D 2020. Available online: https://arxiv.org/pdf/2007.15345.pdf (accessed on 10 October 2020).
- Capozziello, S.; Harko, T.; Lobo, F.S.N.; Olmo, G.J. Hybrid modified gravity unifying local tests, galactic dynamics and late-time cosmic acceleration. Int. J. Mod. Phys. D 2013, 22, 1342006. [Google Scholar] [CrossRef]
- Capozziello, S.; Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J. Cosmology of hybrid metric-Palatini f(X)-gravity. J. Cosmol. Astropart. Phys. 2013, 2013, 011. [Google Scholar] [CrossRef]
- Edery, A.; Nakayama, Y. Palatini formulation of pure R2 gravity yields Einstein gravity with no massless scalar. Phys. Rev. D 2019, 99, 124018. [Google Scholar] [CrossRef]
- Dănilă, B.; Harko, T.; Lobo, F.S.N.; Mak, M.K. Spherically symmetric static vacuum solutions in hybrid metric-Palatini gravity. Phys. Rev. D 2019, 99, 064028. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Spherically symmetric black holes and wormholes in hybrid metric-Palatini gravity. Grav. Cosmol. 2019, 25, 331. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Bolokhov, S.V.; Skvortsova, M.V. Hybrid metric-Palatini gravity: black holes, wormholes, singularities and instabilities. Grav. Cosmol. 2020, 26, 212. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; da Silva, H.M.R. Cosmic stringlike objects in hybrid metric-Palatini gravity. Phys. Rev. D 2020, 101, 124050. [Google Scholar] [CrossRef]
- Böhmer, C.G.; Tamanini, N. Generalized hybrid metric-Palatini gravity. Phys. Rev. D 2013, 87, 084031. [Google Scholar]
- Bombacigno, F.; Moretti, F.; Montani, G. Scalar modes in extended hybrid metric-Palatini gravity: Weak field phenomenology. Phys. Rev. D 2019, 100, 124036. [Google Scholar] [CrossRef]
- Rosa, J.L.; Carloni, S.; Lemos, J.P.S. The cosmological phase space of generalized hybrid metric-Palatini theories of gravity. Phys. Rev. D 2020, 101, 104056. [Google Scholar] [CrossRef]
- Rosa, J.L.; Lemos, J.P.S.; Lobo, F.S.N. Stability of Kerr black holes in generalized hybrid metric-Palatini gravity. Phys. Rev. D 2020, 101, 044055. [Google Scholar] [CrossRef]
- Vilenkin, A. Gravitational field of vacuum domain walls and strings. Phys. Rev. D 1981, 23, 852. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Shikin, G.N. Cylindrically symmetric solitons with nonlinear self-gravitating scalar fields. Grav. Cosmol. 2001, 6, 231. [Google Scholar]
- Stephani, H.; Kramer, D.; MacCallum, M.A.H.; Hoenselaers, C.; Herlt, E. Exact Solutions of Einstein’s Field Equations; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bronnikov, K.A.; Santos, N.O.; Wang, A. Cylindrical systems in general relativity. Class. Quantum Grav. 2020, 37, 113002. [Google Scholar] [CrossRef]
- Bergmann, P.G. Comments on the scalar-tensor theory. Int. J. Theor. Phys. 1968, 1, 25. [Google Scholar] [CrossRef]
- Wagoner, R. Scalar-tensor theory and gravitational waves. Phys. Rev. D 1970, 1, 3209. [Google Scholar] [CrossRef]
- Nordtvedt, K. Post-Newtonian metric for a general class of scalar-tensor gravitational theories and observational consequences. Astrophys. J. 1970, 161, 1059. [Google Scholar] [CrossRef]
- Penrose, R. Conformal treatment of the infinity. In Relativity, Groups and Topology; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: London, UK, 1964; p. 565. [Google Scholar]
- Chernikov, N.A.; Tagirov, E.A. Quantum theory of scalar field in de Sitter space-time. Ann. Inst. H. Poincare Phys. Theor. A 1968, 9, 109. [Google Scholar]
- Zaitsev, N.A.; Kolesnikov, S.M. Self-consistent interaction of scalar and tensor gravitational fields. In Problems of Gravitation Theory and Particle Theory, Issue 4; Staniukovich, K.P., Sokolik, G.A., Eds.; Atomizdat: Moscow, Russia, 1970; pp. 24–50. (In Russian) [Google Scholar]
- Bronnikov, K.A. Scalar vacuum structure in general relativity and alternative theories. Conformal continuations. Acta Phys. Polon. B 2001, 32, 3571. [Google Scholar]
- Bronnikov, K.A. Scalar-tensor gravity and conformal continuations. J. Math. Phys. 2002, 43, 6096. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Chernakova, M.S. Generalized theory of gravity and conformal continuations. Grav. Cosmol. 2005, 11, 305–309. [Google Scholar]
- Bocharova, N.M.; Bronnikov, K.A.; Melnikov, V.N. On an exact solution of the Einstein-scalar field equations. Vestn. Mosk Univ., Fiz. Astron. 1970, 6, 706. [Google Scholar]
- Bronnikov, K.A. Scalar-tensor theory and scalar charge. Acta Phys. Pol. B 1973, 4, 251. [Google Scholar]
- Bronnikov, K.A.; Clement, G.; Constantinidis, C.P.; Fabris, J.C. Structure and stability of cold scalar-tensor black holes. Phys. Lett. A 1998, 243, 121. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Chernakova, M.S.; Fabris, J.C.; Pinto-Neto, N.; Rodrigues, M.E. Cold black holes and conformal continuations. Int. J. Mod. Phys. D 2008, 17, 25. [Google Scholar] [CrossRef]
- Kamke, E. Differentialgleichungen: Lösungsmethoden und Lösungen. I. Gewönliche Differentialgleichungen; Springer International Publishing: Cham, Switzerland, 1979. [Google Scholar]
- Bronnikov, K.A. Static fluid cylinders and plane layers in general relativity. J. Phys. A Math. Gen. 1979, 12, 201. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Sushkov, S.V. Trapped ghosts: A new class of wormholes. Class. Quantum Grav. 2010, 27, 095022. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Trapped ghosts as sources for wormholes and regular black holes. The stability problem. In Wormholes, Warp Drives and Energy Conditions; Lobo, F.S.N., Ed.; Springer: New York, NY, USA, 2017; pp. 137–159. [Google Scholar]
- Bronnikov, K.A. Scalar fields as sources for wormholes and regular black holes. Particles 2018, 1, 56–81. [Google Scholar] [CrossRef]
- Levi-Civita, T. ds2 einsteiniani in campi newtoniani. IX: L’analogo del potenziale logaritmico. Rend. Accad. Lincei 1919, 28, 101–109. [Google Scholar]
- Bolokhov, S.V.; Bronnikov, K.A.; Skvortsova, M.V. Rotating cylinders with anisotropic fluids in general relativity. Grav. Cosmol. 2019, 25, 122–130. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Lemos, J.P.S. Cylindrical wormholes. Phys. Rev. D 2009, 79, 104089. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Krechet, V.G.; Lemos, J.P.S. Rotating cylindrical wormholes. Phys. Rev. D 2013, 87, 084060. [Google Scholar] [CrossRef]
- Visser, M. Lorentzian Wormholes: From Einstein to Hawking; AIP: Woodbury, NY, USA, 1995. [Google Scholar]
- Lobo, F.S.N. (Ed.) Wormholes, Warp Drives and Energy Conditions; Springer: Berlin, Germany, 2017. [Google Scholar]
- Bronnikov, K.A.; Krechet, V.G. Potentially observable cylindrical wormholes without exotic matter in GR. Phys. Rev. D 2019, 99, 084051. [Google Scholar] [CrossRef]
- Bolokhov, S.V.; Bronnikov, K.A.; Skvortsova, M.V. Cylindrical wormholes: A search for viable phantom-free models in GR. Int. J. Mod. Phys. D 2019, 28, 1941008. [Google Scholar]
- Bronnikov, K.A.; Krechet, V.G.; Oshurko, V.B. Rotating Melvin-like universes and wormholes in general relativity. Symmetry 2020, 12, 1306. [Google Scholar] [CrossRef]
| 1. | Unlike the papers [6,7,13] etc., we use the metric signature , therefore, the plus before refers to a canonical field, and a minus means that the field is phantom. Also, in what follows we consider only vacuum HMPG solutions () and safely omit the factor near the gravitational part of the action. The Ricci tensor is defined as , thus, for example, the Ricci scalar R is positive for de Sitter space-time. The units are used in which the speed of light and the Newtonian gravitational constant are equal to unity. |
| 2. | We denote by a quantity of either the same order of magnitude as f or smaller in a certain limit, while quantities of the same order are connected by the symbol ∼. |
| 3. | To our knowledge, this coordinate condition was used for the first time for finding cylindrically symmetric solutions in GR in [39]. |


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronnikov, K.; Bolokhov, S.; Skvortsova, M. Hybrid Metric-Palatini Gravity: Regular Stringlike Configurations. Universe 2020, 6, 172. https://doi.org/10.3390/universe6100172
Bronnikov K, Bolokhov S, Skvortsova M. Hybrid Metric-Palatini Gravity: Regular Stringlike Configurations. Universe. 2020; 6(10):172. https://doi.org/10.3390/universe6100172
Chicago/Turabian StyleBronnikov, Kirill, Sergey Bolokhov, and Milena Skvortsova. 2020. "Hybrid Metric-Palatini Gravity: Regular Stringlike Configurations" Universe 6, no. 10: 172. https://doi.org/10.3390/universe6100172
APA StyleBronnikov, K., Bolokhov, S., & Skvortsova, M. (2020). Hybrid Metric-Palatini Gravity: Regular Stringlike Configurations. Universe, 6(10), 172. https://doi.org/10.3390/universe6100172





