1. Introduction
Processes in strong electromagnetic fields are currently studied in applied and fundamental research papers [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21]. Sufficient attention is paid to processes in strong X-ray fields near neutron stars [
22,
23,
24,
25,
26,
27]. However, there is still no explanation for the anomalous flows of electron–positron pairs near these objects. It is important to emphasize that higher-order QED processes with respect to the fine-structure constant in the electromagnetic field (QED processes modified by the electromagnetic field) can occur in a resonant channel. In the electromagnetic field, so-called Oleinik resonances may occur [
1,
2], as lower-order processes are possible in the external field by the fine-structure constant (QED processes stimulated by the external field) [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
28,
29]. It is important to note that the probability of resonant QED processes, occurring in an external field may significantly (by several orders of magnitude) exceed the corresponding probability of such processes without an external field.
In this paper, we develop the theory of resonant production of an ultrarelativistic electron–positron pair when a gamma-quantum collides with an X-ray wave, provided that the angle of the resulting momentum (of the final gamma quantum and the electron–positron pair) has small dispersion with respect to the initial gamma quantum momentum. It should be noted that this problem has a classic relativistic-invariant parameter [
10]:
numerically equal to the ratio of the work field at the wavelength to the rest energy of the electron (
e and
m are the electron charge and the electron mass,
F and
are the electric field strength and the wave length,
is the wave frequency). In the X-ray frequency range (
), the classic parameter
is approximately equal to 1 for fields
We further assume that the X-ray fields for this process are weak, i.e.,
In the future, we will use the relativistic system of units: .
2. The Process Amplitude
Lets us consider the 4-potential of an external circular polarized electromagnetic wave propagating along the z-axis as follows
where
,
and
are 4-vectors of polarization and momentum of the photon of the external field, where,
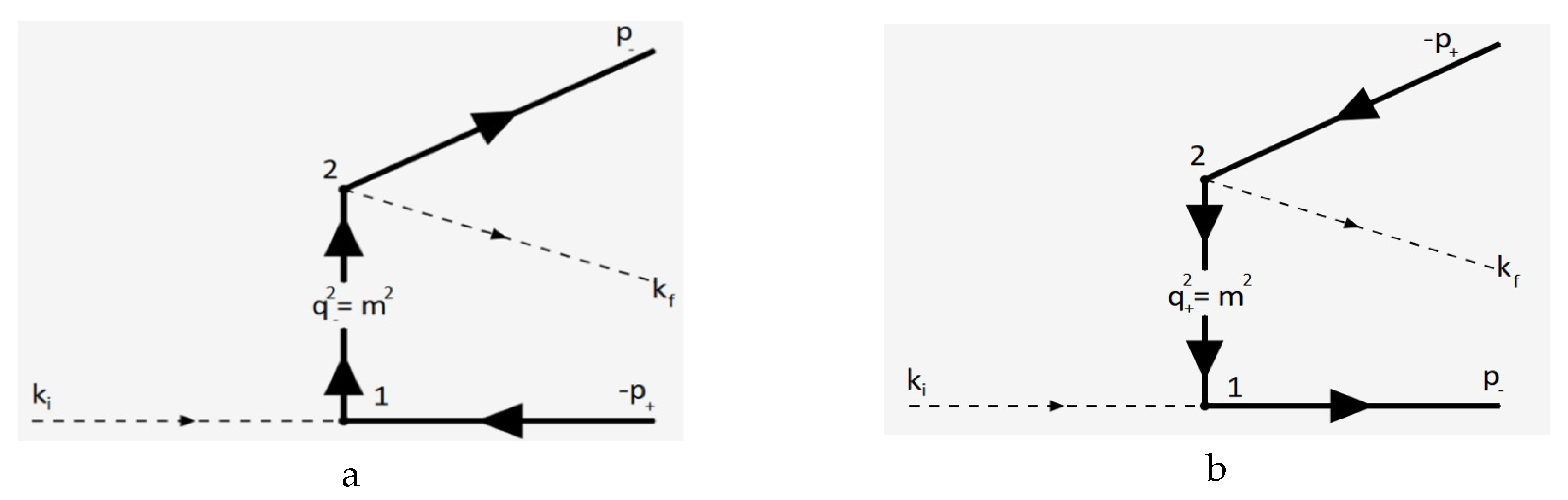
The problem of electron–positron pair production is studied when a gamma-quantum collides with a plane electromagnetic wave field. This is a second-order process with a fine-structure constant and is described by two Feynman diagrams (see
Figure 1). The amplitude of this process can be represented in the following form:
where
are the wave functions of the positron and the electron in the field of a plane monochromatic wave (Volkov’s function) [
16,
17],
is the electron (positron) Green’s function in the plane wave field [
21,
28],
are 4-momentum of the electron and the positron,
are the 4-potentials of the initial and final gamma quanta,
are 4-momentum of the initial and the final gamma quantum. In Formulas (
4)–(
7), expressions with cap mean scalar products of the corresponding 4-vector on the Dirac’s gamma matrix. For example:
(
are the Dirac’s matrices). Substituting the Equations (
5)–(
9) and taking into account the weak field condition (
2) after simple calculations, the amplitude of the process Equation (
4) will take the form:
where the partial amplitude with radiation
or absorption
,
photons wave has the form:
In square brackets in the expression (
12) the first term corresponds to a channel A, and the second term to a channel B,
are 4-momenta of the intermediate electron and a positron, and the corresponding matrices are equal:
In Equations (
14)–(
17), 4-momenta
and
p, as well as the integer index n, take the corresponding values according to expression Equation (
12). Note that the amplitude
determines the external field-stimulated Breit–Wheeler process and the amplitude
determines the external field-stimulated Compton process [
10].
3. Resonance Kinematics
The resonant behavior of the amplitude Equations (
11) and (
12) occurs when an intermediate electron (for a channel A) or a positron (for a channel B) enters the mass shell. In this case, the following relations are valid (see
Figure 2):
In the present paper, we study the process for the high-energy gamma quanta and an ultrarelativistic electron and a positron. In this case, all the final particles are produced in a narrow cone along the momentum of the initial gamma quantum. We assume that this narrow cone lies far from the direction of the wave propagation (if the narrow cone of particles lies along the direction of the wave, the resonances disappear).
Let us first analyze the resonances for a channel A. The conservation law of the 4-momentum at the first vertex is
Given the resonant condition (
18),
and
, the relation in Equation (
22) holds only for
. Thus, under the conditions of a resonance Equation (
18), the conservation law of the 4-momentum Equation (
22) along with the amplitude Equation (
14) determine the X-ray field-stimulated Breit–Wheeler process with the
photon absorption [
10]. Putting the expression for the intermediate 4-momentum of electron
Equation (
13) in the ratio Equation (
18) and taking into account the conditions Equations (
20) and (
21), we obtain a square equation for the positron energy:
where,
As follows from Equation (
23), a positron can have two possible energies:
The expression under the square root must be positive. Therefore, there are two conditions:
Condition (
27) means that there is a threshold energy
for the energy of the initial gamma quantum. Condition (
28) defines the positron’s possible outgoing angles. It is important to emphasize that the outgoing angles of the positron vary from zero to the maximum value, which is determined by the energy of the initial gamma quantum (in units of threshold energy). It should be noted that in the X-ray field frequency range
, the threshold energy has the following order of magnitude
.
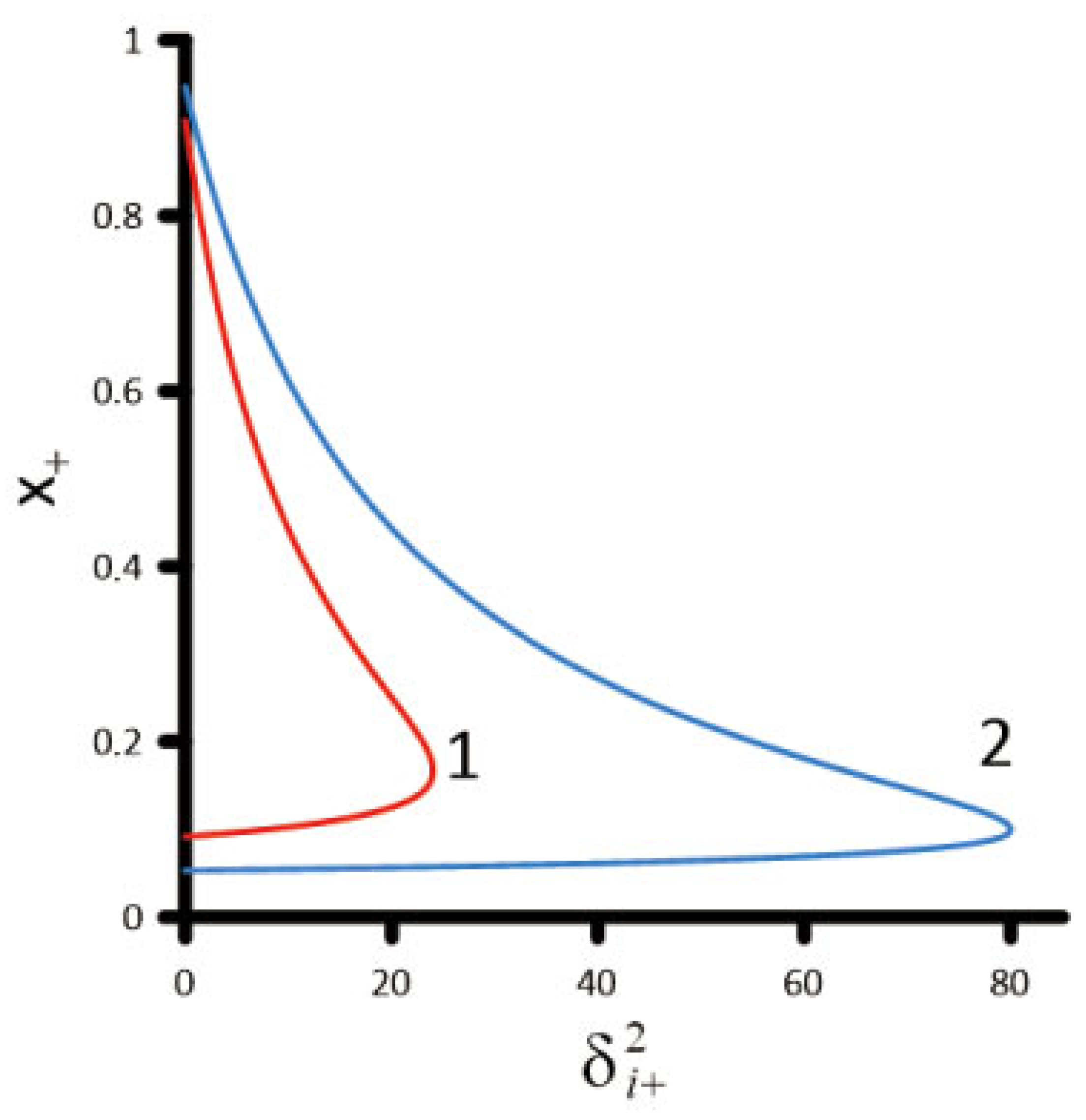
Figure 3 shows the dependence of the positron energy on its outgoing angle for the two energies of the initial gamma quantum
and
. It becomes clear that at zero outgoing angle, the positron energy difference between the maximum and minimum values is the largest. As the outgoing angle increases, this positron energy difference decreases, and for the maximum outgoing angle, the positron energy takes a single value.
The conservation law of the 4-momentum in the second vertex of a channel A:
Given that
and
, the relation Equation (
29) holds only for
. Thus, under the conditions of resonance Equation (
18), the conservation law of the 4-momentum Equation (
29) is determined locally with the amplitude Equation (
15) by the X-ray field-stimulated Compton process with
photon absorption [
10]. Substituting the expression for the intermediate 4-momentum of an electron
, Equation (
29), into Equation (
18) and taking into account the conditions in Equations (
20) and (
21), we obtain a cubic equation for the electron energy:
where,
Note that
here is the positron energy, which can have two values and is determined by the ratio (
26). If an electron flies out along the momentum of a finite gamma-ray quantum
, then Equation (
30) implies that the electron energy takes a minimum value equal to
Analysis of Equation (
30) at
shows that there are two different areas of
parameter values in which the electron energies are significantly different. So, in the area of
The energy of an electron takes a single value equal to
where,
In this case, the outgoing angle of the electron in the range:
Figure 4 shows the dependence of the electron energy on its outgoing angle in the initial electron energy range Equation (
33) at a fixed outgoing angle of the positron (two possible positron energies). The figure shows that the electron energy spectrum at fixed values for the maximum outgoing angle Equation (
38) of the positron energy vary from the minimum Equation (
32) to the maximum value.
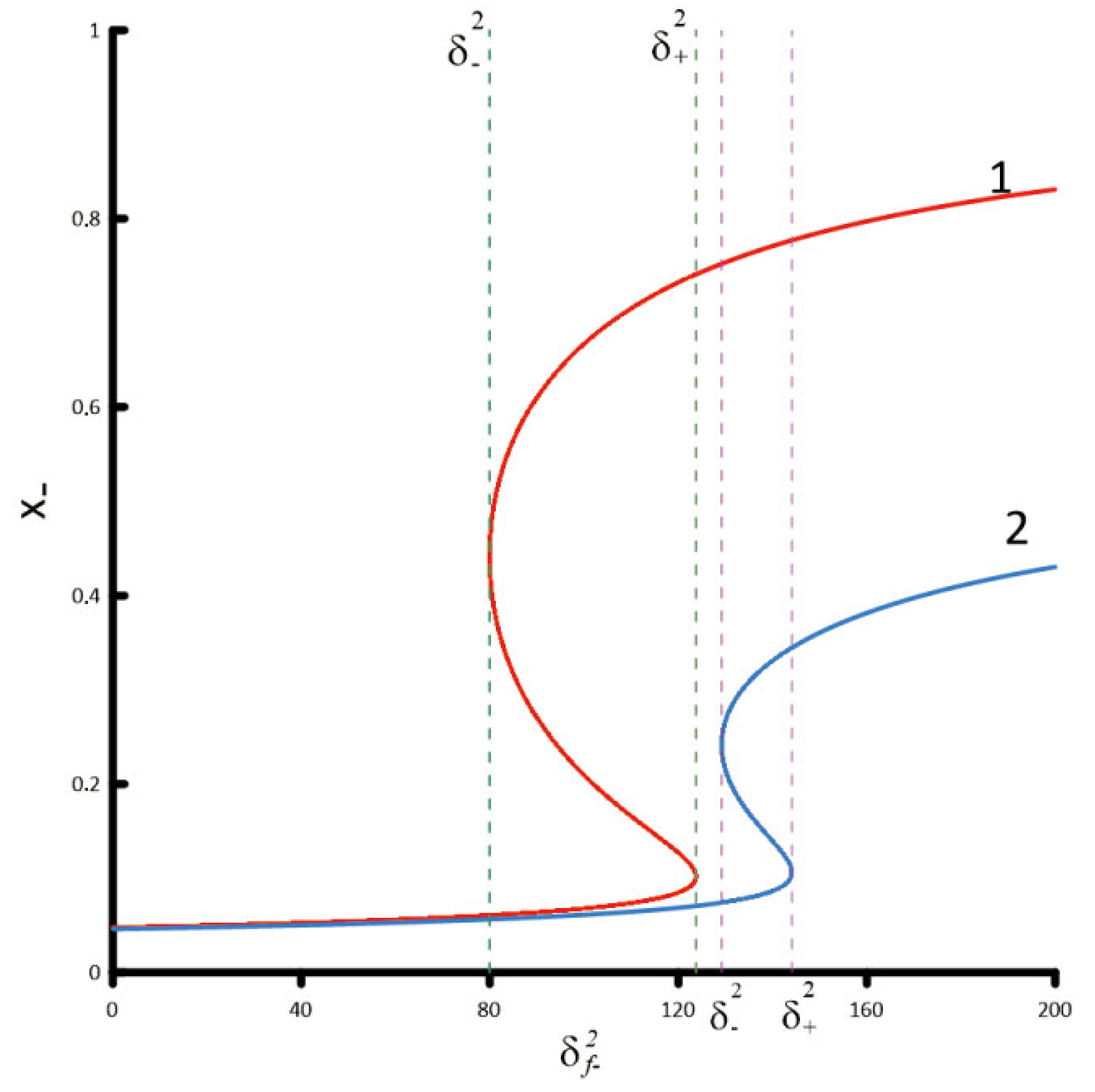
If the energies of the initial gamma quantum and a positron are in the range:
then in the area of outgoing angles:
where,
we have three valid solutions for the electron energy:
where,
At the same time, in the area of angles
we have a unique solution by the relations Equations (
34)–(
37). It should be noted that conditions Equation (
39) follow from inequality Equation (
42).
Figure 5 shows the dependence of the electron energy on its outgoing angle in the energy range of the initial gamma quantum and a positron Equation (
39).
We emphasize that the positron energy spectrum for a channel A depends only on its outgoing angle (relative to the momentum of the initial gamma quantum). In this case, for each outgoing angle, the positron energy can take two values up to the maximum outgoing angle (see
Figure 3). The electron energy depends not only on its outgoing angle relative to the momentum of a finite gamma quantum, but also on the outgoing angle of the positron. In addition, the energy spectrum of an electron is qualitatively different from the corresponding positron spectrum (compare
Figure 3,
Figure 4 and
Figure 5). In the case of a channel B, the situation is reversed (the resonant kinematics for a channel B is obtained from the kinematics of a channel A by replacing the 4-momentum particles of the pair:
⇌
). Now the energy spectrum of an electron depends only on its outgoing angle relative to the momentum of the initial gamma quantum, and the energy spectrum of a positron depends on its outgoing angle relative to the momentum of the final gamma quantum and the outgoing angle of the electron. Because of this, channels A and B are distinguishable and do not interfere.
4. Resonant Differential Probability
In the weak wave field Equation (
2), the processes with absorption of one photon of the wave at the first and second vertices are most alike (see
Figure 2). Because of this, the relations for amplitude Equations (
11)–(
17) should be
and
. Since channels A and B do not interfere, we firstly start by calculating the probability of the process for a channel A (the corresponding probability for a channel B is obtained by replacing 4-momenta
⇌
). The probability (per unit of time and unit of volume) is obtained from the amplitude [
29]:
Averaging and summation by polarization of the initial and final particles are performed [
29]. After simple calculations, we get the probability (per unit of time) in the following form:
Here
is a fine structure constant,
, the function
determines the probability of the external field-stimulated Breit–Wheeler process and the function
determines the probability of the external field-stimulated Compton effect [
10].
Here, the corresponding relativistic-invariant parameters have the form:
Integration by three-dimensional momentum of a finite gamma quantum, and by the energy of an electron is performed by using the following replacement:
Here,
and
are the corresponding polar angles of the positron and electron. The elimination of the resonant infinity in channels A and B can be accomplished by an imaginary addition to the mass of an intermediate electron or a positron. So, for a channel A, we have:
Here,
is the full probability (per unit of time) of the external field-stimulated Breit–Wheeler process [
10].
Taking into account the relations (
56), the resonant denominator represented as:
where the parameter
is related to the resonant frequency of the incident gamma quantum for a channel A by the ratio (
23). Given the relations (
55), (
59), the expression for the resonant differential probability (
50):
When
the value of the resonant probability takes the maximum value
This equation shows that the maximum resonant probability for fields
at can exceed the non-resonant differential probability of this process by eight orders of magnitude. It is important to emphasize the essential difference between the kinematics of the process and the electron–positron pair energy spectrum for the resonant and non-resonant channels of this reaction. Thus, under resonance conditions, there is a reaction threshold for the energy of the gamma-ray quantum (see (
27)). The threshold energy depends significantly on the X-ray photon energy and the angle between the momenta of the initial gamma quantum and the X-ray photon. In this case, the electron–positron pair production energies have a specific dependence both on the initial gamma quantum energy and on their outgoing angles (see (
26), (
34)). In the case of a non-resonant process, there is no threshold energy and the energy spectrum of the electron–positron pair is determined only by the general energy conservation law (see (
11)). At the same time, there is also no dependence of the pair energy on the outgoing angles of the electron and positron.
5. Conclusions
The study of the process of resonant electron–positron pair production in the collision of a gamma quantum with an X-ray wave, allows us to formulate the main results:
1. The resonant process has a threshold for the energy of the initial gamma quantum. In the X-ray frequency range, the threshold energy has an order of magnitude . Because of this, the initial gamma quantum must be high-energy .
2. Under resonant conditions, the initial second order process by the fine-structure constant in the wave field effectively splits into two first order processes: the X-ray field-stimulated Breit–Wheeler process and the X-ray field-stimulated Compton effect. The final gamma quantum and the resulting electron–positron pair are ultrarelativistic and fly in a narrow cone along the momentum of the initial gamma quantum.
3. The energy spectra of the electron and the positron differ qualitatively and transfer into each other from a channel A to a channel B. Thus, for a channel A, the energy of the positron is determined by its outgoing angle and can take two values up to the maximum outgoing angle. In this case, the energy of an electron is determined not only by its outgoing angle, but also by the outgoing angle of the positron and can take from one to three values.
4. The resonant differential probability (per unit of time) can exceed the non-resonant differential probability by 8 orders of magnitude.
5. The positron energy spectrum in pulsar X-ray field depends significantly on their outgoing angles and the energy of the initial gamma quantum. When the outgoing angles of the positron are small
and the energies of the initial gamma quanta are high
we have high-energy positron production
with a high probability (by eight orders of magnitude) (see
Figure 3). This result may explain the anomalous high-energy positrons flows near neutron stars.