In the Quest for Cosmic Rotation
Abstract
1. Introduction
2. Metric and Matter vs. Dark Energy and Oscillating Physics
3. In the Theoretical Quest for Cosmic Rotation
4. In the Experimental Quest for Cosmic Rotation
4.1. RCSED (Reference Catalog of Spectral Energy Distributions of Galaxies) Catalog
4.2. Kuminski and Shamir Catalogs
4.3. GAIA Data Release 2 Quasar Catalog
4.4. Milliquas 6.3 Catalog
4.5. KQCG (Known Quasars Catalog for GAIA Mission)
5. Numerical Experiments
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587727177915301989 | 6.31801788 | −11.12899674 | 0.164466 |
| 587734894366425177 | 186.3215957 | 11.12945461 | 0.167687 | |
| (2) | 587727177911304300 | 356.9463884 | −11.1131664 | 0.11336 |
| 587734894362427519 | 176.9362082 | 11.12183186 | 0.10569 | |
| (3) | 587727177915367567 | 6.473508 | −11.08978967 | 0.109483 |
| 587734894366490714 | 186.4752183 | 11.09098806 | 0.103002 | |
| (4) | 587727225157451822 | 9.78490157 | −10.97586123 | 0.0656358 |
| 587732772669292660 | 189.7803892 | 10.98178272 | 0.0667346 | |
| (5) | 587727177921069125 | 19.65932903 | −10.93368609 | 0.141083 |
| 588017569241432335 | 199.6689547 | 10.93044205 | 0.145941 | |
| (6) | 587727177921069119 | 19.64324854 | −10.90207866 | 0.140991 |
| 588017569241432309 | 199.6421776 | 10.89885453 | 0.149119 | |
| (7) | 587727225157779575 | 10.47400922 | −10.89314855 | 0.115176 |
| 587732772669554736 | 190.4693767 | 10.88349483 | 0.113392 | |
| (8) | 587727873696006248 | 354.4140938 | −10.76728771 | 0.0980759 |
| 587732772662673520 | 174.4078391 | 10.76580767 | 0.0941737 | |
| (9) | 587727178450665633 | 2.84320186 | −10.72060849 | 0.0626986 |
| 587734893828112436 | 182.834768 | 10.72901371 | 0.0684232 | |
| (10) | 587727178453483585 | 9.28275768 | −10.70100563 | 0.130024 |
| 587734893830864981 | 189.2821245 | 10.70562335 | 0.128155 | |
| (11) | 587727178451452024 | 4.57186615 | −10.67135056 | 0.061156 |
| 587734893828833380 | 184.568407 | 10.66631434 | 0.0513871 | |
| (12) | 587727225693536361 | 7.83605949 | −10.59958384 | 0.0905357 |
| 587732772131569821 | 187.8259964 | 10.59469904 | 0.0927822 | |
| (13) | 587727229447962769 | 23.72675428 | −10.51170548 | 0.0992561 |
| 587736543623839915 | 203.7347943 | 10.50510464 | 0.103054 | |
| (14) | 587727178458333267 | 20.61377325 | −10.47315078 | 0.109546 |
| 587736543622529169 | 200.6164952 | 10.48116533 | 0.10888 | |
| (15) | 587727229448028286 | 23.8634114 | −10.4420383 | 0.0872344 |
| 587736543623905435 | 203.8644965 | 10.44923329 | 0.083543 | |
| (16) | 587727874233335894 | 355.4913684 | −10.41356256 | 0.0980471 |
| 587732772126261484 | 175.4967819 | 10.419777 | 0.106774 | |
| (17) | 587727178459644099 | 23.56363216 | −10.30676641 | 0.087484 |
| 588017992299970676 | 203.560364 | 10.29826366 | 0.0842322 | |
| (18) | 587727874232942672 | 354.5407195 | −10.2905162 | 0.115404 |
| 587732772125802696 | 174.5311941 | 10.29906788 | 0.112148 | |
| (19) | 587727178989240463 | 6.75089715 | −10.28452672 | 0.141096 |
| 587734893292879988 | 186.7541572 | 10.2905859 | 0.138833 | |
| (20) | 587727178459775095 | 23.99049618 | −10.24662329 | 0.16844 |
| 588017992300167307 | 203.9854969 | 10.23670831 | 0.159882 | |
| (21) | 587727178992320618 | 13.92268478 | −10.23798263 | 0.0545347 |
| 588017991758970941 | 193.9286925 | 10.23919618 | 0.0576316 | |
| (22) | 587726877275324641 | 341.4198226 | −10.22775339 | 0.0854893 |
| 587732772657037548 | 161.4250258 | 10.2288603 | 0.0864014 | |
| (23) | 587727178459775058 | 23.95379218 | −10.20892227 | 0.170874 |
| 588017992300167290 | 203.9605329 | 10.21263285 | 0.16155 | |
| (24) | 587727178459775059 | 23.9542841 | −10.20863418 | 0.167602 |
| 588017992300167290 | 203.9605329 | 10.21263285 | 0.16155 | |
| (25) | 587727178992386152 | 14.00945119 | −10.16938834 | 0.0582089 |
| 588017991758971000 | 194.0154632 | 10.17011785 | 0.0547655 | |
| (26) | 587727178983473249 | 353.3035011 | −10.11314013 | 0.175384 |
| 587734893287112784 | 173.3054337 | 10.10802598 | 0.171464 | |
| (27) | 587730815751291175 | 336.940361 | −9.95373677 | 0.0563963 |
| 587734864295166164 | 156.9394599 | 9.94507402 | 0.046747 | |
| (28) | 587727179526701090 | 8.03597019 | −9.91194747 | 0.0790208 |
| 587734892756598903 | 188.0361662 | 9.91573124 | 0.0763644 | |
| (29) | 587727178995335253 | 20.82821245 | −9.86158021 | 0.128453 |
| 588017991761920153 | 200.8255428 | 9.86031309 | 0.125208 | |
| (30) | 587730815750045949 | 334.0325931 | −9.85353658 | 0.349603 |
| 588017702382403743 | 154.0277586 | 9.85157764 | 0.356585 | |
| (31) | 587727178996449304 | 23.51060112 | −9.77414538 | 0.0408057 |
| 588017991763099797 | 203.5206978 | 9.78398572 | 0.0398321 | |
| (32) | 587730815749980360 | 334.0089931 | −9.76351938 | 0.0919012 |
| 588017702382403698 | 154.016896 | 9.76374758 | 0.0834979 | |
| (33) | 587727179531354122 | 18.84193042 | −9.69197199 | 0.0623454 |
| 588017991224197282 | 198.8506924 | 9.7002904 | 0.0665447 | |
| (34) | 587727230521311310 | 22.64387404 | −9.63632312 | 0.121776 |
| 587736542549704781 | 202.645084 | 9.64360108 | 0.123518 | |
| (35) | 587730815749128409 | 331.9847156 | −9.62353845 | 0.105015 |
| 587735342655471787 | 151.9840169 | 9.63233216 | 0.114253 | |
| (36) | 587730815748866357 | 331.395196 | −9.60640427 | 0.0800119 |
| 587735342655209578 | 151.3870255 | 9.60693788 | 0.0783352 | |
| (37) | 587726877811934142 | 340.8324856 | −9.59191986 | 0.439336 |
| 587732772119904870 | 160.8394092 | 9.59742067 | 0.433453 | |
| (38) | 587730816827326649 | 342.3741793 | −9.56574501 | 0.0821777 |
| 587746210520367211 | 162.3699937 | 9.56609192 | 0.0862479 | |
| (39) | 587727230522163362 | 24.74103715 | −9.56325433 | 0.0862579 |
| 587736542550556886 | 204.7496386 | 9.55691982 | 0.0868169 | |
| (40) | 587727177929457776 | 39.13882791 | −9.51991056 | 0.081008 |
| 588017702410453175 | 219.1457622 | 9.51836998 | 0.088222 | |
| (41) | 587727180061868049 | 4.08337588 | −9.46368127 | 0.0872652 |
| 587734892218023997 | 184.0819229 | 9.45884063 | 0.094822 | |
| (42) | 587727230522425495 | 25.33108177 | −9.42130098 | 0.104163 |
| 587736542550818989 | 205.3372284 | 9.41874675 | 0.0996079 | |
| (43) | 587727177929785591 | 39.92521168 | −9.33831191 | 0.0532149 |
| 588017702410846353 | 219.9175712 | 9.34391573 | 0.0516048 | |
| (44) | 587727177930113154 | 40.58369451 | −9.32630004 | 0.155765 |
| 588017702411108409 | 220.5908395 | 9.3201034 | 0.1517 | |
| (45) | 587730816826212465 | 339.7809475 | −9.28473191 | 0.0631319 |
| 587734863222669402 | 159.7726217 | 9.27776767 | 0.0686803 | |
| (46) | 587727230524260481 | 29.54831241 | −9.28065885 | 0.0912357 |
| 587736542552653969 | 209.5405473 | 9.27495593 | 0.0982227 | |
| (47) | 587730816287113330 | 334.562248 | −9.27926377 | 0.097067 |
| 587732772117217405 | 154.5603312 | 9.27525384 | 0.1006 | |
| (48) | 587726877808787613 | 333.5596377 | −9.10873 | 0.125766 |
| 587732772116758696 | 153.5547995 | 9.10677581 | 0.117325 | |
| (49) | 587727227308802155 | 18.62293278 | −9.09116739 | 0.0828624 |
| 587736541474193627 | 198.6259619 | 9.08656038 | 0.0928012 | |
| (50) | 587727231058837640 | 24.24960403 | −9.07220804 | 0.116431 |
| 587736542013489445 | 204.258942 | 9.07093891 | 0.122971 | |
| (51) | 587727231059034221 | 24.70990827 | −9.050773 | 0.0766974 |
| 587736542013685982 | 204.707667 | 9.05688215 | 0.0775408 | |
| (52) | 587724240688382034 | 38.55751214 | −8.98833628 | 0.111355 |
| 588017992306458874 | 218.563633 | 8.99273253 | 0.116682 | |
| (53) | 587727180595134577 | 355.7997977 | −8.987712 | 0.0753556 |
| 587734891677548628 | 175.8078012 | 8.98622382 | 0.0829316 | |
| (54) | 587727180594479192 | 354.2791585 | −8.98725868 | 0.0806326 |
| 587732770515124373 | 174.277534 | 8.99625689 | 0.0760123 | |
| (55) | 587726878886723739 | 343.2696496 | −8.98547579 | 0.170464 |
| 587732771047211211 | 163.2757834 | 8.99239073 | 0.166468 | |
| (56) | 587726879426150556 | 349.2821756 | −8.9139055 | 0.0837956 |
| 587732770512961595 | 169.2765643 | 8.90951915 | 0.0850834 | |
| (57) | 587726877269229794 | 327.3372251 | −8.88489879 | 0.0911886 |
| 587732772650942640 | 147.3341982 | 8.8846179 | 0.0977782 | |
| (58) | 587727227843510349 | 13.58226852 | −8.82669194 | 0.0775205 |
| 587732769986576485 | 193.5776433 | 8.82324646 | 0.0802786 | |
| (59) | 587727227841544334 | 9.17385956 | −8.81343367 | 0.161788 |
| 587732769984675893 | 189.1800829 | 8.81570619 | 0.165148 | |
| (60) | 587727227840823364 | 7.41474543 | −8.78739786 | 0.134174 |
| 587732769983889559 | 187.4173796 | 8.79260319 | 0.141713 | |
| (61) | 587726879424774256 | 346.0556579 | −8.74818209 | 0.097193 |
| 587732770511519918 | 166.0566685 | 8.740358 | 0.0875037 | |
| (62) | 587727180071501902 | 26.40085465 | −8.73107212 | 0.121164 |
| 588017990690603214 | 206.3924788 | 8.73386769 | 0.120342 | |
| (63) | 587726877268902222 | 326.6199672 | −8.72026028 | 0.135262 |
| 587734863753838722 | 146.6245995 | 8.71266702 | 0.134986 | |
| (64) | 587727227842986122 | 12.49783122 | −8.70198555 | 0.0739487 |
| 587732769986117760 | 192.5043783 | 8.69610353 | 0.0837418 | |
| (65) | 587726878345265364 | 332.6514376 | −8.66253229 | 0.103393 |
| 587732771579494537 | 152.6458706 | 8.66485751 | 0.0973786 | |
| (66) | 587730817361182802 | 335.363148 | −8.64716609 | 0.0373209 |
| 587734862683832453 | 155.3597555 | 8.64438959 | 0.0450276 | |
| (67) | 587724240689102969 | 40.22878711 | −8.64369517 | 0.0380482 |
| 587736543094177958 | 220.2206679 | 8.64675197 | 0.0308106 | |
| (68) | 587726877268312182 | 325.2592388 | −8.63777296 | 0.0863781 |
| 587732772650025128 | 145.2509033 | 8.63971077 | 0.0846345 | |
| (69) | 587727227843510316 | 13.66287605 | −8.63255357 | 0.0778701 |
| 588017730839642176 | 193.6626503 | 8.63958689 | 0.0827405 | |
| (70) | 587730818439512260 | 346.092724 | −8.50560084 | 0.172473 |
| 587734891673354322 | 166.094645 | 8.51369065 | 0.175036 | |
| (71) | 587727231597478004 | 28.3056497 | −8.42097287 | 0.0471675 |
| 587736541478387896 | 208.3127137 | 8.41497984 | 0.0450439 | |
| (72) | 587730818439053410 | 344.9876466 | −8.39745108 | 0.0779055 |
| 587734891672895587 | 164.9894861 | 8.39564562 | 0.073904 | |
| (73) | 587727212272943399 | 320.8338911 | −8.39485218 | 0.117779 |
| 587734948049912071 | 140.8422313 | 8.39661384 | 0.11207 | |
| (74) | 587727212273271140 | 321.5992953 | −8.37544229 | 0.158414 |
| 587734948050239774 | 141.6072698 | 8.3832973 | 0.152886 | |
| (75) | 587724240155705507 | 48.22814118 | −8.33581316 | 0.0735155 |
| 587736477058990249 | 228.2378153 | 8.33940235 | 0.0804487 | |
| (76) | 587727177934307453 | 50.24970865 | −8.29951375 | 0.0330458 |
| 588017702952173868 | 230.2488442 | 8.308433 | 0.0393475 | |
| (77) | 587726878343823623 | 329.4183427 | −8.27673436 | 0.148898 |
| 587732771578052774 | 149.4134499 | 8.27527956 | 0.15852 | |
| (78) | 587726877804855542 | 324.4594709 | −8.21209911 | 0.0871732 |
| 587732772112826583 | 144.4574674 | 8.20228244 | 0.0867666 | |
| (79) | 587727178469802145 | 46.9844432 | −8.18224969 | 0.0744629 |
| 588017992310128884 | 226.9932375 | 8.19029998 | 0.0765801 | |
| (80) | 587726878882332761 | 333.2058322 | −8.14083953 | 0.0837303 |
| 587732771042820325 | 153.2151481 | 8.1369431 | 0.0842566 | |
| (81) | 587727232134873177 | 29.37707349 | −7.94639568 | 0.10361 |
| 587736526444560520 | 209.3793586 | 7.94487803 | 0.103126 | |
| (82) | 587727232134742064 | 29.16828094 | −7.91303927 | 0.0989567 |
| 587736526444429478 | 209.1635351 | 7.91749915 | 0.103407 | |
| (83) | 587730817895629069 | 329.9017868 | −7.78737555 | 0.0856975 |
| 587732771041378462 | 149.8929509 | 7.78668911 | 0.0914809 | |
| (84) | 587726878341726580 | 324.6422074 | −7.75110002 | 0.0880603 |
| 587732771576021174 | 144.6379017 | 7.74239199 | 0.0931418 | |
| (85) | 587730818435317875 | 336.3522559 | −7.7508616 | 0.109669 |
| 587732769970454629 | 156.3434173 | 7.74177121 | 0.103487 | |
| (86) | 587726877264839112 | 317.3101898 | −7.73854853 | 0.0732018 |
| 587734948048404618 | 137.3147516 | 7.72945807 | 0.0821823 | |
| (87) | 587730818433155251 | 331.3679425 | −7.45623643 | 0.0592957 |
| 587734861608321127 | 151.3713518 | 7.46400606 | 0.0621482 | |
| (88) | 587724240694542491 | 52.76892686 | −7.35645715 | 0.138503 |
| 587736543099617547 | 232.7601059 | 7.34722426 | 0.129012 | |
| (89) | 587724241765007480 | 45.13170845 | −7.34640725 | 0.161412 |
| 587736542022598934 | 225.1285679 | 7.34491587 | 0.154524 | |
| (90) | 587727179008311337 | 50.7121024 | −7.32739104 | 0.0845821 |
| 588017991774896410 | 230.7190341 | 7.3349747 | 0.0783759 | |
| (91) | 587724240694673500 | 52.96494777 | −7.25533989 | 0.133988 |
| 587736543099683339 | 232.959273 | 7.24727706 | 0.128557 | |
| (92) | 587730818432041321 | 328.9376199 | −7.06320875 | 0.0592138 |
| 587732579378724931 | 148.9383586 | 7.06251179 | 0.0602015 | |
| (93) | 587726879954370763 | 329.3517007 | −7.04637715 | 0.0859399 |
| 587732579378921673 | 149.3440319 | 7.03988761 | 0.0784532 | |
| (94) | 587724242302533699 | 46.63534829 | −6.83786511 | 0.028473 |
| 587736541486383232 | 226.6284051 | 6.83905419 | 0.0376736 | |
| (95) | 587726879953322317 | 327.0174505 | −6.78848336 | 0.0898924 |
| 587732579377873009 | 147.0128383 | 6.79790707 | 0.0932444 | |
| (96) | 587727180081660026 | 49.76721128 | −6.65462997 | 0.171731 |
| 588017990700826690 | 229.7751332 | 6.65265276 | 0.17779 | |
| (97) | 587726879952732589 | 325.6644648 | −6.53424217 | 0.0882166 |
| 587732703396430084 | 145.6718053 | 6.52802864 | 0.0933982 | |
| (98) | 587727179011195092 | 57.28409909 | −6.5146857 | 0.0656059 |
| 588017991777780111 | 237.2916735 | 6.51711338 | 0.0727241 | |
| (99) | 587726879413371300 | 319.8134098 | −6.4153901 | 0.0633028 |
| 587732770500116746 | 139.8142344 | 6.40937891 | 0.0725347 | |
| (100) | 587726879950045526 | 319.5050187 | −5.89992385 | 0.0887226 |
| 587732578837725451 | 139.5035274 | 5.89314752 | 0.090063 | |
| (101) | 587724241234690202 | 60.1469532 | −5.82246607 | 0.128101 |
| 587736542566023562 | 240.1442599 | 5.81544137 | 0.120623 | |
| (102) | 587724241771102391 | 59.12398332 | −5.6749918 | 0.0597927 |
| 587736542028693952 | 239.1163388 | 5.66555938 | 0.0621059 | |
| (103) | 587724241770709041 | 58.1813494 | −5.66402869 | 0.124912 |
| 587736542028300451 | 238.1814968 | 5.66896383 | 0.132543 | |
| (104) | 587724242307448950 | 57.81327563 | −5.44193649 | 0.12508 |
| 587736541491298661 | 237.8139452 | 5.4320315 | 0.117586 | |
| (105) | 587727180085919882 | 59.45274909 | −5.37776939 | 0.112835 |
| 588017990705086634 | 239.459686 | 5.3730717 | 0.114617 | |
| (106) | 587726879409635950 | 311.3361796 | −5.13025247 | 0.100322 |
| 587732703390204231 | 131.3358794 | 5.12942269 | 0.0944183 | |
| (107) | 587727214952710451 | 310.6951216 | −5.00957318 | 0.0533286 |
| 587732578833859013 | 130.7039891 | 5.01590373 | 0.0516006 | |
| (108) | 587726879408915112 | 309.7014626 | −5.00378611 | 0.0822278 |
| 587732703389483300 | 129.7102373 | 5.0038262 | 0.0759225 | |
| (109) | 587727180622528725 | 58.85069515 | −4.88213314 | 0.0739501 |
| 587730023336902902 | 238.8427352 | 4.88395362 | 0.0681825 | |
| (110) | 587724650869686415 | 184.6727131 | −1.25620133 | 0.0803352 |
| 587731187816595528 | 4.66679487 | 1.26085556 | 0.0876818 | |
| (111) | 587724650869424248 | 184.0892593 | −1.25371914 | 0.108284 |
| 587731187816333417 | 4.09325126 | 1.25789316 | 0.105123 | |
| (112) | 588015507671089581 | 28.14765501 | −1.22061106 | 0.174438 |
| 587726031187148932 | 208.1479272 | 1.22578036 | 0.174331 | |
| (113) | 587729971792052457 | 228.9119379 | −1.22029557 | 0.120609 |
| 587731514229588106 | 48.91797559 | 1.21584566 | 0.112363 | |
| (114) | 587748927626608776 | 172.1310313 | −1.21504223 | 0.113913 |
| 587731187811090545 | 352.1225299 | 1.21974134 | 0.119537 | |
| (115) | 587734303270764663 | 341.5351663 | −1.20503473 | 0.0583548 |
| 587726031166701712 | 161.5251899 | 1.20328815 | 0.0671257 | |
| (116) | 587722981747458159 | 196.8323221 | −1.10495117 | 0.0858605 |
| 587731514215563418 | 16.84068508 | 1.10383695 | 0.0941228 | |
| (117) | 588015507676987550 | 41.62918519 | −1.09799691 | 0.0740636 |
| 587726014013440008 | 221.6264322 | 1.10413737 | 0.0735006 | |
| (118) | 587722981750931657 | 204.8306575 | −1.06369837 | 0.0707877 |
| 587731514219036795 | 24.83154818 | 1.06710408 | 0.078975 | |
| (119) | 587731511532454043 | 19.75110345 | −0.99674932 | 0.044761 |
| 587722984433057983 | 199.7536973 | 0.99668931 | 0.0541101 | |
| (120) | 587731185125359869 | 349.0427567 | −0.98745757 | 0.091398 |
| 587748930309587102 | 169.0524929 | 0.9931595 | 0.0962012 | |
| (121) | 587731185116315784 | 328.3852669 | −0.92491413 | 0.0954053 |
| 587728950120612023 | 148.3899618 | 0.92361081 | 0.0948823 | |
| (122) | 588848898860056883 | 228.2742186 | −0.90832571 | 0.129659 |
| 588015510364225797 | 48.27957041 | 0.91491284 | 0.131263 | |
| (123) | 587731185119723924 | 336.1672691 | −0.89711779 | 0.0991819 |
| 587728950124019803 | 156.1666319 | 0.89373435 | 0.0938088 | |
| (124) | 588848898847539378 | 199.7024399 | −0.8926827 | 0.0818081 |
| 588015510351708322 | 19.70776073 | 0.89908792 | 0.0800928 | |
| (125) | 588848898830172339 | 159.9730114 | −0.85567902 | 0.0908891 |
| 587734305954463933 | 339.9668426 | 0.86319413 | 0.0873762 | |
| (126) | 588848898843279472 | 189.8915184 | −0.85366277 | 0.0242445 |
| 588015510347448339 | 9.89514685 | 0.85996826 | 0.0146933 | |
| (127) | 587728947975291011 | 153.3264231 | −0.8327221 | 0.0490744 |
| 587731187265962312 | 333.3213035 | 0.83853245 | 0.0571919 | |
| (128) | 587729778526781840 | 234.5183544 | −0.8262151 | 0.144058 |
| 587731513695142080 | 54.52663634 | 0.82450886 | 0.139076 | |
| (129) | 587722982293176752 | 217.0007899 | −0.82291535 | 0.399234 |
| 587731513687474437 | 36.99722415 | 0.81755209 | 0.397598 | |
| (130) | 587734303804031262 | 333.3022362 | −0.80519986 | 0.129767 |
| 588848900974706861 | 153.3035057 | 0.80991503 | 0.120938 | |
| (131) | 587722982300123441 | 232.9101284 | −0.79167934 | 0.0766653 |
| 587731513694421196 | 52.90549275 | 0.79102086 | 0.0856506 | |
| (132) | 587722982285508856 | 199.6286217 | −0.78745739 | 0.0882834 |
| 587731513679872138 | 19.62375817 | 0.78798276 | 0.0898079 | |
| (133) | 587734303805866210 | 337.4814454 | −0.7517174 | 0.0903008 |
| 588848900976541910 | 157.4856125 | 0.75898364 | 0.099725 | |
| (134) | 588015508192624827 | 353.1832021 | −0.74826734 | 0.0574768 |
| 588848900983423150 | 173.1767412 | 0.75630883 | 0.0674753 | |
| (135) | 588015508203241620 | 17.35657948 | −0.73451621 | 0.103116 |
| 588848900994039948 | 197.3614164 | 0.72866873 | 0.0944896 | |
| (136) | 588015508216873237 | 48.61535843 | −0.71640599 | 0.0873679 |
| 588848901007671746 | 228.6074205 | 0.70948451 | 0.0915592 | |
| (137) | 588015508218904634 | 53.23858074 | −0.70414471 | 0.0331694 |
| 588848901009703095 | 233.2419617 | 0.71068808 | 0.0378785 | |
| (138) | 587722982280593611 | 188.3839313 | −0.69206406 | 0.0716765 |
| 587731187281297523 | 8.38761185 | 0.69265965 | 0.0666569 | |
| (139) | 587748928166887621 | 179.9836371 | −0.68306759 | 0.0800753 |
| 587731187277627630 | 359.9849222 | 0.67510242 | 0.0848031 | |
| 140) | 588015508212285576 | 38.07654238 | −0.66091986 | 0.152935 |
| 588848901003084008 | 218.0833898 | 0.65782354 | 0.148348 | |
| (141) | 587722982275154175 | 175.8949958 | −0.63154972 | 0.0777659 |
| 587731187275858096 | 355.9025156 | 0.63455671 | 0.0830219 | |
| (142) | 588848899399090470 | 233.1265588 | −0.60318561 | 0.0834699 |
| 588015509829517446 | 53.12424142 | 0.60899384 | 0.0888991 | |
| (143) | 588848899394830608 | 223.4164629 | −0.59793901 | 0.0757585 |
| 588015509825257582 | 43.4242485 | 0.59779667 | 0.0674929 | |
| (144) | 587731172768809842 | 312.9796387 | −0.5957954 | 0.0542642 |
| 587725075526189422 | 132.9735106 | 0.58860398 | 0.0512173 | |
| (145) | 588848899367698514 | 161.4291165 | −0.59321324 | 0.0850623 |
| 587734305418182948 | 341.4353393 | 0.59869345 | 0.0853401 | |
| (146) | 588848899377791164 | 184.5422801 | −0.54941729 | 0.0806642 |
| 588015509808218204 | 4.53334222 | 0.54320436 | 0.0883403 | |
| (147) | 588848899381395678 | 192.8322052 | −0.54359022 | 0.0823546 |
| 588015509811822661 | 12.82661496 | 0.54938195 | 0.0838967 | |
| (148) | 587731512070570074 | 22.52506877 | −0.53886851 | 0.0752843 |
| 587722983897432095 | 202.5292389 | 0.53144561 | 0.0753058 | |
| (149) | 588848899365142729 | 155.7201062 | −0.52903144 | 0.161499 |
| 587734305415692542 | 335.7266832 | 0.52749615 | 0.161789 | |
| (150) | 587731185656922427 | 336.925539 | −0.52188082 | 0.142554 |
| 587728949587476580 | 156.9318551 | 0.51420834 | 0.147027 | |
| (151) | 587731512085708963 | 57.24298571 | −0.52109991 | 0.0398141 |
| 587722983912636747 | 237.2401798 | 0.51948336 | 0.0326624 | |
| (152) | 588848899365208074 | 155.7345006 | −0.52048483 | 0.152984 |
| 587734305415692542 | 335.7266832 | 0.52749615 | 0.161789 | |
| (153) | 587731512075026623 | 32.7941736 | −0.51697122 | 0.104186 |
| 587722983901888776 | 212.7874643 | 0.51757655 | 0.10494 | |
| (154) | 587731512070570080 | 22.53092957 | −0.51301286 | 0.0754378 |
| 587722983897432249 | 202.5290072 | 0.50960505 | 0.0842453 | |
| (155) | 588848899367567503 | 161.1736846 | −0.50354558 | 0.116059 |
| 587734305418117322 | 341.1713409 | 0.49887529 | 0.10686 | |
| (156) | 587731185663738041 | 352.414892 | −0.49559734 | 0.0610491 |
| 587748929774223562 | 172.4212536 | 0.49196292 | 0.0617746 | |
| (157) | 587731185657315605 | 337.8171047 | −0.46714883 | 0.089706 |
| 587728949587869853 | 157.8165583 | 0.46875388 | 0.0972739 | |
| (158) | 588848899365011498 | 155.3428317 | −0.46621861 | 0.0616145 |
| 587734305415561419 | 335.3404111 | 0.46782104 | 0.0585452 | |
| (159) | 587731185654825160 | 332.0329757 | −0.45305431 | 0.0966575 |
| 587728949585314077 | 152.0316255 | 0.44515599 | 0.096859 | |
| (160) | 588848899369599194 | 165.777933 | −0.43232161 | 0.408335 |
| 588015509800026315 | 345.7681431 | 0.42889055 | 0.406645 | |
| (161) | 588848899392012585 | 217.0954067 | −0.42921954 | 0.13692 |
| 588015509822505078 | 37.10056005 | 0.42263247 | 0.13819 | |
| (162) | 587748928964460711 | 162.3131562 | −0.4126741 | 0.0631013 |
| 587731186733023422 | 342.3072456 | 0.40960475 | 0.0687452 | |
| (163) | 588015508738474102 | 13.66692127 | −0.40711197 | 0.0431046 |
| 588848900455530621 | 193.6587778 | 0.40977996 | 0.048432 | |
| (164) | 588015508744241268 | 26.76827379 | −0.39658262 | 0.0921257 |
| 588848900461232473 | 206.7714106 | 0.39999281 | 0.0904585 | |
| (165) | 587730846891377212 | 322.2164035 | −0.36530606 | 0.0524633 |
| 588848900432986349 | 142.2201617 | 0.3629534 | 0.0564073 | |
| (166) | 587722982818971844 | 191.8125016 | −0.35898776 | 0.126037 |
| 587731186745933956 | 11.82036541 | 0.35818073 | 0.117239 | |
| (167) | 588015508741030001 | 19.45674285 | −0.34082464 | 0.0468492 |
| 588848900458086553 | 199.4599698 | 0.34994819 | 0.048473 | |
| (168) | 588015508727529597 | 348.5866992 | −0.33249466 | 0.0806627 |
| 588848900444520624 | 168.5870372 | 0.32365469 | 0.0784033 | |
| (169) | 588015508727136416 | 347.7652686 | −0.32576489 | 0.0983488 |
| 588848900444192846 | 167.7733221 | 0.32533721 | 0.0968191 | |
| (170) | 587730846890132061 | 319.3488484 | −0.31274778 | 0.0580555 |
| 588848900431741191 | 139.3414636 | 0.32191469 | 0.0540347 | |
| (171) | 587734304341426385 | 334.4289933 | −0.29072537 | 0.0946837 |
| 588848900438360204 | 154.434898 | 0.2951535 | 0.0948182 | |
| (172) | 587734304340640020 | 332.7387428 | −0.26301595 | 0.180004 |
| 588848900437573950 | 152.7359484 | 0.25633147 | 0.186205 | |
| (173) | 587722982822772953 | 200.5231175 | −0.25712776 | 0.0755962 |
| 587731513143394377 | 20.52539083 | 0.26106339 | 0.0739661 | |
| (174) | 587730846892097872 | 323.7534775 | −0.25580372 | 0.23578 |
| 588848900433641580 | 143.7508871 | 0.25087206 | 0.230907 | |
| (175) | 587722982818578564 | 190.8538024 | −0.25574711 | 0.108047 |
| 587731186745540781 | 10.85230943 | 0.25272055 | 0.108846 | |
| (176) | 587728948512882891 | 155.0284918 | −0.24893939 | 0.0946879 |
| 587731186729877696 | 335.0272875 | 0.25118887 | 0.0976836 | |
| (177) | 587722982829588620 | 215.9538986 | −0.24834938 | 0.0845643 |
| 587731513150144670 | 35.96309274 | 0.24429916 | 0.0878976 | |
| (178) | 587728948515438760 | 160.8665986 | −0.24408333 | 0.0612075 |
| 587731186732433592 | 340.8655553 | 0.23643433 | 0.0602342 | |
| (179) | 587728948515438760 | 160.8665986 | −0.24408333 | 0.0612075 |
| 587731186732433605 | 340.8750138 | 0.24261057 | 0.0586656 | |
| (180) | 587722982817202308 | 187.6635646 | −0.21513005 | 0.112303 |
| 587731186744164449 | 7.6553343 | 0.21555044 | 0.114242 | |
| (181) | 587731512609996966 | 28.42414238 | −0.20766632 | 0.116707 |
| 587722983363117368 | 208.4229163 | 0.20947298 | 0.116208 | |
| (182) | 587731512620351626 | 52.0486704 | −0.18938222 | 0.0851471 |
| 587722983373472062 | 232.0581374 | 0.18368629 | 0.0798633 | |
| (183) | 588848899901030743 | 153.4421478 | −0.13358412 | 0.096212 |
| 587734304877838573 | 333.4461883 | 0.14101877 | 0.0959779 | |
| (184) | 588848899931963795 | 224.1292204 | −0.10150706 | 0.37695 |
| 588015509288648969 | 44.12854088 | 0.10090797 | 0.37109 | |
| (185) | 587731512620613919 | 52.66581732 | −0.08391774 | 0.0747399 |
| 587722983373733982 | 232.6567434 | 0.09144794 | 0.0712474 | |
| (186) | 587731512616550555 | 43.4068315 | −0.02922721 | 0.0437379 |
| 587722983369670840 | 223.4084883 | 0.02099328 | 0.0447694 | |
| (187) | 587731186188353997 | 324.4826276 | −0.02063334 | 0.0912575 |
| 587725074994364633 | 144.4802056 | 0.02165878 | 0.0908592 |
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587727227839578254 | 4.62339359 | −8.82776469 | 0.104797 |
| 587732769982709974 | 184.6230609 | 8.826889 | 0.481948 | |
| (2) | 587726877268312182 | 325.2592388 | −8.63777296 | 0.0863781 |
| 587732772650025129 | 145.2584188 | 8.63747987 | 0.182619 | |
| (3) | 587727227845804151 | 19.00360312 | −8.53841652 | 0.125065 |
| 587736540937519274 | 199.003274 | 8.53767648 | 0.0523744 | |
| (4) | 587726879422152915 | 340.0250784 | −8.32576871 | 0.211179 |
| 587732770508898457 | 160.0243395 | 8.32579967 | 0.46663 | |
| (5) | 587727212272943498 | 320.9004948 | −8.31734032 | 0.118795 |
| 587734948049977496 | 140.900737 | 8.31661374 | 0.132243 | |
| (6) | 587724240691855395 | 46.59481629 | −8.02287019 | 0.119974 |
| 587736543096930620 | 226.5946368 | 8.0234898 | 0.141641 | |
| (7) | 587726879416648036 | 327.4332687 | −7.24482558 | 0.120794 |
| 587732770503458957 | 147.4334035 | 7.24510724 | 0.172101 | |
| (8) | 587730818432041321 | 328.9376199 | −7.06320875 | 0.0592138 |
| 587732579378724931 | 148.9383586 | 7.06251179 | 0.0602015 | |
| (9) | 587726879951618320 | 323.0326676 | −6.24542716 | 0.0835999 |
| 587732703395315898 | 143.0324689 | 6.2463979 | 0.152482 | |
| (10) | 587726879409635950 | 311.3361796 | −5.13025247 | 0.100322 |
| 587732703390204231 | 131.3358794 | 5.12942269 | 0.0944183 | |
| (11) | 587724242308432093 | 60.09682211 | −5.0670592 | 0.139483 |
| 587736541492281504 | 240.0961397 | 5.06798605 | 0.161674 | |
| (12) | 587722981749620931 | 201.8110903 | −1.15290891 | 0.0672574 |
| 587731514217726115 | 21.81094788 | 1.15332655 | 0.0825304 | |
| (13) | 588848898840002840 | 182.4290969 | −0.99010277 | 0.101162 |
| 588015510344171606 | 2.42945951 | 0.99083329 | 0.0595599 | |
| (14) | 587731511542349980 | 42.40717742 | −0.84245813 | 0.023485 |
| 587722984443019391 | 222.4075711 | 0.84279922 | 0.211561 | |
| (15) | 588848899373138039 | 173.8651882 | −0.55499635 | 0.105208 |
| 588015509803565082 | 353.8651982 | 0.55470851 | 0.241575 | |
| (16) | 588015508736114824 | 8.29352396 | −0.35022869 | 0.0803753 |
| 588848900453171355 | 188.2937459 | 0.35119113 | 0.091289 | |
| (17) | 587722982819365056 | 192.6996089 | −0.24023107 | 0.082066 |
| 587731186746327197 | 12.69923244 | 0.23965712 | 0.243192 | |
| (18) | 588848899913482481 | 181.8731715 | −0.20286898 | 0.086595 |
| 588015509270167718 | 1.87315452 | 0.20227552 | 0.139049 | |
| (19) | 587731186189599168 | 327.3151749 | −0.17472973 | 0.475598 |
| 587725074995609777 | 147.314463 | 0.17484814 | 0.0847248 | |
| (20) | 587731512608817253 | 25.67986817 | −0.10862577 | 0.114301 |
| 587722983361937622 | 205.6799242 | 0.10944099 | 0.0763704 | |
| (21) | 588848899931963795 | 224.1292204 | −0.10150706 | 0.37695 |
| 588015509288648969 | 44.12854088 | 0.10090797 | 0.37109 | |
| (22) | 588848899903258801 | 158.5313323 | −0.04817315 | 0.0649146 |
| 587734304880066822 | 338.5305229 | 0.04819563 | 0.212747 |
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587726877268312182 | 325.2592388 | −8.63777296 | 0.0863781 |
| 587732772650025129 | 145.2584188 | 8.63747987 | 0.182619 | |
| (2) | 587727227845804151 | 19.00360312 | −8.53841652 | 0.125065 |
| 587736540937519274 | 199.003274 | 8.53767648 | 0.0523744 | |
| (3) | 587726879422152915 | 340.0250784 | −8.32576871 | 0.211179 |
| 587732770508898457 | 160.0243395 | 8.32579967 | 0.46663 | |
| (4) | 587727212272943498 | 320.9004948 | −8.31734032 | 0.118795 |
| 587734948049977496 | 140.900737 | 8.31661374 | 0.132243 | |
| (5) | 587724240691855395 | 46.59481629 | −8.02287019 | 0.119974 |
| 587736543096930620 | 226.5946368 | 8.0234898 | 0.141641 | |
| (6) | 587726879416648036 | 327.4332687 | −7.24482558 | 0.120794 |
| 587732770503458957 | 147.4334035 | 7.24510724 | 0.172101 | |
| (7) | 587730818432041321 | 328.9376199 | −7.06320875 | 0.0592138 |
| 587732579378724931 | 148.9383586 | 7.06251179 | 0.0602015 | |
| (8) | 587726879951618320 | 323.0326676 | −6.24542716 | 0.0835999 |
| 587732703395315898 | 143.0324689 | 6.2463979 | 0.152482 | |
| (9) | 587726879409635950 | 311.3361796 | −5.13025247 | 0.100322 |
| 587732703390204231 | 131.3358794 | 5.12942269 | 0.0944183 | |
| (10) | 587724242308432093 | 60.09682211 | −5.0670592 | 0.139483 |
| 587736541492281504 | 240.0961397 | 5.06798605 | 0.161674 | |
| (11) | 587722981749620931 | 201.8110903 | −1.15290891 | 0.0672574 |
| 587731514217726115 | 21.81094788 | 1.15332655 | 0.0825304 | |
| (12) | 588848898840002840 | 182.4290969 | −0.99010277 | 0.101162 |
| 588015510344171606 | 2.42945951 | 0.99083329 | 0.0595599 | |
| (13) | 588848899373138039 | 173.8651882 | −0.55499635 | 0.105208 |
| 588015509803565082 | 353.8651982 | 0.55470851 | 0.241575 | |
| (14) | 588015508736114824 | 8.29352396 | −0.35022869 | 0.0803753 |
| 588848900453171355 | 188.2937459 | 0.35119113 | 0.091289 | |
| (15) | 587722982819365056 | 192.6996089 | −0.24023107 | 0.082066 |
| 587731186746327197 | 12.69923244 | 0.23965712 | 0.243192 | |
| (16) | 588848899913482481 | 181.8731715 | −0.20286898 | 0.086595 |
| 588015509270167718 | 1.87315452 | 0.20227552 | 0.139049 | |
| (17) | 587731512608817253 | 25.67986817 | −0.10862577 | 0.114301 |
| 587722983361937622 | 205.6799242 | 0.10944099 | 0.0763704 | |
| (18) | 588848899931963795 | 224.1292204 | −0.10150706 | 0.37695 |
| 588015509288648969 | 44.12854088 | 0.10090797 | 0.37109 |
Appendix B
| Id SDSS DR8 | Ra | Dec | Ell | Sp | |
|---|---|---|---|---|---|
| (1) | 1237678888521237047 | 26.56961575 | −3.036690882 | 0.009671 | 0.990329 |
| 1237674469000413487 | 206.569743 | 3.036761704 | 0.147295 | 0.852705 | |
| (2) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237646588233974200 | 51.12707011 | 1.237392067 | 0.471205 | 0.528795 | |
| (3) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237657815275471153 | 51.12706887 | 1.237400496 | 0.52382 | 0.47618 | |
| (4) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237653000613921219 | 51.12707746 | 1.237402214 | 0.486234 | 0.513766 | |
| (5) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237659915511726413 | 51.12707585 | 1.237404045 | 0.484072 | 0.515928 | |
| (6) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237666516881834000 | 51.12704369 | 1.237412566 | 0.545912 | 0.454088 | |
| (7) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237666662937788799 | 51.12706696 | 1.23741968 | 0.492949 | 0.507051 | |
| (8) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237663330011251042 | 51.127083 | 1.237427134 | 0.502022 | 0.497978 | |
| (9) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237666409538519489 | 51.12708146 | 1.237445228 | 0.461594 | 0.538406 | |
| (10) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237666340814716950 | 51.12708141 | 1.237451208 | 0.435734 | 0.564266 | |
| (11) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237657587639386438 | 51.12708243 | 1.237457695 | 0.432267 | 0.567733 | |
| (12) | 1237655693017940456 | 231.1268834 | −1.237362786 | 0.153929 | 0.846071 |
| 1237657587639321096 | 51.12707884 | 1.237457919 | 0.457914 | 0.542086 | |
| (13) | 1237646748740026642 | 62.17470211 | −1.016792147 | 0.095611 | 0.904389 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (14) | 1237646748740026642 | 62.17470211 | −1.016792147 | 0.095611 | 0.904389 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (15) | 1237652997934416225 | 62.1747088 | −1.016787397 | 0.108173 | 0.891827 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (16) | 1237652997934416225 | 62.1747088 | −1.016787397 | 0.108173 | 0.891827 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (17) | 1237657761048166683 | 62.17471976 | −1.016786518 | 0.114383 | 0.885617 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (18) | 1237657761048166683 | 62.17471976 | −1.016786518 | 0.114383 | 0.885617 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (19) | 1237646748740026643 | 62.17475111 | −1.016781419 | 0.097682 | 0.902318 |
| 1237655551815123559 | 242.1749457 | 1.01671526 | 0.083047 | 0.916953 | |
| (20) | 1237646748740026643 | 62.17475111 | −1.016781419 | 0.097682 | 0.902318 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (21) | 1237646748740026643 | 62.17475111 | −1.016781419 | 0.097682 | 0.902318 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (22) | 1237649823937986797 | 62.17470476 | −1.016778157 | 0.109712 | 0.890288 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (23) | 1237649823937986797 | 62.17470476 | −1.016778157 | 0.109712 | 0.890288 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (24) | 1237646585554469394 | 62.17471262 | −1.016759557 | 0.087926 | 0.912074 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (25) | 1237646585554469394 | 62.17471262 | −1.016759557 | 0.087926 | 0.912074 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (26) | 1237666497028096411 | 62.17470133 | −1.016724343 | 0.06974 | 0.93026 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (27) | 1237666497028096411 | 62.17470133 | −1.016724343 | 0.06974 | 0.93026 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (28) | 1237666497028096412 | 62.17471675 | −1.016711222 | 0.07633 | 0.92367 |
| 1237648705676575427 | 242.1748881 | 1.016716451 | 0.092952 | 0.907048 | |
| (29) | 1237666497028096412 | 62.17471675 | −1.016711222 | 0.07633 | 0.92367 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.078252 | 0.921748 | |
| (30) | 1237655177615638991 | 128.668235 | −0.926547264 | 0.883225 | 0.116775 |
| 1237649942587703356 | 308.6681411 | 0.926418898 | 0.861631 | 0.138369 | |
| (31) | 1237648720134537650 | 128.6682518 | −0.926538368 | 0.902699 | 0.097301 |
| 1237649942587703356 | 308.6681411 | 0.926418898 | 0.861631 | 0.138369 | |
| (32) | 1237648720166060380 | 200.6434022 | −0.866110951 | 0.989174 | 0.010826 |
| 1237663480353259732 | 20.64339386 | 0.86631035 | 0.958359 | 0.041641 |
| Id SDSS DR8 | Ra | Dec | Sp | Zphot | |
|---|---|---|---|---|---|
| (1) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237666662924943502 | 21.81093325 | 1.15332143 | 0.56 | 0.070 | |
| (2) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237660237652623499 | 21.81093366 | 1.15333317 | 0.64 | 0.071 | |
| (3) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237663205460607081 | 21.81092528 | 1.15333562 | 0.61 | 0.070 | |
| (4) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237660010021060695 | 21.8109353 | 1.15333828 | 0.58 | 0.069 | |
| (5) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237660010021060693 | 21.8109426 | 1.1533383 | 0.58 | 0.069 | |
| (6) | 1237650372102127690 | 201.8110906 | −1.1529332 | 0.80 | 0.061 |
| 1237646588221128874 | 21.81095251 | 1.15334338 | 0.54 | 0.071 | |
| (7) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237656909048971424 | 21.81094041 | 1.1533158 | 0.59 | 0.072 | |
| (8) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237666662924943502 | 21.81093325 | 1.15332143 | 0.56 | 0.070 | |
| (9) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237657235442630860 | 21.8109474 | 1.15332466 | 0.57 | 0.078 | |
| (10) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237657815262625899 | 21.81092583 | 1.15333002 | 0.57 | 0.075 | |
| (11) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237646588221128876 | 21.81094599 | 1.15333221 | 0.67 | 0.074 | |
| (12) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237666340801871988 | 21.81093809 | 1.15333261 | 0.59 | 0.072 | |
| (13) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237660237652623499 | 21.81093366 | 1.15333317 | 0.64 | 0.071 | |
| (14) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237662969220497579 | 21.81093606 | 1.15333365 | 0.67 | 0.073 | |
| (15) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237663205460607081 | 21.81092528 | 1.15333562 | 0.61 | 0.070 | |
| (16) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237657106606063792 | 21.81092612 | 1.15333705 | 0.65 | 0.077 | |
| (17) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237659915498881211 | 21.81093881 | 1.15333749 | 0.64 | 0.076 | |
| (18) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237660010021060693 | 21.8109426 | 1.1533383 | 0.58 | 0.069 | |
| (19) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237663544779276481 | 21.8109381 | 1.15334331 | 0.59 | 0.074 | |
| (20) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237646588221128874 | 21.81095251 | 1.15334338 | 0.54 | 0.071 | |
| (21) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237657737950789725 | 21.81092483 | 1.15334534 | 0.64 | 0.073 | |
| (22) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237666409525739588 | 21.81091124 | 1.15334613 | 0.60 | 0.080 | |
| (23) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237656513889894587 | 21.81092948 | 1.15334793 | 0.59 | 0.072 | |
| (24) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237656513889894586 | 21.81093578 | 1.15334862 | 0.64 | 0.073 | |
| (25) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237657072230400220 | 21.81093259 | 1.15334873 | 0.61 | 0.076 | |
| (26) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237678617427378399 | 21.81092545 | 1.15335605 | 0.66 | 0.079 | |
| (27) | 1237651709428367652 | 201.8110888 | −1.1529142 | 0.82 | 0.079 |
| 1237678617427378397 | 21.81093158 | 1.15336241 | 0.59 | 0.076 | |
| (28) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237657235442630860 | 21.8109474 | 1.15332466 | 0.57 | 0.078 | |
| (29) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237657815262625899 | 21.81092583 | 1.15333002 | 0.57 | 0.075 | |
| (30) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237657106606063792 | 21.81092612 | 1.15333705 | 0.65 | 0.077 | |
| (31) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237659915498881211 | 21.81093881 | 1.15333749 | 0.64 | 0.076 | |
| (32) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237666409525739588 | 21.81091124 | 1.15334613 | 0.60 | 0.080 | |
| (33) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237657072230400220 | 21.81093259 | 1.15334873 | 0.61 | 0.076 | |
| (34) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237678617427378399 | 21.81092545 | 1.15335605 | 0.66 | 0.079 | |
| (35) | 1237651279931506991 | 201.8110746 | −1.1529118 | 0.76 | 0.085 |
| 1237678617427378397 | 21.81093158 | 1.15336241 | 0.59 | 0.076 | |
| (36) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237656909048971424 | 21.81094041 | 1.1533158 | 0.59 | 0.072 | |
| (37) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237666662924943502 | 21.81093325 | 1.15332143 | 0.56 | 0.070 | |
| (38) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237657235442630860 | 21.8109474 | 1.15332466 | 0.57 | 0.078 | |
| (39) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237657815262625899 | 21.81092583 | 1.15333002 | 0.57 | 0.075 | |
| (40) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237646588221128876 | 21.81094599 | 1.15333221 | 0.67 | 0.074 | |
| (41) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237666340801871988 | 21.81093809 | 1.15333261 | 0.59 | 0.072 | |
| (42) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237660237652623499 | 21.81093366 | 1.15333317 | 0.64 | 0.071 | |
| (43) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237662969220497579 | 21.81093606 | 1.15333365 | 0.67 | 0.073 | |
| (44) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237663205460607081 | 21.81092528 | 1.15333562 | 0.61 | 0.070 | |
| (45) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237657106606063792 | 21.81092612 | 1.15333705 | 0.65 | 0.077 | |
| (46) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237659915498881211 | 21.81093881 | 1.15333749 | 0.64 | 0.076 | |
| (47) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237660010021060695 | 21.8109353 | 1.15333828 | 0.58 | 0.069 | |
| (48) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237660010021060693 | 21.8109426 | 1.1533383 | 0.58 | 0.069 | |
| (49) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237663544779276481 | 21.8109381 | 1.15334331 | 0.59 | 0.074 | |
| (50) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237646588221128874 | 21.81095251 | 1.15334338 | 0.54 | 0.071 | |
| (51) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237657737950789725 | 21.81092483 | 1.15334534 | 0.64 | 0.073 | |
| (52) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237666409525739588 | 21.81091124 | 1.15334613 | 0.60 | 0.080 | |
| (53) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237656513889894587 | 21.81092948 | 1.15334793 | 0.59 | 0.072 | |
| (54) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237656513889894586 | 21.81093578 | 1.15334862 | 0.64 | 0.073 | |
| (55) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237657072230400220 | 21.81093259 | 1.15334873 | 0.61 | 0.076 | |
| (56) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237678617427378399 | 21.81092545 | 1.15335605 | 0.66 | 0.079 | |
| (57) | 1237648702974525748 | 201.8110905 | −1.1529069 | 0.82 | 0.071 |
| 1237678617427378397 | 21.81093158 | 1.15336241 | 0.59 | 0.076 | |
| (58) | 1237666406859014666 | 62.17467447 | −1.016796 | 0.90 | 0.081 |
| 1237655551815123559 | 242.1749457 | 1.01671526 | 0.92 | 0.088 | |
| (59) | 1237666406859014666 | 62.17467447 | −1.016796 | 0.90 | 0.081 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (60) | 1237666406859014666 | 62.17467447 | −1.016796 | 0.90 | 0.081 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (61) | 1237652997934416225 | 62.1747088 | −1.0167874 | 0.89 | 0.074 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (62) | 1237652997934416225 | 62.1747088 | −1.0167874 | 0.89 | 0.074 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (63) | 1237646748740026643 | 62.17475111 | −1.0167814 | 0.90 | 0.076 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (64) | 1237646748740026643 | 62.17475111 | −1.0167814 | 0.90 | 0.076 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (65) | 1237649823937986797 | 62.17470476 | −1.0167782 | 0.89 | 0.071 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (66) | 1237646585554469394 | 62.17471262 | −1.0167596 | 0.91 | 0.083 |
| 1237655551815123559 | 242.1749457 | 1.01671526 | 0.92 | 0.088 | |
| (67) | 1237646585554469394 | 62.17471262 | −1.0167596 | 0.91 | 0.083 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (68) | 1237646585554469394 | 62.17471262 | −1.0167596 | 0.91 | 0.083 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (69) | 1237666497028096411 | 62.17470133 | −1.0167243 | 0.93 | 0.085 |
| 1237655551815123559 | 242.1749457 | 1.01671526 | 0.92 | 0.088 | |
| (70) | 1237666497028096411 | 62.17470133 | −1.0167243 | 0.93 | 0.085 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (71) | 1237666497028096411 | 62.17470133 | −1.0167243 | 0.93 | 0.085 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (72) | 1237660007354335814 | 62.17467871 | −1.016717 | 0.89 | 0.068 |
| 1237648705676575428 | 242.1748845 | 1.01672036 | 0.92 | 0.076 | |
| (73) | 1237666497028096412 | 62.17471675 | −1.0167112 | 0.92 | 0.089 |
| 1237655551815123559 | 242.1749457 | 1.01671526 | 0.92 | 0.088 | |
| (74) | 1237666497028096412 | 62.17471675 | −1.0167112 | 0.92 | 0.089 |
| 1237648705676575427 | 242.1748881 | 1.01671645 | 0.91 | 0.084 | |
| (75) | 1237648721222828169 | 161.910801 | −0.1931421 | 0.69 | 0.123 |
| 1237653012428554879 | 341.9117668 | 0.19238554 | 0.59 | 0.131 | |
| (76) | 1237648721222828169 | 161.910801 | −0.1931421 | 0.69 | 0.123 |
| 1237663479262544284 | 341.9117693 | 0.19240627 | 0.63 | 0.119 | |
| (77) | 1237648721222828169 | 161.910801 | −0.1931421 | 0.69 | 0.123 |
| 1237663479262544283 | 341.9117693 | 0.19240627 | 0.62 | 0.116 |
| Id SDSS DR8 | Ra | Dec | Sp | Zphot | |
|---|---|---|---|---|---|
| (1) | 1237671139859628503 | 164.797490 | −21.936403 | 0.99 | 0.103 |
| 1237680273114923318 | 344.796820 | 21.936782 | 0.88 | 0.142 | |
| (2) | 1237671139859628503 | 164.797490 | −21.936403 | 0.99 | 0.103 |
| 1237679478537912674 | 344.796831 | 21.936789 | 0.85 | 0.123 | |
| (3) | 1237671239182254464 | 165.440684 | −20.397881 | 0.56 | 0.079 |
| 1237679476390560006 | 345.439848 | 20.398063 | 0.96 | 0.059 | |
| (4) | 1237671239182254464 | 165.440684 | −20.397881 | 0.56 | 0.079 |
| 1237680270967636262 | 345.439859 | 20.398065 | 0.95 | 0.058 | |
| (5) | 1237671239182254464 | 165.440684 | −20.397881 | 0.56 | 0.079 |
| 1237680270967636263 | 345.439855 | 20.398073 | 0.93 | 0.064 | |
| (6) | 1237671239182254464 | 165.440684 | −20.397881 | 0.56 | 0.079 |
| 1237679476390560005 | 345.439850 | 20.398083 | 0.96 | 0.058 | |
| (7) | 1237668756705771673 | 313.351245 | −17.157470 | 0.99 | 0.092 |
| 1237667539074023810 | 133.351503 | 17.157239 | 0.62 | 0.210 | |
| (8) | 1237668756705771673 | 313.351245 | −17.157470 | 0.99 | 0.092 |
| 1237667292113011156 | 133.351519 | 17.157253 | 0.56 | 0.154 | |
| (9) | 1237667247022604530 | 55.572846 | −11.962790 | 0.96 | 0.099 |
| 1237668350292328878 | 235.572915 | 11.963025 | 0.76 | 0.072 | |
| (10) | 1237667247022604530 | 55.572846 | −11.962790 | 0.96 | 0.099 |
| 1237668270839038355 | 235.572925 | 11.963054 | 0.78 | 0.058 | |
| (11) | 1237667726440530093 | 83.727284 | −6.167019 | 0.63 | 0.274 |
| 1237671693914146439 | 263.726548 | 6.167152 | 0.99 | 0.092 | |
| (12) | 1237680066953806059 | 334.767374 | −3.511891 | 0.99 | 0.067 |
| 1237654600491729036 | 154.766800 | 3.511264 | 0.97 | 0.117 | |
| (13) | 1237679079114932401 | 334.767352 | −3.511879 | 0.99 | 0.076 |
| 1237654600491729036 | 154.766800 | 3.511264 | 0.97 | 0.117 | |
| (14) | 1237679433981362251 | 359.485290 | −3.315196 | 0.65 | 0.063 |
| 1237651737367347360 | 179.485647 | 3.314965 | 0.84 | 0.086 | |
| (15) | 1237679433981362251 | 359.485290 | −3.315196 | 0.65 | 0.063 |
| 1237651737367347361 | 179.485641 | 3.314973 | 0.80 | 0.079 | |
| (16) | 1237679433981362253 | 359.485278 | −3.315192 | 0.74 | 0.066 |
| 1237651737367347360 | 179.485647 | 3.314965 | 0.84 | 0.086 | |
| (17) | 1237679433981362253 | 359.485278 | −3.315192 | 0.74 | 0.066 |
| 1237651737367347361 | 179.485641 | 3.314973 | 0.80 | 0.079 | |
| (18) | 1237672836917362790 | 359.485272 | −3.315190 | 0.71 | 0.061 |
| 1237651737367347360 | 179.485647 | 3.314965 | 0.84 | 0.086 | |
| (19) | 1237672836917362790 | 359.485272 | −3.315190 | 0.71 | 0.061 |
| 1237651737367347361 | 179.485641 | 3.314973 | 0.80 | 0.079 | |
| (20) | 1237678888521237046 | 26.569616 | −3.036691 | 0.99 | 0.076 |
| 1237674469000413486 | 206.569743 | 3.036762 | 0.85 | 0.115 | |
| (21) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237656909048971424 | 21.810940 | 1.153316 | 0.59 | 0.072 | |
| (22) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237666662924943502 | 21.810933 | 1.153321 | 0.56 | 0.070 | |
| (23) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237657235442630860 | 21.810947 | 1.153325 | 0.57 | 0.078 | |
| (24) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237657815262625899 | 21.810926 | 1.153330 | 0.57 | 0.075 | |
| (25) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237646588221128876 | 21.810946 | 1.153332 | 0.67 | 0.074 | |
| (26) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237666340801871988 | 21.810938 | 1.153333 | 0.59 | 0.072 | |
| (27) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237660237652623499 | 21.810934 | 1.153333 | 0.64 | 0.071 | |
| (28) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237662969220497579 | 21.810936 | 1.153334 | 0.67 | 0.073 | |
| (29) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237663205460607081 | 21.810925 | 1.153336 | 0.61 | 0.070 | |
| (30) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237657106606063792 | 21.810926 | 1.153337 | 0.65 | 0.077 | |
| (31) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237659915498881211 | 21.810939 | 1.153337 | 0.64 | 0.076 | |
| (32) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237660010021060695 | 21.810935 | 1.153338 | 0.58 | 0.069 | |
| (33) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237660010021060693 | 21.810943 | 1.153338 | 0.58 | 0.069 | |
| (34) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237663544779276481 | 21.810938 | 1.153343 | 0.59 | 0.074 | |
| (35) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237646588221128874 | 21.810953 | 1.153343 | 0.54 | 0.071 | |
| (36) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237657737950789725 | 21.810925 | 1.153345 | 0.64 | 0.073 | |
| (37) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237666409525739588 | 21.810911 | 1.153346 | 0.60 | 0.080 | |
| (38) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237656513889894587 | 21.810929 | 1.153348 | 0.59 | 0.072 | |
| (39) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237656513889894586 | 21.810936 | 1.153349 | 0.64 | 0.073 | |
| (40) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237657072230400220 | 21.810933 | 1.153349 | 0.61 | 0.076 | |
| (41) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237678617427378399 | 21.810925 | 1.153356 | 0.66 | 0.079 | |
| (42) | 1237650372102127690 | 201.811091 | −1.152933 | 0.80 | 0.061 |
| 1237678617427378397 | 21.810932 | 1.153362 | 0.59 | 0.076 | |
| (43) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237656909048971424 | 21.810940 | 1.153316 | 0.59 | 0.072 | |
| (44) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237666662924943502 | 21.810933 | 1.153321 | 0.56 | 0.070 | |
| (45) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237657235442630860 | 21.810947 | 1.153325 | 0.57 | 0.078 | |
| (46) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237657815262625899 | 21.810926 | 1.153330 | 0.57 | 0.075 | |
| (47) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237646588221128876 | 21.810946 | 1.153332 | 0.67 | 0.074 | |
| (48) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237666340801871988 | 21.810938 | 1.153333 | 0.59 | 0.072 | |
| (49) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237660237652623499 | 21.810934 | 1.153333 | 0.64 | 0.071 | |
| (50) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237662969220497579 | 21.810936 | 1.153334 | 0.67 | 0.073 | |
| (51) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237663205460607081 | 21.810925 | 1.153336 | 0.61 | 0.070 | |
| (52) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237657106606063792 | 21.810926 | 1.153337 | 0.65 | 0.077 | |
| (53) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237659915498881211 | 21.810939 | 1.153337 | 0.64 | 0.076 | |
| (54) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237660010021060695 | 21.810935 | 1.153338 | 0.58 | 0.069 | |
| (55) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237660010021060693 | 21.810943 | 1.153338 | 0.58 | 0.069 | |
| (56) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237663544779276481 | 21.810938 | 1.153343 | 0.59 | 0.074 | |
| (57) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237646588221128874 | 21.810953 | 1.153343 | 0.54 | 0.071 | |
| (58) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237657737950789725 | 21.810925 | 1.153345 | 0.64 | 0.073 | |
| (59) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237666409525739588 | 21.810911 | 1.153346 | 0.60 | 0.080 | |
| (60) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237656513889894587 | 21.810929 | 1.153348 | 0.59 | 0.072 | |
| (61) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237656513889894586 | 21.810936 | 1.153349 | 0.64 | 0.073 | |
| (62) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237657072230400220 | 21.810933 | 1.153349 | 0.61 | 0.076 | |
| (63) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237678617427378399 | 21.810925 | 1.153356 | 0.66 | 0.079 | |
| (64) | 1237655500274270455 | 201.811109 | −1.152926 | 0.76 | 0.116 |
| 1237678617427378397 | 21.810932 | 1.153362 | 0.59 | 0.076 | |
| (65) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237656909048971424 | 21.810940 | 1.153316 | 0.59 | 0.072 | |
| (66) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237666662924943502 | 21.810933 | 1.153321 | 0.56 | 0.070 | |
| (67) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237657235442630860 | 21.810947 | 1.153325 | 0.57 | 0.078 | |
| (68) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237657815262625899 | 21.810926 | 1.153330 | 0.57 | 0.075 | |
| (69) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237646588221128876 | 21.810946 | 1.153332 | 0.67 | 0.074 | |
| (70) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237666340801871988 | 21.810938 | 1.153333 | 0.59 | 0.072 | |
| (71) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237660237652623499 | 21.810934 | 1.153333 | 0.64 | 0.071 | |
| (72) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237662969220497579 | 21.810936 | 1.153334 | 0.67 | 0.073 | |
| (73) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237663205460607081 | 21.810925 | 1.153336 | 0.61 | 0.070 | |
| (74) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237657106606063792 | 21.810926 | 1.153337 | 0.65 | 0.077 | |
| (75) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237659915498881211 | 21.810939 | 1.153337 | 0.64 | 0.076 | |
| (76) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237660010021060695 | 21.810935 | 1.153338 | 0.58 | 0.069 | |
| (77) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237660010021060693 | 21.810943 | 1.153338 | 0.58 | 0.069 | |
| (78) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237663544779276481 | 21.810938 | 1.153343 | 0.59 | 0.074 | |
| (79) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237646588221128874 | 21.810953 | 1.153343 | 0.54 | 0.071 | |
| (80) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237657737950789725 | 21.810925 | 1.153345 | 0.64 | 0.073 | |
| (81) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237666409525739588 | 21.810911 | 1.153346 | 0.60 | 0.080 | |
| (82) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237656513889894587 | 21.810929 | 1.153348 | 0.59 | 0.072 | |
| (83) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237656513889894586 | 21.810936 | 1.153349 | 0.64 | 0.073 | |
| (84) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237657072230400220 | 21.810933 | 1.153349 | 0.61 | 0.076 | |
| (85) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237678617427378399 | 21.810925 | 1.153356 | 0.66 | 0.079 | |
| (86) | 1237651709428367652 | 201.811089 | −1.152914 | 0.82 | 0.079 |
| 1237678617427378397 | 21.810932 | 1.153362 | 0.59 | 0.076 | |
| (87) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237656909048971424 | 21.810940 | 1.153316 | 0.59 | 0.072 | |
| (88) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237666662924943502 | 21.810933 | 1.153321 | 0.56 | 0.070 | |
| (89) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237657235442630860 | 21.810947 | 1.153325 | 0.57 | 0.078 | |
| (90) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237657815262625899 | 21.810926 | 1.153330 | 0.57 | 0.075 | |
| (91) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237646588221128876 | 21.810946 | 1.153332 | 0.67 | 0.074 | |
| (92) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237666340801871988 | 21.810938 | 1.153333 | 0.59 | 0.072 | |
| (93) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237660237652623499 | 21.810934 | 1.153333 | 0.64 | 0.071 | |
| (94) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237662969220497579 | 21.810936 | 1.153334 | 0.67 | 0.073 | |
| (95) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237663205460607081 | 21.810925 | 1.153336 | 0.61 | 0.070 | |
| (96) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237657106606063792 | 21.810926 | 1.153337 | 0.65 | 0.077 | |
| (97) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237659915498881211 | 21.810939 | 1.153337 | 0.64 | 0.076 | |
| (98) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237660010021060695 | 21.810935 | 1.153338 | 0.58 | 0.069 | |
| (99) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237660010021060693 | 21.810943 | 1.153338 | 0.58 | 0.069 | |
| (100) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237663544779276481 | 21.810938 | 1.153343 | 0.59 | 0.074 | |
| (101) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237646588221128874 | 21.810953 | 1.153343 | 0.54 | 0.071 | |
| (102) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237657737950789725 | 21.810925 | 1.153345 | 0.64 | 0.073 | |
| (103) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237666409525739588 | 21.810911 | 1.153346 | 0.60 | 0.080 | |
| (104) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237656513889894587 | 21.810929 | 1.153348 | 0.59 | 0.072 | |
| (105) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237656513889894586 | 21.810936 | 1.153349 | 0.64 | 0.073 | |
| (106) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237657072230400220 | 21.810933 | 1.153349 | 0.61 | 0.076 | |
| (107) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237678617427378399 | 21.810925 | 1.153356 | 0.66 | 0.079 | |
| (108) | 1237651279931506991 | 201.811075 | −1.152912 | 0.76 | 0.085 |
| 1237678617427378397 | 21.810932 | 1.153362 | 0.59 | 0.076 | |
| (109) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237656909048971424 | 21.810940 | 1.153316 | 0.59 | 0.072 | |
| (110) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237666662924943502 | 21.810933 | 1.153321 | 0.56 | 0.070 | |
| (111) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237657235442630860 | 21.810947 | 1.153325 | 0.57 | 0.078 | |
| (112) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237657815262625899 | 21.810926 | 1.153330 | 0.57 | 0.075 | |
| (113) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237646588221128876 | 21.810946 | 1.153332 | 0.67 | 0.074 | |
| (114) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237666340801871988 | 21.810938 | 1.153333 | 0.59 | 0.072 | |
| (115) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237660237652623499 | 21.810934 | 1.153333 | 0.64 | 0.071 | |
| (116) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237662969220497579 | 21.810936 | 1.153334 | 0.67 | 0.073 | |
| (117) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237663205460607081 | 21.810925 | 1.153336 | 0.61 | 0.070 | |
| (118) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237657106606063792 | 21.810926 | 1.153337 | 0.65 | 0.077 | |
| (119) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237659915498881211 | 21.810939 | 1.153337 | 0.64 | 0.076 | |
| (120) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237660010021060695 | 21.810935 | 1.153338 | 0.58 | 0.069 | |
| (121) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237660010021060693 | 21.810943 | 1.153338 | 0.58 | 0.069 | |
| (122) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237663544779276481 | 21.810938 | 1.153343 | 0.59 | 0.074 | |
| (123) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237646588221128874 | 21.810953 | 1.153343 | 0.54 | 0.071 | |
| (124) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237657737950789725 | 21.810925 | 1.153345 | 0.64 | 0.073 | |
| (125) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237666409525739588 | 21.810911 | 1.153346 | 0.60 | 0.080 | |
| (126) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237656513889894587 | 21.810929 | 1.153348 | 0.59 | 0.072 | |
| (127) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237656513889894586 | 21.810936 | 1.153349 | 0.64 | 0.073 | |
| (128) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237657072230400220 | 21.810933 | 1.153349 | 0.61 | 0.076 | |
| (129) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237678617427378399 | 21.810925 | 1.153356 | 0.66 | 0.079 | |
| (130) | 1237648702974525748 | 201.811090 | −1.152907 | 0.82 | 0.071 |
| 1237678617427378397 | 21.810932 | 1.153362 | 0.59 | 0.076 | |
| (131) | 1237666406859014666 | 62.174674 | −1.016796 | 0.90 | 0.081 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (132) | 1237666406859014666 | 62.174674 | −1.016796 | 0.90 | 0.081 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (133) | 1237666406859014666 | 62.174674 | −1.016796 | 0.90 | 0.081 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (134) | 1237646748740026642 | 62.174702 | −1.016792 | 0.90 | 0.099 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (135) | 1237646748740026642 | 62.174702 | −1.016792 | 0.90 | 0.099 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (136) | 1237646748740026642 | 62.174702 | −1.016792 | 0.90 | 0.099 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (137) | 1237652997934416225 | 62.174709 | −1.016787 | 0.89 | 0.074 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (138) | 1237652997934416225 | 62.174709 | −1.016787 | 0.89 | 0.074 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (139) | 1237652997934416225 | 62.174709 | −1.016787 | 0.89 | 0.074 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (140) | 1237657761048166683 | 62.174720 | −1.016787 | 0.89 | 0.113 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (141) | 1237657761048166683 | 62.174720 | −1.016787 | 0.89 | 0.113 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (142) | 1237657761048166683 | 62.174720 | −1.016787 | 0.89 | 0.113 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (143) | 1237646748740026643 | 62.174751 | −1.016781 | 0.90 | 0.076 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (144) | 1237646748740026643 | 62.174751 | −1.016781 | 0.90 | 0.076 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (145) | 1237646748740026643 | 62.174751 | −1.016781 | 0.90 | 0.076 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (146) | 1237649823937986797 | 62.174705 | −1.016778 | 0.89 | 0.071 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (147) | 1237649823937986797 | 62.174705 | −1.016778 | 0.89 | 0.071 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (148) | 1237649823937986797 | 62.174705 | −1.016778 | 0.89 | 0.071 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (149) | 1237646585554469394 | 62.174713 | −1.016760 | 0.91 | 0.083 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (150) | 1237646585554469394 | 62.174713 | −1.016760 | 0.91 | 0.083 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (151) | 1237646585554469394 | 62.174713 | −1.016760 | 0.91 | 0.083 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (152) | 1237666497028096411 | 62.174701 | −1.016724 | 0.93 | 0.085 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (153) | 1237666497028096411 | 62.174701 | −1.016724 | 0.93 | 0.085 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (154) | 1237666497028096411 | 62.174701 | −1.016724 | 0.93 | 0.085 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (155) | 1237660007354335814 | 62.174679 | −1.016717 | 0.89 | 0.068 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (156) | 1237660007354335814 | 62.174679 | −1.016717 | 0.89 | 0.068 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (157) | 1237660007354335814 | 62.174679 | −1.016717 | 0.89 | 0.068 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (158) | 1237666497028096412 | 62.174717 | −1.016711 | 0.92 | 0.089 |
| 1237655551815123559 | 242.174946 | 1.016715 | 0.92 | 0.088 | |
| (159) | 1237666497028096412 | 62.174717 | −1.016711 | 0.92 | 0.089 |
| 1237648705676575427 | 242.174888 | 1.016716 | 0.91 | 0.084 | |
| (160) | 1237666497028096412 | 62.174717 | −1.016711 | 0.92 | 0.089 |
| 1237648705676575428 | 242.174884 | 1.016720 | 0.92 | 0.076 | |
| (161) | 1237666497538883899 | 2.523832 | −0.444620 | 0.66 | 0.260 |
| 1237648705113555092 | 182.524814 | 0.444527 | 0.57 | 0.110 | |
| (162) | 1237666497538883899 | 2.523832 | −0.444620 | 0.66 | 0.260 |
| 1237674651003519212 | 182.524830 | 0.444553 | 0.68 | 0.088 | |
| (163) | 1237666299997782594 | 2.523821 | −0.444607 | 0.72 | 0.310 |
| 1237648705113555092 | 182.524814 | 0.444527 | 0.57 | 0.110 | |
| (164) | 1237648673959378974 | 161.910785 | −0.193158 | 0.79 | 0.150 |
| 1237653012428554879 | 341.911767 | 0.192386 | 0.59 | 0.131 | |
| (165) | 1237648673959378974 | 161.910785 | −0.193158 | 0.79 | 0.150 |
| 1237663479262544284 | 341.911769 | 0.192406 | 0.63 | 0.119 | |
| (166) | 1237648673959378974 | 161.910785 | −0.193158 | 0.79 | 0.150 |
| 1237663479262544283 | 341.911769 | 0.192406 | 0.62 | 0.116 | |
| (167) | 1237648673959378974 | 161.910785 | −0.193158 | 0.79 | 0.150 |
| 1237663526510395758 | 341.911752 | 0.192409 | 0.74 | 0.135 | |
| (168) | 1237648721222828169 | 161.910801 | −0.193142 | 0.69 | 0.123 |
| 1237653012428554879 | 341.911767 | 0.192386 | 0.59 | 0.131 | |
| (169) | 1237648721222828169 | 161.910801 | −0.193142 | 0.69 | 0.123 |
| 1237663479262544284 | 341.911769 | 0.192406 | 0.63 | 0.119 | |
| (170) | 1237648721222828169 | 161.910801 | −0.193142 | 0.69 | 0.123 |
| 1237663479262544283 | 341.911769 | 0.192406 | 0.62 | 0.116 | |
| (171) | 1237648721222828169 | 161.910801 | −0.193142 | 0.69 | 0.123 |
| 1237663526510395758 | 341.911752 | 0.192409 | 0.74 | 0.135 |
| SpecObjID | Ra | Dec | z | Elliptical | |
|---|---|---|---|---|---|
| (1) | 4839208601778651136 | 2.66932 | 1.37162 | 0.2678 | 0.935 |
| 4329151476691107840 | 182.669 | −1.3722 | 0.5809 | 0.892 | |
| (2) | 4914588370669666304 | 2.99248 | −3.2495 | 0.0003 | 0.861 |
| 5346040858121076736 | 182.993 | 3.24996 | 0.6052 | 0.958 | |
| (3) | 734224488962484224 | 4.30274 | −9.4565 | 0.1170 | 0.663 |
| 6075454403388112896 | 184.303 | 9.45639 | 2.4796 | 0.730 | |
| (4) | 734242081148528640 | 4.62338 | −8.8278 | 0.1047 | 0.686 |
| 1384895138274240512 | 184.623 | 8.82687 | 0.4819 | 0.997 | |
| (5) | 1680006812310464512 | 5.91966 | 0.54668 | 0.0596 | 0.709 |
| 4331440114590285824 | 185.92 | −0.546 | 0.5116 | 0.995 | |
| (6) | 735378151655368704 | 6.86606 | −8.8217 | 0.1888 | 0.550 |
| 1830869162549864448 | 186.866 | 8.822 | 0.0855 | 0.911 | |
| (7) | 4844864764419506176 | 8.16193 | 2.99506 | 0.4595 | 0.708 |
| 376056649636407296 | 188.161 | −2.9954 | 0.0991 | 0.792 | |
| (8) | 4919173338989330432 | 9.19367 | −2.8909 | 0.4721 | 0.999 |
| 5351416371190693888 | 189.193 | 2.89151 | 0.5333 | 0.999 | |
| (9) | 4753611070676402176 | 10.3652 | −0.5698 | 0.4595 | 0.994 |
| 4333736164478943232 | 190.365 | 0.5689 | 0.0006 | 0.661 | |
| (10) | 4039789700742381568 | 10.3652 | −0.5698 | 0.4594 | 0.995 |
| 4333736164478943232 | 190.365 | 0.5689 | 0.0006 | 0.661 | |
| (11) | 4920278343259521024 | 11.2634 | −2.7318 | 0.3479 | 0.998 |
| 5353712700990423040 | 191.263 | 2.73184 | 0.4950 | 0.636 | |
| (12) | 1683253395470706688 | 11.3174 | −0.1229 | 0.4762 | 0.913 |
| 4333669644025462784 | 191.318 | 0.12199 | 0.0004 | 0.788 | |
| (13) | 778123041480665088 | 11.5428 | 1.11225 | 0.2160 | 0.885 |
| 4270781151322832896 | 191.542 | −1.1128 | 0.5737 | 0.877 | |
| (14) | 4920246732300222464 | 11.7652 | −2.4001 | 0.5587 | 0.995 |
| 5354974390096756736 | 191.766 | 2.40077 | 0.4318 | 0.966 | |
| (15) | 779218704851298304 | 12.1667 | 0.06339 | 0.3315 | 0.827 |
| 4333606696984772608 | 192.167 | −0.0629 | 0.6460 | 0.988 | |
| (16) | 4848371932909273088 | 12.7862 | 2.31558 | 0.3916 | 0.995 |
| 4254850052604297216 | 192.786 | −2.3157 | 0.3638 | 0.927 | |
| (17) | 4755887885000376320 | 13.4472 | −0.2816 | 0.6521 | 0.988 |
| 4334910722825256960 | 193.448 | 0.28142 | 0.6379 | 0.998 | |
| (18) | 4921514474173104128 | 13.5581 | −1.4265 | 0.6410 | 0.891 |
| 4334919244040372224 | 193.559 | 1.42684 | 2.7379 | 0.512 | |
| (19) | 1219440076220557312 | 13.8081 | 1.19783 | 0.1501 | 0.630 |
| 4334772459238064128 | 193.809 | −1.1978 | 0.0008 | 0.784 | |
| (20) | 445869587716663296 | 16.9041 | −1.2101 | 0.1278 | 0.744 |
| 4511605535782993920 | 196.904 | 1.21051 | 0.6376 | 0.920 | |
| (21) | 4858431363432841216 | 17.7868 | 2.55229 | 0.1187 | 0.975 |
| 4563366149601361920 | 197.787 | −2.5522 | 0.4748 | 0.999 | |
| (22) | 781377596066654208 | 18.153 | −0.8043 | 0.4344 | 0.825 |
| 4511537915817885696 | 198.152 | 0.8038 | 0.4538 | 0.743 | |
| (23) | 447132651329972224 | 18.6371 | 0.23377 | 0.0449 | 0.812 |
| 3294404095737096192 | 198.638 | −0.233 | 0.0003 | 0.524 | |
| (24) | 743193205964564480 | 19.0036 | −8.5384 | 0.1251 | 0.834 |
| 2023364803757631488 | 199.003 | 8.53769 | 0.0524 | 0.910 | |
| (25) | 783713783397771264 | 19.6607 | −0.1202 | 0.0774 | 0.815 |
| 4508350431508299776 | 199.66 | 0.12022 | 0.4957 | 0.989 | |
| (26) | 4900146835093979136 | 21.7069 | −1.6754 | 0.3576 | 0.814 |
| 4554394684994617344 | 201.707 | 1.67542 | 0.5282 | 0.995 | |
| (27) | 4898954139939635200 | 22.8196 | −1.7604 | 0.6082 | 0.997 |
| 4554317994058579968 | 202.82 | 1.76101 | −0.0006 | 0.797 | |
| (28) | 3240357324111505408 | 22.9715 | −9.9891 | 1.7556 | 0.784 |
| 2028969828722698240 | 202.972 | 9.98944 | 0.0708 | 0.740 | |
| (29) | 2156103604883187712 | 25.3766 | −10.301 | 0.0001 | 0.616 |
| 6125025335974559744 | 205.376 | 10.3015 | 0.0976 | 0.768 | |
| (30) | 4808852734936088576 | 28.5418 | 1.69838 | 0.0835 | 0.889 |
| 1029209999458461696 | 208.541 | −1.6974 | 0.9782 | 0.728 | |
| (31) | 4950684244306821120 | 30.6002 | −9.3223 | 0.2858 | 0.994 |
| 2036853600411478016 | 210.6 | 9.32152 | 0.1129 | 0.612 | |
| (32) | 4767095206971965440 | 31.0675 | −1.1378 | 0.5428 | 0.819 |
| 599056024569145344 | 211.067 | 1.13788 | 0.2413 | 0.941 | |
| (33) | 4950627894335897600 | 31.3118 | −9.568 | 0.5654 | 0.996 |
| 6136202696354955264 | 211.312 | 9.56828 | 0.5225 | 0.994 | |
| (34) | 4946296918419963904 | 32.0863 | −3.3337 | 0.5013 | 0.994 |
| 599121995266811904 | 212.086 | 3.33396 | 0.1804 | 0.941 | |
| (35) | 1753144407835568128 | 33.0844 | 0.47945 | 0.1208 | 0.788 |
| 4541919901161881600 | 213.085 | −0.4803 | 0.3592 | 0.973 | |
| (36) | 4942780405423538176 | 33.8174 | −4.757 | 0.2931 | 0.973 |
| 5384229646118682624 | 213.817 | 4.75723 | 0.5377 | 0.731 | |
| (37) | 4948567407985164288 | 34.7932 | −7.0072 | 0.3011 | 0.990 |
| 5473179862867378176 | 214.793 | 7.00645 | 0.3060 | 0.977 | |
| (38) | 4770627388076195840 | 35.1163 | 0.11026 | 4.2378 | 0.744 |
| 4538720871560773632 | 215.117 | −0.1095 | 0.3080 | 0.869 | |
| (39) | 4802194917118443520 | 36.5091 | 2.8207 | 0.5139 | 0.999 |
| 1033647348191881216 | 216.509 | −2.8206 | 0.1083 | 0.759 | |
| (40) | 793836711925803008 | 36.9665 | −1.1694 | 0.0705 | 0.937 |
| 4533999294172626944 | 216.967 | 1.16883 | 0.5898 | 0.998 | |
| (41) | 4941630309399003136 | 38.565 | −9.3922 | 3.1585 | 0.552 |
| 6155479883750834176 | 218.565 | 9.39272 | 1.7961 | 0.540 | |
| (42) | 1700186150221670400 | 39.1133 | −1.1598 | 0.1325 | 0.765 |
| 4530637812533821440 | 219.113 | 1.15965 | −0.0001 | 0.768 | |
| (43) | 4938232268730138624 | 39.5952 | −5.0323 | 0.3833 | 0.999 |
| 5470806016826802176 | 219.596 | 5.033 | 0.3147 | 0.747 | |
| (44) | 1204870173954172928 | 40.3719 | 0.94366 | 0.3124 | 0.984 |
| 4533100713194553344 | 220.371 | −0.9445 | 0.9001 | 0.959 | |
| (45) | 1701291433513740288 | 41.581 | −1.0697 | 0.1536 | 0.707 |
| 604667932487739392 | 221.582 | 1.0688 | 2.7213 | 0.593 | |
| (46) | 1757550146414995456 | 42.5052 | −1.2479 | 0.1107 | 0.895 |
| 4523926393155223552 | 222.505 | 1.24716 | 0.5312 | 0.998 | |
| (47) | 4776111202286174208 | 44.2673 | −0.0568 | 0.4766 | 0.923 |
| 4525024526048165888 | 224.268 | 0.05648 | 0.6359 | 0.870 | |
| (48) | 913192280402192384 | 46.5123 | −0.1553 | 0.1095 | 0.768 |
| 4521668546195357696 | 226.512 | 0.15569 | 0.3529 | 0.986 | |
| (49) | 909757953937008640 | 46.6698 | −0.1322 | 0.3371 | 0.977 |
| 4521657276201172992 | 226.669 | 0.13306 | 0.5010 | 0.994 | |
| (50) | 517948624043272192 | 50.282 | −8.0389 | 0.0723 | 0.852 |
| 6181271678262706176 | 230.281 | 8.03859 | 0.4335 | 0.896 | |
| (51) | 1835370579998304256 | 53.5805 | −6.229 | 0.2550 | 0.979 |
| 2049174459813750784 | 233.581 | 6.2284 | 0.1394 | 0.787 | |
| (52) | 2970257888494249984 | 55.4657 | 0.6257 | 0.5709 | 0.991 |
| 354686810980378624 | 235.466 | −0.6265 | 0.0809 | 0.870 | |
| (53) | 521458539768604672 | 58.4107 | −4.9795 | 0.1134 | 0.770 |
| 5491059571152125952 | 238.41 | 4.97862 | 0.9057 | 0.767 | |
| (54) | 522580316506843136 | 60.0968 | −5.0671 | 0.1395 | 0.861 |
| 2051397380066011136 | 240.096 | 5.06799 | 0.1615 | 0.712 | |
| (55) | 2727025575481862144 | 124.032 | 13.3341 | 0.2018 | 0.588 |
| 3532033024394895360 | 304.032 | −13.334 | −0.0004 | 0.551 | |
| (56) | 5482152155748499456 | 136.731 | 6.56935 | 0.5701 | 0.995 |
| 718431927618529280 | 316.73 | −6.5703 | 0.1258 | 0.880 | |
| (57) | 5482200534260121600 | 137.823 | 7.38189 | 0.5085 | 0.882 |
| 718370629845280768 | 317.822 | −7.3824 | 0.1306 | 0.874 | |
| (58) | 531483062945474560 | 138.414 | −0.6326 | 0.2941 | 0.824 |
| 1155301165563406336 | 318.414 | 0.63161 | 0.1408 | 0.831 | |
| (59) | 4303412737826357248 | 139.318 | 2.8441 | 0.4084 | 0.997 |
| 4934949682486444032 | 319.319 | −2.8444 | 1.2665 | 0.589 | |
| (60) | 4302094698111565824 | 139.494 | −0.1787 | 0.4557 | 0.997 |
| 1155338274080843776 | 319.493 | 0.17935 | 0.1378 | 0.978 | |
| (61) | 532577351456811008 | 140.024 | 1.07582 | 0.0880 | 0.845 |
| 4719817306338230272 | 320.024 | −1.0758 | 0.5385 | 0.970 | |
| (62) | 533708750112974848 | 142.116 | −0.1828 | 1.1383 | 0.770 |
| 1112513395053062144 | 322.115 | 0.18204 | 0.1382 | 0.581 | |
| (63) | 4306817925153030144 | 143.7 | 1.11628 | 0.0002 | 0.732 |
| 4722047115600592896 | 323.699 | −1.116 | 0.5033 | 0.986 | |
| (64) | 4241523696663527424 | 144.728 | −0.9367 | 0.0001 | 0.637 |
| 1114734407618422784 | 324.727 | 0.93737 | 0.0914 | 0.707 | |
| (65) | 4258301419972984832 | 144.786 | −1.7252 | 0.4087 | 0.560 |
| 5792911249252024320 | 324.785 | 1.72534 | 0.1804 | 0.908 | |
| (66) | 1468184248975386624 | 145.258 | 8.63748 | 0.1826 | 0.954 |
| 1325221896005904384 | 325.259 | −8.6378 | 0.0862 | 0.751 | |
| (67) | 5332337919582011392 | 145.395 | 1.96721 | 0.2884 | 0.985 |
| 4937343042257944576 | 325.394 | −1.9665 | 0.5580 | 0.992 | |
| (68) | 4258354471409025024 | 146.058 | −1.6501 | 0.5357 | 0.992 |
| 5792991238722945024 | 326.059 | 1.64999 | 0.5321 | 0.980 | |
| (69) | 5340192281129910272 | 147.855 | 1.6496 | 0.4277 | 0.612 |
| 4926010103331028992 | 327.856 | −1.6498 | 0.3152 | 0.806 | |
| (70) | 5333521268954628096 | 148.617 | 2.03358 | 0.4854 | 0.875 |
| 4926055458185674752 | 328.617 | −2.0334 | 0.4969 | 0.998 | |
| (71) | 300635368191977472 | 149.071 | −0.1031 | 0.0844 | 0.660 |
| 1162049428530423808 | 329.071 | 0.10394 | 0.1914 | 0.936 | |
| (72) | 6000020484002414592 | 150.64 | 7.2737 | 0.5548 | 0.996 |
| 807373628705368064 | 330.639 | −7.2731 | 0.0585 | 0.558 | |
| (73) | 6000135382967517184 | 151.226 | 9.18359 | 0.5679 | 0.998 |
| 808475060082862080 | 331.225 | −9.1836 | 0.1162 | 0.960 | |
| (74) | 564246864883378176 | 152.036 | 2.60955 | 0.2255 | 0.550 |
| 4928117316342251520 | 332.035 | −2.6104 | −0.0011 | 0.525 | |
| (75) | 4312372383706513408 | 152.52 | 0.79 | 0.4913 | 0.962 |
| 421174006381570048 | 332.519 | −0.7906 | 0.0954 | 0.729 | |
| (76) | 4312233570363506688 | 153.639 | −0.8249 | 0.0003 | 0.716 |
| 1243118065701382144 | 333.639 | 0.82408 | 0.2721 | 0.978 | |
| (77) | 567537979422173184 | 155.631 | 1.86663 | 0.2492 | 0.983 |
| 4930524972818366464 | 335.632 | −1.8675 | 1.2607 | 0.995 | |
| (78) | 4314694547482869760 | 157.533 | 0.24703 | 0.4817 | 0.995 |
| 4731051565992378368 | 337.533 | −0.2472 | 0.4740 | 0.999 | |
| (79) | 4315711870633246720 | 157.653 | 0.02593 | 1.4246 | 0.742 |
| 4732332497072291840 | 337.652 | −0.026 | 0.5039 | 0.669 | |
| (80) | 307417161767348224 | 158.238 | −0.4138 | 0.1182 | 0.769 |
| 757890377641388032 | 338.239 | 0.41328 | −0.0003 | 0.744 | |
| (81) | 4315788836447191040 | 159.178 | 0.27608 | 0.6207 | 0.772 |
| 4733403696661528576 | 339.177 | −0.2753 | 0.2538 | 0.973 | |
| (82) | 570967906565777408 | 162.893 | 2.27202 | 0.1158 | 0.731 |
| 4913639497436495872 | 342.893 | −2.2713 | −0.0006 | 0.566 | |
| (83) | 4318991988898136064 | 165.716 | −0.3594 | 0.5770 | 0.981 |
| 4737931210767466496 | 345.715 | 0.35921 | 0.4103 | 0.999 | |
| (84) | 4318962576962093056 | 166.315 | −0.0114 | 0.4667 | 0.999 |
| 762409377880631296 | 346.316 | 0.01125 | 0.2943 | 0.908 | |
| (85) | 4318962576962093056 | 166.315 | −0.0114 | 0.4667 | 0.999 |
| 4736665947745026048 | 346.316 | 0.01125 | 0.2940 | 0.894 | |
| (86) | 313068375699908608 | 166.741 | −1.0969 | 0.0896 | 0.716 |
| 763483055649220608 | 346.741 | 1.09744 | 0.2620 | 0.826 | |
| (87) | 574323066767697920 | 168.514 | 3.22425 | 0.0752 | 0.585 |
| 4909015221106376704 | 348.514 | −3.2248 | 0.2472 | 0.992 | |
| (88) | 5326812049438146560 | 168.772 | 2.64553 | 0.5162 | 0.895 |
| 4908998453554053120 | 348.773 | −2.6464 | 0.3090 | 0.975 | |
| (89) | 4321409544887992320 | 169.357 | 0.84778 | 0.6557 | 0.958 |
| 4740153048352423936 | 349.358 | −0.8468 | 0.3819 | 0.682 | |
| (90) | 5325629249368358912 | 170.61 | 1.43599 | 0.2828 | 0.962 |
| 4907992950069788672 | 350.61 | −1.4356 | 0.4622 | 0.977 | |
| (91) | 315397411373606912 | 170.823 | 1.21037 | 0.0736 | 0.711 |
| 1232915690747357184 | 350.822 | −1.2105 | 0.1875 | 0.953 | |
| (92) | 4322558259443007488 | 171.391 | 0.9829 | 0.5939 | 0.998 |
| 4741256958060265472 | 351.39 | −0.9824 | 0.3199 | 0.850 | |
| (93) | 5325578671833481216 | 171.703 | 1.74119 | 0.7231 | 0.965 |
| 4906813179126349824 | 351.704 | −1.7413 | 0.0639 | 0.502 | |
| (94) | 4266153857560084480 | 171.74 | −2.1658 | 0.4919 | 0.997 |
| 4823580149407023104 | 351.74 | 2.16561 | 0.0877 | 0.694 | |
| (95) | 576595475898066944 | 171.814 | 2.39126 | 0.1273 | 0.864 |
| 4906808781079838720 | 351.814 | −2.3912 | 0.4541 | 0.996 | |
| (96) | 316509842296563712 | 171.978 | 0.46955 | 0.1836 | 0.982 |
| 4741226446612594688 | 351.979 | −0.4687 | 0.5093 | 0.989 | |
| (97) | 5325776034170667008 | 172.454 | 3.30746 | 3.9018 | 0.821 |
| 4906774146463563776 | 352.455 | −3.3076 | 2.2473 | 0.963 | |
| (98) | 4323644302036566016 | 173.063 | 0.77839 | 0.2855 | 0.966 |
| 4742391654076907520 | 353.062 | −0.7788 | 0.3492 | 0.979 | |
| (99) | 4266283325054255104 | 173.131 | −0.3697 | 0.4066 | 0.946 |
| 1673219253177706496 | 353.131 | 0.36908 | 0.1208 | 0.963 | |
| (100) | 5336938551446077440 | 173.505 | 3.17503 | 0.5416 | 0.962 |
| 4906696356015898624 | 353.504 | −3.1742 | 0.6170 | 0.892 | |
| (101) | 368204767274493952 | 173.585 | −3.5904 | 0.0001 | 0.668 |
| 4822247541330935808 | 353.584 | 3.59006 | 0.3967 | 0.978 | |
| (102) | 577726048678995968 | 174.184 | 2.67686 | 0.4598 | 0.998 |
| 4905651545024495616 | 354.183 | −2.6774 | 0.5341 | 0.999 | |
| (103) | 368325163797735424 | 174.441 | −1.3075 | 0.0774 | 0.630 |
| 4821148298591600640 | 354.441 | 1.30798 | 0.5238 | 0.994 | |
| (104) | 6057568923170635776 | 176.508 | 10.675 | 0.5038 | 0.601 |
| 729620840840194048 | 356.507 | −10.676 | 0.1151 | 0.626 | |
| (105) | 578737599460435968 | 176.726 | 1.68594 | 0.1707 | 0.866 |
| 4904637795303686144 | 356.727 | −1.6865 | 0.0800 | 0.745 | |
| (106) | 4326846349808500736 | 179.997 | −0.6119 | 0.1915 | 0.757 |
| 1676605474079795200 | 359.998 | 0.61259 | 0.1477 | 0.591 |
| SpecObjID | Ra | Dec | z | Spiral | |
|---|---|---|---|---|---|
| (1) | 734165115334584320 | 3.13101 | −11.1988 | 0.1065 | 0.667 |
| 1383900905740462080 | 183.132 | 11.1974 | 0.0782 | 0.733 | |
| (2) | 734165115334584320 | 3.13101 | −11.1988 | 0.1065 | 0.667 |
| 6073191609364119552 | 183.129 | 11.2007 | 0.4462 | 0.671 | |
| (3) | 743129709168060416 | 19.6432 | −10.9021 | 0.1409 | 0.832 |
| 1911855335291774976 | 199.642 | 10.8989 | 0.1491 | 0.844 | |
| (4) | 731860813924558848 | 0.62585 | −10.9018 | 0.0288 | 0.743 |
| 1382729651062859776 | 180.622 | 10.8979 | 0.0616 | 0.572 | |
| (5) | 731920737308272640 | 358.864 | −10.4171 | 0.2912 | 0.588 |
| 1381612822210832384 | 178.866 | 10.415 | 0.1168 | 0.544 | |
| (6) | 735277821219334144 | 5.62372 | −10.3846 | 0.0877 | 0.634 |
| 1385018008698644480 | 185.628 | 10.3872 | 0.0216 | 0.707 | |
| (7) | 743125036243642368 | 19.8544 | −10.0195 | 0.1420 | 0.655 |
| 2024520104594663424 | 199.85 | 10.0161 | 0.0486 | 0.772 | |
| (8) | 748746839045466112 | 28.8179 | −9.94469 | 0.1934 | 0.714 |
| 2033534720653944832 | 208.821 | 9.94239 | 0.1512 | 0.721 | |
| 99) | 749919467877722112 | 29.7612 | −9.64619 | 0.3374 | 0.511 |
| 2034618849453697024 | 209.757 | 9.64868 | 0.0704 | 0.902 | |
| (10) | 738753377525065728 | 12.1847 | −9.44537 | 0.0958 | 0.633 |
| 6092283803341422592 | 192.18 | 9.44541 | 0.4549 | 0.600 | |
| (11) | 735331972167002112 | 5.53528 | −9.40561 | 0.0530 | 0.717 |
| 1386048526860969984 | 185.532 | 9.4091 | 0.1333 | 0.786 | |
| (12) | 735345166306535424 | 6.11665 | −9.38702 | 0.1427 | 0.630 |
| 1386035332721436672 | 186.119 | 9.38824 | 0.0708 | 0.749 | |
| (13) | 752127287444400128 | 34.9428 | −9.36809 | 0.0684 | 0.760 |
| 2039106770269399040 | 214.939 | 9.36446 | 0.0042 | 0.623 | |
| (14) | 737601914207758336 | 10.3014 | −9.34322 | 0.0559 | 0.512 |
| 2014319942068889600 | 190.302 | 9.34553 | 0.0952 | 0.786 | |
| (15) | 4949578408943681536 | 31.7084 | −9.32514 | 0.2485 | 0.564 |
| 2036888509905659904 | 211.713 | 9.3212 | 0.0240 | 0.602 | |
| (16) | 730872079066359808 | 358.978 | −9.22965 | 0.0756 | 0.764 |
| 1381502596170147840 | 178.983 | 9.2295 | 0.1318 | 0.695 | |
| (17) | 737567279591483392 | 9.46966 | −8.87285 | 2.7401 | 0.690 |
| 1388259919773329408 | 189.471 | 8.87691 | 0.1868 | 0.607 | |
| (18) | 809694968183547904 | 335.363 | −8.64717 | 0.0373 | 0.754 |
| 1393917732184942592 | 155.36 | 8.6444 | 0.0450 | 0.871 | |
| (19) | 809695792817268736 | 335.426 | −8.40569 | 0.0705 | 0.685 |
| 1393918556818663424 | 155.43 | 8.40975 | 0.0865 | 0.599 | |
| (20) | 749954102493997056 | 29.4351 | −8.39294 | 0.0792 | 0.737 |
| 2033379689514428416 | 209.439 | 8.39684 | 0.0629 | 0.851 | |
| (21) | 811867328701556736 | 336.686 | −8.18604 | 0.1324 | 0.738 |
| 1395060674505238528 | 156.685 | 8.18211 | 0.0321 | 0.696 | |
| (22) | 519107509064067072 | 52.3919 | −7.93974 | 0.1274 | 0.780 |
| 1939981130342098944 | 232.395 | 7.93993 | 0.0749 | 0.853 | |
| (23) | 811897015515506688 | 337.822 | −7.80632 | 0.1330 | 0.828 |
| 1395012845749430272 | 157.821 | 7.80735 | 0.0667 | 0.557 | |
| (24) | 811928351596898304 | 338.431 | −7.72959 | 0.1669 | 0.638 |
| 1124917262550067200 | 158.428 | 7.73371 | 0.0673 | 0.678 | |
| (25) | 808545978582853632 | 332.595 | −7.52507 | 0.0563 | 0.742 |
| 1392816571306502144 | 152.598 | 7.52229 | 0.0707 | 0.647 | |
| (26) | 4949674616211111936 | 32.8596 | −7.47662 | 0.2186 | 0.677 |
| 2037965481578620928 | 212.857 | 7.47175 | 0.1091 | 0.501 | |
| (27) | 519084419319883776 | 52.782 | −6.98112 | 0.2000 | 0.591 |
| 2048172260535068672 | 232.778 | 6.98277 | 0.0348 | 0.750 | |
| (28) | 719544634476357632 | 318.955 | −6.6414 | −0.0001 | 0.822 |
| 1343369057658759168 | 138.954 | 6.63737 | 0.0453 | 0.668 | |
| (29) | 4951848077784252416 | 30.0436 | −6.05043 | 0.2459 | 0.537 |
| 2035663110638954496 | 210.045 | 6.04801 | 0.0804 | 0.700 | |
| (30) | 717316199754524672 | 315.639 | −5.41605 | 0.0911 | 0.781 |
| 1342204125038798848 | 135.644 | 5.4139 | 0.1766 | 0.553 | |
| (31) | 717315649998710784 | 315.543 | −5.41414 | 0.0631 | 0.741 |
| 1341003733638604800 | 135.54 | 5.41015 | 0.1514 | 0.932 | |
| (32) | 4937148978455642112 | 324.03 | −3.01385 | 0.5287 | 0.563 |
| 640660174721280000 | 144.029 | 3.01168 | 0.0186 | 0.644 | |
| (33) | 4557716584164491264 | 202.738 | −2.64609 | 0.3604 | 0.507 |
| 4814542157820461056 | 22.7336 | 2.64401 | 0.0437 | 0.727 | |
| (34) | 4908072664662802432 | 352.216 | −2.11621 | 0.0609 | 0.730 |
| 576509713991100416 | 172.212 | 2.11888 | 0.0743 | 0.757 | |
| (35) | 4891051125555855360 | 36.2809 | −2.02219 | 0.3070 | 0.670 |
| 601262744473200640 | 216.278 | 2.01777 | 0.0261 | 0.716 | |
| (36) | 4892303194623311872 | 36.2808 | −2.02121 | 0.8932 | 0.607 |
| 601262744473200640 | 216.278 | 2.01777 | 0.0261 | 0.716 | |
| (37) | 1106828368889800704 | 312.725 | −1.24782 | 0.1293 | 0.630 |
| 525966537325045760 | 132.72 | 1.25011 | 0.0347 | 0.708 | |
| (38) | 304075195369416704 | 151.728 | −1.23313 | 0.0335 | 0.700 |
| 1244241217248585728 | 331.733 | 1.23424 | 0.0495 | 0.703 | |
| (39) | 1680994448646891520 | 7.38777 | −1.10037 | 0.0591 | 0.694 |
| 325539587847907328 | 187.385 | 1.1025 | 0.0782 | 0.504 | |
| (40) | 1659576786771535872 | 330.756 | −1.0931 | 0.4383 | 0.697 |
| 564131141284554752 | 150.752 | 1.08967 | 0.1729 | 0.898 | |
| (41) | 336658118953953280 | 206.035 | −1.07384 | 0.0886 | 0.630 |
| 1212741028830799872 | 26.0389 | 1.07793 | 0.0592 | 0.584 | |
| (42) | 774688716978415616 | 5.28659 | −1.03586 | 0.1077 | 0.711 |
| 324403517626279936 | 185.29 | 1.03245 | 0.0993 | 0.710 | |
| (43) | 422226519742507008 | 336.167 | −0.89711 | 0.0990 | 0.505 |
| 306369326917642240 | 156.167 | 0.893717 | 0.0937 | 0.583 | |
| (44) | 315310824832919552 | 170.316 | −0.89299 | 0.0403 | 0.681 |
| 1234154023318218752 | 350.319 | 0.892361 | 0.1263 | 0.802 | |
| (45) | 427900268781266944 | 344.85 | −0.78249 | 0.1220 | 0.874 |
| 311974911520303104 | 164.846 | 0.777527 | 0.0403 | 0.748 | |
| (46) | 1658520430555719680 | 327.446 | −0.75649 | 0.3044 | 0.681 |
| 300719755709409280 | 147.45 | 0.758068 | 0.0732 | 0.850 | |
| (47) | 794950517187962880 | 39.1814 | −0.71337 | 0.0879 | 0.724 |
| 345754653394233344 | 219.186 | 0.710053 | 0.0562 | 0.720 | |
| (48) | 803929404051843072 | 55.401 | −0.67076 | 0.0367 | 0.836 |
| 354808032137340928 | 235.399 | 0.674322 | 0.0865 | 0.760 | |
| (49) | 1659619117969205248 | 329.993 | −0.63486 | 0.1275 | 0.595 |
| 562961531747198976 | 149.997 | 0.638209 | 0.0329 | 0.757 | |
| (50) | 1679888065054664704 | 5.2273 | −0.60555 | 0.1595 | 0.919 |
| 324402692992559104 | 185.224 | 0.608647 | 0.1025 | 0.566 | |
| (51) | 306262399411841024 | 157.048 | −0.54237 | 0.2214 | 0.805 |
| 423454949158971392 | 337.053 | 0.543207 | 0.0584 | 0.632 | |
| (52) | 309696723461105664 | 161.174 | −0.50356 | 0.1161 | 0.866 |
| 425721592429963264 | 341.171 | 0.498878 | 0.1068 | 0.780 | |
| (53) | 533738162049017856 | 140.545 | −0.46001 | 0.3197 | 0.664 |
| 1111393817388410880 | 320.544 | 0.464496 | 0.1344 | 0.613 | |
| (54) | 325434309609547776 | 186.904 | −0.38401 | 0.1155 | 0.691 |
| 1681098352495716352 | 6.90859 | 0.387528 | 0.1697 | 0.874 | |
| (55) | 1239663120406833152 | 339.376 | −0.1986 | 0.1883 | 0.616 |
| 307543330726635520 | 159.371 | 0.194265 | 0.0965 | 0.508 | |
| (56) | 773536159199422464 | 4.18587 | −0.10027 | 0.1272 | 0.732 |
| 324366134230935552 | 184.19 | 0.099486 | 0.0721 | 0.599 | |
| (57) | 305206317520283648 | 153.857 | −0.07052 | 0.1443 | 0.836 |
| 421228432207144960 | 333.859 | 0.073314 | 0.0452 | 0.701 | |
| (58) | 385078137475590144 | 237.596 | −0.00662 | 0.0830 | 0.536 |
| 1399629972804495360 | 57.6003 | 0.011409 | 0.0839 | 0.629 |
| SpecObjID | Ra | Dec | z | Star | |
|---|---|---|---|---|---|
| (1) | 2954423276568340480 | 0.694712 | −5.24687 | −0.0002 | 0.974 |
| 948114688929982464 | 180.694 | 5.24762 | 0.1423 | 0.791 | |
| (2) | 1676640383573977088 | 0.9439 | 0.28991 | −0.0002 | 0.968 |
| 322071453446989824 | 180.944 | −0.289746 | 1.0926 | 0.765 | |
| (3) | 1227362888558077952 | 1.52502 | 0.610184 | 0.0000 | 0.980 |
| 322044240534202368 | 181.525 | −0.610271 | 0.1814 | 0.546 | |
| (4) | 1224979697541081088 | 5.97699 | −1.04043 | −0.0001 | 0.997 |
| 2891434450627880960 | 185.977 | 1.04139 | 0.0001 | 0.592 | |
| (5) | 4841613233993809920 | 6.05869 | 2.55233 | 1.6621 | 0.928 |
| 4269537328760356864 | 186.058 | −2.5523 | 0.0006 | 0.758 | |
| (6) | 1265610500226443264 | 7.42917 | 0.131164 | 0.0001 | 0.773 |
| 2880060552376248320 | 187.429 | −0.131837 | 0.0001 | 1.000 | |
| (7) | 1276880489881298944 | 8.18923 | 0.647915 | −0.0001 | 0.875 |
| 3259547102262355968 | 188.189 | −0.648561 | 0.0006 | 0.992 | |
| (8) | 1275677080259946496 | 9.27467 | −0.0541519 | 0.0000 | 0.988 |
| 3259523737640265728 | 189.275 | 0.05479 | −0.0004 | 0.990 | |
| 9) | 739725621168465920 | 14.4364 | −10.0952 | 1.9325 | 0.609 |
| 3336213574535112704 | 194.437 | 10.0945 | 0.0001 | 0.998 | |
| (10) | 1217134125643753472 | 18.1146 | −0.700653 | −0.0003 | 0.961 |
| 3294508274463827968 | 198.115 | 0.700001 | 0.0005 | 0.814 | |
| (11) | 3224609293978331136 | 19.2516 | −9.86777 | 0.0004 | 0.997 |
| 6109206662252855296 | 199.252 | 9.86821 | 2.1820 | 0.866 | |
| (12) | 4760371418590871552 | 20.3504 | −0.882473 | 2.5398 | 0.621 |
| 3723477244270714880 | 200.351 | 0.882389 | 0.0000 | 0.599 | |
| (13) | 4940696823976689664 | 38.2399 | −5.23203 | 3.4576 | 0.582 |
| 658818330399893504 | 218.239 | 5.2316 | 0.2002 | 0.976 | |
| (14) | 1703605094194374656 | 45.1314 | 0.64229 | 2.6116 | 0.852 |
| 3731245568798859264 | 225.132 | −0.642758 | −0.0002 | 0.995 | |
| (15) | 2328467167030306816 | 46.0127 | 0.329006 | −0.0004 | 0.904 |
| 4521696583741865984 | 226.013 | −0.32927 | 0.0001 | 0.996 | |
| (16) | 531439632236177408 | 139.112 | −0.747577 | 0.6402 | 0.627 |
| 1252158529679157248 | 319.113 | 0.74727 | −0.0002 | 1.000 | |
| (17) | 2681979409950337024 | 140.333 | 6.52503 | 0.0005 | 1.000 |
| 719600434691467264 | 320.333 | −6.52547 | 0.0000 | 0.995 | |
| (18) | 4306676088153047040 | 142.445 | 0.0328297 | 3.0603 | 0.627 |
| 1112430931680978944 | 322.444 | −0.0324278 | −0.0002 | 0.805 | |
| (19) | 533850312235051008 | 142.445 | 0.0328401 | 3.0611 | 0.635 |
| 1112430931680978944 | 322.444 | −0.0324278 | −0.0002 | 0.805 | |
| (20) | 305140071944710144 | 155.122 | −0.10081 | 0.8089 | 0.683 |
| 1241932791512328192 | 335.123 | 0.101456 | −0.0001 | 0.827 | |
| (21) | 567512965532641280 | 156.507 | 0.887376 | 0.0000 | 0.791 |
| 1240819811034884096 | 336.506 | −0.887341 | −0.0001 | 0.995 | |
| (22) | 4320303161044107264 | 167.537 | 0.858582 | 0.6269 | 0.566 |
| 4739039243643912192 | 347.537 | −0.857903 | −0.0003 | 0.997 | |
| (23) | 315371023094540288 | 170.337 | 0.306388 | 0.0000 | 0.913 |
| 1672033429870372864 | 350.336 | −0.306994 | 0.0002 | 0.775 | |
| (24) | 3640122716687802368 | 171.106 | −0.155472 | 0.0005 | 0.999 |
| 1672091978864551936 | 351.106 | 0.155463 | −0.0005 | 0.657 | |
| (25) | 315279763629434880 | 171.106 | −0.155471 | 0.0006 | 0.999 |
| 1672091978864551936 | 351.106 | 0.155463 | −0.0005 | 0.657 | |
| (26) | 316494998889588736 | 171.432 | 0.43459 | 0.0000 | 1.000 |
| 1232900572462475264 | 351.432 | −0.433976 | −0.0004 | 0.972 | |
| (27) | 4322575576751144960 | 171.712 | 0.731312 | 2.4768 | 0.950 |
| 1232886553689221120 | 351.711 | −0.730549 | 0.0931 | 0.798 | |
| (28) | 367067598732421120 | 172.137 | −3.61907 | 0.0004 | 0.991 |
| 4822344848109993984 | 352.138 | 3.61852 | 1.5191 | 0.508 | |
| (29) | 369354306480007168 | 175.039 | −3.43229 | 0.0004 | 0.930 |
| 4820051266384691200 | 355.039 | 3.43141 | 0.4810 | 0.549 | |
| (30) | 3256182321551796224 | 179.776 | −0.658958 | 0.0006 | 0.999 |
| 1228487139180701696 | 359.777 | 0.658661 | −0.0003 | 1.000 |
| SpecObjID | Ra | Dec | z | Spiral | |
|---|---|---|---|---|---|
| (1) | 734165115334584320 | 3.13101 | −11.1988 | 0.1065 | 0.667 |
| 1383900905740462080 | 183.132 | 11.1974 | 0.0782 | 0.733 | |
| (2) | 743129709168060416 | 19.6432 | −10.9021 | 0.1409 | 0.832 |
| 1911855335291774976 | 199.642 | 10.8989 | 0.1491 | 0.844 | |
| (3) | 731860813924558848 | 0.625854 | −10.9018 | 0.0288 | 0.743 |
| 1382729651062859776 | 180.622 | 10.8979 | 0.0616 | 0.572 | |
| (4) | 731920737308272640 | 358.864 | −10.4171 | 0.2912 | 0.588 |
| 1381612822210832384 | 178.866 | 10.415 | 0.1168 | 0.544 | |
| (5) | 743125036243642368 | 19.8544 | −10.0195 | 0.1420 | 0.655 |
| 2024520104594663424 | 199.85 | 10.0161 | 0.0486 | 0.772 | |
| (6) | 748746839045466112 | 28.8179 | −9.94469 | 0.1934 | 0.714 |
| 2033534720653944832 | 208.821 | 9.94239 | 0.1512 | 0.721 | |
| (7) | 735331972167002112 | 5.53528 | −9.40561 | 0.0530 | 0.717 |
| 1386048526860969984 | 185.532 | 9.4091 | 0.1333 | 0.786 | |
| (8) | 735345166306535424 | 6.11665 | −9.38702 | 0.1427 | 0.630 |
| 1386035332721436672 | 186.119 | 9.38824 | 0.0708 | 0.749 | |
| (9) | 737601914207758336 | 10.3014 | −9.34322 | 0.0559 | 0.512 |
| 2014319942068889600 | 190.302 | 9.34553 | 0.0952 | 0.786 | |
| (10) | 730872079066359808 | 358.978 | −9.22965 | 0.0756 | 0.764 |
| 1381502596170147840 | 178.983 | 9.2295 | 0.1318 | 0.695 | |
| (11) | 809694968183547904 | 335.363 | −8.64717 | 0.0373 | 0.754 |
| 1393917732184942592 | 155.36 | 8.6444 | 0.0450 | 0.871 | |
| (12) | 809695792817268736 | 335.426 | −8.40569 | 0.0705 | 0.685 |
| 1393918556818663424 | 155.43 | 8.40975 | 0.0865 | 0.599 | |
| (13) | 749954102493997056 | 29.4351 | −8.39294 | 0.0792 | 0.737 |
| 2033379689514428416 | 209.439 | 8.39684 | 0.0629 | 0.851 | |
| (14) | 519107509064067072 | 52.3919 | −7.93974 | 0.1274 | 0.780 |
| 1939981130342098944 | 232.395 | 7.93993 | 0.0749 | 0.853 | |
| (15) | 811897015515506688 | 337.822 | −7.80632 | 0.1330 | 0.828 |
| 1395012845749430272 | 157.821 | 7.80735 | 0.0667 | 0.557 | |
| (16) | 811928351596898304 | 338.431 | −7.72959 | 0.1669 | 0.638 |
| 1124917262550067200 | 158.428 | 7.73371 | 0.0673 | 0.678 | |
| (17) | 808545978582853632 | 332.595 | −7.52507 | 0.0563 | 0.742 |
| 1392816571306502144 | 152.598 | 7.52229 | 0.0707 | 0.647 | |
| (18) | 4949674616211111936 | 32.8596 | −7.47662 | 0.2186 | 0.677 |
| 2037965481578620928 | 212.857 | 7.47175 | 0.1091 | 0.501 | |
| (19) | 717316199754524672 | 315.639 | −5.41605 | 0.0911 | 0.781 |
| 1342204125038798848 | 135.644 | 5.4139 | 0.1766 | 0.553 | |
| (20) | 717315649998710784 | 315.543 | −5.41414 | 0.0631 | 0.741 |
| 1341003733638604800 | 135.54 | 5.41015 | 0.1514 | 0.932 | |
| (21) | 4908072664662802432 | 352.216 | −2.11621 | 0.0609 | 0.730 |
| 576509713991100416 | 172.212 | 2.11888 | 0.0743 | 0.757 | |
| (22) | 304075195369416704 | 151.728 | −1.23313 | 0.0335 | 0.700 |
| 1244241217248585728 | 331.733 | 1.23424 | 0.0495 | 0.703 | |
| (23) | 1680994448646891520 | 7.38777 | −1.10037 | 0.0591 | 0.694 |
| 325539587847907328 | 187.385 | 1.1025 | 0.0782 | 0.504 | |
| (24) | 1659576786771535872 | 330.756 | −1.0931 | 0.4383 | 0.697 |
| 564131141284554752 | 150.752 | 1.08967 | 0.1729 | 0.898 | |
| (25) | 336658118953953280 | 206.035 | −1.07384 | 0.0886 | 0.630 |
| 1212741028830799872 | 26.0389 | 1.07793 | 0.0592 | 0.584 | |
| (26) | 774688716978415616 | 5.28659 | −1.03586 | 0.1077 | 0.711 |
| 324403517626279936 | 185.29 | 1.03245 | 0.0993 | 0.710 | |
| (27) | 422226519742507008 | 336.167 | −0.897112 | 0.0990 | 0.505 |
| 306369326917642240 | 156.167 | 0.893717 | 0.0937 | 0.583 | |
| (28) | 794950517187962880 | 39.1814 | −0.713369 | 0.0879 | 0.724 |
| 345754653394233344 | 219.186 | 0.710053 | 0.0562 | 0.720 | |
| (29) | 803929404051843072 | 55.401 | −0.670755 | 0.0367 | 0.836 |
| 354808032137340928 | 235.399 | 0.674322 | 0.0865 | 0.760 | |
| (30) | 1679888065054664704 | 5.2273 | −0.605546 | 0.1595 | 0.919 |
| 324402692992559104 | 185.224 | 0.608647 | 0.1025 | 0.566 | |
| (31) | 309696723461105664 | 161.174 | −0.503556 | 0.1161 | 0.866 |
| 425721592429963264 | 341.171 | 0.498878 | 0.1068 | 0.780 | |
| (32) | 533738162049017856 | 140.545 | −0.460014 | 0.3197 | 0.664 |
| 1111393817388410880 | 320.544 | 0.464496 | 0.1344 | 0.613 | |
| (33) | 325434309609547776 | 186.904 | −0.38401 | 0.1155 | 0.691 |
| 1681098352495716352 | 6.90859 | 0.387528 | 0.1697 | 0.874 | |
| (34) | 1239663120406833152 | 339.376 | −0.1986 | 0.1883 | 0.616 |
| 307543330726635520 | 159.371 | 0.194265 | 0.0965 | 0.508 | |
| (35) | 773536159199422464 | 4.18587 | −0.100271 | 0.1272 | 0.732 |
| 324366134230935552 | 184.19 | 0.0994864 | 0.0721 | 0.599 | |
| (36) | 385078137475590144 | 237.596 | −0.00662 | 0.0830 | 0.536 |
| 1399629972804495360 | 57.6003 | 0.0114088 | 0.0839 | 0.629 |
Appendix C
| Allwise_Name | Source_Id | Ra | Dec | |
|---|---|---|---|---|
| (1) | J210304.14-762224.9 | 6368528062846000640 | 315.7673682 | −76.37360527 |
| J090304.41+762224.0 | 1125452302531483520 | 135.7684166 | 76.37343393 | |
| (2) | J000923.83-752826.7 | 4685204141864675840 | 2.349349915 | −75.47408959 |
| J120924.56+752830.2 | 1692570332734552320 | 182.3515394 | 75.47502083 | |
| (3) | J005511.81-723727.8 | 4688988630882739328 | 13.79922983 | −72.6245651 |
| J125511.51+723731.8 | 1689619312245569024 | 193.7978223 | 72.62551077 | |
| (4) | J054056.36-604959.0 | 4759331807060038272 | 85.23483284 | −60.83306433 |
| J174056.57+605000.8 | 1435781247493233280 | 265.2357231 | 60.83356526 | |
| (5) | J042637.98-602917.9 | 4678309551123478016 | 66.65829152 | −60.4883202 |
| J162638.53+602917.1 | 1624874054648019712 | 246.6600443 | 60.48800541 | |
| (6) | J003634.96-450211.3 | 4979663732423902336 | 9.145683022 | −45.03652837 |
| J123635.26+450208.0 | 1541170364728499840 | 189.1469143 | 45.03558095 | |
| (7) | J023912.05-424657.5 | 4947107506659554304 | 39.80039767 | −42.78281482 |
| J143911.83+424655.0 | 1492995984312364928 | 219.7994728 | 42.78193739 | |
| (8) | J010933.66-415122.0 | 4984721382832208000 | 17.39027938 | −41.85614291 |
| J130933.48+415122.3 | 1525961816813896576 | 197.3894785 | 41.8561489 | |
| (9) | J030635.12-342620.5 | 5048328852053654272 | 46.6464308 | −34.43910643 |
| J150634.97+342621.0 | 1290665847434238336 | 226.6455941 | 34.43914596 | |
| (10) | J144620.40-322022.3 | 6215805347992022144 | 221.5850719 | −32.33959386 |
| J024620.21+322020.8 | 133564171416873728 | 41.58418524 | 32.33907625 | |
| (11) | J020549.77-245224.7 | 5121462661817011712 | 31.45738864 | −24.87356749 |
| J140549.73+245227.4 | 1257473141874860032 | 211.457199 | 24.87428879 | |
| (12) | J120429.60-215735.5 | 3493448195802870400 | 181.1233688 | −21.95989953 |
| J000429.68+215736.0 | 2847161965440082176 | 1.123715043 | 21.9600063 | |
| (13) | J043710.51-215420.2 | 4898466860297217536 | 69.29392704 | −21.90553489 |
| J163710.55+215416.4 | 1297817517737857024 | 249.2939377 | 21.90458255 | |
| (14) | J040147.38-180917.4 | 5096949256234108800 | 60.4473916 | −18.15484375 |
| J160147.61+180917.7 | 1199646075865168128 | 240.4484116 | 18.155046 | |
| (15) | J124510.71-180851.9 | 3522237773904469248 | 191.294554 | −18.1478664 |
| J004510.62+180851.9 | 2782801120299995520 | 11.29451879 | 18.14802663 | |
| (16) | J150108.76-134935.8 | 6311851640047858048 | 225.2865151 | −13.82676674 |
| J030108.57+134935.1 | 29187876189414144 | 45.28574655 | 13.8264156 | |
| (17) | J035733.19-083041.3 | 3194958963846806144 | 59.38814002 | −8.511587953 |
| J155733.13+083042.9 | 4454299557503538688 | 239.3880677 | 8.511930041 |
Appendix D
| Ra | Dec | Name | Descrip | Z | |
|---|---|---|---|---|---|
| (1) | 255.5777892 | −77.0249529 | WISEA J170218.69-770129.2 | q | 2.3 |
| 75.5809969 | 77.0255634 | WISEA J050219.24+770131.4 | q | 2.3 | |
| (2) | 315.7673595 | −76.3736026 | WISEA J210304.14-762224.9 | q | 1 |
| 135.7683983 | 76.3734303 | WISEA J090304.41+762224.0 | q | 2.4 | |
| (3) | 2.3493535 | −75.4740875 | WISEA J000923.83-752826.7 | q | 0.8 |
| 182.3515932 | 75.4750181 | WISEA J120924.56+752830.2 | q | 0.7 | |
| (4) | 85.679027 | −68.1421484 | WISEA J054242.99-680831.9 | q | 1.4 |
| 265.6773749 | 68.1413691 | SDSS J174242.55+680829.1 | q | 1.5 | |
| (5) | 352.8305884 | −66.7005686 | WISEA J233119.35-664201.9 | q | |
| 172.8287239 | 66.7011287 | SDSS J113118.89+664204.0 | q | 1.5 | |
| (6) | 350.1300997 | −64.0960807 | WISEA J232031.22-640545.8 | q | 0.8 |
| 170.1297219 | 64.0966844 | SDSS J112031.12+640548.1 | q | 1.4 | |
| (7) | 77.2847276 | −61.1581631 | WISEA J050908.30-610929.5 | q | 0.6 |
| 257.2851687 | 61.1587398 | SDSS J170908.44+610931.4 | q | 0.9 | |
| (8) | 85.2348298 | −60.8330635 | WISEA J054056.36-604959.0 | q | 0.6 |
| 265.2357267 | 60.8335658 | WISEA J174056.57+605000.8 | q | 1.9 | |
| (9) | 66.6582972 | −60.4883083 | WISEA J042637.98-602917.9 | q | 2.8 |
| 246.6600372 | 60.4879967 | WISEA J162638.53+602917.1 | q | ||
| (10) | 55.6305834 | −55.3800834 | J034231.34-552248.3 | X | |
| 235.6289338 | 55.3794316 | SDSS J154230.94+552245.9 | Q | 2.268 | |
| (11) | 12.2865176 | −55.3358661 | WISEA J004908.81-552009.3 | q | 1.3 |
| 192.2854767 | 55.3366013 | SDSS J124908.51+552011.7 | q | 1.9 | |
| (12) | 18.9229286 | −55.1625237 | WISEA J011541.50-550945.0 | qR | 0.7 |
| 198.9241743 | 55.16331 | SDSS J131541.80+550947.9 | Q | 2.518 | |
| (13) | 350.4801742 | −55.0232756 | XXLS J232155.23-550123.3 | QX | 1.788 |
| 170.4785659 | 55.0239884 | SDSS J112154.85+550126.3 | Q | 1.73 | |
| (14) | 13.9470844 | −54.2692763 | WISEA J005547.29-541609.5 | q | 2 |
| 193.9459076 | 54.2689056 | SDSS J125547.01+541608.0 | q | 0.3 | |
| (15) | 2.4579845 | −53.9814555 | WISEA J000949.91-535853.2 | q | 0.2 |
| 182.4575348 | 53.980648 | SDSS J120949.80+535850.3 | q | 0.3 | |
| (16) | 323.9286029 | −53.3487347 | WISEA J213542.85-532055.4 | q | 0.9 |
| 143.9271545 | 53.3484154 | SDSS J093542.51+532054.2 | q | 0.5 | |
| (17) | 348.3491422 | −53.3478756 | XXLS J231323.75-532051.9 | QX | 0.496 |
| 168.3507385 | 53.3479691 | SDSS J111324.17+532052.6 | q | 0.3 | |
| (18) | 80.7328764 | −52.4533568 | WISEA J052255.89-522712.0 | q | |
| 260.732699 | 52.4532957 | SDSS J172255.84+522712.0 | q | 2.1 | |
| (19) | 38.535212 | −50.9830297 | WISEA J023408.44-505858.7 | q | |
| 218.5348844 | 50.9840003 | SDSS J143408.35+505902.3 | Q | 3.175 | |
| (20) | 315.5807126 | −50.5996161 | WISEA J210219.36-503558.6 | q | 2.2 |
| 135.5799944 | 50.6005463 | SDSS J090219.19+503601.9 | Q | 2.619 | |
| (21) | 68.3167757 | −50.5098938 | WISEA J043316.02-503035.6 | q | 1.1 |
| 248.3167223 | 50.5106667 | PGC 2375138 | GR2 | ||
| (22) | 27.2491308 | −50.0692574 | WISEA J014859.79-500409.4 | q | 1.8 |
| 207.2486497 | 50.0702154 | SDSS J134859.67+500412.8 | Q | 1.559 | |
| (23) | 70.1774106 | −49.1605048 | WISEA J044042.58-490937.9 | q | 0.9 |
| 250.1779433 | 49.1604959 | SDSS J164042.70+490937.7 | q | 3.2 | |
| (24) | 352.4638668 | −46.4933229 | WISEA J232951.30-462936.0 | q | |
| 172.4629902 | 46.4929967 | SDSS J112951.12+462934.8 | Q | 1.874 | |
| (25) | 51.7544779 | −45.8163472 | WISEA J032701.07-454859.0 | q | 2.1 |
| 231.753214 | 45.816666 | SDSS J152700.77+454859.9 | q | 0.9 | |
| (26) | 13.7156676 | −45.5401862 | WISEA J005451.73-453224.7 | q | 1 |
| 193.7148005 | 45.5407984 | SDSS J125451.55+453226.8 | Q | 0.599 | |
| (27) | 9.1456769 | −45.036539 | WISEA J003634.96-450211.3 | q | 1.6 |
| 189.1469172 | 45.0355819 | SDSS J123635.25+450208.0 | Q | 0.401 | |
| (28) | 312.4572617 | −43.5311298 | WISEA J204949.73-433151.7 | q | 1.7 |
| 132.4578712 | 43.5314134 | SDSS J084949.88+433153.1 | q | 2.6 | |
| (29) | 39.8003988 | −42.7828145 | WISEA J023912.05-424657.5 | q | 1.8 |
| 219.7994764 | 42.7819417 | SDSS J143911.87+424655.0 | Q | 2.376 | |
| (30) | 58.8593889 | −42.1836389 | J035526.25-421101.1 | X | |
| 238.859031 | 42.1833947 | SDSS J155526.16+421100.1 | Q | 1.222 | |
| (31) | 75.7744245 | −40.7936211 | WISEA J050305.91-404736.8 | q | 2.3 |
| 255.7743683 | 40.7937126 | SDSS J170305.84+404737.3 | q | 0.3 | |
| (32) | 327.4360427 | −38.6604478 | WISEA J214944.65-383937.5 | q | 0.6 |
| 147.4361286 | 38.659581 | SDSS J094944.67+383934.5 | Q | 1.326 | |
| (33) | 17.7159333 | −38.4864674 | WISEA J011051.83-382911.3 | q | 2.2 |
| 197.7147558 | 38.4865089 | SDSS J131051.54+382911.4 | Q | 0.817 | |
| (34) | 35.9159531 | −37.2880557 | WISEA J022339.81-371716.8 | q | 0.7 |
| 215.9154018 | 37.2873321 | SDSS J142339.69+371714.3 | q | 1.4 | |
| (35) | 5.4863222 | −36.9636832 | WISEA J002156.72-365749.2 | q | 1.6 |
| 185.4861944 | 36.9634266 | SDSS J122156.67+365748.3 | Q | 2.097 | |
| (36) | 288.7726299 | −36.2604918 | WISEA J191505.43-361537.9 | q | 1 |
| 108.771553 | 36.2600021 | SDSS J071505.17+361536.0 | q | 0.4 | |
| (37) | 48.2374301 | −35.2506342 | WISEA J031256.97-351502.2 | qX | 1.9 |
| 228.2368457 | 35.250557 | SDSS J151256.83+351502.0 | q | 1.3 | |
| (38) | 71.9969184 | −34.9231867 | WISEA J044759.25-345523.3 | q | 2.5 |
| 251.99809 | 34.922451 | DEEP J164759.54+345520.8 | A | 0.743 | |
| (39) | 51.0522347 | −34.8159832 | WISEA J032412.53-344857.3 | q | 0.7 |
| 231.051651 | 34.815155 | SDSS J152412.39+344854.5 | q | 0 | |
| (40) | 64.4053066 | −34.4443255 | WISEA J041737.25-342639.2 | q | 2.3 |
| 244.4049248 | 34.4447566 | SDSS J161737.18+342641.1 | q | 1.9 | |
| (41) | 46.6464316 | −34.4391069 | WISEA J030635.12-342620.5 | q | 1.5 |
| 226.6455899 | 34.4391456 | SDSS J150634.94+342620.9 | Q | 2.275 | |
| (42) | 13.9539794 | −33.5205216 | Q 0053-3347 | Q | 2.08 |
| 193.9543304 | 33.519737 | SDSS J125549.03+333111.0 | q | 0.9 | |
| (43) | 61.3792872 | −33.3589696 | WISEA J040531.02-332132.4 | q | 1.3 |
| 241.3804819 | 33.3584594 | SDSS J160531.31+332130.4 | q | 0.6 | |
| (44) | 52.3380705 | −33.1624587 | WISEA J032921.13-330944.7 | q | 1 |
| 232.3374622 | 33.1619242 | SDSS J152921.00+330942.9 | q | 0.9 | |
| (45) | 35.6523275 | −32.9501625 | WISEA J022236.55-325700.5 | q | 2 |
| 215.6517237 | 32.9500411 | SDSS J142236.40+325700.2 | q | 1.8 | |
| (46) | 24.818008 | −32.6980218 | WISEA J013916.33-324152.7 | q | 1.6 |
| 204.8176575 | 32.6980515 | SDSS J133916.23+324152.9 | q | 0 | |
| (47) | 331.3013548 | −31.5723459 | 2QZ J220512.3-313421 | Q | 1.934 |
| 151.3004456 | 31.5727386 | SDSS J100512.10+313421.8 | q | 0.9 | |
| (48) | 178.0274651 | −31.4001968 | WISEA J115206.58-312400.4 | q | 2.4 |
| 358.026947 | 31.4004002 | SDSS J235206.46+312401.4 | q | 1 | |
| (49) | 341.9315476 | −31.0519246 | 6QZ J224743.5-310306 | Q | 2.614 |
| 161.9314813 | 31.0522394 | SDSS J104743.55+310308.0 | q | 0 | |
| (50) | 309.9034723 | −30.9013056 | J203936.83-305404.7 | X | |
| 129.9024969 | 30.9010042 | SDSS J083936.60+305403.6 | Q | 1.1 | |
| (51) | 15.5519167 | −30.6883056 | 2QZ J010212.4-304118 | N | 0.201 |
| 195.5513019 | 30.6890974 | SDSS J130212.30+304120.7 | QX | 0.897 | |
| (52) | 188.680682 | −30.5578933 | WISEA J123443.36-303328.3 | q | 1 |
| 8.6803036 | 30.558761 | SDSS J003443.27+303331.6 | Q | 1.254 | |
| (53) | 300.1895832 | −30.1375161 | WISEA J200045.51-300814.8 | q | 0.6 |
| 120.1898279 | 30.1370937 | SDSS J080045.55+300813.5 | Q | 1.343 | |
| (54) | 332.1756094 | −29.9838041 | 2QZ J220842.1-295902 | Q | 1.023 |
| 152.1766832 | 29.9847166 | SDSS J100842.39+295905.0 | Q | 2.56 | |
| (55) | 12.3530442 | −29.9213175 | Q 0046-3011 | Q | 1.081 |
| 192.3529914 | 29.9214458 | SDSS J124924.71+295517.2 | q | 2.2 | |
| (56) | 183.3282018 | −29.1793456 | WISEA J121318.77-291045.5 | q | 0.3 |
| 3.327841 | 29.1787777 | SDSS J001318.68+291043.5 | q | 0.9 | |
| (57) | 338.8539592 | −28.7111297 | 2QZ J223525.0-284240 | Q | 2.567 |
| 158.8546667 | 28.71175 | J103525.12+284242.3 | R | ||
| (58) | 333.8811688 | −28.3336528 | 2QZ J221531.4-282001 | Q | 1.909 |
| 153.8815524 | 28.3342401 | SDSS J101531.57+282003.3 | Q | 2.395 | |
| (59) | 80.438152 | −28.1840351 | WISEA J052145.16-281102.6 | q | 0.6 |
| 260.437853 | 28.1849529 | SDSS J172145.08+281105.8 | q | 1.3 | |
| (60) | 65.5058337 | −27.9944556 | WISEA J042201.40-275940.0 | q | 0.2 |
| 245.5051373 | 27.993782 | SDSS J162201.23+275937.6 | Q | 2.29 | |
| (61) | 189.5249477 | −27.4782258 | WISEA J123805.97-272841.7 | q | 2.3 |
| 9.5243507 | 27.4772773 | SDSS J003805.84+272838.2 | Q | 1.937 | |
| (62) | 44.5344194 | −26.5790235 | WISEA J025808.26-263444.5 | q | 1.5 |
| 224.5352818 | 26.5780647 | SDSS J145808.46+263441.0 | q | 2.1 | |
| (63) | 42.3864196 | −26.4011219 | WISEA J024932.73-262404.3 | q | 3 |
| 222.3872658 | 26.401885 | SDSS J144932.94+262406.7 | qR | 0.3 | |
| (64) | 197.0438404 | −25.791086 | WISEA J130810.53-254728.0 | q | 1.1 |
| 17.0442989 | 25.7919436 | SDSS J010810.62+254730.9 | Q | 1.843 | |
| (65) | 47.3495546 | −25.1085428 | WISEA J030923.89-250630.5 | q | 1 |
| 227.3495813 | 25.1081434 | SDSS J150923.90+250629.2 | q | 1.8 | |
| (66) | 31.4573892 | −24.8735666 | WISEA J020549.77-245224.7 | q | 0.3 |
| 211.4572001 | 24.8742878 | SDSS J140549.72+245227.4 | QX | 0.93 | |
| (67) | 48.9227 | −24.5943481 | WISEA J031541.43-243539.7 | qR | 1 |
| 228.9221526 | 24.5946659 | SDSS J151541.31+243540.7 | Q | 3.21 | |
| (68) | 314.8735964 | −23.9469948 | WISEA J205929.66-235649.1 | q | 0.4 |
| 134.8731466 | 23.946707 | SDSS J085929.56+235648.1 | Q | 1.085 | |
| (69) | 211.3857165 | −23.9417462 | WISEA J140532.57-235630.1 | q | 2.3 |
| 31.3864591 | 23.9416464 | SDSS J020532.75+235629.9 | Q | 2.005 | |
| (70) | 9.3024771 | −23.7730802 | SDSS J003712.58-234622.9 | q | 1.7 |
| 189.3025669 | 23.7724481 | SDSS J123712.61+234620.8 | Q | 2.644 | |
| (71) | 55.1065124 | −23.5058167 | WISEA J034025.56-233020.9 | q | 2.5 |
| 235.1074677 | 23.5059795 | SDSS J154025.79+233021.5 | q | 0.1 | |
| (72) | 325.6254779 | −23.1632401 | WISEA J214230.10-230947.5 | q | 0.9 |
| 145.6252854 | 23.1622808 | SDSS J094230.07+230944.1 | q | 1.4 | |
| (73) | 40.1013553 | −23.0486453 | J024024.32-230255.1 | X | |
| 220.1017934 | 23.0486683 | SDSS J144024.43+230255.2 | q | 1.6 | |
| (74) | 330.2260385 | −23.0089209 | WISEA J220054.23-230032.0 | q | 0.6 |
| 150.2259947 | 23.0087942 | SDSS J100054.23+230031.6 | Q | 3.027 | |
| (75) | 15.629173 | −22.6311972 | WISEA J010230.99-223752.2 | qR | 1.9 |
| 195.6286965 | 22.6311474 | SDSS J130230.88+223752.2 | Q | 3.405 | |
| (76) | 152.8034904 | −22.2785203 | WISEA J101112.84-221642.2 | qR | 0.4 |
| 332.802887 | 22.2781582 | SDSS J221112.69+221641.3 | q | 0 | |
| (77) | 181.1233682 | −21.9598988 | WISEA J120429.60-215735.5 | q | 0.8 |
| 1.1237153 | 21.9600067 | WISEA J000429.68+215736.0 | q | 1.4 | |
| (78) | 69.293922 | −21.9055291 | WISEA J043710.51-215420.2 | q | 0.7 |
| 249.293937 | 21.9045811 | SDSS J163710.55+215416.4 | Q | 1.411 | |
| (79) | 199.0397778 | −21.5273612 | J131609.54-213138.5 | R | |
| 19.0390736 | 21.5264408 | SDSS J011609.37+213135.1 | Q | 2.088 | |
| (80) | 22.013869 | −20.8937502 | SDSS J012803.33-205337.4 | q | 1.6 |
| 202.0134583 | 20.8942223 | SDSS J132803.22+205339.2 | q | 0.3 | |
| (81) | 341.8649478 | −20.6885193 | WISEA J224727.58-204119.2 | q | 1.2 |
| 161.8640315 | 20.6894371 | SDSS J104727.36+204121.9 | Q | 2.262 | |
| (82) | 347.9339167 | −20.5751112 | J231144.14-203430.4 | R | |
| 167.9335297 | 20.5758125 | SDSS J111144.05+203432.9 | q | 0 | |
| (83) | 191.7714081 | −20.2647247 | SDSS J124705.13-201553.0 | q | 0.3 |
| 11.7713099 | 20.2641487 | SDSS J004705.11+201550.9 | q | 4.5 | |
| (84) | 29.9053228 | −19.4208582 | WISEA J015937.24-192514.6 | q | 0.3 |
| 209.9044189 | 19.4200344 | SDSS J135937.06+192512.1 | q | 0 | |
| (85) | 315.432881 | −19.3894197 | WISEA J210143.86-192321.5 | q | 1.8 |
| 135.4334805 | 19.3888631 | SDSS J090144.03+192319.9 | q | 1.4 | |
| (86) | 315.2686772 | −19.0978465 | WISEA J210104.48-190552.1 | q | 1.1 |
| 135.2689056 | 19.0972805 | SDSS J090104.53+190550.2 | q | 0.4 | |
| (87) | 331.1935682 | −18.7863235 | QSM3:36 | QX | 0.873 |
| 151.1930394 | 18.7867023 | SDSS J100446.32+184712.1 | q | 1.5 | |
| (88) | 190.1060207 | −18.3141455 | WISEA J124025.44-181851.0 | q | 0.3 |
| 10.105106 | 18.314339 | SDSS J004025.23+181851.6 | Q | 1.156 | |
| (89) | 60.4473986 | −18.154863 | WISEA J040147.38-180917.4 | q | 0.4 |
| 240.4484093 | 18.1550387 | WISEA J160147.61+180917.7 | q | 0.8 | |
| (90) | 191.2945552 | −18.1478667 | WISEA J124510.71-180851.9 | q | 1.5 |
| 11.2945118 | 18.1480237 | SDSS J004510.68+180852.8 | Q | 2.955 | |
| (91) | 173.7006562 | −18.0690647 | WISEA J113448.15-180408.7 | q | 2.3 |
| 353.7006507 | 18.0682592 | SDSS J233448.15+180405.7 | Q | 2.881 | |
| (92) | 24.9069328 | −17.90944 | SDSS J013937.65-175434.1 | qX | 2 |
| 204.9072341 | 17.910056 | SDSS J133937.73+175436.2 | q | 1.3 | |
| (93) | 352.4344723 | −17.8641457 | WISEA J232944.27-175150.9 | q | 1.3 |
| 172.4351845 | 17.8639806 | SDSS J112944.45+175150.4 | q | 3.3 | |
| (94) | 16.7804723 | −17.6221112 | J010707.31-173719.6 | X | |
| 196.7801056 | 17.6227665 | SDSS J130707.22+173721.9 | q | 0 | |
| (95) | 29.9174996 | −17.2967528 | SDSS J015940.19-171747.7 | q | 0.9 |
| 209.9180908 | 17.2973289 | SDSS J135940.34+171750.3 | q | 1.8 | |
| (96) | 166.796621 | −17.1482174 | SDSS J110711.18-170853.6 | q | 1.1 |
| 346.7956543 | 17.1488914 | SDSS J230710.95+170856.0 | q | 1.1 | |
| (97) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 | |
| (98) | 354.8260594 | −16.8908891 | WISEA J233918.25-165327.1 | q | 1.5 |
| 174.8269911 | 16.8898926 | SDSS J113918.48+165323.6 | N | 0.062 | |
| (99) | 165.3264823 | −16.8833416 | SDSS J110118.35-165300.0 | q | 2 |
| 345.3268127 | 16.8840275 | SDSS J230118.43+165302.4 | q | 0.9 | |
| (100) | 43.6272916 | −16.2718962 | SDSS J025430.54-161618.8 | q | 0.3 |
| 223.6267804 | 16.2723981 | SDSS J145430.42+161620.6 | N | 0.158 | |
| (101) | 310.9503012 | −16.1176807 | SDSS J204348.07-160703.6 | q | 2.1 |
| 130.9494101 | 16.1168221 | SDSS J084347.85+160700.5 | q | 0.5 | |
| (102) | 352.1153529 | −16.006742 | WISEA J232827.67-160024.4 | q | 0.8 |
| 172.1161957 | 16.0070877 | SDSS J112827.88+160025.5 | q | 3.1 | |
| (103) | 149.4813563 | −15.5088164 | WISEA J095755.52-153031.8 | q | 2.2 |
| 329.4811707 | 15.5078583 | SDSS J215755.48+153028.2 | q | 0.8 | |
| (104) | 5.3051921 | −14.5195128 | SDSS J002113.24-143110.2 | q | 2 |
| 185.3048056 | 14.5204167 | J122113.15+143113.5 | X | ||
| (105) | 310.7940674 | −14.2887297 | SDSS J204310.57-141719.4 | q | 4.1 |
| 130.7950205 | 14.2880621 | SDSS J084310.80+141717.0 | Q | 0.887 | |
| (106) | 321.3724784 | −14.2055432 | WISEA J212529.39-141219.9 | q | 1 |
| 141.3732103 | 14.2057221 | SDSS J092529.57+141220.5 | A | 0.473 | |
| (107) | 335.04035 | −13.9567208 | J222009.68-135724.1 | R | |
| 155.0393304 | 13.9561601 | WISEA J102009.42+135722.3 | q | 1.2 | |
| (108) | 225.2865096 | −13.8267692 | WISEA J150108.76-134935.8 | q | 1.8 |
| 45.2857528 | 13.8264077 | WISEA J030108.57+134935.1 | q | 0.7 | |
| (109) | 22.4869537 | −13.2917978 | WISEA J012956.87-131730.2 | q | 1.6 |
| 202.4875051 | 13.2909737 | SDSS J132957.00+131727.5 | Q | 3.144 | |
| (110) | 190.3695441 | −13.095317 | SDSS J124128.69-130543.1 | q | 0.6 |
| 10.3688927 | 13.0956669 | SDSS J004128.53+130544.4 | q | 0.4 | |
| (111) | 178.5013735 | −12.8384611 | WISEA J115400.32-125018.4 | q | 0.9 |
| 358.501349 | 12.8377738 | SDSS J235400.32+125015.9 | q | 1.7 | |
| (112) | 56.1097236 | −12.7916261 | WISEA J034426.33-124729.7 | q | 0.3 |
| 236.109024 | 12.7923546 | SDSS J154426.16+124732.4 | q | 0.5 | |
| (113) | 39.5398838 | −11.856346 | WISEA J023809.57-115122.9 | q | 1.1 |
| 219.5404339 | 11.8565365 | SDSS J143809.70+115123.5 | q | 1.1 | |
| (114) | 304.7146082 | −11.8357393 | SDSS J201851.51-115008.7 | q | 3 |
| 124.7154201 | 11.8347625 | SDSS J081851.70+115005.1 | Q | 3.092 | |
| (115) | 18.0162381 | −10.9062962 | SDSS J011203.89-105422.6 | q | 1.9 |
| 198.0161728 | 10.9057355 | SDSS J131203.88+105420.7 | q | 0.8 | |
| (116) | 9.0308609 | −10.8671694 | SDSS J003607.40-105201.8 | q | 0 |
| 189.0314246 | 10.867996 | SDSS J123607.54+105204.8 | q | 1.4 | |
| (117) | 33.4777451 | −10.6369173 | SDSS J021354.65-103812.8 | q | 1.7 |
| 213.4776649 | 10.6378738 | SDSS J141354.63+103816.3 | q | 2.1 | |
| (118) | 24.1238435 | −10.5259013 | SDSS J013629.72-103133.2 | q | 2.3 |
| 204.1232718 | 10.5261989 | SDSS J133629.58+103134.3 | QX | 2.83 | |
| (119) | 4.7525 | −10.4661945 | J001900.60-102758.3 | X | |
| 184.7530212 | 10.4664478 | SDSS J121900.72+102759.2 | q | 0.3 | |
| (120) | 3.1000975 | −10.3740423 | FIRST J0012-1022 | QRX | 0.228 |
| 183.0995052 | 10.3736727 | SDSS J121223.88+102225.2 | q | 1.8 | |
| (121) | 334.8985316 | −9.69364 | SDSS J221935.64-094137.1 | q | 2 |
| 154.8980454 | 9.6929715 | SDSS J101935.52+094134.7 | Q | 2.313 | |
| (122) | 38.5649712 | −9.3922666 | SDSS J023415.59-092332.0 | Q | 3.159 |
| 218.5647491 | 9.3927159 | SDSS J143415.53+092333.7 | Q | 1.796 | |
| (123) | 140.4377101 | −9.3709292 | WISEA J092145.05-092215.4 | q | 0.8 |
| 320.4374695 | 9.3712921 | SDSS J212144.99+092216.6 | q | 1.2 | |
| (124) | 158.5661086 | −9.1451916 | WISEA J103415.86-090842.6 | q | |
| 338.56533 | 9.1442883 | SDSS J223415.68+090839.5 | q | 1.6 | |
| (125) | 37.7328056 | −9.0068612 | J023055.87-090024.7 | X | |
| 217.7330967 | 9.0059802 | SDSS J143055.94+090021.5 | Q | 2.383 | |
| (126) | 30.7570701 | −8.6899451 | SDSS J020301.69-084123.8 | q | 2.2 |
| 210.757843 | 8.6908655 | SDSS J140301.88+084127.1 | q | 0 | |
| (127) | 59.3881301 | −8.5115865 | WISEA J035733.19-083041.3 | q | 0.3 |
| 239.388068 | 8.511933 | SDSS J155733.13+083042.9 | A | 0.047 | |
| (128) | 358.0582864 | −8.2121914 | SDSS J235213.99-081244.0 | q | 2 |
| 178.0589787 | 8.211923 | SDSS J115214.15+081242.8 | q | 1.1 | |
| (129) | 338.7737732 | −8.142704 | SDSS J223505.70-080833.7 | q | 0.4 |
| 158.773734 | 8.1430363 | SDSS J103505.69+080834.9 | q | 0.9 | |
| (130) | 332.3883082 | −7.9754252 | SDSS J220933.20-075831.4 | q | 2 |
| 152.3875951 | 7.9759758 | SDSS J100933.02+075833.4 | Q | 2.532 | |
| (131) | 9.7862066 | −7.7658426 | SDSS J003908.70-074557.1 | q | 1.7 |
| 189.7870789 | 7.765204 | SDSS J123908.89+074554.7 | q | 0.3 | |
| (132) | 47.6100042 | −7.6891097 | SDSS J031026.40-074120.8 | q | 1.6 |
| 227.6091204 | 7.6900591 | AX J1510+0742 | AX | 0.459 | |
| (133) | 16.9498272 | −7.6777906 | SDSS J010747.95-074040.0 | q | 1 |
| 196.9504416 | 7.6768407 | WISEA J130748.10+074036.6 | q | 0.1 | |
| (134) | 25.2191067 | −7.6683216 | SDSS J014052.58-074005.9 | q | 0 |
| 205.2184797 | 7.668935 | SDSS J134052.43+074008.1 | Q | 1.077 | |
| (135) | 46.2892799 | −7.2429566 | SDSS J030509.42-071434.6 | q | 0.5 |
| 226.2901611 | 7.2421827 | SDSS J150509.63+071431.8 | q | 1 | |
| (136) | 42.2919481 | −7.135162 | SDSS J024910.06-070806.6 | Q | 2.561 |
| 222.2917609 | 7.1344065 | SDSS J144910.02+070803.8 | q | 1.5 | |
| (137) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | |
| (138) | 328.3192139 | −6.7707705 | SDSS J215316.61-064614.7 | q | 1.7 |
| 148.3194775 | 6.7699293 | SDSS J095316.66+064611.7 | Q | 1.092 | |
| (139) | 209.4759723 | −6.7408847 | SDSS J135754.23-064427.1 | q | 1.7 |
| 29.4751402 | 6.7413482 | LAMOSTJ015754.04+064428.9 | Q | 1.565 | |
| (140) | 28.0452862 | −6.7327127 | SDSS J015210.86-064357.7 | q | 0.4 |
| 208.0451896 | 6.732888 | SDSS J135210.84+064358.3 | q | 1.6 | |
| (141) | 310.9553801 | −6.521875 | SDSS J204349.29-063118.7 | q | 2.2 |
| 130.9551195 | 6.521617 | SDSS J084349.22+063117.8 | q | 1.1 | |
| (142) | 10.7848358 | −6.4319367 | SDSS J004308.36-062554.9 | q | 0.7 |
| 190.7848032 | 6.4326671 | SDSS J124308.35+062557.6 | q | 2.2 | |
| (143) | 17.3667355 | −6.3337412 | SDSS J010928.01-062001.4 | q | 0.3 |
| 197.3658023 | 6.3341348 | WISEA J130927.78+062002.7 | q | 1.4 | |
| (144) | 42.0314865 | −6.0404835 | SDSS J024807.55-060225.7 | q | 1.1 |
| 222.031267 | 6.0407225 | SDSS J144807.50+060226.5 | Q | 2.324 | |
| (145) | 155.888588 | −5.987767 | WISEA J102333.26-055915.9 | q | 1 |
| 335.8882692 | 5.9887381 | WISEA J222333.18+055919.4 | q | 0.8 | |
| (146) | 30.4249489 | −5.8591802 | VIPERS 101146840 | Q | 2.126 |
| 210.4239741 | 5.858464 | SDSS J140141.75+055130.4 | q | 1.1 | |
| (147) | 345.5845337 | −5.7119699 | SDSS J230220.28-054243.0 | q | 5.5 |
| 165.5838875 | 5.7116443 | SDSS J110220.13+054242.0 | q | 1.2 | |
| (148) | 38.2399412 | −5.2320188 | SDSS J023257.58-051355.2 | Q | 3.458 |
| 218.2393005 | 5.2315766 | MS 14304+0527 | QX | 0.2 | |
| (149) | 318.9673157 | −5.08287 | SDSS J211552.15-050458.3 | q | 0.4 |
| 138.967392 | 5.0823555 | SDSS J091552.17+050456.4 | q | 0.6 | |
| (150) | 2.9218395 | −4.9358745 | SDSS J001141.24-045609.1 | q | 3.1 |
| 182.9209776 | 4.9351431 | SDSS J121141.03+045606.5 | q | 2 | |
| (151) | 339.1091419 | −4.9108333 | SDSS J223626.19-045438.9 | q | 1.6 |
| 159.1097246 | 4.9101383 | Q 1033+051 | Q | 1.048 | |
| (152) | 44.1149634 | −4.8954605 | SDSS J025627.59-045343.6 | Q | 1.645 |
| 224.1147795 | 4.8951414 | SDSS J145627.54+045342.5 | q | 0.4 | |
| (153) | 318.953949 | −4.8887081 | SDSS J211548.94-045319.3 | q | 0.5 |
| 138.9544497 | 4.8892847 | LAMOSTJ091549.07+045321.5 | Q | 1.974 | |
| (154) | 11.8971845 | −4.6937364 | SDSS J004735.33-044137.5 | Q | 1.931 |
| 191.8971312 | 4.6943342 | SDSS J124735.31+044139.5 | Q | 0.868 | |
| (155) | 215.4113925 | −4.6316734 | WISEA J142138.70-043753.9 | q | 1.5 |
| 35.4120872 | 4.6310081 | SDSS J022138.89+043751.6 | Q | 2.018 | |
| (156) | 44.1504799 | −4.5690993 | SDSS J025636.11-043408.8 | Q | 3.094 |
| 224.1496194 | 4.5693052 | WISEA J145635.91+043409.4 | q | 1.9 | |
| (157) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | |
| (158) | 313.1420516 | −4.4458056 | WISEA J205234.08-042644.8 | q | 2.3 |
| 133.1429183 | 4.4466583 | SDSS J085234.29+042648.0 | Q | 2.745 | |
| (159) | 28.6933545 | −3.9445188 | SDSS J015446.40-035640.2 | Q | 2.322 |
| 208.6934509 | 3.9447002 | SDSS J135446.42+035640.9 | q | 0.8 | |
| (160) | 190.871543 | −3.9282525 | SDSS J124329.17-035541.7 | qR | 2.2 |
| 10.8722192 | 3.9287007 | SDSS J004329.33+035543.2 | q | 0.1 | |
| (161) | 36.0865531 | −3.5906219 | SDSS J022420.77-033526.2 | QX | 0.552 |
| 216.0868377 | 3.5907531 | SDSS J142420.83+033526.7 | q | 1.8 | |
| (162) | 23.3642954 | −3.508162 | SDSS J013327.43-033029.3 | Q | 1.724 |
| 203.3644091 | 3.5075679 | SDSS J133327.45+033027.2 | q | 1 | |
| (163) | 342.6967773 | −3.4136071 | SDSS J225047.22-032448.9 | q | 1.3 |
| 162.6963654 | 3.4144416 | SDSS J105047.12+032451.9 | q | 0.3 | |
| (164) | 29.2919507 | −3.3900862 | SDSS J015710.06-032324.3 | Q | 1.504 |
| 209.2925571 | 3.3891148 | WISEA J135710.20+032320.9 | q | 0.7 | |
| (165) | 351.8889506 | −3.1861348 | SDSS J232733.34-031109.9 | q | 2.6 |
| 171.889383 | 3.186412 | SDSS J112733.45+031111.0 | q | ||
| (166) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | Q | 2.173 | |
| (167) | 59.7010545 | −3.0252538 | WISEA J035848.22-030131.3 | q | 0.9 |
| 239.7015228 | 3.0244355 | SDSS J155848.36+030127.9 | q | 1 | |
| (168) | 357.4388055 | −2.8983433 | SDSS J234945.32-025354.0 | Q | 0.938 |
| 177.4378903 | 2.899283 | SDSS J114945.07+025357.3 | q | 1.5 | |
| (169) | 316.7376204 | −2.8595332 | WISEA J210657.03-025134.3 | q | 1.5 |
| 136.7379203 | 2.8594311 | SDSS J090657.10+025133.9 | A | 0.194 | |
| (170) | 11.9639927 | −2.8499138 | SDSS J004751.36-025059.6 | Q | 1.262 |
| 191.9631892 | 2.849156 | SDSS J124751.16+025056.9 | Q | 1.568 | |
| (171) | 323.6482118 | −2.7731332 | SDSS J213435.57-024623.2 | Q | 3.228 |
| 143.6486958 | 2.7735964 | SDSS J093435.68+024624.9 | Q | 0.763 | |
| (172) | 31.1501826 | −2.6833719 | SDSS J020436.04-024100.0 | Q | 2.149 |
| 211.1496969 | 2.6833621 | SDSS J140435.92+024100.1 | q | 0.4 | |
| (173) | 11.428722 | −2.6318303 | SDSS J004542.89-023754.5 | q | 1 |
| 191.4280252 | 2.6316203 | WISEA J124542.71+023753.8 | qX | 0.7 | |
| (174) | 9.1659024 | −2.4347542 | SDSS J003639.81-022604.9 | Q | 1.055 |
| 189.165748 | 2.4344829 | SDSS J123639.77+022604.1 | q | 2 | |
| (175) | 17.5345544 | −2.4323457 | SDSS J011008.29-022556.4 | Q | 1.068 |
| 197.5339023 | 2.4329717 | SDSS J131008.13+022558.6 | q | 1.6 | |
| (176) | 145.7966766 | −2.4094768 | SDSS J094311.20-022434.1 | q | 0.9 |
| 325.7966554 | 2.410309 | SDSS J214311.19+022437.1 | q | 1.2 | |
| (177) | 73.1702424 | −2.260853 | WISEA J045240.88-021539.0 | q | 2.4 |
| 253.170835 | 2.2612845 | J165241.00+021540.6 | X | ||
| (178) | 181.200555 | −2.225128 | 2QZ J120448.1-021331 | Q | 0.888 |
| 1.2006668 | 2.2249101 | SDSS J000448.16+021329.6 | q | 1.2 | |
| (179) | 21.4036505 | −2.1947235 | SDSS J012536.87-021141.0 | Q | 2.542 |
| 201.4034175 | 2.1940664 | SDSS J132536.82+021138.6 | q | 1.2 | |
| (180) | 172.9620056 | −2.1642234 | SDSS J113150.88-020951.2 | q | 0.9 |
| 352.9627548 | 2.1647976 | SDSS J233151.04+020953.2 | q | 1.4 | |
| (181) | 221.5816508 | −2.0546804 | 2QZ J144619.5-020317 | Q | 1.021 |
| 41.5820598 | 2.0548802 | SDSS J024619.69+020317.5 | Q | 1.611 | |
| (182) | 42.9641686 | −1.8095775 | SDSS J025151.40-014834.4 | Q | 1.943 |
| 222.9651434 | 1.8088515 | SDSS J145151.63+014831.8 | q | 0.6 | |
| (183) | 325.6085362 | −1.7636978 | SDSS J214226.05-014549.2 | q | 1.4 |
| 145.6089432 | 1.7631901 | SDSS J094226.14+014547.5 | Q | 2.335 | |
| (184) | 133.334329 | −1.6598129 | SDSS J085320.23-013935.3 | qX | 1.4 |
| 313.3345032 | 1.6590253 | SDSS J205320.28+013932.4 | q | 0.1 | |
| (185) | 14.2851195 | −1.5772589 | SDSS J005708.42-013438.1 | Q | 1.329 |
| 194.2848358 | 1.5782201 | SDSS J125708.36+013441.5 | qX | 0.8 | |
| (186) | 316.4041208 | −1.4412537 | SDSS J210536.98-012628.4 | q | 2 |
| 136.4042816 | 1.4411682 | SDSS J090537.02+012628.2 | q | 0 | |
| (187) | 36.4121461 | −1.4221784 | SDSS J022538.91-012519.8 | Q | 0.727 |
| 216.412656 | 1.4224802 | 2QZ J142539.0+012521 | Q | 1.136 | |
| (188) | 179.9376714 | −1.3721402 | 2QZ J115945.0-012220 | Q | 1.275 |
| 359.9384294 | 1.3712088 | SDSS J235945.22+012216.3 | Q | 1.222 | |
| (189) | 309.459063 | −1.3256484 | J203750.17-011932.3 | X | |
| 129.4598151 | 1.3266144 | SDSS J083750.35+011935.7 | q | 2.5 | |
| (190) | 169.1804623 | −1.2787242 | SDSS J111643.31-011643.4 | Q | 0.878 |
| 349.1801163 | 1.2778387 | SDSS J231643.23+011640.2 | qX | 2.1 | |
| (191) | 40.8886891 | −1.1553956 | SDSS J024333.28-010919.3 | Q | 2.265 |
| 220.889267 | 1.1561131 | SDSS J144333.42+010922.0 | q | 1.5 | |
| (192) | 181.0820052 | −1.1238078 | J120419.68-010725.7 | X | |
| 1.0822232 | 1.1242868 | SDSS J000419.73+010727.4 | Q | 2.086 | |
| (193) | 322.0407105 | −1.1103891 | 2SLAQ J212809.77-010637.4 | Q | 2.016 |
| 142.0406886 | 1.109918 | SDSS J092809.76+010635.6 | Q | 0.691 | |
| (194) | 323.8986908 | −1.1047641 | SDSS J213535.68-010617.1 | q | 0.1 |
| 143.898949 | 1.1039692 | SDSS J093535.74+010614.2 | q | 1.4 | |
| (195) | 359.5996406 | −1.1012612 | SDSS J235823.91-010604.5 | A | 0.172 |
| 179.5999641 | 1.1017779 | SDSS J115823.98+010606.4 | q | 1.1 | |
| (196) | 333.6993254 | −1.0151735 | SDSS J221447.83-010054.6 | q | 2.1 |
| 153.700119 | 1.0157703 | SDSS J101448.02+010056.7 | q | 0.4 | |
| (197) | 191.5187354 | −0.947775 | 2QZ J124604.4-005652 | Q | 1.74 |
| 11.5188728 | 0.9486683 | SDSS J004604.52+005655.1 | Q | 2.394 | |
| (198) | 136.812282 | −0.9465473 | WISEA J090714.94-005647.5 | q | 0.4 |
| 316.8128149 | 0.9471022 | SDSS J210715.08+005649.5 | q | 0.6 | |
| (199) | 335.2752368 | −0.9282428 | SDSS J222106.05-005541.6 | Q | 2.32 |
| 155.27575 | 0.92775 | 2QZ J102106.1+005539 | K | 0.246 | |
| (200) | 322.1036971 | −0.8306041 | SDSS J212824.88-004950.1 | q | 3.8 |
| 142.1045748 | 0.8311082 | SDSS J092825.09+004951.9 | Q | 0.85 | |
| (201) | 318.5432739 | −0.6772609 | SDSS J211410.38-004038.1 | q | 1 |
| 138.5425553 | 0.6770332 | SDSS J091410.21+004037.3 | q | 2.2 | |
| (202) | 149.5630798 | −0.6754175 | LAMOSTJ095815.14-004031.4 | Q | 0.954 |
| 329.5624984 | 0.6744513 | SDSS J215814.99+004028.0 | q | 3.6 | |
| (203) | 176.6971288 | −0.6466236 | SDSS J114647.31-003847.8 | q | 1.6 |
| 356.6970072 | 0.6459298 | SDSS J234647.28+003845.3 | q | 3.2 | |
| (204) | 10.1452528 | −0.6391804 | SDSS J004034.86-003821.0 | Q | 1.836 |
| 190.1442813 | 0.638343 | 2QZ J124034.6+003816 | Q | 1.856 | |
| (205) | 322.7183019 | −0.5829681 | SDSS J213052.39-003458.6 | Q | 2.654 |
| 142.7177224 | 0.5830358 | PKS 0928+008 | QRX | 1.769 | |
| (206) | 321.3839569 | −0.535798 | SDSS J212532.14-003208.8 | q | 3.6 |
| 141.3843083 | 0.5359621 | 2SLAQ J092532.23+003209.5 | Q | 1.451 | |
| (207) | 359.9532206 | −0.5350152 | SDSS J235948.77-003206.0 | Q | 1.443 |
| 179.9524587 | 0.5345278 | 2QZ J115948.5+003203 | Q | 2.27 | |
| (208) | 328.4185019 | −0.4744671 | SDSS J215340.44-002828.0 | q | 4.7 |
| 148.4176331 | 0.4748041 | SDSS J095340.23+002829.2 | q | 2 | |
| (209) | 158.5922393 | −0.4348561 | 2SLAQ J103422.14-002605.5 | Q | 1.161 |
| 338.5917053 | 0.434891 | SDSS J223422.00+002605.6 | qR | 0.1 | |
| (210) | 348.1098247 | −0.4195352 | 2SLAQ J231226.35-002510.3 | Q | 1.105 |
| 168.1100567 | 0.4190823 | 2QZ J111226.3+002508 | Q | 1.309 | |
| (211) | 44.7576857 | −0.2819373 | SDSS J025901.84-001654.9 | Q | 1.406 |
| 224.7571 | 0.2811774 | 2SLAQ J145901.70+001652.2 | Q | 1.58 | |
| (212) | 358.9575115 | −0.2437697 | SDSS J235549.80-001437.5 | q | 1.3 |
| 178.9582363 | 0.243 | SDSS J115549.97+001434.7 | q | 1.2 | |
| (213) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | Q | 0.284 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 | |
| (214) | 182.3428955 | −0.097823 | SDSS J120922.29-000552.1 | q | 0.3 |
| 2.3425216 | 0.098785 | SDSS J000922.19+000555.6 | Q | 1.99 | |
| (215) | 321.2974555 | −0.0852931 | 2SLAQ J212511.38-000507.0 | Q | 2.308 |
| 141.2979338 | 0.08586 | 2SLAQ J092511.51+000509.0 | Q | 2.698 | |
| (216) | 314.6144714 | −0.0745742 | SDSS J205827.47-000428.4 | q | 1.2 |
| 134.6143136 | 0.073984 | SDSS J085827.43+000426.3 | q | 2 | |
| (217) | 309.3637298 | −0.0379301 | SDSS J203727.29-000216.5 | q | 2.1 |
| 129.3627777 | 0.037032 | SDSS J083727.06+000213.3 | q | 0.6 | |
| (218) | 9.8680615 | −0.0269525 | 2SLAQ J003928.32-000137.0 | Q | 2.478 |
| 189.8671854 | 0.0272719 | SDSS J123928.12+000138.1 | q | 0.6 | |
| (219) | 129.7712982 | −0.0251763 | SDSS J083905.11-000130.6 | Q | 2.511 |
| 309.7715133 | 0.0243675 | SDSS J203905.16+000127.7 | q | 2.5 |
| Ra | Dec | Name | Descrip | Z | |
|---|---|---|---|---|---|
| (1) | 315.7673595 | −76.3736026 | WISEA J210304.14-762224.9 | q | 1 |
| 135.7683983 | 76.3734303 | WISEA J090304.41+762224.0 | q | 2.4 | |
| (2) | 80.7328764 | −52.4533568 | WISEA J052255.89-522712.0 | q | |
| 260.732699 | 52.4532957 | SDSS J172255.84+522712.0 | q | 2.1 | |
| (3) | 70.1774106 | −49.1605048 | WISEA J044042.58-490937.9 | q | 0.9 |
| 250.1779433 | 49.1604959 | SDSS J164042.70+490937.7 | q | 3.2 | |
| (4) | 312.4572617 | −43.5311298 | WISEA J204949.73-433151.7 | q | 1.7 |
| 132.4578712 | 43.5314134 | SDSS J084949.88+433153.1 | q | 2.6 | |
| (5) | 58.8593889 | −42.1836389 | J035526.25-421101.1 | X | |
| 238.859031 | 42.1833947 | SDSS J155526.16+421100.1 | Q | 1.222 | |
| (6) | 75.7744245 | −40.7936211 | WISEA J050305.91-404736.8 | q | 2.3 |
| 255.7743683 | 40.7937126 | SDSS J170305.84+404737.3 | q | 0.3 | |
| (7) | 5.4863222 | −36.9636832 | WISEA J002156.72-365749.2 | q | 1.6 |
| 185.4861944 | 36.9634266 | SDSS J122156.67+365748.3 | Q | 2.097 | |
| (8) | 48.2374301 | −35.2506342 | WISEA J031256.97-351502.2 | qX | 1.9 |
| 228.2368457 | 35.250557 | SDSS J151256.83+351502.0 | q | 1.3 | |
| (9) | 64.4053066 | −34.4443255 | WISEA J041737.25-342639.2 | q | 2.3 |
| 244.4049248 | 34.4447566 | SDSS J161737.18+342641.1 | q | 1.9 | |
| (10) | 24.818008 | −32.6980218 | WISEA J013916.33-324152.7 | q | 1.6 |
| 204.8176575 | 32.6980515 | SDSS J133916.23+324152.9 | q | 0 | |
| (11) | 178.0274651 | −31.4001968 | WISEA J115206.58-312400.4 | q | 2.4 |
| 358.026947 | 31.4004002 | SDSS J235206.46+312401.4 | q | 1 | |
| (12) | 341.9315476 | −31.0519246 | 6QZ J224743.5-310306 | Q | 2.614 |
| 161.9314813 | 31.0522394 | SDSS J104743.55+310308.0 | q | 0 | |
| (13) | 300.1895832 | −30.1375161 | WISEA J200045.51-300814.8 | q | 0.6 |
| 120.1898279 | 30.1370937 | SDSS J080045.55+300813.5 | Q | 1.343 | |
| (14) | 12.3530442 | −29.9213175 | Q 0046-3011 | Q | 1.081 |
| 192.3529914 | 29.9214458 | SDSS J124924.71+295517.2 | q | 2.2 | |
| (15) | 47.3495546 | −25.1085428 | WISEA J030923.89-250630.5 | q | 1 |
| 227.3495813 | 25.1081434 | SDSS J150923.90+250629.2 | q | 1.8 | |
| (16) | 48.9227 | −24.5943481 | WISEA J031541.43-243539.7 | qR | 1 |
| 228.9221526 | 24.5946659 | SDSS J151541.31+243540.7 | Q | 3.21 | |
| (17) | 314.8735964 | −23.9469948 | WISEA J205929.66-235649.1 | q | 0.4 |
| 134.8731466 | 23.946707 | SDSS J085929.56+235648.1 | Q | 1.085 | |
| (18) | 40.1013553 | −23.0486453 | J024024.32-230255.1 | X | |
| 220.1017934 | 23.0486683 | SDSS J144024.43+230255.2 | q | 1.6 | |
| (19) | 330.2260385 | −23.0089209 | WISEA J220054.23-230032.0 | q | 0.6 |
| 150.2259947 | 23.0087942 | SDSS J100054.23+230031.6 | Q | 3.027 | |
| (20) | 15.629173 | −22.6311972 | WISEA J010230.99-223752.2 | qR | 1.9 |
| 195.6286965 | 22.6311474 | SDSS J130230.88+223752.2 | Q | 3.405 | |
| (21) | 181.1233682 | −21.9598988 | WISEA J120429.60-215735.5 | q | 0.8 |
| 1.1237153 | 21.9600067 | WISEA J000429.68+215736.0 | q | 1.4 | |
| (22) | 22.013869 | −20.8937502 | SDSS J012803.33-205337.4 | q | 1.6 |
| 202.0134583 | 20.8942223 | SDSS J132803.22+205339.2 | q | 0.3 | |
| (23) | 191.2945552 | −18.1478667 | WISEA J124510.71-180851.9 | q | 1.5 |
| 11.2945118 | 18.1480237 | SDSS J004510.68+180852.8 | Q | 2.955 | |
| (24) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 | |
| (25) | 38.5649712 | −9.3922666 | SDSS J023415.59-092332.0 | Q | 3.159 |
| 218.5647491 | 9.3927159 | SDSS J143415.53+092333.7 | Q | 1.796 | |
| (26) | 140.4377101 | −9.3709292 | WISEA J092145.05-092215.4 | q | 0.8 |
| 320.4374695 | 9.3712921 | SDSS J212144.99+092216.6 | q | 1.2 | |
| (27) | 59.3881301 | −8.5115865 | WISEA J035733.19-083041.3 | q | 0.3 |
| 239.388068 | 8.511933 | SDSS J155733.13+083042.9 | A | 0.047 | |
| (28) | 338.7737732 | −8.142704 | SDSS J223505.70-080833.7 | q | 0.4 |
| 158.773734 | 8.1430363 | SDSS J103505.69+080834.9 | q | 0.9 | |
| (29) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | |
| (30) | 28.0452862 | −6.7327127 | SDSS J015210.86-064357.7 | q | 0.4 |
| 208.0451896 | 6.732888 | SDSS J135210.84+064358.3 | q | 1.6 | |
| (31) | 310.9553801 | −6.521875 | SDSS J204349.29-063118.7 | q | 2.2 |
| 130.9551195 | 6.521617 | SDSS J084349.22+063117.8 | q | 1.1 | |
| (32) | 42.0314865 | −6.0404835 | SDSS J024807.55-060225.7 | q | 1.1 |
| 222.031267 | 6.0407225 | SDSS J144807.50+060226.5 | Q | 2.324 | |
| (33) | 44.1149634 | −4.8954605 | SDSS J025627.59-045343.6 | Q | 1.645 |
| 224.1147795 | 4.8951414 | SDSS J145627.54+045342.5 | q | 0.4 | |
| (34) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | |
| (35) | 28.6933545 | −3.9445188 | SDSS J015446.40-035640.2 | Q | 2.322 |
| 208.6934509 | 3.9447002 | SDSS J135446.42+035640.9 | q | 0.8 | |
| (36) | 36.0865531 | −3.5906219 | SDSS J022420.77-033526.2 | QX | 0.552 |
| 216.0868377 | 3.5907531 | SDSS J142420.83+033526.7 | q | 1.8 | |
| (37) | 351.8889506 | −3.1861348 | SDSS J232733.34-031109.9 | q | 2.6 |
| 171.889383 | 3.186412 | SDSS J112733.45+031111.0 | q | ||
| (38) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | Q | 2.173 | |
| (39) | 316.7376204 | −2.8595332 | WISEA J210657.03-025134.3 | q | 1.5 |
| 136.7379203 | 2.8594311 | SDSS J090657.10+025133.9 | A | 0.194 | |
| (40) | 323.6482118 | −2.7731332 | SDSS J213435.57-024623.2 | Q | 3.228 |
| 143.6486958 | 2.7735964 | SDSS J093435.68+024624.9 | Q | 0.763 | |
| (41) | 31.1501826 | −2.6833719 | SDSS J020436.04-024100.0 | Q | 2.149 |
| 211.1496969 | 2.6833621 | SDSS J140435.92+024100.1 | q | 0.4 | |
| (42) | 9.1659024 | −2.4347542 | SDSS J003639.81-022604.9 | Q | 1.055 |
| 189.165748 | 2.4344829 | SDSS J123639.77+022604.1 | q | 2 | |
| (43) | 181.200555 | −2.225128 | 2QZ J120448.1-021331 | Q | 0.888 |
| 1.2006668 | 2.2249101 | SDSS J000448.16+021329.6 | q | 1.2 | |
| (44) | 221.5816508 | −2.0546804 | 2QZ J144619.5-020317 | Q | 1.021 |
| 41.5820598 | 2.0548802 | SDSS J024619.69+020317.5 | Q | 1.611 | |
| (45) | 316.4041208 | −1.4412537 | SDSS J210536.98-012628.4 | q | 2 |
| 136.4042816 | 1.4411682 | SDSS J090537.02+012628.2 | q | 0 | |
| (46) | 181.0820052 | −1.1238078 | J120419.68-010725.7 | X | |
| 1.0822232 | 1.1242868 | SDSS J000419.73+010727.4 | Q | 2.086 | |
| (47) | 322.0407105 | −1.1103891 | 2SLAQ J212809.77-010637.4 | Q | 2.016 |
| 142.0406886 | 1.109918 | SDSS J092809.76+010635.6 | Q | 0.691 | |
| (48) | 321.3839569 | −0.535798 | SDSS J212532.14-003208.8 | q | 3.6 |
| 141.3843083 | 0.5359621 | 2SLAQ J092532.23+003209.5 | Q | 1.451 | |
| (49) | 348.1098247 | −0.4195352 | 2SLAQ J231226.35-002510.3 | Q | 1.105 |
| 168.1100567 | 0.4190823 | 2QZ J111226.3+002508 | Q | 1.309 | |
| (50) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | Q | 0.284 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 |
| Ra | Dec | Name | Descrip | Z | |
|---|---|---|---|---|---|
| (1) | 255.5777892 | −77.0249529 | WISEA J170218.69-770129.2 | q | 2.3 |
| 75.5809969 | 77.0255634 | WISEA J050219.24+770131.4 | q | 2.3 | |
| (2) | 2.3493535 | −75.4740875 | WISEA J000923.83-752826.7 | q | 0.8 |
| 182.3515932 | 75.4750181 | WISEA J120924.56+752830.2 | q | 0.7 | |
| (3) | 85.679027 | −68.1421484 | WISEA J054242.99-680831.9 | q | 1.4 |
| 265.6773749 | 68.1413691 | SDSS J174242.55+680829.1 | q | 1.5 | |
| (4) | 350.4801742 | −55.0232756 | XXLS J232155.23-550123.3 | QX | 1.788 |
| 170.4785659 | 55.0239884 | SDSS J112154.85+550126.3 | Q | 1.73 | |
| (5) | 2.4579845 | −53.9814555 | WISEA J000949.91-535853.2 | q | 0.2 |
| 182.4575348 | 53.980648 | SDSS J120949.80+535850.3 | q | 0.3 | |
| (6) | 348.3491422 | −53.3478756 | XXLS J231323.75-532051.9 | QX | 0.496 |
| 168.3507385 | 53.3479691 | SDSS J111324.17+532052.6 | q | 0.3 | |
| (7) | 52.3380705 | −33.1624587 | WISEA J032921.13-330944.7 | q | 1 |
| 232.3374622 | 33.1619242 | SDSS J152921.00+330942.9 | q | 0.9 | |
| (8) | 35.6523275 | −32.9501625 | WISEA J022236.55-325700.5 | q | 2 |
| 215.6517237 | 32.9500411 | SDSS J142236.40+325700.2 | q | 1.8 | |
| (9) | 166.796621 | −17.1482174 | SDSS J110711.18-170853.6 | q | 1.1 |
| 346.7956543 | 17.1488914 | SDSS J230710.95+170856.0 | q | 1.1 | |
| (10) | 43.6272916 | −16.2718962 | SDSS J025430.54-161618.8 | q | 0.3 |
| 223.6267804 | 16.2723981 | SDSS J145430.42+161620.6 | N | 0.158 | |
| (11) | 190.3695441 | −13.095317 | SDSS J124128.69-130543.1 | q | 0.6 |
| 10.3688927 | 13.0956669 | SDSS J004128.53+130544.4 | q | 0.4 | |
| (12) | 39.5398838 | −11.856346 | WISEA J023809.57-115122.9 | q | 1.1 |
| 219.5404339 | 11.8565365 | SDSS J143809.70+115123.5 | q | 1.1 | |
| (13) | 304.7146082 | −11.8357393 | SDSS J201851.51-115008.7 | q | 3 |
| 124.7154201 | 11.8347625 | SDSS J081851.70+115005.1 | Q | 3.092 | |
| (14) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | |
| (15) | 209.4759723 | −6.7408847 | SDSS J135754.23-064427.1 | q | 1.7 |
| 29.4751402 | 6.7413482 | LAMOSTJ015754.04+064428.9 | Q | 1.565 | |
| (16) | 155.888588 | −5.987767 | WISEA J102333.26-055915.9 | q | 1 |
| 335.8882692 | 5.9887381 | WISEA J222333.18+055919.4 | q | 0.8 | |
| (17) | 318.9673157 | −5.08287 | SDSS J211552.15-050458.3 | q | 0.4 |
| 138.967392 | 5.0823555 | SDSS J091552.17+050456.4 | q | 0.6 | |
| (18) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | |
| (19) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | Q | 2.173 | |
| (20) | 59.7010545 | −3.0252538 | WISEA J035848.22-030131.3 | q | 0.9 |
| 239.7015228 | 3.0244355 | SDSS J155848.36+030127.9 | q | 1 | |
| (21) | 179.9376714 | −1.3721402 | 2QZ J115945.0-012220 | Q | 1.275 |
| 359.9384294 | 1.3712088 | SDSS J235945.22+012216.3 | Q | 1.222 | |
| (22) | 136.812282 | −0.9465473 | WISEA J090714.94-005647.5 | q | 0.4 |
| 316.8128149 | 0.9471022 | SDSS J210715.08+005649.5 | q | 0.6 | |
| (23) | 10.1452528 | −0.6391804 | SDSS J004034.86-003821.0 | Q | 1.836 |
| 190.1442813 | 0.638343 | 2QZ J124034.6+003816 | Q | 1.856 | |
| (24) | 44.7576857 | −0.2819373 | SDSS J025901.84-001654.9 | Q | 1.406 |
| 224.7571 | 0.2811774 | 2SLAQ J145901.70+001652.2 | Q | 1.58 | |
| (25) | 358.9575115 | −0.2437697 | SDSS J235549.80-001437.5 | q | 1.3 |
| 178.9582363 | 0.243 | SDSS J115549.97+001434.7 | q | 1.2 | |
| (26) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | Q | 0.284 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 | |
| (27) | 129.7712982 | −0.0251763 | SDSS J083905.11-000130.6 | Q | 2.511 |
| 309.7715133 | 0.0243675 | SDSS J203905.16+000127.7 | q | 2.5 |
| Ra | Dec | Name | Descrip | Z | |
|---|---|---|---|---|---|
| (1) | 255.5777892 | −77.0249529 | WISEA J170218.69-770129.2 | q | 2.3 |
| 75.5809969 | 77.0255634 | WISEA J050219.24+770131.4 | q | 2.3 | |
| (2) | 315.7673595 | −76.3736026 | WISEA J210304.14-762224.9 | q | 1 |
| 135.7683983 | 76.3734303 | WISEA J090304.41+762224.0 | q | 2.4 | |
| (3) | 2.3493535 | −75.4740875 | WISEA J000923.83-752826.7 | q | 0.8 |
| 182.3515932 | 75.4750181 | WISEA J120924.56+752830.2 | q | 0.7 | |
| (4) | 85.679027 | −68.1421484 | WISEA J054242.99-680831.9 | q | 1.4 |
| 265.6773749 | 68.1413691 | SDSS J174242.55+680829.1 | q | 1.5 | |
| (5) | 350.1300997 | −64.0960807 | WISEA J232031.22-640545.8 | q | 0.8 |
| 170.1297219 | 64.0966844 | SDSS J112031.12+640548.1 | q | 1.4 | |
| (6) | 77.2847276 | −61.1581631 | WISEA J050908.30-610929.5 | q | 0.6 |
| 257.2851687 | 61.1587398 | SDSS J170908.44+610931.4 | q | 0.9 | |
| (7) | 12.2865176 | −55.3358661 | WISEA J004908.81-552009.3 | q | 1.3 |
| 192.2854767 | 55.3366013 | SDSS J124908.51+552011.7 | q | 1.9 | |
| (8) | 350.4801742 | −55.0232756 | XXLS J232155.23-550123.3 | QX | 1.788 |
| 170.4785659 | 55.0239884 | SDSS J112154.85+550126.3 | Q | 1.73 | |
| (9) | 2.4579845 | −53.9814555 | WISEA J000949.91-535853.2 | q | 0.2 |
| 182.4575348 | 53.980648 | SDSS J120949.80+535850.3 | q | 0.3 | |
| (10) | 323.9286029 | −53.3487347 | WISEA J213542.85-532055.4 | q | 0.9 |
| 143.9271545 | 53.3484154 | SDSS J093542.51+532054.2 | q | 0.5 | |
| (11) | 348.3491422 | −53.3478756 | XXLS J231323.75-532051.9 | QX | 0.496 |
| 168.3507385 | 53.3479691 | SDSS J111324.17+532052.6 | q | 0.3 | |
| (12) | 315.5807126 | −50.5996161 | WISEA J210219.36-503558.6 | q | 2.2 |
| 135.5799944 | 50.6005463 | SDSS J090219.19+503601.9 | Q | 2.619 | |
| (13) | 27.2491308 | −50.0692574 | WISEA J014859.79-500409.4 | q | 1.8 |
| 207.2486497 | 50.0702154 | SDSS J134859.67+500412.8 | Q | 1.559 | |
| (14) | 51.7544779 | −45.8163472 | WISEA J032701.07-454859.0 | q | 2.1 |
| 231.753214 | 45.816666 | SDSS J152700.77+454859.9 | q | 0.9 | |
| (15) | 13.7156676 | −45.5401862 | WISEA J005451.73-453224.7 | q | 1 |
| 193.7148005 | 45.5407984 | SDSS J125451.55+453226.8 | Q | 0.599 | |
| (16) | 312.4572617 | −43.5311298 | WISEA J204949.73-433151.7 | q | 1.7 |
| 132.4578712 | 43.5314134 | SDSS J084949.88+433153.1 | q | 2.6 | |
| (17) | 39.8003988 | −42.7828145 | WISEA J023912.05-424657.5 | q | 1.8 |
| 219.7994764 | 42.7819417 | SDSS J143911.87+424655.0 | Q | 2.376 | |
| (18) | 327.4360427 | −38.6604478 | WISEA J214944.65-383937.5 | q | 0.6 |
| 147.4361286 | 38.659581 | SDSS J094944.67+383934.5 | Q | 1.326 | |
| (19) | 17.7159333 | −38.4864674 | WISEA J011051.83-382911.3 | q | 2.2 |
| 197.7147558 | 38.4865089 | SDSS J131051.54+382911.4 | Q | 0.817 | |
| (20) | 35.9159531 | −37.2880557 | WISEA J022339.81-371716.8 | q | 0.7 |
| 215.9154018 | 37.2873321 | SDSS J142339.69+371714.3 | q | 1.4 | |
| (21) | 5.4863222 | −36.9636832 | WISEA J002156.72-365749.2 | q | 1.6 |
| 185.4861944 | 36.9634266 | SDSS J122156.67+365748.3 | Q | 2.097 | |
| (22) | 288.7726299 | −36.2604918 | WISEA J191505.43-361537.9 | q | 1 |
| 108.771553 | 36.2600021 | SDSS J071505.17+361536.0 | q | 0.4 | |
| (23) | 48.2374301 | −35.2506342 | WISEA J031256.97-351502.2 | qX | 1.9 |
| 228.2368457 | 35.250557 | SDSS J151256.83+351502.0 | q | 1.3 | |
| (24) | 64.4053066 | −34.4443255 | WISEA J041737.25-342639.2 | q | 2.3 |
| 244.4049248 | 34.4447566 | SDSS J161737.18+342641.1 | q | 1.9 | |
| (25) | 46.6464316 | −34.4391069 | WISEA J030635.12-342620.5 | q | 1.5 |
| 226.6455899 | 34.4391456 | SDSS J150634.94+342620.9 | Q | 2.275 | |
| (26) | 13.9539794 | −33.5205216 | Q 0053-3347 | Q | 2.08 |
| 193.9543304 | 33.519737 | SDSS J125549.03+333111.0 | q | 0.9 | |
| (27) | 61.3792872 | −33.3589696 | WISEA J040531.02-332132.4 | q | 1.3 |
| 241.3804819 | 33.3584594 | SDSS J160531.31+332130.4 | q | 0.6 | |
| (28) | 52.3380705 | −33.1624587 | WISEA J032921.13-330944.7 | q | 1 |
| 232.3374622 | 33.1619242 | SDSS J152921.00+330942.9 | q | 0.9 | |
| (29) | 35.6523275 | −32.9501625 | WISEA J022236.55-325700.5 | q | 2 |
| 215.6517237 | 32.9500411 | SDSS J142236.40+325700.2 | q | 1.8 | |
| (30) | 331.3013548 | −31.5723459 | 2QZ J220512.3-313421 | Q | 1.934 |
| 151.3004456 | 31.5727386 | SDSS J100512.10+313421.8 | q | 0.9 | |
| (31) | 178.0274651 | −31.4001968 | WISEA J115206.58-312400.4 | q | 2.4 |
| 358.026947 | 31.4004002 | SDSS J235206.46+312401.4 | q | 1 | |
| (32) | 188.680682 | −30.5578933 | WISEA J123443.36-303328.3 | q | 1 |
| 8.6803036 | 30.558761 | SDSS J003443.27+303331.6 | Q | 1.254 | |
| (33) | 300.1895832 | −30.1375161 | WISEA J200045.51-300814.8 | q | 0.6 |
| 120.1898279 | 30.1370937 | SDSS J080045.55+300813.5 | Q | 1.343 | |
| (34) | 332.1756094 | −29.9838041 | 2QZ J220842.1-295902 | Q | 1.023 |
| 152.1766832 | 29.9847166 | SDSS J100842.39+295905.0 | Q | 2.56 | |
| (35) | 12.3530442 | −29.9213175 | Q 0046-3011 | Q | 1.081 |
| 192.3529914 | 29.9214458 | SDSS J124924.71+295517.2 | q | 2.2 | |
| (36) | 333.8811688 | −28.3336528 | 2QZ J221531.4-282001 | Q | 1.909 |
| 153.8815524 | 28.3342401 | SDSS J101531.57+282003.3 | Q | 2.395 | |
| (37) | 80.438152 | −28.1840351 | WISEA J052145.16-281102.6 | q | 0.6 |
| 260.437853 | 28.1849529 | SDSS J172145.08+281105.8 | q | 1.3 | |
| (38) | 189.5249477 | −27.4782258 | WISEA J123805.97-272841.7 | q | 2.3 |
| 9.5243507 | 27.4772773 | SDSS J003805.84+272838.2 | Q | 1.937 | |
| (39) | 44.5344194 | −26.5790235 | WISEA J025808.26-263444.5 | q | 1.5 |
| 224.5352818 | 26.5780647 | SDSS J145808.46+263441.0 | q | 2.1 | |
| (40) | 197.0438404 | −25.791086 | WISEA J130810.53-254728.0 | q | 1.1 |
| 17.0442989 | 25.7919436 | SDSS J010810.62+254730.9 | Q | 1.843 | |
| (41) | 47.3495546 | −25.1085428 | WISEA J030923.89-250630.5 | q | 1 |
| 227.3495813 | 25.1081434 | SDSS J150923.90+250629.2 | q | 1.8 | |
| (42) | 314.8735964 | −23.9469948 | WISEA J205929.66-235649.1 | q | 0.4 |
| 134.8731466 | 23.946707 | SDSS J085929.56+235648.1 | Q | 1.085 | |
| (43) | 211.3857165 | −23.9417462 | WISEA J140532.57-235630.1 | q | 2.3 |
| 31.3864591 | 23.9416464 | SDSS J020532.75+235629.9 | Q | 2.005 | |
| (44) | 9.3024771 | −23.7730802 | SDSS J003712.58-234622.9 | q | 1.7 |
| 189.3025669 | 23.7724481 | SDSS J123712.61+234620.8 | Q | 2.644 | |
| (45) | 325.6254779 | −23.1632401 | WISEA J214230.10-230947.5 | q | 0.9 |
| 145.6252854 | 23.1622808 | SDSS J094230.07+230944.1 | q | 1.4 | |
| (46) | 15.629173 | −22.6311972 | WISEA J010230.99-223752.2 | qR | 1.9 |
| 195.6286965 | 22.6311474 | SDSS J130230.88+223752.2 | Q | 3.405 | |
| (47) | 181.1233682 | −21.9598988 | WISEA J120429.60-215735.5 | q | 0.8 |
| 1.1237153 | 21.9600067 | WISEA J000429.68+215736.0 | q | 1.4 | |
| (48) | 69.293922 | −21.9055291 | WISEA J043710.51-215420.2 | q | 0.7 |
| 249.293937 | 21.9045811 | SDSS J163710.55+215416.4 | Q | 1.411 | |
| (49) | 341.8649478 | −20.6885193 | WISEA J224727.58-204119.2 | q | 1.2 |
| 161.8640315 | 20.6894371 | SDSS J104727.36+204121.9 | Q | 2.262 | |
| (50) | 315.432881 | −19.3894197 | WISEA J210143.86-192321.5 | q | 1.8 |
| 135.4334805 | 19.3888631 | SDSS J090144.03+192319.9 | q | 1.4 | |
| (51) | 315.2686772 | −19.0978465 | WISEA J210104.48-190552.1 | q | 1.1 |
| 135.2689056 | 19.0972805 | SDSS J090104.53+190550.2 | q | 0.4 | |
| (52) | 331.1935682 | −18.7863235 | QSM3:36 | QX | 0.873 |
| 151.1930394 | 18.7867023 | SDSS J100446.32+184712.1 | q | 1.5 | |
| (53) | 60.4473986 | −18.154863 | WISEA J040147.38-180917.4 | q | 0.4 |
| 240.4484093 | 18.1550387 | WISEA J160147.61+180917.7 | q | 0.8 | |
| (54) | 191.2945552 | −18.1478667 | WISEA J124510.71-180851.9 | q | 1.5 |
| 11.2945118 | 18.1480237 | SDSS J004510.68+180852.8 | Q | 2.955 | |
| (55) | 173.7006562 | −18.0690647 | WISEA J113448.15-180408.7 | q | 2.3 |
| 353.7006507 | 18.0682592 | SDSS J233448.15+180405.7 | Q | 2.881 | |
| (56) | 24.9069328 | −17.90944 | SDSS J013937.65-175434.1 | qX | 2 |
| 204.9072341 | 17.910056 | SDSS J133937.73+175436.2 | q | 1.3 | |
| (57) | 352.4344723 | −17.8641457 | WISEA J232944.27-175150.9 | q | 1.3 |
| 172.4351845 | 17.8639806 | SDSS J112944.45+175150.4 | q | 3.3 | |
| (58) | 29.9174996 | −17.2967528 | SDSS J015940.19-171747.7 | q | 0.9 |
| 209.9180908 | 17.2973289 | SDSS J135940.34+171750.3 | q | 1.8 | |
| (59) | 166.796621 | −17.1482174 | SDSS J110711.18-170853.6 | q | 1.1 |
| 346.7956543 | 17.1488914 | SDSS J230710.95+170856.0 | q | 1.1 | |
| (60) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 | |
| (61) | 165.3264823 | −16.8833416 | SDSS J110118.35-165300.0 | q | 2 |
| 345.3268127 | 16.8840275 | SDSS J230118.43+165302.4 | q | 0.9 | |
| (62) | 43.6272916 | −16.2718962 | SDSS J025430.54-161618.8 | q | 0.3 |
| 223.6267804 | 16.2723981 | SDSS J145430.42+161620.6 | N | 0.158 | |
| (63) | 149.4813563 | −15.5088164 | WISEA J095755.52-153031.8 | q | 2.2 |
| 329.4811707 | 15.5078583 | SDSS J215755.48+153028.2 | q | 0.8 | |
| (64) | 321.3724784 | −14.2055432 | WISEA J212529.39-141219.9 | q | 1 |
| 141.3732103 | 14.2057221 | SDSS J092529.57+141220.5 | A | 0.473 | |
| (65) | 225.2865096 | −13.8267692 | WISEA J150108.76-134935.8 | q | 1.8 |
| 45.2857528 | 13.8264077 | WISEA J030108.57+134935.1 | q | 0.7 | |
| (66) | 22.4869537 | −13.2917978 | WISEA J012956.87-131730.2 | q | 1.6 |
| 202.4875051 | 13.2909737 | SDSS J132957.00+131727.5 | Q | 3.144 | |
| (67) | 190.3695441 | −13.095317 | SDSS J124128.69-130543.1 | q | 0.6 |
| 10.3688927 | 13.0956669 | SDSS J004128.53+130544.4 | q | 0.4 | |
| (68) | 178.5013735 | −12.8384611 | WISEA J115400.32-125018.4 | q | 0.9 |
| 358.501349 | 12.8377738 | SDSS J235400.32+125015.9 | q | 1.7 | |
| (69) | 56.1097236 | −12.7916261 | WISEA J034426.33-124729.7 | q | 0.3 |
| 236.109024 | 12.7923546 | SDSS J154426.16+124732.4 | q | 0.5 | |
| (70) | 39.5398838 | −11.856346 | WISEA J023809.57-115122.9 | q | 1.1 |
| 219.5404339 | 11.8565365 | SDSS J143809.70+115123.5 | q | 1.1 | |
| (71) | 304.7146082 | −11.8357393 | SDSS J201851.51-115008.7 | q | 3 |
| 124.7154201 | 11.8347625 | SDSS J081851.70+115005.1 | Q | 3.092 | |
| (72) | 18.0162381 | −10.9062962 | SDSS J011203.89-105422.6 | q | 1.9 |
| 198.0161728 | 10.9057355 | SDSS J131203.88+105420.7 | q | 0.8 | |
| (73) | 33.4777451 | −10.6369173 | SDSS J021354.65-103812.8 | q | 1.7 |
| 213.4776649 | 10.6378738 | SDSS J141354.63+103816.3 | q | 2.1 | |
| (74) | 24.1238435 | −10.5259013 | SDSS J013629.72-103133.2 | q | 2.3 |
| 204.1232718 | 10.5261989 | SDSS J133629.58+103134.3 | QX | 2.83 | |
| (75) | 334.8985316 | −9.69364 | SDSS J221935.64-094137.1 | q | 2 |
| 154.8980454 | 9.6929715 | SDSS J101935.52+094134.7 | Q | 2.313 | |
| (76) | 38.5649712 | −9.3922666 | SDSS J023415.59-092332.0 | Q | 3.159 |
| 218.5647491 | 9.3927159 | SDSS J143415.53+092333.7 | Q | 1.796 | |
| (77) | 140.4377101 | −9.3709292 | WISEA J092145.05-092215.4 | q | 0.8 |
| 320.4374695 | 9.3712921 | SDSS J212144.99+092216.6 | q | 1.2 | |
| (78) | 358.0582864 | −8.2121914 | SDSS J235213.99-081244.0 | q | 2 |
| 178.0589787 | 8.211923 | SDSS J115214.15+081242.8 | q | 1.1 | |
| (79) | 338.7737732 | −8.142704 | SDSS J223505.70-080833.7 | q | 0.4 |
| 158.773734 | 8.1430363 | SDSS J103505.69+080834.9 | q | 0.9 | |
| (80) | 332.3883082 | −7.9754252 | SDSS J220933.20-075831.4 | q | 2 |
| 152.3875951 | 7.9759758 | SDSS J100933.02+075833.4 | Q | 2.532 | |
| (81) | 46.2892799 | −7.2429566 | SDSS J030509.42-071434.6 | q | 0.5 |
| 226.2901611 | 7.2421827 | SDSS J150509.63+071431.8 | q | 1 | |
| (82) | 42.2919481 | −7.135162 | SDSS J024910.06-070806.6 | Q | 2.561 |
| 222.2917609 | 7.1344065 | SDSS J144910.02+070803.8 | q | 1.5 | |
| (83) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | |
| (84) | 328.3192139 | −6.7707705 | SDSS J215316.61-064614.7 | q | 1.7 |
| 148.3194775 | 6.7699293 | SDSS J095316.66+064611.7 | Q | 1.092 | |
| (85) | 209.4759723 | −6.7408847 | SDSS J135754.23-064427.1 | q | 1.7 |
| 29.4751402 | 6.7413482 | LAMOSTJ015754.04+064428.9 | Q | 1.565 | |
| (86) | 310.9553801 | −6.521875 | SDSS J204349.29-063118.7 | q | 2.2 |
| 130.9551195 | 6.521617 | SDSS J084349.22+063117.8 | q | 1.1 | |
| (87) | 42.0314865 | −6.0404835 | SDSS J024807.55-060225.7 | q | 1.1 |
| 222.031267 | 6.0407225 | SDSS J144807.50+060226.5 | Q | 2.324 | |
| (88) | 155.888588 | −5.987767 | WISEA J102333.26-055915.9 | q | 1 |
| 335.8882692 | 5.9887381 | WISEA J222333.18+055919.4 | q | 0.8 | |
| (89) | 30.4249489 | −5.8591802 | VIPERS 101146840 | Q | 2.126 |
| 210.4239741 | 5.858464 | SDSS J140141.75+055130.4 | q | 1.1 | |
| (90) | 318.9673157 | −5.08287 | SDSS J211552.15-050458.3 | q | 0.4 |
| 138.967392 | 5.0823555 | SDSS J091552.17+050456.4 | q | 0.6 | |
| (91) | 2.9218395 | −4.9358745 | SDSS J001141.24-045609.1 | q | 3.1 |
| 182.9209776 | 4.9351431 | SDSS J121141.03+045606.5 | q | 2 | |
| (92) | 339.1091419 | −4.9108333 | SDSS J223626.19-045438.9 | q | 1.6 |
| 159.1097246 | 4.9101383 | Q 1033+051 | Q | 1.048 | |
| (93) | 11.8971845 | −4.6937364 | SDSS J004735.33-044137.5 | Q | 1.931 |
| 191.8971312 | 4.6943342 | SDSS J124735.31+044139.5 | Q | 0.868 | |
| (94) | 215.4113925 | −4.6316734 | WISEA J142138.70-043753.9 | q | 1.5 |
| 35.4120872 | 4.6310081 | SDSS J022138.89+043751.6 | Q | 2.018 | |
| (95) | 44.1504799 | −4.5690993 | SDSS J025636.11-043408.8 | Q | 3.094 |
| 224.1496194 | 4.5693052 | WISEA J145635.91+043409.4 | q | 1.9 | |
| (96) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | |
| (97) | 313.1420516 | −4.4458056 | WISEA J205234.08-042644.8 | q | 2.3 |
| 133.1429183 | 4.4466583 | SDSS J085234.29+042648.0 | Q | 2.745 | |
| (98) | 28.6933545 | −3.9445188 | SDSS J015446.40-035640.2 | Q | 2.322 |
| 208.6934509 | 3.9447002 | SDSS J135446.42+035640.9 | q | 0.8 | |
| (99) | 23.3642954 | −3.508162 | SDSS J013327.43-033029.3 | Q | 1.724 |
| 203.3644091 | 3.5075679 | SDSS J133327.45+033027.2 | q | 1 | |
| (100) | 29.2919507 | −3.3900862 | SDSS J015710.06-032324.3 | Q | 1.504 |
| 209.2925571 | 3.3891148 | WISEA J135710.20+032320.9 | q | 0.7 | |
| (101) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | Q | 2.173 | |
| (102) | 59.7010545 | −3.0252538 | WISEA J035848.22-030131.3 | q | 0.9 |
| 239.7015228 | 3.0244355 | SDSS J155848.36+030127.9 | q | 1 | |
| (103) | 357.4388055 | −2.8983433 | SDSS J234945.32-025354.0 | Q | 0.938 |
| 177.4378903 | 2.899283 | SDSS J114945.07+025357.3 | q | 1.5 | |
| (104) | 11.9639927 | −2.8499138 | SDSS J004751.36-025059.6 | Q | 1.262 |
| 191.9631892 | 2.849156 | SDSS J124751.16+025056.9 | Q | 1.568 | |
| (105) | 11.428722 | −2.6318303 | SDSS J004542.89-023754.5 | q | 1 |
| 191.4280252 | 2.6316203 | WISEA J124542.71+023753.8 | qX | 0.7 | |
| (106) | 9.1659024 | −2.4347542 | SDSS J003639.81-022604.9 | Q | 1.055 |
| 189.165748 | 2.4344829 | SDSS J123639.77+022604.1 | q | 2 | |
| (107) | 17.5345544 | −2.4323457 | SDSS J011008.29-022556.4 | Q | 1.068 |
| 197.5339023 | 2.4329717 | SDSS J131008.13+022558.6 | q | 1.6 | |
| (108) | 145.7966766 | −2.4094768 | SDSS J094311.20-022434.1 | q | 0.9 |
| 325.7966554 | 2.410309 | SDSS J214311.19+022437.1 | q | 1.2 | |
| (109) | 181.200555 | −2.225128 | 2QZ J120448.1-021331 | Q | 0.888 |
| 1.2006668 | 2.2249101 | SDSS J000448.16+021329.6 | q | 1.2 | |
| (110) | 21.4036505 | −2.1947235 | SDSS J012536.87-021141.0 | Q | 2.542 |
| 201.4034175 | 2.1940664 | SDSS J132536.82+021138.6 | q | 1.2 | |
| (111) | 172.9620056 | −2.1642234 | SDSS J113150.88-020951.2 | q | 0.9 |
| 352.9627548 | 2.1647976 | SDSS J233151.04+020953.2 | q | 1.4 | |
| (112) | 221.5816508 | −2.0546804 | 2QZ J144619.5-020317 | Q | 1.021 |
| 41.5820598 | 2.0548802 | SDSS J024619.69+020317.5 | Q | 1.611 | |
| (113) | 325.6085362 | −1.7636978 | SDSS J214226.05-014549.2 | q | 1.4 |
| 145.6089432 | 1.7631901 | SDSS J094226.14+014547.5 | Q | 2.335 | |
| (114) | 14.2851195 | −1.5772589 | SDSS J005708.42-013438.1 | Q | 1.329 |
| 194.2848358 | 1.5782201 | SDSS J125708.36+013441.5 | qX | 0.8 | |
| (115) | 36.4121461 | −1.4221784 | SDSS J022538.91-012519.8 | Q | 0.727 |
| 216.412656 | 1.4224802 | 2QZ J142539.0+012521 | Q | 1.136 | |
| (116) | 179.9376714 | −1.3721402 | 2QZ J115945.0-012220 | Q | 1.275 |
| 359.9384294 | 1.3712088 | SDSS J235945.22+012216.3 | Q | 1.222 | |
| (117) | 169.1804623 | −1.2787242 | SDSS J111643.31-011643.4 | Q | 0.878 |
| 349.1801163 | 1.2778387 | SDSS J231643.23+011640.2 | qX | 2.1 | |
| (118) | 40.8886891 | −1.1553956 | SDSS J024333.28-010919.3 | Q | 2.265 |
| 220.889267 | 1.1561131 | SDSS J144333.42+010922.0 | q | 1.5 | |
| (119) | 322.0407105 | −1.1103891 | 2SLAQ J212809.77-010637.4 | Q | 2.016 |
| 142.0406886 | 1.109918 | SDSS J092809.76+010635.6 | Q | 0.691 | |
| (120) | 191.5187354 | −0.947775 | 2QZ J124604.4-005652 | Q | 1.74 |
| 11.5188728 | 0.9486683 | SDSS J004604.52+005655.1 | Q | 2.394 | |
| (121) | 136.812282 | −0.9465473 | WISEA J090714.94-005647.5 | q | 0.4 |
| 316.8128149 | 0.9471022 | SDSS J210715.08+005649.5 | q | 0.6 | |
| (122) | 318.5432739 | −0.6772609 | SDSS J211410.38-004038.1 | q | 1 |
| 138.5425553 | 0.6770332 | SDSS J091410.21+004037.3 | q | 2.2 | |
| (123) | 176.6971288 | −0.6466236 | SDSS J114647.31-003847.8 | q | 1.6 |
| 356.6970072 | 0.6459298 | SDSS J234647.28+003845.3 | q | 3.2 | |
| (124) | 10.1452528 | −0.6391804 | SDSS J004034.86-003821.0 | Q | 1.836 |
| 190.1442813 | 0.638343 | 2QZ J124034.6+003816 | Q | 1.856 | |
| (125) | 322.7183019 | −0.5829681 | SDSS J213052.39-003458.6 | Q | 2.654 |
| 142.7177224 | 0.5830358 | PKS 0928+008 | QRX | 1.769 | |
| (126) | 321.3839569 | −0.535798 | SDSS J212532.14-003208.8 | q | 3.6 |
| 141.3843083 | 0.5359621 | 2SLAQ J092532.23+003209.5 | Q | 1.451 | |
| (127) | 359.9532206 | −0.5350152 | SDSS J235948.77-003206.0 | Q | 1.443 |
| 179.9524587 | 0.5345278 | 2QZ J115948.5+003203 | Q | 2.27 | |
| (128) | 328.4185019 | −0.4744671 | SDSS J215340.44-002828.0 | q | 4.7 |
| 148.4176331 | 0.4748041 | SDSS J095340.23+002829.2 | q | 2 | |
| (129) | 348.1098247 | −0.4195352 | 2SLAQ J231226.35-002510.3 | Q | 1.105 |
| 168.1100567 | 0.4190823 | 2QZ J111226.3+002508 | Q | 1.309 | |
| (130) | 44.7576857 | −0.2819373 | SDSS J025901.84-001654.9 | Q | 1.406 |
| 224.7571 | 0.2811774 | 2SLAQ J145901.70+001652.2 | Q | 1.58 | |
| (131) | 358.9575115 | −0.2437697 | SDSS J235549.80-001437.5 | q | 1.3 |
| 178.9582363 | 0.243 | SDSS J115549.97+001434.7 | q | 1.2 | |
| (132) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | Q | 0.284 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 | |
| (133) | 321.2974555 | −0.0852931 | 2SLAQ J212511.38-000507.0 | Q | 2.308 |
| 141.2979338 | 0.08586 | 2SLAQ J092511.51+000509.0 | Q | 2.698 | |
| (134) | 314.6144714 | −0.0745742 | SDSS J205827.47-000428.4 | q | 1.2 |
| 134.6143136 | 0.073984 | SDSS J085827.43+000426.3 | q | 2 | |
| (135) | 129.7712982 | −0.0251763 | SDSS J083905.11-000130.6 | Q | 2.511 |
| 309.7715133 | 0.0243675 | SDSS J203905.16+000127.7 | q | 2.5 |
| Ra | Dec | Name | Descrip | Z | |
|---|---|---|---|---|---|
| (1) | 315.7673595 | −76.3736026 | WISEA J210304.14-762224.9 | q | 1 |
| 135.7683983 | 76.3734303 | WISEA J090304.41+762224.0 | q | 2.4 | |
| (2) | 312.4572617 | −43.5311298 | WISEA J204949.73-433151.7 | q | 1.7 |
| 132.4578712 | 43.5314134 | SDSS J084949.88+433153.1 | q | 2.6 | |
| (3) | 5.4863222 | −36.9636832 | WISEA J002156.72-365749.2 | q | 1.6 |
| 185.4861944 | 36.9634266 | SDSS J122156.67+365748.3 | Q | 2.097 | |
| (4) | 48.2374301 | −35.2506342 | WISEA J031256.97-351502.2 | qX | 1.9 |
| 228.2368457 | 35.250557 | SDSS J151256.83+351502.0 | q | 1.3 | |
| (5) | 64.4053066 | −34.4443255 | WISEA J041737.25-342639.2 | q | 2.3 |
| 244.4049248 | 34.4447566 | SDSS J161737.18+342641.1 | q | 1.9 | |
| (6) | 178.0274651 | −31.4001968 | WISEA J115206.58-312400.4 | q | 2.4 |
| 358.026947 | 31.4004002 | SDSS J235206.46+312401.4 | q | 1 | |
| (7) | 300.1895832 | −30.1375161 | WISEA J200045.51-300814.8 | q | 0.6 |
| 120.1898279 | 30.1370937 | SDSS J080045.55+300813.5 | Q | 1.343 | |
| (8) | 12.3530442 | −29.9213175 | Q 0046-3011 | Q | 1.081 |
| 192.3529914 | 29.9214458 | SDSS J124924.71+295517.2 | q | 2.2 | |
| (9) | 47.3495546 | −25.1085428 | WISEA J030923.89-250630.5 | q | 1 |
| 227.3495813 | 25.1081434 | SDSS J150923.90+250629.2 | q | 1.8 | |
| (10) | 314.8735964 | −23.9469948 | WISEA J205929.66-235649.1 | q | 0.4 |
| 134.8731466 | 23.946707 | SDSS J085929.56+235648.1 | Q | 1.085 | |
| (11) | 15.629173 | −22.6311972 | WISEA J010230.99-223752.2 | qR | 1.9 |
| 195.6286965 | 22.6311474 | SDSS J130230.88+223752.2 | Q | 3.405 | |
| (12) | 181.1233682 | −21.9598988 | WISEA J120429.60-215735.5 | q | 0.8 |
| 1.1237153 | 21.9600067 | WISEA J000429.68+215736.0 | q | 1.4 | |
| (13) | 191.2945552 | −18.1478667 | WISEA J124510.71-180851.9 | q | 1.5 |
| 11.2945118 | 18.1480237 | SDSS J004510.68+180852.8 | Q | 2.955 | |
| (14) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 | |
| (15) | 38.5649712 | −9.3922666 | SDSS J023415.59-092332.0 | Q | 3.159 |
| 218.5647491 | 9.3927159 | SDSS J143415.53+092333.7 | Q | 1.796 | |
| (16) | 140.4377101 | −9.3709292 | WISEA J092145.05-092215.4 | q | 0.8 |
| 320.4374695 | 9.3712921 | SDSS J212144.99+092216.6 | q | 1.2 | |
| (17) | 338.7737732 | −8.142704 | SDSS J223505.70-080833.7 | q | 0.4 |
| 158.773734 | 8.1430363 | SDSS J103505.69+080834.9 | q | 0.9 | |
| (18) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | |
| (19) | 310.9553801 | −6.521875 | SDSS J204349.29-063118.7 | q | 2.2 |
| 130.9551195 | 6.521617 | SDSS J084349.22+063117.8 | q | 1.1 | |
| (20) | 42.0314865 | −6.0404835 | SDSS J024807.55-060225.7 | q | 1.1 |
| 222.031267 | 6.0407225 | SDSS J144807.50+060226.5 | Q | 2.324 | |
| (21) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | |
| (22) | 28.6933545 | −3.9445188 | SDSS J015446.40-035640.2 | Q | 2.322 |
| 208.6934509 | 3.9447002 | SDSS J135446.42+035640.9 | q | 0.8 | |
| (23) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | Q | 2.173 | |
| (24) | 9.1659024 | −2.4347542 | SDSS J003639.81-022604.9 | Q | 1.055 |
| 189.165748 | 2.4344829 | SDSS J123639.77+022604.1 | q | 2 | |
| (25) | 181.200555 | −2.225128 | 2QZ J120448.1-021331 | Q | 0.888 |
| 1.2006668 | 2.2249101 | SDSS J000448.16+021329.6 | q | 1.2 | |
| (26) | 221.5816508 | −2.0546804 | 2QZ J144619.5-020317 | Q | 1.021 |
| 41.5820598 | 2.0548802 | SDSS J024619.69+020317.5 | Q | 1.611 | |
| (27) | 322.0407105 | −1.1103891 | 2SLAQ J212809.77-010637.4 | Q | 2.016 |
| 142.0406886 | 1.109918 | SDSS J092809.76+010635.6 | Q | 0.691 | |
| (28) | 321.3839569 | −0.535798 | SDSS J212532.14-003208.8 | q | 3.6 |
| 141.3843083 | 0.5359621 | 2SLAQ J092532.23+003209.5 | Q | 1.451 | |
| (29) | 348.1098247 | −0.4195352 | 2SLAQ J231226.35-002510.3 | Q | 1.105 |
| 168.1100567 | 0.4190823 | 2QZ J111226.3+002508 | Q | 1.309 | |
| (30) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | Q | 0.284 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 |
Appendix E
| Name | Ra | Dec | Z | |
|---|---|---|---|---|
| (1) | J065013.57-814217.6 | 102.5565628 | −81.7049143 | |
| J185012.45+814220.5 | 282.5519004 | 81.7056967 | ||
| (2) | J104815.79-775517.6 | 162.0658158 | −77.9215763 | |
| J224816.91+775517.5 | 342.0704902 | 77.9215426 | ||
| (3) | J015410.35-770145.4 | 28.5431453 | −77.0292865 | |
| J135410.15+770146.8 | 208.5423058 | 77.0296683 | ||
| (4) | J170218.69-770129.2 | 255.5779108 | −77.0247821 | |
| J050219.24+770131.4 | 75.5802066 | 77.0253936 | ||
| (5) | LQAC_048-076_004 | 48.2412 | −76.8556 | 2.251 |
| J151258.42+765116.6 | 228.2434304 | 76.8546334 | ||
| (6) | J031257.86-765119.5 | 48.2411239 | −76.855429 | |
| J151258.42+765116.6 | 228.2434304 | 76.8546334 | ||
| (7) | J201452.82-764705.1 | 303.7201147 | −76.7847541 | |
| J081453.75+764706.8 | 123.7239922 | 76.7852418 | ||
| (8) | J210304.14-762224.9 | 315.7672779 | −76.3735957 | |
| J090304.41+762224.0 | 135.7684133 | 76.3733506 | ||
| (9) | J000923.83-752826.7 | 2.3493314 | −75.4740891 | |
| J120924.56+752830.2 | 182.3523545 | 75.4750639 | ||
| (10) | J082102.98-732201.4 | 125.2624384 | −73.3670587 | |
| J202103.69+732201.4 | 305.2653831 | 73.3670564 | ||
| (11) | J152625.82-732045.8 | 231.6076131 | −73.346071 | |
| J032626.02+732043.5 | 51.6084447 | 73.3454428 | ||
| (12) | J075055.11-665252.9 | 117.7296651 | −66.8813702 | |
| J195054.52+665252.8 | 297.7271938 | 66.8813334 | ||
| (13) | J003923.34-661033.4 | 9.8472514 | −66.1759482 | |
| J123923.49+661035.8 | 189.8478948 | 66.176629 | ||
| (14) | J170820.10-623913.0 | 257.0837815 | −62.6536341 | |
| J050820.40+623912.3 | 77.0850212 | 62.6534285 | ||
| (15) | J224505.82-621922.8 | 341.2742892 | −62.3230084 | |
| 104505.93+621922.8 | 161.2747324 | 62.32302149 | 1.342 | |
| (16) | J054056.36-604959.0 | 85.2348533 | −60.8330709 | |
| J174056.57+605000.8 | 265.2357489 | 60.8335817 | ||
| (17) | J093154.04-604552.0 | 142.9751737 | −60.7644677 | |
| J213154.02+604550.2 | 322.975094 | 60.7639456 | ||
| (18) | J073745.76-601648.0 | 114.4407021 | −60.2800092 | |
| J193745.89+601650.5 | 294.441231 | 60.2807195 | ||
| (19) | J043547.94-593444.6 | 68.9497681 | −59.5790668 | |
| J163548.00+593441.4 | 248.9500066 | 59.5781862 | ||
| (20) | J044902.05-585105.9 | 72.2585651 | −58.8516409 | |
| J164902.23+585109.5 | 252.2593095 | 58.8526408 | ||
| (21) | J023030.16-584734.1 | 37.6256709 | −58.7928136 | |
| 143030.20+584736.9 | 217.6258429 | 58.79360186 | 2.603 | |
| (22) | J021037.60-574807.6 | 32.656701 | −57.8021278 | |
| J141037.99+574804.5 | 212.6583135 | 57.8012742 | ||
| (23) | J234926.29-564624.9 | 357.3595443 | −56.7735858 | |
| 114926.22+564624.9 | 177.359266 | 56.77360707 | 1.459 | |
| (24) | J014942.21-561417.0 | 27.4258981 | −56.2380595 | |
| 134942.26+561415.1 | 207.4260912 | 56.23755146 | 1.513 | |
| (25) | J232326.69-560831.7 | 350.861225 | −56.1421439 | |
| J112326.28+560829.4 | 170.8595139 | 56.1415184 | ||
| (26) | J033029.28-553249.4 | 52.6220047 | −55.5470669 | |
| LQAC_232+055_010 | 232.6210224 | 55.5466683 | 1.732 | |
| (27) | J014520.31-551733.1 | 26.3346552 | −55.2925322 | |
| J134520.13+551734.6 | 206.3338867 | 55.2929689 | ||
| (28) | J035335.57-551116.1 | 58.398228 | −55.1878328 | |
| 155335.97+551115.7 | 238.3998764 | 55.18770389 | 2.801 | |
| (29) | J011541.50-550945.0 | 18.9229286 | −55.1625237 | |
| 131541.80+550947.9 | 198.924174 | 55.1633099 | 2.518 | |
| (30) | J004443.92-544532.5 | 11.183014 | −54.7590464 | |
| J124443.89+544531.9 | 191.1828838 | 54.7588612 | ||
| (31) | J020849.23-534047.4 | 32.2051551 | −53.6798564 | |
| 140849.42+534050.9 | 212.2059195 | 53.68083276 | 2.594 | |
| (32) | J032510.30-532527.4 | 51.2929271 | −53.4242888 | |
| LQAC_231+053_004 | 231.2946008 | 53.42329979 | 3.62 | |
| (33) | J013702.04-513252.3 | 24.2585004 | −51.5478865 | |
| 133702.07+513252.1 | 204.2586596 | 51.54780646 | 3.123 | |
| (34) | J005717.66-505253.0 | 14.3236008 | −50.8814119 | |
| 125717.65+505255.6 | 194.3235824 | 50.88212363 | 1.642 | |
| (35) | J210219.36-503558.6 | 315.580702 | −50.5996365 | |
| 090219.19+503601.9 | 135.579984 | 50.60054742 | 2.619 | |
| (36) | J014423.74-502934.8 | 26.0989274 | −50.4930215 | |
| 134424.09+502935.3 | 206.1004142 | 50.49316354 | 1.542 | |
| (37) | J025356.53-502734.2 | 43.4855594 | −50.4595093 | |
| J145356.47+502732.3 | 223.4853141 | 50.4589903 | ||
| (38) | J045351.32-500446.4 | 73.4638512 | −50.0795633 | |
| J165351.61+500448.1 | 253.4650669 | 50.0800473 | ||
| (39) | J014859.79-500409.4 | 27.249139 | −50.0693006 | |
| 134859.67+500412.8 | 207.2486344 | 50.07024035 | 1.559 | |
| (40) | J115039.86-483126.9 | 177.6660978 | −48.5241579 | |
| J235039.73+483125.6 | 357.665564 | 48.5237961 | ||
| (41) | J121222.32-470945.7 | 183.0930407 | −47.1627214 | |
| L_3.092+47.16228 | 3.0919976 | 47.162279 | 0.435 | |
| (42) | J121222.32-470945.7 | 183.0930407 | −47.1627214 | |
| J001222.08+470944.3 | 3.0920057 | 47.1623169 | ||
| (43) | J234921.38-463939.4 | 357.3391246 | −46.6609453 | |
| 114921.37+463937.4 | 177.3390734 | 46.66041384 | 2.209 | |
| (44) | J000333.34-463348.8 | 0.8889306 | −46.5635617 | |
| J120333.26+463349.2 | 180.888613 | 46.5636756 | ||
| (45) | J232951.30-462936.0 | 352.4637617 | −46.4933383 | |
| 112951.12+462934.8 | 172.4630068 | 46.49300281 | 1.874 | |
| (46) | J001522.25-462711.2 | 3.8427405 | −46.4531156 | |
| 121521.94+462708.3 | 183.841433 | 46.45232349 | 0.706 | |
| (47) | J235842.78-462119.9 | 359.6782761 | −46.3555539 | |
| 115842.73+462119.3 | 179.6780673 | 46.35538626 | 1.441 | |
| (48) | J102546.91-460551.1 | 156.4454829 | −46.0975459 | |
| J222546.61+460552.2 | 336.444224 | 46.0978546 | ||
| (49) | J022714.20-455207.2 | 36.8091778 | −45.8686727 | |
| 142713.98+455209.2 | 216.808284 | 45.86923886 | 0.89 | |
| (50) | J005451.73-453224.7 | 13.7155508 | −45.5401987 | |
| 125451.55+453226.8 | 193.7148002 | 45.54079833 | 0.599 | |
| (51) | J002525.65-451116.2 | 6.3569101 | −45.1878378 | |
| 122525.90+451119.4 | 186.3579518 | 45.18873483 | 2.012 | |
| (52) | J003634.96-450211.3 | 9.1456971 | −45.0364828 | |
| LQAC_189+045_001 | 189.1468986 | 45.03557266 | 0.401 | |
| (53) | J032340.76-445219.8 | 50.9198579 | −44.8721899 | |
| J152340.96+445222.6 | 230.9206887 | 44.8729639 | ||
| (54) | J142118.81-444959.4 | 215.3284148 | −44.8331713 | |
| J022118.56+444959.6 | 35.3273534 | 44.8332385 | ||
| (55) | J040922.63-434237.6 | 62.3443021 | −43.7104529 | |
| J160922.90+434238.0 | 242.3454381 | 43.710576 | ||
| (56) | J023912.05-424657.5 | 39.80023 | −42.78266 | |
| LQAC_219+042_028 | 219.7994832 | 42.78195298 | 2.376 | |
| (57) | J011902.18-423527.9 | 19.7591123 | −42.5911066 | |
| 131901.96+423525.1 | 199.7581772 | 42.59031464 | 2.418 | |
| (58) | J194357.17-423230.3 | 295.9882428 | −42.5417658 | |
| LQAC_115+042_034 | 115.9881497 | 42.54250971 | 0.785 | |
| (59) | J010933.66-415122.0 | 17.3902687 | −41.856116 | |
| LQAC_197+041_004 | 197.3894588 | 41.85616598 | 1.128 | |
| (60) | J065832.76-413600.0 | 104.6365048 | −41.6000057 | |
| J185832.85+413601.2 | 284.6368963 | 41.6003466 | ||
| (61) | J225003.90-404750.0 | 342.5162501 | −40.7972425 | |
| J105003.82+404752.3 | 162.5159468 | 40.7978721 | ||
| (62) | J054106.29-393853.6 | 85.2762311 | −39.6482362 | |
| J174106.48+393851.1 | 265.2770063 | 39.6475475 | ||
| (63) | J214944.65-383937.5 | 327.4360536 | −38.6604439 | |
| 094944.67+383934.5 | 147.4361304 | 38.6595897 | 1.326 | |
| (64) | J011051.83-382911.3 | 17.7159682 | −38.4864762 | |
| LQAC_197+038_041 | 197.7147781 | 38.48651802 | 0.816 | |
| (65) | J121926.97-381141.0 | 184.8623806 | −38.1947475 | |
| J001926.76+381141.9 | 4.8615332 | 38.1949744 | ||
| (66) | J140113.73-375749.9 | 210.3072125 | −37.9638751 | |
| J020113.48+375746.6 | 30.3062011 | 37.9629542 | ||
| (67) | J034937.91-374902.4 | 57.4079661 | −37.8173499 | |
| J154937.76+374904.2 | 237.407344 | 37.8178398 | ||
| (68) | J032742.65-372227.2 | 51.9277313 | −37.3742363 | |
| LQAC_231+037_033 | 231.9276563 | 37.37406082 | 2.635 | |
| (69) | J002156.72-365749.2 | 5.4863348 | −36.9636685 | |
| LQAC_185+036_009 | 185.4861573 | 36.96344034 | 2.097 | |
| (70) | J015857.83-364051.5 | 29.74099 | −36.6809782 | |
| LQAC_209+036_041 | 209.7415028 | 36.68102127 | 1.325 | |
| (71) | J020724.39-363533.9 | 31.8516579 | −36.5927588 | |
| J140724.46+363534.6 | 211.8519458 | 36.5929712 | ||
| (72) | J221949.29-361508.3 | 334.9553981 | −36.2523091 | |
| 101949.33+361511.6 | 154.9555568 | 36.25323484 | 2.072 | |
| (73) | J201205.95-353252.6 | 303.0248152 | −35.5479606 | |
| J081206.08+353250.7 | 123.0253608 | 35.5474366 | ||
| (74) | J041151.56-351610.1 | 62.9648363 | −35.2694838 | |
| J161151.26+351608.7 | 242.9636226 | 35.2690879 | ||
| (75) | J135450.16-351503.3 | 208.7090077 | −35.2509374 | |
| J015450.31+351503.4 | 28.7096451 | 35.2509711 | ||
| (76) | J032412.53-344857.3 | 51.0522435 | −34.8159276 | |
| J152412.33+344855.8 | 231.0513838 | 34.8155136 | ||
| (77) | J030635.12-342620.5 | 46.6463591 | −34.4390464 | |
| LQAC_226+034_022 | 226.6456048 | 34.43915382 | 2.267 | |
| (78) | J022031.39-335746.0 | 35.1308163 | −33.9627784 | |
| J142031.67+335745.7 | 215.1319667 | 33.9626953 | ||
| (79) | J201529.89-334536.3 | 303.8745553 | −33.7601054 | |
| LQAC_123+033_045 | 123.8749216 | 33.76069163 | 2.263 | |
| (80) | J023025.90-331514.2 | 37.6079221 | −33.2539609 | |
| J143026.02+331515.8 | 217.6084382 | 33.2543894 | ||
| (81) | J144620.40-322022.3 | 221.5850027 | −32.3395303 | |
| J024620.21+322020.8 | 41.5842294 | 32.3391357 | ||
| (82) | LQAC_031-030_002 | 31.13416667 | −30.7485 | 1.665 |
| J140432.01+304451.1 | 211.1334154 | 30.7475457 | ||
| (83) | J123443.36-303328.3 | 188.6806682 | −30.5578886 | |
| 003443.27+303331.6 | 8.680297194 | 30.55878763 | 1.254 | |
| (84) | J200045.51-300814.8 | 300.1896576 | −30.1374469 | |
| LQAC_120+030_023 | 120.1897932 | 30.13710584 | 1.344 | |
| (85) | LQAC_332-029_006 | 332.17575 | −29.98391667 | 1.023 |
| 100842.39+295905.0 | 152.176654 | 29.98472533 | 2.56 | |
| (86) | J091949.60-295507.2 | 139.956669 | −29.9186772 | |
| J211949.69+295510.1 | 319.9570695 | 29.9194956 | ||
| (87) | J223635.72-294646.1 | 339.1488693 | −29.7794728 | |
| LQAC_159+029_002 | 159.1497968 | 29.77935241 | 0.969 | |
| (88) | J031933.05-293711.2 | 49.8877165 | −29.6197972 | |
| J151933.28+293714.8 | 229.888686 | 29.6207837 | ||
| (89) | J001806.16-292855.6 | 4.5256732 | −29.4821238 | |
| J121806.13+292853.5 | 184.5255438 | 29.4815289 | ||
| (90) | J192614.75-292450.8 | 291.56146 | −29.4141247 | |
| J072614.78+292453.4 | 111.5615925 | 29.4148538 | ||
| (91) | LQAC_333-028_039 | 333.8812083 | −28.33372222 | 1.909 |
| 101531.57+282003.3 | 153.8815418 | 28.33425215 | 2.395 | |
| (92) | J042201.40-275940.0 | 65.5058587 | −27.9944693 | |
| LQAC_245+027_035 | 245.5051328 | 27.99378112 | 2.283 | |
| (93) | J105219.42-275107.3 | 163.0809198 | −27.8520433 | |
| 225219.63+275104.7 | 343.0817958 | 27.85131359 | 2.107 | |
| (94) | J123805.97-272841.7 | 189.524903 | −27.4782619 | |
| 003805.84+272838.2 | 9.524363473 | 27.4772968 | 1.937 | |
| (95) | J130810.53-254728.0 | 197.0439145 | −25.7911368 | |
| 010810.62+254730.9 | 17.04428773 | 25.79192277 | 1.843 | |
| (96) | J024444.36-252255.5 | 41.1848409 | −25.3821032 | |
| J144444.41+252254.9 | 221.1850503 | 25.3819393 | ||
| (97) | J223704.99-251338.9 | 339.2708283 | −25.2274835 | |
| 103704.76+251336.6 | 159.2698378 | 25.22684044 | 0.531 | |
| (98) | J014622.54-251130.4 | 26.5939276 | −25.1917856 | |
| LQAC_206+025_027 | 206.5933002 | 25.19165212 | 2.456 | |
| (99) | J020549.77-245224.7 | 31.4574 | −24.87353 | |
| LQAC_211+024_008 | 211.4571845 | 24.87429322 | 0.928 | |
| (100) | J031541.43-243539.7 | 48.9226614 | −24.5943802 | |
| LQAC_228+024_039 | 228.9221594 | 24.59465727 | 3.209 | |
| (101) | J205929.66-235649.1 | 314.8735964 | −23.9469948 | |
| LQAC_134+023_015 | 134.873161 | 23.9466925 | 1.078 | |
| (102) | J140532.57-235630.1 | 211.3857207 | −23.9417186 | |
| 020532.75+235629.9 | 31.38646701 | 23.94164901 | 2.005 | |
| (103) | J150948.30-232343.7 | 227.4512769 | −23.3954723 | |
| J030948.53+232346.1 | 47.4522222 | 23.3961525 | ||
| (104) | J220054.23-230032.0 | 330.2259757 | −23.0089119 | |
| 100054.23+230031.6 | 150.2259966 | 23.00878724 | 3.027 | |
| (105) | J010230.99-223752.2 | 15.6291536 | −22.6311827 | |
| LQAC_195+022_028 | 195.6286998 | 22.63117677 | 3.406 | |
| (106) | J120429.60-215735.5 | 181.1233627 | −21.9598782 | |
| J000429.68+215736.0 | 1.1236965 | 21.9600236 | ||
| (107) | J065001.37-212358.7 | 102.5057101 | −21.399642 | |
| J185001.25+212355.6 | 282.5052397 | 21.398792 | ||
| (108) | J005650.87-212138.7 | 14.2119971 | −21.3607693 | |
| LQAC_194+021_035 | 194.2109514 | 21.36031333 | 3.127 | |
| (109) | J013938.67-212010.0 | 24.9111441 | −21.3361154 | |
| LQAC_204+021_041 | 204.9120593 | 21.33514981 | 2.552 | |
| (110) | J035233.36-211221.7 | 58.1390267 | −21.2060385 | |
| J155233.38+211221.7 | 238.1391178 | 21.2060426 | ||
| (111) | J224727.58-204119.2 | 341.8649405 | −20.6886935 | |
| LQAC_161+020_031 | 161.8640312 | 20.68943703 | 2.263 | |
| (112) | J031653.77-202303.1 | 49.2240677 | −20.3842205 | |
| LQAC_229+020_017 | 229.2243051 | 20.38391551 | 2.662 | |
| (113) | J193418.18-193048.3 | 293.575751 | −19.5134425 | |
| J073418.08+193051.5 | 113.5753484 | 19.5143209 | ||
| (114) | J100124.33-192443.5 | 150.3514045 | −19.4120913 | |
| 220124.59+192440.4 | 330.3524601 | 19.41123813 | 2.248 | |
| (115) | J220218.01-182459.7 | 330.5750658 | −18.4166105 | |
| LQAC_150+018_009 | 150.5756637 | 18.41574009 | 3.27 | |
| (116) | J025347.91-182055.5 | 43.4496403 | −18.3487653 | |
| J145347.66+182057.6 | 223.4485908 | 18.3493384 | ||
| (117) | J124025.44-181851.0 | 190.1060315 | −18.3141709 | |
| 004025.23+181851.6 | 10.10516218 | 18.31436067 | 1.156 | |
| (118) | J040147.38-180917.4 | 60.4474285 | −18.1548374 | |
| J160147.61+180917.7 | 240.448394 | 18.1549427 | ||
| (119) | J124510.71-180851.9 | 191.2946306 | −18.147767 | |
| J004510.62+180851.9 | 11.294273 | 18.147755 | ||
| (120) | J113448.15-180408.7 | 173.7006493 | −18.0690897 | |
| 233448.15+180405.7 | 353.7006501 | 18.06825912 | 2.881 | |
| (121) | J101559.49-174442.2 | 153.9979125 | −17.7450573 | |
| LQAC_333+017_020 | 333.9971774 | 17.74470031 | 2.384 | |
| (122) | J150108.76-134935.8 | 225.2865111 | −13.8266261 | |
| J030108.57+134935.1 | 45.2857099 | 13.8264198 | ||
| (123) | J012956.87-131730.2 | 22.4869978 | −13.2917386 | |
| LQAC_202+013_037 | 202.4875015 | 13.2909928 | 3.144 | |
| (124) | J055239.68-125839.6 | 88.1653641 | −12.9776924 | |
| J175239.90+125836.8 | 268.1662789 | 12.9768908 | ||
| (125) | J143527.45-115442.8 | 218.8644074 | −11.9119024 | |
| J023527.48+115445.4 | 38.8645354 | 11.9126238 | ||
| (126) | J000055.44-113218.8 | 0.2310389 | −11.5385816 | |
| J120055.36+113219.3 | 180.2306821 | 11.5387135 | ||
| (127) | J123939.37-104706.9 | 189.9140688 | −10.7852747 | |
| LQAC_009+010_017 | 9.913255077 | 10.78543594 | 2.425 | |
| (128) | J000622.70-095633.6 | 1.5946224 | −9.9426718 | |
| LQAC_181+009_011 | 181.5946887 | 9.941953343 | 1.534 | |
| (129) | J202753.35-094134.4 | 306.9723332 | −9.6928923 | |
| LQAC_126+009_048 | 126.9724849 | 9.693554141 | 0.83 | |
| (130) | J145149.26-093928.7 | 222.9552738 | −9.6579802 | |
| J025149.19+093931.4 | 42.9549795 | 9.6587312 | ||
| (131) | LQAC_038-009_025 | 38.5649606 | −9.392240877 | 3.159 |
| LQAC_218+009_031 | 218.5647428 | 9.392719278 | 1.796 | |
| (132) | J000505.01-090230.9 | 1.2708766 | −9.041933 | |
| J120505.01+090230.4 | 181.2708763 | 9.0417792 | ||
| (133) | J035733.19-083041.3 | 59.388302 | −8.5114804 | |
| J155733.13+083042.9 | 239.3880664 | 8.5119305 | 0.047 | |
| (134) | J204510.69-081616.2 | 311.2945797 | −8.2711881 | |
| LQAC_131+008_030 | 131.2935706 | 8.271914842 | 2.247 | |
| (135) | J110555.82-080323.2 | 166.4826173 | −8.0564548 | |
| J230555.63+080319.9 | 346.4818073 | 8.0555318 | ||
| (136) | J110555.82-080323.2 | 166.4826173 | −8.0564548 | |
| L_346.482+8.05556 | 346.4818408 | 8.0555638 | 1.52 | |
| (137) | J224014.32-072909.9 | 340.059673 | −7.4861023 | |
| LQAC_160+007_019 | 160.0601378 | 7.487028237 | 3.14 | |
| (138) | J144108.90-070313.6 | 220.2870849 | −7.053796 | |
| J024108.85+070311.3 | 40.2869077 | 7.053151 | ||
| (139) | J102333.26-055915.9 | 155.888588 | −5.987767 | |
| J222333.18+055919.4 | 335.8882806 | 5.988737 | ||
| (140) | LQAC_038-005_001 | 38.2399343 | −5.232025068 | 3.458 |
| LQAC_218+005_005 | 218.2393199 | 5.231581596 | 0.2 | |
| (141) | J213604.22-050152.0 | 324.0175956 | −5.0311184 | |
| LQAC_144+005_022 | 144.0166292 | 5.031056212 | 2.409 | |
| (142) | 025627.59-045343.6 | 44.11496329 | −4.895460489 | 1.645 |
| J145627.50+045340.4 | 224.1146139 | 4.8945605 | ||
| (143) | 004735.33-044137.5 | 11.89721807 | −4.693753563 | 1.931 |
| LQAC_191+004_014 | 191.8971418 | 4.694341169 | 0.868 | |
| (144) | J142138.70-043753.9 | 215.4112822 | −4.6316548 | |
| 022138.89+043751.6 | 35.41205565 | 4.631021039 | 2.018 | |
| (145) | 025636.11-043408.8 | 44.15049337 | −4.569125414 | 3.094 |
| J145635.91+043409.4 | 224.1496303 | 4.5692848 | ||
| (146) | J205234.08-042644.8 | 313.1420064 | −4.4457967 | |
| LQAC_133+004_022 | 133.1429082 | 4.446671684 | 2.745 | |
| (147) | J014824.02-033047.7 | 27.100084 | −3.5132583 | |
| J134823.84+033045.8 | 207.0993466 | 3.5127227 | ||
| (148) | 015710.06-032324.3 | 29.29195061 | −3.390086166 | 1.504 |
| J135710.20+032320.9 | 209.2925121 | 3.3891406 | ||
| (149) | J210657.03-025134.3 | 316.7376479 | −2.8595533 | |
| LQAC_136+002_017 | 136.7379 | 2.8592 | 0.194 | |
| (150) | 004751.36-025059.6 | 11.96401317 | −2.84989781 | 1.262 |
| LQAC_191+002_029 | 191.9631831 | 2.849151807 | 1.569 | |
| (151) | LQAC_323-002_008 | 323.6482112 | −2.773133154 | 3.227 |
| LQAC_143+002_018 | 143.648699 | 2.773614173 | 0.763 | |
| (152) | LQAC_197-002_026 | 197.6704167 | −2.227027778 | 1.765 |
| J011040.87+021336.5 | 17.6703106 | 2.2268189 | ||
| (153) | LQAC_221-002_011 | 221.5815417 | −2.054722222 | 1.021 |
| 024619.69+020317.5 | 41.58205972 | 2.054880133 | 1.611 | |
| (154) | 022538.91-012519.8 | 36.41214596 | −1.422178345 | 0.727 |
| LQAC_216+001_018 | 216.4125417 | 1.4225 | 1.136 | |
| (155) | LQAC_179-001_037 | 179.9377083 | −1.372166667 | 1.275 |
| 235945.22+012216.3 | 359.9384346 | 1.371206026 | 1.222 | |
| (156) | LQAC_322-001_003 | 322.04071 | −1.110389 | 2.017 |
| LQAC_142+001_019 | 142.0406947 | 1.109906236 | 0.691 | |
| (157) | J134857.45-005815.3 | 207.2393956 | −0.9709267 | |
| LQAC_027+000_061 | 27.23865057 | 0.970120818 | 2.259 | |
| (158) | LQAC_191-000_049 | 191.5187217 | −0.947792721 | 1.734 |
| LQAC_011+000_123 | 11.51886623 | 0.948653301 | 2.394 | |
| (159) | 004034.86-003821.0 | 10.14525273 | −0.63918039 | 1.836 |
| LQAC_190+000_011 | 190.1443333 | 0.638194444 | 1.856 | |
| (160) | LQAC_322-000_101 | 322.7183014 | −0.582968066 | 2.654 |
| LQAC_142+000_040 | 142.7177231 | 0.583039252 | 1.771 | |
| (161) | LQAC_158-000_052 | 158.592239 | −0.434856 | 1.161 |
| J223422.00+002605.4 | 338.5917077 | 0.4348598 | ||
| (162) | LQAC_348-000_009 | 348.109802 | −0.419542 | 1.105 |
| LQAC_168+000_003 | 168.1099167 | 0.419027778 | 1.309 | |
| (163) | 025901.84-001654.9 | 44.75769361 | −0.281929479 | 1.406 |
| LQAC_224+000_062 | 224.757095 | 0.281169 | 1.58 | |
| (164) | 01281.493-001442.6 | 22.00622083 | −0.245181678 | 1.088 |
| J132801.70+001440.0 | 202.007088 | 0.2444674 | ||
| (165) | J125103.72-001224.5 | 192.7655083 | −0.2068329 | |
| 005103.89+001227.4 | 12.766223 | 0.207611943 | 2.12 | |
| (166) | LQAC_352-000_049 | 352.8172404 | −0.117229211 | 1.696 |
| LQAC_172+000_041 | 172.8182083 | 0.118 | 1.784 | |
| (167) | LQAC_321-000_023 | 321.297455 | −0.085293 | 2.308 |
| LQAC_141+000_022 | 141.2979311 | 0.085854987 | 2.698 |
| Name | Ra | Dec | Z | |
|---|---|---|---|---|
| (1) | J015410.35-770145.4 | 28.5431453 | −77.0292865 | |
| J135410.15+770146.8 | 208.5423058 | 77.0296683 | ||
| (2) | J210304.14-762224.9 | 315.7672779 | −76.3735957 | |
| J090304.41+762224.0 | 135.7684133 | 76.3733506 | ||
| (3) | J224505.82-621922.8 | 341.2742892 | −62.3230084 | |
| 104505.93+621922.8 | 161.2747324 | 62.32302149 | 1.342 | |
| (4) | J234926.29-564624.9 | 357.3595443 | −56.7735858 | |
| 114926.22+564624.9 | 177.359266 | 56.77360707 | 1.459 | |
| (5) | J014520.31-551733.1 | 26.3346552 | −55.2925322 | |
| J134520.13+551734.6 | 206.3338867 | 55.2929689 | ||
| (6) | J004443.92-544532.5 | 11.183014 | −54.7590464 | |
| J124443.89+544531.9 | 191.1828838 | 54.7588612 | ||
| (7) | J013702.04-513252.3 | 24.2585004 | −51.5478865 | |
| 133702.07+513252.1 | 204.2586596 | 51.54780646 | 3.123 | |
| (8) | J115039.86-483126.9 | 177.6660978 | −48.5241579 | |
| J235039.73+483125.6 | 357.665564 | 48.5237961 | ||
| (9) | J000333.34-463348.8 | 0.8889306 | −46.5635617 | |
| J120333.26+463349.2 | 180.888613 | 46.5636756 | ||
| (10) | J235842.78-462119.9 | 359.6782761 | −46.3555539 | |
| 115842.73+462119.3 | 179.6780673 | 46.35538626 | 1.441 | |
| (11) | J065832.76-413600.0 | 104.6365048 | −41.6000057 | |
| J185832.85+413601.2 | 284.6368963 | 41.6003466 | ||
| (12) | J034937.91-374902.4 | 57.4079661 | −37.8173499 | |
| J154937.76+374904.2 | 237.407344 | 37.8178398 | ||
| (13) | J032742.65-372227.2 | 51.9277313 | −37.3742363 | |
| LQAC_231+037_033 | 231.9276563 | 37.37406082 | 2.635 | |
| (14) | J002156.72-365749.2 | 5.4863348 | −36.9636685 | |
| LQAC_185+036_009 | 185.4861573 | 36.96344034 | 2.097 | |
| (15) | J015857.83-364051.5 | 29.74099 | −36.6809782 | |
| LQAC_209+036_041 | 209.7415028 | 36.68102127 | 1.325 | |
| (16) | J020724.39-363533.9 | 31.8516579 | −36.5927588 | |
| J140724.46+363534.6 | 211.8519458 | 36.5929712 | ||
| (17) | J023025.90-331514.2 | 37.6079221 | −33.2539609 | |
| J143026.02+331515.8 | 217.6084382 | 33.2543894 | ||
| (18) | J200045.51-300814.8 | 300.1896576 | −30.1374469 | |
| LQAC_120+030_023 | 120.1897932 | 30.13710584 | 1.344 | |
| (19) | J024444.36-252255.5 | 41.1848409 | −25.3821032 | |
| J144444.41+252254.9 | 221.1850503 | 25.3819393 | ||
| (20) | J031541.43-243539.7 | 48.9226614 | −24.5943802 | |
| LQAC_228+024_039 | 228.9221594 | 24.59465727 | 3.209 | |
| (21) | J205929.66-235649.1 | 314.8735964 | −23.9469948 | |
| LQAC_134+023_015 | 134.873161 | 23.9466925 | 1.078 | |
| (22) | J220054.23-230032.0 | 330.2259757 | −23.0089119 | |
| 100054.23+230031.6 | 150.2259966 | 23.00878724 | 3.027 | |
| (23) | J010230.99-223752.2 | 15.6291536 | −22.6311827 | |
| LQAC_195+022_028 | 195.6286998 | 22.63117677 | 3.406 | |
| (24) | J120429.60-215735.5 | 181.1233627 | −21.9598782 | |
| J000429.68+215736.0 | 1.1236965 | 21.9600236 | ||
| (25) | J035233.36-211221.7 | 58.1390267 | −21.2060385 | |
| J155233.38+211221.7 | 238.1391178 | 21.2060426 | ||
| (26) | J031653.77-202303.1 | 49.2240677 | −20.3842205 | |
| LQAC_229+020_017 | 229.2243051 | 20.38391551 | 2.662 | |
| (27) | J124510.71-180851.9 | 191.2946306 | −18.147767 | |
| J004510.62+180851.9 | 11.294273 | 18.147755 | ||
| (28) | J000055.44-113218.8 | 0.2310389 | −11.5385816 | |
| J120055.36+113219.3 | 180.2306821 | 11.5387135 | ||
| (29) | LQAC_038-009_025 | 38.5649606 | −9.392240877 | 3.159 |
| LQAC_218+009_031 | 218.5647428 | 9.392719278 | 1.796 | |
| (30) | J000505.01-090230.9 | 1.2708766 | −9.041933 | |
| J120505.01+090230.4 | 181.2708763 | 9.0417792 | ||
| (31) | J035733.19-083041.3 | 59.388302 | −8.5114804 | |
| J155733.13+083042.9 | 239.3880664 | 8.5119305 | 0.047 | |
| (32) | J210657.03-025134.3 | 316.7376479 | −2.8595533 | |
| LQAC_136+002_017 | 136.7379 | 2.8592 | 0.194 | |
| (33) | LQAC_323-002_008 | 323.6482112 | −2.773133154 | 3.227 |
| LQAC_143+002_018 | 143.648699 | 2.773614173 | 0.763 | |
| (34) | LQAC_197-002_026 | 197.6704167 | −2.227027778 | 1.765 |
| J011040.87+021336.5 | 17.6703106 | 2.2268189 | ||
| (35) | 022538.91-012519.8 | 36.41214596 | −1.422178345 | 0.727 |
| LQAC_216+001_018 | 216.4125417 | 1.4225 | 1.136 | |
| (36) | LQAC_322-001_003 | 322.04071 | −1.110389 | 2.017 |
| LQAC_142+001_019 | 142.0406947 | 1.109906236 | 0.691 |
| Name | Ra | Dec | Z | |
|---|---|---|---|---|
| (1) | LQAC_323-045_002 | 323.0704 | −45.8867 | 1.025 |
| 093214.29+455249.2 | 143.059556 | 45.8803591 | 1.094 | |
| (2) | LQAC_001-041_001 | 1.0375 | −41.9756 | 1.72 |
| 120411.17+415814.6 | 181.0465681 | 41.97072878 | 1.691 | |
| (3) | LQAC_024-041_004 | 24.1579 | −41.7931 | 2.2 |
| 133639.64+414711.0 | 204.1651671 | 41.78641438 | 2.166 | |
| (4) | LQAC_352-041_001 | 352.816472 | −41.149396 | 0.252 |
| 113113.06+410907.9 | 172.8044242 | 41.15221529 | 0.27 | |
| (5) | LQAC_341-038_001 | 341.686232 | −38.454078 | 2.16 |
| LQAC_161+038_026 | 161.6971609 | 38.45968469 | 2.224 | |
| (6) | LQAC_338-037_002 | 338.196898 | −37.619514 | 2.33 |
| LQAC_158+037_019 | 158.2064503 | 37.61361655 | 2.353 | |
| (7) | LQAC_329-036_002 | 329.2175 | −36.8133 | 1.94 |
| 095651.30+364813.9 | 149.2137769 | 36.80387676 | 1.898 | |
| (8) | LQAC_338-036_001 | 338.1892 | −36.5347 | 2.262 |
| 103246.43+363154.9 | 158.1934861 | 36.5319377 | 2.199 | |
| (9) | LQAC_017-032_009 | 17.217685 | −32.875892 | 2.23 |
| J130849.50+325201.7 | 197.2062585 | 32.8671451 | 2.239 | |
| (10) | LQAC_012-031_011 | 12.378625 | −31.54333333 | 1.577 |
| LQAC_192+031_011 | 192.3716769 | 31.5394031 | 1.582 | |
| (11) | LQAC_343-031_010 | 343.14375 | −31.32902778 | 0.805 |
| 105237.20+311957.6 | 163.1550379 | 31.33268011 | 0.801 | |
| (12) | LQAC_339-030_005 | 339.202 | −30.62991667 | 0.856 |
| J103648.90+303806.7 | 159.2037895 | 30.6352135 | 0.926 | |
| (13) | LQAC_326-030_015 | 326.3645 | −30.50294444 | 1.142 |
| LQAC_146+030_004 | 146.3607191 | 30.49396248 | 1.165 | |
| (14) | LQAC_042-030_018 | 42.34833333 | −30.40694444 | 2.033 |
| LQAC_222+030_024 | 222.3522302 | 30.4163666 | 2.029 | |
| (15) | LQAC_035-030_020 | 35.70970833 | −30.39716667 | 1.654 |
| L_215.718+30.39543 | 215.7180284 | 30.3954277 | 1.657 | |
| (16) | LQAC_337-030_014 | 337.3667083 | −30.11483333 | 0.555 |
| LQAC_157+030_003 | 157.3651363 | 30.11835308 | 0.561 | |
| (17) | LQAC_015-029_022 | 15.41258333 | −29.54566667 | 1.418 |
| L_195.403+29.55539 | 195.403134 | 29.5553877 | 1.445 | |
| (18) | LQAC_037-029_003 | 37.03429167 | −29.39491667 | 1.939 |
| L_217.024+29.40348 | 217.0237318 | 29.4034762 | 1.916 | |
| (19) | LQAC_337-029_001 | 337.0180833 | −29.26602778 | 1.5 |
| 102804.15+291620.6 | 157.0173061 | 29.27240187 | 1.53 | |
| (20) | LQAC_341-028_031 | 341.8202917 | −28.21711111 | 2.062 |
| 104714.52+281330.9 | 161.8105168 | 28.2252619 | 2.019 | |
| (21) | LQAC_005-028_016 | 5.404041667 | −28.20741667 | 1.208 |
| J122139.32+281151.6 | 185.4138653 | 28.1976789 | 1.128 | |
| (22) | LQAC_345-027_028 | 345.88075 | −27.661 | 1.35 |
| J110329.85+273905.9 | 165.8743991 | 27.6516402 | 1.428 | |
| (23) | LQAC_043-027_005 | 43.17745833 | −27.55630556 | 1.661 |
| L_223.187+27.55884 | 223.1867024 | 27.5588391 | 1.666 | |
| (24) | LQAC_332-027_003 | 332.1489167 | −27.53458333 | 0.792 |
| LQAC_152+027_003 | 152.1399094 | 27.54382611 | 0.886 | |
| (25) | LQAC_022-009_008 | 22.30469877 | −9.012753558 | 1.949 |
| LQAC_202+009_021 | 202.312047 | 9.022032441 | 2.03 | |
| (26) | 024703.63-083644.3 | 41.76514018 | −8.612317408 | 3.168 |
| LQAC_221+008_036 | 221.7690357 | 8.602943548 | 3.172 | |
| (27) | LQAC_046-008_008 | 46.38831776 | −8.530334761 | 2.258 |
| LQAC_226+008_021 | 226.3879189 | 8.53907539 | 2.34 | |
| (28) | 021642.26-051801.7 | 34.17612153 | −5.300498064 | 1.043 |
| LQAC_214+005_001 | 214.1790392 | 5.303307824 | 1.09 | |
| (29) | 024509.67-045526.6 | 41.29030614 | −4.924073165 | 1.814 |
| LQAC_221+004_007 | 221.2829568 | 4.920292343 | 1.854 | |
| (30) | J021504.48-044619.0 | 33.7686732 | −4.7719598 | 0.3 |
| LQAC_213+004_010 | 213.7746265 | 4.762817113 | 0.241 | |
| (31) | 020427.68-043739.2 | 31.11533444 | −4.62757387 | 0.212 |
| LQAC_211+004_004 | 211.1183809 | 4.635500685 | 0.258 | |
| (32) | LQAC_031-004_020 | 31.63195811 | −4.613700851 | 2.301 |
| LQAC_211+004_022 | 211.6411524 | 4.606115539 | 2.261 | |
| (33) | 022142.03-042712.6 | 35.4251408 | −4.453523132 | 2.841 |
| LQAC_215+004_028 | 215.4293621 | 4.460833849 | 2.832 | |
| (34) | 005202.36-041315.2 | 13.00984088 | −4.220910489 | 2.127 |
| LQAC_193+004_006 | 193.0041244 | 4.226636732 | 2.173 | |
| (35) | 002316.99-035309.0 | 5.82080727 | −3.885844542 | 2.179 |
| LQAC_185+003_036 | 185.8174826 | 3.894175851 | 2.221 | |
| (36) | 001214.99-034351.5 | 3.062461902 | −3.730985145 | 1.602 |
| LQAC_183+003_004 | 183.0584417 | 3.738243028 | 1.505 | |
| (37) | 023848.33-032632.8 | 39.7013883 | −3.44244926 | 1.356 |
| LQAC_219+003_009 | 219.7041461 | 3.44386827 | 1.443 | |
| (38) | LQAC_195-003_002 | 195.2479809 | −3.42588229 | 1.708 |
| 010057.65+032504.1 | 15.24021079 | 3.417809261 | 1.778 | |
| (39) | 010115.16-031401.5 | 15.31318916 | −3.233765642 | 2.088 |
| LQAC_195+003_006 | 195.3180605 | 3.240485078 | 2.102 | |
| (40) | 020823.25-025701.2 | 32.09690554 | −2.950335837 | 1.44 |
| LQAC_212+002_003 | 212.0902993 | 2.959248154 | 1.344 | |
| (41) | LQAC_163-002_014 | 163.3850417 | −2.929666667 | 2.059 |
| L_343.376+2.93350 | 343.376148 | 2.9334976 | 2.1 | |
| (42) | 023823.01-025529.0 | 39.59588451 | −2.924741709 | 2.149 |
| LQAC_219+002_035 | 219.5861076 | 2.924167023 | 2.171 | |
| (43) | LQAC_222-002_009 | 222.2378325 | −2.873268642 | 1.104 |
| 024854.69+025153.4 | 42.22789614 | 2.864856903 | 1.154 | |
| (44) | LQAC_195-002_015 | 195.4199167 | −2.823055556 | 1.645 |
| 010142.45+024933.5 | 15.42690572 | 2.825980823 | 1.721 | |
| (45) | LQAC_179-002_034 | 179.1020791 | −2.777284206 | 1.896 |
| 235622.51+024641.2 | 359.0937999 | 2.778136548 | 1.841 | |
| (46) | LQAC_213-002_014 | 213.5926667 | −2.653888889 | 1.583 |
| 021424.01+023911.0 | 33.60007716 | 2.653061423 | 1.587 | |
| (47) | LQAC_176-002_051 | 176.783068 | −2.542637898 | 2.769 |
| LQAC_356+002_027 | 356.7779822 | 2.549142614 | 2.749 | |
| (48) | LQAC_206-002_018 | 206.5271667 | −2.509166667 | 1.916 |
| 014608.18+023051.8 | 26.53412076 | 2.514405525 | 2.008 | |
| (49) | LQAC_208-002_045 | 208.7652311 | −2.485529271 | 2.354 |
| LQAC_028+002_027 | 28.77499853 | 2.480155238 | 2.358 | |
| (50) | LQAC_215-002_027 | 215.8487083 | −2.356361111 | 0.757 |
| LQAC_035+002_026 | 35.84129832 | 2.362110145 | 0.84 | |
| (51) | LQAC_148-002_037 | 148.4734564 | −2.321739174 | 2.224 |
| LQAC_328+002_011 | 328.4781814 | 2.316791172 | 2.299 | |
| (52) | LQAC_179-002_002 | 179.020875 | −2.246777778 | 1.14 |
| 235603.14+021446.8 | 359.0130905 | 2.246339818 | 1.206 | |
| (53) | LQAC_174-002_024 | 174.7015417 | −2.005444444 | 0.992 |
| L_354.707+1.99734 | 354.7073047 | 1.9973398 | 1.059 | |
| (54) | 004013.64-013749.5 | 10.05686326 | −1.630422554 | 1.25 |
| LQAC_190+001_003 | 190.0556247 | 1.635763502 | 1.341 | |
| (55) | LQAC_179-001_037 | 179.9377083 | −1.372166667 | 1.275 |
| 235945.22+012216.3 | 359.9384346 | 1.371206026 | 1.222 | |
| (56) | 024059.55-011946.1 | 40.24816336 | −1.329490927 | 0.829 |
| LQAC_220+001_009 | 220.2400454 | 1.337454418 | 0.732 | |
| (57) | LQAC_207-001_015 | 207.3852083 | −1.317583333 | 2.123 |
| 014932.65+011923.8 | 27.38605106 | 1.323303146 | 2.114 | |
| (58) | LQAC_189-001_016 | 189.5481398 | −1.272113467 | 1.192 |
| 003811.30+011630.5 | 9.547112026 | 1.275139173 | 1.29 | |
| (59) | LQAC_052-001_011 | 52.90720523 | −1.205552203 | 2.205 |
| LQAC_232+001_028 | 232.9102632 | 1.200941917 | 2.261 | |
| (60) | LQAC_196-001_048 | 196.9642917 | −1.092222222 | 1.296 |
| 010749.71+010541.9 | 16.95715341 | 1.094976798 | 1.199 | |
| (61) | 002538.20-010416.9 | 6.409207232 | −1.071365841 | 1.179 |
| LQAC_186+001_018 | 186.4122083 | 1.067027778 | 1.199 | |
| (62) | LQAC_187-001_015 | 187.3914685 | −1.03950696 | 2.33 |
| LQAC_007+001_037 | 7.389802282 | 1.037764215 | 2.276 | |
| (63) | LQAC_206-001_014 | 206.325195 | −1.032847 | 1.891 |
| 014517.74+010212.0 | 26.32392414 | 1.036693288 | 1.88 | |
| (64) | 023532.16-010157.7 | 38.88400215 | −1.032720469 | 2.084 |
| LQAC_218+001_024 | 218.8835417 | 1.038777778 | 2.012 | |
| (65) | LQAC_176-001_017 | 176.4090716 | −1.002939638 | 0.88 |
| LQAC_356+001_034 | 356.4154007 | 1.009270159 | 0.783 | |
| (66) | LQAC_012-001_011 | 12.6204 | −1.0025 | 0.103 |
| LQAC_192+001_025 | 192.6208 | 1.0053 | 0.147 | |
| (67) | LQAC_034-000_125 | 34.16339129 | −0.98950573 | 2.214 |
| LQAC_214+000_030 | 214.1595018 | 0.998719425 | 2.154 | |
| (68) | LQAC_034-000_107 | 34.94479384 | −0.97750017 | 1.155 |
| LQAC_214+000_027 | 214.946027 | 0.984763668 | 1.125 | |
| (69) | LQAC_033-000_121 | 33.45681868 | −0.972846554 | 2.862 |
| LQAC_213+000_041 | 213.4528988 | 0.967259011 | 2.842 | |
| (70) | L_332.899-0.95608 | 332.89911 | −0.95608 | 1.064 |
| LQAC_152+000_068 | 152.8977796 | 0.961987871 | 1.072 | |
| (71) | 025749.51-005615.4 | 44.45630123 | −0.937630641 | 1.448 |
| L_224.466+0.92774 | 224.4661485 | 0.9277391 | 1.465 | |
| (72) | LQAC_234-000_006 | 234.3883287 | −0.92714033 | 0.542 |
| LQAC_054+000_035 | 54.38578906 | 0.92988287 | 0.625 | |
| (73) | LQAC_217-000_018 | 217.538268 | −0.888678729 | 0.809 |
| 023008.27+005323.1 | 37.53447644 | 0.889773333 | 0.748 | |
| (74) | LQAC_220-000_041 | 220.4374167 | −0.874083333 | 1.474 |
| 024147.26+005202.0 | 40.44692945 | 0.867240769 | 1.491 | |
| (75) | LQAC_213-000_072 | 213.805206 | −0.839989 | 1.013 |
| 021511.24+005017.3 | 33.79686409 | 0.838139499 | 1.091 | |
| (76) | LQAC_206-000_070 | 206.7435 | −0.8315 | 1.758 |
| 014659.79+004932.6 | 26.74914722 | 0.825734516 | 1.706 | |
| (77) | LQAC_000-000_043 | 0.669873496 | −0.801015302 | 1.735 |
| L_180.661+0.79757 | 180.6608942 | 0.7975713 | 1.786 | |
| (78) | J032945.45-004637.9 | 52.4393772 | −0.7772181 | 0.572 |
| LQAC_232+000_027 | 232.4304194 | 0.77602973 | 0.647 | |
| (79) | LQAC_141-000_050 | 141.571304 | −0.697299 | 1.358 |
| LQAC_321+000_037 | 321.5625466 | 0.692807157 | 1.316 | |
| (80) | LQAC_165-000_005 | 165.096619 | −0.674177 | 1.016 |
| LQAC_345+000_062 | 345.0945234 | 0.680428018 | 1.007 | |
| (81) | LQAC_184-000_054 | 184.0036197 | −0.66664066 | 1.843 |
| LQAC_004+000_050 | 4.010976393 | 0.675646913 | 1.796 | |
| (82) | 001902.13-003854.1 | 4.758914043 | −0.648366254 | 1.149 |
| LQAC_184+000_035 | 184.761625 | 0.651361111 | 1.206 | |
| (83) | 004034.86-003821.0 | 10.14525273 | −0.63918039 | 1.836 |
| LQAC_190+000_011 | 190.1443333 | 0.638194444 | 1.856 | |
| (84) | LQAC_191-000_046 | 191.4796594 | −0.626509606 | 1.041 |
| 004557.02+003756.0 | 11.48759265 | 0.632247161 | 1.021 | |
| (85) | 013943.85-003612.0 | 24.93271241 | −0.603355207 | 1.599 |
| LQAC_204+000_072 | 204.927017 | 0.600137 | 1.513 | |
| (86) | LQAC_200-000_080 | 200.864944 | −0.591986 | 1.278 |
| 012326.07+003526.9 | 20.85864192 | 0.590813358 | 1.237 | |
| (87) | LQAC_190-000_051 | 190.427048 | −0.591902 | 1.12 |
| LQAC_010+000_031 | 10.42275671 | 0.595793629 | 1.163 | |
| (88) | LQAC_011-000_090 | 11.99853783 | −0.573200853 | 1.029 |
| LQAC_192+000_001 | 192.0050833 | 0.571 | 0.947 | |
| (89) | LQAC_153-000_082 | 153.0728207 | −0.52940076 | 2.449 |
| LQAC_333+000_064 | 333.0824573 | 0.526179819 | 2.382 | |
| (90) | 025457.39-003121.2 | 43.73915361 | −0.52258078 | 1.637 |
| LQAC_223+000_056 | 223.736237 | 0.51361 | 1.724 | |
| (91) | 014437.46-003109.0 | 26.15609597 | −0.519180884 | 1.484 |
| LQAC_206+000_013 | 206.1542083 | 0.515277778 | 1.519 | |
| (92) | LQAC_193-000_021 | 193.4251667 | −0.501277778 | 1.732 |
| 005341.92+002946.8 | 13.42470551 | 0.496353312 | 1.641 | |
| (93) | LQAC_329-000_018 | 329.3428611 | −0.492357153 | 1.92 |
| LQAC_149+000_015 | 149.3335 | 0.4955 | 1.975 | |
| (94) | LQAC_177-000_044 | 177.2740753 | −0.490986415 | 2.361 |
| LQAC_357+000_032 | 357.2708931 | 0.481955999 | 2.369 | |
| (95) | LQAC_209-000_091 | 209.930389 | −0.487416 | 2.146 |
| 015941.34+002901.8 | 29.92227712 | 0.48385759 | 2.079 | |
| (96) | LQAC_358-000_006 | 358.0841585 | −0.46555538 | 0.879 |
| LQAC_178+000_006 | 178.0850417 | 0.459777778 | 0.796 | |
| 97) | LQAC_137-000_008 | 137.1205388 | −0.411421257 | 2.629 |
| LQAC_317+000_030 | 317.1176049 | 0.409202564 | 2.641 | |
| (98) | LQAC_207-000_063 | 207.787033 | −0.390158 | 1.378 |
| 015110.52+002310.9 | 27.79384904 | 0.386374118 | 1.438 | |
| (99) | LQAC_200-000_054 | 200.618759 | −0.322608 | 1.633 |
| 012229.74+001916.2 | 20.62394575 | 0.321178062 | 1.594 | |
| (100) | LQAC_039-000_023 | 39.52240355 | −0.281156871 | 1.237 |
| LQAC_219+000_042 | 219.530411 | 0.271528 | 1.213 | |
| (101) | 011435.92-000715.2 | 18.64967272 | −0.120890254 | 1.643 |
| LQAC_198+000_052 | 198.652847 | 0.122162 | 1.661 | |
| (102) | LQAC_352-000_049 | 352.8172404 | −0.117229211 | 1.696 |
| LQAC_172+000_041 | 172.8182083 | 0.118 | 1.784 | |
| (103) | 025702.92-000634.0 | 44.26220206 | −0.109449378 | 2.155 |
| LQAC_224+000_019 | 224.2601385 | 0.108301193 | 2.167 | |
| (104) | LQAC_011-000_070 | 11.75031949 | −0.049399404 | 1.685 |
| LQAC_191+000_059 | 191.752487 | 0.054056 | 1.622 | |
| (105) | 012505.61-000246.1 | 21.27338412 | −0.046155587 | 1.98 |
| LQAC_201+000_012 | 201.278641 | 0.042633 | 2.075 | |
| (106) | LQAC_346-000_064 | 346.859192 | −0.037073 | 0.704 |
| LQAC_166+000_061 | 166.862991 | 0.0435 | 0.664 | |
| (107) | LQAC_039-000_036 | 39.74662363 | −0.032826977 | 0.813 |
| LQAC_219+000_061 | 219.744125 | 0.025444444 | 0.829 | |
| (108) | 000448.01-000108.7 | 1.2000593 | −0.019109312 | 2.259 |
| LQAC_181+000_059 | 181.2008147 | 0.026026332 | 2.257 | |
| (109) | LQAC_345-000_001 | 345.012421 | −0.00797 | 1.703 |
| LQAC_165+000_003 | 165.0160833 | 0.006333333 | 1.787 |
| Name | Ra | Dec | Z | |
|---|---|---|---|---|
| (1) | LQAC_332-029_006 | 332.17575 | −29.98391667 | 1.0232 |
| 100842.39+295905.0 | 152.176654 | 29.98472533 | 2.56 | |
| (2) | LQAC_333-028_039 | 333.8812083 | −28.33372222 | 1.9087 |
| 101531.57+282003.3 | 153.8815418 | 28.33425215 | 2.395 | |
| (3) | LQAC_038-009_025 | 38.5649606 | −9.392240877 | 3.15853 |
| LQAC_218+009_031 | 218.5647428 | 9.392719278 | 1.79609 | |
| (4) | 004735.33-044137.5 | 11.89721807 | −4.693753563 | 1.93149 |
| LQAC_191+004_014 | 191.8971418 | 4.694341169 | 0.86833 | |
| (5) | 004751.36-025059.6 | 11.96401317 | −2.84989781 | 1.262066 |
| LQAC_191+002_029 | 191.9631831 | 2.849151807 | 1.56871 | |
| (6) | LQAC_221-002_011 | 221.5815417 | −2.054722222 | 1.0214 |
| 024619.69+020317.5 | 41.58205972 | 2.054880133 | 1.610928 | |
| (7) | 022538.91-012519.8 | 36.41214596 | −1.422178345 | 0.72737 |
| LQAC_216+001_018 | 216.4125417 | 1.4225 | 1.1363 | |
| (8) | LQAC_179-001_037 | 179.9377083 | −1.372166667 | 1.2752 |
| 235945.22+012216.3 | 359.9384346 | 1.371206026 | 1.222477 | |
| (9) | LQAC_322-001_003 | 322.04071 | −1.110389 | 2.0165 |
| LQAC_142+001_019 | 142.0406947 | 1.109906236 | 0.69137 | |
| (10) | LQAC_191-000_049 | 191.5187217 | −0.947792721 | 1.73388 |
| LQAC_011+000_123 | 11.51886623 | 0.948653301 | 2.3943 | |
| (11) | 004034.86-003821.0 | 10.14525273 | −0.63918039 | 1.835918 |
| LQAC_190+000_011 | 190.1443333 | 0.638194444 | 1.8557 | |
| (12) | LQAC_322-000_101 | 322.7183014 | −0.582968066 | 2.65398 |
| LQAC_142+000_040 | 142.7177231 | 0.583039252 | 1.7708 | |
| (13) | LQAC_348-000_009 | 348.109802 | −0.419542 | 1.1047 |
| LQAC_168+000_003 | 168.1099167 | 0.419027778 | 1.3086 | |
| (14) | 025901.84-001654.9 | 44.75769361 | −0.281929479 | 1.405797 |
| LQAC_224+000_062 | 224.757095 | 0.281169 | 1.5796 | |
| (15) | LQAC_352-000_049 | 352.8172404 | −0.117229211 | 1.69638 |
| LQAC_172+000_041 | 172.8182083 | 0.118 | 1.7844 | |
| (16) | LQAC_321-000_023 | 321.297455 | −0.085293 | 2.3081 |
| LQAC_141+000_022 | 141.2979311 | 0.085854987 | 2.69755 |
References
- Whittaker, E. Spin in the Universe. In Yearbook of Roy.Soc.Edinburgh; The University of Edinburgh: Edinburgh, UK, 1945; pp. 5–13. [Google Scholar]
- Lemaıtre, G. L’Hypothèse de L’atome Primitif: Essai de Cosmogonie; Griffon: Neuchâtel, Switzerland, 1946; p. 201. [Google Scholar]
- Weyssenhoff, J.; Raabe, A. Relativistic dynamics of spin fluids and spin particles. Acta Phys. Polon. 1947, 9, 7–18. [Google Scholar]
- Korotkii, V.A.; Obukhov, Y.N. Generalized model of fluid with spin. Sov. Phys. J. 1991, 34, 165–168. [Google Scholar] [CrossRef]
- Balachandran, A.; Мапnо, G.; Skagerstram, B.; Stern, A. Gauge fields, extended objects and states of matter. J. Phys. G 1981, 7, 1001–1017. [Google Scholar] [CrossRef]
- Petrova, N.; Sandina, I. On the method of obtaining equations of motion in general relativity theory. In Fizika; Kazahskii Gosudarstvennii universitet: Almaty, Kazakhstan, 1970; pp. 220–221. (In Russian) [Google Scholar]
- Sandina, I. Motion of extended bodies in general relativity and gravitational radiation. Sov. Phys. J. 1985, 28, 9–12. [Google Scholar] [CrossRef]
- Korotky, V.A.; Obukhov, Y.N. Microwave Background Radiation in Rotating Cosmology; Warsaw University: Warsaw, Poland, 1987. [Google Scholar]
- Нawking, S. Оn the rotation of the Universe. Mon. Not. R. Astron. Soc. 1969, 142, 129–141. [Google Scholar] [CrossRef]
- Obukhov, Y.N. Observations in Rotating Cosmologies. In Gauge Theories of Fundamental Interactions; Raczka, R., Pawlowski, M., Eds.; World Scientific: Singapore, 1990; pp. 341–366. [Google Scholar]
- Hasse, W.; Perlick, V. Geometrical and kinematical characterization of parallax-free world models. J. Math. Phys. 1988, 29, 2064–2068. [Google Scholar] [CrossRef]
- Treder, H.-J. Abberrations-Konstante und Rotation des Kosmos. Ann. Phys. 1985, 42, 71–72. [Google Scholar] [CrossRef]
- Ruben, G. Die Rotation des Kosmos aus der Aberration von Quasaren. Ann. Phys. 1987, 44, 150–152. [Google Scholar] [CrossRef]
- Gödel, K. An Example of a New Type of Cosmological Solutions of Einstein’s Field Equations of Gravitation. Rev. Mod. Phys. 1949, 21, 447–450. [Google Scholar] [CrossRef]
- Maitra, S. Stationary Dust-Filled Cosmological Solution with Λ = 0 and without Closed Timelike Lines. J. Math. Phys. 1966, 7, 1025–1030. [Google Scholar] [CrossRef]
- Lee, J.H.; Pak, M.; Lee, H.-R.; Song, H. Galaxy Rotation Coherent with the Motions of Neighbors: Discovery of Observational Evidence. Astrophys. J. 2019, 872, 78. [Google Scholar] [CrossRef]
- Lee, J.H.; Pak, M.; Song, H.; Lee, H.-R.; Kim, S.; Jeong, H. Mysterious coherence in several-megaparsec scales between galaxy rotation and neighbor motion. Astrophys. J. 2019, 884, 104. [Google Scholar] [CrossRef]
- Ray, J.; Smalley, L. Improved perfect fluid energy-momentum tensor with spin in Einstein-Cartan space-time. Phys. Rev. Lett. 1982, 49, 1059–1061. [Google Scholar] [CrossRef]
- Korotkii, V.A.; Obukhov, Y.N. Bianchi-II cosmological models with rotation in general relativity theory. Russ. Phys. J. 1994, 37, 961–970. [Google Scholar] [CrossRef]
- Korotkii, V.A.; Obukhov, Y.N. General-relativistic cosmology with expansion and rotation. Russ. Phys. J. 1993, 36, 568–573. [Google Scholar] [CrossRef]
- Korotkii, V.A.; Obukhov, Y.N. Bianchi-IX cosmological models with rotation in general relativity. Russ. Phys. J. 1994, 37, 909–914. [Google Scholar] [CrossRef]
- Korotky, V.A.; Obukhov, Y.N. Rotating cosmologies in Poincare gauge gravity. In The Universe Rotation: Pro and Contra; Myrzakulov, R., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2017; pp. 157–205. [Google Scholar]
- Korotkii, V.A.; Obukhov, Y.N. Rotating and expanding cosmology in ECSK-theory. Astrophys. Space Sci. 1992, 198, 1–12. [Google Scholar] [CrossRef]
- Riess, A.; Filippenko, A.; Challis, P.; Clocchiattia, A.; Diercks, A.; Garnavich, P.M.; Gilliand, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1072. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–598. [Google Scholar] [CrossRef]
- Broadhurst, Т.; Ellis, R.; Коо, D.; Szalay, А.S. Large-scale distribution of galaxies at the Galactic poles. Nature 1990, 343, 726–728. [Google Scholar] [CrossRef]
- Hill, С.; Steinhardt, Р.; Тurner, М. Can oscillating physics explain an apparently periodic universe? Phys. Lett. B 1990, 252, 343–348. [Google Scholar] [CrossRef]
- Korotky, V.A.; Obukhov, Y.N. Can Cosmic Rotation Explain an Apparently Periodic Universe? Gen. Relativ. Gravit. 1994, 26, 429–435. [Google Scholar] [CrossRef]
- Birch, P. Is the Universe rotating? Nature 1982, 298, 451–454. [Google Scholar] [CrossRef]
- Korotkii, V.A.; Obukhov, Y.N. Kinematic analysis of cosmological models with rotation. Sov. J. Exp. Theor. Phys. 1991, 72, 11–15. [Google Scholar]
- Korotkii, V.A.; Obukhov, Y.N. Polarization of radiation in а rotating universe. Sov. J. Exp. Theor. Phys. 1995, 81, 1031–1035. [Google Scholar]
- Panov, V.; Sbytov, Y. Accounting for Birch's observed anisotropy of the universe: Cosmological rotation? Sov. J. Exp. Theor. Phys. 1992, 74, 411–415. [Google Scholar]
- Korotky, V.A.; Obukhov, Y.N. On cosmic rotation. In Particles and Space-Time; Pronin, P., Sardanashvily, G., Eds.; World Scientific: Singapore, 1996; pp. 421–439. [Google Scholar]
- Korotky, V.A.; Obukhov, Y.N. Bianchi-II rotating world. Astrophys. Space Sci. 1999, 260, 425–439. [Google Scholar] [CrossRef]
- Obukhov, Y.N.; Korotky, V.A. The Weyssenhoff fluid in Einstein-Cartan Theory. Class. Quantum Gravity 1987, 4, 1633–1657. [Google Scholar] [CrossRef]
- Chilingarian, I.V.; Zolotukhin, I.Y.; Katkov, I.Y.; Melchior, A.-L.; Rubtsov, E.V.; Grishin, K.A. RCSED—A value-added reference catalog of spectral energy distributions of 800,299 galaxies in 11 ultraviolet, optical, and near-infrared bands: Morphologies, colors, ionized gas, and stellar population properties. Astrophys. J. Suppl. 2017, 228, 14. [Google Scholar] [CrossRef]
- Kuminski, E.; Shamir, L. Computer-generated visual morphology catalog of ~3,000,000 SDSS galaxies. Astrophys. J. Suppl. 2016, 223, 20. [Google Scholar] [CrossRef]
- Catalog of Broad Morphology of SDSS Galaxies. Available online: http://vfacstaff.ltu.edu/lshamir/data/morph_catalog/wndchrm_w_catalog.csv.gz (accessed on 10 January 2020).
- Catalog of Broad Morphology of SDSS Galaxies. Available online: http://vfacstaff.ltu.edu/lshamir/data/morph_catalog/wndchrm_spec_catalog.csv.gz (accessed on 10 January 2020).
- Catalog of Broad Morphology of SDSS Galaxies. Available online: http://vfacstaff.ltu.edu/lshamir/data/morph_catalog/wndchrm_catalog_n.csv.gz (accessed on 10 January 2020).
- Paul, N.; Virag, N.; Shamir, L. A Catalog of Photometric Redshift and the Distribution of Broad Galaxy Morphologies. Galaxies 2018, 6, 64. [Google Scholar] [CrossRef]
- Lindegren, L.; Hernández, J.; Bombrun, A.; Klioner, S.; Bastian, U.; Ramos-Lerate, M.; de Torres, A.; Steidelmuller, H.; Stephenson, C.; Hobbs, D.; et al. Gaia Data Release 2 The astrometric solution. Astron. Astrophys. 2018, 616, A2. [Google Scholar] [CrossRef]
- Mignard, F.; Klioner, S.A.; Lindegren, L.; Hernandez, J.; Bastian, U.; Bombrun, A.; Hobbs, D.; Lammers, U.; Michalik, D.; Ramos-Lerate, M.; et al. Gaia Data Release 2 The celestial reference frame (Gaia-CRF2). Astron. Astrophys. 2018, 616, A14. [Google Scholar]
- Brown, A.G.A.; Vallenari, A.; Prusti, T.; de Bruijne, J.H.J.; Babusiaux, C.; Barler-Jones, C.A.L.; Biermann, M.; Evans, D.W.; Eyer, L.; Jansen, F.; et al. Gaia Data Release 2 Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar]
- Flesch, E. The Half Million Quasars (HMQ) Catalogue. Publ. Astron. Soc. Aust. 2015, 32, E010. [Google Scholar] [CrossRef]
- The Million Quasars (Milliquas) Catalog, v6.3. 15 June 2019. Available online: http://quasars.org/milliquas.htm (accessed on 23 July 2019).
- MILLIQUAS—Million Quasars Catalog, Version 6.3. 16 June 2019. Available online: https://heasarc.gsfc.nasa.gov/W3Browse/all/milliquas.html (accessed on 23 July 2019).
- Liao, S.-L.; Qi, Z.-X.; Guo, S.-F.; Cao, Z.-H. A compilation of known QSOs for the Gaia mission. Res. Astron. Astrophys. 2019, 19, 29. [Google Scholar] [CrossRef]
- Prokhorov, G.Y.; Teryaev, O.V.; Zakharov, V.I. Axial current in rotating and accelerating medium. Phys. Rev. D 2018, 98. [Google Scholar] [CrossRef]
- Prokhorov, G.Y.; Teryaev, O.V.; Zakharov, V.I. Unruh effect for fermions from the Zubarev density operator. Phys. Rev. D 2019, 99. [Google Scholar] [CrossRef]
- Prokhorov, G.Y.; Teryaev, O.V.; Zakharov, V.I. Effects of rotation and acceleration in the axial current: Density operator vs Wigner function. J. High Energy Phys. 2019, 146. [Google Scholar] [CrossRef]
- Teryaev, O.; Usubov, R. Vorticity and hydrodynamic helicity in heavy-ion collisions in the hadron-string dynamics model. Phys. Rev. C 2015, 92. [Google Scholar] [CrossRef]
- Baznat, M.; Gudima, K.; Sorin, A.; Teryaev, O. Femto-vortex sheets and hyperon polarization in heavy-ion collisions. Phys. Rev. C 2016, 93. [Google Scholar] [CrossRef]
- Rustamov, A.; Rustamov, J.N. On the spiral structures in heavy-ion collisions. arXiv 2016, arXiv:1602.01812. [Google Scholar]
- Martynova, A.; Teryaev, O.V. Search for spiral structures in heavy ion physics and astrometry. In Proceedings of the Talk at XVIII Workshop on High Energy Spin Physics (DSPIN19), Dubna, Russia, 2–6 September 2019. [Google Scholar]
| 1 | Let us note that without filtering original catalog to have only unique objects, one would have instead 1533 pairs of galaxies, composed of 802 galaxies where 448 galaxies are in more than one pair. However, only 725 from these 802 galaxies are unique objects so 77 galaxies are repeating objects with different IDs. |
| 2 | |
| 3 | It also tests our filtering which, for evenly distributed objects, should give approximately 100-times less pairs when eps decreases 10 times. |
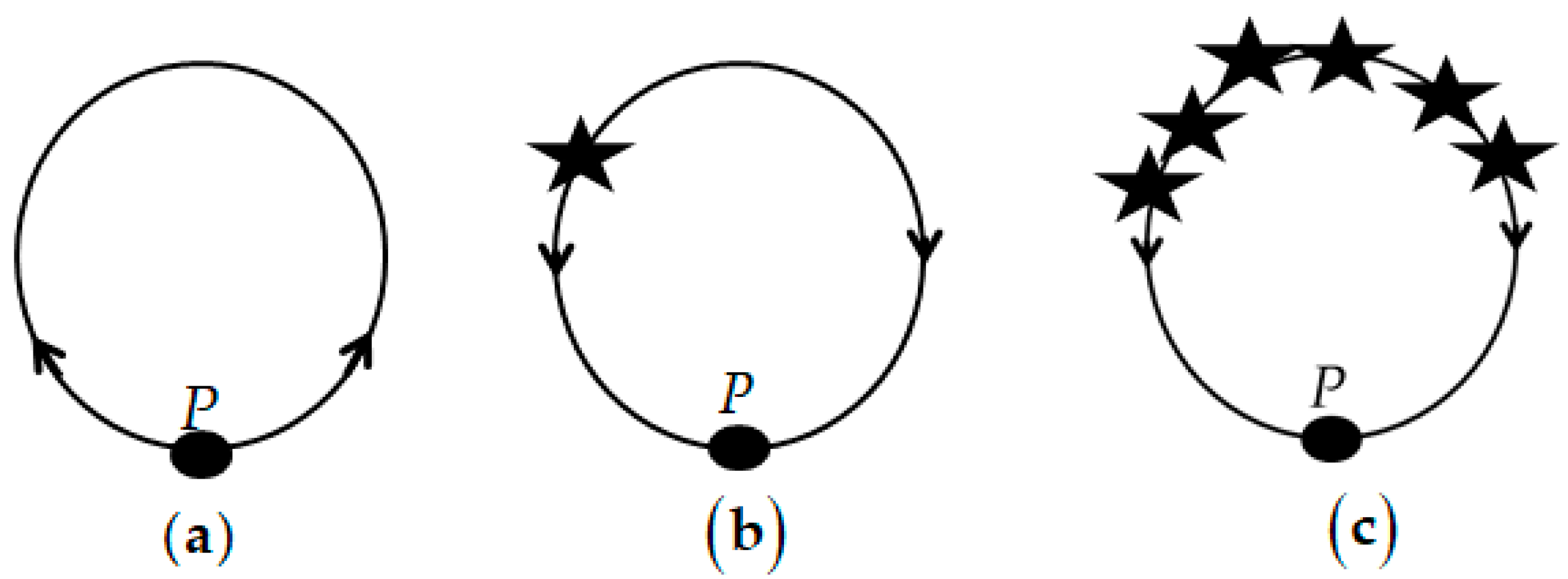

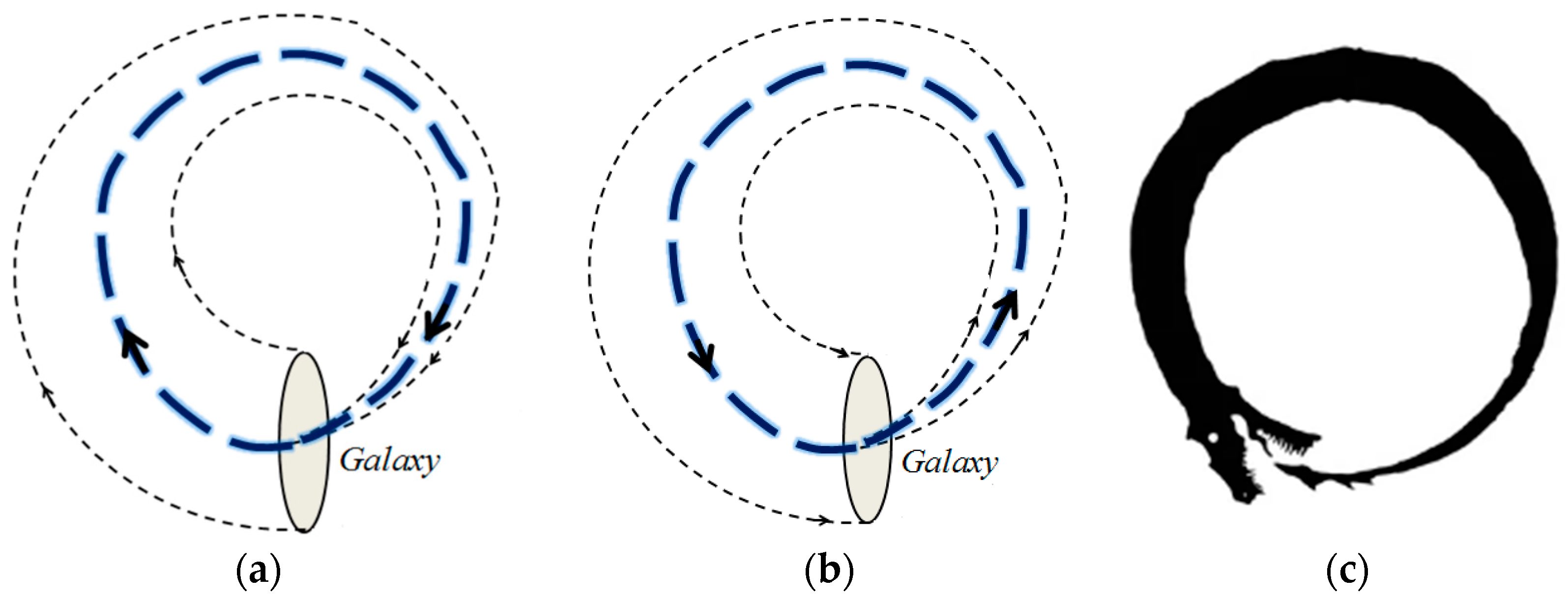
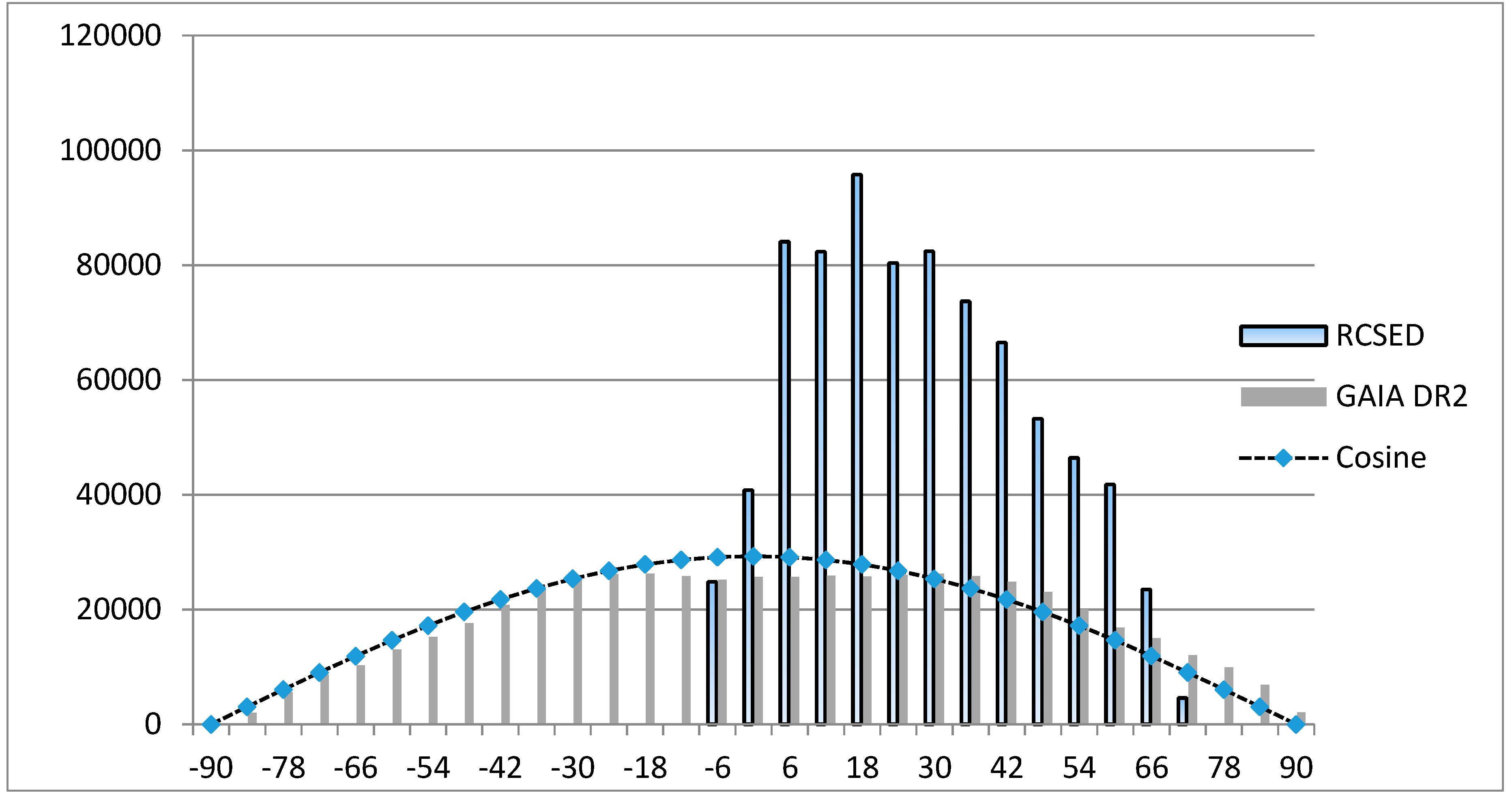
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587730818432041321 | 328.93761990 | −7.06320875 | 0.0592138 |
| 587732579378724931 | 148.93835864 | 7.06251179 | 0.0602015 | |
| (2) | 587726879409635950 | 311.33617957 | −5.13025247 | 0.100322 |
| 587732703390204231 | 131.33587944 | 5.12942269 | 0.094418 | |
| (3) | 588848899931963795 | 224.12922043 | −0.10150706 | 0.376950 |
| 588015509288648969 | 44.128540880 | 0.10090797 | 0.371090 |
| Id SDSS DR7 | ra | dec | z | |
|---|---|---|---|---|
| (1) | 587730818432041321 | 328.93761990 | −7.06320875 | 0.0592138 |
| 587732579378724931 | 148.93835864 | 7.06251179 | 0.0602015 |
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587726879416648036 | 327.43326873 | −7.24482558 | 0.120794 |
| 587732770503458957 | 147.43340352 | 7.24510724 | 0.172101 | |
| (2) | 587722981749620931 | 201.81109033 | −1.15290891 | 0.0672574 |
| 587731514217726115 | 21.810947880 | 1.15332655 | 0.0825304 | |
| (3) | 588848899373138039 | 173.86518822 | −0.55499635 | 0.105208 |
| 588015509803565082 | 353.86519822 | 0.55470851 | 0.241575 |
| Id SDSS DR7 | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | 587726879416648036 | 327.43326873 | −7.24482558 | 0.120794 |
| 587732770503458957 | 147.43340352 | 7.24510724 | 0.172101 | |
| (2) | 587722981749620931 | 201.81109033 | −1.15290891 | 0.0672574 |
| 587731514217726115 | 21.810947880 | 1.15332655 | 0.0825304 | |
| (3) | 588848899373138039 | 173.86518822 | −0.55499635 | 0.105208 |
| 588015509803565082 | 353.86519822 | 0.55470851 | 0.241575 | |
| (4) | 587731511542349980 | 42.407177420 | −0.84245813 | 0.023485 |
| 587722984443019391 | 222.40757112 | 0.84279922 | 0.211561 |
| Id SDSS DR8 | Ra | Dec | Elliptical | Spiral | |
|---|---|---|---|---|---|
| (1) | 1237678888521237047 | 26.5696157538807 | −3.036690882053760 | 0.009671 | 0.990329 |
| 1237674469000413487 | 206.5697430121670 | 3.036761704248740 | 0.147295 | 0.852705 | |
| (2) | 1237646748740026643 | 62.1747511145106 | −1.016781419414090 | 0.097682 | 0.902318 |
| 1237648705676575427 | 242.1748881053750 | 1.016716451442130 | 0.092952 | 0.907048 | |
| (3) | 1237646748740026643 | 62.1747511145106 | −1.016781419414090 | 0.097682 | 0.902318 |
| 1237648705676575428 | 242.1748844511030 | 1.016720360108510 | 0.078252 | 0.921748 | |
| (4) | 1237655177615638991 | 128.6682349968410 | −0.926547264053684 | 0.883225 | 0.116775 |
| 1237649942587703356 | 308.6681411440870 | 0.926418898103171 | 0.861631 | 0.138369 | |
| (5) | 1237648720134537650 | 128.6682518312900 | −0.926538367783351 | 0.902699 | 0.097301 |
| 1237649942587703356 | 308.6681411440870 | 0.926418898103171 | 0.861631 | 0.138369 |
| Id SDSS DR8 | Ra | Dec | Elliptical | Spiral | Zphot | |
|---|---|---|---|---|---|---|
| (1) | 1237666409525739588 | 21.8109112443 | 1.15334613372 | 0.398 | 0.602 | 0.0798 |
| 1237651709428367652 | 201.811088818 | −1.15291424464 | 0.185 | 0.815 | 0.0789 | |
| (2) | 1237678617427378399 | 21.8109254471 | 1.15335605428 | 0.343 | 0.657 | 0.0794 |
| 1237651709428367652 | 201.811088818 | −1.15291424464 | 0.185 | 0.815 | 0.0789 | |
| (3) | 1237660237652623499 | 21.8109336601 | 1.15333316620 | 0.356 | 0.644 | 0.0710 |
| 1237648702974525748 | 201.811090479 | −1.15290686150 | 0.179 | 0.821 | 0.0713 | |
| (4) | 1237666340801871988 | 21.8109380881 | 1.15333261091 | 0.413 | 0.587 | 0.0717 |
| 1237648702974525748 | 201.811090479 | −1.15290686150 | 0.179 | 0.821 | 0.0713 | |
| (5) | 1237646588221128874 | 21.8109525056 | 1.15334337704 | 0.465 | 0.535 | 0.0707 |
| 1237648702974525748 | 201.811090479 | −1.15290686150 | 0.179 | 0.821 | 0.0713 | |
| (6) | 1237646748740026643 | 62.1747511145 | −1.01678141941 | 0.098 | 0.902 | 0.0756 |
| 1237648705676575428 | 242.174884451 | 1.01672036011 | 0.078 | 0.922 | 0.0757 | |
| (7) | 1237660776104657068 | 171.086130380 | −0.99648723534 | 0.212 | 0.788 | 0.0294 |
| 1237650011315241011 | 351.087087401 | 0.99670903212 | 0.738 | 0.262 | 0.0287 |
| Id SDSS DR8 | Ra | Dec | Elliptical | Spiral | Zphot | |
|---|---|---|---|---|---|---|
| (1) | 1237646748740026643 | 62.1747511145 | −1.01678141941 | 0.098 | 0.902 | 0.0756 |
| 1237648705676575428 | 242.174884451 | 1.01672036011 | 0.078 | 0.922 | 0.0757 |
| Id SDSS DR8 | Ra | Dec | Elliptical | Spiral | Zphot | |
|---|---|---|---|---|---|---|
| (1) | 1237678888521237046 | 26.5696157538807 | −3.036690882053760 | 0.009671 | 0.99033 | 0.0757 |
| 1237674469000413486 | 206.5697430121670 | 3.036761704248740 | 0.147295 | 0.85271 | 0.1149 | |
| (2) | 1237646748740026643 | 62.1747511145106 | −1.016781419414090 | 0.097682 | 0.90232 | 0.0756 |
| 1237648705676575428 | 242.1748844511030 | 1.016720360108510 | 0.078252 | 0.92175 | 0.0757 | |
| (3) | 1237646748740026643 | 62.1747511145106 | −1.016781419414090 | 0.097682 | 0.90232 | 0.0756 |
| 1237648705676575427 | 242.1748881053750 | 1.016716451442130 | 0.092952 | 0.90705 | 0.0839 |
| SpecObjID | Ra | Dec | z | Elliptical | Spiral | |
|---|---|---|---|---|---|---|
| (1) | 774688716978415616 | 5.28659 | −1.03586 | 0.1077 | 0.29 | 0.71 |
| 324403517626279936 | 185.29 | 1.03245 | 0.0993 | 0.29 | 0.71 | |
| (2) | 743129709168060416 | 19.6432 | −10.9021 | 0.1409 | 0.17 | 0.83 |
| 1911855335291774976 | 199.642 | 10.8989 | 0.1491 | 0.16 | 0.84 | |
| (3) | 1399629972804495360 | 57.6003 | 0.0114088 | 0.0839 | 0.37 | 0.63 |
| 385078137475590144 | 237.596 | −0.00662002 | 0.0830 | 0.46 | 0.54 | |
| (4) | 1393917732184942592 | 155.36 | 8.6444 | 0.0450 | 0.13 | 0.87 |
| 809694968183547904 | 335.363 | −8.64717 | 0.0373 | 0.24 | 0.75 | |
| (5) | 306369326917642240 | 156.167 | 0.893717 | 0.0937 | 0.41 | 0.58 |
| 422226519742507008 | 336.167 | −0.897112 | 0.0990 | 0.42 | 0.51 | |
| (6) | 309696723461105664 | 161.174 | −0.503556 | 0.1161 | 0.13 | 0.87 |
| 425721592429963264 | 341.171 | 0.498878 | 0.1068 | 0.22 | 0.78 |
| SpecObjID | Ra | Dec | z | Elliptical | Spiral | |
|---|---|---|---|---|---|---|
| (1) | 1399629972804495360 | 57.6003 | 0.0114088 | 0.0839 | 0.37 | 0.63 |
| 385078137475590144 | 237.596 | −0.00662002 | 0.0830 | 0.46 | 0.54 |
| Allwise_Name | Source_Id | Ra | Dec | |
|---|---|---|---|---|
| (1) | J210304.14-762224.9 | 6368528062846000640 | 315.7673682 | −76.37360527 |
| J090304.41+762224.0 | 1125452302531483520 | 135.7684166 | 76.37343393 | |
| (2) | J120429.60-215735.5 | 3493448195802870400 | 181.1233688 | −21.95989953 |
| J000429.68+215736.0 | 2847161965440082176 | 1.123715043 | 21.9600063 | |
| (3) | J124510.71-180851.9 | 3522237773904469248 | 191.294554 | −18.1478664 |
| J004510.62+180851.9 | 2782801120299995520 | 11.29451879 | 18.14802663 | |
| (4) | J035733.19-083041.3 | 3194958963846806144 | 59.38814002 | −8.511587953 |
| J155733.13+083042.9 | 4454299557503538688 | 239.3880677 | 8.511930041 |
| Ra | Dec | Name | Descrip | z | |
|---|---|---|---|---|---|
| (1) | 75.7744245 | −40.7936211 | WISEA J050305.91-404736.8 | q | 2.3 |
| 255.7743683 | 40.7937126 | SDSS J170305.84+404737.3 | q | 0.3 | |
| (2) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 |
| Ra | Dec | Name | Descrip | z | Rmag | Bmag | |
|---|---|---|---|---|---|---|---|
| (1) | 5.8514071 | −7.0936418 | SDSS J002324.33-070537.1 | q | 0.6 | 21.75 | 21.73 |
| 185.8513794 | 7.093749 | SDSS J122324.33+070537.4 | qX | 0.6 | 21.82 | 21.61 | |
| (2) | 356.0054037 | −4.4881222 | SDSS J234401.30-042917.1 | q | 2.1 | 19.79 | 20.52 |
| 176.0057901 | 4.4880115 | SDSS J114401.38+042916.8 | q | 2.2 | 21.32 | 21.32 | |
| (3) | 215.9122427 | −3.1485981 | SDSS J142338.93-030854.9 | q | 2 | 21.54 | 21.34 |
| 35.911743 | 3.1485686 | SDSS J022338.81+030854.7 | q | 2.173 | 20.03 | 20.59 | |
| (4) | 148.4235067 | −0.1395639 | 2QZ J095341.5-000822 | q | 0.284 | 19.06 | 19.96 |
| 328.4236129 | 0.1398213 | SDSS J215341.66+000823.3 | q | 0.1 | 22.55 | 23.38 |
| Ra | Dec | Name | Descrip | z | |
|---|---|---|---|---|---|
| (1) | 43.6995104 | −17.1177057 | WISEA J025447.88-170703.8 | q | 1.9 |
| 223.699538 | 17.1176163 | SDSS J145447.88+170703.4 | q | 1.1 |
| Name | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | J013702.04-513252.3 | 24.2585004 | −51.5478865 | |
| 133702.07+513252.1 | 204.2586596 | 51.54780646 | 3.123 | |
| (2) | J035233.36-211221.7 | 58.1390267 | −21.2060385 | |
| J155233.38+211221.7 | 238.1391178 | 21.2060426 |
| Name | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | LQAC_179-001_037 | 179.9377083 | −1.372166667 | 1.2752 |
| 235945.22+012216.3 | 359.9384346 | 1.371206026 | 1.2224771 | |
| (2) | 004034.86-003821.0 | 10.14525273 | −0.63918039 | 1.8359182 |
| LQAC_190+000_011 | 190.1443333 | 0.638194444 | 1.8557 | |
| (3) | LQAC_352-000_049 | 352.8172404 | −0.117229211 | 1.69638 |
| LQAC_172+000_041 | 172.8182083 | 0.118 | 1.7844 |
| Name | Ra | Dec | z | |
|---|---|---|---|---|
| (1) | LQAC_038-009_025 | 38.5649606 | −9.392240877 | 3.15853 |
| LQAC_218+009_031 | 218.5647428 | 9.392719278 | 1.79609 | |
| (2) | 022538.91-012519.8 | 36.41214596 | −1.422178345 | 0.7273704 |
| LQAC_216+001_018 | 216.4125417 | 1.4225 | 1.1363 | |
| (3) | LQAC_322-001_003 | 322.04071 | −1.110389 | 2.0165 |
| LQAC_142+001_019 | 142.0406947 | 1.109906236 | 0.69137 |
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 | № of Objects | Dec Interval |
|---|---|---|---|---|---|---|---|---|
| RCSED | 214,050 | 2127 | 542 | 22 | 4 | 0 | 800,299 | −11.25 … 70.29 |
| Random 1 | 121,672 | 1204 | 288 | 14 | 2 | 0 | 221,502 | −11.25 ... 11.25 |
| Random 2 | 121,918 | 1261 | 332 | 14 | 4 | 0 | 221,502 | −11.25 ... 11.25 |
| Random 3 | 121,391 | 1269 | 323 | 14 | 4 | 0 | 221,502 | −11.25 ... 11.25 |
| Random 4 | 121,263 | 1250 | 284 | 11 | 0 | 0 | 221,502 | −11.25 ... 11.25 |
| Random 5 | 121,192 | 1163 | 288 | 6 | 0 | 0 | 221,502 | −11.25 ... 11.26 |
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| GAIADR2Q | 198,621 | 1945 | 485 | 17 | 4 | 0 |
| Random 1 | 150,489 | 1506 | 401 | 15 | 5 | 0 |
| Random 2 | 150,358 | 1512 | 381 | 15 | 3 | 0 |
| Random 3 | 150,550 | 1495 | 382 | 13 | 5 | 0 |
| Random 4 | 151,013 | 1520 | 372 | 14 | 4 | 1 |
| Random 5 | 150,306 | 1503 | 357 | 16 | 6 | 0 |
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| RCSED | 214,050 | 2127 | 542 | 22 | 4 | 0 |
| Random18_1 | 176,055 | 1676 | 417 | 21 | 4 | 2 |
| Random18_2 | 176,584 | 1723 | 440 | 20 | 6 | 1 |
| Random18_3 | 175,916 | 1728 | 428 | 22 | 9 | 0 |
| Random18_4 | 176,006 | 1826 | 429 | 15 | 6 | 0 |
| Random18_5 | 175,810 | 1789 | 425 | 13 | 4 | 0 |
| Random30_1 | 185,460 | 1794 | 423 | 14 | 5 | 1 |
| Random30_2 | 185,681 | 1881 | 467 | 26 | 7 | 0 |
| Random30_3 | 187,713 | 1827 | 428 | 20 | 8 | 1 |
| Random30_4 | 185,976 | 1862 | 466 | 18 | 5 | 0 |
| Random30_5 | 184,818 | 1883 | 462 | 17 | 4 | 0 |
| Random90_1 | 208,266 | 2062 | 496 | 27 | 11 | 0 |
| Random90_2 | 208,645 | 2092 | 562 | 23 | 6 | 0 |
| Random90_3 | 207,692 | 2051 | 491 | 22 | 4 | 0 |
| Random90_4 | 208,046 | 2029 | 513 | 15 | 6 | 0 |
| Random90_5 | 208,289 | 2077 | 517 | 25 | 10 | 1 |
| Random180_1 | 212,404 | 2107 | 591 | 32 | 11 | 1 |
| Random180_2 | 213,252 | 2201 | 559 | 22 | 4 | 0 |
| Random180_3 | 212,848 | 2080 | 529 | 29 | 7 | 1 |
| Random180_4 | 212,768 | 2077 | 482 | 16 | 5 | 0 |
| Random180_5 | 213,511 | 2077 | 529 | 19 | 8 | 1 |
| Average of 20 runs with N = 180 | 21.95 | 5.3 | 0.15 | |||
| Standard deviation | 3.43 | 1.95 | 0.36 | |||
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| GAIADR2 | 198,621 | 1945 | 485 | 17 | 4 | 0 |
| Random18_1 | 196,114 | 1893 | 483 | 17 | 3 | 0 |
| Random18_2 | 197,388 | 1972 | 479 | 16 | 5 | 0 |
| Random18_3 | 196,415 | 1972 | 502 | 18 | 4 | 1 |
| Random18_4 | 197,010 | 1984 | 475 | 22 | 3 | 0 |
| Random18_5 | 198,107 | 1961 | 511 | 12 | 2 | 0 |
| Random30_1 | 196,396 | 1979 | 470 | 16 | 2 | 0 |
| Random30_2 | 198,441 | 2039 | 491 | 17 | 4 | 0 |
| Random30_3 | 198,034 | 1926 | 476 | 19 | 5 | 0 |
| Random30_4 | 198,060 | 2009 | 490 | 21 | 5 | 0 |
| Random30_5 | 198,763 | 1984 | 510 | 23 | 3 | 0 |
| Random90_1 | 198,481 | 2020 | 491 | 11 | 2 | 0 |
| Random90_2 | 198,438 | 2044 | 500 | 21 | 7 | 0 |
| Random90_3 | 197,632 | 2020 | 517 | 21 | 2 | 0 |
| Random90_4 | 198,300 | 1958 | 472 | 20 | 2 | 0 |
| Random90_5 | 199,184 | 1967 | 501 | 23 | 4 | 0 |
| Random180_1 | 197,900 | 1888 | 489 | 14 | 4 | 1 |
| Random180_2 | 198,556 | 2002 | 511 | 21 | 2 | 0 |
| Random180_3 | 198,563 | 2007 | 487 | 18 | 5 | 0 |
| Random180_4 | 199,210 | 1980 | 492 | 21 | 7 | 0 |
| Random180_5 | 199,532 | 1962 | 499 | 19 | 4 | 0 |
| Average of 20 runs with N = 180 | 19.2 | 4.65 | 0.5 | |||
| Standard deviation | 3.72 | 1.49 | 0.81 | |||
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| K&S [40] | 7,612,266 | 76,867 | 18,024 | 1222 | 605 | 0 |
| Random18_1 | 4,475,466 | 45,104 | 11,333 | 441 | 126 | 7 |
| Random18_2 | 4,468,199 | 44,838 | 11,320 | 456 | 114 | 6 |
| Random18_3 | 4,526,555 | 44,884 | 11,162 | 448 | 118 | 2 |
| Random18_4 | 4,475,244 | 44,714 | 11,163 | 462 | 113 | 4 |
| Random18_5 | 4,478,613 | 44,762 | 11,166 | 473 | 137 | 6 |
| Random90_1 | 6,533,538 | 65,955 | 16,568 | 720 | 185 | 6 |
| Random90_2 | 6,534,673 | 65,300 | 16,417 | 616 | 161 | 6 |
| Random90_3 | 6,538,237 | 65,311 | 16,266 | 674 | 187 | 5 |
| Random90_4 | 6,538,688 | 65,529 | 16,250 | 663 | 155 | 5 |
| Random90_5 | 6,536,033 | 65,938 | 16,531 | 643 | 152 | 8 |
| Random180_1 | 7,005,872 | 70,357 | 17,657 | 702 | 178 | 3 |
| Random180_2 | 7,010,050 | 70,260 | 17,538 | 663 | 172 | 6 |
| Random180_3 | 7,006,156 | 70,465 | 17,578 | 729 | 174 | 6 |
| Random180_4 | 7,008,239 | 70,197 | 17,455 | 678 | 182 | 3 |
| Random180_5 | 7,006,665 | 70,257 | 17,669 | 708 | 178 | 11 |
| Average of 20 runs with N = 180 | 697.3 | 174.5 | 7.35 | |||
| Standard deviation | 26.7 | 13.8 | 2.52 | |||
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| Milliquas 6.3 | 2,272,887 | 23,024 | 5795 | 219 | 50 | 2 |
| Random90_1 | 2,261,589 | 22,473 | 5564 | 214 | 60 | 1 |
| Random90_2 | 2,259,751 | 22,559 | 5581 | 215 | 66 | 3 |
| Random90_3 | 2,261,151 | 22,391 | 5496 | 245 | 70 | 2 |
| Random90_4 | 2,262,077 | 22,672 | 5702 | 264 | 55 | 2 |
| Random90_5 | 2,262,742 | 22,643 | 5683 | 239 | 59 | 2 |
| Random180_1 | 2,270,577 | 22,426 | 5527 | 219 | 59 | 2 |
| Random180_2 | 2,270,319 | 22,829 | 5722 | 219 | 59 | 2 |
| Random180_3 | 2,269,632 | 22,637 | 5630 | 224 | 53 | 3 |
| Random180_4 | 2,270,186 | 23,136 | 5814 | 233 | 48 | 1 |
| Random180_5 | 2,270,844 | 22,680 | 5738 | 237 | 59 | 1 |
| Average of 20 runs with N = 180 | 225.7 | 57.25 | 2.3 | |||
| Standard deviation | 13.28 | 8.12 | 1.7 | |||
| Eps | 0.1 | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 |
|---|---|---|---|---|---|---|
| KQCG | 1,933,692 | 19,250 | 4735 | 167 | 36 | 2 |
| Random90_1 | 1,930,091 | 19,298 | 4838 | 217 | 49 | 3 |
| Random90_2 | 1,928,432 | 19,588 | 4806 | 201 | 50 | 5 |
| Random90_3 | 1,930,965 | 19,463 | 4774 | 191 | 46 | 1 |
| Random90_4 | 1,927,537 | 19,340 | 4821 | 196 | 48 | 0 |
| Random90_5 | 1,930,231 | 19,183 | 4787 | 189 | 50 | 2 |
| Random180_1 | 1,929,688 | 19,326 | 4745 | 182 | 53 | 2 |
| Random180_2 | 1,933,921 | 19,436 | 4810 | 175 | 49 | 4 |
| Random180_3 | 1,931,871 | 19,442 | 4892 | 213 | 43 | 3 |
| Random180_4 | 1,930,751 | 19,212 | 4800 | 206 | 53 | 1 |
| Random180_5 | 1,934,750 | 19,483 | 4785 | 161 | 36 | 4 |
| Average of 20 runs with N = 180 | 190.9 | 47.8 | 1.5 | |||
| Standard deviation | 16.14 | 6 | 1.2 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korotky, V.A.; Masár, E.; Obukhov, Y.N. In the Quest for Cosmic Rotation. Universe 2020, 6, 14. https://doi.org/10.3390/universe6010014
Korotky VA, Masár E, Obukhov YN. In the Quest for Cosmic Rotation. Universe. 2020; 6(1):14. https://doi.org/10.3390/universe6010014
Chicago/Turabian StyleKorotky, Vladimir A., Eduard Masár, and Yuri N. Obukhov. 2020. "In the Quest for Cosmic Rotation" Universe 6, no. 1: 14. https://doi.org/10.3390/universe6010014
APA StyleKorotky, V. A., Masár, E., & Obukhov, Y. N. (2020). In the Quest for Cosmic Rotation. Universe, 6(1), 14. https://doi.org/10.3390/universe6010014





