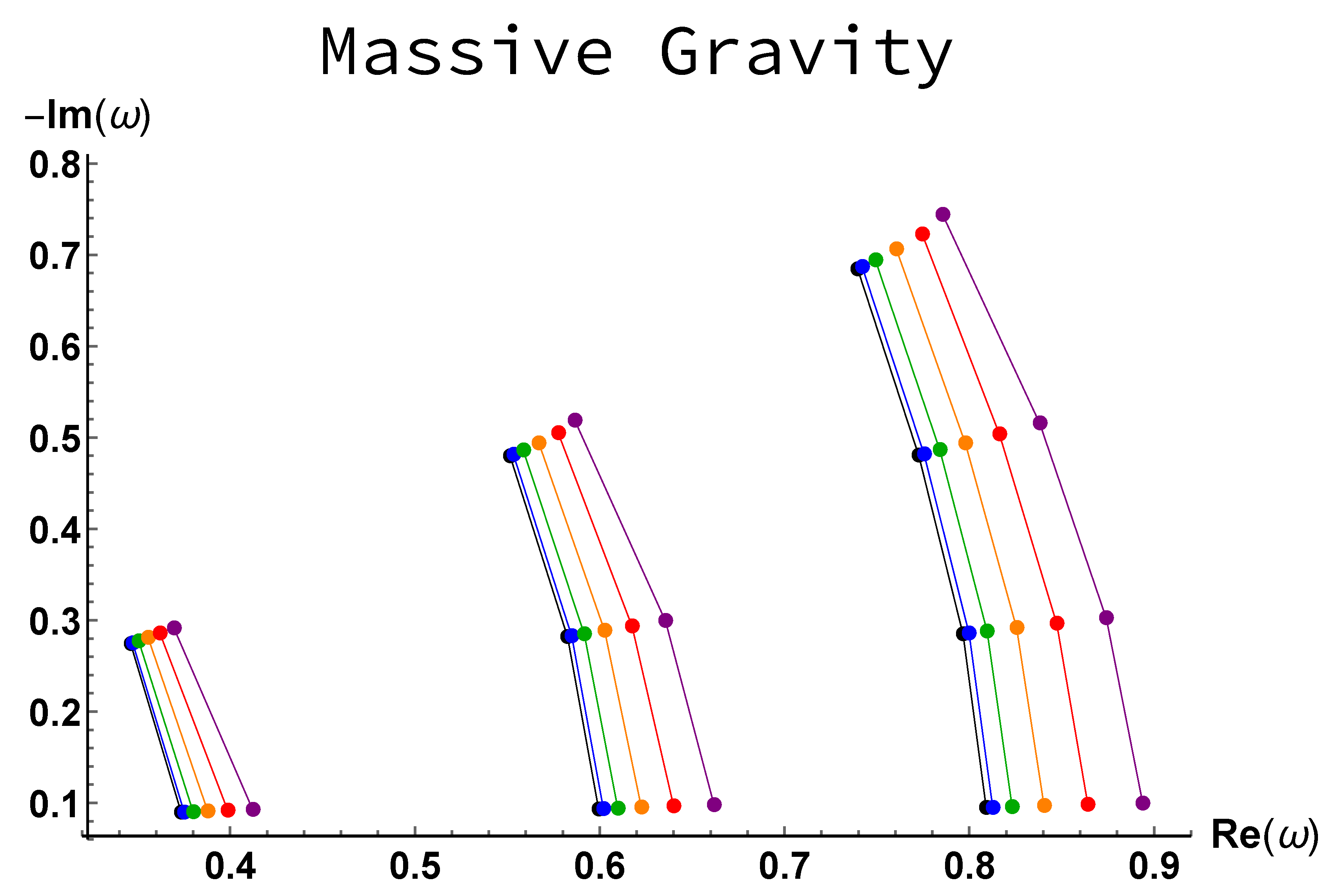1. Introduction
General relativity (GR) is our best theory of spacetime. While the Lovelock theorem [
1] ensures that it cannot be easily modified, there are quite a lot of attempts to relax some hypotheses and build a deeper model to describe the gravitational field. From effective quantum gravity to improved infrared properties, the motivations to go beyond GR are countless. So are the situations, both in astrophysics and cosmology, where extended gravity theories can, in principle, be tested. In practice, reaching the level of accuracy useful to probe the relevant range of parameters is obviously far from trivial. In this article we focus on a specific aspect of gravitational waves that would be emitted during the relaxation phase of a deformed black hole (BH).
We will consider quasinormal modes associated with the ringdown phase of a BH merger. The modes are not strictly normal due to energy losses of the system through gravitational waves. The boundary conditions for the equation of motion are unusual as the wave has to be purely outgoing at infinity and purely ingoing at the event horizon. The time component of the radial part reads (an introductory review can be found in [
2]):
the complex pulsation
being split into a real part
, which corresponds to the frequency, and an imaginary one
, which is the inverse timescale of the damping. Stability requires
. While real-life BHs are spinning, we focus on Schwarzschild solutions in this article. The details of these predictions can not be used to directly compare with observations. We, however, expect the general tendencies and orders of magnitudes to remain correct, as they can be checked for the general relativistic case in [
3].
Whether one considers “axial” or “polar” perturbations, the linearized Einstein equations lead to wave equations with different potentials. In GR, the (so-called Regge-Wheeler) potential for axial perturbations is:
while the (so-called Zerilli) one for polar perturbations is:
where
. Throughout the paper we use Planck units. In the purely gravitational sector, one needs
. Interestingly, both those equations have the very same spectrum of quasinormal modes (QNMs). This property, called isospectrality [
4], is not always true in modified gravity (see [
5] for an extension and a discussion of the original proof). Basically, quasinomal modes are described by their multipole number
ℓ and their overtone number
n. The fundamental quadrupolar mode (
and
) for a Schwarzschild BH in GR is given by
.
There are many different ways to calculate the QNMs: Continued fractions, Frobenius series, Mashhoon’s method, confluent Heun’s equation, characteristic integration, shooting, Wentzel-Kramers-Brillouin (WKB) approximations, etc. In this article we focus on the last approach. For most models considered here, the QNMs have already been calculated in previous studies. However, this has most of the time been done for or , not for as we have done it here. More importantly, it is in addition very useful to rely on the very same method to investigate all models so that the differences underlined are actually due to physical effects and not to numerical issues. Even when the same approach is considered, the way it is implemented is often different enough, between articles, so that it is hard to directly compare the results. This is why we have here tried to methodically consider several modified gravity models with a well controlled WKB approximation scheme used in the same way in all cases so as to compare the tendencies between modified gravity proposals. This is not mandatory for this qualitative step but this will become useful in future quantitative studies.
The determination of the complex frequencies of QNMs is difficult (see [
6,
7] for historical reviews and [
8,
9] for results based on numerical approaches). This work is based on the WKB approach described in [
10]. Following the pioneering work in [
11], the WKB method for QNMs was developed in [
12,
13,
14,
15]. This formalism leads to fairly good approximations, especially for high multipole and low overtone numbers. In the following, we restrict ourselves to
and use the sixth order WKB method developed by Konoplya [
10] (see also [
16,
17,
18]). This allows one to recast the potential appearing in the effective Schrödinger equation felt by gravitational perturbations in a complex but tractable form.
The aim of this introductory paper is to investigate how several modified gravity theories impact the QNMs at the qualitative level. There are several ways to go beyond GR: Extra dimensions, weak equivalence principle violations, extra fields, diffeomorphism–invariance violations, etc. Beyond those technicalities, there are strong conceptual motivations to consider extended gravity approaches, from the building of an effective quantum gravity theory to the improvements of the renormalisation properties, through the implementation of a dynamical cosmological constant. Among many others, examples of recent relevant works on QNMs can be found in [
19,
20,
21,
22].
2. Perturbation Dynamics
The QNMs are solutions of a perturbation equation with the specific boundary conditions given in the previous section. The radial and angular parts can be separated. The radial part is governed by a Schrödinger-like equation:
where Z is the radial part of the “perturbation” variable, assumed to have a time-dependance
, and
is the tortoise coordinate. For a metric such that:
the tortoise coordinate is defined by:
It tends to at the event horizon and to at spatial infinity.
As explained previously, BH gravitational perturbations can be of two different types distinguished by their behavior under a parity transformation. For an angular momentum
l, axial perturbations transform as
under parity, while polar perturbations transform as
. This leads to the two different potentials in Equation (
4). The potential for the gravitational axial perturbations reads in full generality (see [
2] and references therein) for the metric given by Equation (
5):
In this work we will not consider the isospectrality-violation issues and we will focus only on such perturbations. It should anyway be kept in mind that, in principle, isospectrality might not hold.
The boundary conditions can be expressed as:
We shall now derive the Regge-Wheeler equation for the more general (spherical and static) metric:
For this metric, the tortoise coordinate is defined by:
The general form of an axisymmetric metric can be written as [
4]:
where
,
,
and
. For the metric given by Equation (
10), the correspondence is:
A perturbation of this kind of spacetime is described by
,
and
, assumed to be first order quantities, and by infinitesimal increments,
,
,
, of the other quantities. We focus here on axial perturbations. The point is to linearize the field equations about the solution given by Equation (
10), considering components where
,
and
are only functions of
t,
and
. The equations governing
,
and
are described by the vanishing of the Ricci tensor components:
For Equation (
12), one has [
4]:
with:
where the comma indicates the derivative. The notation
is used to mean
. The component
is also given by Equation (
15) by switching indices 2 and 3.
The perturbed field equations are obtain by
. After replacing
,
,
and
by their expressions,
leads to:
For
, one is led to:
We assume that perturbations have a time dependance given by:
This implies that Equations (
19) and (
20) read:
Taking the derivative of Equation (
21) with respect to
and the derivative of Equation (
22) with respect to
r and combining the results leads to:
As suggested in [
4], one can then separate the variables
r and
using:
with
the Gegenbauer function satisfying:
Inserting Equation (
24) into Equation (
23), one is led to following radial equation:
where
. Defining
Z so that
and using the tortoise coordinate, we are led to a Schrödinger-like equation:
where the potential is:
The potential reduces to Equation (
7) for
and
. This derivation is useful to calculate QNMs for general static and spherically symmetric metrics.
3. The WKB Approximation
The WKB approximation [
12,
13,
14] is known for leading to good approximations (compared to numerical results) for the QNMs. The potential is written using the tortoise coordinate so as to be constant at
(which represent the horizon of the BH) and at
(which represents spatial infinity). The maximum of the potential is reached at
. Three regions can be identified: Region
I from
to
, the first turning point (where the potential vanishes), region
from
to
, the second turning point, and region
from
to
. In region
, a Taylor expansion is performed around
. In regions
I and
, the solution is approximated by an exponential function:
This expression can be inserted into Equation (
4) so as to obtain
as a function of the potential and its derivative. We then impose the boundary conditions given by Equation (9) and match the solutions of regions
I and
with the solution for region
at the turning points
and
, respectively. The WKB approximation has been usefully extended from the third to the sixth order in [
10].
This allows one to derive the complex frequencies as a function of the potential and its derivatives evaluated at the maximum. For the sixth order treatment, one is led to:
where the expressions of the
s can be found in [
10]. In the following, we use this scheme to compare different modified gravity models and we present results only in the range of validity of the WKB approximations.
Interesting recent considerations on the convergence on the WKB series are given in [
23]. Details on the expansion parameter used in this work can be found in [
17]. The consistency of the WKB approximation has been checked for the presented results.
4. Modified Gravity Models and Results
Throughout this section we investigate some properties of the QNMs for several extended gravity approaches. We pretend in no way to do justice to the subtleties of those models and, when necessary, we explicitly choose specific simplified settings to make the calculations easily tractable.
As we focus on phenomenological aspects, the more interesting mode is the fundamental one: and . We therefore focus on a few points around this one (keeping in mind that the accuracy is better for higher values of l). In all the figures, the lower overtone n is the one with the smallest imaginary part.
We first consider models with a metric of the form:
and then investigate a model with two different metric functions, using the result obtained in Equation (
28).
4.1. Massive Gravity
In GR, the graviton is a massless spin-2 particle. One of the first motivations for modern massive gravity—which can be seen as a generalization of GR—was the hope to account for the accelerated expansion of the Universe by generating a kind of Yukawa-like potential for gravitation [
24]. The initial linear approach to massive gravity contained a Boulware-Deser ghost, which was cured in the dRGT version [
25,
26,
27,
28]. Massive gravity also features interesting properties for holography (see, e.g., [
29]).
Starting from the action:
where
R is the Ricci scalar and
is the potential for the graviton, the following black hole solution can be derived [
30,
31]:
where
,
and
are, respectively:
with
a and
b being two dimensionless constants and
c being positive. It should also be pointed out that a positive value of
might raise consistency issues [
31].
The results are presented in
Figure 1. The values chosen for the constants do, of course, change the amplitude of the displacement of the QNMs. The global trend, which is the point of this study, however, remains the same. Increasing the graviton mass
m tends to increase the real part of QNMs, that is the frequency of the oscillations. The difference in frequency between the fundamental and the first overtone also increases with
m. The effect on the imaginary part is hardly noticeable on the plot, even though a slight increase, which is actually 50% less important, in relative variation, than the shift in frequency, should be noticed. The values considered here for the mass are, of course, way out of the known bounds, but this is clearly not the point. As a specific feature, one can notice that the frequency shift due to massive corrections decreases for higher overtones. The shift patterns are mostly the same whatever the multipole number considered.
4.2. Modified Scalar–Tensor–Vector (STV) Gravity
The scalar–tensor–vector modified gravitational theory (MOG) allows the gravitational constant, a vector field coupling, and the vector field mass to vary with space and time [
32]. The equations of motion lead to an effective modified acceleration law that can account for galaxy rotation curves and cluster observation without dark matter. While it has recently been much debated and put under pressure, the theory is still worth considering seriously. We consider the field equation for the metric tensor [
33]:
where the gravitational coupling is
, with
being the Newton’s constant. The gravitational strength of the vector field
(spin 1 graviton) is
. With
, the energy-momentum tensor for the vector field is:
with the constant
of [
32] being set to one. Solving the vacuum field equations:
and:
with the appropriate symmetry leads to the metric:
We focus on the case where the field equations for
are non-linear, as the phenomenology is then richer, and we consider the relevant choice
where there are two horizons and appropriate potential behavior for the WKB approximation to hold. An up-to-date investigation of QNMs in MOG can be found in [
34].
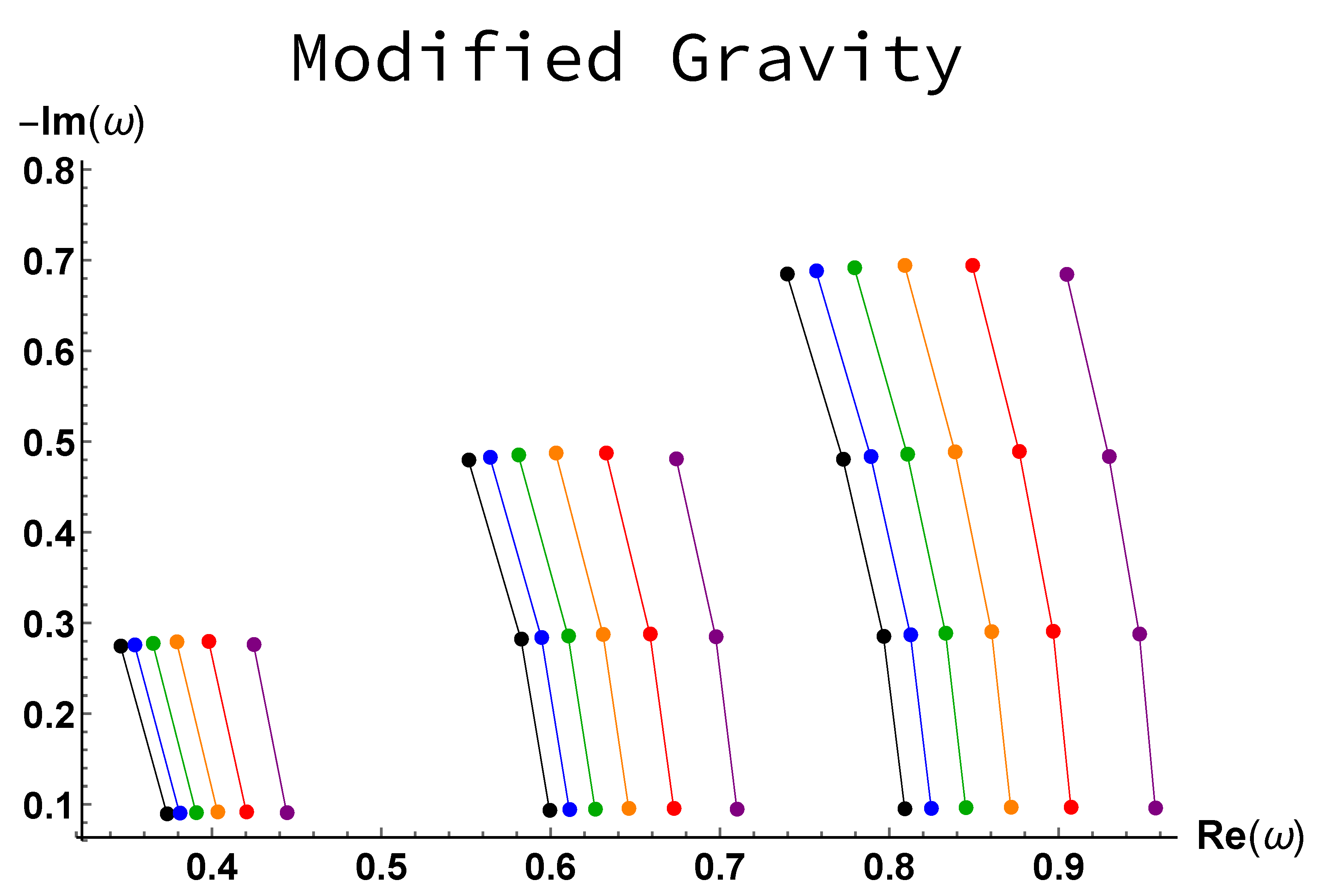
The results are given in
Figure 2. The imaginary part of the QNMs is nearly the same whatever the value of
: The modified metric has no effect on the damping rate. However, increasing
does increase of the real part, that is the frequency. The effect is important for values near the critical value
. The slope of the Imaginary part versus the real one, at a given
l for different values of
n, is nearly independent of
. This slope is not directly observable but it shows how the structure of the QNMs changes with the overtone number. The curves remain here parallel one to the other: This means that increasing the deformation parameter does not change the frequency shift between overtones.
4.3. Hořava-Lifshitz Gravity
Hořava-Lifshitz gravity bets on the fundamental nature of the quantum theory instead of relying on GR principles. It is a renormalizable UV-complete gravitational theory which is not Lorentz invariant in 3 + 1 dimensions [
35]. The relativistic time with its Lorentz invariance emerges only at large distances. Black hole solutions have been found [
36,
37,
38] and QNMs were studied [
39].
Using the ansatz:
in the action, one is led to the Lagrangian:
where
. For
, the solution is:
with
,
w being the deformation parameter enterring the action given in [
37]. There are two horizons for
.
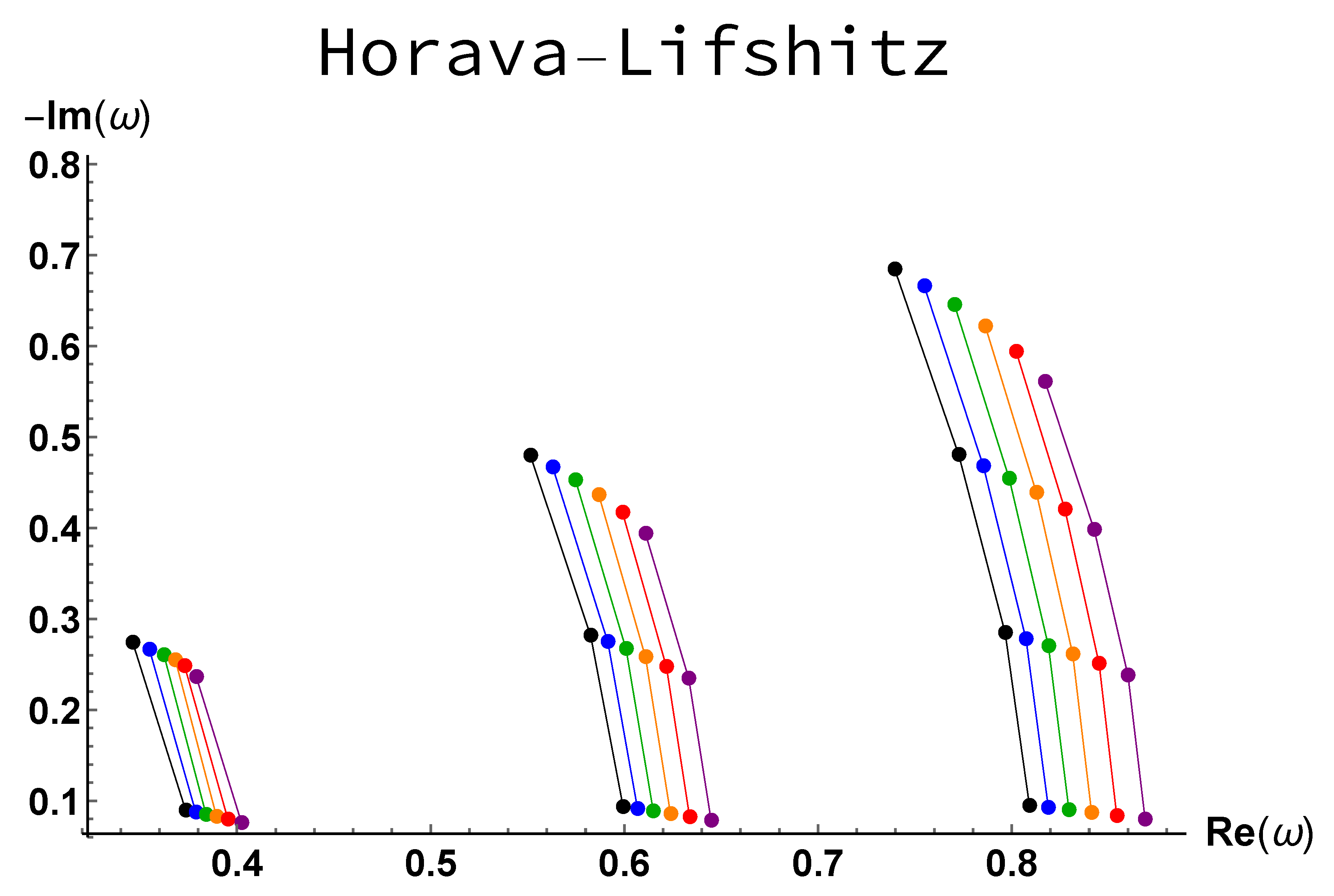
The results are given in
Figure 3. The frequency increases with an increase of
. Interestingly, the imaginary part of the overtones is highly sensitive to
. This remains true for higher multipoles. The relative variation of the imaginary part is nearly the same whatever the overtone number. It therefore becomes large in absolute value for high
n values.
4.4. ℏ Correction
It has been known for a long time that quantum corrections to the Newtonian gravitational potential can be rigorously derived without having a full quantum theory of gravity at disposal (see, e.g., [
40,
41,
42,
43,
44] to cite only a few works from a very long list). Recently, a quite similar approach was developed [
45] requiring that the quantum mechanically corrected metric reproduces the corrected Newtonian limit, reproduces the standard result for the entropy of black holes including the known corrections and fulfills some consistency conditions regarding the geodesic motion.
We use, as previously, natural units and the coefficients of the last term, , is proportional to ℏ in these models. It is worth noticing that there has been a long controversy about the value and the sign of the factor. From the phenomenological perspective, we do not fix it to a particular value but we keep it negative, in agreement with the latest expectations.
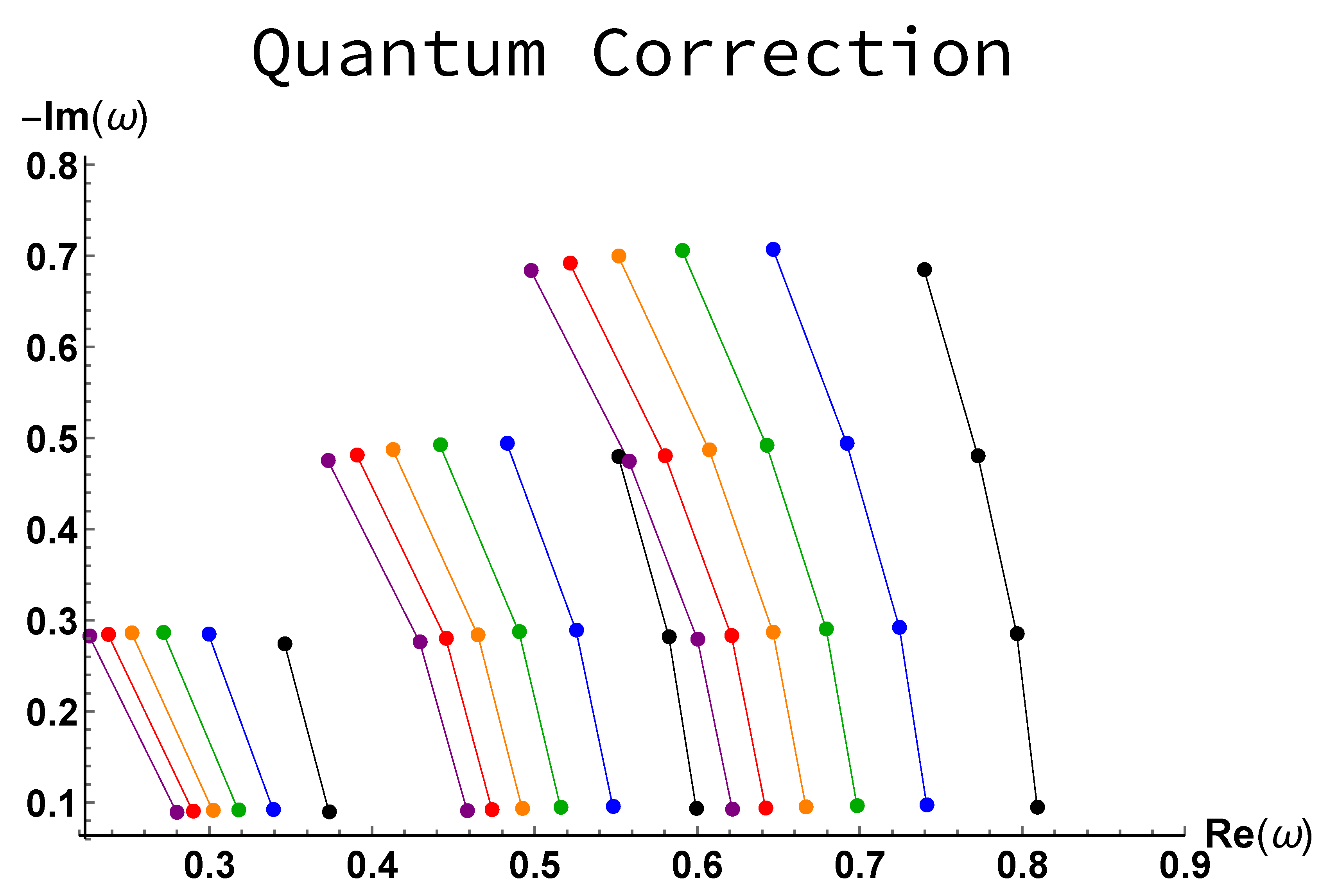
The results are given in
Figure 4. For large values of
, the effects are noticeable on the frequency. It is remarkable that, from our analysis, the real part of the complex frequency is only decreased, which is not the case for the other models that have been considered in this study. The higher the absolute value of
, the larger the difference of frequency between the fundamental and the overtones. This effect, however, remains quite subtle.
4.5. LQG Polymeric BH
Loop quantum gravity (LQG) is a non-perturbative and background-independant quantum theory of gravity [
46]. In the covariant formulation, space is described by a spin network [
47]. Each edge carries a “quantum of area”, labelled by a half integer
j, associated with a irreducible representations of
. Each node carries a “quantum of space” associated with an intertwiner. A key result is that the area is quantized according to:
with
being the Barbero-Immirzi parameter. Black holes are usually described in LQG through an isolated horizon puncturing a spin network [
48] and the phenomenology is very rich, depending on the precise setting chosen [
49]. We focus here on the model developed in [
50], as this is the one leading to metric modifications outside the horizon, where a regular lattice with edges of lengths
and
is considered. Requiring the minimal area to be one derived in LQG, one is left with only one free parameter
. From this minisuperspace approximation, a static spherical solution can be derived and is given by:
where
,
and
are the two horizons, and
,
P is the polymeric function defined by
with
, and the area parameter
is given by
,
being the minimum area appearing in LQG. The parameter
m in the solution is related to the ADM mass
M by
.
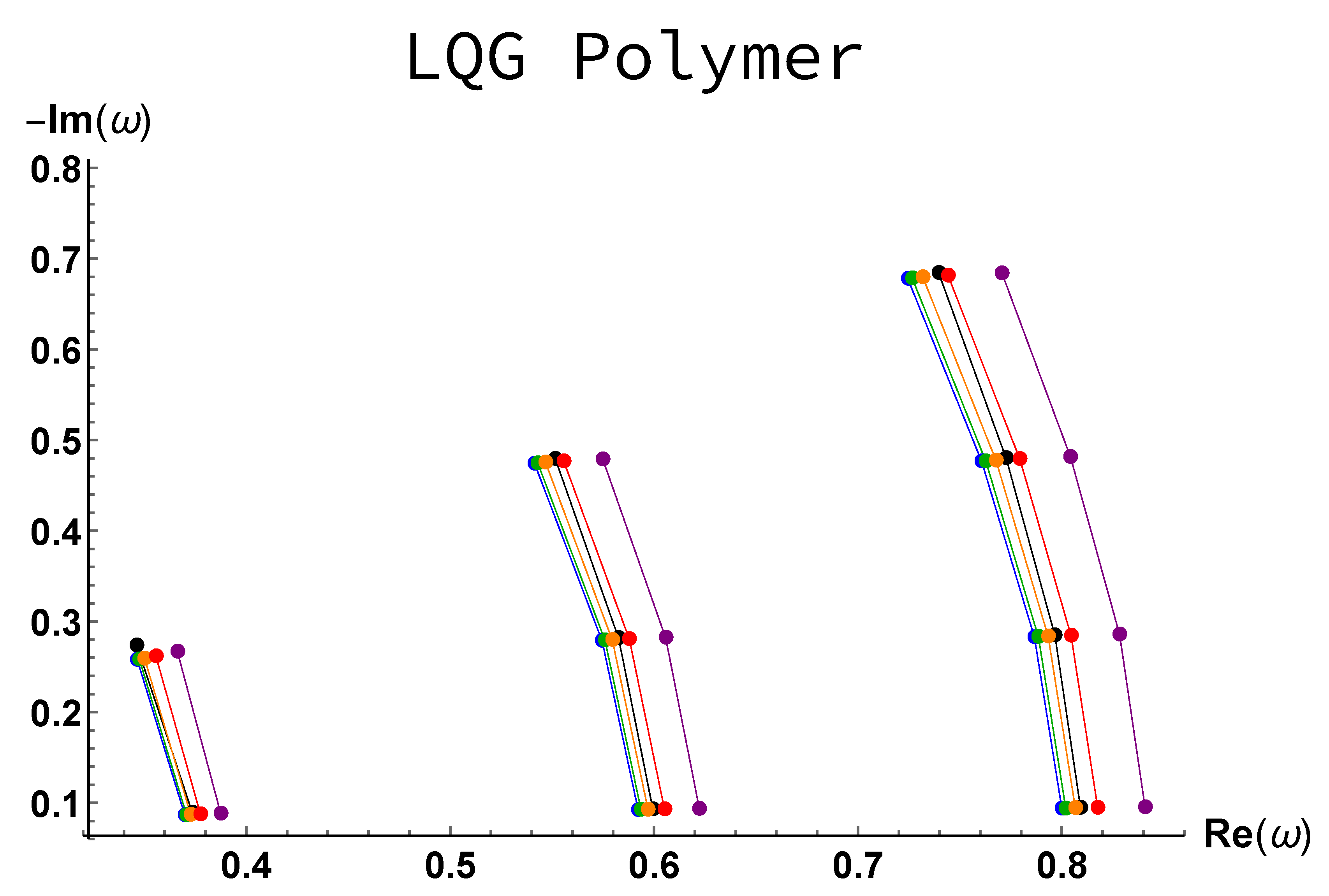
The results are given in
Figure 5. The damping rate does not depend at all on the polymerization parameter. The real part of the complex frequency does, however, first decrease with
. Noticeably, the slope is unchanged, and varying the deformation parameter just leads to a horizontal translation of the QNM frequency in the complex plane. This means that the frequency shift between the fundamental and the overtones does not depend on the amplitude of the quantum gravity corrections, as in modified gravity. Interestingly, for higher values of
, the frequency begins to increase. This is the only model considered in this study with non-monotonic behavior. For
the “polymerization” effect nearly exactly compensates the “area discretization" effect and one recovers the GR frequencies (and damping rates).
5. Conclusions
This study shows the evolution of the complex frequency of quasinormal modes of a Schwarzschild black hole for the fundamental and the first overtones for a few multipole numbers. We have considered massive gravity, STV gravity, Hořava-Lifshitz gravity, quantum corrected gravity and loop quantum gravity. All the results were derived using the very same WKB approximation scheme which makes a meaningful comparison possible. It will be especially useful for future quantitative studies.
Obviously, distinguishing between those models with observations is more than challenging. First, because there exist degeneracies, for given overtone and multipole numbers, between the models—when taking into account that the values of the parameters controlling the deformation are unknown. Second, because the intrinsic characteristics of the observed black holes are also unknown, which induces other degeneracies. In addition, this study should be extended to Kerr black holes, which also add some degeneracies in addition to the complexity.
Some interesting trends can, however, be underlined. For all models, the effects of modifying the gravitational theory are more important for the real part than for the imaginary part of the complex frequency of the QNMs. Stated in another way, the frequency shift is more important than the change in the damping rate. Obviously, it does not make sense to quantitatively compare the results from various models, as the deformation parameters are different. However, the “trends” are clearly specific to each studied theory and there is no need to define comparable “steps” in the deformation parameters (which do not have the same units anyway) to draw significant conclusions about the directions in which the different models considered deviate from GR. In addition, the sign of the frequency shift, and its dependance upon the overtone and multipole numbers, is characteristic of a given extension of GR. The accurate patterns are never the same, which is an excellent point for phenomenology. It can basically be concluded that a meaningful use of QNMs to efficiently investigate modified gravity requires the measurement of several relaxation modes. This is in principle possible [
51], but way beyond the sensitivity of current interferometers. If features beyond GR were to be observed, the direction of the frequency shift in the complex plane would already allow the exclusion of models, as this article shows. The goal of this study was not to perform a detailed analysis of the discrimination capabilities of gravitational wave experiments, it simply aimed at exhibiting the main tendencies for currently considered extended gravity models, as an introduction to this special issue on “probing new physics with black holes”.