Gauss–Bonnet Inflation and the String Swampland
Abstract
1. Introduction
- Swampland Criterion I (I) [8]: The scalar field excursion, normalized by the reduced Planck mass, in field space is bounded from abovewhere the reduced Planck mass and the order one constant .
2. The Gauss–Bonnet Inflation
3. The Models
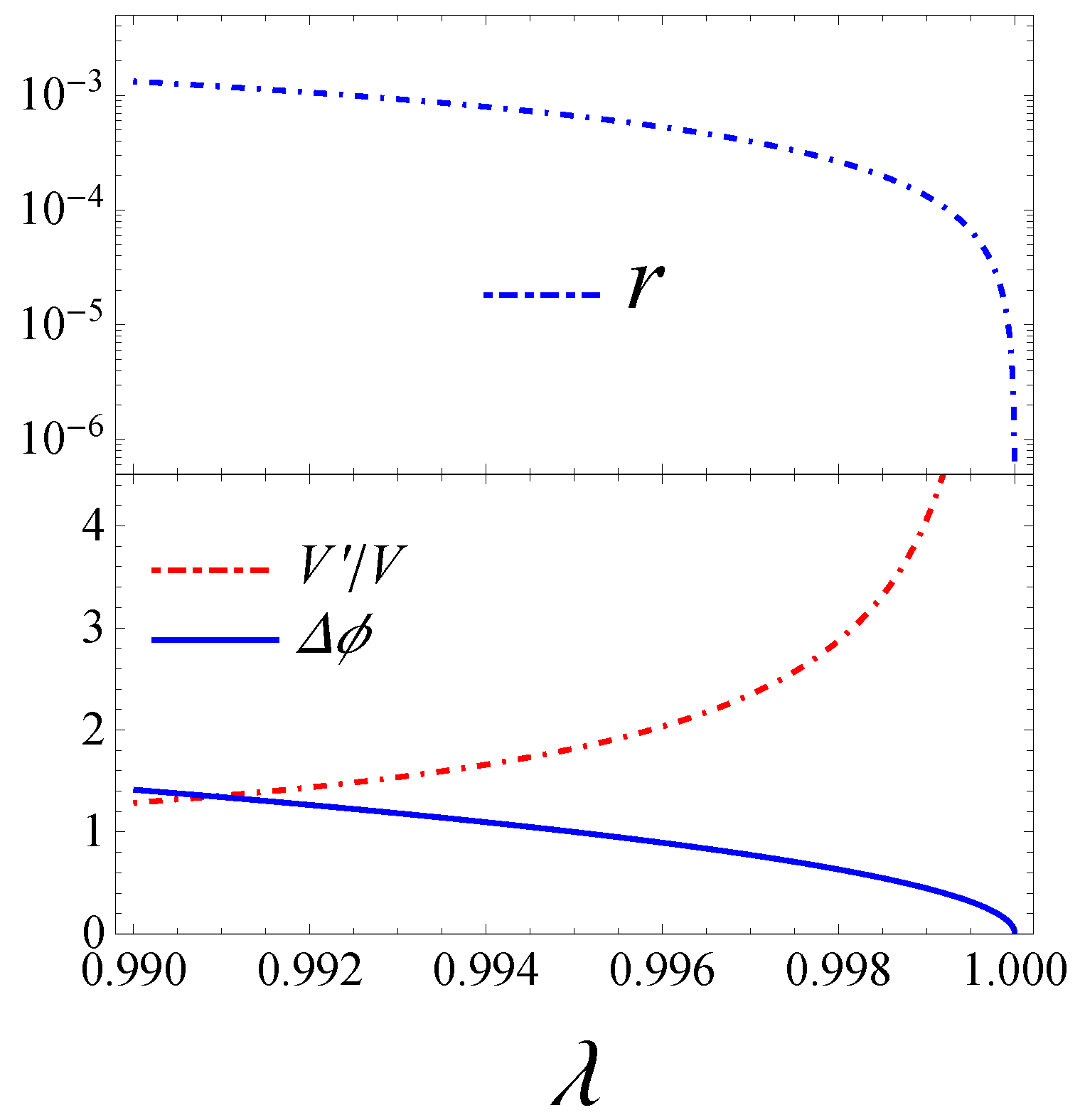
3.1. The Power-Law Potential
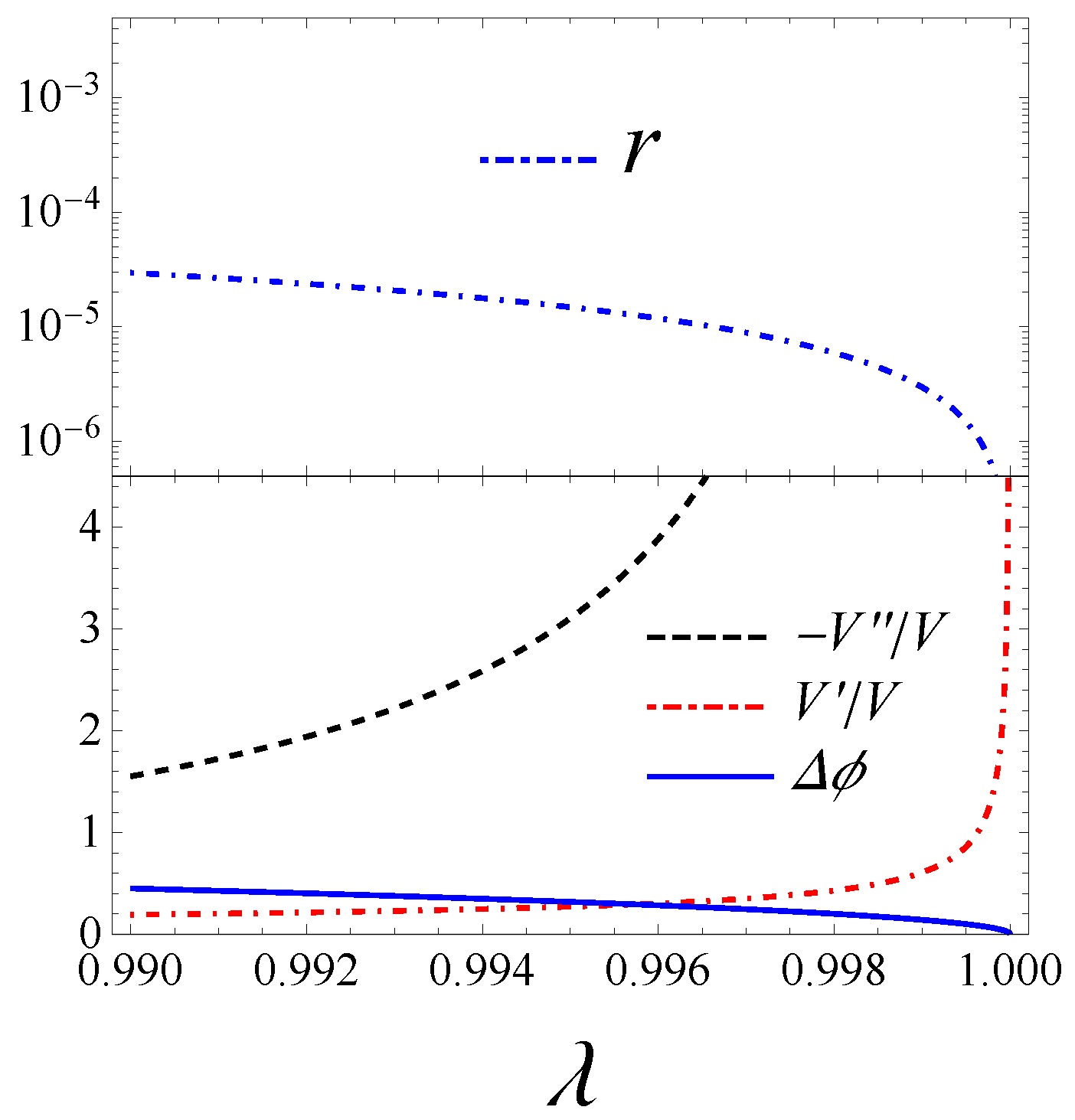
3.2. The E-Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Sato, K. First Order Phase Transition of a Vacuum and Expansion of the Universe. Mon. Not. R. Astron. Soc. 1981, 195, 467–479. [Google Scholar] [CrossRef]
- Ooguri, H.; Vafa, C. On the Geometry of the String Landscape and the Swampland. Nucl. Phys. B 2007, 766, 21–33. [Google Scholar] [CrossRef]
- Vafa, C. The String landscape and the swampland. arXiv 2005, arXiv:hep-th/0509212. [Google Scholar]
- Ooguri, H.; Vafa, C. Non-supersymmetric AdS and the Swampland. Adv. Theor. Math. Phys. 2017, 21, 1787–1801. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:hep-th/1806.08362. [Google Scholar]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Kehagias, A.; Riotto, A. A note on Inflation and the Swampland. arXiv 2018, arXiv:hep-th/1807.05445. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. arXiv 2018, arXiv:1807.06211. [Google Scholar]
- Ade, P.A.R.; Ahmed, Z.; Aikin, R.W.; Alexander, K.D.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bowens-Rubin, R.; Brevik, J.A.; et al. BICEP2 / Keck Array x: Constraints on Primordial Gravitational Waves using Planck, WMAP, and New BICEP2/Keck Observations through the 2015 Season. Phys. Rev. Lett. 2018, 121, 221301. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G.; Steinhardt, P.J.; Vafa, C. On the Cosmological Implications of the String Swampland. Phys. Lett. B 2018, 784, 271–276. [Google Scholar] [CrossRef]
- Lyth, D.H. What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy? Phys. Rev. Lett. 1997, 78, 1861–1863. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef]
- Brennan, T.D.; Carta, F.; Vafa, C. The String Landscape, the Swampland, and the Missing Corner. arXiv 2017, arXiv:1711.00864. [Google Scholar]
- Das, S. Note on single-field inflation and the swampland criteria. Phys. Rev. D 2019, 99, 083510. [Google Scholar] [CrossRef]
- Das, S. Warm Inflation in the light of Swampland Criteria. Phys. Rev. D 2019, 99, 063514. [Google Scholar] [CrossRef]
- Motaharfar, M.; Kamali, V.; Ramos, R.O. Warm inflation as a way out of the swampland. Phys. Rev. D 2019, 99, 063513. [Google Scholar] [CrossRef]
- Ashoorioon, A. Rescuing Single Field Inflation from the Swampland. Phys. Lett. B 2019, 790, 568–573. [Google Scholar] [CrossRef]
- Lin, C.M.; Ng, K.W.; Cheung, K. Chaotic inflation on the brane and the Swampland Criteria. Phys. Rev. D 2019, 100, 023545. [Google Scholar] [CrossRef]
- Lin, C.M. Type I Hilltop Inflation and the Refined Swampland Criteria. Phys. Rev. D 2019, 99, 023519. [Google Scholar] [CrossRef]
- Kinney, W.H.; Vagnozzi, S.; Visinelli, L. The zoo plot meets the swampland: Mutual (in)consistency of single-field inflation, string conjectures, and cosmological data. Class. Quant. Grav. 2019, 36, 117001. [Google Scholar] [CrossRef]
- Achúcarro, A.; Palma, G.A. The string swampland constraints require multi-field inflation. J. Cosmol. Astropart. Phys. 2019, 2019, 041. [Google Scholar] [CrossRef]
- Andriot, D. On the de Sitter swampland criterion. Phys. Lett. B 2018, 785, 570–573. [Google Scholar] [CrossRef]
- Park, S.C. Minimal gauge inflation and the refined Swampland conjecture. J. Cosmol. Astropart. Phys. 2019, 2019, 053. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. arXiv 2018, arXiv:1807.05193. [Google Scholar]
- Garg, S.K.; Krishnan, C.; Zaid Zaz, M. Bounds on Slow Roll at the Boundary of the Landscape. J. High Energy Phys. 2019, 2019, 029. [Google Scholar] [CrossRef]
- Schimmrigk, R. The Swampland Spectrum Conjecture in Inflation. arXiv 2018, arXiv:1810.11699. [Google Scholar]
- Dimopoulos, K. Steep Eternal Inflation and the Swampland. Phys. Rev. D 2018, 98, 123516. [Google Scholar] [CrossRef]
- Matsui, H.; Takahashi, F. Eternal Inflation and Swampland Conjectures. Phys. Rev. D 2019, 99, 023533. [Google Scholar] [CrossRef]
- Ben-Dayan, I. Draining the Swampland. Phys. Rev. D 2019, 99, 101301. [Google Scholar] [CrossRef]
- Brahma, S.; Wali Hossain, M. Avoiding the string swampland in single-field inflation: Excited initial states. J. High Energy Phys. 2019, 2019, 006. [Google Scholar] [CrossRef]
- Roupec, C.; Wrase, T. De Sitter Extrema and the Swampland. Fortsch. Phys. 2019, 67, 1800082. [Google Scholar] [CrossRef]
- Blåbäck, J.; Danielsson, U.; Dibitetto, G. A new light on the darkest corner of the landscape. arXiv 2018, arXiv:1810.11365. [Google Scholar]
- Odintsov, S.D.; Oikonomou, V.K. Finite-time Singularities in Swampland-related Dark Energy Models. Europhys. Lett. 2019, 126, 20002. [Google Scholar] [CrossRef]
- Kawasaki, M.; Takhistov, V. Primordial Black Holes and the String Swampland. Phys. Rev. D 2018, 98, 123514. [Google Scholar] [CrossRef]
- Wang, S.J. Electroweak relaxation of cosmological hierarchy. Phys. Rev. D 2019, 99, 023529. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Dark Energy in the Swampland. Phys. Rev. D 2018, 98, 123502. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G. Dark Energy and the Refined de Sitter Conjecture. J. High Energy Phys. 2019, 2019, 103. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C.; Zell, S. Quantum Breaking Bound on de Sitter and Swampland. Fortsch. Phys. 2019, 67, 1800094. [Google Scholar] [CrossRef]
- Fukuda, H.; Saito, R.; Shirai, S.; Yamazaki, M. Phenomenological Consequences of the Refined Swampland Conjecture. Phys. Rev. D 2019, 99, 083520. [Google Scholar] [CrossRef]
- Chiang, C.I.; Leedom, J.M.; Murayama, H. What does inflation say about dark energy given the swampland conjectures? Phys. Rev. D 2019, D100, 043505. [Google Scholar] [CrossRef]
- Sabir, M.; Ahmed, W.; Gong, Y.; Lu, Y. Superconformal attractor E-models in brane inflation under swampland criteria. arXiv 2019, arXiv:1903.08435. [Google Scholar]
- Channuie, P. Refined Swampland conjecture in deformed Starobinsky gravity. arXiv 2019, arXiv:1907.10605. [Google Scholar]
- Palti, E. The Swampland: Introduction and Review. Fortsch. Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Kamali, V. Reheating After Swampland Conjecture. arXiv 2019, arXiv:1902.00701. [Google Scholar]
- Yi, Z.; Gong, Y.; Sabir, M. Inflation with Gauss-Bonnet coupling. Phys. Rev. D 2018, 98, 083521. [Google Scholar] [CrossRef]
- Antoniadis, I.; Rizos, J.; Tamvakis, K. Singularity—Free cosmological solutions of the superstring effective action. Nucl. Phys. B 1994, 415, 497–514. [Google Scholar] [CrossRef]
- Kawai, S.; Sakagami, M.A.; Soda, J. Instability of one loop superstring cosmology. Phys. Lett. B 1998, 437, 284–290. [Google Scholar] [CrossRef]
- Kawai, S.; Soda, J. Evolution of fluctuations during graceful exit in string cosmology. Phys. Lett. B 1999, 460, 41–46. [Google Scholar] [CrossRef]
- Tsujikawa, S. Density perturbations in the ekpyrotic universe and string inspired generalizations. Phys. Lett. B 2002, 526, 179–185. [Google Scholar] [CrossRef]
- Toporensky, A.; Tsujikawa, S. Nature of singularities in anisotropic string cosmology. Phys. Rev. D 2002, 65, 123509. [Google Scholar] [CrossRef]
- Gong, Y.; Papantonopoulos, E.; Yi, Z. Constraints on scalar–tensor theory of gravity by the recent observational results on gravitational waves. Eur. Phys. J. C 2018, 78, 738. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. 2017, 848, L13. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary Phenomenology of Einstein Gauss-Bonnet Gravity Compatible with GW170817. arXiv 2019, arXiv:1908.07555. [Google Scholar] [CrossRef]
- Rizos, J.; Tamvakis, K. On the existence of singularity free solutions in quadratic gravity. Phys. Lett. B 1994, 326, 57–61. [Google Scholar] [CrossRef][Green Version]
- Kanti, P.; Rizos, J.; Tamvakis, K. Singularity free cosmological solutions in quadratic gravity. Phys. Rev. D 1999, 59, 083512. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Sasaki, M. Gauss-Bonnet dark energy. Phys. Rev. D 2005, 71, 123509. [Google Scholar] [CrossRef]
- Satoh, M.; Soda, J. Higher Curvature Corrections to Primordial Fluctuations in Slow-roll Inflation. J. Cosmol. Astropart. Phys. 2008, 2008, 019. [Google Scholar] [CrossRef]
- Kanti, P.; Gannouji, R.; Dadhich, N. Gauss-Bonnet Inflation. Phys. Rev. D 2015, 92, 041302. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D.; Oikonomou, V.K. Modified Gauss–Bonnet gravity with the Lagrange multiplier constraint as mimetic theory. Class. Quant. Grav. 2015, 32, 185007. [Google Scholar] [CrossRef]
- Chakraborty, S.; Paul, T.; SenGupta, S. Inflation driven by Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2018, 98, 083539. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Viable Inflation in Scalar-Gauss-Bonnet Gravity and Reconstruction from Observational Indices. Phys. Rev. D 2018, 98, 044039. [Google Scholar] [CrossRef]
- Chatzarakis, N.; Oikonomou, V.K. Autonomous Dynamical System of Einstein-Gauss-Bonnet Cosmologies. arXiv 2019, arXiv:1908.08141. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Van de Bruck, C.; Dimopoulos, K.; Longden, C. Reheating in Gauss-Bonnet-coupled inflation. Phys. Rev. D 2016, 94, 023506. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Terrero-Escalante, C.A.; Garcia, A.A. Higher order corrections to primordial spectra from cosmological inflation. Phys. Lett. B 2001, 517, 243–249. [Google Scholar] [CrossRef]
- Guo, Z.K.; Schwarz, D.J. Slow-roll inflation with a Gauss-Bonnet correction. Phys. Rev. D 2010, 81, 123520. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Gerbino, M.; Freese, K.; Vagnozzi, S.; Lattanzi, M.; Mena, O.; Giusarma, E.; Ho, S. Impact of neutrino properties on the estimation of inflationary parameters from current and future observations. Phys. Rev. 2017, D95, 043512. [Google Scholar] [CrossRef]
- Kallosh, R.; Linde, A. Non-minimal Inflationary Attractors. JCAP 2013, 2013, 033. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Kallosh, R.; Linde, A. Cosmological Attractors and Initial Conditions for Inflation. Phys. Rev. D 2015, 92, 063519. [Google Scholar] [CrossRef]
- Yi, Z.; Gong, Y. Nonminimal coupling and inflationary attractors. Phys. Rev. D 2016, 94, 103527. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, Z.; Gong, Y. Gauss–Bonnet Inflation and the String Swampland. Universe 2019, 5, 200. https://doi.org/10.3390/universe5090200
Yi Z, Gong Y. Gauss–Bonnet Inflation and the String Swampland. Universe. 2019; 5(9):200. https://doi.org/10.3390/universe5090200
Chicago/Turabian StyleYi, Zhu, and Yungui Gong. 2019. "Gauss–Bonnet Inflation and the String Swampland" Universe 5, no. 9: 200. https://doi.org/10.3390/universe5090200
APA StyleYi, Z., & Gong, Y. (2019). Gauss–Bonnet Inflation and the String Swampland. Universe, 5(9), 200. https://doi.org/10.3390/universe5090200




