Selected Topics in Numerical Methods for Cosmology
Abstract
1. Introduction
2. Numerical Methods
2.1. Background
2.2. Time Variables
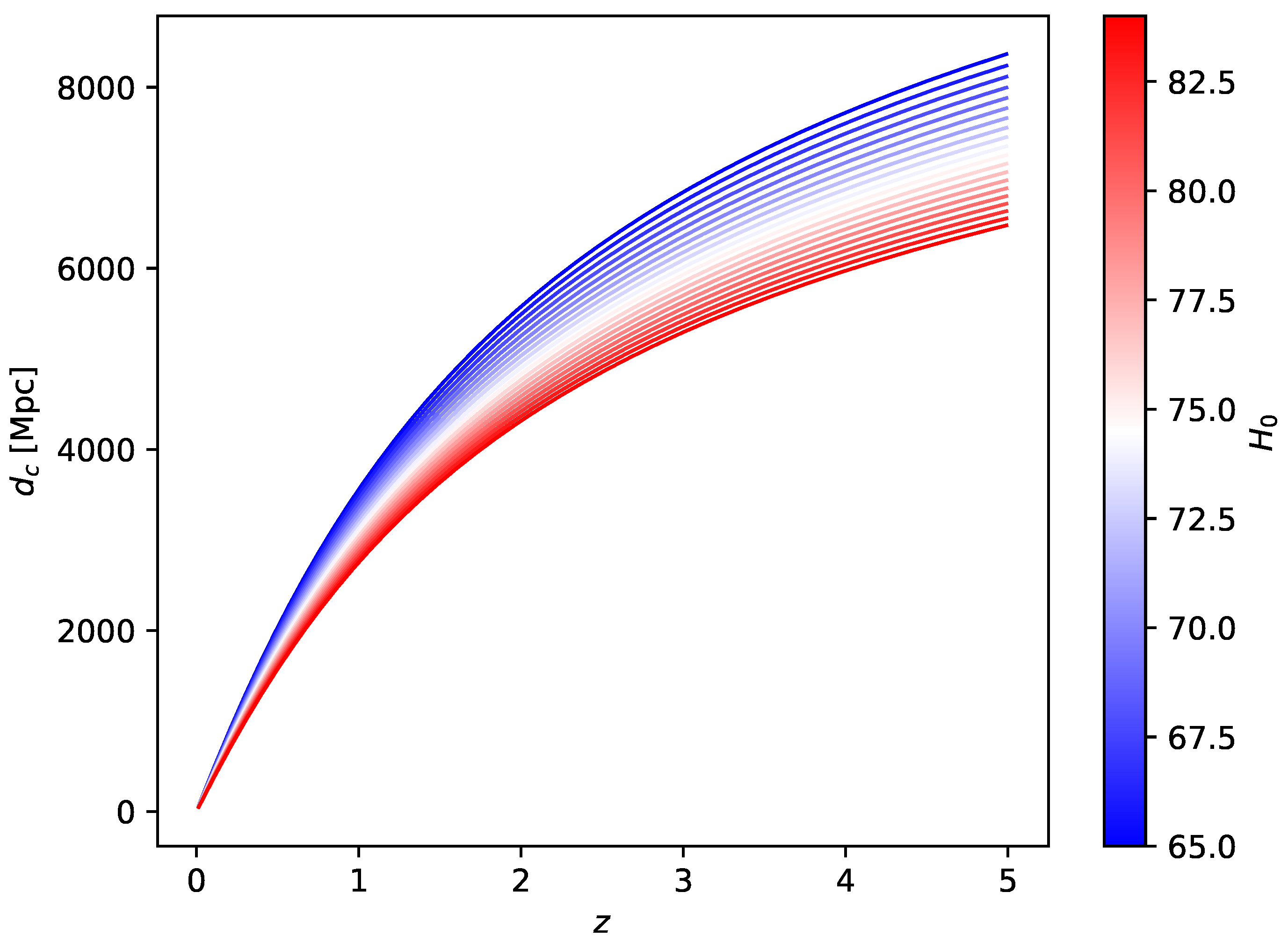
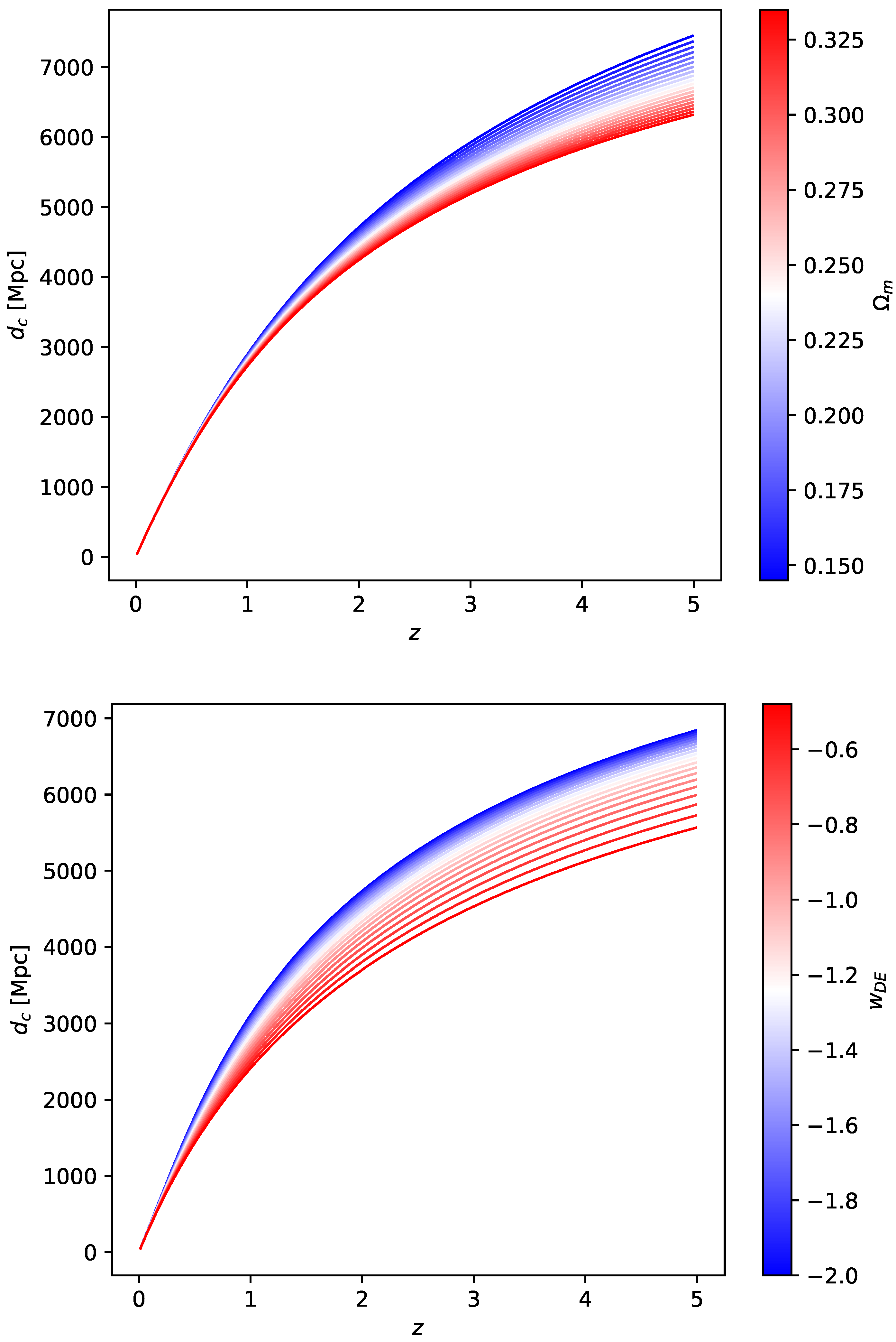
2.3. Distances
2.4. Equations of Motion
2.5. Integrating and Evaluating the Background
2.5.1. Integration Strategies
- simplicity, one needs to integrate a system of variables with respect to time just once;
- less integration overhead, the integration software itself has a computational cost. Each time it is used, there are the costs of initialization, step computation and destruction.
- step sizes smaller than necessary. When performing the integration, the Ordinary Differential Equations (ODE) solver evaluates the steps of all components being integrated and adapts the time step such that the error bounds are respected by all components. For this reason, including the ‘C’ set in the integration can result in a larger set of steps for all quantities ‘B + C’;
- difficult to efficiently modularize, in some analysis, just a few (or just one) observables from ‘C’ are necessary. When performing all integration at once, you have two options, integrate everything every time, even when they are not all necessary, or to create a set of flags that control which quantities should be integrated by branching (e.g., if-statements). Naturally, the if-clauses create an unnecessary overhead if they are placed inside the integration loop. Alternatively, if one decides to create a loop for every combination to avoid this overhead, then he/she will end-up with different loops (where n is the number of variables in ‘C’) which creates new problems such as code repetition and harder code maintenance.
2.5.2. Evaluating the Background
3. Linear Perturbations
Numerical Solution
4. Cancellation Errors
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GR | General Relativity |
| SNeIa | Type Ia Supernovae |
| ODE | Ordinary Differential Equation |
| CMB | Cosmic Microwave Background |
| LSS | Large Scale Structure |
| NumCosmo | Numerical Cosmology |
| CAMB | Code for Anisotropies in the Microwave Background |
| CLASS | The Cosmic Linear Anisotropy Solving System |
| MCMC | Markov Chain Monte Carlo |
| FLRW | Friedmann–Lemaître–Robertson–Walker |
| DM | Dark Matter |
| DE | Dark Energy |
| WKB | Wentzel–Kramers–Brillouin |
| FP | Floating-Point |
References
- Linde, A. On the problem of initial conditions for inflation. arXiv 2017, arXiv:1710.04278v1. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Observational constraints on quantum decoherence during inflation. arXiv 2018, arXiv:1801.09949v1. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year wilkinson microwave anisotropy probe (wmap) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- SDSS-III Collaboration. SDSS-III: Massive Spectroscopic Surveys of the Distant Universe, the Milky Way Galaxy, and Extra-Solar Planetary Systems. Available online: www.sdss3.org/collaboration/description.pdf (accessed on 28 September 2019).
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2015, 594, A13. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Allam, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; Ballester, O.; Banerji, M.; Barkhouse, W.; et al. The Dark Energy Survey Data Release 1. arXiv 2018, arXiv:1801.03181v1. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Penna-Lima, M. Numerical Cosmology—NumCosmo. arXiv 2014, arXiv:1408.013. [Google Scholar]
- Lewis, A.; Challinor, A.; Lasenby, A. Efficient Computation of CMB anisotropies in closed FRW models. Astrophys. J. 2000, 538, 473–476. [Google Scholar] [CrossRef]
- Howlett, C.; Lewis, A.; Hall, A.; Challinor, A. CMB power spectrum parameter degeneracies in the era of precision cosmology. J. Cosmol. Astropart. Phys. 2012, 2012, 027. [Google Scholar] [CrossRef]
- Lewis, A. CAMB Notes. Available online: http://cosmologist.info/notes/CAMB.pdf (accessed on 28 September 2019).
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview. arXiv 2011, arXiv:1104.2932. [Google Scholar]
- Blas, D.; Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes. J. Cosmol. Astropart. Phys. 2011, 2011, 034. [Google Scholar] [CrossRef]
- Lesgourgues, J. The Cosmic Linear Anisotropy Solving System (CLASS) III: Comparision with CAMB for LambdaCDM. arXiv 2011, arXiv:1104.2934. [Google Scholar]
- Lesgourgues, J.; Tram, T. The Cosmic Linear Anisotropy Solving System (CLASS) IV: Efficient implementation of non-cold relics. J. Cosmol. Astropart. Phys. 2011, 9, 32. [Google Scholar] [CrossRef]
- Lewis, A.; Bridle, S. Cosmological parameters from CMB and other data: A Monte Carlo approach. Phys. Rev. 2002, D66, 103511. [Google Scholar] [CrossRef]
- Lewis, A. Efficient sampling of fast and slow cosmological parameters. Phys. Rev. D 2013, 87, 103529. [Google Scholar] [CrossRef]
- Audren, B.; Lesgourgues, J.; Benabed, K.; Prunet, S. Conservative constraints on early cosmology with MONTE PYTHON. J. Cosmol. Astropart. Phys. 2013, 2013, 001. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Peter, P.; Uzan, J.P. Primordial Cosmology; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Hogg, D.W. Distance measures in cosmology. arXiv 2007, arXiv:9905116. [Google Scholar]
- Vitenti, S.D.P. Unitary evolution, canonical variables and vacuum choice for general quadratic Hamiltonians in spatially homogeneous and isotropic space-times. arXiv 2015, arXiv:1505.01541. [Google Scholar]
- Branch, D.; Miller, D.L. Type IA supernovae as standard candles. Astrophys. J. Lett. 1993, 405, L5–L8. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Bassett, B.; Hlozek, R. Baryon acoustic oscillations. In Dark Energy: Observational and Theoretical Approaches; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2010; p. 246. [Google Scholar]
- De Boor, C. A Practical Guide to Splines; Springer: Berlin, Germany, 2001. [Google Scholar]
- GSL Project Contributors. GSL—GNU Scientific Library—GNU Project—Free Software Foundation; Free Software Foundation, Inc.: Boston, MA, USA, 2010. [Google Scholar]
- Behforooz, G.H.; Papamichael, N. End conditions for cubic spline interpolation. IMA J. Appl. Math. 1979, 23, 355–366. [Google Scholar] [CrossRef]
- Chisari, N.E.; Alonso, D.; Krause, E.; Leonard, C.D.; Bull, P.; Neveu, J.; Villarreal, A.; Singh, S.; McClintock, T.; Ellison, J.; et al. [LSST Dark Energy Science Collaboration]Core Cosmology Library: Precision Cosmological Predictions for LSST. arXiv 2018, arXiv:1812.05995. [Google Scholar]
- Heineman, G.; Pollice, G.; Selkow, S. Algorithms in a Nutshell (In a Nutshell (O’Reilly)); O’Reilly Media: Springfield, MO, USA, 2008. [Google Scholar]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Bardeen, J.M. Gauge-invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882–1905. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Feldman, H.A.; Brandenberger, R.H. Theory of cosmological perturbations. Phys. Rep. 1992, 215, 203–333. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Falciano, F.T.; Pinto-Neto, N. Covariant Bardeen perturbation formalism. Phys. Rev. D 2014, 89, 103538. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Pinto-Neto, N. Large Adiabatic Scalar Perturbations in a Regular Bouncing Universe. Phys. Rev. D 2012, 85, 023524. [Google Scholar] [CrossRef]
- Pinto-Neto, N.; Vitenti, S.D.P. Comment on “Growth of covariant perturbations in the contracting phase of a bouncing universe”. Phys. Rev. D 2014, 89, 028301. [Google Scholar] [CrossRef]
- Vitenti, S.D.P.; Falciano, F.T.; Pinto-Neto, N. Quantum Cosmological Perturbations of Generic Fluids in Quantum Universes. Phys. Rev. D 2013, 87, 103503. [Google Scholar] [CrossRef]
- Falciano, F.T.; Pinto-Neto, N.; Vitenti, S.D.P. Scalar field perturbations with arbitrary potentials in quantum backgrounds. Phys. Rev. D 2013, 87, 103514. [Google Scholar] [CrossRef]
- Peter, P.; Pinto-Neto, N.; Vitenti, S.D.P. Quantum cosmological perturbations of multiple fluids. Phys. Rev. D 2016, 93, 023520. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory; Springer: Berlin, Germany, 1978. [Google Scholar]
- Kincaid, D.; Cheney, W. Numerical Analysis: Mathematics of Scientific Computing; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Higham, N. Accuracy and Stability of Numerical Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Penna-Lima, M.; Makler, M.; Wuensche, C.A. Biases on cosmological parameter estimators from galaxy cluster number counts. J. Cosmol. Astropart. Phys. 2014, 2014, 39. [Google Scholar] [CrossRef]
| 1 | The observed anisotropies in the CMB are very small (), and, for this reason, they are within the regime of validity of the first order perturbation theory. |
| 2 | |
| 3 | |
| 4 | Briefly speaking, GObject provides an object-oriented framework for C programs, while GObject Introspection generates bindings for other languages, such as Python, Perl and JavaScript. |
| 5 | The relation between z and is monotonic since . |
| 6 | The ± sign in the definition of is included in order to have it monotonically increasing with t or in the expansion/contraction, respectively. |
| 7 | Note that here we are defining as a constant evaluated today, in the literature, the definition as a function of z is also frequently found, i.e., , where . |
| 8 | It would be necessary to save/read the last evaluation interval in a per-thread basis. |
| 9 | When are not positive definite one can use a similar algorithm with and , where the is a scale s controls the transition between linear and log scale. |
| 10 | Usually, the relative tolerance controls the final error of the code while the absolute tolerance is application specific and, in the few cases where it is used, it serves to avoid excess in the tolerance. For example, if a given function f is zero at a point x and we want to compute its approximation p, the error control is
Thus, without the absolute tolerance, the error control would never accept the approximation, unless it was a perfect approximation . |
| 11 | We can write and , for an eigenfunction of with eigenvalue , i.e., . |
| 12 | It is for this reason that some authors use the expressions super-/sub-Hubble scales, scales much larger/smaller than . We can also find the expressions super-/sub-horizon to refer to the same scales. Nevertheless, this nomenclature is based on the fact that, for some simple models, the horizon is also proportional to , which can be wrong and counter-intuitive in many cases and as such should be avoided. |
| 13 | For a complete exposition about this subject see [39]. |
| 14 | The precision is usually defined in binary basis, since it is that which are used in the computer representation. This precision does not translate to a fixed number of decimal places. For instance, in the IEEE 754 standard, the common used double precision FP number has a 53 bits base and 11 bits exponent; this basis roughly translates to decimal places. |
| 15 | However, in practice, we have the addition of positive and negative numbers. In this case, the error sign of the individual operations are mixed and, consequently, some cancel out. As a rule of thumb, some authors suggest the use of the square root of the number of operations to estimate the roundoff error, see [41] for more details about the statistical analysis of the accumulated roundoff error. |
| 16 | With the exception of computations that involves a very large number of operations, n must be of the order of trillions () to produce a error. |
| 17 | In many cases, the order of the operations follow a restrict precedence rule dependent on the compiler/specification. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias Pinto Vitenti, S.; Penna-Lima, M. Selected Topics in Numerical Methods for Cosmology. Universe 2019, 5, 192. https://doi.org/10.3390/universe5090192
Dias Pinto Vitenti S, Penna-Lima M. Selected Topics in Numerical Methods for Cosmology. Universe. 2019; 5(9):192. https://doi.org/10.3390/universe5090192
Chicago/Turabian StyleDias Pinto Vitenti, Sandro, and Mariana Penna-Lima. 2019. "Selected Topics in Numerical Methods for Cosmology" Universe 5, no. 9: 192. https://doi.org/10.3390/universe5090192
APA StyleDias Pinto Vitenti, S., & Penna-Lima, M. (2019). Selected Topics in Numerical Methods for Cosmology. Universe, 5(9), 192. https://doi.org/10.3390/universe5090192




