1. Introduction
The General Relativity (GR) is one of the best tested theories [
1]. Recently, the detection of gravitational waves [
2] and the first optical resolution of the black hole in M87 [
3,
4,
5,
6,
7,
8] are all consistent with GR, i.e., one observes a shadow of the black hole. The size of it can be understood within GR and its radius is about
. Unfortunately, the resolution is only of
, which will smooth detailed structures, which are predicted by us (see the discussion in the main body of the text).
There are some concerns that, for strong gravitational fields, compared to the solar system, modifications to GR probably have to be applied. This did lead to several attempts to modify GR, which will be all resumed briefly in the next section. Here, we will concentrate on the so-called pseudo-complex General Relativity (pc-GR).
A complete review on the pc-GR, its motivation and relations to other approaches can be found in the book by Hess, Schäfer and Greiner [
9]. The mathematics of the pc-GR is explained in the first and last chapter of the book, using differential geometry. Information on this can also be found in [
10]. The pc-GR was first proposed in [
11]. A general formulation, besides in [
9], can also be found in [
12,
13], where, in [
12], circular stable orbits were investigated and the last stable orbits, compared to GR. One important result is that, for small
a, the last stable orbit in pc-GR is a little bit closer to the black hole than in GR. From a limiting value of
a on, stable orbits up to the surface of the star exist. In this review, we will elaborate on the consequences of it. The theory predicts a different behavior of an accretion disc near the black hole, showing a dark ring followed by a bright one further in. Studies on this were also published in [
14,
15] and more recently in [
16,
17]. The main feature is the ring structure, mentioned above, which is quite independent from the mass of the black hole and the type of the accretion disc (if it is thin, thick, a torus, ...), save that the positions of the structures scale with the mass. The intensities of the light emission are larger in pc-GR than in GR (see also the discussion in the main body of this review).
In addition, neutron stars were studied in [
18,
19,
20], in addition to [
9]. Including the effects of the pc-GR, stars up to six solar masses were obtained in [
18,
20] and up to 200 solar masses in [
19].
Cosmological models were investigated in [
21,
22], which agree with current observations, but with different outcomes in the far future. Due to many parameters, the predictive power is rather limited. Except for a big rip, possibilities were found that the universe approaches a constant acceleration, or approaches to zero acceleration, or it can collapse again. There are different approaches to study future outcomes (see, for example [
23,
24], where possible future evolutions of the universe are investigated, using a thermodynamic approach). Though interesting and worth mentioning, it differs from the path taken in pc-GR. It would be interesting in the future to connect both approaches, i.e., to consider the thermodynamic approach in pc-GR. Another proposal could be that the authors of [
23,
24] use the modified metric of pc-GR.
Gravitational waves were considered in pc-GR: in [
25], the gravitational wave event GW150914 was treated within pc-GR, with the result that probably the masses and distances involved are larger; however, a very simple model was used. The main reason for this behavior is that the orbital frequency becomes very small when the two masses in a black hole merger approach each other and, in order to obtain the observed frequencies, larger masses are required. In [
26], the axial and polar modes of the ring down phase were calculated, however, with some problems of convergence, due to the method used for solving the differential equation. All, except for the discussion of gravitational waves, are neatly summarized in [
9].
The main motivation for the development of pc-GR was to investigate what kind of theory emerges when the coordinates are algebraically extended (where only the pseudo-complex extension makes sense, as will be discussed further below): Is there a possibility to avoid the event horizon? What are the observable effects (particles in a circular orbit, behavior of accretion discs, position of the light-ring, neutron stars, etc.)? As we will point out in the next section, a minimal length element parameter may be involved. What is its effect? Are there consequences or at least suggestions for quantum effects in gravity? Not all has been answered up to now, due to mathematical problems, but most of the above questions have been treated.
Up to now, the main parameter (
, see main body of the text) of the theory was chosen such that no event horizon appears. For
, the standard GR is recovered. In this review, we will not cover all aspects of the theory (please also consult [
13]), but it would be interesting to vary the parameter
from 0 to the value, from which no event horizon appears, as done also in [
27,
28] for gravitational waves. In this manner, the GR and pc-GR can be connected smoothly. One can also study the behavior of the event horizon and the light-ring as a function in the rotational parameter
a and
.
The description is completely classical, though a dark energy contribution will be introduced in a classical language.
In
Section 2, the motivation for the algebraic extension of GR is described in more detail and the structure of pc-GR is discussed. The modified metric of a rotating star is listed (Kerr solution) and the corresponding Einstein equations are presented. In
Section 3, various consequences and structural changes are considered. The condition for the existence of an event horizon and a light-ring depends on a parameter (
), introduced in a phenomenological manner, which varies from zero (GR) to a maximal value (pc-GR). Structural changes, related to
phase transitions, can be described within the theory of catastrophes [
29]. The difference in structure (between GR and pc-GR) of an accretion disc around a black hole is also presented, important for the comparison to the observational data. One recent big advance in this direction was reported by the
Event Horizon Telescope Collaboration [
3,
4,
5,
6,
7,
8], where, for the first time, the black hole shadow of M87 was resolved. These references contain a huge amount of information, still to be analyzed. We also will compare some of the results to the recent observation of a black hole [
3,
4,
5,
6,
7,
8] and if one can distinguish pc-GR from GR. This part represents new results.
We use the signature for the metric. Furthermore, the light velocity c and the gravitational constant are set to one (i.e., ).
2. The Modified Theory: Pseudo-Complex General Relativity
At first, a historical overview on attempts to extend the GR is given, in addition to the reasons for it and why we decided for the pc-GR:
Extensions of the GR have been discussed several times in the past: Einstein extended the metric to a complex one [
30,
31], in an attempt to unify GR and the Electro-Magnetism. He defined a complex metric
where the real part is the standard metric of GR and the imaginary part is the electromagnetic tensor. The real part is symmetric while interchanging the indices and the imaginary part is anti-symmetric. This can be seen as follows:
Comparing both sides leads to
Why a complex extension did not work will become obvious in a moment.
The motivations of Born [
32,
33] were quite different. His concern is that, in Quantum Mechanics, the coordinates and momenta are treated on an equal footing. Canonical transformations of all kinds are allowed, which leave the commutation relations invariant, and one can even interchange coordinates and momenta. On the contrary, in GR, the coordinates play a singular role—in the length element square, only coordinates appear. He tried to recover the symmetry between the coordinates and momenta, leading to a modification of the length element, including momentum dependent terms, however, with the price of a mass dependence on a particle. The attempt by Born was retaken by Caianiello [
34], who introduced in the length element squared an infinitesimal quadratic 4-velocity term, without the reference to a particle, implying an infinitesimal length scale, equivalent to a maximal acceleration:
The l is a length parameter and is not subject to a Lorentz (or Poincaré) transformation. Thus, Lorentz invariance is guaranteed with an infinitesimal length scale in the model! Extracting an eigentime , taking into account that is an acceleration and using that = = ( is the Minkowski metric), we obtain = , i.e., it corresponds to a new metric = . The acceleration is then limited by .
We will see that these modifications are included in pc-GR in a particular limit. A more detailed resume on former intentions to extend the GR is given in [
9].
In [
35], all kinds of
algebraic extensions of the coordinates were considered and the field equations for weak gravitational fields were obtained. It was shown that nearly all algebraic extensions contain solutions for tachyons or ghosts, which shows that nonphysical solutions appear. Only real and pseudo-complex (called in [
35]
hyper-complex) coordinates did not have this problem. This is the reason why we discuss only this particular extension:
In pc-GR, the coordinates of GR are extended to these so-called
pseudo-complex (pc) variables:
(
), with
, which justifies its name (though the name is not universal in the literature, where these variables are denoted as para-complex, etc.). The complex conjugate is defined as
. In [
34], the variable
is proportional to a minimal length scale,
l, multiplied by the 4-velocity component
. It is important to stress that the parameter
l is
not a physical length and, thus, is not effected by a Lorentz transformation. Unfortunately, the relation of
to the 4-velocity is only correct in flat space, where the constraint used further below in (
9) reduces to the standard dispersion relation
, with the solution
. The minimal length parameter
l is required as a factor by dimensional considerations. When the space is not flat, no easy solution has been found yet, but, in principle, can be found by solving the constraint (
9).
An important nature of these variables is revealed when we change to the basis
It implies that there are variables of the type that have a zero norm. Thus, the variables form a ring and not a field. The components of are called zero divisor components.
The division into the zero divisor components can be done for any pc-function
. Mathematical manipulations are independent from each other (see also [
9]).
The fact that
allows for formulating in each zero-divisor component a theory of General Relativity! In order to get a consistent theory, both zero-divisor components have to be connected. In [
9,
11], this is done introducing a modified variational principle, where the variation of the action is proportional to a “general zero”, i.e., a function with a zero norm. However, this is not necessary: in [
36] and the last chapter of [
11], it is shown that a constraint can be implemented and a usual variational principle leads to modified Einstein equations. In what follows, we will resume the main steps.
The constraint requires that the pc length element
is real. We used the definitions
In addition, the representation of
in the zero-divisor is indicated and in the original basis (
-basis). (
7) coincides with the one of [
34], when
is substituted by
. In each component of the zero divisor basis, only Riemannian manifolds are considered, thus other types of manifolds are not included yet.
Setting the pseudo-imaginary part to zero leads to the constraint
The action, without the constraint, is given by
where
is the Riemann scalar. The last term in the action integral allows for introducing the cosmological constant in cosmological models, where
has to be constant in order not to violate the Lorentz symmetry. This, however, changes when a system with a uniquely defined center is considered, which has spherical (Schwarzschild) or axial (Kerr) symmetry. In these cases, the
is allowed to be a function in
r, for the Schwarzschild solution, and a function in
r and
, for the Kerr solution.
The variation is independent in each zero-divisor basis. The result is the set of the modified Einstein equations (see [
36])
with
The energy-momentum tensor corresponds to the one of an asymmetric ideal fluid. The
is related to the appearance of a minimal scale, as explained in the case of the proposal given in [
34]. Because these effects are practically impossible to measure due to their smallness, it suffices to restrict to the real part of the equations, which leads to the only one equation:
The energy-momentum tensor acquires under this approximation the form
The relations to the parameter in the action are (see [
36])
where
are the components of a space-like vector, orthogonal to the 4-velocity.
Because we do not know the exact solution for
, we cannot derive the exact form of the energy- momentum tensor and, thus, we are left to propose a phenomenological model. The energy-momentum tensor describes an ideal anisotropic fluid. That it has to be anisotropic is explained in [
9]: First of all, as explained further below, the energy-momentum tensor on the right-hand side of the Einstein equations is assumed to be related to the contribution of vacuum fluctuations, which represents a dark energy. This dark energy can be calculated within the one-loop approximation of GR as described in [
37] and done in [
38]. The equation of state of a dark energy in the radial pressure is
, where
is its pressure and
is the dark energy density. Within the
Tolmann–Oppenheimer–Volkoff (TOV) equations, the radial derivative of the pressure is proportional to the sum of the radial pressure (which is equal to the tangential one in case of an isotropic fluid) and the density, i.e., it is zero. An anisotropic fluid is characterized by an addition term, proportional to the difference of the radial and tangential pressure (
). Without this term, the radial derivative of the pressure is zero and thus constant in
r. Because of the proportionality of the energy density to the pressure, this also implies a constant energy density. Requiring that the density has to vanish at infinity results in a zero density, contrary to the requirement that the density is building up toward smaller distances. Only an anisotropic fluid can resolve this contradiction (see [
9]).
In the absence of a quantized theory of gravity, it is impossible to deduce, for example, the radial dependence of the dark-energy density. Here, we rely on information from one-loop calculations in GR [
37], which where performed in [
38] for a static Schwarzschild back-ground metric. In [
38], the energy density rises proportional to
toward the center, i.e., it is singular at the Schwarszschild radius. Clearly, the assumption of a static metric fails when the gravitational field increases too much. In this case, one has to include back-reaction effects, which is very difficult to do. This tells us that the fluctuations increase toward the center and they can become large. To avoid the singularity at the Schwarzschild radius, we propose a phenomenological model, where the dark-energy density is treated
classically and behaves as
where, in a first attempt,
was taken. It is strong enough in order not to contribute to the known observations within the solar system and other systems with not too strong gravitational fields [
1]. There may be other dependencies with
and, in fact, in [
27,
28], it was shown that the fall-off of the dark-energy density has to be stronger. We will discuss other cases of the fall-off, ordered by a number
n as in (
16); however, the main conclusions and structural predictions of the theory remain similar.
In [
12], the pc-Kerr solution was derived and here we list it for any
nThe a is the spin parameter in units of . The solution is identical to the standard Kerr solution, except for the term . The is the mass value observed at infinite distance and occasionally it will be abbreviated in the figures simply by m, clear from the context.
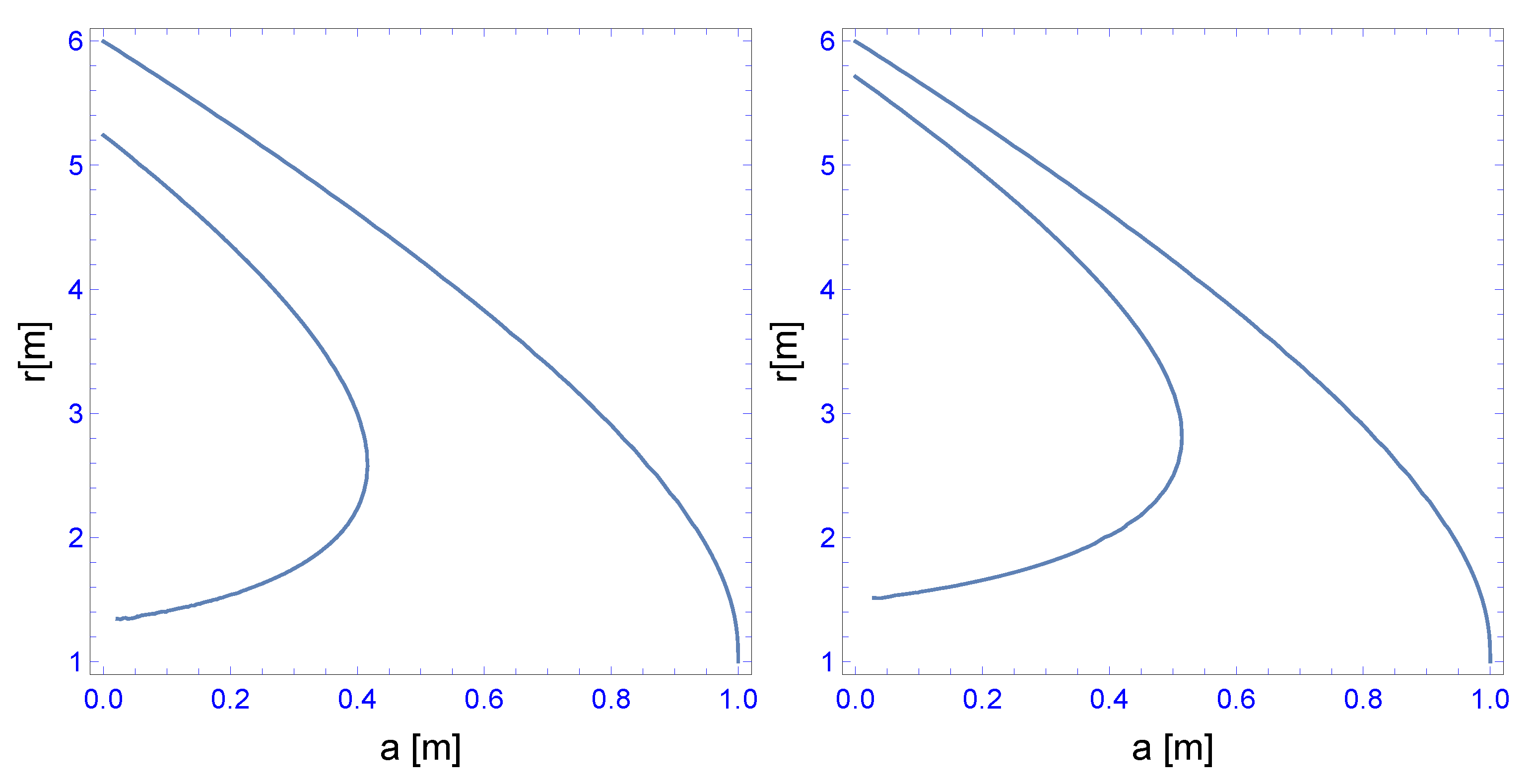
For the equal sign, an event horizon is located at
In this contribution, some examples are calculated with or and we will vary the parameter in from zero to a maximal value for and for . For a larger value, there is no event horizon present anymore. We will also vary the spin-parameter a from zero to and show that, already for , there is a region of large a values where this horizon disappears. For example, the question is, if there is or is not an event horizon already becomes relevant for tiny admixtures of vacuum fluctuations! This is similar, but not equal, to the so-called naked singularities: First, there is no singularity within the pc-GR and, second, what is exposed is the surface of a star. However, seeing the surface will be very difficult because the red-shift tends to infinity.
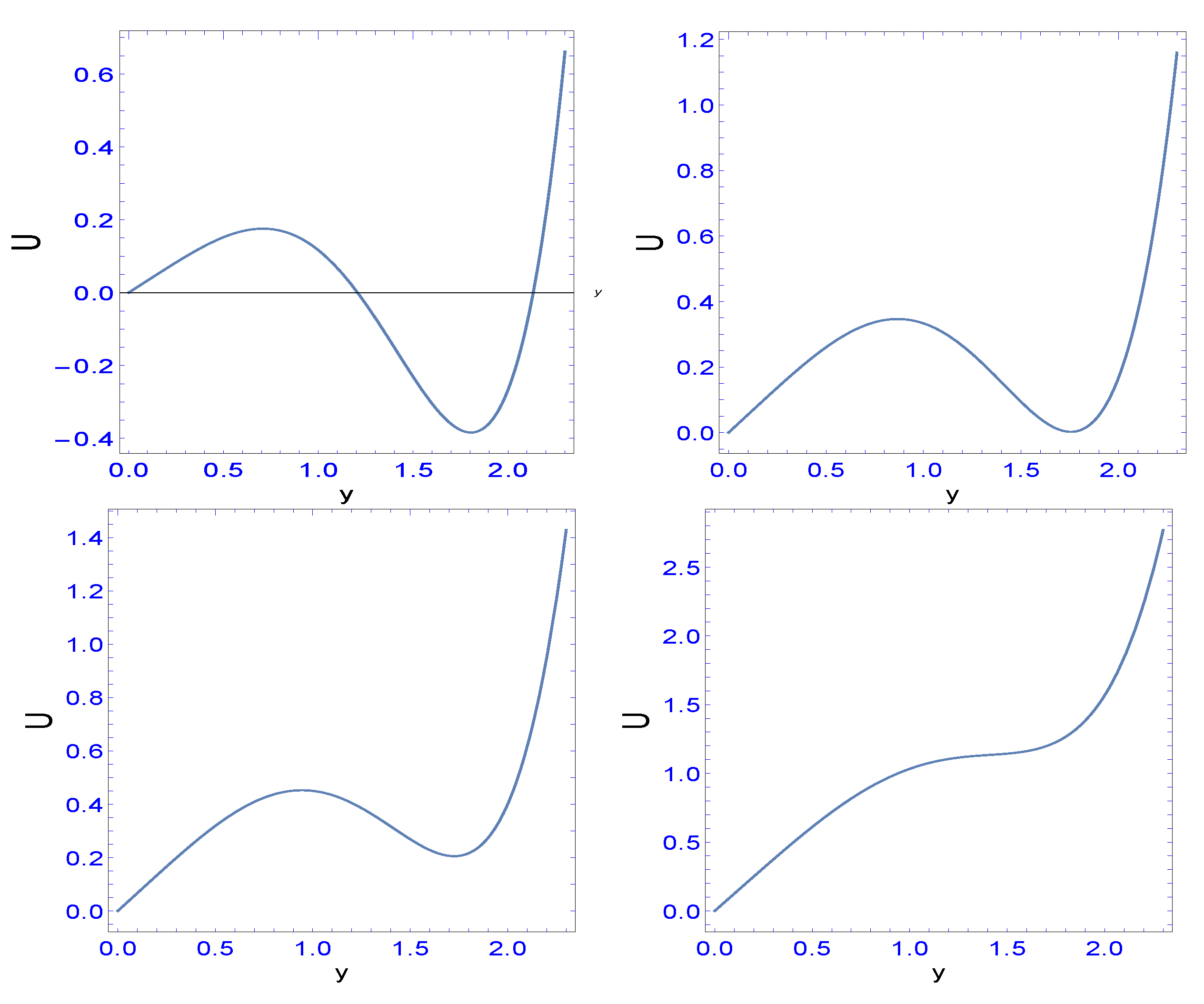
Another topic will be the calculation of the position of the light-ring. A light-ring is defined as the geodesic of a photon in a circular orbit (
const). In GR, there is, for
, only one light-ring at
and the value is slightly lowered for larger
a. In contrast, in pc-GR and, for values
, the structure becomes quite involved. We will investigate this property and relate it to phase transitions, using the
Catastrophe Theory [
29].
The application of pc-GR is not only limited to the region outside of a mass distribution, but also was applied to the interior of the star [
18,
19,
39,
40,
41,
42,
43]. The main problem is to propose a coupling of the dark energy to the mass distribution, which, due to not knowing it from first principles, is always charged with phenomenological assumptions. In [
18], a linear relation was assumed, which, however, leads to an upper limit of six solar masses for a star. The reason is that, near the surface, the repulsion is strong enough that the star sheds its upper parts of the surface. In [
19], this was resolved partially, applying a calculation within the one-loop approximation of quantized gravity [
37] and using the monopole approximation. As a result, the distribution of the dark energy turns out to fall off stronger near the surface. With that, stars with up to 200 solar masses were found to be stable. This already indicated that any mass of a star can probably be stabilized, i.e., even the large masses in the center of galaxies of billions of solar masses are stable and rather dark stars than black holes. There are different, alternative, approaches, e.g., in [
39,
40,
41,
42,
43] compact and dense objects were investigated within the pc-GR and maximal masses were also deduced.
4. Conclusions
We presented a report on the current status of the
pseudo-complec General Relativity (pc-GR). This theory requires that, around a mass, dark energy has to accumulate, for which we constructed a phenomenological ansatz, i.e., that it falls off proportional to
. This is multiplied by a parameter
that describes the coupling of the dark energy to the central mass. In most applications, the parameter
is chosen such that there is no event horizon for any
a-value. For this case, there is a lower value for
, which is
for
and
for
. In this contribution, we also investigated the range of
-values from zero on, i.e., we considered small vacuum fluctuation too, which by force is there [
37,
38]. We found that, even a tiny amount of vacuum fluctuations erase the event horizon near
and also the light-ring ceases to exit for small values of
and
a near
, which is
a new interesting feature. This has nothing to do with the so-called naked singularities because there is no singularity in pc-GR and what is exposed most is the surface of a star. However, the red-shift tends to infinity and the surface can not be seen.
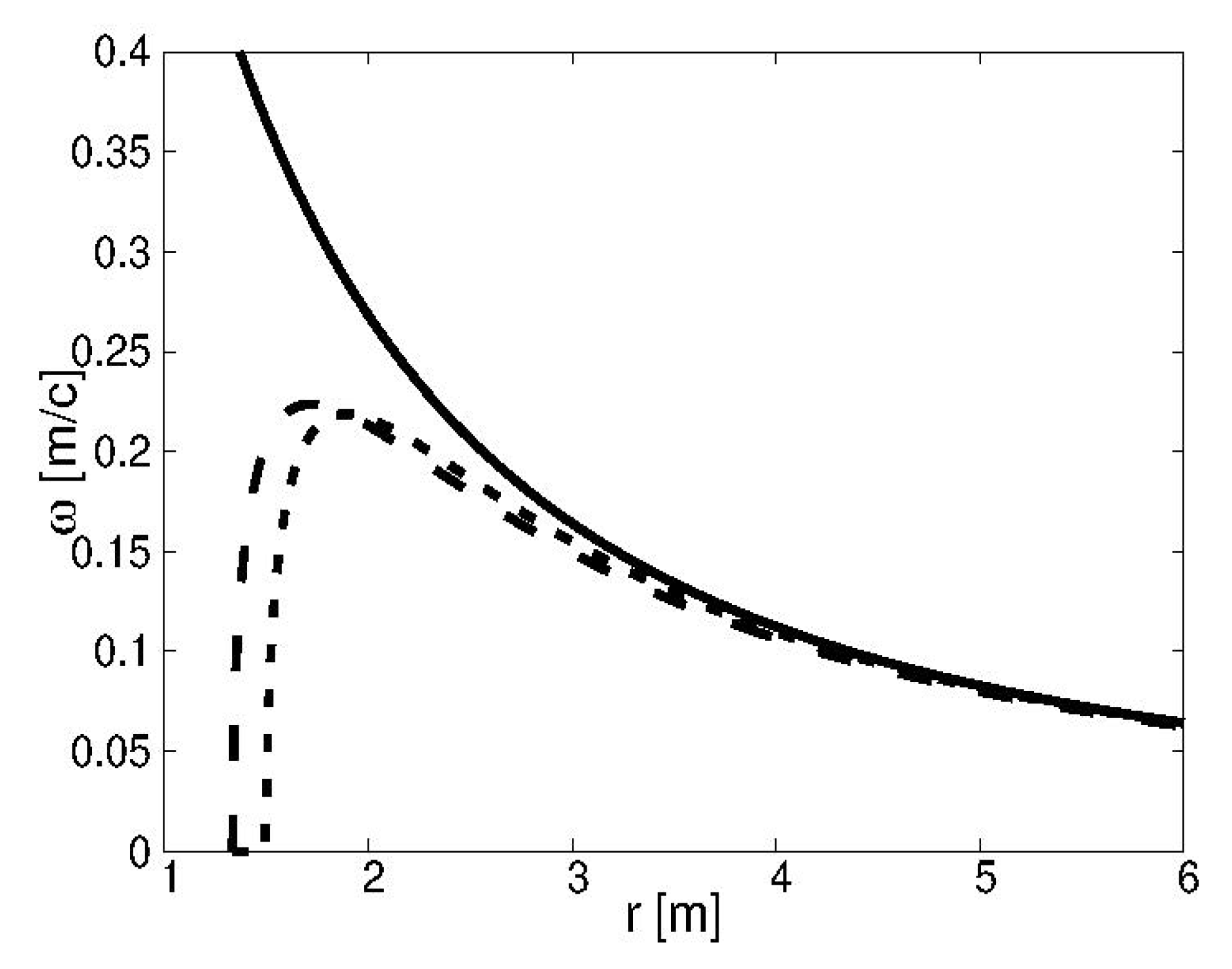
One of the most important predictions is that, when an accretion disc is present and for a rotation large enough, described by the parameter a, it shows a dark ring followed further in by a bright one. This is an effect of the dependence of a particle in a circular orbit, whose frequency shows a maximum and falls off for smaller r. At the maximum, neighboring orbitals have approximately the same orbital frequency, thus friction is low and no light emission is produced. Below and above the position of the maximum in the orbital frequency, it shows a change for neighboring orbital and friction is large, resulting in a stronger light emission. We also compared the GR simulation with the pc-GR one, taking into account the low resolution of , similar to the EHT observation. From this we can conclude that there is, for now, little possibility to see any structural differences. Only an increase in the resolution by a factor of 5 can probably show differences between GR and pc-GR. Until such a resolution can be obtained, a couple of decades have to pass because it will imply to put radio-telescopes in the orbit of the moon and beyond. Nevertheless, the pc-GR can be tested with these telescopes in future. We are currently in contact with members of the EHT on how to obtain a Fourier transform from our pictures, which is what the EHT observes. We plan to look for details in the intensity distribution and its Fourier transform. Unfortunately, we cannot present any results on this yet.
This phenomenon of rings depends on the rotational parameter a: For low a, the last stable orbit follows the one of GR, only further in. The result is a similar pattern of light emission in pc-GR, but, at a higher value, because the last stable orbit reaches further in and, thus, more energy is released which is distributed within the disc. Note that, for also in GR, no light ring can be observed because the inner edge of the accretion disk is at , while the light ring is at larger r. Thus, the light ring is hidden by the accretion disk.
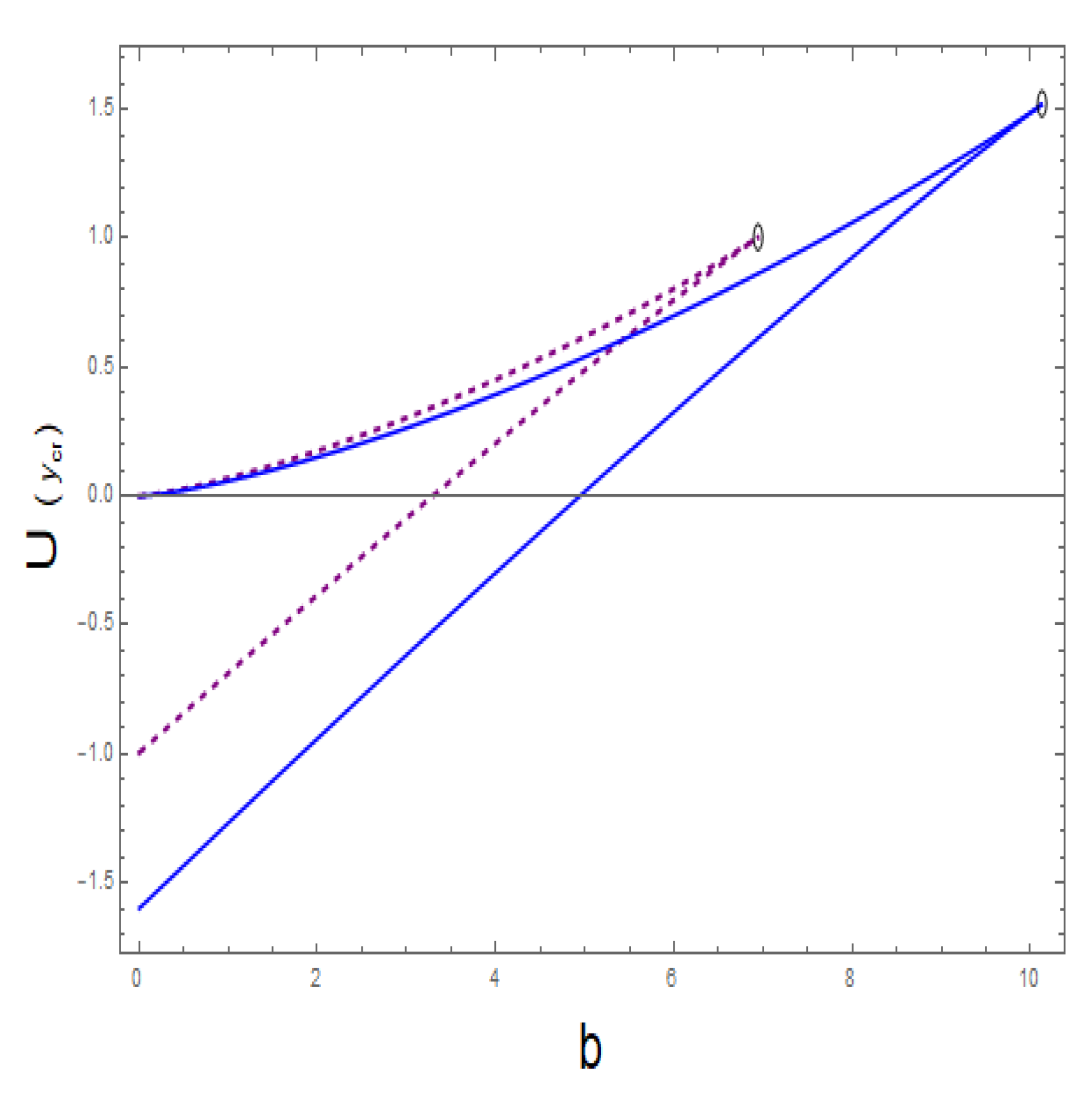
As a new contribution, we showed that the disappearance of the event horizon can be related to a phase transition, which is of the order of 3 when we reach the points where the surface of critical points has a singularity in its derivative. What consequences it may have is not clear to us and we are investigating it further.
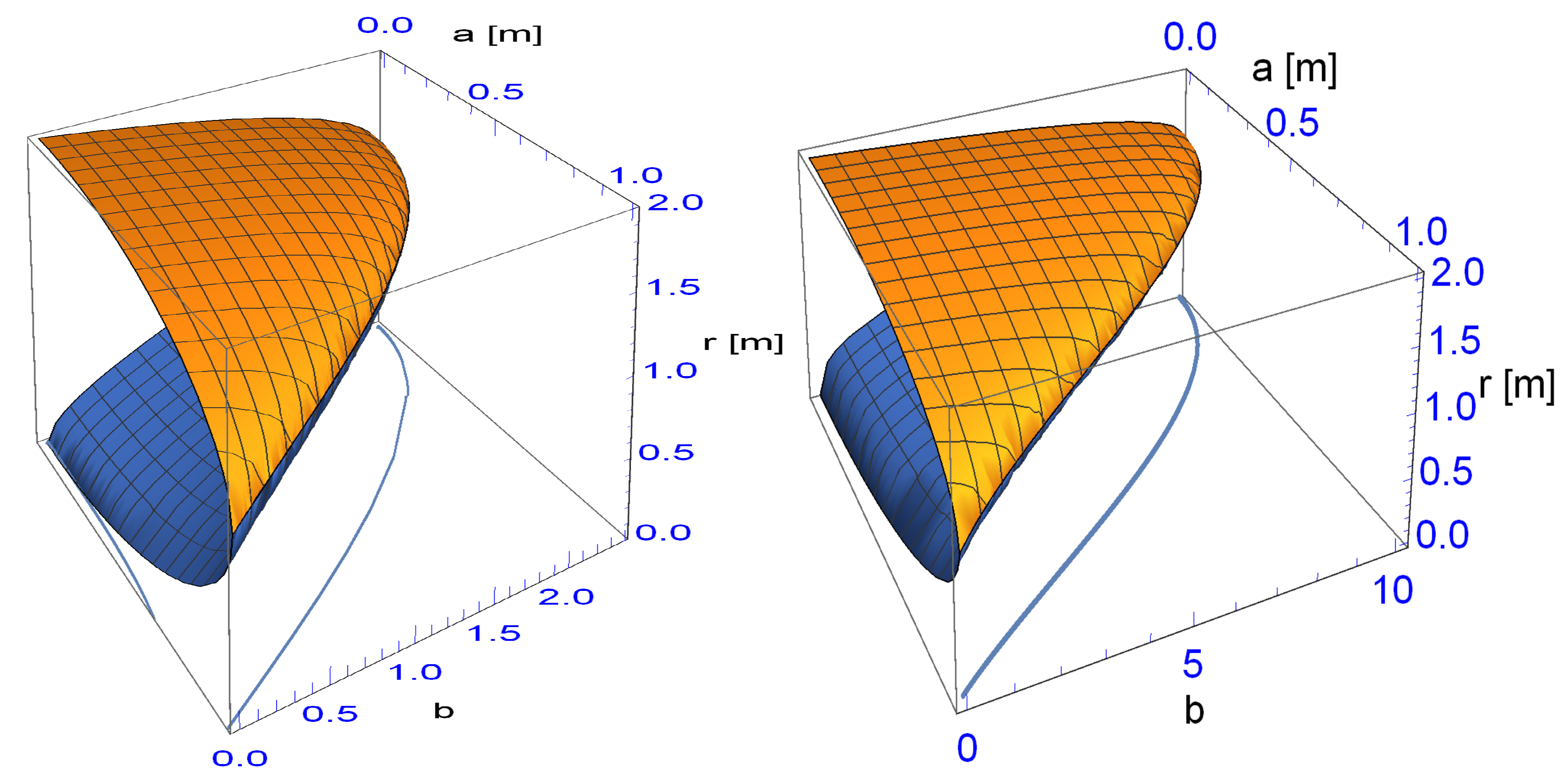
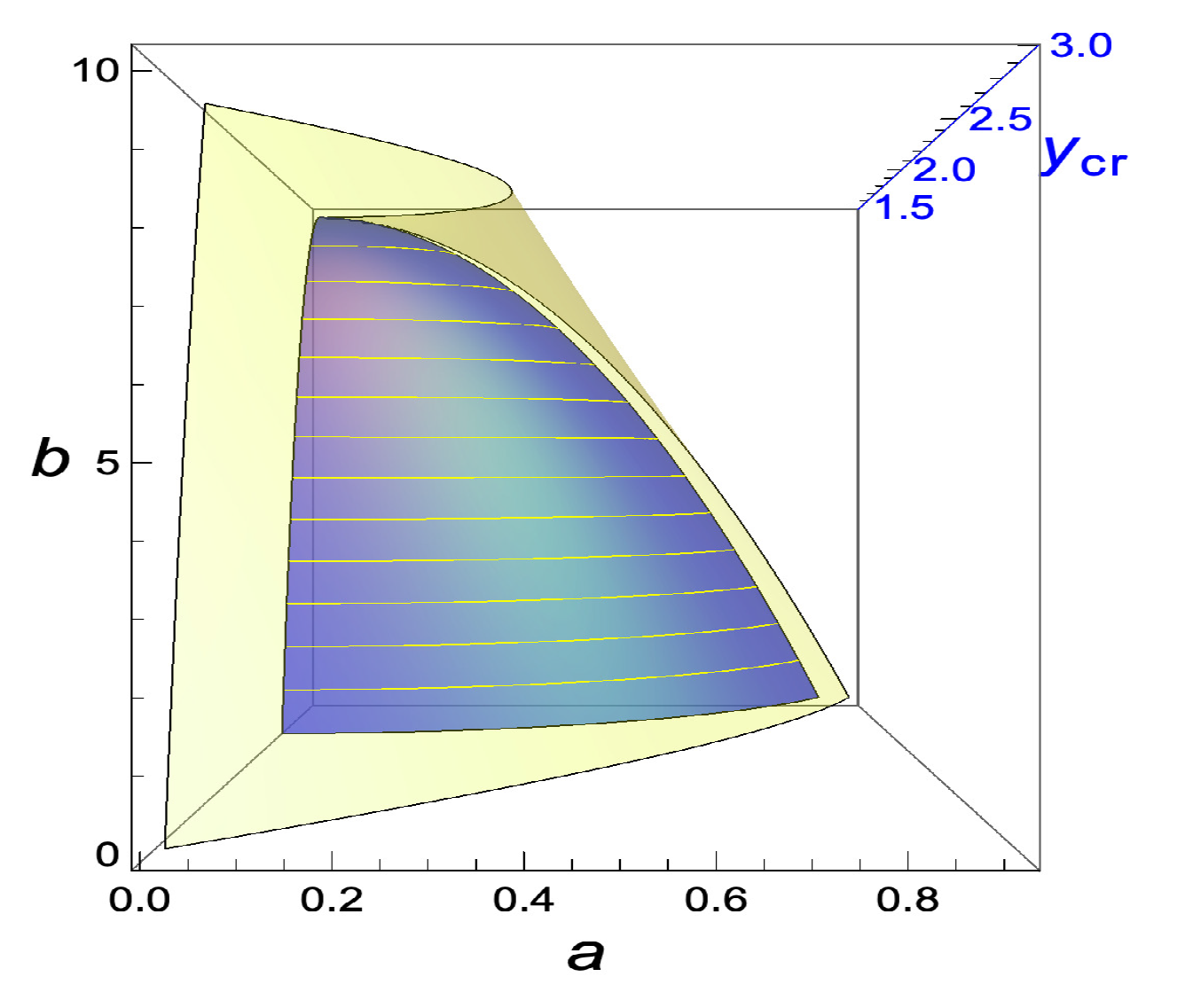
Finally, we discussed the light-ring in the orbital plane (). We also found that, at the moment, some dark energy is accumulated around a black hole, and there is a region where the light-ring ceases to exist from a certain a-value on! The range increases with . We found that the critical surface of the light-ring engulfs the one of the event horizon.
Thus, adding even a small amount of dark energy around a large mass, leads for a certain a-value on to the disappearance of the event horizon and also eliminates the existence of a light-ring! One has to not assume a sufficient large value of in order for no event horizon or light-ring to exist, though the limiting value of serves that, for any a, no horizon exists.
Though a fluid identified with a dark energy is introduced, this fluid is treated classically, as all of the approaches presented in this review. We hope that the results may shed some light on how to include quantum mechanical effects directly. Often, classical treatments can shed some light on the quantum mechanical extension of the theory. The connection to a quantum mechanical description may be the reproduction of the dark energy behavior near a large mass, requiring first the observational confirmation of the structures predicted by the pc-GR.