Identification of a Regular Black Hole by Its Shadow
Abstract
1. Introduction
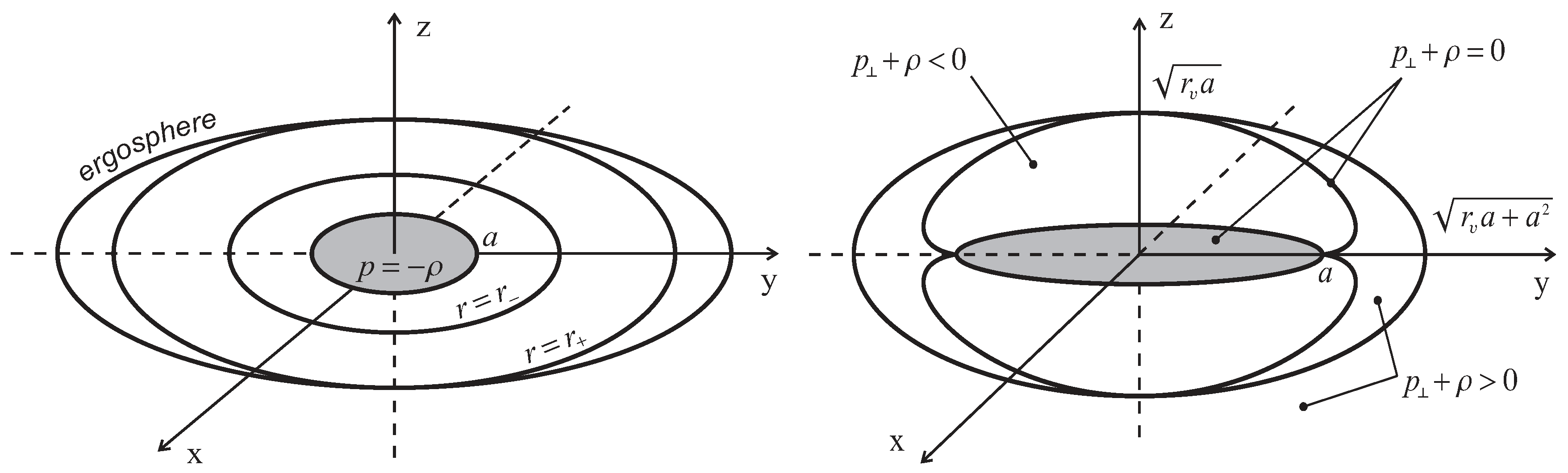
2. Basic Generic Properties of de Sitter-Kerr Black Holes
3. Shadows of Regular de Sitter-Kerr Black Holes
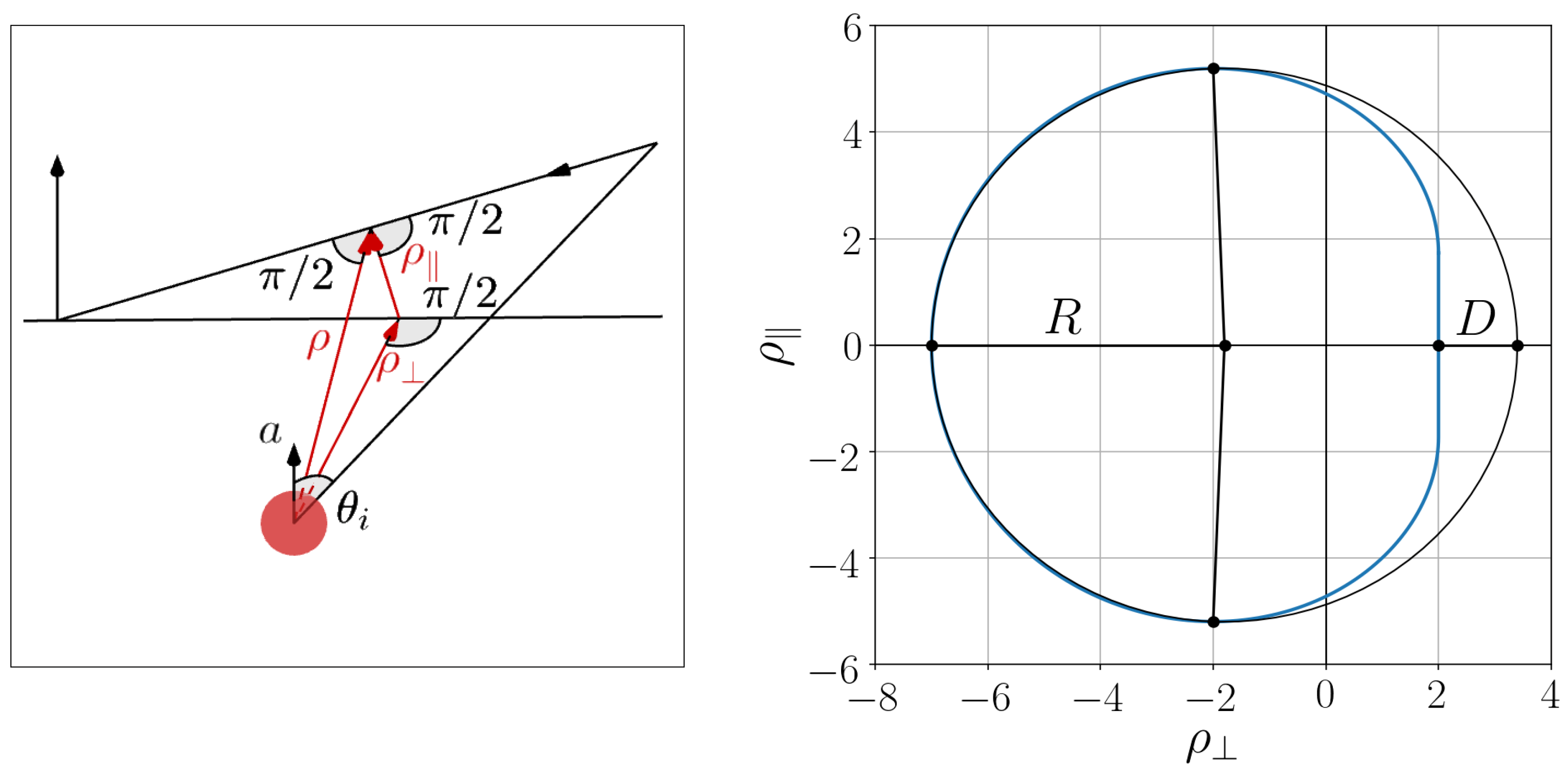
3.1. Integrals of Motion Defining the Boundary of Shadow
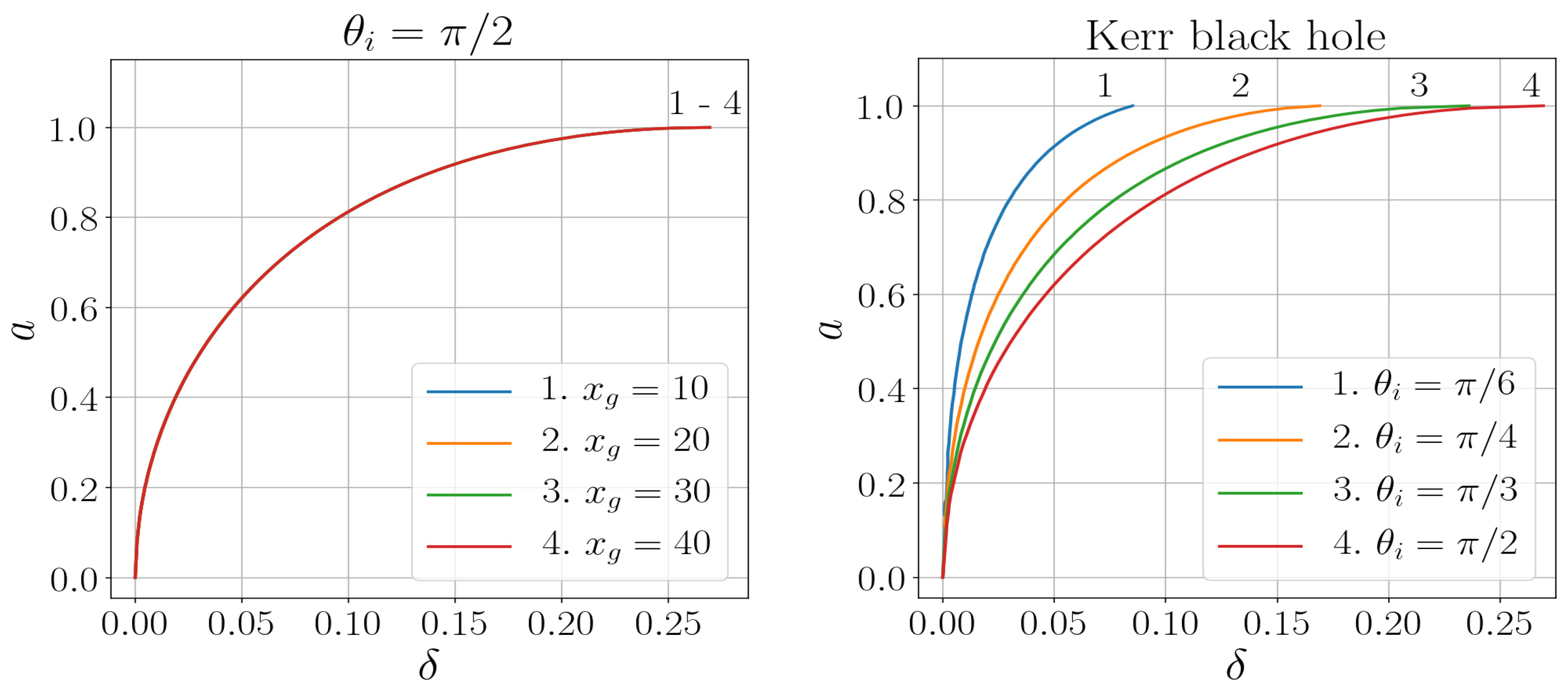
3.2. Information About a Black Hole from Its Shadow
4. Shadows for Two Particular Regular Black Holes
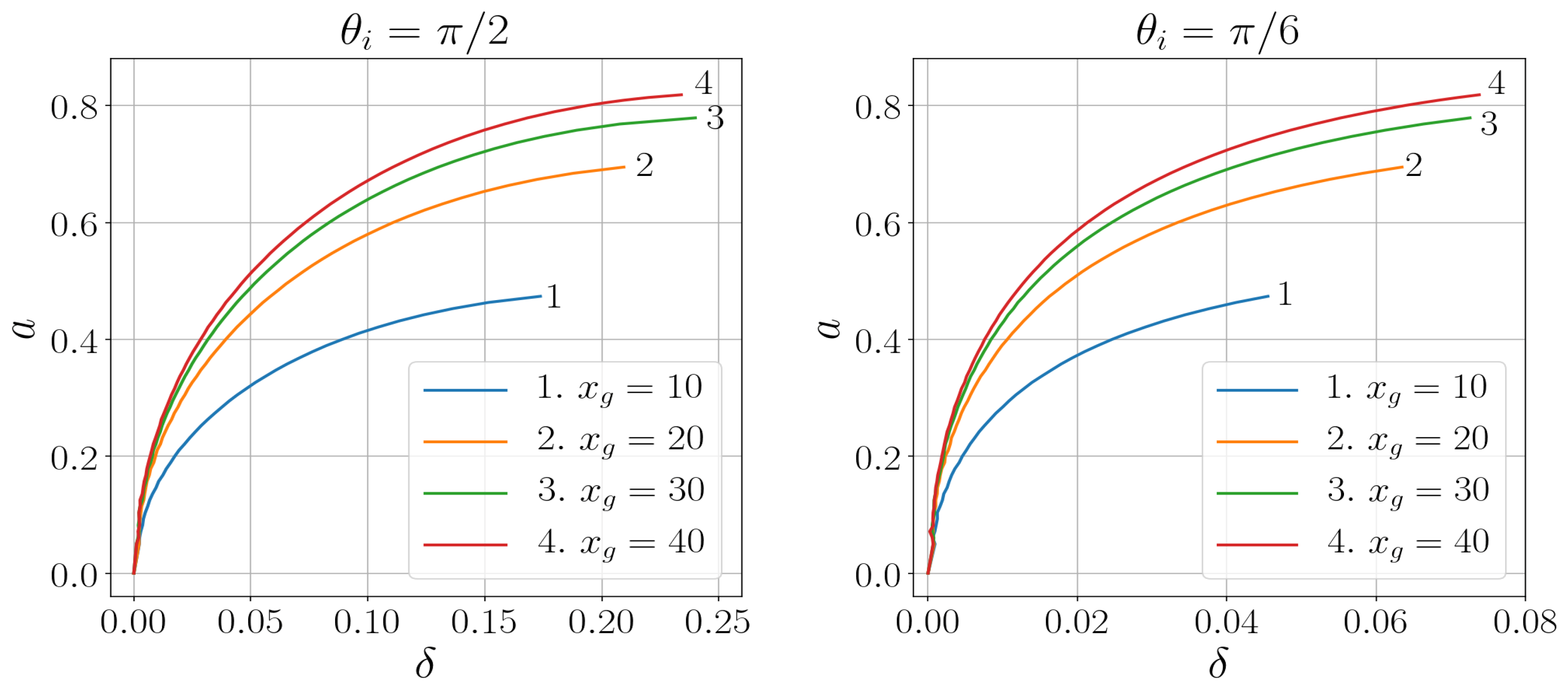
5. Comparison of Shadows for Black Holes with Quickly and Slowly Decreasing Densities
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Dymnikova, I.G. Motion of particles and photons in the gravitational field of a rotating body (In memory of Vladimir Afanas’evich Ruban). Sov. Phys. Uspekhi 1986, 29, 215–237. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the Galactic Center. Astrophys. J. Lett. 2000, 528, L13–L16. [Google Scholar] [CrossRef]
- Takahashi, R. Shapes and positions of black hole shadows in accretion disks and spin parameters of black holes. Astrophys. J. 2004, 611, 996–1004. [Google Scholar] [CrossRef]
- Doeleman, S.S.; Weintroub, J.; Rogers, A.E.E.; Plambeck, R.; Freund, R.; Tilanus, R.P.J.; Friberg, P.; Ziurys, L.M.; Moran, J.M.; Corey, B.; et al. Event-horizon-scale structure in the supermassive black hole candidate at the Galactic Center. Nature 2008, 455, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Alberdi, A.; Gómez Fernández, J.L.; The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Hioki, K.; Maeda, K. Measurement of the Kerr spin parameter by observation of a compact object’s shadow. Phys. Rev. D 2009, 80, 024042. [Google Scholar] [CrossRef]
- Li, Z.; Bambi, C. Measuring the Kerr spin parameter of regular black holes from their shadow. J. Cosmol. Astropart. Phys. 2014, 2014, 41–61. [Google Scholar] [CrossRef]
- Grenzebach, A. Aberration effects for shadows of black holes. Fundam. Theor. Phys. 2015, 179, 823–832. [Google Scholar]
- Mars, K.; Paganini, C.F.; Oancea, M.A. The fingerprints of black holes - shadows and their degeneracies. Class. Quant. Grav. 2018, 35, 025005. [Google Scholar] [CrossRef]
- Grenzebach, A.; Perlick, V.; Lámmerzahl, C. Photon regions and shadows of Kerr-Newman-NUT black holes with a cosmological constant. Phys. Rev. 2014, D89, 124004. [Google Scholar] [CrossRef]
- Repin, S.V.; Kompaneets, D.A.; Novikov, I.D.; Mityagina, V.A. Shadow of rotating black holes on a standard background screen. arXiv 2018, arXiv:1802.04667 [gr-qc]. [Google Scholar]
- Bambi, C.; Freese, K. Apparent shape of super-spinning black holes. Phys. Rev. D 2009, 79, 043002. [Google Scholar] [CrossRef]
- Bambi, C.; Yoshida, N. Shape and position of the shadow in the ? = 2 Tomimatsu-Sato spacetime. Class. Quant. Grav. 2010, 27, 205006. [Google Scholar] [CrossRef]
- Johannsen, T.; Psaltis, D. Testing the No-Hair theorem with observations in the electromagnetic specrum. II. Black hole images. Astrophys. J. 2010, 718, 446–454. [Google Scholar] [CrossRef]
- Ayon-Beato, A.; Garcia, A. The Bardeen model as a nonlinear magnetic monopole. Phys. Lett. B 2000, 493, 149–152. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of nonsingular black holes. Phys. Rev. Lett. 2006, 96, 031103–031105. [Google Scholar] [CrossRef] [PubMed]
- Mizuno, Y.; Younsi, Z.; Fromm, C.M.; Porth, O.; De Laurentis, M.; Olivares, H.; Falcke, H.; Kramer, M.; Rezzolla, L. The current ability to test theories of gravity with black hole shadows. Nat. Astron. Lett. 2018, 2, 585–590. [Google Scholar] [CrossRef]
- Younsi, Z.; Wu, K.; Fuerst, S.V. General relativistic radiative transfer: formulation and emission from structured tori around black holes. Astron. Astrophys. 2012, 545, A13. [Google Scholar] [CrossRef]
- Chan, C.-K.; Psaltis, D.; Oezel, F.; Narayan, R.; Sadowski, A. The power of imaging: constraining the plasma properties of GRMHD simulations using EHT observations of Sgr A*. Astrophys. J. 2015, 799, 1. [Google Scholar] [CrossRef]
- Rezzolla, L.; Zhidenko, A. New parametrization for spherically symmetric black holes in metric theories of gravity. Phys. Rev. D 2014, 90, 084009. [Google Scholar] [CrossRef]
- Garca, A.; Galtsov, D.; Kechkin, O. Class of stationary axisymmetric solutions of the Einstein-Maxwell-dilaton-axion field equations. Phys. Rev. Lett. 1995, 74, 1276–1279. [Google Scholar] [CrossRef] [PubMed]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Rel. Grav. 2018, 50, 42. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.J. Note on the Kerr Spinning-Particle Metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385–2391. [Google Scholar] [CrossRef]
- Kerr, R.P.; Schild, A. Some algebraically degenerate solutions of Einstein’s gravitational field equations. Proc. Symp. Appl. Math. 1965, 17, 199. [Google Scholar]
- Shaikh, R. Black hole shadow in a general rotating spacetime obtained through Newman-Janis algorithm. arXiv 2019, arXiv:1904.08322 [gr-qc]. [Google Scholar]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725–740. [Google Scholar] [CrossRef]
- Dymnikova, I. Spherically symmetric space-time with regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef]
- Burinskii, A.; Elizalde, E.; Hildebrandt, S.R.; Magli, G. Regular sources of the Kerr-Schild class for rotating and nonrotating black hole solutions. Phys. Rev. D 2002, 65, 064039. [Google Scholar] [CrossRef]
- Dymnikova, I. Spinning superconducting electrovacuum soliton. Phys. Lett. B 2006, 639, 368–372. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Regular rotating de Sitter-Kerr black holes and solitons. Class. Quant. Grav. 2016, 33, 145010. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Basic Generic Properties of Regular Rotating Black Holes and Solitons. Adv. Math. Phys. 2017, 2017, 1035381. [Google Scholar] [CrossRef]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular electrically charged vacuum structures with de Sitter center in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, 21, 4417–4428. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Cosmological constant and elementary particles. JETP Lett. 1967, 6, 883–884. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quant. Grav. 1988, 5, L201–L205. [Google Scholar] [CrossRef]
| 1 | Generalization of the Newman–Janis algorithm to the more general case has been considered in [27]. |
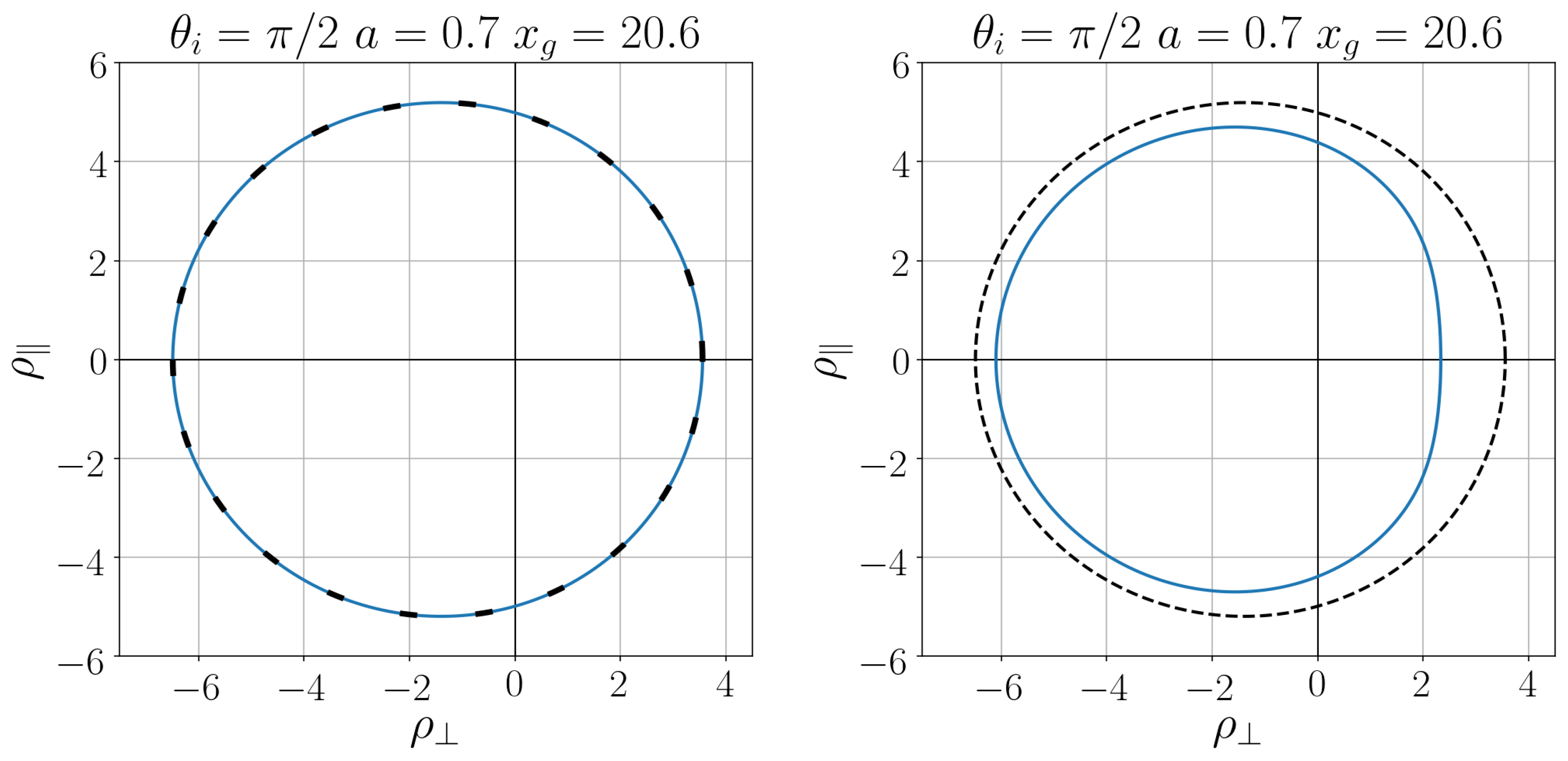
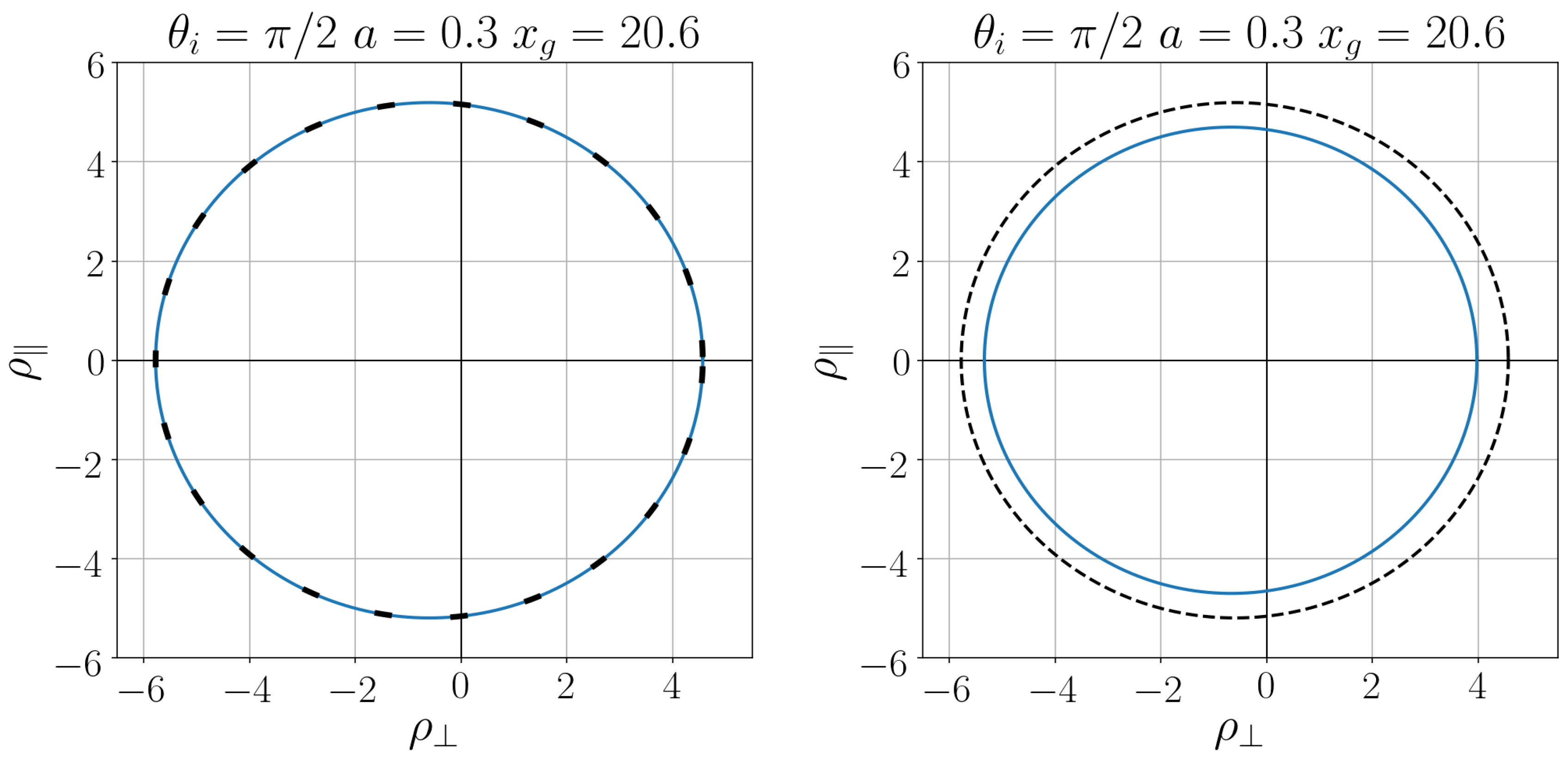

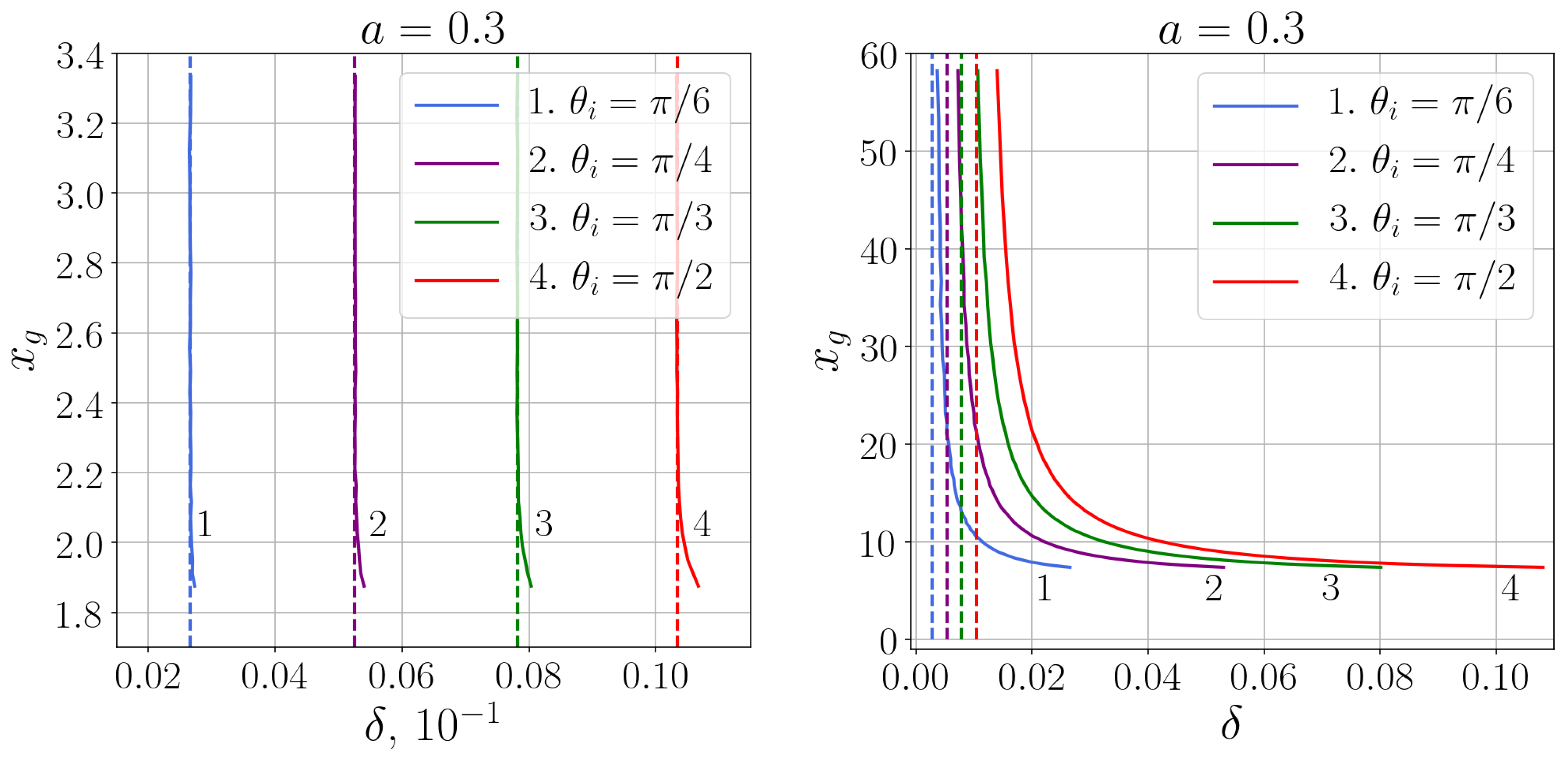
| ∞ | 4.0 | 3.5 | 3.0 | 2.8 | 2.6 | 2.4 | 2.2 | 2.0 | 1.8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 2.0 | 2.0 | 2.0 | 1.9998 | 1.9992 | 1.9976 | 1.9933 | 1.9820 | 1.9513 | 1.8387 |
| 0.1 | 1.995 | 1.995 | 1.995 | 1.9947 | 1.9941 | 1.9925 | 1.988 | 1.9762 | 1.9441 | 1.8215 |
| 0.2 | 1.9798 | 1.9798 | 1.9798 | 1.9795 | 1.9788 | 1.9768 | 1.9717 | 1.9583 | 1.9216 | 1.7415 |
| 0.3 | 1.9539 | 1.9539 | 1.9539 | 1.9535 | 1.9525 | 1.95 | 1.9436 | 1.9269 | 1.88 | – |
| 0.4 | 1.9165 | 1.9165 | 1.9165 | 1.9157 | 1.9144 | 1.9108 | 1.9017 | 1.8786 | 1.8065 | – |
| 0.5 | 1.866 | 1.866 | 1.8659 | 1.8646 | 1.8622 | 1.8563 | 1.8421 | 1.8041 | – | – |
| 0.6 | 1.8 | 1.8 | 1.7997 | 1.7967 | 1.792 | 1.781 | 1.7535 | 1.6489 | – | – |
| 0.7 | 1.7141 | 1.714 | 1.7131 | 1.705 | 1.6935 | 1.6654 | – | – | – | – |
| 0.8 | 1.6 | 1.5993 | 1.5946 | 1.5635 | 1.5005 | – | – | – | – | – |
| 0.9 | 1.4359 | 1.4258 | 1.369 | – | – | – | – | – | – | – |
| 1.0 | 1.0 | – | – | – | – | – | – | – | – | – |
| 0.0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | |
| ∞ | 163.934 | 58.140 | 31.746 | 20.619 | 14.749 | 11.211 | 8.897 | 7.283 | 6.105 | |
| 0.0 | 2.0 | 1.9342 | 1.8636 | 1.7873 | 1.7038 | 1.6111 | 1.5056 | 1.3806 | 1.2193 | 0.9038 |
| 0.1 | 1.995 | 1.9288 | 1.8578 | 1.7809 | 1.6967 | 1.6029 | 1.4958 | 1.3681 | 1.2001 | – |
| 0.2 | 1.9798 | 1.9125 | 1.8402 | 1.7615 | 1.6749 | 1.5778 | 1.4654 | 1.328 | 1.1327 | – |
| 0.3 | 1.9539 | 1.8847 | 1.8099 | 1.728 | 1.637 | 1.5333 | 1.4101 | 1.2496 | – | – |
| 0.4 | 1.9165 | 1.8442 | 1.7654 | 1.6783 | 1.5797 | 1.4642 | 1.3182 | 1.0775 | – | – |
| 0.5 | 1.866 | 1.7891 | 1.7042 | 1.6085 | 1.4967 | 1.3569 | 1.139 | – | – | – |
| 0.6 | 1.8 | 1.7161 | 1.6213 | 1.5104 | 1.3712 | 1.1504 | – | – | – | – |
| 0.7 | 1.7141 | 1.6187 | 1.5061 | 1.3621 | 1.1071 | – | – | – | – | – |
| 0.8 | 1.6 | 1.4825 | 1.3261 | – | – | – | – | – | – | – |
| 0.9 | 1.4359 | 1.2506 | – | – | – | – | – | – | – | – |
| 1.0 | 1.0 | – | – | – | – | – | – | – | – | – |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dymnikova, I.; Kraav, K. Identification of a Regular Black Hole by Its Shadow. Universe 2019, 5, 163. https://doi.org/10.3390/universe5070163
Dymnikova I, Kraav K. Identification of a Regular Black Hole by Its Shadow. Universe. 2019; 5(7):163. https://doi.org/10.3390/universe5070163
Chicago/Turabian StyleDymnikova, Irina, and Kirill Kraav. 2019. "Identification of a Regular Black Hole by Its Shadow" Universe 5, no. 7: 163. https://doi.org/10.3390/universe5070163
APA StyleDymnikova, I., & Kraav, K. (2019). Identification of a Regular Black Hole by Its Shadow. Universe, 5(7), 163. https://doi.org/10.3390/universe5070163




