1. Introduction
There is a formal analogy between the evolution of the universe in the minisuperspace and the trajectory of a test particle in a curved spacetime. The former is given, for a homogeneous and isotropic universe, by the solutions of the field equation and , where a is the scale factor and are n scalar fields that represent the matter content of the universe. The evolution of the universe can then be seen as a parametrised trajectory in the dimensional space formed by the coordinates a and , which is called the minisuperspace. The trajectory is the worldline that extremizes the Einstein–Hilbert action, the time variable t is the parameter that parametrises the worldline, and the parametric coordinates along the worldline are the classical solutions, .
From that point of view, the time reversal invariance of the laws of physics translates in the minisuperspace into the invariance that we have in running the worldline in the two possible directions, forward and backward, along the worldline. It is similar to what happens with the trajectory of a test particle in the spacetime. In particle physics, Feynman interpreted the time-forward and the time-backward solutions of the trajectory of a test particle as the trajectories of the particles and antiparticles of the Dirac’s theory [
1]. In cosmology, we can also assume that the two symmetric solutions may form a universe–antiuniverse pair. In the universe, however, a forward oriented trajectory with respect to the scale factor component,
, means an increasing value of the scale factor, so it represents an expanding universe. Similarly, a backward solution (
) represents a contracting universe. Therefore, the created pair contains, in terms of the same time variable, a contracting universe and an expanding universe.
However, the analysis of the emergence of the classical spacetime in quantum cosmology suggests that the time variables of the two universes should be reversely related [
2,
3],
. In that case, the matter that propagates in one of the universes can naturally be identified from the point of view of the symmetric universe with antimatter, and vice versa. Note that from the quantum cosmology perspective, the semiclassical picture of quantum matter fields propagating in a classical background spacetime is an emergent feature that appears, after some decoherence process, in the semiclassical regime [
4,
5]. In that case, we shall see in this paper that in order to obtain the correct value of the Schrödinger equation in the two universes their time variables would be reversely related. Then, the time variables measured by the internal observers in their particle physics experiments (i.e., the time variables that appear in the Schrödinger equation of their physical experiments) would be reversely related and, from that point of view, the matter that propagates in a hypothetical partner universe could naturally be identified with the primordial antimatter that is absent in the observer’s universe. From the global perspective of the composite state, then, the apparent asymmetry between matter and antimatter would be restored.
However, a caveat should be made on the assumptions of homogeneity and isotropy for the initial spacetime manifold, which is in the basis of the time reversal symmetry of the cosmological field equations, and is therefore a condition for the creation of universes in pairs with reversely related time variables. From the point of view of a full quantum theory of gravity, the creation of all kinds of universes with all kinds of (even exotic) spacetime geometries is expected, so the creation of a homogeneous and isotropic universe should be considered as a particular case, and the consequent scenario of the creation of a universe–antiuniverse pair only as a plausible one. This is said even though the scenario might be rather realistic provided that we assume that the fluctuations of the spacetime are relatively small from the very onset of the universe. The observational data suggest that at least from a very remote past our universe essentially looks homogeneous and isotropic, with relatively small inhomogeneities and anisotropies compared with the energy of the homogeneous and isotropic background. Accordingly, we shall assume in this paper that the universe left the Euclidean gravitational vacuum and started inflating from an initial spatial hypersurface,
, that is small but large enough to assume that the fluctuations of the spacetime are subdominant (i.e.,
). This is not an unrealistic scenario. For instance, in the Higgs inflation scenario [
6],
, where
V is the potential of the Higgs in the initial slow roll regime and
is the strong coupling between the Higgs and gravity. We shall later on comment on the effect that the fluctuations of the spacetime would have on the breaking of the time reversal symmetry.
In this paper we review and gather the main results of previous works [
2,
3,
7,
8,
9] and extend the hypothesis presented in [
10] for the restoration of the primordial matter–antimatter asymmetry to the more general scenario of two homogeneous and isotropic pieces of the spacetime whose time variables, according to the time reversal symmetry of the Einstein–Hilbert action, are reversely related. This will prepare the arena for more detailed future developments on the subject. In
Section 2, we present the analogy between the classical evolution of the universe in the minisuperspace and the trajectory of a test particle in a curved spacetime. It is shown that the time reversal symmetry of the action and the conservation of the total momentum in the process of creation of the universe would imply that the universes should be created in pairs with opposite values of their momenta so that the total momentum is zero.
Section 3 analyses the correlations between the spacetimes that emerge from the two wave functions that are associated to the opposite values of the momenta conjugated to the scale factor. It is determined that in order to obtain the correct value of the Schrödinger equation in the two universes, their physical time variables must be reversely related. Thus, the particles that propagate in one of the universes are naturally identified with the antiparticles that are left in the partner universe. In
Section 4, we summarise and make some conclusions.
2. Time Reversal Symmetry in Classical Cosmology
Let us consider a homogeneous and isotropic spacetime and a scalar field
, which represents the matter content of the universe, that propagates minimally coupled to gravity under the action of the potential,
. The spacetime is then foliated in homogeneous and isotropic slices, with a total line element given by
where
is the scale factor and
is the lapse function that parametrises the time variable (
corresponds to cosmic time), and the homogeneous mode of the scalar field is
. Small inhomogeneities around this homogeneous and isotropic background can also be considered [
11,
12], but as far as the inhomogeneities remain small, the dynamics of the background essentially depends on the values of the scale factor and the homogeneous mode of the scalar field,
and
. From this point of view, the evolution of the universe is determined by the functions
and
that extremise the Hilbert–Einstein action, which for the present case can be written as [
13]:
where
are the coordinates of the configuration space
1,
is given by
and
contains all the potential terms of the spacetime and the scalar field
where
for flat, closed and open spatial slices of the whole spacetime. An explicit term for a cosmological constant is implicitly included in the case of a constant value of the potential,
. The Euler–Lagrange equations derived from the variation of the action (
2) are [
13]:
The Friedmann equation [
14]
turns out to be the Hamiltonian constraint that appears in quantum cosmology from the invariance of the Hilbert–Einstein action (
2) under time reparametrisation,
. The field Equations (
5) and (
6) can generally be difficult to solve analytically, but the exact or the approximate solutions of the field equations basically give the evolution of the universe. It is easy to see that these equations are invariant under the reversal change in the time variable,
. This means that for any given solution
and
one may also consider the symmetric solution,
and
.
The action (
2) and the minisupermetric (
3) clearly reveal the geometric character of the configuration space, which is called the minisuperspace
2, where the scale factor would formally play the role of the time-like variable and the scalar field would formally play the role of the space-like variable
3. Therefore, an alternative but equivalent point of view for the evolution of the universe considers that the time-dependent solutions of the scale factor and the scalar field,
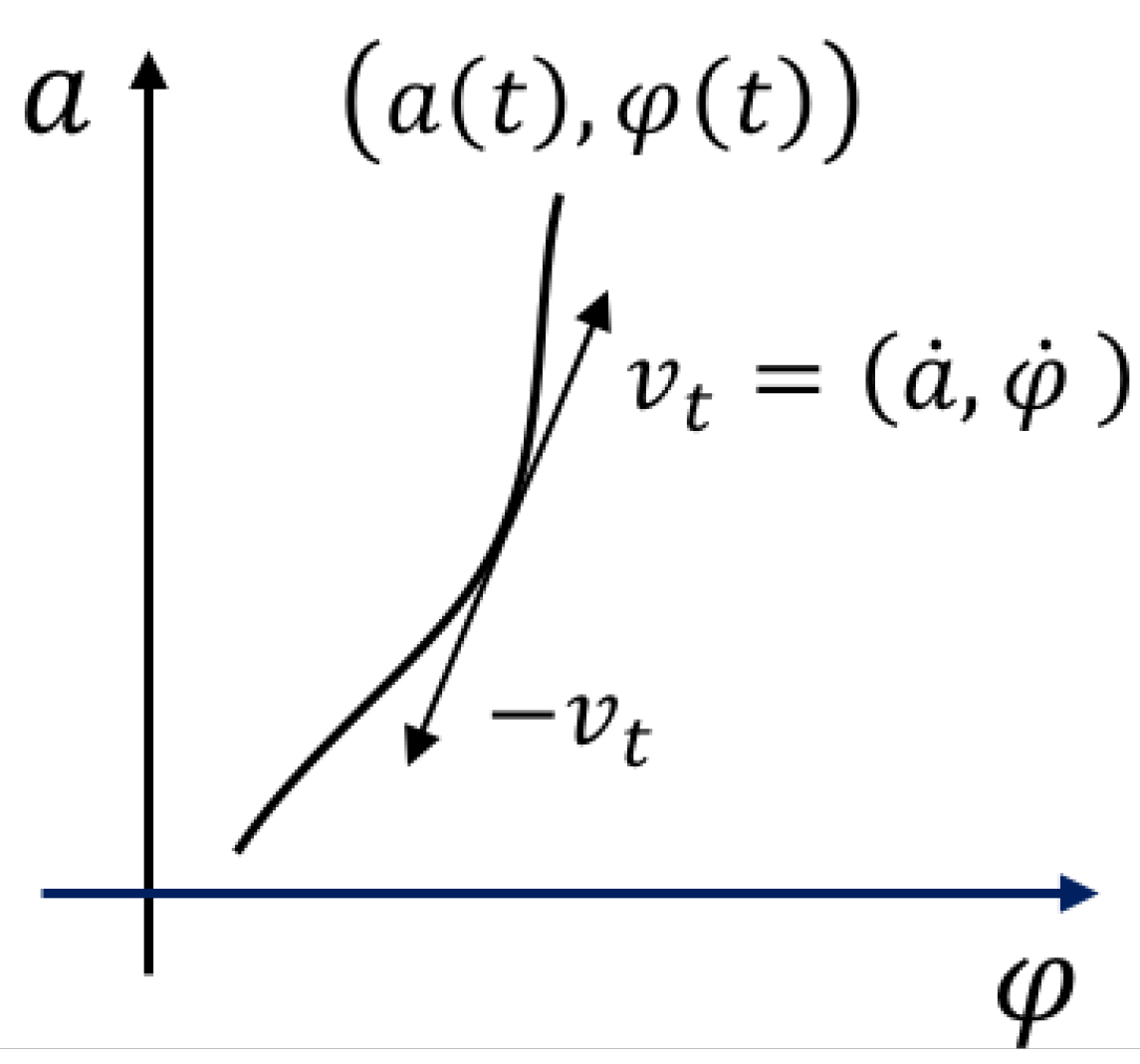
and
, are the parametric equations of a trajectory in the minisuperspace, where the time variable
t acts as the (non-affine) parameter in terms of which the trajectory of a “test universe” is described (
Figure 1). The Euler–Lagrange equations associated with the action (
2), given by (
5), can be rewritten as the equations of the non-geodesic curves
where
is the inverse of the minisupermetric
. The momentum conjugated to the minisuperspace variables can be directly obtained from (
2),
and the Hamiltonian constraint,
, then reads
where for convenience we have defined
4 . In the present case, it yields
which is the Friedmann Equation (
6) expressed in terms of the momenta instead of in terms of the time derivatives of the minisuperspace variables. As pointed out above, the geodesic Equation (
7) and the momentum constraint (
9) and (
10) are invariant under a reversal change of the time variable. This means that the solutions may come in pairs with opposite values of the associated momenta (note that the momenta given in (
8) are not invariant under the same change). From (
8) and (
10), it is easy to see that in terms of the cosmological time (
), the two symmetric solutions are
This is clearly reminiscent of the solutions of the trajectory of a test particle moving in spacetime [
16]. For instance, in Minkowski spacetime
5, the time component of the geodesics satisfies
where
is an affine parameter and
is the energy of the test particle. In the spacetime, the two signs in (
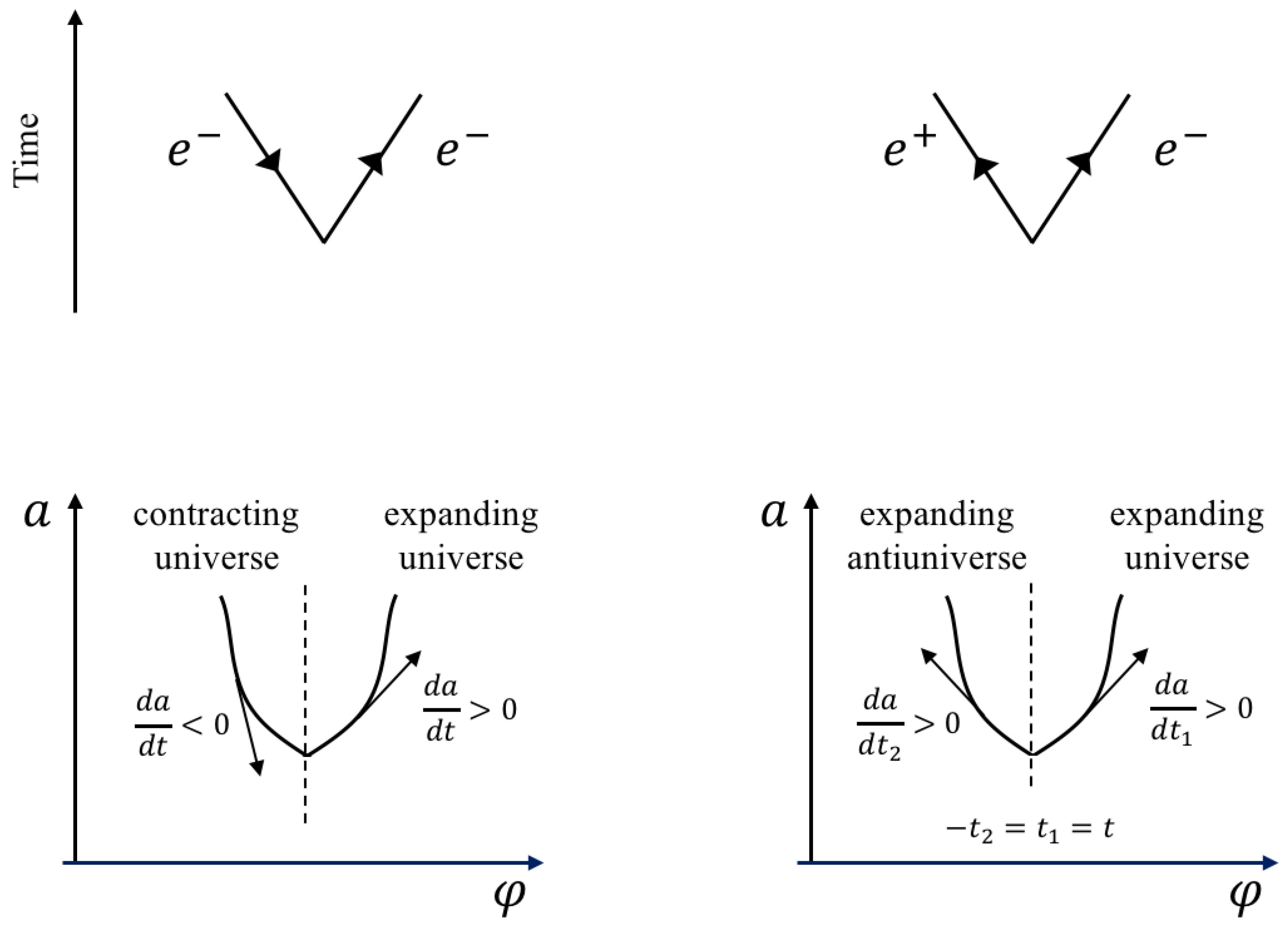
12) represent the opposite values of the time component of the tangent vector to the geodesic—that is, the two ways in which the geodesic can be run: forward in time and backward in time. This was used by Feynman [
1] to interpret the trajectories of an electron and a positron as the trajectory of one single electron bouncing from backwards to forwards in time (
Figure 2 Top).
In the case of the universe, the two solutions given in (
11) also represent two universes: one universe moving forward in the scale factor component and the other moving backward in the scale factor component. In the minisuperspace, however, moving forward in the scale factor component entails an increasing value of the scale factor, so the associated solution represents an expanding universe; and moving backward in the scale factor component entails a decreasing value of the scale factor, so the symmetric solution represents a contracting universe. Therefore, the two symmetric solutions form an expanding–contracting pair of universes (
Figure 2 Bottom-Left). The total momentum conjugated to minisuperspace variables is conserved because the values of the momenta associated to the two symmetric solutions are reversely related. However, let us notice that the field Equation (
5) and the Friedmann Equation (
6) are invariant under a reversal change in the time variable,
, so from a theoretical point of view we could have chosen
as the time variable and then the solutions that represent an expanding and a contracting universe would have been interchanged. In this paper we are interested in the creation of the universe from the spacetime foam [
17], so we shall interpret a contracting–expanding pair of symmetric solutions as the trajectories in the minisuperspace of two newborn universes, both expanding in terms of their reversely related time variables,
(
Figure 2 Bottom-Right).
Therefore, we shall assume that the universes are created in pairs, both expanding in terms of their internal, reversely related time variables. In terms of the same time variable, however, one of the universes is an expanding universe and the other is a contracting universe. For instance, for an inhabitant of one of the universes, say Alice, her universe is the expanding one and the partner universe (that she does not see) would be the contracting one. However, it is not contracting for Bob, an inhabitant of the partner universe, for whom things are the other way around, it is his universe the one that is expanding (in terms of his time variable) and Alice’s universe, from his point of view, the one that is contracting. Thus, the particles that move in the two universes look like they were propagating backward and forward in time, depending on the observer’s point of view. Assuming the CPT theorem, the particles that propagate in the disconnected pieces of the spacetime have consequently opposite values of their charge and parity, so they can be identified in the quantum theory of the composite system with particles and antiparticles. The inhabitants of the two universes can only see the particles that propagate in their own spacetimes, but if they would find any signature of the existence of a time reversely related universe, then they could infer that at the onset primordial antimatter was mainly created in the partner universe, and thus they could conclude that the matter–antimatter asymmetry that they observe in their universes is only an apparent asymmetry that becomes restored in the composite picture of the two symmetric universes.
3. Quantum Cosmology and the Creation of Universes
One would expect that the creation of the universe should have a quantum origin. Therefore, let us analyse the creation of a pair of time reversely related universes in quantum cosmology. The quantum state of the universe is described by a wave function that depends on the metric components of the spacetime as well as on the degrees of freedom of the matter fields. It is the solution of the Wheeler–DeWitt equation, which is essentially the canonically quantised version of the classical Hamiltonian constraint. This is generally a very complicated function. However, as was pointed out in
Section 1, we are assuming that the universe emerges from the gravitational vacuum and starts inflating from an initial spatial hypersurface
that is small but large enough to consider that the fluctuations of the spacetime are subdominant. In that case, we can model the universe as weakly coupled fields propagating in an essentially homogeneous and isotropic background spacetime. Then, the Hamiltonian of the whole universe can be split into the Hamiltonian of the background and the Hamiltonian of the matter fields [
11,
12]
where the Hamiltonian of the background spacetime,
, is given by the quantum version of the classical Hamiltonian (
10)
and
contains the Hamiltonian of all the matter fields and their interactions. The wave function,
, where
are the variables of the local matter fields, can then be expressed in the semiclassical regime as a linear combination of WKB solutions, that is [
4,
5]:
where
is a real slow-varying function of the background variables,
is the action of the background spacetime,
is a complex wave function that contains all the dependence on the matter degrees of freedom, with
, and the sum in (
15) extends to all possible classical configurations. A relevant feature to be noticed here is that, because of the Hermitian character of the Hamiltonian (
13)—which in turn is rooted in the time reversal symmetry of the classical Hamiltonian constraint (
10)—the general solution of the Wheeler–DeWitt equation can always be expressed in terms of the two complex conjugated, independent solutions that correspond to the two possible signs in the exponentials of (
15). We shall now see that these two wave functions represent similar universes with essentially the same evolution of their spacetimes and similar matter fields propagating therein. However, because the momenta conjugated to the scale factor associated to the two complex conjugated solutions in (
15) are reversely related, the time variables of their spacetimes are also reversely related.
In order to see how the wave functions
and
of (
15) represent a particular universe, one can insert them into the Wheeler–DeWitt Equation (
13). After some decoherence process between the two wave functions, which is a guarantee for the smallness of the fluctuations of the spacetime [
5,
18], one can expect that the Wheeler–DeWitt equation must be satisfied order by order in an expansion in
ℏ. At order
one obtains the following Hamilton–Jacobi equation [
3,
12]:
This equation contains the dynamics of the background spacetime. It can be converted into the Friedmann equation by defining the WKB time variable given by [
12]
where ∇ is the gradient of the minisuperspace [
12]. In terms of the WKB time variable,
so that the Hamilton–Jacobi Equation (
16) turns out to be the Friedmann Equation (
6). It thus describes the evolution of the background spacetime. Furthermore, let us notice that at order
the momentum conjugated to the scale factor associated to the wave functions
and
is given by
where the plus sign corresponds to
and the minus sign to
. They are thus reversely related and the total momentum associated to the creation of the two universes represented by
and
is zero.
Furthermore, at first order in
ℏ in the expansion of the Wheeler–DeWitt equation, one obtains [
3,
12]:
where the positive and negative signs correspond to
and
(
15), respectively. The term in brackets in (
20) is actually the WKB time variable defined in the background spacetime, given by (
17), meaning that (
20) is essentially the Schrödinger equation for the matter fields that propagate in the classical background spacetime represented by
and
. We then recover the semiclassical picture of quantum matter fields propagating in a classical background. However, in order to have the proper sign in the Schrödinger equation in each single universe, we need to choose the positive sign in the definition of the time variable
t in (
17) for the wave function
and the negative sign of the time variable for the wave function
. If we assume that the time variable involved in the Schrödinger equation is the
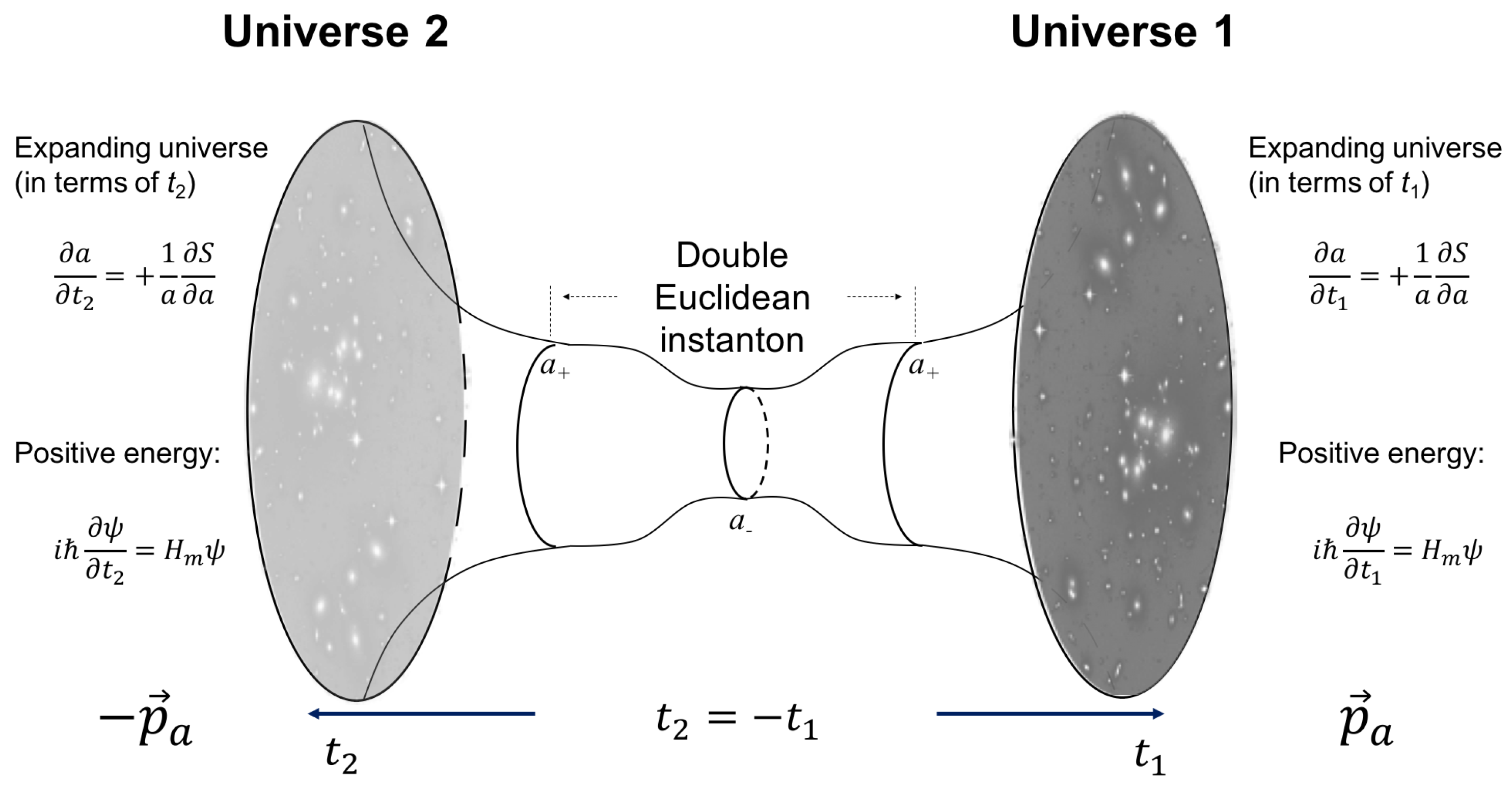
physical time variable in the sense that it is the time measured by the observers in their particle physics experiments (so it is the time variable measured by actual clocks, which are eventually made of matter), then the physical time variables of the two universes are reversely related. Note that the eventual inhabitants of the universes will only see the matter of their respective universes and therefore cannot observe the antimatter (from their point of view) that propagates in the symmetric universe. There is also a Euclidean gap between the two universes that prevents matter and antimatter from collapse (
Figure 3). Therefore, from the point of view of an individual observer there is nothing in principle that makes him suspect the existence of a time reversely symmetric universe except perhaps the occurrence of an asymmetry that is hard to explain within the single universe scenario. In principle, it is only from a symmetry consideration that the observer can pose the existence of another universe that justifies the apparent primordial asymmetry between matter and antimatter
6.
The creation of particles and antiparticles would follow a similar procedure to that customary considered in the context of a single universe (e.g., [
19]). After the slow roll regime the inflaton field eventually approaches a minimum of the potential and starts oscillating. In each oscillation it decays through different channels and in subsequent stages into the particles of the standard model. The interaction with the inflaton field produces a series of consecutive, non-adiabatic changes of the vacuum of the matter fields. The associated particle production can then be derived from the Bogolyubov transformation that relates the vacuum states before and after the non-adiabatic change, with a particle production given by
where
is the vacuum state of the corresponding matter field before the oscillation and
is the state representing the number of particles and antiparticles created with momentum
k after the interaction. The functions
and
are the coefficients of the Bogolyubov transformation that relates the wave functions of the modes before and after the interaction, and they contain the effect of the interaction between the inflaton and the matter fields. In the single-universe scenario, because the symmetries of the background, particles and antiparticles are created in perfectly correlated pairs
so the number of them is exactly balanced, at least in principle. Different mechanisms that would produce some asymmetry in the creation of matter and antimatter are invoked [
19]. However, they usually consider some modification or extension of the standard model of particle physics.
In the scenario of the twin universes with reversely related time variables presented here, the state of the matter field would still be given by (
21). However, matter and antimatter would be created in different universes, so (
21) should be rewritten as:
where
are the particles in the mode
k created in one of the universes, labeled as 1, and
are the particles in the mode
k created in the other universe, labeled as 2. For the inhabitants of the two universes, the primordial antimatter is essentially created in the partner universe, that is, for an observer in universe 1,
are the antiparticles that she misses in her universe and, analogously,
are the antiparticles in mode
k that are left from the point of view of an observer of universe 2. Particles and antiparticles cannot interact, and therefore cannot annihilate each other, because of the Euclidean gap (a quantum barrier) that separates the universes (see
Figure 3 and Refs. [
3,
10]).
Let us now make a comment about the influence that the fluctuations of the spacetime could have in the global picture of the creation of the universes in symmetric pairs and the subsequent creation of matter and antimatter separately. The assumption of homogeneity and isotropy made from the very beginning is determining for the time reversal symmetry of the field equations, and eventually for the creation of the universes in symmetric pairs. This means that the scenario presented here is at most a plausible scenario. However, one would expect that as long as the deviation from the homogeneous and isotropic background is relatively small, the picture would essentially be rather similar. The small fluctuations of the spacetime would cause the symmetry to stop being an exact symmetry to become an approximate symmetry. It would be expected that the creation of particles and antiparticles would cease to occur in perfectly correlated pairs and that (
22) would only be approximate, with corrections at different levels. However, one might expect that this mechanism of creating matter and antimatter separately could still be dominant, as long as the deviations from the homogeneous and isotropic spacetime were small. In addition, other mechanisms that produce matter and antimatter asymmetry can still be considered, and they could work jointly to produce the observed amount of asymmetry. Perhaps the creation of universes in (imperfectly) symmetric pairs could relax the tensions or the anomalous fine tuning that might exist between the theoretical models and the observational data. It might also entail other observable effects [
20]. Therefore, we believe that it is an appealing scenario that deserves further analysis and a deeper understanding.
4. Conclusions
The evolution of the universe can be seen as a worldline of the minisuperspace formed by the scale factor, which formally plays the role of a time-like variable, and the scalar fields, which formally play the role of the spatial components. From that point of view, the time reversal symmetry of the field equations becomes equivalent to the invariance of the geodesics of the minisuperspace under a reversal parametrisation of their non-affine parameter.
Positively oriented paths with respect to the scale factor component in the minisuperspace entail an increasing value of the scale factor, so they represent expanding universes. On the contrary, negatively oriented worldlines with respect to the scale factor component represent contracting universes. However, because of the time reversal invariance of the Lagrangian of a homogeneous and isotropic spacetime, the terms “expansion” and “contraction” can be interchanged so we end up with four symmetric solutions—two oriented forward and two oriented backwards. The former represent two expanding universes with their time variables reversely related and the latter represent two virtual universes that rapidly return to the gravitational vacuum from which they emerged.
Quantum mechanically, the solutions of the Wheeler–DeWitt equation can always be given in complex conjugated pairs because of the Hermitian character of the Hamiltonian constraint. Two complex conjugated solutions entail opposite values of the momentum conjugated to their scale factors, so the creation of universes in pairs whose wave functions are complex conjugated has an associated total zero momentum. Furthermore, the analysis of the emergence of the semiclassical spacetime in the universes that they represent suggests that the physical time variables of their spacetimes should be reversely related. Then, the inhabitants of the two universes would naturally identify matter with the particles that propagate in their spacetimes and the unobserved primordial antimatter with the particles that would propagate in the symmetric universe.
The consideration of a homogeneous and isotropic spacetime makes the scenario presented here at most a plausible one. However, it might be realistic if our universe was created and started inflating from an initial hypersurface that is small but large enough to assume that the fluctuations of the spacetime are subdominant. In that case, small deviations from the homogeneous and isotropy of the spacetime would transform the exact time reversal symmetry into an approximate one. Nevertheless, as long as the deviations are relatively small, one would expect that the global picture would not differ very much from the one depicted here. The creation of matter and antimatter in separated universes might still be the dominant one, or at least it could help or enhance other mechanisms that are already considered in the context of a single scenario.
Finally, this work sets the arena for a deeper and more detailed study, which might eventually unveil whether the universe is actually part of a universe–antiuniverse pair.