Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process †
Abstract
:1. Introduction
2. Electromagnetized Black Hole
2.1. Magnetization of Black Holes
2.2. Black Hole Charge
3. Magnetic Penrose Process
3.1. Dynamics of Charged Particles around Black Hole
3.2. Split of Infalling Particle
3.3. Three Regimes of MPP
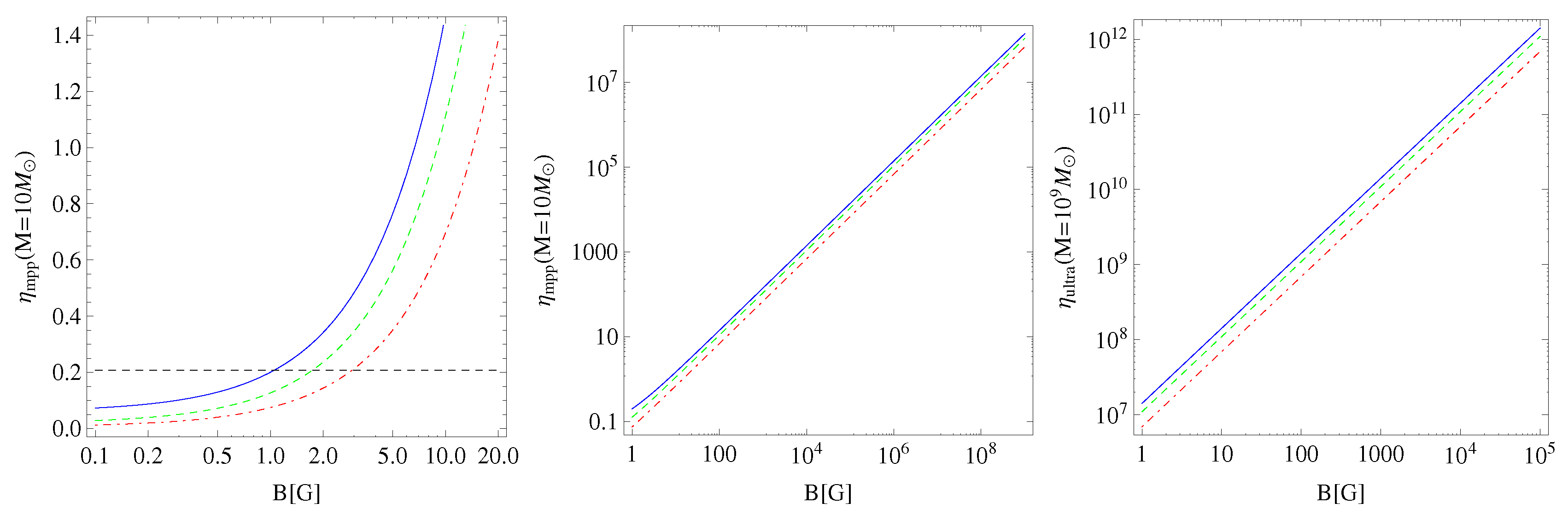
3.4. Quantitative Estimates
4. Astrophysical Applications
4.1. Ultra High Energy Cosmic Rays
4.1.1. State of the Art
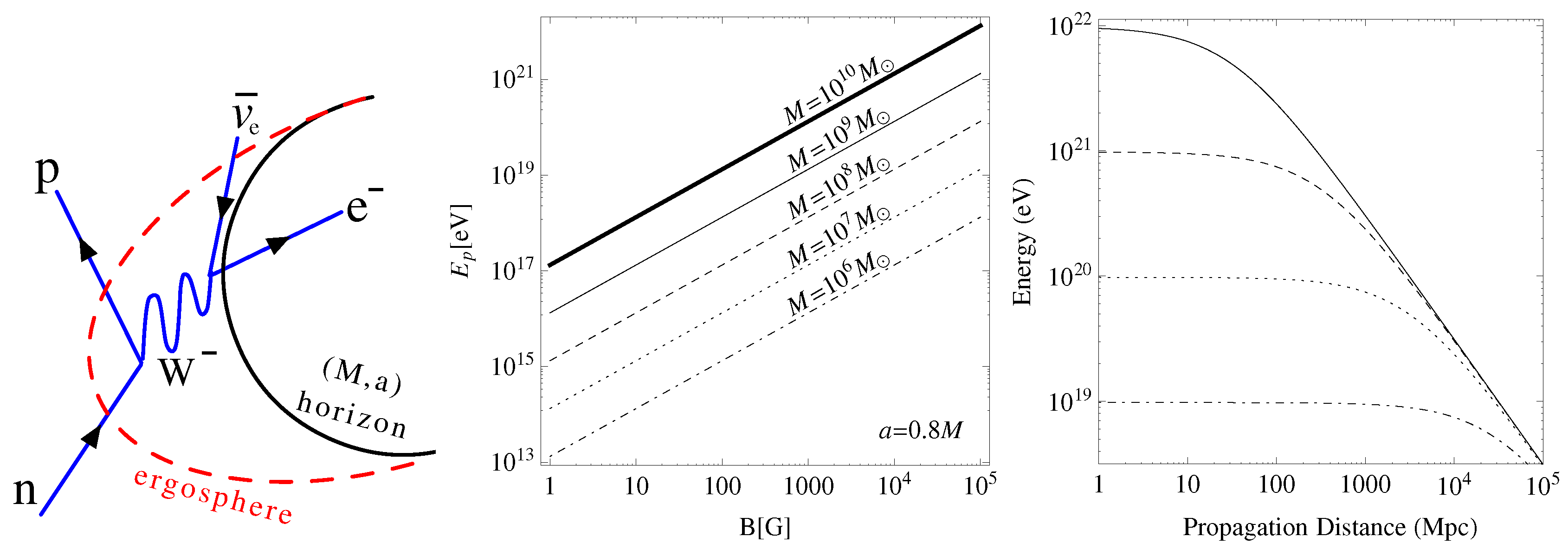
4.1.2. Maximum Energy of Proton
4.1.3. Propagation of Cosmic Rays in Magnetic Field
4.1.4. CosmicRays from Galactic Center Black Hole
4.2. Relativistic Jets
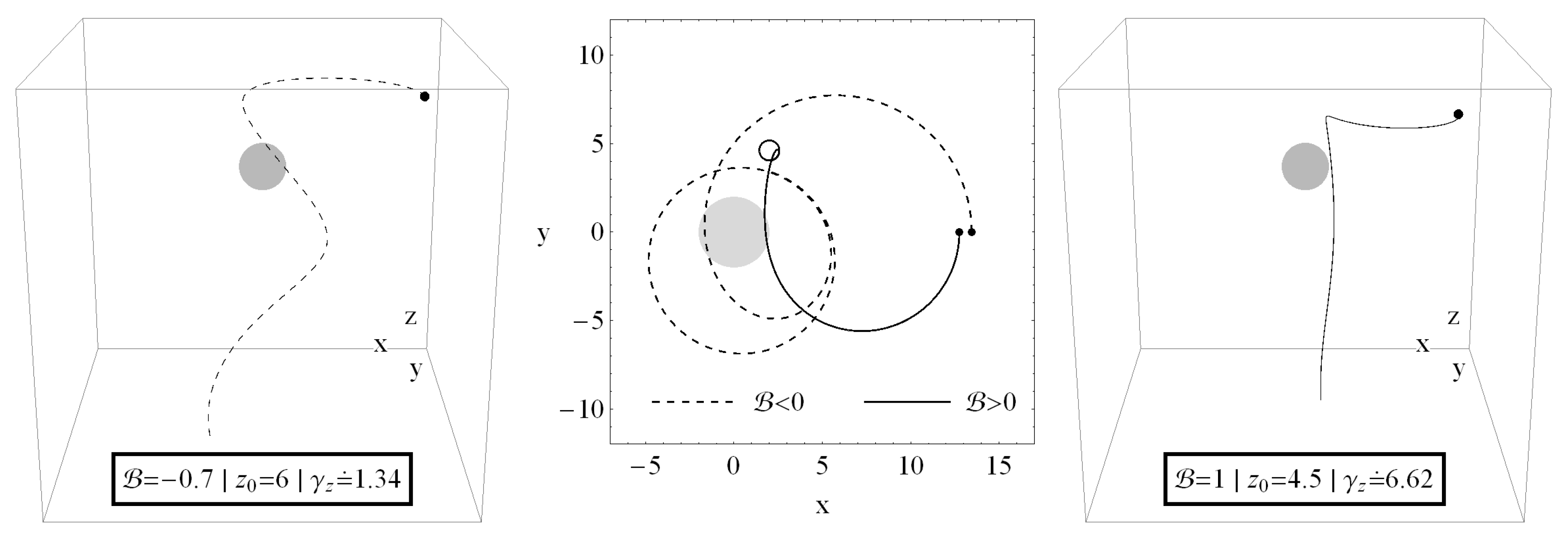
4.2.1. Chaotic Scattering of Ionized Particles
4.2.2. Escape Velocity
4.3. Charge Separation in the Accretion Disk
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MPP | magnetic Penrose process |
| BZ | Blandford–Znajek mechanism |
| SMBH | supermassive black hole |
| UHECR | ultra-high-energy cosmic ray |
| MF | magnetic field |
| NEO | negative energy orbit |
| AGN | active galactic nuclei |
| FRB | fast radio burst |
| GRB | gamma ray burst |
References
- Hulse, R.A. The discovery of the binary pulsar. Rev. Mod. Phys. 1994, 66, 699–710. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Eckart, A.; Hüttemann, A.; Kiefer, C.; Britzen, S.; Zajaček, M.; Lämmerzahl, C.; Stöckler, M.; Valencia, S.M.; Karas, V.; García-Marín, M. The Milky Way’s Supermassive Black Hole: How Good a Case Is It? Found. Phys. 2017, 47, 553–624. [Google Scholar] [CrossRef]
- Abuter, R.; et al. [Gravity Collaboration] Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar]
- McClintock, J.E.; Narayan, R.; Davis, S.W.; Gou, L.; Kulkarni, A.; Orosz, J.A.; Penna, R.F.; Remillard, R.A.; Steiner, J.F. Measuring the spins of accreting black holes. Class. Quantum Gravity 2011, 28, 114009. [Google Scholar] [CrossRef]
- Babak, S.; Gair, J.; Sesana, A.; Barausse, E.; Sopuerta, C.F.; Berry, C.P.; Berti, E.; Amaro-Seoane, P.; Petiteau, A.; Klein, A. Science with the space-based interferometer LISA. V. Extreme mass-ratio inspirals. Phys. Rev. D 2017, 95, 103012. [Google Scholar] [CrossRef] [Green Version]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Harrison, E.R. Electrified black holes. Nature 1976, 264, 525–528. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S. On the charge of the Galactic centre black hole. Mon. Not. R. Astron. Soc. 2018, 480, 4408–4423. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Padmanabhan, T. Thermodynamical aspects of gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef]
- Christodoulou, D.; Ruffini, R. Reversible Transformations of a Charged Black Hole. Phys. Rev. D 1971, 4, 3552–3555. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Extraction of Energy and Charge from a Black Hole. Phys. Rev. D 1973, 7, 949–953. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Nuovo Cimento Riv. Serie 1969, 34, 252–276. [Google Scholar]
- Wald, R.M. Energy Limits on the Penrose Process. Astrophys. J. 1974, 191, 231–234. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Press, W.H.; Teukolsky, S.A. Rotating Black Holes: Locally Nonrotating Frames, Energy Extraction, and Scalar Synchrotron Radiation. Astrophys. J. 1972, 178, 347–370. [Google Scholar] [CrossRef]
- Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. Revival of the Penrose process for astrophysical applications. Astrophys. J. 1985, 290, 12–14. [Google Scholar] [CrossRef]
- Parthasarathy, S.; Wagh, S.M.; Dhurandhar, S.V.; Dadhich, N. High efficiency of the Penrose process of energy extraction from rotating black holes immersed in electromagnetic fields. Astrophys. J. 1986, 307, 38–46. [Google Scholar] [CrossRef]
- Bhat, M.; Dhurandhar, S.; Dadhich, N. Energetics of the Kerr-Newman black hole by the Penrose process. J. Astrophys. Astron. 1985, 6, 85–100. [Google Scholar] [CrossRef]
- Wagh, S.M.; Dadhich, N. The energetics of black holes in electromagnetic fields by the penrose process. Phys. Rep. 1989, 183, 137–192. [Google Scholar] [CrossRef]
- Dadhich, N.; Tursunov, A.; Ahmedov, B.; Stuchlík, Z. The distinguishing signature of magnetic Penrose process. Mon. Not. R. Astron. Soc. 2018, 478, L89–L94. [Google Scholar] [CrossRef] [Green Version]
- Narayan, R.; McClintock, J.E.; Tchekhovskoy, A. Energy Extraction from Spinning Black Holes Via Relativistic Jets. In General Relativity, Cosmology and Astrophysics; Bičák, J., Ledvinka, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Ruffini, R.; Wilson, J.R. Relativistic magnetohydrodynamical effects of plasma accreting into a black hole. Phys. Rev. D 1975, 12, 2959–2962. [Google Scholar] [CrossRef]
- Williams, R.K. Collimated Escaping Vortical Polar e−e+ Jets Intrinsically Produced by Rotating Black Holes and Penrose Processes. Astrophys. J. 2004, 611, 952–963. [Google Scholar] [CrossRef]
- Piran, T.; Shaham, J.; Katz, J. High Efficiency of the Penrose Mechanism for Particle Collisions. Astrophys. J. Lett. 1975, 196, L107. [Google Scholar] [CrossRef]
- Piran, T.; Shaham, J. Production of gamma-ray bursts near rapidly rotating accreting black holes. Astrophys. J. 1977, 214, 268–299. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. Maximum efficiency of the collisional Penrose process. Phys. Rev. D 2016, 94, 064048. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Brito, R.; Cardoso, V. Ultrahigh-Energy Debris from the Collisional Penrose Process. Phys. Rev. Lett. 2015, 114, 251103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnittman, J.D. The collisional Penrose process. Gen. Relativ. Gravit. 2018, 50, 77. [Google Scholar] [CrossRef]
- Leiderschneider, E.; Piran, T. Maximal efficiency of the collisional Penrose process. Phys. Rev. D 2016, 93, 043015. [Google Scholar] [CrossRef] [Green Version]
- Stuchlik, Z. Equatorial circular orbits and the motion of the shell of dust in the field of a rotating naked singularity. Bull. Astron. Inst. Czechoslov. 1980, 31, 129–144. [Google Scholar]
- Morozova, V.; Rezzolla, L.; Ahmedov, B. Nonsingular electrodynamics of a rotating black hole moving in an asymptotically uniform magnetic test field. Phys. Rev. D 2014, 418, 104030. [Google Scholar] [CrossRef]
- Penna, R.F. Energy extraction from boosted black holes: Penrose process, jets, and the membrane at infinity. Phys. Rev. D 2015, 91, 084044. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P. Weakly magnetized black holes as particle accelerators. Phys. Rev. D 2012, 85, 024020. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Atamurotov, F.; Dadhich, N.; Ahmedov, B.; Stuchlík, Z. Energetics and optical properties of 6-dimensional rotating black hole in pure Gauss-Bonnet gravity. Eur. Phys. J. C 2015, 75, 399. [Google Scholar] [CrossRef]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Motion and high energy collision of magnetized particles around a Hořava-Lifshitz black hole. Astrophys. Space Sci. 2015, 360, 19. [Google Scholar] [CrossRef]
- Rayimbaev, J.R. Magnetized particle motion around non-Schwarzschild black hole immersed in an external uniform magnetic field. Astrophys. Space Sci. 2016, 361, 288. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Schee, J.; Abdujabbarov, A. Ultra-high-energy collisions of particles in the field of near-extreme Kehagias-Sfetsos naked singularities and their appearance to distant observers. Phys. Rev. D 2014, 89, 104048. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Abdujabbarov, A.; Ahmedov, B.; Stuchlík, Z. Acceleration of particles in spacetimes of black string. Phys. Rev. D 2013, 88, 124001. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Tursunov, A.A.; Ahmedov, B.J.; Kuvatov, A. Acceleration of particles by black hole with gravitomagnetic charge immersed in magnetic field. Astrophys. Space Sci. 2013, 343, 173–179. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Dadhich, N.; Ahmedov, B.; Eshkuvatov, H. Particle acceleration around a five-dimensional Kerr black hole. Phys. Rev. D 2013, 88, 084036. [Google Scholar] [CrossRef]
- Shaymatov, S.R.; Ahmedov, B.J.; Abdujabbarov, A.A. Particle acceleration near a rotating black hole in a Randall-Sundrum brane with a cosmological constant. Phys. Rev. D 2013, 88, 024016. [Google Scholar] [CrossRef]
- Abdujabbarov, A.A.; Ahmedov, B.J.; Ahmedov, B.B. Energy extraction and particle acceleration around a rotating black hole in Horava-Lifshitz gravity. Phys. Rev. D 2011, 84, 044044. [Google Scholar] [CrossRef]
- Morris, M.R. Manifestations of the Galactic Center Magnetic Field. In Lessons from the Local Group: A Conference in honor of David Block and Bruce Elmegreen; Freeman, K., Elmegreen, B., Block, D., Woolway, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; p. 391. [Google Scholar]
- Eatough, R.P.; Falcke, H.; Karuppusamy, R.; Lee, K.J.; Champion, D.J.; Keane, E.F.; Desvignes, G.; Schnitzeler, D.H.F.M.; Spitler, L.G.; Kramer, M.; et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 2013, 501, 391–394. [Google Scholar] [CrossRef] [Green Version]
- Abuter, R.; et al. [Gravity Collaboration] Detection of orbital motions near the last stable circular orbit of the massive black hole SgrA*. Astron. Astrophys. 2018, 618, L10. [Google Scholar] [Green Version]
- Gal’Tsov, D.V.; Petukhov, V.I. Black hole in an external magnetic field. Sov. J. Exp. Theor. Phys. 1978, 47, 419. [Google Scholar]
- Piotrovich, M.Y.; Gnedin, Y.N.; Buliga, S.D.; Natsvlishvili, T.M.; Silant’ev, N.A.; Nikitenko, A.S. Magnetic Fields of Compact Objects in Close X-ray Binary Systems. In Physics and Evolution of Magnetic and Related Stars; Astronomical Society of the Pacific Conference Series; Balega, Y.Y., Romanyuk, I.I., Kudryavtsev, D.O., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2015; Volume 494, p. 114. [Google Scholar]
- Wald, R.M. General Relativity; The University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Bicak, J.; Janis, V. Magnetic fluxes across black holes. Mon. Not. R. Astron. Soc. 1985, 212, 899–915. [Google Scholar] [CrossRef] [Green Version]
- Petterson, J.A. Magnetic field of a current loop around a Schwarzschild black hole. Phys. Rev. D 1974, 10, 3166–3170. [Google Scholar] [CrossRef]
- Levin, J.; D’Orazio, D.J.; Garcia-Saenz, S. Black hole pulsar. Phys. Rev. D 2018, 98, 123002. [Google Scholar] [CrossRef] [Green Version]
- Bičák, J.; Ledvinka, T. Electromagnetic fields around black holes and Meissner effect. Nuovo Cimento B Serie 2000, 115, 739. [Google Scholar]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Komissarov, S.S. Blandford-Znajek Mechanism versus Penrose Process. J. Korean Phys. Soc. 2009, 54, 2503. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M. Circular orbits and related quasiharmonic oscillatory motion of charged particles around weakly magnetized rotating black holes. Phys. Rev. D 2016, 93, 084012. [Google Scholar] [CrossRef] [Green Version]
- Punsly, B. Black Hole Gravitohydromagnetics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Beskin, V.S. REVIEWS OF TOPICAL PROBLEMS: Axisymmetric stationary flows in compact astrophysical objects. Physics Uspekhi 1997, 40, 659–688. [Google Scholar] [CrossRef]
- Komissarov, S.S. Electrodynamics of black hole magnetospheres. Mon. Not. R. Astron. Soc. 2004, 350, 427–448. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.P.; Shoom, A.A. Motion of charged particles near a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2010, 82, 084034. [Google Scholar] [CrossRef]
- Kološ, M.; Stuchlík, Z.; Tursunov, A. Quasi-harmonic oscillatory motion of charged particles around a Schwarzschild black hole immersed in a uniform magnetic field. Class. Quantum Gravity 2015, 32, 165009. [Google Scholar] [CrossRef]
- Kovář, J.; Kopáček, O.; Karas, V.; Stuchlík, Z. Off-equatorial orbits in strong gravitational fields near compact objects—II: halo motion around magnetic compact stars and magnetized black holes. Class. Quantum Gravity 2010, 27, 135006. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Ternov, I.M.; Aliev, A.N.; Gal’Tsov, D.V. Synchrotron radiation in curved space-time. Soviet Phys. J. 1983, 26, 36–40. [Google Scholar] [CrossRef]
- Sokolov, A.A.; Gal’tsov, D.V.; Petukhov, V.I. Radiation emitted by relativistic particles moving in the vicinity of the Schwarzschild black hole, immersed in an external magnetic field. Phys. Lett. A 1978, 68, 1–2. [Google Scholar] [CrossRef]
- Shoom, A.A. Synchrotron radiation from a weakly magnetized Schwarzschild black hole. Phys. Rev. D 2015, 92, 124066. [Google Scholar] [CrossRef]
- Tursunov, A.; Kološ, M.; Stuchlík, Z.; Gal’tsov, D.V. Radiation Reaction of Charged Particles Orbiting a Magnetized Schwarzschild Black Hole. Astrophys. J. 2018, 861, 2. [Google Scholar] [CrossRef]
- DeWitt, B.S.; Brehme, R.W. Radiation damping in a gravitational field. Ann. Phys. 1960, 9, 220–259. [Google Scholar] [CrossRef]
- Hobbs, J. A vierbein formalism of radiation damping. Ann. Phys. 1968, 47, 141–165. [Google Scholar] [CrossRef]
- Poisson, E. The Motion of Point Particles in Curved Spacetime. Living Rev. Relativ. 2004, 7, 6. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. I. Negative-energy states. Phys. Rev. D 1984, 29, 2712–2720. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Dadhich, N. Energy-extraction processes from a Kerr black hole immersed in a magnetic field. II. The formalism. Phys. Rev. D 1984, 30, 1625–1631. [Google Scholar] [CrossRef]
- Aab, A.; et al. [Pierre Auger Collaboration] An Indication of Anisotropy in Arrival Directions of Ultra-high-energy Cosmic Rays through Comparison to the Flux Pattern of Extragalactic Gamma-Ray Sources. Astrophys. J. Lett. 2018, 853, L29. [Google Scholar] [CrossRef]
- Aab, A.; et al. [Pierre Auger Collaboration] Observation of a large-scale anisotropy in the arrival directions of cosmic rays above 8×1018 eV. Science 2017, 357, 1266–1270. [Google Scholar]
- Greisen, K. End to the cosmic ray spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78–80. [Google Scholar]
- Aartsen, M.G.; et al. [IceCube Collaboration] Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar]
- Aartsen, M.G.; et al. [IceCube Collaboration] Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147–151. [Google Scholar]
- Aab, A.; et al. [The Pierre Auger Collaboration] The Pierre Auger Observatory: Contributions to the 35th International Cosmic Ray Conference (ICRC 2017). arXiv 2017, arXiv:1708.06592. [Google Scholar]
- Aab, A.; Abreu, P.; Aglietta, M.; Al Samarai, I.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Castillo, J.A.; Alvarez-Muñiz, J.; Anastasi, G.A.; et al. Combined fit of spectrum and composition data as measured by the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2017, 2017, 038, Erratum in J. Cosmol. Astropart. Phys. 2018, 2018, E02. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abe, M.; Abu-Zayyad, T.; Allen, M.; Anderson, R.; Azuma, R.; Barcikowski, E.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; et al. Study of Ultra-High Energy Cosmic Ray composition using Telescope Array’s Middle Drum detector and surface array in hybrid mode. Astropart. Phys. 2015, 64, 49–62. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abu-Zayyad, T.; Al-Seady, M.; Allen, M.; Amman, J.F.; Anderson, R.J.; Archbold, G.; Belov, K.; Belz, J.W.; Bergman, D.R.; et al. Indications of Proton-Dominated Cosmic-Ray Composition above 1.6 EeV. Phys. Rev. Lett. 2010, 104, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, R.U.; Abe, M.; Abu-Zayyad, T.; Allen, M.; Azuma, R.; Barcikowski, E.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; Cady, R.; et al. Search for EeV protons of galactic origin. Astropart. Phys. 2017, 86, 21–26. [Google Scholar] [CrossRef]
- Góra, D.; Cheminant, K.A.; Alvarez-Castillo, D.; Bratek, L.; Dhital, N.; Duffy, A.R.; Homola, P.; Jagoda, P.; Jalocha, J.; Kasztelan, M.; et al. Cosmic-Ray Extremely Distributed Observatory: Status and Perspectives. Universe 2018, 4, 111. [Google Scholar] [CrossRef]
- Blandford, R.D. Acceleration of Ultra High Energy Cosmic Rays. Phys. Scripta Volume T 2000, 85, 191–194. [Google Scholar] [CrossRef]
- Tursunov, A.; Stuchlík, Z.; Kološ, M.; Dadhich, N.; Ahmedov, B. Supermassive Black Holes as sources of Ultra-High-Energy Cosmic Rays. 2019; submitted. [Google Scholar]
- Abraham, J.; et al. [Pierre Auger Collaboration] Correlation of the Highest-Energy Cosmic Rays with Nearby Extragalactic Objects. Science 2007, 318, 938–943. [Google Scholar] [Green Version]
- Parsa, M.; Eckart, A.; Shahzamanian, B.; Karas, V.; Zajaček, M.; Zensus, J.A.; Straubmeier, C. Investigating the Relativistic Motion of the Stars Near the Supermassive Black Hole in the Galactic Center. Astrophys. J. 2017, 845, 22. [Google Scholar] [CrossRef] [Green Version]
- Eckart, A.; Schödel, R.; Meyer, L.; Trippe, S.; Ott, T.; Genzel, R. Polarimetry of near-infrared flares from Sagittarius A*. Astron. Astrophys. 2006, 455, 1–10. [Google Scholar] [CrossRef]
- Abbasi, R.U.; Abe, M.; Abu-Zayyad, T.; Allen, M.; Azuma, R.; Barcikowski, E.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; Cady, R.; et al. The Cosmic Ray Energy Spectrum between 2 PeV and 2 EeV Observed with the TALE Detector in Monocular Mode. Astrophys. J. 2018, 865, 74. [Google Scholar] [CrossRef] [Green Version]
- Erlykin, A.D.; Wolfendale, A.W. The nature of the ‘knee’ in the cosmic ray energy spectrum. J. Phys. G Nuclear Part. Phys. 2005, 32, 1–7. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Acceleration of the charged particles due to chaotic scattering in the combined black hole gravitational field and asymptotically uniform magnetic field. Eur. Phys. J. C 2016, 76, 32. [Google Scholar] [CrossRef]
- Goldreich, P.; Julian, W.H. Pulsar Electrodynamics. Astrophys. J. 1969, 157, 869. [Google Scholar] [CrossRef]
| 1 | As for energy E, sign of would be dependent upon the location of observer, whether inside or outside ergosphere. There could exist no static observer in ergosphere, it could at best be stationary with non-zero frame dragging angular velocity. |
| B (Gauss) | (s) | (s) | (s) |
|---|---|---|---|
| 1 | |||
| 1 | |||
| Decay Mode | Generic Equation | Esc. p. | Efficiency | Regime of MPP |
|---|---|---|---|---|
| decay | XY | Y | <0 | - |
| ultra | ||||
| XY | Y | <0 | – | |
| ∼1 | moderate | |||
| XY | Y | ∼2 | moderate | |
| - | ||||
| decay | XY | Y | ultra | |
| <0 | – | |||
| low | ||||
| decay | XY | Y | <0 | – |
| ∼0 | low/– | |||
| <0 | – | |||
| emission | XX’ | X′ | low | |
| low | ||||
| Pair production | <0 | – | ||
| ultra |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tursunov, A.; Dadhich, N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe 2019, 5, 125. https://doi.org/10.3390/universe5050125
Tursunov A, Dadhich N. Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process. Universe. 2019; 5(5):125. https://doi.org/10.3390/universe5050125
Chicago/Turabian StyleTursunov, Arman, and Naresh Dadhich. 2019. "Fifty Years of Energy Extraction from Rotating Black Hole: Revisiting Magnetic Penrose Process" Universe 5, no. 5: 125. https://doi.org/10.3390/universe5050125





