Induced Gravitational Collapse, Binary-Driven Hypernovae, Long Gramma-ray Bursts and Their Connection with Short Gamma-ray Bursts
Abstract
1. Introduction
1.1. The Quest for the Binary Nature of GRB Progenitors
- SNe Ic as the ones associated with GRBs lack hydrogen and helium in their spectra. It has been recognized that they most likely originate in helium stars, CO, or Wolf-Rayet stars, that have lost their outermost layers (see e.g., [26], and references therein). The pre-SN star, very likely, does not follow a single-star evolution but it belongs to a tight binary with a compact star companion (e.g., a NS). The compact star strips off the pre-SN star outermost layers via binary interactions such as mass-transfer and tidal effects (see e.g., [26,27,28,29,30]).
- Denoting the beaming angle by , to an observed isotropic energy it would correspond to a reduced intrinsic source energy released , where . Extremely small beaming factors (i.e., ) are inferred to reduce the observed energetics of erg to the expected energy release by such a scenario ∼10 erg [31]. However, the existence of such extremely narrow beaming angles have never been observationally corroborated [32,33,34].
- An additional drawback of this scenario is that it implies a dense and strong wind-like circumburst medium (CBM) in contrast with the one observed in most GRBs (see e.g., [35]). Indeed, the average CBM density inferred from GRB afterglows is of the order of 1 baryon per cubic centimeter [36]. The baryonic matter component in the GRB process is represented by the so-called baryon load [37]. The GRB plasma should engulf a limited amount of baryons in order to be able to expand at ultrarelativistic velocities with Lorentz factors as requested by the observed non-thermal component in the prompt Gamma-ray emission spectrum [16,17,18]. The amount of baryonic mass is thus limited by the prompt emission to a maximum value of the baryon-load parameter, , where is the total energy of the plasma [37].
- GRBs and SNe have markedly different energetics. SNe emit energies in the range – erg, while GRBs emit in the range – erg. Thus, the origin of GRB energetics point to the gravitational collapse to a stellar-mass BH. The SN origin points to evolutionary stages of a massive star leading to a NS or to a complete disrupting explosion, but not to a BH. The direct formation of a BH in a core-collapse SN is currently ruled out by the observed masses of pre-SN progenitors, ≲18 [38]. It is theoretically known that massive stars with such a relatively low mass do not lead to a direct collapse to a BH (see [38,39] for details).
- It was recently shown in [40] that the observed thermal emission in the X-ray flares present in the early (rest-frame time s) afterglow implies an emitter of size ∼10 cm expanding at mildly-relativistic velocity, e.g., . This is clearly in contrast with the “collapsar-fireball” scenario in which there is an ultrarelativistic emitter (the jet) with – extending from the prompt emission all the way to the afterglow.
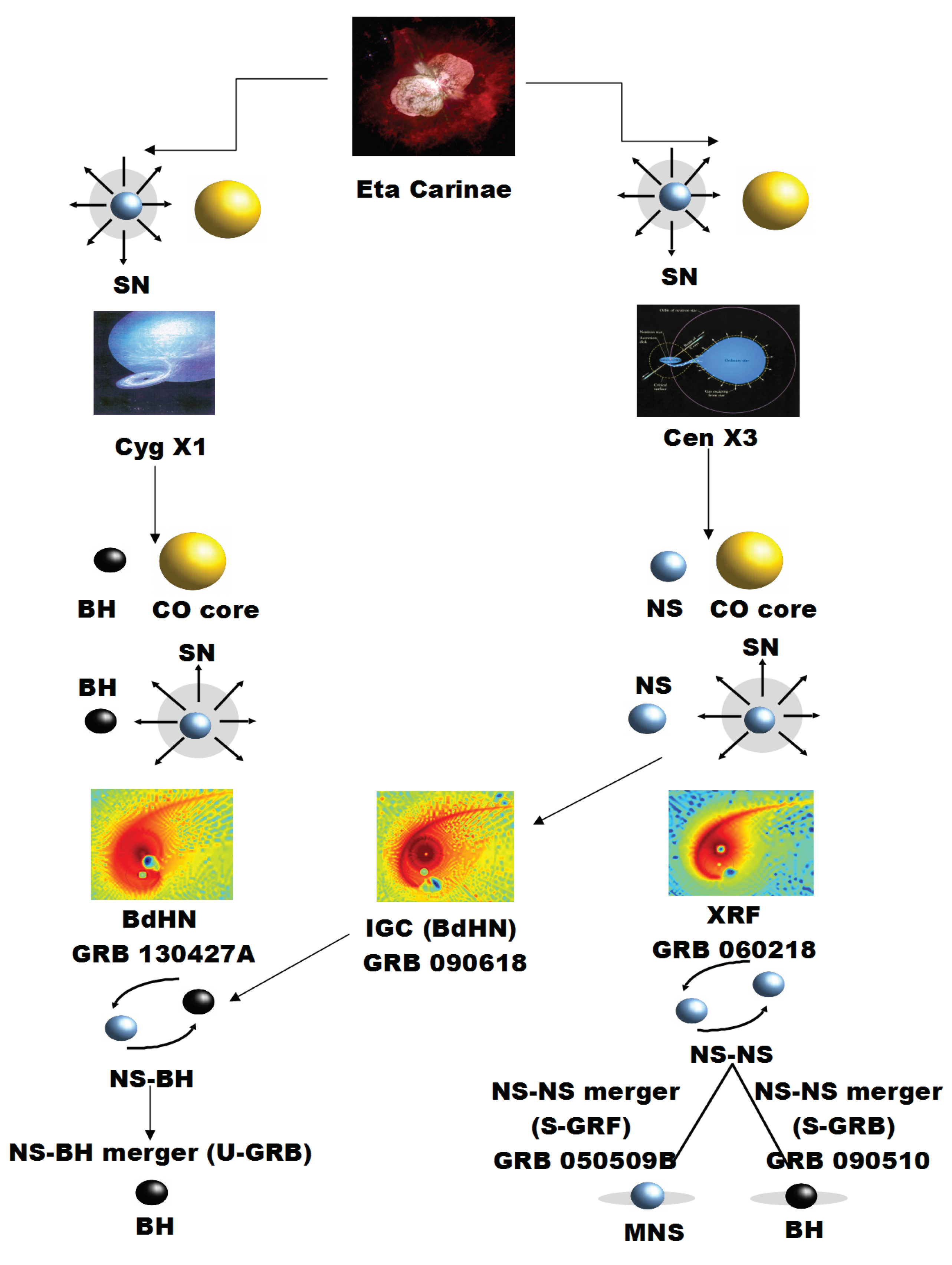
1.2. GRB Subclasses
- i.
- X-ray flashes (XRFs). These systems have CO-NS binary progenitors in which the NS companion does not reach the critical mass for gravitational collapse [52,53]. In the SN explosion, the binary might or might not be disrupted depending on the mass loss and/or the kick imparted [54]. Thus XRFs lead either to two NSs ejected by the disruption, or to binaries composed of a newly-formed ∼1.4–1.5 NS (hereafter NS) born at the center of the SN, and a massive NS (MNS) which accreted matter from the SN ejecta. Some observational properties are: Gamma-ray isotropic energy erg, rest-frame spectral peak energy keV and a local observed rate of Gpc yr [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49], this class has been divided into BdHN type II, the sources with erg, and BdHN type III, the sources with erg.
- ii.
- Binary-driven hypernovae (BdHNe). Originate in compact CO-NS binaries where the accretion onto the NS becomes high enough to bring it to the point of gravitational collapse, hence forming a BH. We showed that most of these binaries survive to the SN explosion owing to the short orbital periods ( min) for which the mass loss cannot be considered as instantaneous, allowing the binary to keep bound even if more than half of the total binary mass is lost [55]. Therefore, BdHNe produce NS-BH binaries. Some observational properties are: erg, keV and a local observed rate of Gpc yr [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BdHN type I.
- iii.
- BH-SN. These systems originate in CO (or Helium or Wolf-Rayet star)-BH binaries, hence the hypercritical accretion of the SN explosion of the CO occurs onto a BH previously formed in the evolution path of the binary. They might be the late evolutionary stages of X-ray binaries such as Cyg X-1 [56,57], or microquasars [58]. Alternatively, they can form following the evolutionary scenario XI in [59]. If the binary survives to the SN explosion BH-SNe produce NS-BH, or BH-BH binaries when the central remnant of the SN explosion collapses directly to a BH (see, although, [38,39]). Some observational properties are: erg, MeV and an upper limit to their rate is Gpc yr, namely the estimated observed rate of BdHNe type I which by definition covers systems with the above and range [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BdHN type IV.
- iv.
- Short Gamma-ray flashes (S-GRFs). They are produced by NS-NS mergers leading to a MNS, namely when the merged core does not reach the critical mass of a NS. Some observational properties are: erg, MeV and a local observed rate of Gpc yr [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BM type I.
- v.
- Authentic short GRBs (S-GRBs). They are produced by NS-NS mergers leading to a BH, namely when the merged core reaches the critical mass of a NS, hence it forms a BH as a central remnant [67,68,69]. Some observational properties are: erg, MeV and a local observed rate of Gpc yr [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BM type II.
- vi.
- Ultra-short GRBs (U-GRBs). This is a theoretical GRB subclass subjected for observational verification. U-GRBs are expected to be produced by NS-BH mergers whose binary progenitors can be the outcome of BdHNe type I (see II above) or of BdHNe type IV (BH-SN; see III above). The following observational properties are expected: erg, MeV and a local observed rate similar to the one of BdHNe type I since we have shown that most of them are expected to remain bound [55], i.e., Gpc yr [45]. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BM type V.
- vii.
- Gamma-ray flashes (GRFs). These sources show an extended and softer emission, i.e., they have hybrid properties between long and short bursts and have no associated SNe [70]. It has been proposed that they are produced by NS-WD mergers [45]. These binaries are expected to be very numerous [71] and a variety of evolutionary scenarios for their formation have been proposed [72,73,74,75]. GRFs form a MNS and not a BH [45]. Some observational properties are: erg, MeV and a local observed rate of Gpc yr [45]. It is worth noting that this rate is low with respect to the one expected from the current number of known NS-WD in the Galaxy [71]. From the GRB observations only one NS-WD merger has been identified (GRB 060614 [76]). This implies that most NS-WD mergers are probably under the threshold of current X and Gamma-ray instruments. We refer the reader to Table 1 and [45,47] for further details on this class. In [49] this class has been renominated as BM type III.
- viii.
- Fallback kilonovae (FB-KNe). This is a recently introduced GRB subclass having as progenitors WD-WD mergers [50,51]. The WD-WD mergers of interest are those that do not produce type Ia SNe but that lead to a massive (), fast rotating (–10 s), highly-magnetized (– G) WD. Some observational properties are: erg, MeV and a local observed rate = (3.7–6.7) × 105 Gpc yr [50,51,77,78]. The coined name FB-KN is due to the fact that they are expected to produce an infrared-optical transient by the cooling of the ejecta expelled in the dynamical phase of the merger and heated up by fallback accretion onto the newly-formed massive WD.
1.3. The Specific Case of BdHNe
2. A Chronological Summary of the IGC Simulations: 2012–2016
2.1. First Analytic Estimates
2.2. First Numerical Simulations: 1D Approximation
2.3. 2D Simulations including Angular Momentum Transfer
2.4. First 3D Simulations
3. The Hypercritical Accretion Process
3.1. Accretion Rate and NS Evolution
- The density profile included finite size/thickness effects and additional CO progenitors, leading to different SN ejecta masses being considered.
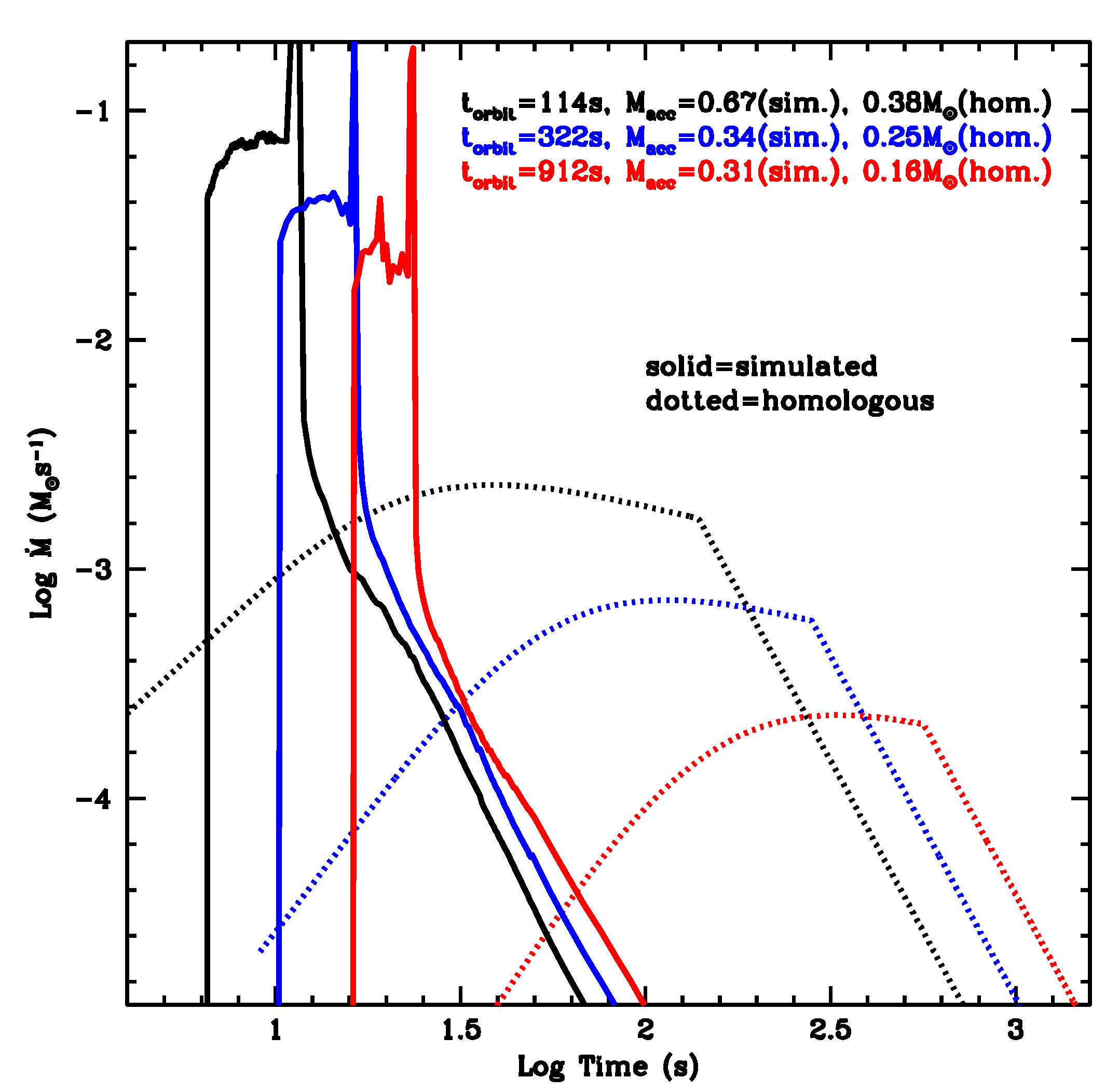
- In [53] the maximum orbital period, , over which the accretion onto NS companion is not sufficient to bring it to the critical mass, was inferred. Thus, binaries with lead to XRFs while the ones with lead to BdHNe. Becerra et al. [52] extended the determination of for all the possible initial values of the NS mass. They also examined the outcomes for different values of the angular momentum transfer efficiency parameter.
- The expected luminosity during the process of hypercritical accretion for a wide range of binary periods covering both XRFs and BdHNe was estimated.
- It was shown that the presence of the NS companion originates asymmetries in the SN ejecta (see, e.g., Figure 6 in [52]). The signatures of such asymmetries in the X-ray emission was there shown in the specific example of XRF 060218.
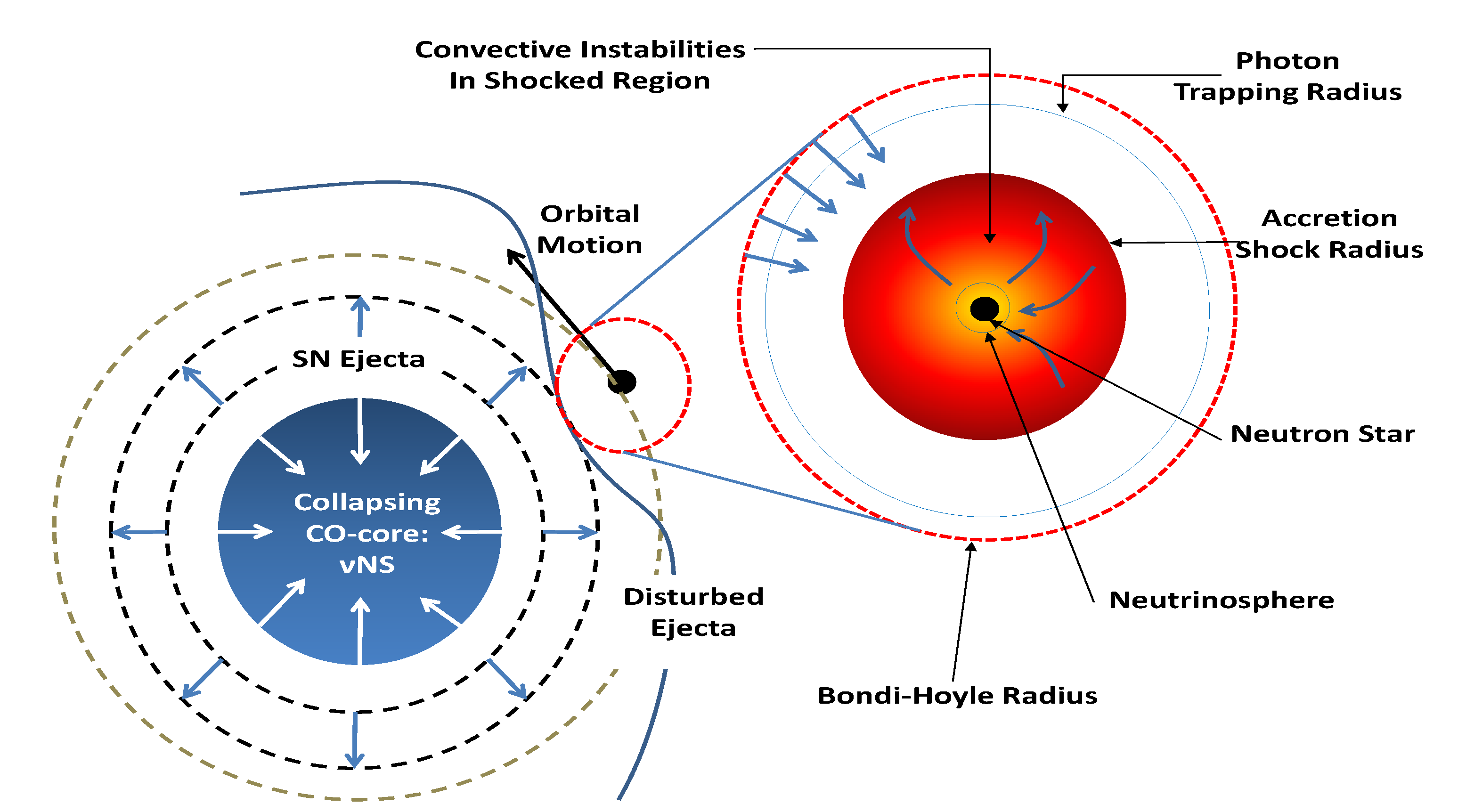
3.2. Hydrodynamics in the Accretion Region
- The photons are trapped within the infalling matter, hence the Eddington limit does not apply and hypercritical accretion occurs. The trapping radius is defined as [97]: , where is the opacity. [83] estimated a Rosseland mean opacity of ≈5 × 10 cm g for the CO. This, together with our typical accretion rates, lead to – cm. This radius is much bigger than the Bondi-Hoyle radius.
3.3. Neutrino Emission and Effective Accretion Rate
3.4. Accretion Luminosity
4. New 3D SPH Simulations
5. Consequences on GRB Data Analysis and Interpretation
5.1. X-ray Precursor
5.2. GRB Prompt Emission
5.3. Early X-ray Afterglow: Flares
5.4. Late X-ray Afterglow
5.5. High-Energy GeV Emission
5.6. Additional Considerations
- (1)
- the hypercritical accretion occurs not only on the NS companion but also on the NS and with a comparable rate.
- (2)
- This implies that BdHNe might be also be able to form, in special cases, BH-BH binaries. Since the system remains bound the binary will quickly merge by emitting gravitational waves. Clearly, no electromagnetic emission is expected from these mergers. However, the typically large cosmological distances of BdHNe would make it extremely difficult to detect their gravitational waves e.g., by LIGO/Virgo.
- (3)
- Relatively weak SN explosions produce a long-lived hypercritical accretion process leading and enhance, at late times, the accretion onto the NS. The revival of the accretion process at late times is a unique feature of our binary and does not occur for single SNe, namely in the absence of the NS companion. This feature increases the probability of detection of weak SNe by X-ray detectors via the accretion phase in an XRF/BdHN.
- (4)
- For asymmetric SN explosions the accretion rate shows a quasi-periodic behavior that might be detected by X-rays instruments, possibly allowing a test of the binary nature and the identification of the orbital period of the progenitor.
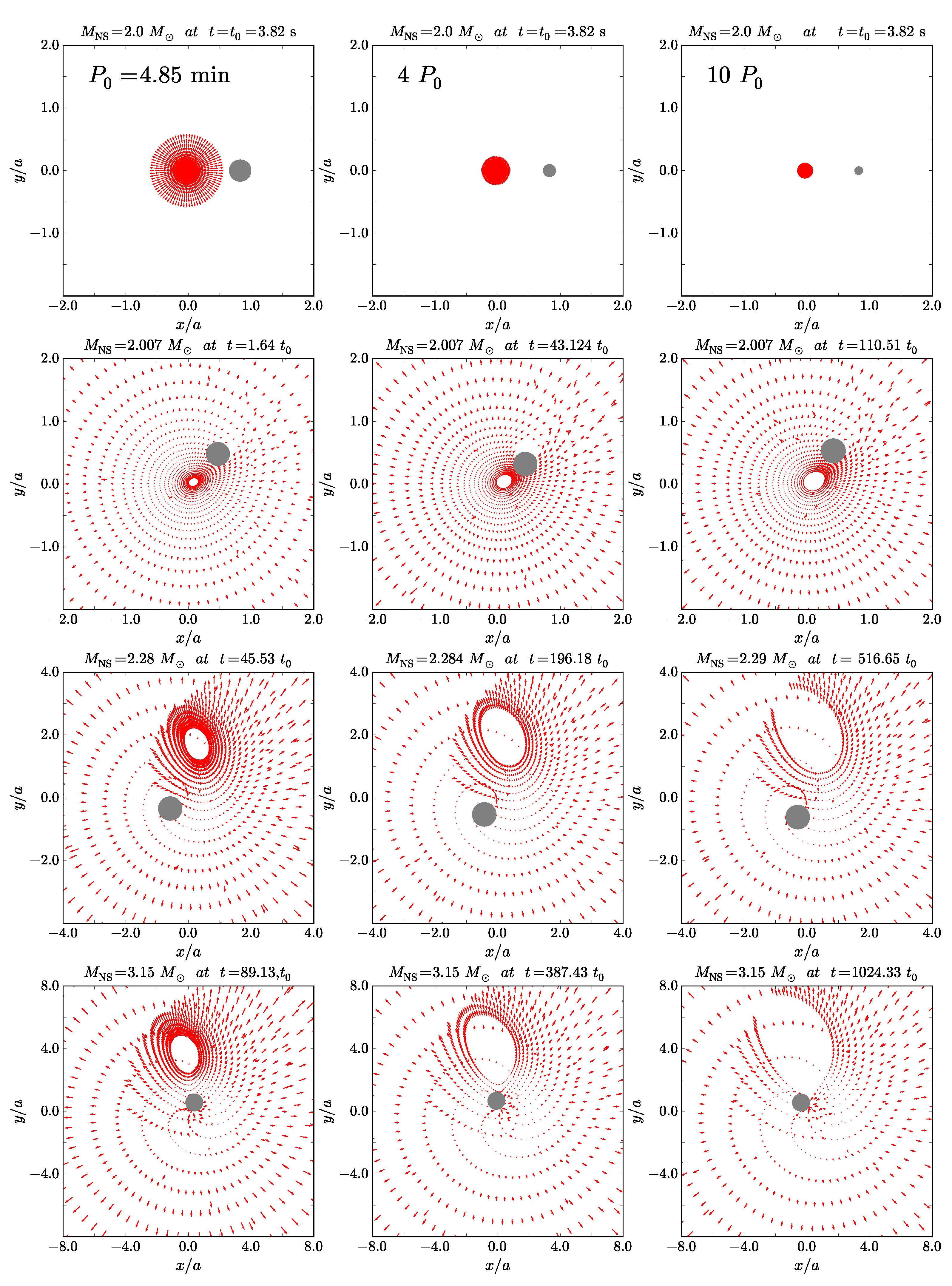
6. Post-Explosion Orbits and Formation of NS-BH Binaries
7. BdHN Formation, Occurrence Rate and Connection with Short GRBs
7.1. An Evolutionary Scenario
7.2. Occurrence Rate
7.3. Connection with Short GRBs
8. Conclusions
- (1)
- the SN explosion;
- (2)
- the hypercritical accretion onto the NS companion;
- (3)
- the NS collapse with consequent BH formation;
- (4)
- the initiation of the inner engine;
- (5)
- the plasma production;
- (6)
- the plasma feedback onto the SN which converts the SN into a HN;
- (7)
- the formation of the cavity around the newborn BH;
- (8)
- the transparency of the plasma along different directions;
- (9)
- the HN emission powered by the NS;
- (10)
- the action of the inner engine in accelerating protons leading to UHECRs and to the high-energy emission.
Funding
Conflicts of Interest
References
- Mazets, E.P.; Golenetskii, S.V.; Ilinskii, V.N.; Panov, V.N.; Aptekar, R.L.; Gurian, I.A.; Proskura, M.P.; Sokolov, I.A.; Sokolova, Z.I.; Kharitonova, T.V. Catalog of cosmic Gamma-ray bursts from the KONUS experiment data. I. Astrophys. Space Sci. 1981, 80, 3–83. [Google Scholar] [CrossRef]
- Klebesadel, R.W. The durations of Gamma-ray bursts. In Gamma-ray Bursts—Observations, Analyses and Theories; Ho, C., Epstein, R.I., Fenimore, E.E., Eds.; Cambridge University Press: Cambridge, UK, 1992; pp. 161–168. [Google Scholar]
- Dezalay, J.P.; Barat, C.; Talon, R.; Syunyaev, R.; Terekhov, O.; Kuznetsov, A. Short cosmic events—A subset of classical GRBs? In American Institute of Physics Conference Series; Paciesas, W.S., Fishman, G.J., Eds.; American Institute of Physics: College Park, MD, USA, 1992; Volume 265, pp. 304–309. [Google Scholar]
- Kouveliotou, C.; Meegan, C.A.; Fishman, G.J.; Bhat, N.P.; Briggs, M.S.; Koshut, T.M.; Paciesas, W.S.; Pendleton, G.N. Identification of two classes of Gamma-ray bursts. Astrophys. J. Lett. 1993, 413, L101–L104. [Google Scholar] [CrossRef]
- Tavani, M. Euclidean versus Non-Euclidean Gamma-ray Bursts. Astrophys. J. Lett. 1998, 497, L21–L24. [Google Scholar] [CrossRef]
- Goodman, J. Are Gamma-ray bursts optically thick? Astrophys. J. Lett. 1986, 308, L47. [Google Scholar] [CrossRef]
- Paczynski, B. Gamma-ray bursters at cosmological distances. Astrophys. J. Lett. 1986, 308, L43. [Google Scholar] [CrossRef]
- Eichler, D.; Livio, M.; Piran, T.; Schramm, D.N. Nucleosynthesis, neutrino bursts and Gamma-rays from coalescing neutron stars. Nature 1989, 340, 126–128. [Google Scholar] [CrossRef]
- Narayan, R.; Piran, T.; Shemi, A. Neutron star and black hole binaries in the Galaxy. Astrophys. J. Lett. 1991, 379, L17–L20. [Google Scholar] [CrossRef]
- Pian, E.; Amati, L.; Antonelli, L.A.; Butler, R.C.; Costa, E.; Cusumano, G.; Danziger, J.; Feroci, M.; Fiore, F.; Frontera, F.; et al. BEPPOSAX Observations of GRB 980425: Detection of the Prompt Event and Monitoring of the Error Box. Astrophys. J. Lett. 2000, 536, 778–787. [Google Scholar] [CrossRef][Green Version]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An unusual supernova in the error box of the γ-ray burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Della Valle, M. Supernovae and Gamma-ray Bursts: A Decade of Observations. Int. J. Mod. Phys. D 2011, 20, 1745–1754. [Google Scholar] [CrossRef]
- Cano, Z.; Wang, S.Q.; Dai, Z.G.; Wu, X.F. The Observer’s Guide to the Gamma-ray Burst Supernova Connection. Adv. Astron. 2017, 2017, 8929054. [Google Scholar] [CrossRef]
- Woosley, S.E.; Bloom, J.S. The Supernova Gamma-ray Burst Connection. Annu. Rev. Astron. Astrophys. 2006, 44, 507–556. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Shemi, A.; Piran, T. The appearance of cosmic fireballs. Astrophys. J. Lett. 1990, 365, L55–L58. [Google Scholar] [CrossRef]
- Meszaros, P.; Laguna, P.; Rees, M.J. Gasdynamics of relativistically expanding Gamma-ray burst sources—Kinematics, energetics, magnetic fields, and efficiency. Astrophys. J. Lett. 1993, 415, 181–190. [Google Scholar] [CrossRef]
- Piran, T.; Shemi, A.; Narayan, R. Hydrodynamics of Relativistic Fireballs. MNRAS 1993, 263, 861. [Google Scholar] [CrossRef]
- Mao, S.; Yi, I. Relativistic beaming and Gamma-ray bursts. Astrophys. J. Lett. 1994, 424, L131–L134. [Google Scholar] [CrossRef]
- Piran, T. Gamma-ray bursts and the fireball model. Phys. Rep. 1999, 314, 575–667. [Google Scholar] [CrossRef]
- Piran, T. The physics of Gamma-ray bursts. Rev. Mod. Phys. 2004, 76, 1143–1210. [Google Scholar] [CrossRef]
- Mészáros, P. Theories of Gamma-ray Bursts. Annu. Rev. Astron. Astrophys. 2002, 40, 137. [Google Scholar] [CrossRef]
- Mészáros, P. Gamma-ray bursts. Rep. Prog. Phys. 2006, 69, 2259–2321. [Google Scholar] [CrossRef]
- Berger, E. Short-Duration Gamma-ray Bursts. Annu. Rev. Astron. Astrophys. 2014, 52, 43–105. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of Gamma-ray bursts and relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Smith, N.; Li, W.; Silverman, J.M.; Ganeshalingam, M.; Filippenko, A.V. Luminous blue variable eruptions and related transients: Diversity of progenitors and outburst properties. MNRAS 2011, 415, 773–810. [Google Scholar] [CrossRef]
- Nomoto, K.; Hashimoto, M. Presupernova evolution of massive stars. Phys. Rep. 1988, 163, 13–36. [Google Scholar] [CrossRef]
- Iwamoto, K.; Nomoto, K.; Höflich, P.; Yamaoka, H.; Kumagai, S.; Shigeyama, T. Theoretical light curves for the type IC supernova SN 1994I. Astrophys. J. Lett. 1994, 437, L115–L118. [Google Scholar] [CrossRef]
- Fryer, C.L.; Mazzali, P.A.; Prochaska, J.; Cappellaro, E.; Panaitescu, A.; Berger, E.; van Putten, M.; van den Heuvel, E.P.J.; Young, P.; Hungerford, A.; et al. Constraints on Type Ib/c Supernovae and Gamma-ray Burst Progenitors. Publ. Astron. Soc. Pac. 2007, 119, 1211–1232. [Google Scholar] [CrossRef]
- Yoon, S.C.; Woosley, S.E.; Langer, N. Type Ib/c Supernovae in Binary Systems. I. Evolution and Properties of the Progenitor Stars. Astrophys. J. Lett. 2010, 725, 940–954. [Google Scholar] [CrossRef]
- Frail, D.A.; Kulkarni, S.R.; Sari, R.; Djorgovski, S.G.; Bloom, J.S.; Galama, T.J.; Reichart, D.E.; Berger, E.; Harrison, F.A.; Price, P.A.; et al. Beaming in Gamma-ray Bursts: Evidence for a Standard Energy Reservoir. Astrophys. J. Lett. 2001, 562, L55–L58. [Google Scholar] [CrossRef]
- Covino, S.; Malesani, D.; Tagliaferri, G.; Vergani, S.D.; Chincarini, G.; Kann, D.A.; Moretti, A.; Stella, L.; Mistici Collaboration. Achromatic breaks for Swift GRBs: Any evidence? Nuovo C. Ser. 2006, 121, 1171–1176. [Google Scholar]
- Sato, G.; Yamazaki, R.; Ioka, K.; Sakamoto, T.; Takahashi, T.; Nakazawa, K.; Nakamura, T.; Toma, K.; Hullinger, D.; Tashiro, M.; et al. Swift Discovery of Gamma-ray Bursts without a Jet Break Feature in Their X-ray Afterglows. Astrophys. J. Lett. 2007, 657, 359–366. [Google Scholar] [CrossRef][Green Version]
- Burrows, D.; Garmire, G.; Ricker, G.; Bautz, M.; Nousek, J.; Grupe, D.; Racusin, J. Chandra Searches for Late-Time Jet Breaks in GRB X-ray Afterglows. In Chandra’s First Decade of Discovery; Wolk, S., Fruscione, A., Swartz, D., Eds.; Chandra X-ray Center: Cambridge, MA, USA, 2009. [Google Scholar]
- Izzo, L.; Ruffini, R.; Penacchioni, A.V.; Bianco, C.L.; Caito, L.; Chakrabarti, S.K.; Rueda, J.A.; Nandi, A.; Patricelli, B. A double component in GRB 090618: A proto-black hole and a genuinely long Gamma-ray burst. A&A 2012, 543, A10. [Google Scholar]
- Ruffini, R. Fundamental Physics from Black Holes, Neutron Stars and Gamma-ray Bursts. Int. J. Mod. Phys. D 2011, 20, 1797–1872. [Google Scholar] [CrossRef]
- Ruffini, R.; Salmonson, J.D.; Wilson, J.R.; Xue, S.S. On the pair-electromagnetic pulse from an electromagnetic black hole surrounded by a baryonic remnant. A&A 2000, 359, 855–864. [Google Scholar]
- Smartt, S.J. Observational Constraints on the Progenitors of Core-Collapse Supernovae: The Case for Missing High-Mass Stars. PASA 2015, 32, e016. [Google Scholar] [CrossRef]
- Smartt, S.J. Progenitors of Core-Collapse Supernovae. Annu. Rev. Astron. Astrophys. 2009, 47, 63–106. [Google Scholar] [CrossRef]
- Ruffini, R.; Wang, Y.; Aimuratov, Y.; Barres de Almeida, U.; Becerra, L.; Bianco, C.L.; Chen, Y.C.; Karlica, M.; Kovacevic, M.; Li, L.; et al. Early X-ray Flares in GRBs. Astrophys. J. Lett. 2018, 852, 53. [Google Scholar] [CrossRef]
- Ruffini, R.; Bianco, C.L.; Fraschetti, F.; Xue, S.S.; Chardonnet, P. On a Possible Gamma-ray Burst-Supernova Time Sequence. Astrophys. J. Lett. 2001, 555, L117–L120. [Google Scholar] [CrossRef]
- Ruffini, R.; Bernardini, M.G.; Bianco, C.L.; Caito, L.; Chardonnet, P.; Cherubini, C.; Dainotti, M.G.; Fraschetti, F.; Geralico, A.; Guida, R.; et al. On Gamma-ray Bursts. In The Eleventh Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories; Kleinert, H., Jantzen, R.T., Ruffini, R., Eds.; World Scientific Publishing Co. Pte Ltd.: Hackensack, NJ, USA, 2008; pp. 368–505. [Google Scholar]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444. [Google Scholar] [CrossRef]
- Smith, N. Mass Loss: Its Effect on the Evolution and Fate of High-Mass Stars. Annu. Rev. Astron. Astrophys. 2014, 52, 487–528. [Google Scholar] [CrossRef]
- Ruffini, R.; Rueda, J.A.; Muccino, M.; Aimuratov, Y.; Becerra, L.M.; Bianco, C.L.; Kovacevic, M.; Moradi, R.; Oliveira, F.G.; Pisani, G.B.; et al. On the Classification of GRBs and Their Occurrence Rates. Astrophys. J. Lett. 2016, 832, 136. [Google Scholar] [CrossRef]
- Rueda, J.A.; Aimuratov, Y.; de Almeida, U.B.; Becerra, L.; Bianco, C.L.; Cherubini, C.; Filippi, S.; Karlica, M.; Kovacevic, M.; Fuksman, J.D.M.; et al. The binary systems associated with short and long Gamma-ray bursts and their detectability. Int. J. Mod. Phys. D 2017, 26, 1730016. [Google Scholar] [CrossRef]
- Ruffini, R.; Rodriguez, J.; Muccino, M.; Rueda, J.A.; Aimuratov, Y.; Barres de Almeida, U.; Becerra, L.; Bianco, C.L.; Cherubini, C.; Filippi, S.; et al. On the Rate and on the Gravitational Wave Emission of Short and Long GRBs. Astrophys. J. Lett. 2018, 859, 30. [Google Scholar] [CrossRef]
- Ruffini, R.; Moradi, R.; Wang, Y.; Aimuratov, Y.; Amiri, M.; Becerra, L.; Bianco, C.L.; Chen, Y.C.; Eslam Panah, B.; Mathews, G.J.; et al. On the universal GeV emission in binary-driven hypernovae and their inferred morphological structure. arXiv 2018, arXiv:1803.05476. [Google Scholar]
- Wang, Y.; Rueda, J.A.; Ruffini, R.; Becerra, L.; Bianco, C.; Becerra, L.; Li, L.; Karlica, M. Two Predictions of Supernova: GRB 130427A/SN 2013cq and GRB 180728A/SN 2018fip. Astrophys. J. Lett. 2019, 874, 39. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R.; Wang, Y.; Aimuratov, Y.; Barres de Almeida, U.; Bianco, C.L.; Chen, Y.C.; Lobato, R.V.; Maia, C.; Primorac, D.; et al. GRB 170817A-GW170817-AT 2017gfo and the observations of NS-NS, NS-WD and WD-WD mergers. J. Cosmol. Astropart. Phys. 2018, 2018, 006. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R.; Wang, Y.; Bianco, C.L.; Blanco-Iglesias, J.M.; Karlica, M.; Lorén-Aguilar, P.; Moradi, R.; Sahakyan, N. Electromagnetic emission of white dwarf binary mergers. J. Cosmol. Astropart. Phys. 2019, 2019, 044. [Google Scholar] [CrossRef]
- Becerra, L.; Bianco, C.L.; Fryer, C.L.; Rueda, J.A.; Ruffini, R. On the Induced Gravitational Collapse Scenario of Gamma-ray Bursts Associated with Supernovae. Astrophys. J. Lett. 2016, 833, 107. [Google Scholar] [CrossRef]
- Becerra, L.; Cipolletta, F.; Fryer, C.L.; Rueda, J.A.; Ruffini, R. Angular Momentum Role in the Hypercritical Accretion of Binary-driven Hypernovae. Astrophys. J. Lett. 2015, 812, 100. [Google Scholar] [CrossRef]
- Postnov, K.A.; Yungelson, L.R. The Evolution of Compact Binary Star Systems. Living Rev. Relativ. 2014, 17, 3. [Google Scholar] [CrossRef]
- Fryer, C.L.; Oliveira, F.G.; Rueda, J.A.; Ruffini, R. Neutron-Star-Black-Hole Binaries Produced by Binary-Driven Hypernovae. Phys. Rev. Lett. 2015, 115, 231102. [Google Scholar] [CrossRef]
- Giacconi, R.; Ruffini, R. (Eds.) Physics and Astrophysics of Neutron Stars and Black Holes; North Holland Publishing Co.: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Belczynski, K.; Bulik, T.; Bailyn, C. The Fate of Cyg X-1: An Empirical Lower Limit on Black-hole-Neutron-star Merger Rate. Astrophys. J. Lett. 2011, 742, L2. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodríguez, L.F. Microquasars in our Galaxy. Nature 1998, 392, 673–676. [Google Scholar] [CrossRef]
- Fryer, C.L.; Woosley, S.E.; Hartmann, D.H. Formation Rates of Black Hole Accretion Disk Gamma-ray Bursts. Astrophys. J. Lett. 1999, 526, 152–177. [Google Scholar] [CrossRef]
- Li, L.X.; Paczyński, B. Transient Events from Neutron Star Mergers. Astrophys. J. Lett. 1998, 507, L59–L62. [Google Scholar] [CrossRef]
- Metzger, B.D.; Martínez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.V.; Zinner, N.T. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. MNRAS 2010, 406, 2650–2662. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; Fruchter, A.S.; Hjorth, J.; Hounsell, R.A.; Wiersema, K.; Tunnicliffe, R.L. A ‘kilonova’ associated with the short-duration γ-ray burst GRB 130603B. Nature 2013, 500, 547–549. [Google Scholar] [CrossRef]
- Berger, E.; Fong, W.; Chornock, R. An r-process Kilonova Associated with the Short-hard GRB 130603B. Astrophys. J. Lett. 2013, 774, L23. [Google Scholar] [CrossRef]
- Meszaros, P.; Rees, M.J. Poynting Jets from Black Holes and Cosmological Gamma-ray Bursts. Astrophys. J. Lett. 1997, 482, L29. [Google Scholar] [CrossRef]
- Rosswog, S.; Ramirez-Ruiz, E.; Davies, M.B. High-resolution calculations of merging neutron stars—III. Gamma-ray bursts. MNRAS 2003, 345, 1077–1090. [Google Scholar] [CrossRef]
- Lee, W.H.; Ramirez-Ruiz, E.; Page, D. Opaque or Transparent? A Link between Neutrino Optical Depths and the Characteristic Duration of Short Gamma-ray Bursts. Astrophys. J. Lett. 2004, 608, L5–L8. [Google Scholar] [CrossRef]
- Ruffini, R.; Muccino, M.; Kovacevic, M.; Oliveira, F.G.; Rueda, J.A.; Bianco, C.L.; Enderli, M.; Penacchioni, A.V.; Pisani, G.B.; Wang, Y.; et al. GRB 140619B: A short GRB from a binary neutron star merger leading to black hole formation. Astrophys. J. Lett. 2015, 808, 190. [Google Scholar] [CrossRef]
- Ruffini, R.; Muccino, M.; Aimuratov, Y.; Bianco, C.L.; Cherubini, C.; Enderli, M.; Kovacevic, M.; Moradi, R.; Penacchioni, A.V.; Pisani, G.B.; et al. GRB 090510: A Genuine Short GRB from a Binary Neutron Star Coalescing into a Kerr-Newman Black Hole. Astrophys. J. Lett. 2016, 831, 178. [Google Scholar] [CrossRef]
- Muccino, M.; Ruffini, R.; Bianco, C.L.; Izzo, L.; Penacchioni, A.V. GRB 090227B: The Missing Link between the Genuine Short and Long Gamma-ray Bursts. Astrophys. J. Lett. 2013, 763, 125. [Google Scholar] [CrossRef]
- Della Valle, M.; Chincarini, G.; Panagia, N.; Tagliaferri, G.; Malesani, D.; Testa, V.; Fugazza, D.; Campana, S.; Covino, S.; Mangano, V.; et al. An enigmatic long-lasting γ-ray burst not accompanied by a bright supernova. Nature 2006, 444, 1050. [Google Scholar] [CrossRef]
- Cadelano, M.; Pallanca, C.; Ferraro, F.R.; Salaris, M.; Dalessandro, E.; Lanzoni, B.; Freire, P.C.C. Optical Identification of He White Dwarfs Orbiting Four Millisecond Pulsars in the Globular Cluster 47 Tucanae. Astrophys. J. Lett. 2015, 812, 63. [Google Scholar] [CrossRef]
- Bildsten, L.; Cutler, C. Tidal interactions of inspiraling compact binaries. Astrophys. J. Lett. 1992, 400, 175–180. [Google Scholar] [CrossRef]
- Fryer, C.L.; Woosley, S.E.; Herant, M.; Davies, M.B. Merging White Dwarf/Black Hole Binaries and Gamma-ray Bursts. Astrophys. J. Lett. 1999, 520, 650–660. [Google Scholar] [CrossRef]
- Tauris, T.M.; van den Heuvel, E.P.J.; Savonije, G.J. Formation of Millisecond Pulsars with Heavy White Dwarf Companions:Extreme Mass Transfer on Subthermal Timescales. Astrophys. J. Lett. 2000, 530, L93–L96. [Google Scholar] [CrossRef]
- Lazarus, P.; Tauris, T.M.; Knispel, B.; Freire, P.C.C.; Deneva, J.S.; Kaspi, V.M.; Allen, B.; Bogdanov, S.; Chatterjee, S.; Stairs, I.H.; et al. Timing of a young mildly recycled pulsar with a massive white dwarf companion. MNRAS 2014, 437, 1485–1494. [Google Scholar] [CrossRef]
- Caito, L.; Bernardini, M.G.; Bianco, C.L.; Dainotti, M.G.; Guida, R.; Ruffini, R. GRB060614: A “fake” short GRB from a merging binary system. A&A 2009, 498, 501–507. [Google Scholar]
- Maoz, D.; Hallakoun, N. The binary fraction, separation distribution, and merger rate of white dwarfs from SPY. MNRAS 2017, 467, 1414–1425. [Google Scholar] [CrossRef]
- Maoz, D.; Hallakoun, N.; Badenes, C. The separation distribution and merger rate of double white dwarfs: Improved constraints. MNRAS 2018, 476, 2584–2590. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, B.; Li, Z. Extragalactic High-energy Transients: Event Rate Densities and Luminosity Functions. Astrophys. J. Lett. 2015, 812, 33. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R.; Becerra, L.M.; Fryer, C.L. Simulating the induced gravitational collapse scenario of long Gamma-ray bursts. Int. J. Mod. Phys. A 2018, 33, 1844031. [Google Scholar] [CrossRef]
- Rueda, J.A.; Ruffini, R. On the Induced Gravitational Collapse of a Neutron Star to a Black Hole by a Type Ib/c Supernova. Astrophys. J. Lett. 2012, 758, L7. [Google Scholar] [CrossRef]
- Izzo, L.; Rueda, J.A.; Ruffini, R. GRB 090618: A candidate for a neutron star gravitational collapse onto a black hole induced by a type Ib/c supernova. A&A 2012, 548, L5. [Google Scholar]
- Fryer, C.L.; Rueda, J.A.; Ruffini, R. Hypercritical Accretion, Induced Gravitational Collapse, and Binary-Driven Hypernovae. Astrophys. J. Lett. 2014, 793, L36. [Google Scholar] [CrossRef]
- Ruffini, R.; Rueda, J.A.; Becerra, L.; Bianco, C.L.; Chen, Y.C.; Cherubini, C.; Filippi, S.; Karlica, M.; Melon Fuksman, J.D.; Moradi, R.; et al. The inner engine of GeV-radiation-emitting Gamma-ray bursts. arXiv 2018, arXiv:1811.01839. [Google Scholar]
- Ruffini, R.; Moradi, R.; Rueda, J.A.; Becerra, L.; Bianco, C.L.; Cherubini, C.; Filippi, S.; Chen, Y.C.; Karlica, M.; Sahakyan, N.; et al. On the GeV emission of the type I BdHN GRB 130427A. arXiv 2018, arXiv:1812.00354. [Google Scholar]
- Ruffini, R.; Li, L.; Moradi, R.; Rueda, J.A.; Wang, Y.; Xue, S.S.; Bianco, C.L.; Campion, S.; Melon Fuksman, J.D.; Cherubini, C.; et al. Self-similarity and power-laws in GRB 190114C. arXiv 2019, arXiv:1904.04162. [Google Scholar]
- Ruffini, R.; Melon Fuksman, J.D.; Vereshchagin, G.V. On the role of a cavity in the hypernova ejecta of GRB190114C. arXiv 2019, arXiv:1904.03163. [Google Scholar]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Ruffini, R.; Becerra, L.; Bianco, C.L.; Chen, Y.C.; Karlica, M.; Kovačević, M.; Melon Fuksman, J.D.; Moradi, R.; Muccino, M.; Pisani, G.B.; et al. On the Ultra-relativistic Prompt Emission, the Hard and Soft X-Ray Flares, and the Extended Thermal Emission in GRB 151027A. Astrophys. J. Lett. 2018, 869, 151. [Google Scholar] [CrossRef]
- Becerra, L.; Ellinger, C.L.; Fryer, C.L.; Rueda, J.A.; Ruffini, R. SPH Simulations of the Induced Gravitational Collapse Scenario of Long Gamma-ray Bursts Associated with Supernovae. Astrophys. J. Lett. 2019, 871, 14. [Google Scholar] [CrossRef]
- Ruffini, R.; Karlica, M.; Sahakyan, N.; Rueda, J.A.; Wang, Y.; Mathews, G.J.; Bianco, C.L.; Muccino, M. A GRB Afterglow Model Consistent with Hypernova Observations. Astrophys. J. Lett. 2018, 869, 101. [Google Scholar] [CrossRef]
- Fryer, C.; Benz, W.; Herant, M.; Colgate, S.A. What Can the Accretion-induced Collapse of White Dwarfs Really Explain? Astrophys. J. Lett. 1999, 516, 892–899. [Google Scholar] [CrossRef]
- Becerra, L.; Guzzo, M.M.; Rossi-Torres, F.; Rueda, J.A.; Ruffini, R.; Uribe, J.D. Neutrino Oscillations within the Induced Gravitational Collapse Paradigm of Long Gamma-ray Bursts. Astrophys. J. Lett. 2018, 852, 120. [Google Scholar] [CrossRef]
- Cipolletta, F.; Cherubini, C.; Filippi, S.; Rueda, J.A.; Ruffini, R. Last stable orbit around rapidly rotating neutron stars. PRD 2017, 96, 024046. [Google Scholar] [CrossRef]
- Cipolletta, F.; Cherubini, C.; Filippi, S.; Rueda, J.A.; Ruffini, R. Fast rotating neutron stars with realistic nuclear matter equation of state. Phys. Rev. D 2015, 92, 023007. [Google Scholar] [CrossRef]
- Fryer, C.L.; Benz, W.; Herant, M. The Dynamics and Outcomes of Rapid Infall onto Neutron Stars. Astrophys. J. Lett. 1996, 460, 801. [Google Scholar] [CrossRef]
- Chevalier, R.A. Neutron star accretion in a supernova. Astrophys. J. Lett. 1989, 346, 847–859. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Ivanova, L.N.; Nadezhin, D.K. Nonstationary Hydrodynamical Accretion onto a Neutron Star. Sov. Astron. 1972, 16, 209. [Google Scholar]
- Ruffini, R.; Wilson, J. Possibility of Neutrino Emission from Matter Accreting into a Neutron Star. Phys. Rev. Lett. 1973, 31, 1362–1364. [Google Scholar] [CrossRef]
- Fryer, C.L.; Herwig, F.; Hungerford, A.; Timmes, F.X. Supernova Fallback: A Possible Site for the r-Process. Astrophys. J. Lett. 2006, 646, L131–L134. [Google Scholar] [CrossRef]
- Fryer, C.L. Neutrinos from Fallback onto Newly Formed Neutron Stars. Astrophys. J. Lett. 2009, 699, 409–420. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Kaminker, A.D.; Gnedin, O.Y.; Haensel, P. Neutrino emission from neutron stars. Phys. Rep. 2001, 354, 1–155. [Google Scholar] [CrossRef]
- Fryer, C.L.; Rockefeller, G.; Warren, M.S. SNSPH: A Parallel Three-dimensional Smoothed Particle Radiation Hydrodynamics Code. Astrophys. J. Lett. 2006, 643, 292–305. [Google Scholar] [CrossRef]
- Fryer, C.L.; Warren, M.S. Modeling Core-Collapse Supernovae in Three Dimensions. Astrophys. J. Lett. 2002, 574, L65–L68. [Google Scholar] [CrossRef]
- Young, P.A.; Fryer, C.L.; Hungerford, A.; Arnett, D.; Rockefeller, G.; Timmes, F.X.; Voit, B.; Meakin, C.; Eriksen, K.A. Constraints on the Progenitor of Cassiopeia A. Astrophys. J. Lett. 2006, 640, 891–900. [Google Scholar] [CrossRef]
- Diehl, S.; Fryer, C.; Herwig, F. The Formation of Hydrogen Deficient Stars through Common Envelope Evolution. Hydrogen-Deficient Stars. In Astronomical Society of the Pacific Conference Series; Werner, A., Rauch, T., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2008; Volume 391, p. 221. [Google Scholar]
- Batta, A.; Ramirez-Ruiz, E.; Fryer, C. The Formation of Rapidly Rotating Black Holes in High-mass X-ray Binaries. Astrophys. J. Lett. 2017, 846, L15. [Google Scholar] [CrossRef]
- Arnett, D. Supernovae and Nucleosynthesis: An Investigation of the History of Matter from the Big Bang to the Present; Princeton University Press: Princeton, NJ, USA, 1996. [Google Scholar]
- Ruffini, R.; Vereshchagin, G.; Xue, S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1–140. [Google Scholar] [CrossRef]
- Preparata, G.; Ruffini, R.; Xue, S.S. The dyadosphere of black holes and Gamma-ray bursts. A&A 1998, 338, L87–L90. [Google Scholar]
- Ruffini, R.; Salmonson, J.D.; Wilson, J.R.; Xue, S.S. On evolution of the pair-electromagnetic pulse of a charged black hole. Astron. Astrophys. Suppl. 1999, 138, 511–512. [Google Scholar] [CrossRef]
- Penacchioni, A.V.; Ruffini, R.; Izzo, L.; Muccino, M.; Bianco, C.L.; Caito, L.; Patricelli, B.; Amati, L. Evidence for a proto-black hole and a double astrophysical component in GRB 101023. A&A 2012, 538, A58. [Google Scholar]
- Patricelli, B.; Bernardini, M.G.; Bianco, C.L.; Caito, L.; de Barros, G.; Izzo, L.; Ruffini, R.; Vereshchagin, G.V. Analysis of GRB 080319B and GRB 050904 within the Fireshell Model: Evidence for a Broader Spectral Energy Distribution. Astrophys. J. Lett. 2012, 756, 16. [Google Scholar] [CrossRef]
- Woosley, S.E. Gamma-ray bursts from stellar mass accretion disks around black holes. Astrophys. J. Lett. 1993, 405, 273–277. [Google Scholar] [CrossRef]
- Starling, R.L.C.; Page, K.L.; Pe’Er, A.; Beardmore, A.P.; Osborne, J.P. A search for thermal X-ray signatures in Gamma-ray bursts - I. Swift bursts with optical supernovae. MNRAS 2012, 427, 2950–2964. [Google Scholar] [CrossRef]
- Wang, Y.; Aimuratov, Y.; Moradi, R.; Peresano, M.; Ruffini, R.; Shakeri, S. Revisiting the statistics of X-ray flares in Gamma-ray bursts. Mem. Soc. Astron. Ital. 2018, 89, 293. [Google Scholar]
- Ruffini, R.; Muccino, M.; Bianco, C.L.; Enderli, M.; Izzo, L.; Kovacevic, M.; Penacchioni, A.V.; Pisani, G.B.; Rueda, J.A.; Wang, Y. On binary-driven hypernovae and their nested late X-ray emission. A&A 2014, 565, L10. [Google Scholar]
- Page, K.L.; Starling, R.L.C.; Fitzpatrick, G.; Pandey, S.B.; Osborne, J.P.; Schady, P.; McBreen, S.; Campana, S.; Ukwatta, T.N.; Pagani, C.; et al. GRB 090618: Detection of thermal X-ray emission from a bright Gamma-ray burst. MNRAS 2011, 416, 2078–2089. [Google Scholar] [CrossRef]
- Ruffini, R.; Wang, Y.; Enderli, M.; Muccino, M.; Kovacevic, M.; Bianco, C.L.; Penacchioni, A.V.; Pisani, G.B.; Rueda, J.A. GRB 130427A and SN 2013cq: A Multi-wavelength Analysis of An Induced Gravitational Collapse Event. Astrophys. J. Lett. 2015, 798, 10. [Google Scholar] [CrossRef]
- Wang, Y.; Ruffini, R.; Kovacevic, M.; Bianco, C.L.; Enderli, M.; Muccino, M.; Penacchioni, A.V.; Pisani, G.B.; Rueda, J.A. Predicting supernova associated to Gamma-ray burst 130427a. Astron. Rep. 2015, 59, 667–671. [Google Scholar] [CrossRef]
- Dominik, M.; Belczynski, K.; Fryer, C.; Holz, D.E.; Berti, E.; Bulik, T.; Mandel, I.; O’Shaughnessy, R. Double Compact Objects. I. The Significance of the Common Envelope on Merger Rates. Astrophys. J. Lett. 2012, 759, 52. [Google Scholar] [CrossRef]
- Hills, J.G. The effects of sudden mass loss and a random kick velocity produced in a supernova explosion on the dynamics of a binary star of arbitrary orbital eccentricity—Applications to X-ray binaries and to the binary pulsars. Astrophys. J. Lett. 1983, 267, 322–333. [Google Scholar] [CrossRef]
- Tauris, T.M.; Langer, N.; Podsiadlowski, P. Ultra-stripped supernovae: Progenitors and fate. MNRAS 2015, 451, 2123–2144. [Google Scholar] [CrossRef]
- Tauris, T.M.; Langer, N.; Moriya, T.J.; Podsiadlowski, P.; Yoon, S.C.; Blinnikov, S.I. Ultra-stripped Type Ic Supernovae from Close Binary Evolution. Astrophys. J. Lett. 2013, 778, L23. [Google Scholar] [CrossRef]
- Guetta, D.; Della Valle, M. On the Rates of Gamma-ray Bursts and Type Ib/c Supernovae. Astrophys. J. Lett. 2007, 657, L73–L76. [Google Scholar] [CrossRef]
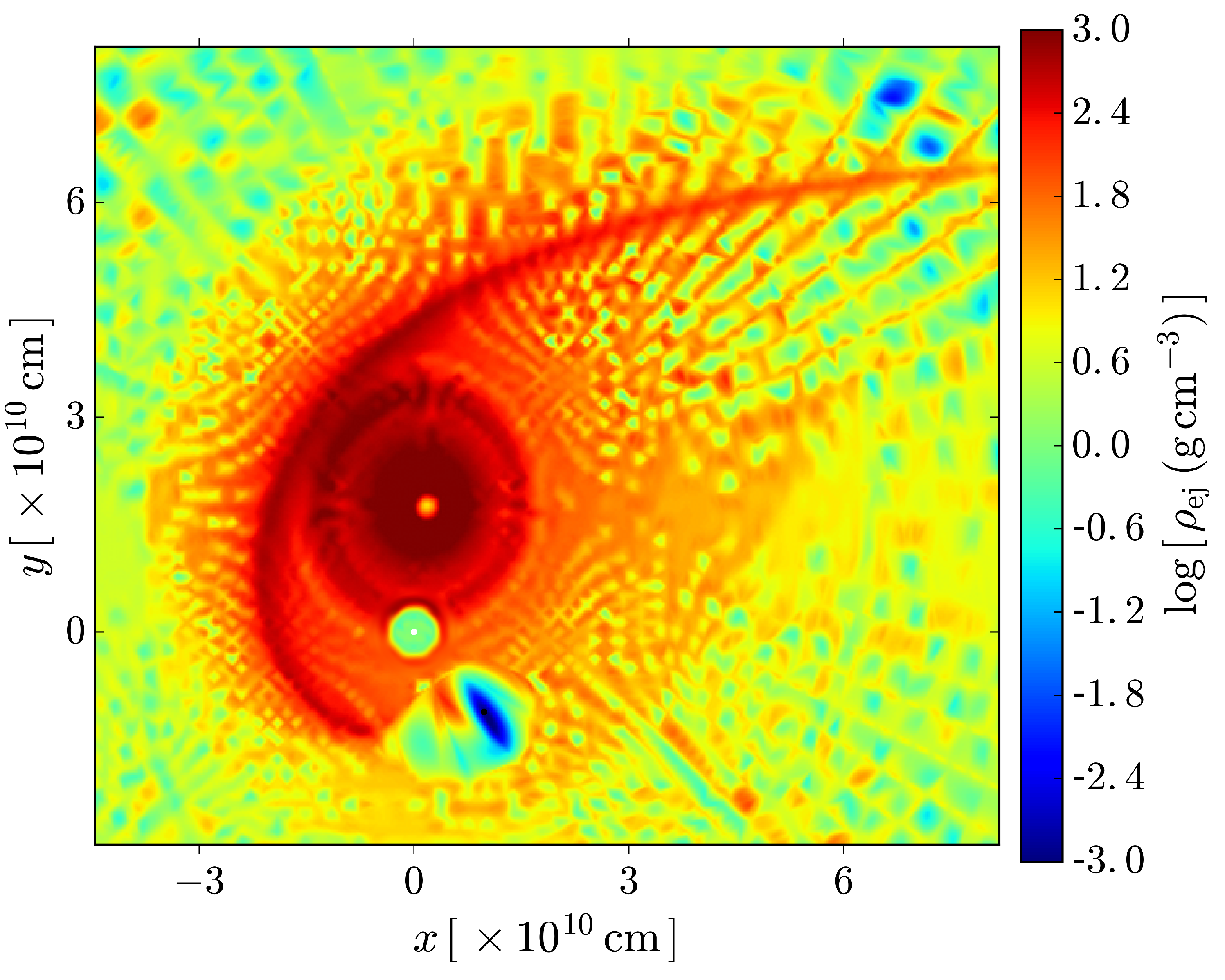
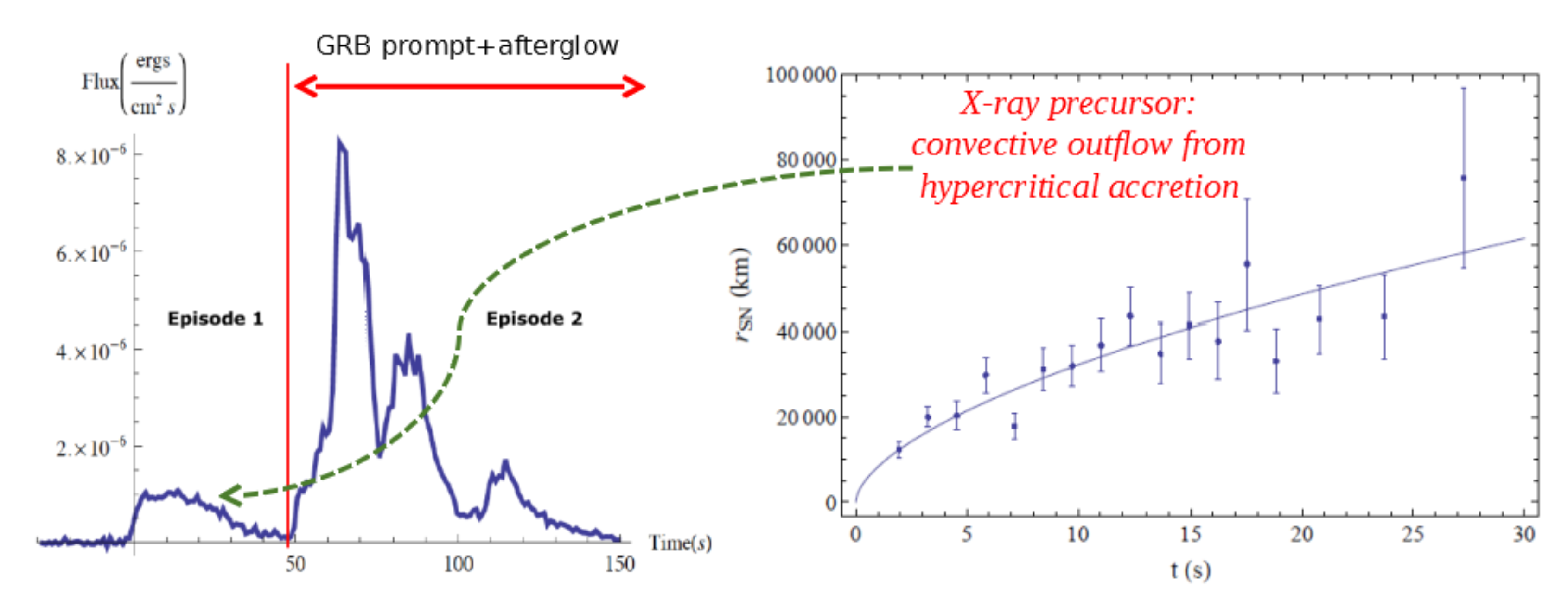
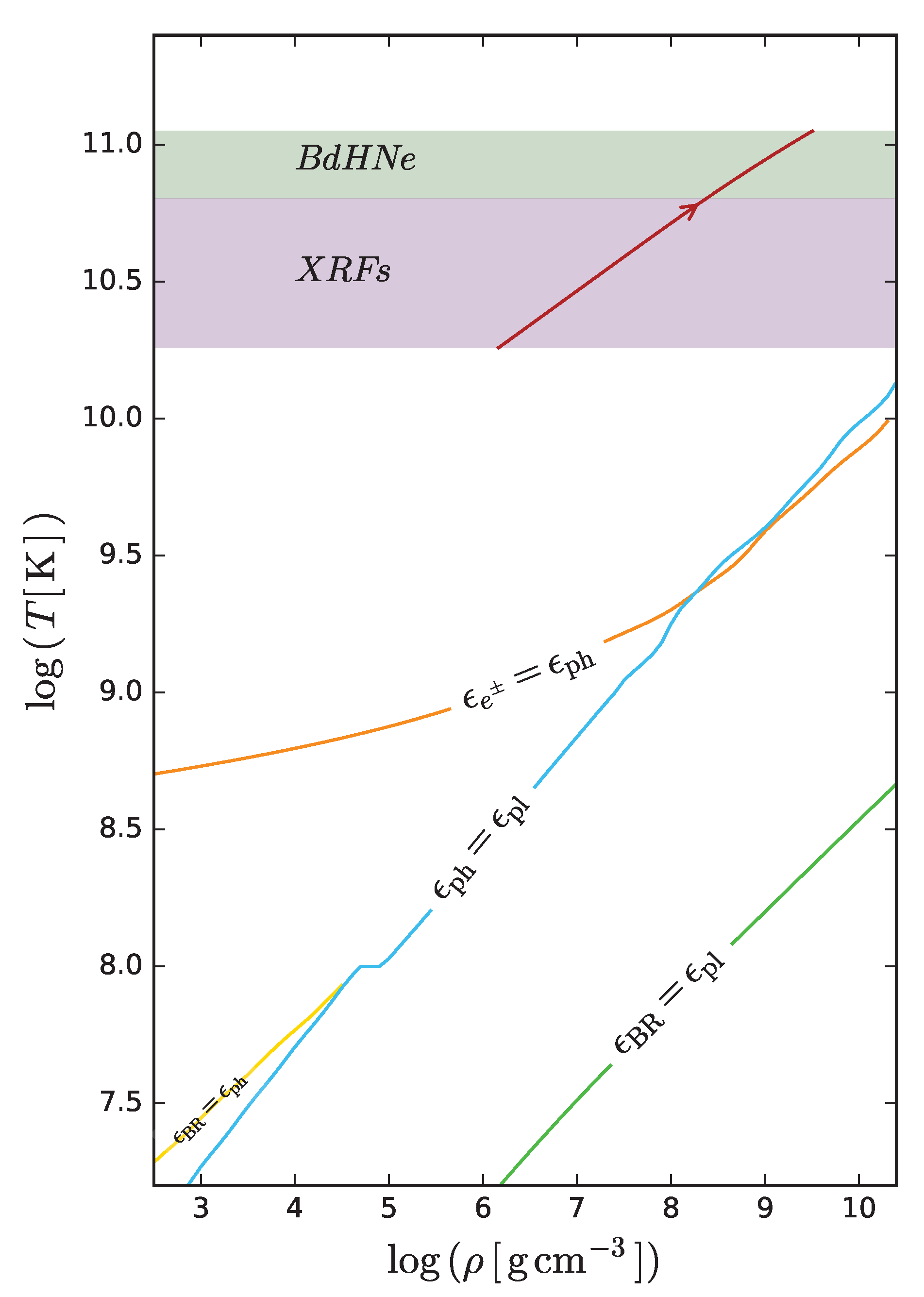
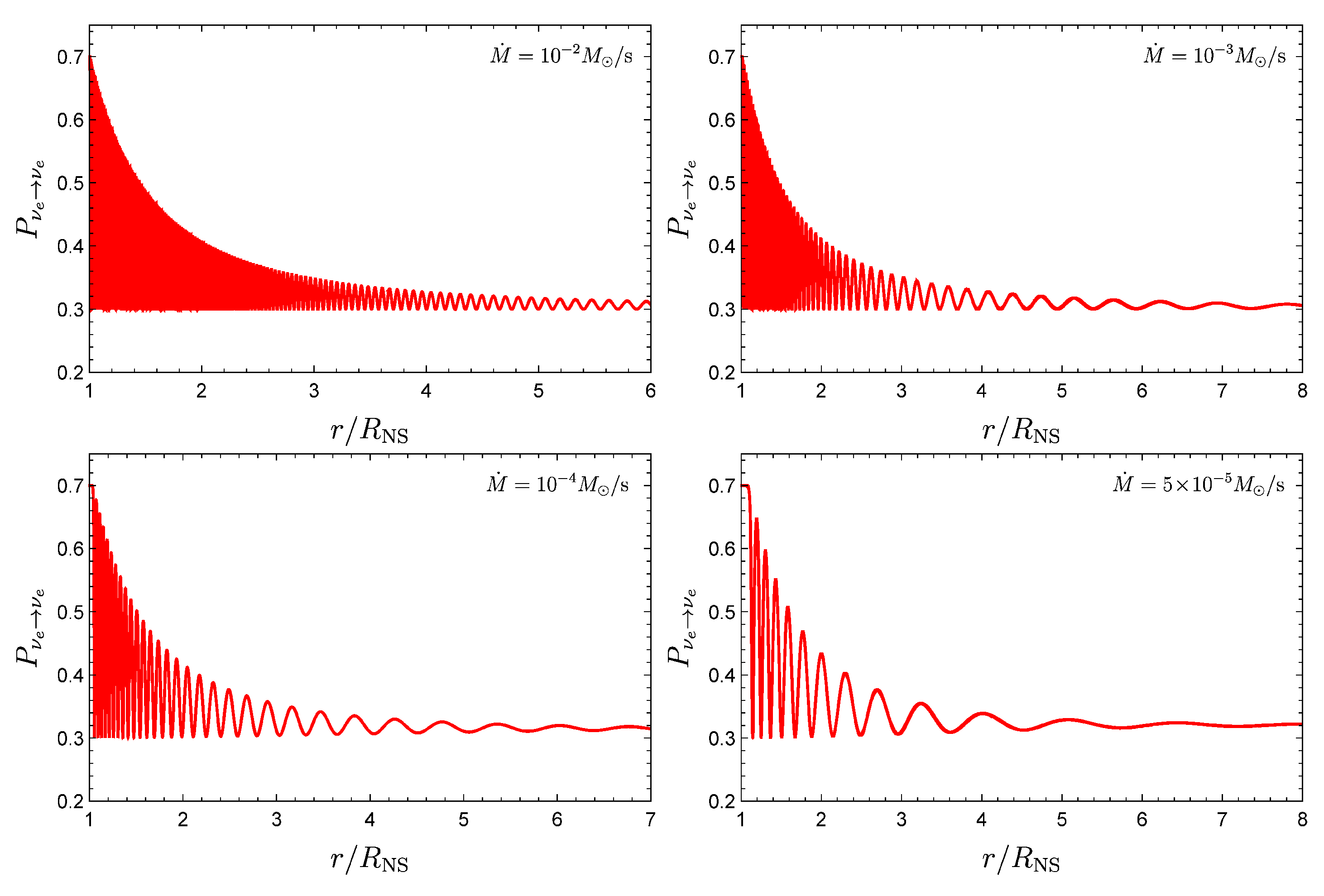
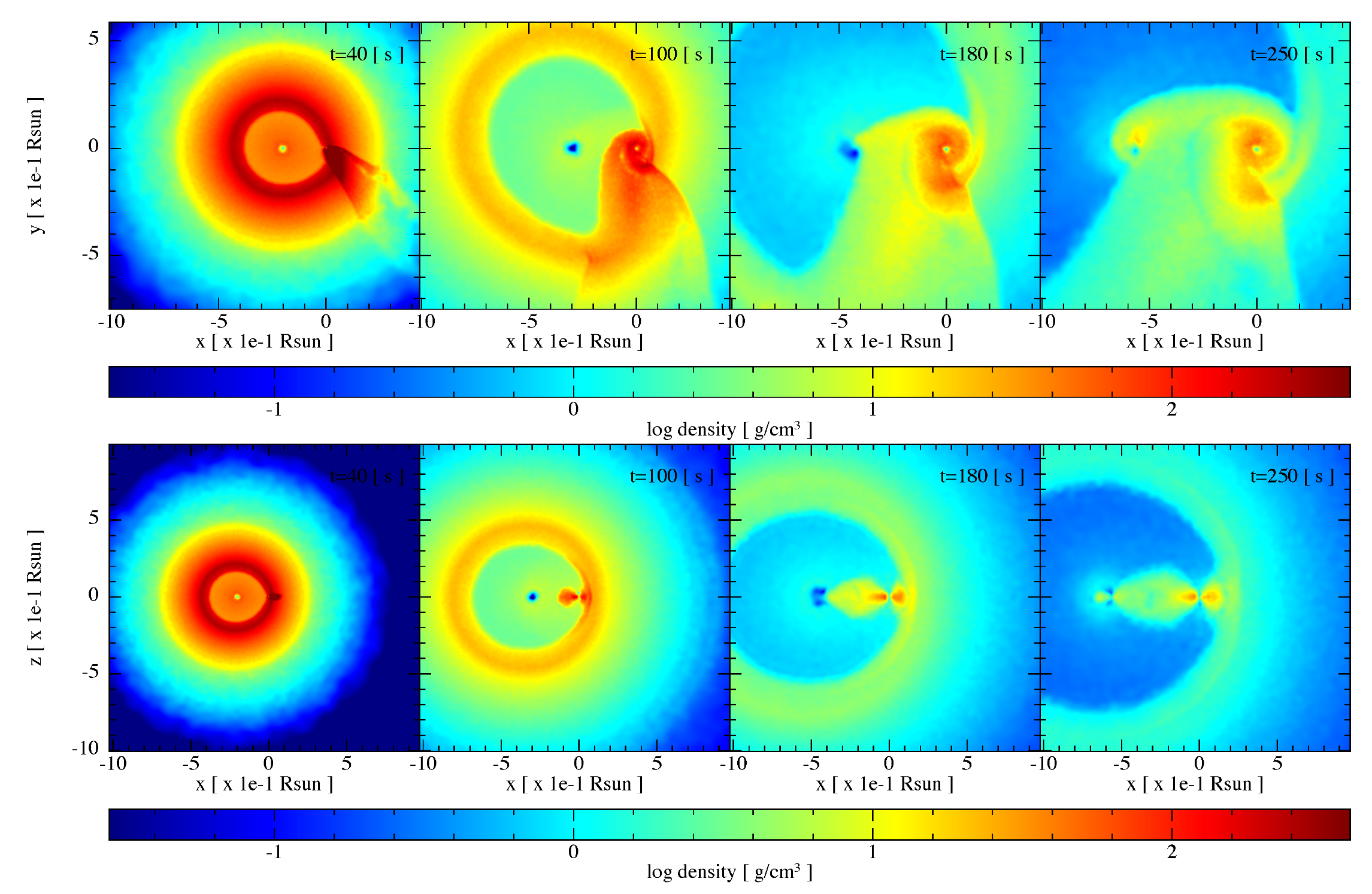
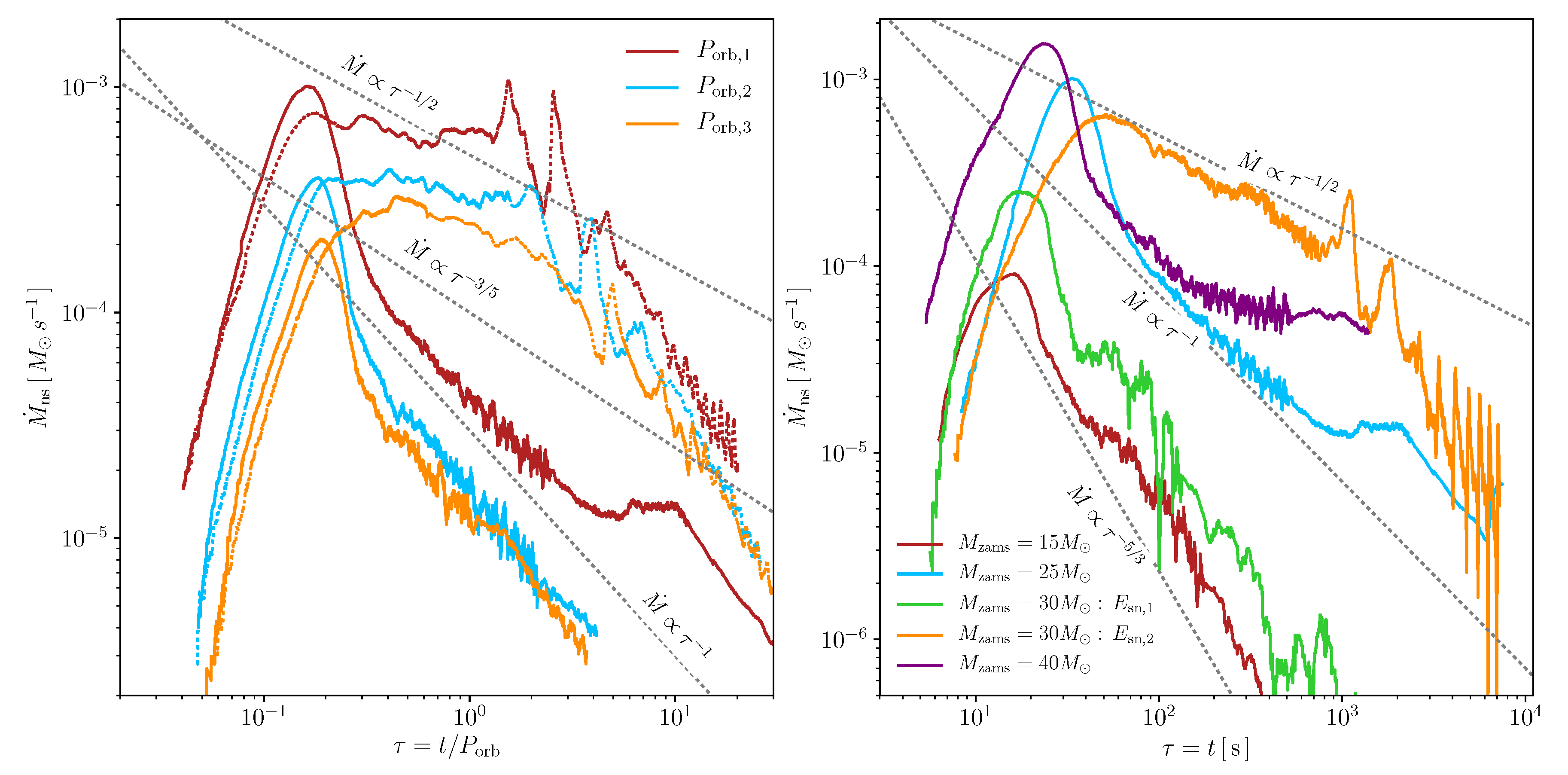
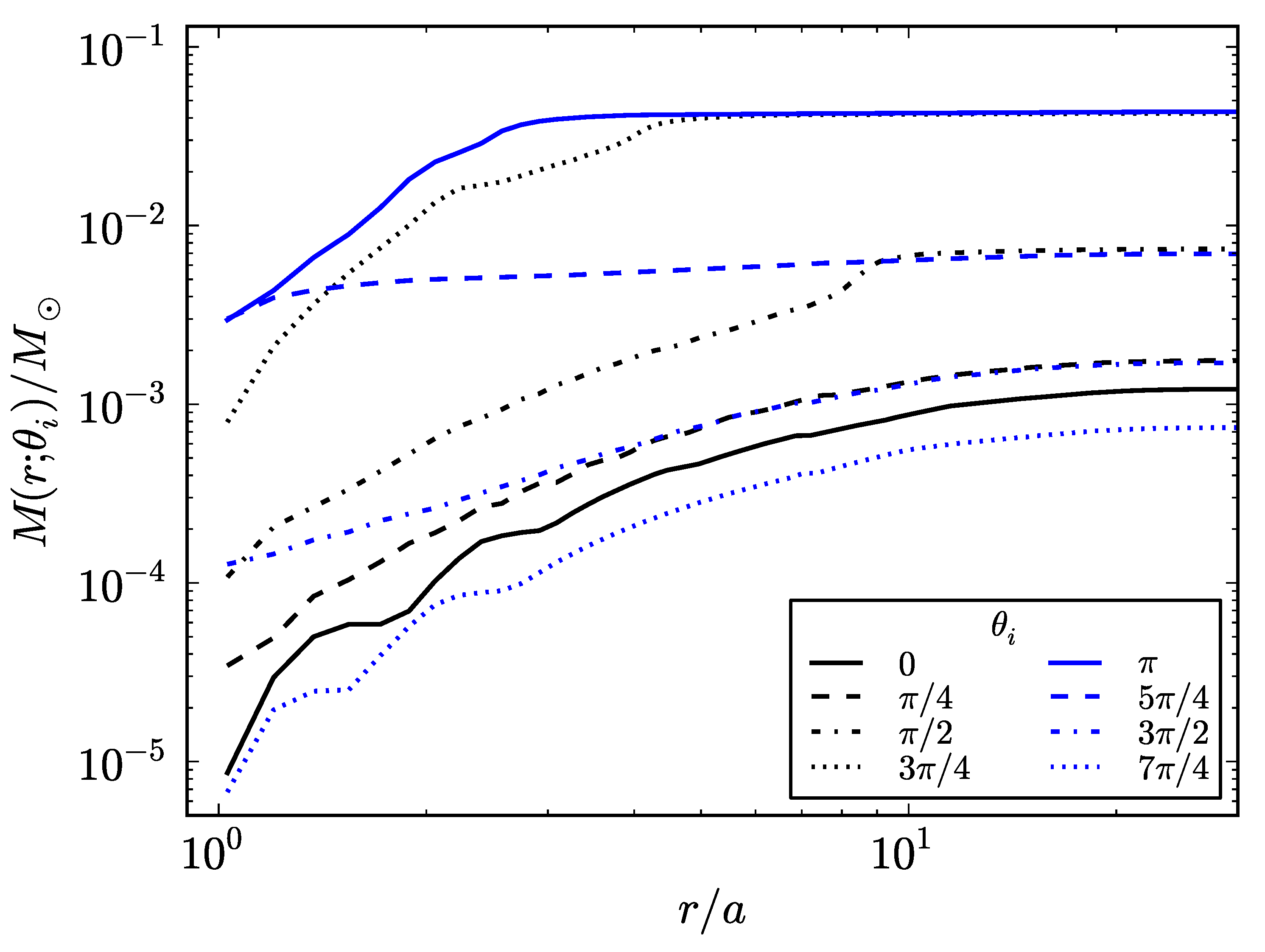
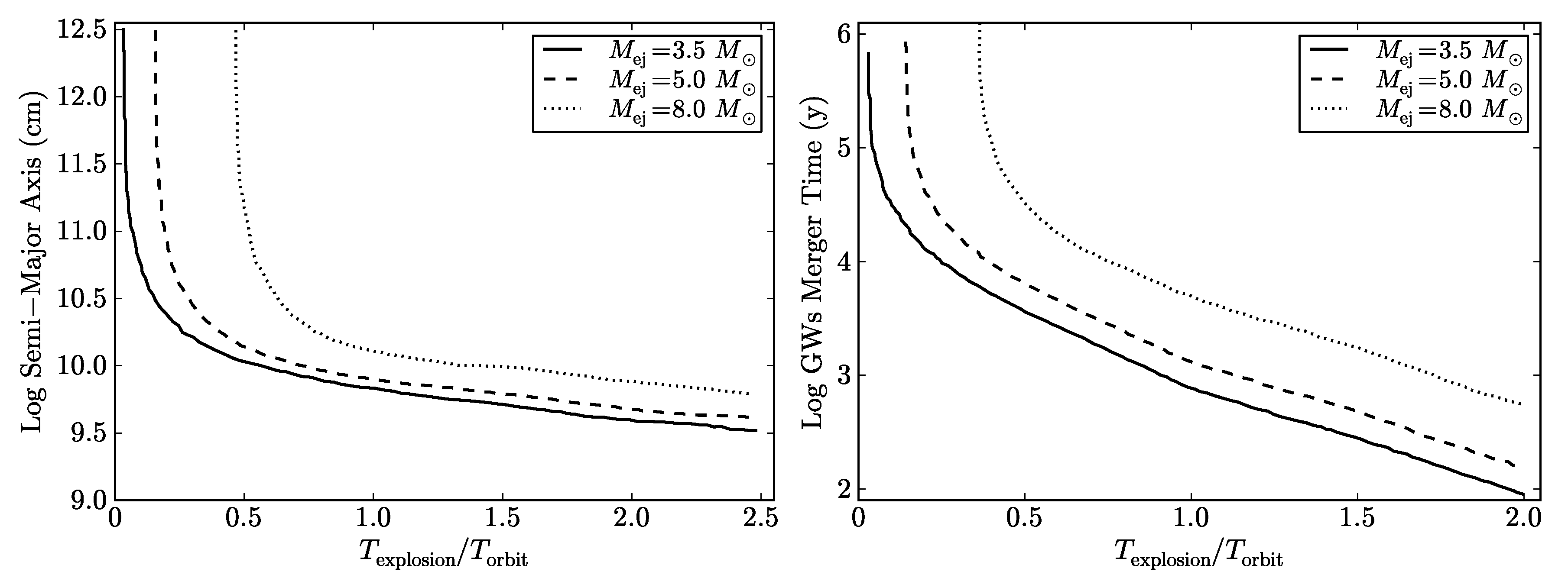
| Class | Type | Previous Alias | Number | In-State | Out-State | (MeV) | (erg) | (Gpc yr) | |
|---|---|---|---|---|---|---|---|---|---|
| Binary-driven | I | BdHN | 329 | CO-NS | NS-BH | ∼0.2–2 | ∼10– | ≳10 | |
| hypernova | II | XRF | CO-NS | NS-NS | ∼0.01– | ∼10– | − | ||
| (BdHN) | III | HN | CO-NS | NS-NS | ∼0.01 | ∼10– | − | − | |
| IV | BH-SN | 5 | CO-BH | NS-BH | ≳2 | >10 | ≳10 | ≲0.77 | |
| I | S-GRF | 18 | NS-NS | MNS | ∼0.2–2 | ∼10– | − | ||
| Binary | II | S-GRB | 6 | NS-NS | BH | ∼2–8 | ∼10– | ≳10 | |
| Merger | III | GRF | NS-WD | MNS | ∼0.2–2 | ∼10– | − | ||
| (BM) | IV | FB-KN | WD-WD | NS/MWD | <0.2 | <10 | − | − | |
| V | U-GRB | NS-BH | BH | ≳2 | >10 | − | ≈0.77 |
| Extended Wording | Acronym |
|---|---|
| Binary-driven hypernova | BdHN |
| Black hole | BH |
| Carbon-oxygen core | CO |
| Gamma-ray burst | GRB |
| Gamma-ray flash | GRF |
| Induced gravitational collapse | IGC |
| Massive neutron star | MNS |
| Neutron star | NS |
| New neutron star created in the SN explosion | NS |
| Short Gamma-ray burst | S-GRB |
| Short Gamma-ray flash | S-GRF |
| Supernova | SN |
| Ultrashort Gamma-ray burst | U-GRB |
| Ultra high-energy cosmic ray | UHECR |
| White dwarf | WD |
| X-ray flash | XRF |
| EOS | p | k | |
|---|---|---|---|
| NL3 | |||
| GM1 | |||
| TM1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rueda, J.A.; Ruffini, R.; Wang, Y. Induced Gravitational Collapse, Binary-Driven Hypernovae, Long Gramma-ray Bursts and Their Connection with Short Gamma-ray Bursts. Universe 2019, 5, 110. https://doi.org/10.3390/universe5050110
Rueda JA, Ruffini R, Wang Y. Induced Gravitational Collapse, Binary-Driven Hypernovae, Long Gramma-ray Bursts and Their Connection with Short Gamma-ray Bursts. Universe. 2019; 5(5):110. https://doi.org/10.3390/universe5050110
Chicago/Turabian StyleRueda, J. A., R. Ruffini, and Y. Wang. 2019. "Induced Gravitational Collapse, Binary-Driven Hypernovae, Long Gramma-ray Bursts and Their Connection with Short Gamma-ray Bursts" Universe 5, no. 5: 110. https://doi.org/10.3390/universe5050110
APA StyleRueda, J. A., Ruffini, R., & Wang, Y. (2019). Induced Gravitational Collapse, Binary-Driven Hypernovae, Long Gramma-ray Bursts and Their Connection with Short Gamma-ray Bursts. Universe, 5(5), 110. https://doi.org/10.3390/universe5050110





