The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine
Abstract
:1. Introduction
- The flares rise rapidly with the rise time of only about a few days. In contrast, the timescales associated with processes like jet turning are several months to years.
- A natural (and powerful) feature of the BBH impact model is its accurate predictive power. Indeed, the model accurately predicted the starting times for the widely observed 1995, 2005, 2007 and 2015 outbursts [8,20,21,22]. It is rather difficult to make testable predictions using the alternative models for OJ 287 as they assume that the flares are strictly periodic which puts the prediction off by up to several years. Random deviations around the strictly periodic times do not suit either, as the deviations are predictable.
2. Construction of the BBH Central Engine Model for OJ 287
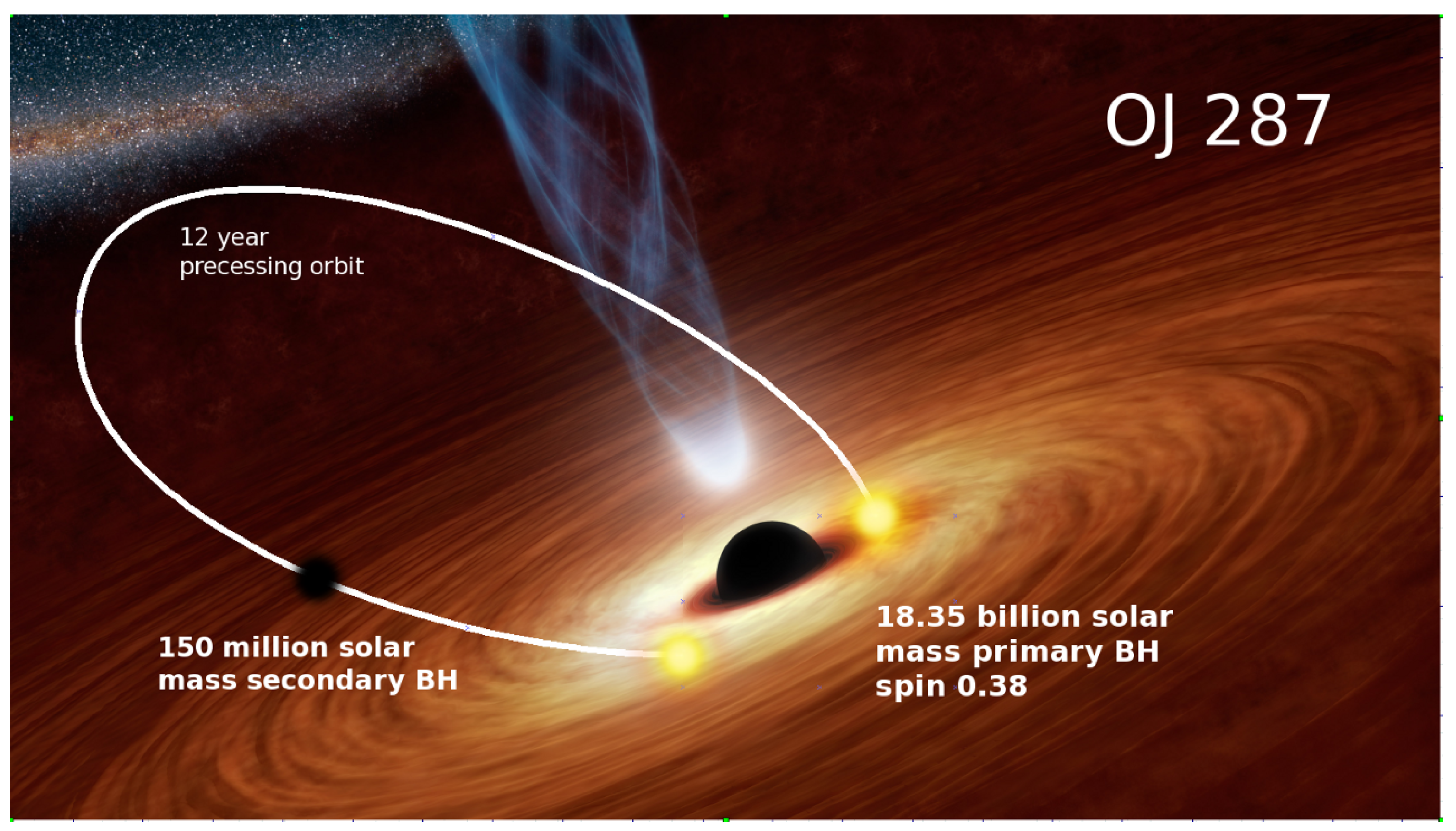
2.1. Elements of the BBH Model from Astrophysical Considerations
2.2. Details of BBH Central Engine from the Timing of Impact Outbursts
2.3. General Relativistic Orbital Trajectory for the Secondary BH
2.4. The Most up to Date Description of the BBH Central Engine
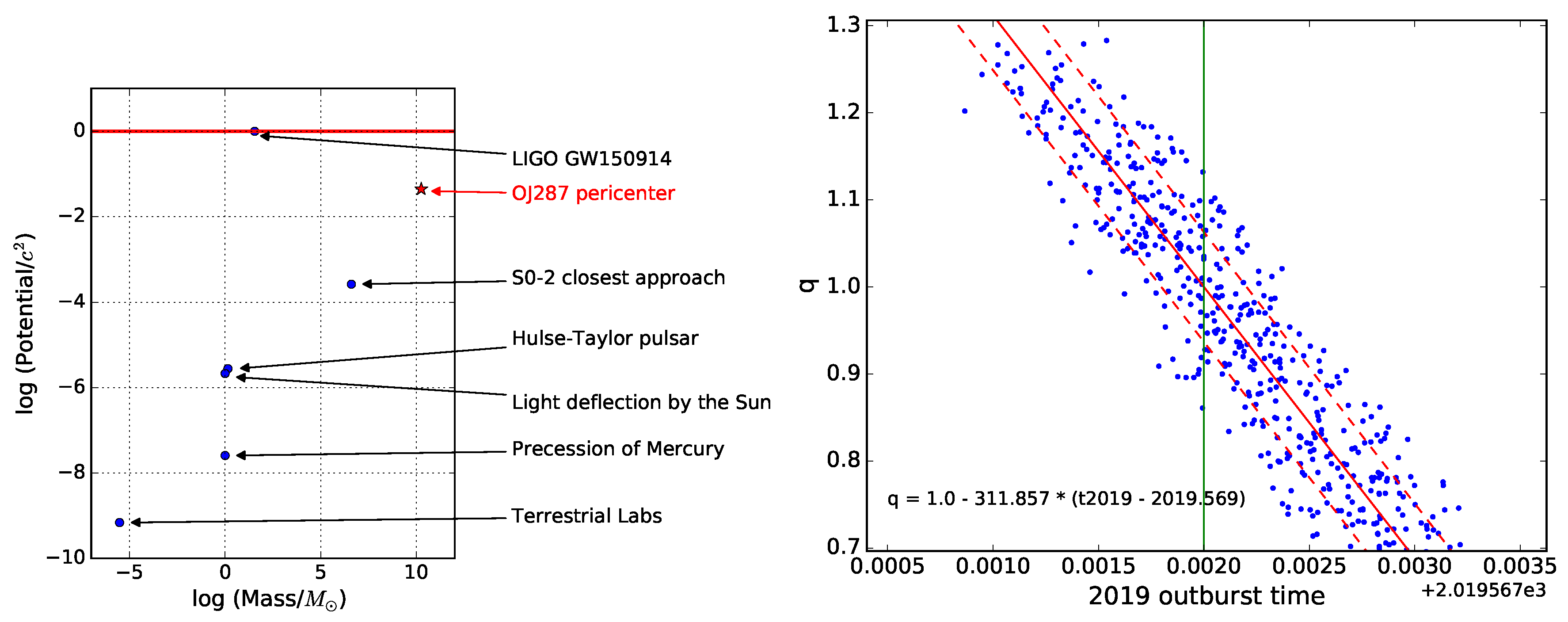
3. Tests of GR Using OJ 287
3.1. First Indirect Evidence for GW Emission from BH-BH Binaries
3.2. Testing the BH ‘No-hair’ Theorem during the Present Decade
4. Describing OJ 287’s BBH Dynamics via GW Phasing Prescription for Eccentric Binaries
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GW | Gravitational Wave |
| SMBBH | Supermassive binary black hole |
| BBH | Binary black hole |
| SMBH | Supermassive black hole |
| AGN | Active galactic nucleus |
| LC | Light curve |
| GR | General Relativity |
Appendix A. Alternative Models for OJ 287
References
- Kormendy, J.; Richstone, D. Inward Bound—The Search For Supermassive Black Holes in Galactic Nuclei. Annu. Rev. Astron. Astrophys. 1995, 33, 581. [Google Scholar] [CrossRef]
- Ferrarese, L.; Ford, H. Supermassive Black Holes in Galactic Nuclei: Past, Present and Future Research. Space Sci. Rev. 2005, 116, 523–624. [Google Scholar] [CrossRef] [Green Version]
- Graham, A.W. Galaxy Bulges and Their Massive Black Holes: A Review. Galact. Bulges 2016, 418, 263–313. [Google Scholar] [Green Version]
- Kembhavi, A.K.; Narlikar, J.V. Quasars and Active Galactic Nuclei: An Introduction; Cambridge University Press: Cambridge, UK, 1999; ISBN 0521474779. [Google Scholar]
- Begelman, M.C.; Blandford, R.D.; Rees, M.J. Massive black hole binaries in active galactic nuclei. Nature 1980, 287, 307. [Google Scholar] [CrossRef]
- Merritt, D.; Milosavljević, M. Massive Black Hole Binary Evolution. Living Rev. Relativ. 2005, 8, 8. [Google Scholar] [CrossRef]
- Komossa, S.; Zensus, J.A. Compact object mergers: Observations of supermassive binary black holes and stellar tidal disruption events. Star Clust. Black Holes Galaxies across Cosm. Time 2016, 312, 13. [Google Scholar] [CrossRef]
- Lehto, H.J.; Valtonen, M.J. OJ 287 Outburst Structure and a Binary Black Hole Model. Astrophys. J. 1996, 460, 207. [Google Scholar] [CrossRef]
- Dey, L.; Valtonen, M.J.; Gopakumar, A.; Zola, S.; Hudec, R.; Pihajoki, P.; Ciprini, S.; Matsumoto, K.; Sadakane, K.; Kidger, M.; et al. Authenticating the Presence of a Relativistic Massive Black Hole Binary in OJ 287 Using Its General Relativity Centenary Flare: Improved Orbital Parameters. Astrophys. J. 2018, 866, 11. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Sillanpää, A.; Haarala, S.; Valtaoja, L.; Valtaoja, E.; Sundelius, B.; Byrd, G.G.; Teräsranta, H.; Urpo, S. OJ 287 as a Binary System. In Active Galactic Nuclei, Proceedings of the Conference Held at the Georgia State University, Atlanta, GA, USA, 28–30 October 1987; Miller, H.R., Wiita, P.J., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany; New York, NY, USA, 1988; Volume 307, p. 68. [Google Scholar]
- Sillanpää, A.; Haarala, S.; Valtonen, M.J.; Sundelius, B.; Byrd, G.G. OJ 287—Binary pair of supermassive black holes. Astrophys. J. 1988, 325, 628. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Sillanpää, A.; Nilsson, K.; Mikkola, S.; Hudec, R.; Basta, M.; Teräsranta, H.; Haque, S.; Rampadarath, H. Predicting the Next Outbursts of OJ 287 in 2006–2010. Astrophys. J. 2006, 646, 36. [Google Scholar] [CrossRef]
- Sundelius, B.; Wahde, M.; Lehto, H.J.; Valtonen, M.J. A Numerical Simulation of the Brightness Variations of OJ 287. Astrophys. J. 1997, 484, 180. [Google Scholar] [CrossRef]
- Ivanov, P.B.; Igumenshchev, I.V.; Novikov, I.D. Hydrodynamics of Black Hole-Accretion Disk Collision. Astrophys. J. 1998, 507, 131. [Google Scholar] [CrossRef]
- Pihajoki, P. Black hole accretion disc impacts. Mon. Not. R. Astron. Soc. 2016, 457, 1145. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Ciprini, S.; Lehto, H.J. On the masses of OJ287 black holes. Mon. Not. R. Astron. Soc. 2012, 427, 77. [Google Scholar] [CrossRef]
- Katz, J.I. A Precessing Disk in OJ 287? Astrophys. J. 1997, 478, 527. [Google Scholar] [CrossRef]
- Tanaka, T.L. Recurring flares from supermassive black hole binaries: Implications for tidal disruption candidates and OJ 287. Mon. Not. R. Astron. Soc. 2013, 434, 2275. [Google Scholar] [CrossRef]
- Britzen, S.; Fendt, C.; Witzel, G.; Qian, S.-J.; Pashchenko, I.N.; Kurtanidze, O.; Zajacek, M.; Martinez, G.; Karas, V.; Aller, M.; et al. OJ287: Deciphering the ‘Rosetta stone of blazars. Mon. Not. R. Astron. Soc. 2018, 478, 3199. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Nilsson, K.; Heidt, J.; Takalo, L.O.; Sillanpää, A.; Villforth, C.; Kidger, M.; Poyner, G.; Pursimo, T.; et al. A massive binary black-hole system in OJ287 and a test of general relativity. Nature 2008, 452, 851. [Google Scholar] [CrossRef] [PubMed]
- Valtonen, M.; Zola, S.; Jermak, H.; Ciprini, S.; Hudec, R.; Dey, L.; Gopakumar, A.; Reichart, D.L.; Caton, D.B.; Gazeas, K.; et al. Polarization and Spectral Energy Distribution in OJ 287 during the 2016/17 Outbursts. Galaxies 2017, 5, 83. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Zola, S.; Ciprini, S.; Gopakumar, A.; Matsumoto, K.; Sadakane, K.; Kidger, M.; Gazeas, K.; Nilsson, K.; Berdyugin, A.; et al. Primary Black Hole Spin in OJ 287 as Determined by the General Relativity Centenary Flare. Astrophys. J. 2016, 819, L37. [Google Scholar] [CrossRef]
- Valtonen, M.J. New Orbit Solutions for the Precessing Binary Black Hole Model of OJ 287. Astrophys. J. 2007, 659, 1074. [Google Scholar] [CrossRef]
- Pihajoki, P.; Valtonen, M.; Zola, S.; Liakos, A.; Drozdz, M.; Winiarski, M.; Ogloza, W.; Koziel-Wierzbowska, D.; Provencal, J.; Nilsson, K. Precursor Flares in OJ 287. Astrophys. J. 2013, 764, 5. [Google Scholar] [CrossRef]
- Hudec, R.; Bašta, M.; Pihajoki, P.; Valtonen, M. The historical 1900 and 1913 outbursts of the binary blazar candidate OJ287. Astron. Astrophys. 2013, 559, A20. [Google Scholar] [CrossRef]
- Wex, N. Testing Relativistic Gravity with Radio Pulsars. arXiv 2014, arXiv:1402.5594. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Tests of General Relativity with GW150914. Phys. Rev. Lett. 2016, 116, 221101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Tests of General Relativity with GW170817. arXiv 2018, arXiv:1811.00364. [Google Scholar]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with Stellar Orbits around the Supermassive Black Hole in Our Galactic Center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kormendy, J.; Bender, R. Supermassive black holes do not correlate with dark matter haloes of galaxies. Nature 2011, 469, 377. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Wiik, K. Optical polarization angle and VLBI jet direction in the binary black hole model of OJ287. Mon. Not. R. Astron. Soc. 2012, 421, 1861. [Google Scholar] [CrossRef]
- Valtonen, M.; Pihajoki, P. A helical jet model for OJ287. Astron. Astrophys. 2013, 557, A28. [Google Scholar] [CrossRef]
- Dey, L.; Valtonen, M.; Gopakumar, A.; Pihajoki, P. Modeling temporal variations of the jet position angle from jet precession in blazar OJ 287. In preparation.
- Pietilä, H. Possibilities and Predictions of the OJ 287 Binary Black Hole Model. Astrophys. J. 1998, 508, 669. [Google Scholar] [CrossRef]
- Valtonen, M.; Zola, S.; Pihajoki, P.; Enestam, S.; Lehto, H.J.; Dey, L.; Gopakumar, A.; Drozdz, M.; Ogloza, W.; Zejmo, M.; et al. Accretion Disc Parameters determined from the General Relativity Centenary Flare of OJ287. In preparation.
- Sakimoto, P.J.; Coroniti, F.V. Accretion disk models for QSOs and active galactic nuclei—The role of magnetic viscosity. Astrophys. J. 1981, 247, 19. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; Sarkissian, J.M.; et al. Tests of General Relativity from Timing the Double Pulsar. Science 2006, 314, 97. [Google Scholar] [CrossRef]
- Blanchet, L. Gravitational Radiation from Post-Newtonian Sources and Inspiralling Compact Binaries. Living Rev. Relativ. 2014, 17, 2. [Google Scholar] [CrossRef] [Green Version]
- Will, C.M.; Maitra, M. Relativistic orbits around spinning supermassive black holes: Secular evolution to 4.5 post-Newtonian order. Phys. Rev. D 2017, 95, 064003. [Google Scholar] [CrossRef] [Green Version]
- Blanchet, L.; Schafer, G. Gravitational wave tails and binary star systems. Class. Quantum Gravity 1993, 10, 2699. [Google Scholar] [CrossRef]
- Yunes, N.; Siemens, X. Gravitational-Wave Tests of General Relativity with Ground-Based Detectors and Pulsar-Timing Arrays. Living Rev. Relativ. 2013, 16, 9. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing general relativity with present and future astrophysical observations. Class. Quantum Gravity 2015, 32, 243001. [Google Scholar] [CrossRef] [Green Version]
- Damour, T. 1974: The discovery of the first binary pulsar. Class. Quantum Gravity 2015, 32, 124009. [Google Scholar] [CrossRef]
- Gürlebeck, N. No-Hair Theorem for Black Holes in Astrophysical Environments. Phys. Rev. Lett. 2015, 114, 151102. [Google Scholar] [CrossRef] [PubMed]
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299. [Google Scholar] [CrossRef]
- Krishnendu, N.V.; Arun, K.G.; Mishra, C.K. Testing the Binary Black Hole Nature of a Compact Binary Coalescence. Phys. Rev. Lett. 2017, 119, 091101. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Barausse, E. Constraining the Quadrupole Moment of Stellar-mass Black Hole Candidates with the Continuum Fitting Method. Astrophys. J. 2011, 731, 121. [Google Scholar] [CrossRef]
- Johannsen, T.; Psaltis, D. Testing the No-hair Theorem with Observations in the Electromagnetic Spectrum. II. Black Hole Images. Astrophys. J. 2010, 718, 446. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Mikkola, S.; Lehto, H.J.; Gopakumar, A.; Hudec, R.; Polednikova, J. Testing the Black Hole No-hair Theorem with OJ287. Astrophys. J. 2011, 742, 22. [Google Scholar] [CrossRef]
- Damour, T.; Gopakumar, A.; Iyer, B.R. Phasing of gravitational waves from inspiralling eccentric binaries. Phys. Rev. D 2004, 70, 064028. [Google Scholar] [CrossRef]
- Königsdörffer, C.; Gopakumar, A. Phasing of gravitational waves from inspiralling eccentric binaries at the third-and-a-half post-Newtonian order. Phys. Rev. D 2006, 73, 124012. [Google Scholar] [CrossRef]
- Tanay, S.; Haney, M.; Gopakumar, A. Frequency and time-domain inspiral templates for comparable mass compact binaries in eccentric orbits. Phys. Rev. D 2016, 93, 064031. [Google Scholar] [CrossRef] [Green Version]
- Mikkola, S. A cubic approximation for Kepler’s equation. Celest. Mech. 1987, 40, 329. [Google Scholar] [CrossRef]
- Memmesheimer, R.-M.; Gopakumar, A.; Schäfer, G. Third post-Newtonian accurate generalized quasi-Keplerian parametrization for compact binaries in eccentric orbits. Phys. Rev. D 2004, 70, 104011. [Google Scholar] [CrossRef]
- Klein, A.; Boetzel, Y.; Gopakumar, A.; Jetzer, P.; de Vittori, L. Fourier domain gravitational waveforms for precessing eccentric binaries. Phys. Rev. D 2018, 98, 104043. [Google Scholar] [CrossRef]
- Arun, K.G.; Blanchet, L.; Iyer, B.R.; Sinha, S. Third post-Newtonian angular momentum flux and the secular evolution of orbital elements for inspiralling compact binaries in quasi-elliptical orbits. Phys. Rev. D 2009, 80, 124018. [Google Scholar] [CrossRef]
- Valtaoja, E.; Teräsranta, H.; Tornikoski, M.; Sillanpää, A.; Aller, M.F.; Aller, H.D.; Hughes, P.A. Radio Monitoring of OJ 287 and Binary Black Hole Models for Periodic Outbursts. Astrophys. J. 2011, 531, 744. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Lehto, H.J.; Takalo, L.O.; Sillanpää, A. Testing the 1995 Binary Black Hole Model of OJ287. Astrophys. J. 2011, 729, 33. [Google Scholar] [CrossRef]
- Valtonen, M.J.; Dey, L.; Hudec, R.; Zola, S.; Gopakumar, A.; Mikkola, S.; Ciprini, S.; Matsumoto, K.; Sadakane, K.; Kidger, M.; et al. High accuracy measurement of gravitational wave back-reaction in the OJ287 black hole binary. In Proceedings of the Gravitational Wave Astrophysics: Early Results from Gravitational Wave Searches and Electromagnetic Counterparts, Baton Rouge, LA, USA, 16–19 October 2017; Volume 338, pp. 29–36. [Google Scholar]
- Villforth, C.; Nilsson, K.; Heidt, J.; Takalo, L.O.; Pursimo, T.; Berdyugin, A.; Lindfors, E.; Pasanen, M.; Winiarski, M.; Drozdz, M.; et al. Variability and stability in blazar jets on time-scales of years: Optical polarization monitoring of OJ 287 in 2005–2009. Mon. Not. R. Astron. Soc. 2018, 402, 2087. [Google Scholar] [CrossRef]
- Qian, S. Model simulation of optical light curves for blazar OJ287. arXiv 2019, arXiv:1904.03357. [Google Scholar]
- Goyal, A.; Stawarz, Ł.; Zola, S.; Marchenko, V.; Soida, M.; Nilsson, K.; Ciprini, S.; Baran, A.; Ostrowski, M.; Wiita, P.J.; et al. Stochastic Modeling of Multiwavelength Variability of the Classical BL Lac Object OJ 287 on Timescales Ranging from Decades to Hours. Astrophys. J. 2018, 863, 175. [Google Scholar] [CrossRef]
- Valtonen, M.J. The OJ 287 Binary Model and the Expected Outburst in November 1995. Available online: http://adsabs.harvard.edu/abs/1996wtyi.conf...64V (accessed on 6 May 2019).
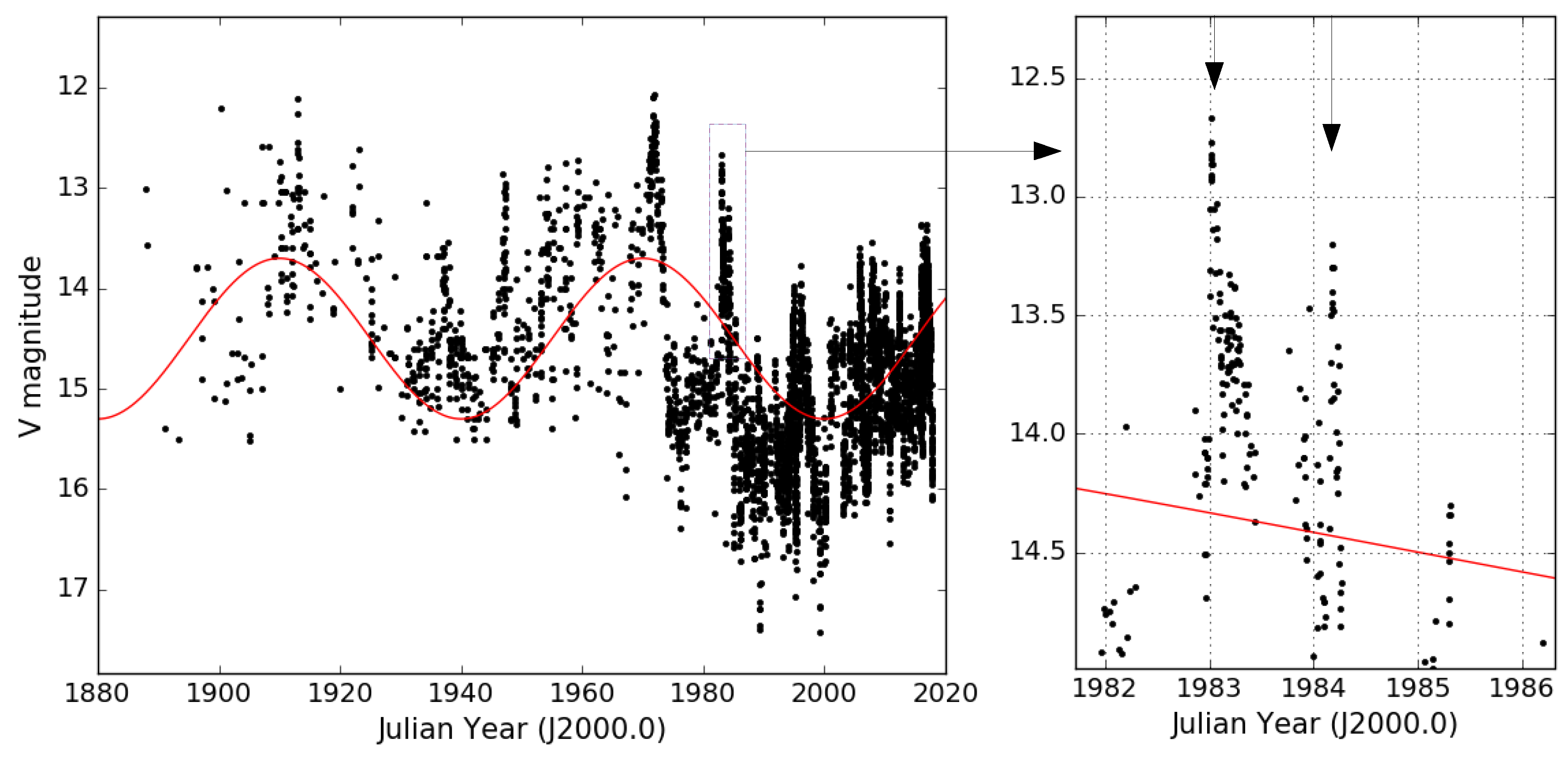
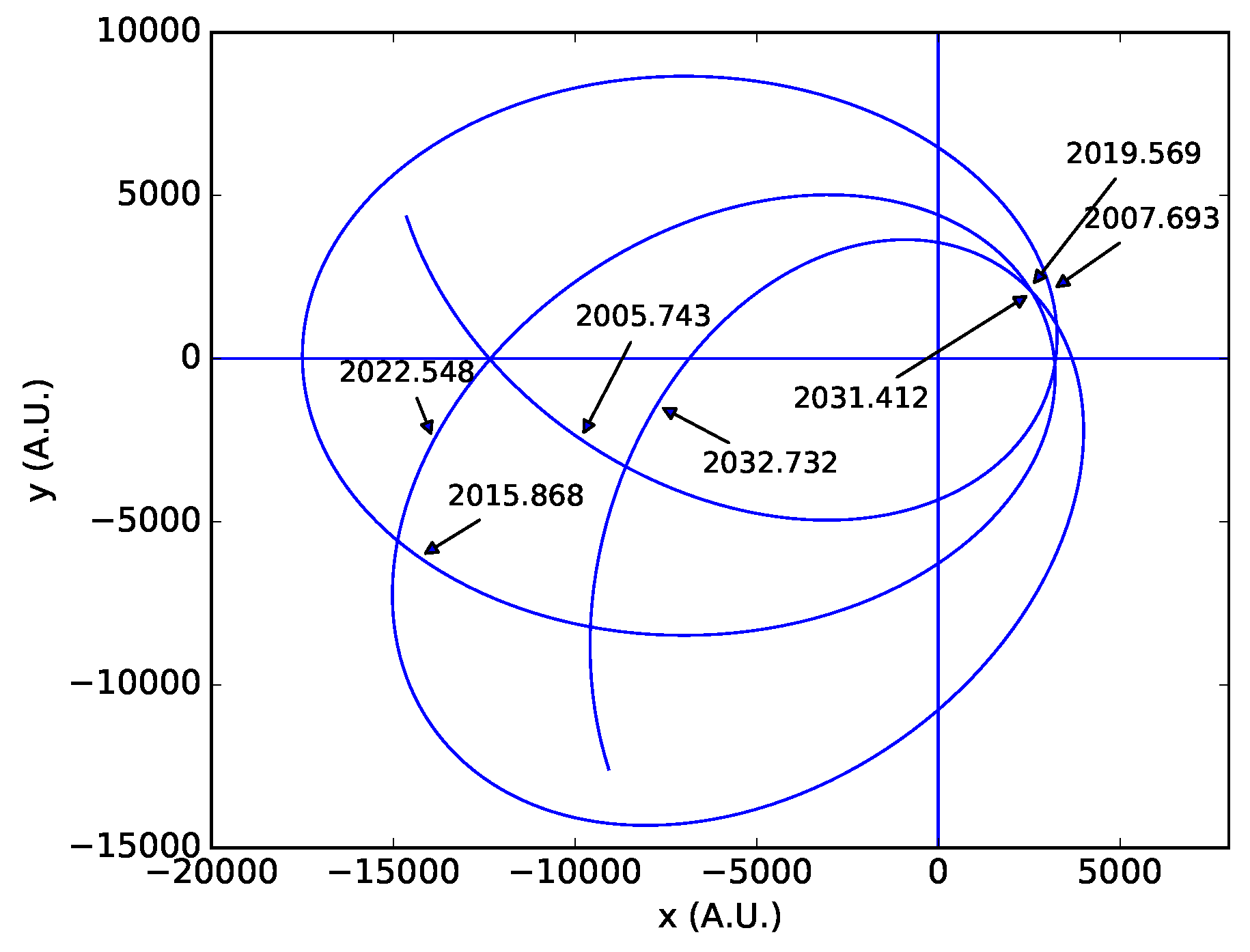
| Outburst Times with Estimated Uncertainty (Julian Year) |
|---|
| 1912.980 ± 0.020 |
| 1947.283 ± 0.002 |
| 1957.095 ± 0.025 |
| 1972.935 ± 0.012 |
| 1982.964 ± 0.0005 |
| 1984.125 ± 0.01 |
| 1995.841 ± 0.002 |
| 2005.745 ± 0.015 |
| 2007.6915 ± 0.0015 |
| 2015.875 ± 0.025 |
| Parameter | Value | Unit |
|---|---|---|
| 18348 | ||
| 150.13 | ||
| 0.381 | ||
| 0.657 | ||
| 38.62 | ||
| 55.42 | ||
| h | 0.900 | |
| d | 0.776 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, L.; Gopakumar, A.; Valtonen, M.; Zola, S.; Susobhanan, A.; Hudec, R.; Pihajoki, P.; Pursimo, T.; Berdyugin, A.; Piirola, V.; et al. The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine. Universe 2019, 5, 108. https://doi.org/10.3390/universe5050108
Dey L, Gopakumar A, Valtonen M, Zola S, Susobhanan A, Hudec R, Pihajoki P, Pursimo T, Berdyugin A, Piirola V, et al. The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine. Universe. 2019; 5(5):108. https://doi.org/10.3390/universe5050108
Chicago/Turabian StyleDey, Lankeswar, Achamveedu Gopakumar, Mauri Valtonen, Stanislaw Zola, Abhimanyu Susobhanan, Rene Hudec, Pauli Pihajoki, Tapio Pursimo, Andrei Berdyugin, Vilppu Piirola, and et al. 2019. "The Unique Blazar OJ 287 and Its Massive Binary Black Hole Central Engine" Universe 5, no. 5: 108. https://doi.org/10.3390/universe5050108





