Equation of State of a Magnetized Dense Neutron System

Abstract

We discuss how a magnetic field can affect the equation of state of a many-particle neutron system. We show that, due to the anisotropy in the pressures, the pressure transverse to the magnetic field direction increases with the magnetic field, while the one along the field direction decreases. We also show that in this medium there exists a significant negative field-dependent contribution associated with the vacuum pressure. This negative pressure demands a neutron density sufficiently high (corresponding to a baryonic chemical potential of $\mu =2.25$ GeV) to produce the necessary positive matter pressure that can compensate for the gravitational pull. The decrease of the parallel pressure with the field limits the maximum magnetic field to a value of the order of ${10}^{18}$ G, where the pressure decays to zero. We show that the combination of all these effects produces an insignificant variation of the system equation of state. We also found that this neutron system exhibits paramagnetic behavior expressed by the Curie’s law in the high-temperature regime. The reported results may be of interest for the astrophysics of compact objects such as magnetars, which are endowed with substantial magnetic fields.

1. Introduction

Neutron stars (NS) are very dense objects produced by the gravitational collapse of very massive stars (stars with masses larger than eight solar masses) or by binary NS merger events such as GW170817 [1]. They can reach densities several times larger than the nuclear density of ${\rho }_n=0.16$ fm${}^{-3}$. An interesting question that is attracting much attention at present is “what is the state of matter that can support such a dense medium?” In this regard, very precise mass measurements for two compact objects, PSR J1614-2230 and PSR J0348+0432 with $M=1.908\pm 0.016M_{\odot }$ [2,3] and $M=2.01\pm 0.04M_{\odot }$ [4], respectively, where $M_{\odot }$ is the solar mass, have provided an important clue to the possible candidates for their interior compositions: the phase of matter there should have an equation of state (EOS) that is rather stiff at high densities.

If the inner density of compact stars is not sufficiently high to produce the deconfinement of quarks, the nuclear star matter below the crust is believed to be formed mainly by neutrons. Nevertheless, the possibility of an interior composition formed mainly by neutrons at a relatively high density, faces the difficulty of reproducing the required EOS stiffness. This is due to the fact that, while under terrestrial conditions, hyperons are unstable and decay into nucleons through weak interactions, in neutron stars, the equilibrium conditions at core densities of order (2–3)${\rho }_n$ can make the inverse process possible. Hence, at a large enough baryon chemical potential, the conversion of nucleons into hyperons becomes energetically favorable. This conversion reduces the Fermi pressure exerted by the nucleons and makes the EOS soft enough to lead to a significant reduction of the star mass [5,6,7].

On the other hand, NSs also exhibit the strongest magnetic fields known in nature. Some radio pulsars are endowed with surface magnetic fields of order ${10}^{13}$–${10}^{14}$ G [8]. From spectroscopic and spin-down studies of soft-gamma ray repeaters (SGRs) and anomalous x-ray pulsars (AXPs), it has been inferred that surface magnetic fields of order ${10}^{14}$–${10}^{15}$ G occur in some special compact objects called magnetars [9]. Moreover, the inner core magnetic fields of magnetars can be even larger as it follows from the magnetic field flux conservation in stellar media with very large electric conductivities. The inner fields have been estimated to range from ${10}^{18}$ G for nuclear matter stars [10] to ${10}^{20}$ G for quark matter stars [11]. The fact that strong magnetic fields populate the vast majority of astrophysical compact objects and that they have significant consequences for several star properties have motivated a lot of work focused on the study of the EOS of magnetized neutron stars (see [12] and references there).

In a more realistic nuclear model of the star interior, other degrees of freedom corresponding to protons, electrons and neutrinos that, together with the neutrons, guarantee the medium $\beta$ equilibrium, and the mesons, which mediate the nuclear forces among the baryons, should be included. However, in this paper, we constrain our investigation only to neutrons, since apart from the fact that they form a substantial component of this medium, they do not suffer in the presence of a magnetic field, from the softening of pressure due to the Landau momentum quatization, thus in the case of an isotropic approach it has been found that they significantly contribute to the system EOS [13]. Nevertheless, an important characteristic of the stellar medium EOS in a uniform magnetic field is that they become anisotropic, with different pressures in directions along and transverse to the field, respectively [11,14,15]. The anisotropy of the EOS produces a significant splitting of the TOV equations at strong magnetic fields in different dense media [16,17]. Since neutrons are composite neutral particles, the magnetic field can only interact with their anomalous magnetic moment. The effect of the magnetic-field/anomalous-magnetic-moment (B-AMM) interaction on the EOS of charged particles was recently investigated by Ferrer et al. [12], who proved that this effect is insignificantly small both in the strong-field and the weak-field approximations. For neutrons, however, it was found by Broderick et al. [13] in an isotropic approach that, for critical fields of order ∼${10}^{18}$ G, the magnetic field can make a substantial contribution to the system EOS. Then, it would be important to investigate by considering the pressure anisotropy if the effect of the magnetic field on the corresponding EOS is significant or not. This is one of the main questions to be answered here.

Thus, we discuss a result found in [18], which shows that due to the pressure anisotropy, while the transverse pressure increases with the magnetic field, the parallel pressure decreases, reaching zero value at a magnetic field strength, which is of the order of the one needed to produce a significant effect under the isotropic neutron-system EOS assumption [13]. This result indicates that, for the magnetic-field range where the system pressure has a positive magnetic pressure, the effect of the B-AMM interaction has a negligibly small effect on the system EOS, similar to the case of charged particles studied in [12]. Another factor that up to now has not been taken into consideration is the effect of the quantum field theory (QFT) contribution to the neutron-system EOS. As shown in [18], this contribution plays an important role for this effective model by pushing the system, through the magneto-hydrostatic equilibrium between the matter and gravitational pressures, to higher density values, corresponding to baryonic chemical potentials of the order of several GeV. Under these conditions, it is naturally expected that other exotic degrees of freedom, such as hyperons, emerge in the magnetized scenario. This fact implies that the magnetic field implicitly helps to soften the EOS of nuclear matter.

We also discuss how the QFT contribution to the system magnetization is not negligible at sufficiently strong fields. This implies that the product of the neutron magnetic moment by the relative number of polarized particles only gives the real system magnetization in the weak-field approximation (i.e., fields smaller than ${10}^{14}$ G), where it coincides with the more general formula, $M=-\partial {\Omega }_N/\partial B$, where ${\Omega }_N$ includes the QFT contribution to the thermodynamic potential, ${\Omega }_{QFT}$.

Finally, we show that the magnetized many-particle neutron system exhibits paramagnetic behavior, as shown by the dependence on temperature of the system magnetic susceptibility, which satisfies Curie’s law in the high-temperature regime at a fixed particle-number density.

2. The Effective Model

We consider an effective theory in which the neutrons, although electrically neutral, interact with a magnetic field via their anomalous magnetic moment (AMM). The magnetic field is taken to be uniform in the $\widehat{z}$ direction. The effective Lagrangian density is then given by

$$\mathcal{L}={\overline{\Psi }}_N(i{\gamma }_{\mu }{\partial }^{\mu }-M_N+i{k}_N{\sigma }_{\mu \nu }{F}^{\mu \nu }){\Psi }_N,$$

(1)

where $k_N$ represents the neutron’s anomalous magnetic moment given by $k_N={\mu }_N{g}_N/2$, ${\mu }_N=\left|e\right|\hslash /2M_P=3.15\times {10}^{-18}$ MeV/G is the nuclear magneton, $M_P$ is the proton mass and $g_N=-3.82$ is the Land$\acute{e}$ g-factor for the neutron [19,20]. The negative sign of $g_N$ indicates that the neutron’s magnetic moment is similar to that of a negatively charged particle. In Equation (1), $M_N=939.56$ MeV is the neutron mass, ${\sigma }_{\mu \nu }=\frac{i}{2}[{\gamma }_{\mu },{\gamma }_{\nu }]$ and $F^{\mu \nu }$ are the electromagnetic field strength tensor corresponding to the applied uniform and constant magnetic field in the z direction, respectively (i.e., $B=F^{21}$).

The Lagrangian density (Equation (1)), corresponds to a non-renormalizable theory, since the parameter $k_N$, which is playing the role of the coupling constant for the B-AMM interaction, has dimensions of inverse energy ($k_N\sim 1/E$), making the dimensionless parameter, $k_{N}E$, small at low energies and large at high energies. This means that we have to consider this model as an effective theory that is reliable only up to a certain energy scale that is defined by the system’s leading parameter. Therefore, in the case of a neutron star, it is natural to consider the baryonic chemical potential as the physical scale ($\Lambda \sim \mu$).

To study the many-particle theory, we calculate the grand-canonical thermodynamic potential in the one-loop approximation

$${\Omega }_N(B,\mu ,T)=\frac{-1}{\beta }\sum _{p_4}\int \frac{d^{3}p}{{\left(2\pi \right)}^3}ln[det(-{\gamma }^{\mu }{p}_{\mu }^{*}-M_N-i{k}_{N}B{\gamma }_2{\gamma }_1)],$$

(2)

where $\beta =1/T$ denotes the inverse of the absolute temperature, and the baryonic chemical potential $\mu$ appears as a shift to the Euclidean four-momentum ($p_0=i{p}_4$, with $p_4=\frac{(2n+1)\pi }{\beta },n=0,\pm 1,\pm 2,\dots$) in $p_{\mu }^{*}=(i{p}_4-\mu ,p_1,p_2,p_3)$.

After taking the determinant in Equation (2), the thermodynamic potential can be given in terms of the energy spectrum, $E_{\eta ,\sigma }$, as

$${\Omega }_N(B,\mu ,T)=\frac{-1}{\beta }\sum _{p_4}\sum _{\eta ,\sigma =\pm }\int \frac{d^{3}p}{{\left(2\pi \right)}^3}\left[ln[{(p_4+i\mu )}^2+{\left(E_{\eta ,\sigma }\right)}^2\right],$$

(3)

where

$$E_{\eta ,\sigma }=\eta \sqrt{{p_3}^2+{\left(\sqrt{{M_N}^2+{p_1}^2+{p_2}^2}+\sigma k_{N}B\right)}^2}$$

(4)

Here, $\eta =\pm$ denotes particle/antiparticle modes and $\sigma =\pm$ denotes spin up/down modes. As expected, the B-AMM interaction breaks the spin degeneracy that exists at zero magnetic field.

Performing in Equation (3) the sum in Matsubara frequencies, we obtain

$${\Omega }_N={\Omega }_0+{\Omega }_{QFT}+{\Omega }_S,$$

(5)

where ${\Omega }_0$ is a constant added to make the vacuum pressure equal to zero when all the physical parameters, $\mu$, T, etc., are zero; ${\Omega }_{QFT}$ is the quantum field theory contribution (the one that does not depend on the chemical potential and temperature) given by

$${\Omega }_{QFT}=-\sum _{\sigma =\pm }{\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\left(E_{+,\sigma }\right);$$

(6)

and ${\Omega }_S$ is the statistical contribution, which depends on the system’s temperature and chemical potential

$${\Omega }_S=-\frac{1}{\beta }\sum _{\sigma =\pm }{\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\left(ln[1+e^{-\beta (E_{+,\sigma }+\mu )}]+ln[1+e^{-\beta (E_{+,\sigma }-\mu )}]\right)$$

(7)

In the following, we analyze the different contributions separately.

2.1. QFT Contribution

We express Equation (6) in cylindrical coordinates ($p_1=p_{\perp }cos\theta$, $p_2=p_{\perp }sin\theta$) as

$${\Omega }_{QFT}=\frac{-1}{2{\pi }^2}\sum _{\sigma }{\int }_0^{\infty }{p}_{\perp }d{p}_{\perp }{\int }_0^{\infty }d{p}_3\sqrt{p_3^2+{\left[\sqrt{M_N^2+p_{\perp }^2}+\sigma k_{N}B\right]}^2}.$$

(8)

These integrals diverge, but since the theory under consideration is an effective theory that is only valid up to certain energy scale, we introduce the energy cutoff $\Lambda$, such that

$${\Lambda }^2=p_3^2+{\left[\sqrt{M_N^2+p_{\perp }^2}+\sigma k_{N}B\right]}^2.$$

(9)

As indicated above, this energy scale should be presumably fixed in a neutron star by the baryonic chemical potential (i.e., $\Lambda \sim \mu$).

In this region, we have

$${\Omega }_{QFT}=\frac{-1}{2{\pi }^2}\sum _{\sigma }{\int }_0^{p_{\perp }^{Max}}{p}_{\perp }d{p}_{\perp }{\int }_0^{p_3^{Max}}d{p}_3\sqrt{p_3^2+{\left[\sqrt{M_N^2+p_{\perp }^2}+\sigma k_{N}B\right]}^2}.$$

(10)

where

$$p_3^{Max}=\sqrt{{\Lambda }^2-{\left[\sqrt{M_N^2+p_{\perp }^2}+\sigma k_{N}B\right]}^2},p_{\perp }^{Max}=\sqrt{{(\Lambda -\sigma k_{N}B)}^2-M_N^2}.$$

(11)

Then, after integrating and performing the sum in $\sigma$, we obtain

$$\begin{array}{l}{\Omega }_{QFT}=\frac{-1}{48{\pi }^2}({\Lambda }^2\left[\sqrt{\frac{{\Lambda }^2-{(M_N+B{k}_N)}^2}{{\Lambda }^2}}({(M_N-B{k}_N)}^2-4M_N^2+6{\Lambda }^2)+(B\to -B)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +8k_N{\Lambda }^3\left[B{sin}^{-1}\left[\frac{B{k}_N-M_N}{\Lambda }\right]+(B\to -B)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} +B^4{k}_N^4\left[ln\left[1+\sqrt{\frac{{\Lambda }^2-{(M_N+B{k}_N)}^2}{{\Lambda }^2}}\right]-ln\left[\frac{M_N-B{k}_N}{\Lambda }\right]+(B\to -B)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} +M_N^2\left[(6B^2{k}_N^2-8B{k}_N{M}_N+3M_N^2)ln\left[\frac{M_N-B{k}_N}{\Lambda }\right]+(B\to -B)\right]\\ -M_N^2\left[(6B^2{k}_N^2+8B{k}_N{M}_N+3M_N^2)ln\left[1+\sqrt{\frac{{\Lambda }^2-{(M_N+B{k}_N)}^2}{{\Lambda }^2}}\right]+(B\to -B)\right]).\end{array}$$

(12)

The introduced notation $(B\to -B)$ stands for the same contribution with a change in the magnetic field sign. The existence of the two terms with different magnetic field signs reflects the contributions of the spin-up and spin-down polarizations in the magnetic-moment/magnetic-field interaction.

From Equation (12), we see that the leading divergent term does not depend on the physical parameters, but only on the cutoff $\Lambda$. Thus, to guarantee that the vacuum pressure vanishes appropriately, we need to take this into account in Equation (5),

$${\Omega }_0=\frac{1}{4{\pi }^2}{\Lambda }^4.$$

(13)

On the other hand, there are terms proportional to ${\Lambda }^2$, which depending on B could makes a large field contribution to the thermodynamic potential for $\Lambda \sim \mu$ and so the QFT contribution should be considered on equal footing with the many-particle contribution when calculating the field dependent EOS. In the following, we show that the QFT contribution will have a significant impact on the system EOS, something that has been pointed out in Ref. [18] for first time.

2.2. Many-Particle Contribution

We concentrate now on the calculation of the $T\to 0$ limit. Then, letting ${\Omega }_{\mu }={lim}_{\beta \to \infty }{\Omega }_S$, we have from Equation (7) that

$${\Omega }_{\mu }=-{\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\left[(\mu -E_{+,-})\Theta (\mu -E_{+,-})+(\mu -E_{+,+})\Theta (\mu -E_{+,+})\right],$$

(14)

which after integration gives

$$\begin{array}{ccc}\hfill {\Omega }_{\mu }& =& \frac{-1}{48{\pi }^2}[2\left(\sqrt{1-{\left(\frac{M_N+k_{N}B}{\mu }\right)}^2}+(B\to -B)\right){\mu }^4+4k_{N}B\left({sin}^{-1}\left(\frac{M_N+K_{N}B}{\mu }\right)-(B\to -B)\right){\mu }^3\hfill \\ & +& \left[{(M_N+k_{N}B)}^3(3M_N-k_{N}B)\left(ln\left[1+\sqrt{1-{\left(\frac{M_N+k_{N}B}{\mu }\right)}^2}\right]-ln\left[\frac{|M_N+k_{N}B|}{\left|\mu \right|}\right]\right)+(B\to -B)\right]\hfill \\ & +& \left[(8k_{N}B(M_N+k_{N}B)-5{(M_N+k_{N}B)}^2)\sqrt{1-{\left(\frac{M_N+k_{N}B}{\mu }\right)}^2}+(B\to -B)\right]{\mu }^2.\hfill \end{array}$$

(15)

From Equation (15), we see that in order for the potential to remain real the arguments of the radical terms must be non negative, which implies

$$\left|\frac{M_N\pm k_{N}B}{\mu }\right|\le 1.$$

(16)

Furthermore, for a given value of the chemical potential the magnitude of the magnetic field is bounded by

$$B\le \left|\frac{\mu -M_N}{k_N}\right|.$$

(17)

Hence, for values of $\mu$ near $2.25$ GeV, the upper bound of the magnetic field strength is approximately $B_{max}(\mu =2.25$ GeV$)\approx 2.0\times {10}^{20}$ G.

3. Anisotropic Equation of State in the Presence of a Magnetic Field

It is well known that, in the presence of a uniform magnetic field, there is a splitting of the pressures in the directions along and transverse to the magnetic field. This is due to the breaking of the rotational symmetry by the magnetic field, which gives rise to new field-dependent structures in the energy-momentum tensor [11,18]. A detailed calculation of the transverse and longitudinal pressures expressed in terms of the thermodynamic potential is presented in [11] by performing a quantum-statistical average of the energy-momentum tensor using the path-integral approach. The obtained results coincide with those obtained years ago by using the many-particle density matrix [14].

The energy density, $\epsilon$, and parallel and transverse pressures, $P_{\Vert }$, $P_{\perp }$, respectively, can be then expressed in terms of the thermodynamic potential ${\Omega }_N$ in the $T\to 0$ limit as [11],

$$\epsilon ={\Omega }_N^{(T=0)}-\mu \frac{\partial {\Omega }_{\mu }}{\partial \mu },$$

(18)

$$P_{\Vert }=-{\Omega }_N^{(T=0)}-\frac{B^2}{2},P_{\perp }=-{\Omega }_N^{(T=0)}-MB+\frac{B^2}{2},$$

(19)

where the quadratic terms in B arise from the Maxwell contribution to the energy momentum tensor.

The system magnetization in Equation (19) is given by

$$M=-\frac{\partial {\Omega }_N^{(T=0)}}{\partial B},$$

(20)

which results in

$$\begin{array}{c}M=\frac{k_N}{12{\pi }^2}(\left[2M_N\left[\sqrt{1-\frac{{(M_N-B{k}_N)}^2}{{\Lambda }^2}}-(B\to -B)\right]+B{k}_N\left[\sqrt{1-\frac{{(M_N-B{k}_N)}^2}{{\Lambda }^2}}+(B\to -B)\right]\right]{\Lambda }^2\\ +(2{\Lambda }^3+{\mu }^3)\left[{sin}^{-1}\left[\frac{B{k}_N+M_N}{\Lambda }\right]-(B\to -B)\right]\\ +\left[(2M_N+B{k}_N){(M_N-B{k}_N)}^{2}ln\left[1+\sqrt{1-\frac{{(M_N-B{k}_N)}^2}{{\Lambda }^2}}\right]-(B\to -B)\right]\\ +\left[(2M_N-B{k}_N){(B{k}_N+M_N)}^{2}ln\left[\frac{{(M_N+B{k}_N)}^2}{{\Lambda }^2}\right]-(B\to -B)\right])\\ +\frac{k_N}{24{\pi }^2}(2{\mu }^2\left[(M_N+2B{k}_N)\sqrt{1-\frac{{(M_N-B{k}_N)}^2}{{\mu }^2}}-(B\to -B)\right]\\ +[2(2M_N-B{k}_N){(M_N+B{k}_N)}^{2}ln\left[1+\sqrt{1-\frac{{(M_N+B{k}_N)}^2}{{\mu }^2}}-(B\to -B)\right]\\ +\left[(2M_N+B{k}_N){(M_N-B{k}_N)}^{2}ln\left[\frac{{(M_N-B{k}_N)}^2}{{\mu }^2}\right]-(B\to -B)\right]).\end{array}$$

(21)

We call attention to the fact that in previous works the ${\Omega }_{QFT}$ contribution to the energy density and pressure was neglected under the assumption that it does not depend on the baryonic chemical potential $\mu$, which is the leading parameter in the stellar medium. Nevertheless, as we found in [18], the non-renormalizable nature of this effective theory makes ${\Omega }_{QFT}$ dependent on terms that couples the cutoff $\Lambda \sim \mu$ with the magnetic field, which results in a significant contribution to the thermodynamic potential. Thus, in our approach, the QFT contribution is taken to be on the same footing as the many-particle one. This is why the magnetization (Equation (21)) depends on $\Lambda$.

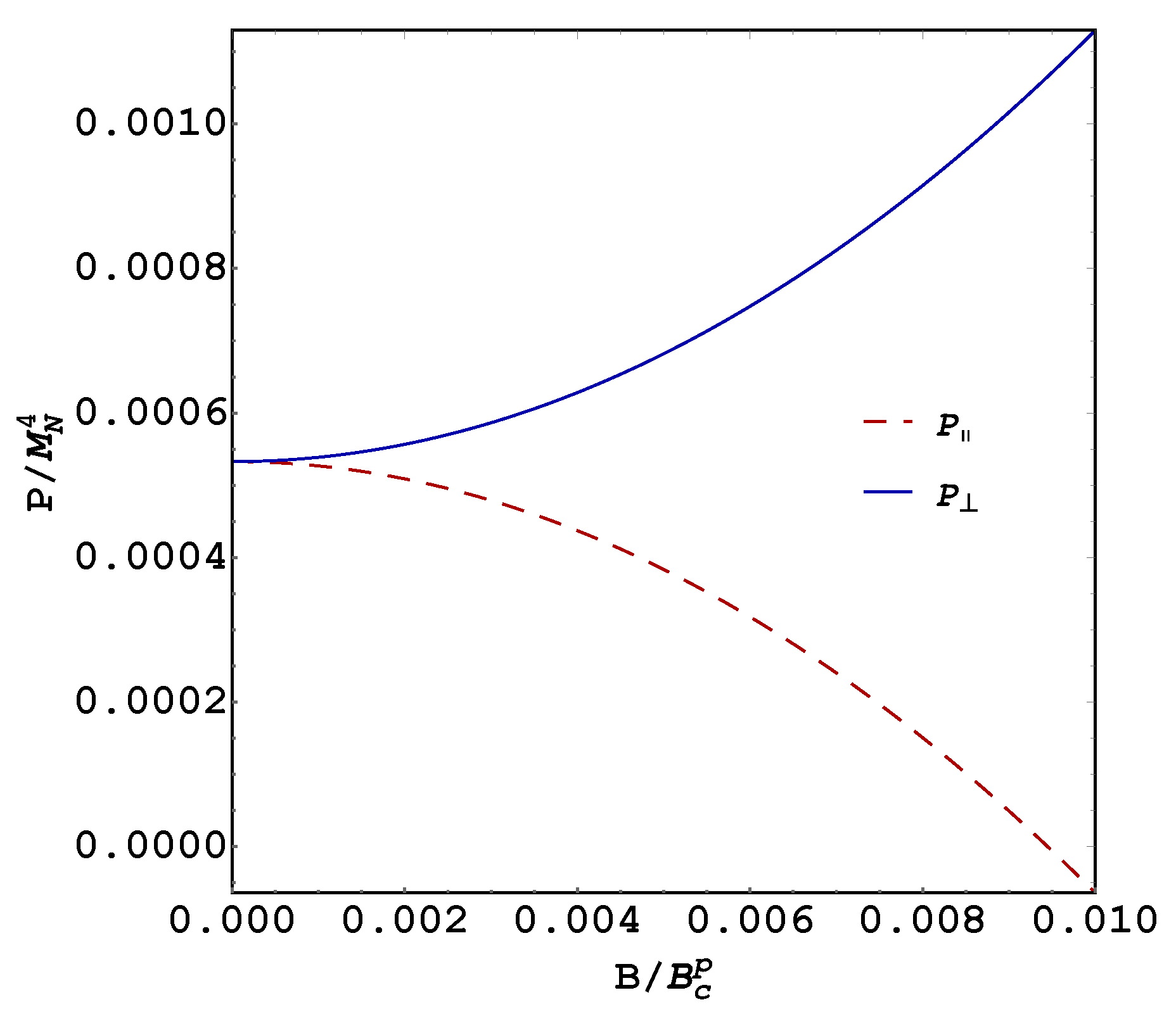
Using Equation (19), the parallel and transverse pressures are plotted versus the magnetic field in Figure 1, for a chemical potential $\mu =2.25$ GeV. The chemical potential value $\mu =2.25$ GeV is needed to produce positive pressures at small field values. We found that the contribution of the QFT thermodynamic potential substantially depletes the pressures making necessary a higher Fermi pressure to produce a net positive pressure, which is necessary to compensate for the gravitational pull. We notice that, while the perpendicular pressure increases with the magnetic field, the parallel pressure decays monotonically due to the negative sign of its Maxwell term and has a root at $B_{\Vert }^{\left(0\right)}$($\mu =2.25$ GeV) $\approx 1.5\times {10}^{18}$ G, which is two orders smaller than $B_{max}$($\mu =2.25$ GeV) $\approx 2.0\times {10}^{20}$ G obtained from Equation (17).

Figure 1. (Color online) Parallel and perpendicular pressures as a function of the magnetic field at a fixed chemical potential $\mu =2.25$ GeV. Here, $B_C^{\left(p\right)}=1.6\times {10}^{20}$ G, is the baryonic critical field obtained by equating the proton magnetic energy to its rest energy.

Here, the following comment is in order. Because neutrons in a magnetic field do not suffer the softening in pressure caused by Landau quantization, it has been found following an isotropic approach and neglecting the Maxwell pressure (i.e., considering $p_{\parallel }=p_{\perp }$ in Equation (19) without the $MB$ and $B^2/2$ terms) that the magnetic field, through its interaction with the neutron magnetic moment, stiffens the system EOS [13] for fields of order ${10}^{18}$ G. However, as shown above, due to the pressure anisotropy produced by the magnetic field [11,12,13,14], the situation is more subtle in the sense that at the magnetic-field strength that was needed to produce significant stiffening of the isotropic EOS, the longitudinal pressure vanishes creating a loss of balance with the gravitational pull in the neutron star. Moreover, because of the softening effect of the QFT contribution, we found that the net magnetic field effect is to soften the system EOS, as can be seen in Figure 2 and Figure 3 for the parallel and transverse pressures, respectively.

Figure 2. (Color online) Equations of state for the parallel pressure versus energy density. With ${\Omega }_{QFT}$ contribution (continuous line) and without (dashed line). The magnetic field under consideration is $B={10}^{16}$ G.

Figure 3. (Color online) Equations of state for the perpendicular pressure versus energy density. With ${\Omega }_{QFT}$ contribution (continuous line) and without (dashed line). The magnetic field under consideration is $B={10}^{16}$ G.

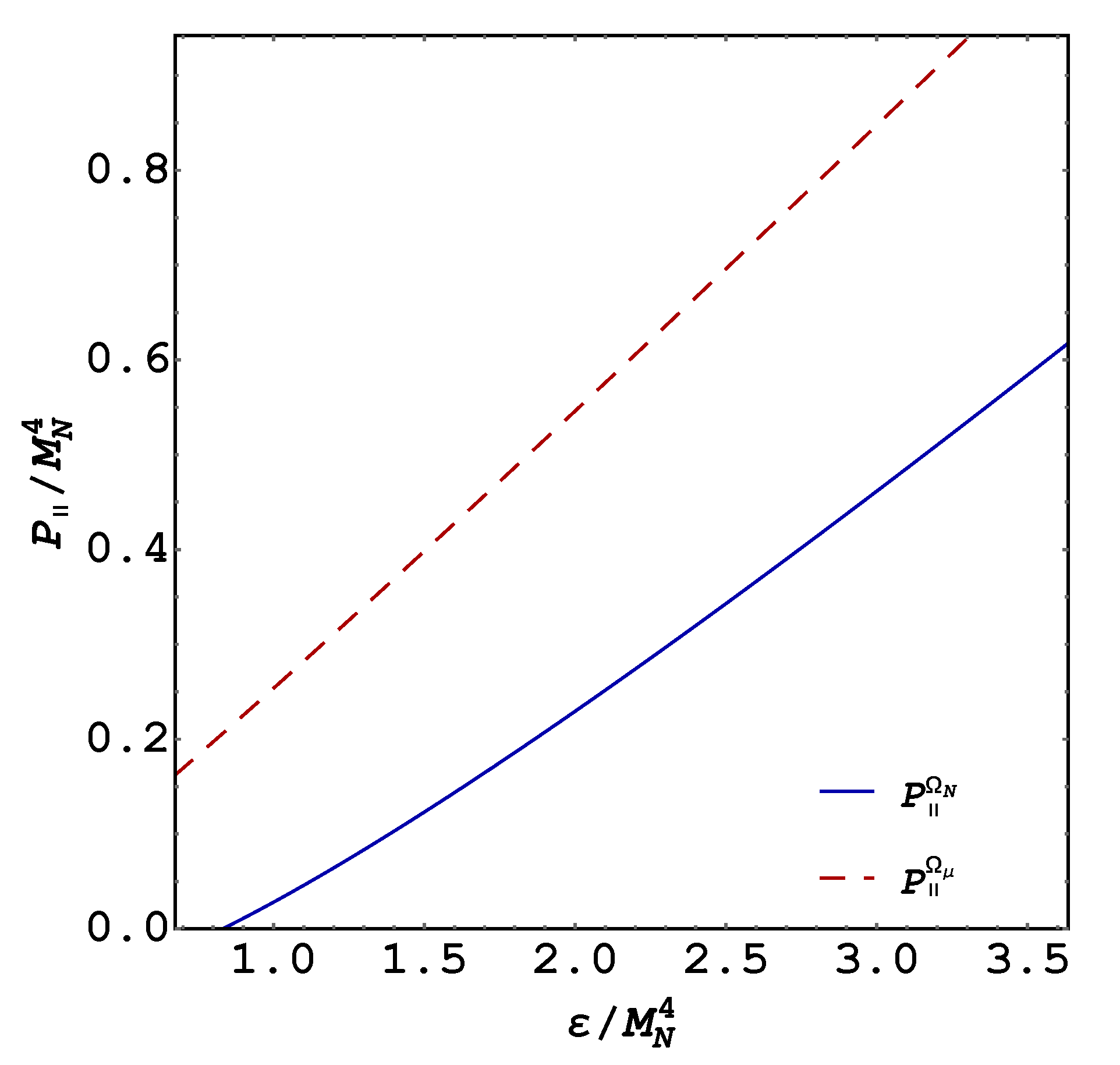
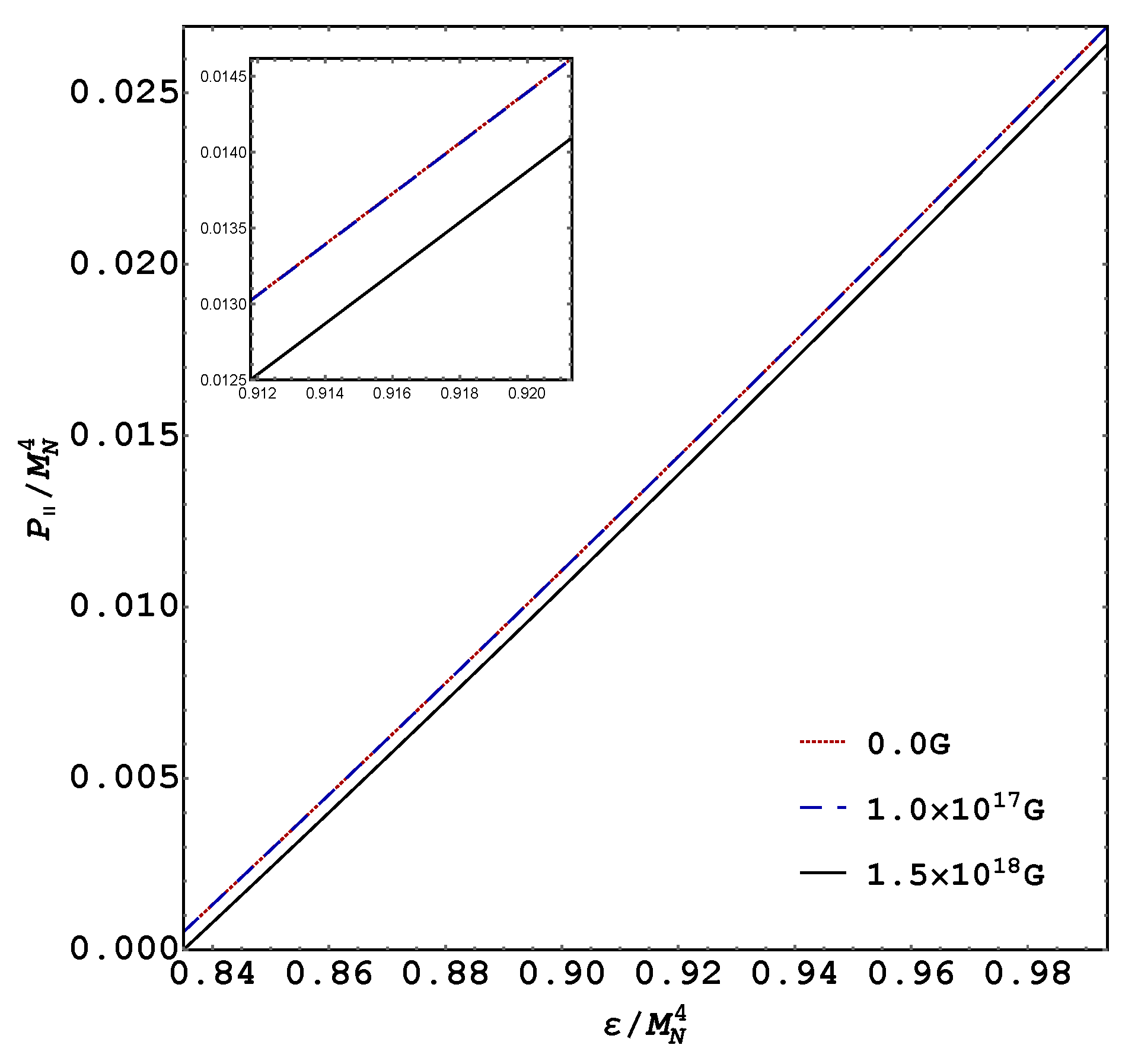
On the other hand, taking into account the anisotropy in the pressures given in Equation (19), and including the QFT contribution, we found that the EOS’s of this system, given in Figure 4 and Figure 5, do not show a significant variation for the range of allowed fields ($B<{10}^{18}$ G) that are considered to maintain a positive pressure at $\mu =2.25$ GeV. In this sense, we found an insignificant effect on the system EOS through the B-AMM interaction, similar to what was obtained for charged particles in [12].

Figure 4. (Color online) Equations of state for the parallel pressure for magnetic field strengths of 0.0 G (dotted), $1.0\times {10}^{17}$ G (dashed), and $1.5\times {10}^{18}$ G (solid). The curves for the two lower fields overlap.

Figure 5. (Color online) Equations of state for the perpendicular pressure, for magnetic field strengths of 0.0 G (dotted), $1.0\times {10}^{17}$ G (dashed), and $1.5\times {10}^{18}$ G (solid). The curves for the two lower fields overlap.

4. Medium Polarization and Magnetization

Since the interaction between the magnetic field and the neutron magnetic moment breaks the spin degeneracy, we can measure the relative polarization of the medium as

$$\Delta =\frac{N_{(+)}-N_{(-)}}{N}$$

(22)

where $N_{(+)}$ and $N_{(-)}$ are the particle number densities of spin up and spin down particles, respectively, and $N=N_{(+)}+N_{(-)}$ is the total particle number density. In this case, they are given by

$$N_{(+/-)}=-\frac{\partial {\Omega }_S(\sigma =+/-)}{\partial \mu }$$

(23)

with corresponding expressions,

$$N_{(+)}={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\left[n_F(E_{+,+}-\mu )-n_F(E_{+,+}+\mu )\right],$$

(24)

$$N_{(-)}={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\left[n_F(E_{+,-}-\mu )-n_F(E_{+,-}+\mu )\right].$$

(25)

Here, $n_F={[1+exp\left(\beta x\right)]}^{-1}]$ is the Fermi–Dirac distribution.

In the zero-temperature limit, they take the forms

$$N_{(+)}^0={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\theta (\mu -E_{+,+}),$$

(26)

$$N_{(-)}^0={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\theta (\mu -E_{+,-}).$$

(27)

where $\theta \left(x\right)$ is the Heaviside step function.

In Figure 6, the polarization at zero temperature $\Delta (\beta \to \infty )$, is plotted versus the magnetic field for different baryon chemical potentials. We can see that the magnetic field in the range allowed for neutron stars produces an increase of the polarization, while the increase of the chemical potential decreases it.

Figure 6. (Color online) Neutron-system polarization versus the magnetic field at zero temperature for three baryonic chemical potentials with values $\mu =2.3,2.4,2.5$ GeV.

The system magnetization is commonly defined as [21,22,23,24,25]

$$M=k_N[N_{(+)}-N_{(-)}]$$

(28)

where the neutron magnetic moment is given by $k_N=-6.03\times {10}^{-18}$ MeV/G [19].

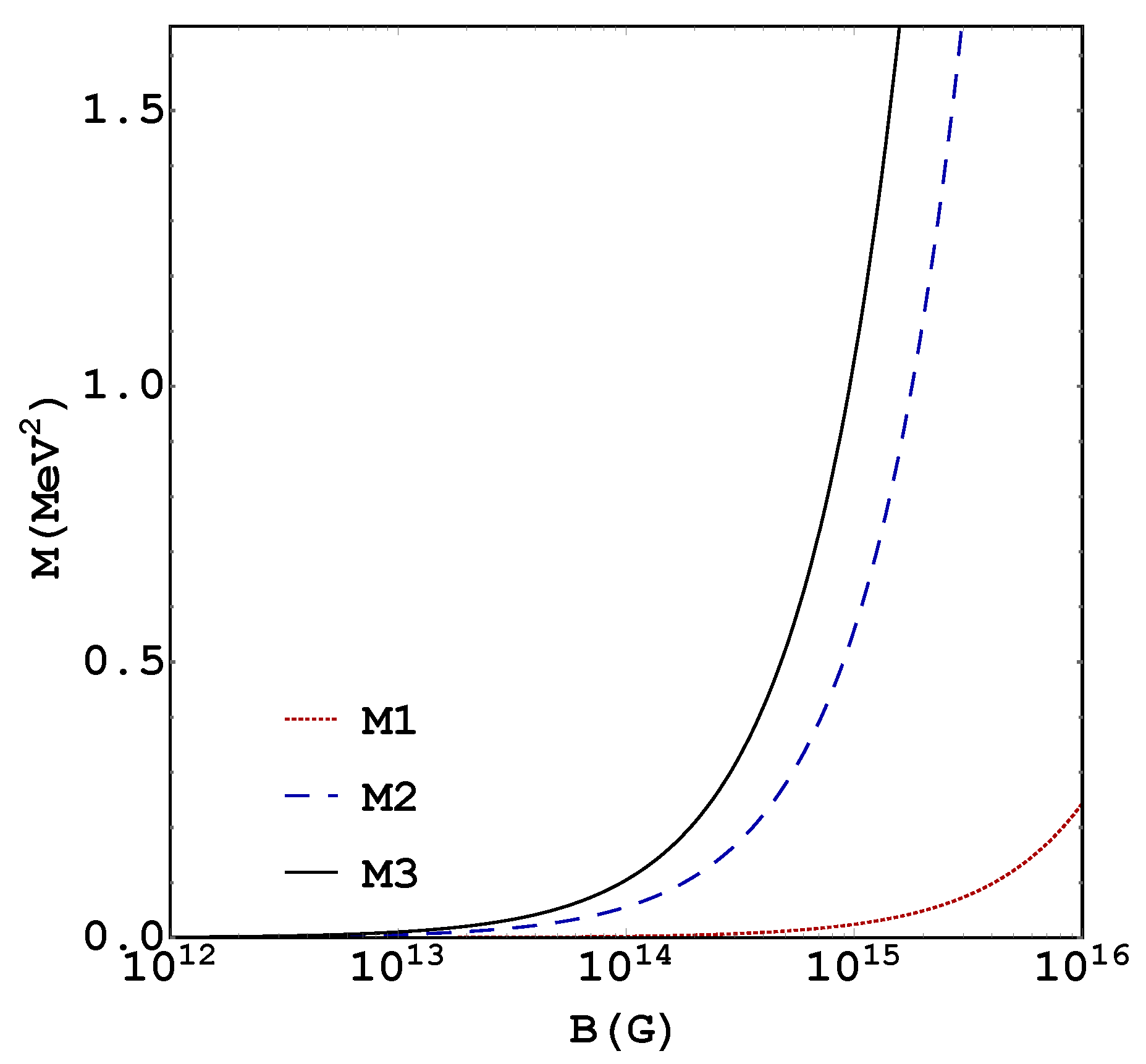
In Figure 7, we compare the magnetizations found with three different methods. In M1, we use Equation (28); in M2, Equation (20), but replacing ${\Omega }_N$ by ${\Omega }_{\mu }$; and, in M3, Equation (20).

Figure 7. (Color online) Neutron-system magnetization versus magnetic field using three different formulations. In M1, we use Equation (28); in M2, Equation (20), but replacing ${\Omega }_N$ by ${\Omega }_{\mu }$; and, in M3, Equation (20).

We can see that the results for the three formulations only coincide in the weak-field approximation, while for fields larger than ${10}^{14}$ G they are significantly split. The difference between the magnetizations M2 and M3, makes apparent the importance of the QFT contribution. Thus, we conclude that in this system the QFT contribution makes a substantial impact to the system’s magnetization, and that Equation (20) is the adequate one at relatively high fields.

5. Magnetic Susceptibility and Curie’s Law for Magnetized Neutrons

The magnetic susceptibility ${\chi }_M$ is defined as the coefficient of the linear expansion of M in the magnetic field

$$M={\chi }_{M}B$$

(29)

Taking into account Equation (28), the susceptibility can be found from

$${\chi }_M=k_N{\left[\frac{\partial N_{(+)}}{\partial B}-\frac{\partial N_{(-)}}{\partial B}\right]}_{B=0}$$

(30)

For paramagnetic material, if the particle number density N is fixed in the high-temperature regime $(T>k_{N}B)$, the susceptibility changes with the temperature as ${\chi }_N\sim 1/T$. This is the famous Curie’s law of paramagnetism. To corroborate that our magnetized many-particle neutron system behaves as a paramagnet, we should check that Curie’s law is satisfied.

Before accomplishing this task let us review, as a preparatory exercise, how it is obtained for a non-relativistic system, which is where it was originally derived.

5.1. Curie’s Law for Non-Relativistic Systems

As is well known, in the high-temperature limit both Fermi–Dirac and Bose–Einstein quantum statistics become the classical Maxwell–Boltzmann statistics. In this case, the particle number densities for spin up and down are given by

$$N_{(+/-)}={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}{e}^{\beta ({ϵ}_{NR}\pm k_{N}B-\mu )},$$

(31)

with the non-relativistic energy spectrum given as ${ϵ}_{NR}=p^2/2m$.

Substituting Equation (31) into Equation (30), we obtain

$${\chi }_M=\beta k_N^{2}N,$$

(32)

which is Curie’s formula, telling us that for fixed N in the high-temperature regime, ${\chi }_M$ decays with the temperature as $1/T$.

5.2. Curie’s Law for Relativistic Magnetized Neutrons

For the neutron system, the particle number densities for spin up and down are given by

$$N_{(+/-)}={\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}{e}^{\beta ({ϵ}_R-\mu )},$$

(33)

with

$${ϵ}_R=\sqrt{p_3^2+{\left(\sqrt{M_N^2+p_{\perp }^2}+\sigma k_{N}B\right)}^2},\sigma =\pm$$

(34)

Substituting Equation (33) into Equation (30), we obtain in the leading approximation (i.e., taking $M_N/T=\mu /T=0$)

$${\chi }_M=\beta C{k}_N^{2}N,$$

(35)

where the coefficient C plays the role here of a relativistic correction to Curie’s law (Equation (32)). It is given in the leading approximation by

$$C=\left[{\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}\frac{|p_{\perp }|}{|\overrightarrow{p}|}{e}^{-|\overrightarrow{p}|}\right]{\left[{\int }_{-\infty }^{\infty }\frac{d^{3}p}{{\left(2\pi \right)}^3}{e}^{-|\overrightarrow{p}|}\right]}^{-1}=\pi /4$$

(36)

Thus, we conclude that, if the particle number density N is constant, the magnetic susceptibility of the magnetized neutron system decays with the temperature as $1/T$. On the contrary, if what is fixed is the baryonic chemical potential $\mu$ instead of the particle number density N, then we can see that ${\chi }_M$ will increases as $T^2$. This is the case considered in Ref. [18] and that is more suited to describe the situation in NS where, because of the $\beta$-equilibrium condition, the number of neutrons is not fixed, but the number of baryons is what is conserved.

6. Conclusions

In this paper, we present the results for the effects of a uniform and constant magnetic field on the EOS of a neutron system at finite density. The neutrons, although electrically neutral, being composite particles formed by charged quarks, are endowed with an anomalous magnetic moment that can interact with an applied magnetic field. Taking into account that NS at moderate densities are mainly comprised by neutrons and that magnetic fields of significant strengths are present in most of these compact objects, the outcomes of our analysis are of interest for the astrophysics of NS.

We analyzed three effects that are present in this system and that imply a softening of the equation of state of nuclear matter. These effects can be enumerated as follows: First, the large neutron mass will require that $\mu >M_N$ in order to have a well defined Fermi sphere for the neutron many-particle system in a magnetic field. This already demands a baryonic chemical potential $\mu \sim 1$ GeV. Second, the presence of the magnetized QFT contribution pulls down the system pressure making necessary a higher density (i.e., $\mu >2.25$ GeV) to produce a positive matter pressure that can sustain the gravitational pull of a neutron star with a mass of $M_{NS}=1.4M_{\odot }$. Third, the magnetic-field-induced decrease in the pressure directed along the field, limits the maximum value of the magnetic field that the NS can sustain. In particular, for this model, the zero pressure is reached at a magnetic field value of order ${10}^{18}$ G, which was the needed value to produce a significant effect in the system EOS in the context of an isotropic model [13]. We should point out that, when the pressure anisotropy in the presence of a magnetic field is taken into account in the magneto-hydrostatic equilibrium between the matter and gravitational pressures the inner maximum value that the magnetic field can reach in a compact star is reduced to one order of magnitude smaller than the value that was obtained by using the scalar virial theorem for nuclear matter in Ref. [10]. Then, the maximum field found in [18] for a $1.4M_{\odot }$, $R=12$ km star is of order ${10}^{17}$ G.

Therefore, in this scenario, the need of a density higher than (2–3)${\rho }_n$ (which corresponds to chemical potentials $\mu \sim 1.2$ GeV) to maintain the star’s magneto-hydrostatic equilibrium in the presence of a magnetic field is mandatory. Thus, as explained in the Introduction, under these conditions, the conversion of nucleons into hyperons becomes energetically favorable with the consequent release of the Fermi pressure exerted by the nucleons making the EOS soft enough to lead to a significant reduction of the star mass [5,6,7]. Hence, we conclude that a magnetic field is negatively affecting the possibility to reach the 2$M_{\odot }$ with a nucleon inner phase.

Here, we also proved that the magnetization of this system gets a significant contribution from the magnetized vacuum. This is a consequence of the appearance of terms that combine the magnetic field with the energy scale $\Lambda$ of this non-renormalizable model. Other situations where the energy scale makes significant contributions in magnetized systems can be found in the value of the chiral condensate of the Nambu–Jona–Lasinio version of QCD [26,27] and in the gap of the magnetic color–flavor–locking phase of color superconductivity [28,29,30]. All this indicates that, in finding the system magnetization at moderately large magnetic fields, neither the particle-contribution alone (given by the curve M2 in Figure 7), nor the calculation from the system polarization (Equation (28)) (given by the curve M1 in Figure 7) will be correct.

An additional point we discussed is the paramagnetic behavior of this system, which is expressed by its temperature dependence at a fixed particle-number density in the high-temperature regime that is given by Curie’s law.

Finally, we want to point out that it would be interesting to expand the study we carried out here only for neutrons to the more realistic situation of the inner composition of NS, where more baryonic and mesonic degrees of freedom will participate, and to see the implications of our results for the system $\beta$ equilibrium, as well as for the superfluidity and superconductivity states that can be realized in the more realistic stellar medium.