Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure
Abstract
1. Introduction
2. Basic Equations and Assumptions
2.1. Vertical Integrated Equations
2.2. Self-Similar Assumptions
3. Results
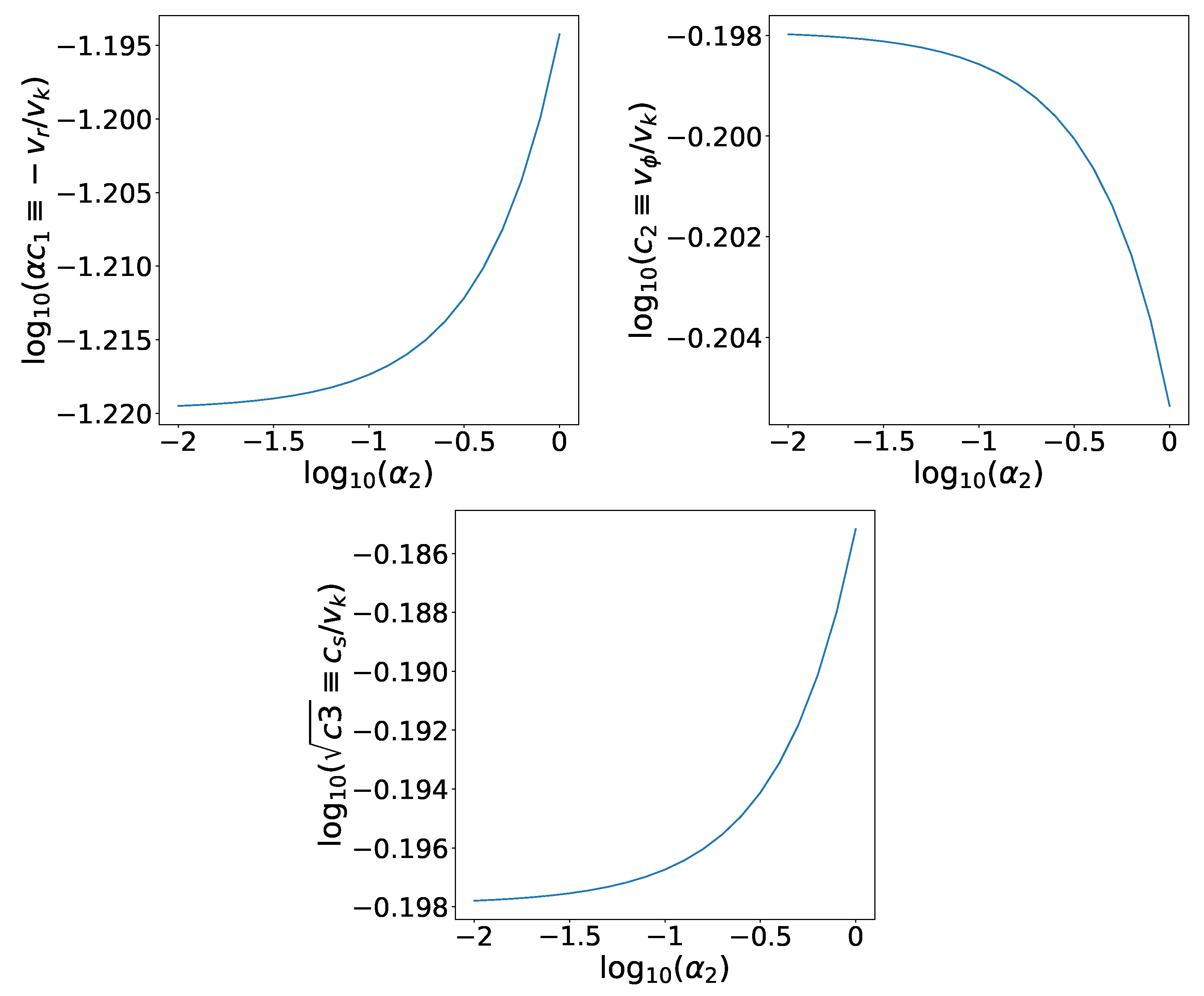
3.1. Accretion Flow without Outflow
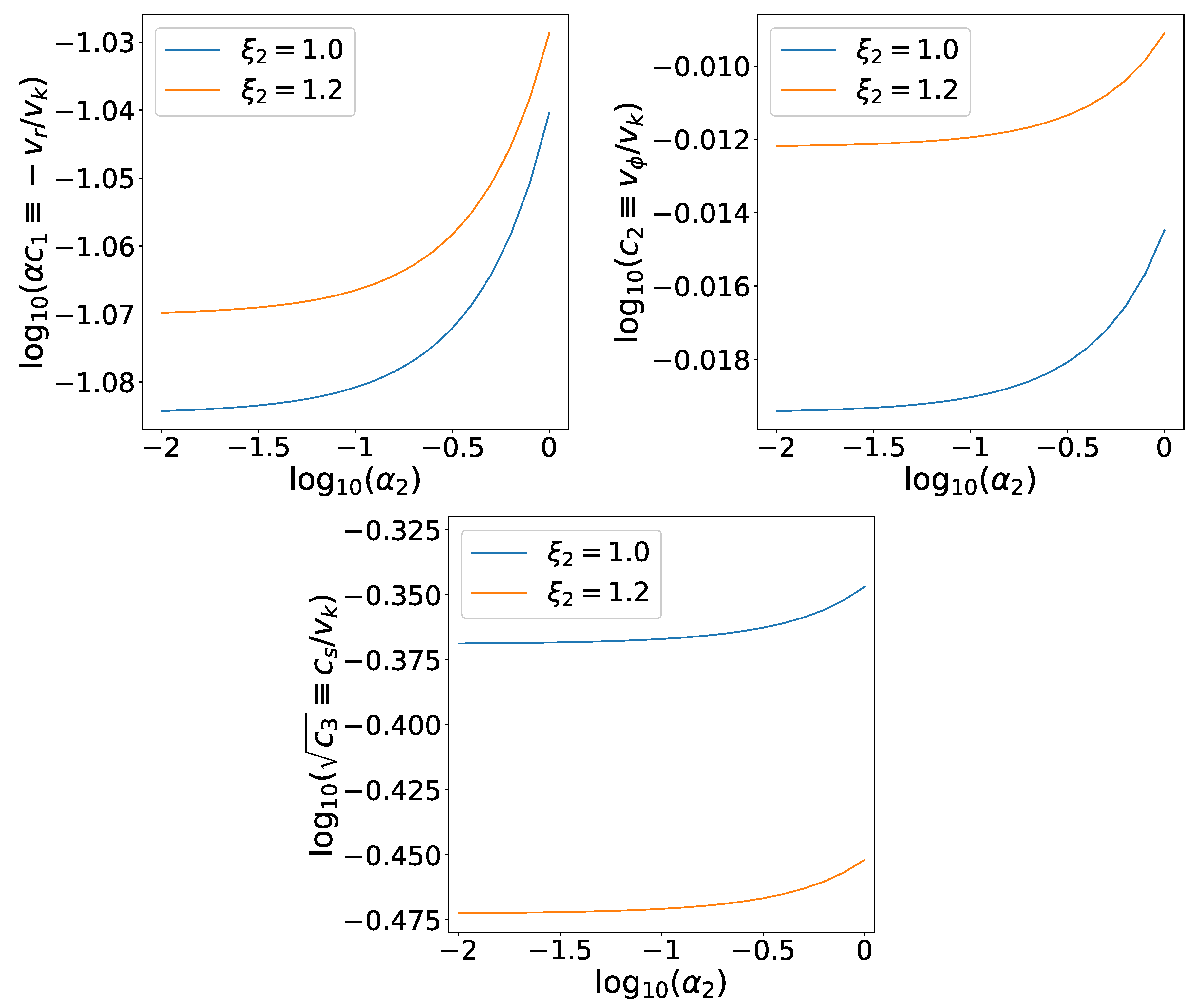
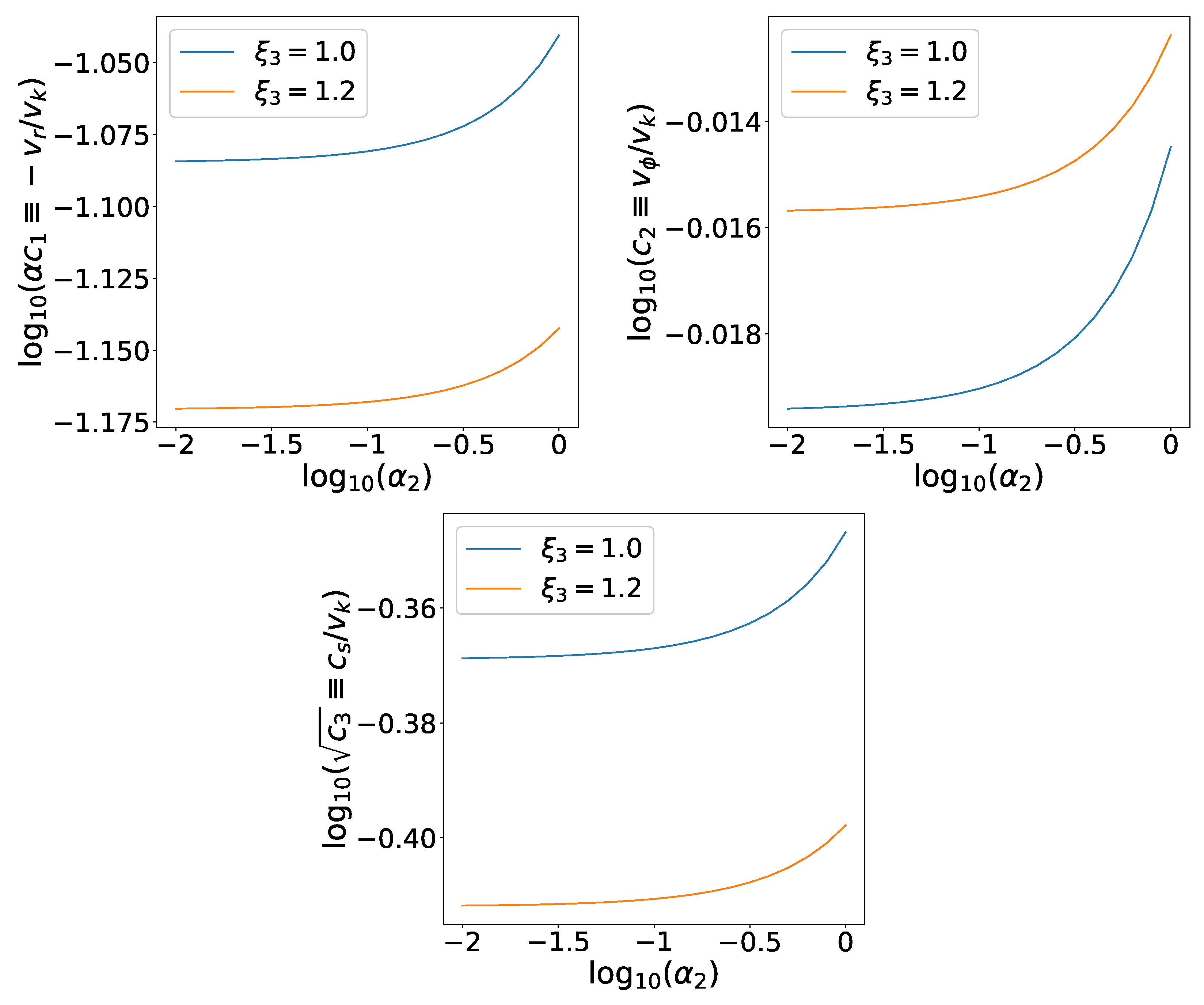
3.2. Accretion Flow with Outflow
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Casse, F.; Keppens, R. Magnetized Accretion-Ejection Structures: 2.5-dimensional Magnetohydrodynamic Simulations of Continuous Ideal Jet Launching from Resistive Accretion Disks. Astrophys. J. 2002, 581, 998–1001. [Google Scholar] [CrossRef]
- Casse, F.; Keppens, R. Radiatively Inefficient Magnetohydrodynamic Accretion-Ejection Structures. Astrophys. J. 2004, 601, 90. [Google Scholar] [CrossRef]
- Zanni, C.; Ferrari, A.; Massaglia, S.; Bodo, G.; Rossi, P. Launching jets from resistive accretion disks. Mem della Soc. Astron. Italiana 2005, 76, 372. [Google Scholar]
- Zanni, C.; Ferrari, A. MHD simulations of jet acceleration from Keplerian accretion disks. The effects of disk resistivity. Astron. Astrophys. 2007, 469, 811. [Google Scholar] [CrossRef]
- Sheikhnezami, S.; Fendt, C.; Porth, O.; Vaidya, B.; Ghanbari, J. Bipolar Jets Launched from Magnetically Diffusive Accretion Disks. I. Ejection Efficiency versus Field Strength and Diffusivity. Astrophys. J. 2012, 757, 65. [Google Scholar] [CrossRef]
- Sheikhnezami, S.; Fendt, C. MHD simulations of jet-launching from diffusive magnetized accretion disks. Eur. Conf. Lab. Astrophys. 2012, 58, 113–116. [Google Scholar] [CrossRef][Green Version]
- Sheikhnezami, S.; Fendt, C. Long-term Simulation of MHD Jet Launching in an Orbiting Star-Disk System. Astrophys. J. 2018, 861, 11. [Google Scholar] [CrossRef]
- Takahashi, M.; Nitta, S.; Yoshinori, T.; Akira, T. Magnetohydrodynamic flows in Kerr geometry—Energy extraction from black holes. Astrophys. J. 1990, 363, 206–217. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F. Three-dimensional Hydrodynamic Simulations of Accretion Tori in Kerr Spacetimes. Astrophys. J. 2002, 577, 866. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F. A Numerical Method for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 458. [Google Scholar] [CrossRef]
- Gammie, C.F.; McKinney, J.C. Tóth, G. HARM: A Numerical Scheme for General Relativistic Magnetohydrodynamics. Astrophys. J. 2003, 589, 444. [Google Scholar] [CrossRef]
- Noble, S.C.; Krolik, J.H.; Schnittman, J.D.; Hawley, J.F. Radiative Efficiency and Thermal Spectrum of Accretion onto Schwarzschild Black Holes. Astrophys. J. 2011, 743, 115. [Google Scholar] [CrossRef]
- Sądowski, A.; Abramowicz, M.; Bursa, M.; Kluzniak, W.; Lasota, J.; Rozanska, A. Relativistic slim disks with vertical structure. Astron. Astrophys. 2011, 527, 17. [Google Scholar] [CrossRef]
- Hawley, J.F.; Fendt, C.; Hardcastle, M.; Nokhrina, E.; Tchekhovskoy, A. Disks and Jets. Gravity, Rotation and Magnetic Fields. Space Sci. Rev. 2015, 191, 441. [Google Scholar] [CrossRef]
- Ho, L. Nuclear activity in nearby galaxies. Annu. Rev. Astron. Astrophys. 2008, 46, 475–539. [Google Scholar] [CrossRef]
- Narayan, R.; Yi, I. Advection-dominated accretion: A self-similar solution. Astrophys. J. 1994, 428, L13. [Google Scholar] [CrossRef]
- Yuan, F.; Narayan, R. Hot accretion flows around black holes. Ann. Rev. Astron. Astrophys. 2014, 52, 529. [Google Scholar] [CrossRef]
- Done, C.; Gierliński, M.; Kubota, A. Modelling the behaviour of accretion flows in X-ray binaries. Everything you always wanted to know about accretion but were afraid to ask. Astron. Astrophys. Rev. 2007, 15, 1–66. [Google Scholar] [CrossRef]
- Qiao, E.; Liu, B. Dependence of spectral state transition and disk truncation on viscosity parameter alpha. Publ. Astron. Soc. Jpn. 2009, 61, 403–410. [Google Scholar] [CrossRef]
- Gilfanov, M. X-ray Emission from Black-Hole Binaries. In Lecture Notes in Physics; The Jet Paradigm-From Microquasars to Quasars; Belloni, T., Ed.; Springer: Berlin, Germany, 2010; Volume 794, p. 17. [Google Scholar]
- Zhang, S.; Liao, J.; Yao, Y. Measuring the black hole masses in accreting X-ray binaries by detecting the Doppler orbital motion of their accretion disc wind absorption lines. Mon. Not. R. Astron. Soc. 2012, 421, 3550. [Google Scholar] [CrossRef][Green Version]
- Yan, Z.; Yu, W. Detection of X-ray spectral state transitions in mini-outbursts of black hole transient GRS 1739-278. Mon. Not. R. Astron. Soc. 2017, 470, 4298–4306. [Google Scholar] [CrossRef]
- Yuan, F.; Bu, D.; Wu, M. Numerical simulation of hot accretion flows. II. nature, origin, and properties of outflows and their possible observational applications. Astrophys. J. 2012, 761, 130. [Google Scholar] [CrossRef]
- Yuan, F.; Gan, Z.; Narayan, R.; Sadowski, A.; Bu, D.; Bai, X. Numerical simulation of hot accretion flows. III. revisiting wind properties using the trajectory approach. Astrophys. J. 2015, 804, 101. [Google Scholar] [CrossRef]
- Narayan, R.; Sadowski, A.; Penna, R.F.; Kulkarni, A.K. GRMHD simulations of magnetized advection- dominated accretion on a non-spinning black hole: Role of outflows. Mon. Not. R. Astron. Soc. 2012, 426, 3241. [Google Scholar] [CrossRef]
- Li, J.; Ostriker, J.; Sunyaev, R. Rotating accretion flows: From infinity to the black hole. Astrophys. J. 2013, 767, 105. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Wu, M.; Cuadra, J. On the role of initial and boundary conditions in numerical simulations of accretion flows. Mon. Not. R. Astron. Soc. 2013, 434, 1692. [Google Scholar] [CrossRef][Green Version]
- Bu, D.; Yuan, F.; Gan, Z.; Yang, X. Hydrodynamical numerical simulation of wind production from black hole hot accretion flows at very large radii. Astrophys. J. 2016, 818, 83. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Gan, Z.; Yang, X. Magnetohydrodynamic numerical simulation of wind production from hot accretion flows around black holes at very large radii. Astrophys. J. 2016, 823, 90. [Google Scholar] [CrossRef]
- Xue, L.; Wang, J. The effect of outflow on advection-dominated accretion. Astrophys. J. 2005, 623, 372. [Google Scholar] [CrossRef][Green Version]
- Akizuki, C.; Fukue, J. Self-similar solutions for ADAF with toroidal magnetic fields. Mon. Not. R. Astron. Soc. 2006, 58, 469–475. [Google Scholar] [CrossRef]
- Bu, D.; Yuan, F.; Xie, F. Self-similar solution of hot accretion flows with ordered magnetic field and outflow. Mon. Not. R. Astron. Soc. 2009, 392, 325. [Google Scholar] [CrossRef]
- Li, S.; Cao, X. Global dynamics of advection-dominated accretion flows with magnetically driven outflow. Mon. Not. R. Astron. Soc. 2009, 400, 1734. [Google Scholar] [CrossRef]
- Jiao, C.; Wu, X. On the structure of accretion disks with outflows. Astrophys. J. 2011, 733, 112. [Google Scholar] [CrossRef]
- Begelman, M.C. Radiatively inefficient accretion: Breezes, winds and hyperaccretion. Mon. Not. R. Astron. Soc. 2012, 420, 2912. [Google Scholar] [CrossRef][Green Version]
- Wu, Q.; Cao, X.; Ho, L.C.; Wang, D. A physical link between jet formation and hot plasma in active galactic nuclei. Astrophys. J. 2013, 770, 31. [Google Scholar] [CrossRef]
- Gu, W. Mechanism of Outflows in Accretion System: Advective Cooling cannot Balance Viscous Heating? Astrophys. J. 2015, 799, 71. [Google Scholar] [CrossRef]
- Cao, X. An accretion disk-outflow model for hysteretic state transition in X-ray binaries. Astrophys. J. 2016, 817, 71. [Google Scholar] [CrossRef]
- Ghasemnezhad, M.; Abbassi, S. The influence of large-scale magnetic field in the structure of supercritical accretion flow with outflow. Mon. Not. R. Astron. Soc. 2017, 469, 3307. [Google Scholar] [CrossRef]
- Kumar, R.; Gu, W. The 2D disk structure with advective transonic inflow-outflow solutions around black holes. Astrophys. J. 2018, 860, 114. [Google Scholar] [CrossRef]
- Crenshaw, D.M.; Kraemer, S.B. Feedback from mass outflows in nearby active galactic nuclei. I. ultraviolet and X-ray absorbers. Astrophys. J. 2012, 753, 75. [Google Scholar] [CrossRef]
- Cheung, E.; Bundy, K.; Cappellari, M.; Peirani, S.; Rujopakarn, W.; Westfall, K.; Yan, R.; Bershady, M.; Greene, J.E.; Heckman, T.M.; et al. Suppressing star formation in quiescent galaxies with supermassive black hole winds. Nature 2016, 533, 504–508. [Google Scholar] [CrossRef] [PubMed]
- Homan, J.; Neilsen, J.; Allen, J.L.; Chakrabarty, D.; Fender, R.; Fridriksson, J.K.; Remillard, R.A.; Schulz, N. Evidence for simultaneous jets and disk winds in luminous low-mass X-ray binaries. Astrophys. J. 2016, 830, L5. [Google Scholar] [CrossRef]
- Ma, R.; Roberts, S.R.; Li, Y.; Wang, Q.D. Spectral energy distribution of the inner accretion flow around Sgr A*—Clue for a weak outflow in the innermost region. Mon. Not. R. Astron. Soc. 2019, 483, 5614. [Google Scholar] [CrossRef]
- Park, J.; Hada, K.; Kino, M.; Nakamura, M.; Ro, H.; Trippe, S. Faraday rotation in the jet of M87 inside the bondi radius: Indication of winds from hot accretion flows confining the relativistic jet. Astrophys. J. 2019, 871, 257. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Choi, E.; Ciotti, L.; Novak, G.S.; Proga, D. Momentum driving: Which physical processes dominate active galactic nucleus feedback? Astrophys. J. 2010, 722, 642. [Google Scholar] [CrossRef]
- Ciotti, L.; Ostriker, J.P.; Proga, D. Feedback from central black holes in elliptical galaxies. III. models with both radiative and mechanical feedback. Astrophys. J. 2010, 717, 708. [Google Scholar] [CrossRef]
- Ciotti, L.; Pellegrini, S.; Negri, A.; Ostriker, J.P. The effect of the AGN feedback on the interstellar medium of early-type galaxies:2D hydrodynamical simulations of the low-rotation case. Astrophys. J. 2017, 835, 15. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Hernquist, L.; Pillepich, A.; Marinacci, F.; Pakmor, R.; Nelson, D.; Genel, S.; Vogelsberger, M.; Naiman, J.; et al. Simulating galaxy formation with black hole driven thermal and kinetic feedback. Mon. Not. R. Astron. Soc. 2017, 465, 3291. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Pakmor, R.; Nelson, D.; Genel, S.; Pillepich, A.; Vogelsberger, M.; Marinacci, F.; Naiman, J.; Torrey, P.; et al. Supermassive black holes and their feedback effects in the IllustrisTNG simulation. Mon. Not. R. Astron. Soc. 2018, 479, 4056–4072. [Google Scholar] [CrossRef]
- Yuan, F.; Yoon, D.; Li, Y.; Gan, Z.-M.; Ho, L.C.; Guo, F. Active galactic nucleus feedback in an elliptical galaxy with the most updated AGN physics. I. low angular momentum case. Astrophys. J. 2018, 857, 121. [Google Scholar] [CrossRef]
- Yoon, D.; Yuan, F.; Gan, Z.; Ostriker, J.P.; Li, Y.; Ciotti, L. Active galactic nucleus feedback in an elliptical galaxy with the most updated AGN physics. II. high angular momentum case. Astrophys. J. 2018, 864, 6. [Google Scholar] [CrossRef]
- Bu, D.; Yang, X. Quenching black hole accretion by active galactic nuclei feedback. Astrophys. J. 2019, 871, 138. [Google Scholar] [CrossRef]
- Tanaka, T.; Menou, K. Hot accretion with conduction: Spontaneous thermal outflows. Astrophys. J. 2006, 649, 345. [Google Scholar] [CrossRef]
- Johnson, B.M.; Quataert, E. The effects of thermal conduction on radiatively inefficient accretion flows. Astrophys. J. 2007, 660, 1273. [Google Scholar] [CrossRef][Green Version]
- Foucart, F.; Chandra, M.; Gammie, C.F.; Quataert, E. Evolution of accretion discs around a kerr black hole using extended magnetohydrodynamics. Mon. Not. R. Astron. Soc. 2016, 456, 1332. [Google Scholar] [CrossRef]
- Kunz, M.W.; Schekochihin, A.A.; Stone, J.M. Firehose and mirror instabilities in a collisionless shearing plasma. Phys. Rev. Lett. 2014, 112, 205003. [Google Scholar] [CrossRef]
- Riquelme, M.A.; Quataert, E.; Verscharen, D. Particle-in-cell simulations of continuously driven mirror and ion clotron instabilities in high beta astrophysical and heliospheric plasmas. Astrophys. J. 2015, 800, 27. [Google Scholar] [CrossRef]
- Sironi, L.; Narayan, R. Electron heating by the ion cyclotron instability in collisionless accretion flows. I. compression-driven instabilities and the electron heating mechanism. Astrophys. J. 2015, 800, 88. [Google Scholar] [CrossRef]
- Parrish, I.J.; Stone, J.M. Saturation of the magnetothermal instability in three dimensions. Astrophys. J. 2007, 664, 135. [Google Scholar] [CrossRef]
- Sharma, P.; Quataert, E.; Stone, J.M. Spherical accretion with anisotropic thermal conduction. Mon. Not. R. Astron. Soc. 2008, 389, 1815. [Google Scholar] [CrossRef][Green Version]
- Bu, D.; Yuan, F.; Stone, J.M. Magnetothermal and magnetorotational instabilities in hot accretion flows. Mon. Not. R. Astron. Soc. 2011, 413, 2808. [Google Scholar] [CrossRef][Green Version]
- Bu, D.; Wu, M.; Yuan, Y. Effects of anisotropic thermal conduction on wind properties in hot accretion flow. Mon. Not. R. Astron. Soc. 2016, 459, 746. [Google Scholar] [CrossRef][Green Version]
- Quataert, E.; Dorland, W.; Hammett, G.W. The magnetorotational instability in a collisionless plasma. Astrophys. J. 2002, 577, 524. [Google Scholar] [CrossRef]
- Sharma, P. Hammett, G.W.; Quataert, E. Transition from collisionless to collisional magnetorotational instability. Astrophys. J. 2003, 596, 1121. [Google Scholar] [CrossRef]
- Chandra, M.; Gammie, C.F.; Foucart, F.; Quataert, E. An extended magnetohydrodynamics model for relativistic weakly collisional plasmas. Astrophys. J. 2015, 810, 162. [Google Scholar] [CrossRef]
- Balbus, S.A. Viscous shear instability in weakly magnetized, dilute plasmas. Astrophys. J. 2004, 616, 857. [Google Scholar] [CrossRef][Green Version]
- Islam, T.; Balbus, S. Dynamics of the magnetoviscous instability. Astrophys. J. 2005, 633, 328. [Google Scholar] [CrossRef][Green Version]
- Wu, M.; Bu, D.; Gan, Z.; Yuan, Y. Hot accretion flow with anisotropic viscosity. Astron. Astrophys. 2017, 608, 114. [Google Scholar] [CrossRef][Green Version]
- Yuan, F.; Quataert, E.; Narayan, R. Nonthermal Electrons in Radiatively Inefficient Accretion Flow Models of Sagittarius A*. Astrophys. J. 2003, 598, 301. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I—Linear analysis. II—Nonlinear evolution. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. Turbulent transport in accretion disks. AIP Conf. Proc. 1998, 431, 79. [Google Scholar]
- King, A.R.; Pringle, J.E.; Livio, M. Accretion disc viscosity: How big is alpha? Mon. Not. R. Astron. Soc. 2007, 376, 1740. [Google Scholar] [CrossRef]
- Machida, M.; Hayashi, M.R.; Matsumoto, R. Global simulations of differentially rotating magnetized disks: Formation of low-beta filaments and structured coronae. Astrophys. J. 2000, 532, L67. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; De Villiers, J.P.; Hawley, J.F. Magnetically driven accretion flows in the kerr metric. II. structure of the magnetic field. Astrophys. J. 2004, 606, 1083. [Google Scholar] [CrossRef]
- Bai, X.; Stone, J.M. Local study of accretion disks with a strong vertical magnetic field: Magnetorotational instability and disk outflow. Astrophys. J. 2013, 767, 30. [Google Scholar] [CrossRef]
- Lavelace, R.E.V.; Romanova, M.M. Implosive accretion and outbursts of active galactic nuclei. Astrophys. J. 1994, 437, 136–143. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; Stone, J.M. Vertical structure of gas pressure-dominated accretion disks with local dissipation of turbulence and radiative transport. Astrophys. J. 2006, 640, 901. [Google Scholar] [CrossRef]
- Braginskii, S.I. Transport processes in a plasma. Rev. Plasma Phys. 1965, 1, 205. [Google Scholar]
- Xie, F.; Yuan, F. The Influences of outflow on the dynamics of inflow. Astrophys. J. 2008, 681, 499. [Google Scholar] [CrossRef]
- Stone, J.M.; Pringle, J.E.; Begelman, M.C. Hydrodynamical non-radiative accretion flows in two dimensions. Mon. Not. R. Astron. Soc. 1999, 310, 1002. [Google Scholar] [CrossRef]
- Wang, Q.D.; Nowak, M.A.; Markoff, S.B.; Baganoff, F.K.; Nayakshin, S.; Yuan, F.; Cuadra, J.; Davis, J.; Dexter, J.; Fabian, A.C.; et al. Dissecting X-ray-emitting gas around the center of our galaxy. Science 2013, 341, 981–983. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, D.-F.; Xu, P.-Y.; Zhu, B.-C. Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure. Universe 2019, 5, 89. https://doi.org/10.3390/universe5040089
Bu D-F, Xu P-Y, Zhu B-C. Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure. Universe. 2019; 5(4):89. https://doi.org/10.3390/universe5040089
Chicago/Turabian StyleBu, De-Fu, Pei-Yao Xu, and Bo-Cheng Zhu. 2019. "Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure" Universe 5, no. 4: 89. https://doi.org/10.3390/universe5040089
APA StyleBu, D.-F., Xu, P.-Y., & Zhu, B.-C. (2019). Self-Similar Solution of Hot Accretion Flow with Anisotropic Pressure. Universe, 5(4), 89. https://doi.org/10.3390/universe5040089




