Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects
Abstract
1. Introduction
1.1. Basics of the Gravitational Radiation Theory
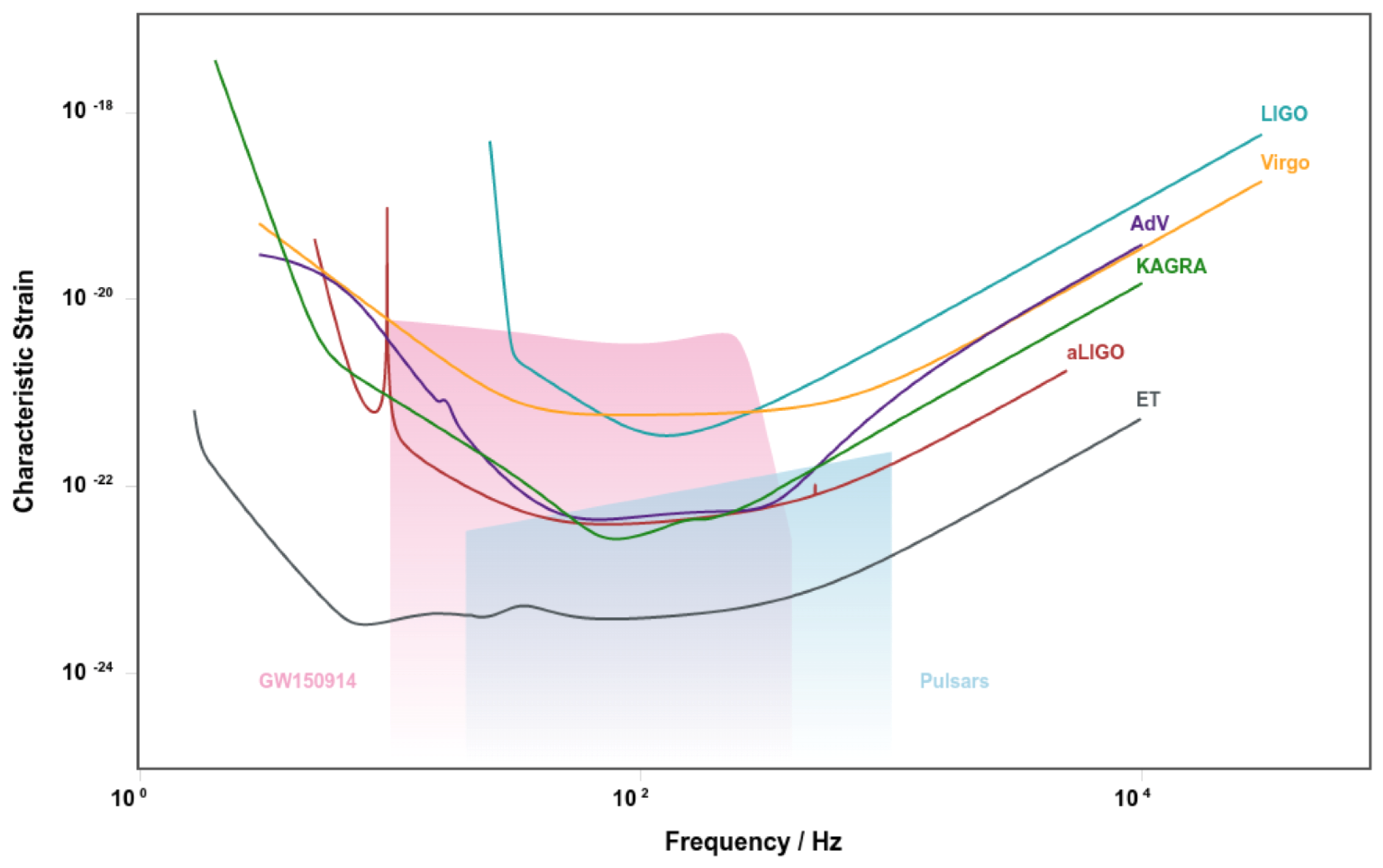
1.2. Brief History of Gravitational Waves Detections
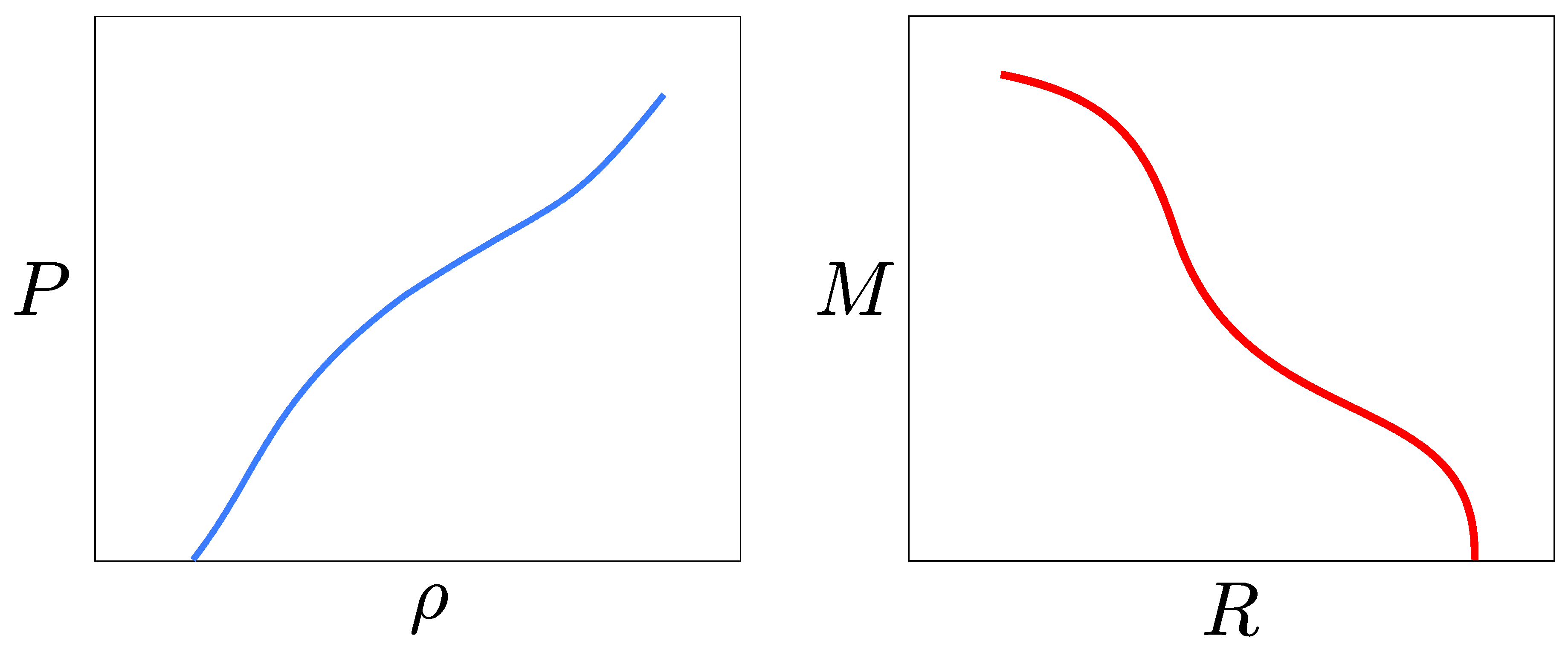
1.3. Properties of Neutron Stars
1.4. General Information about Continuous Gravitational Waves
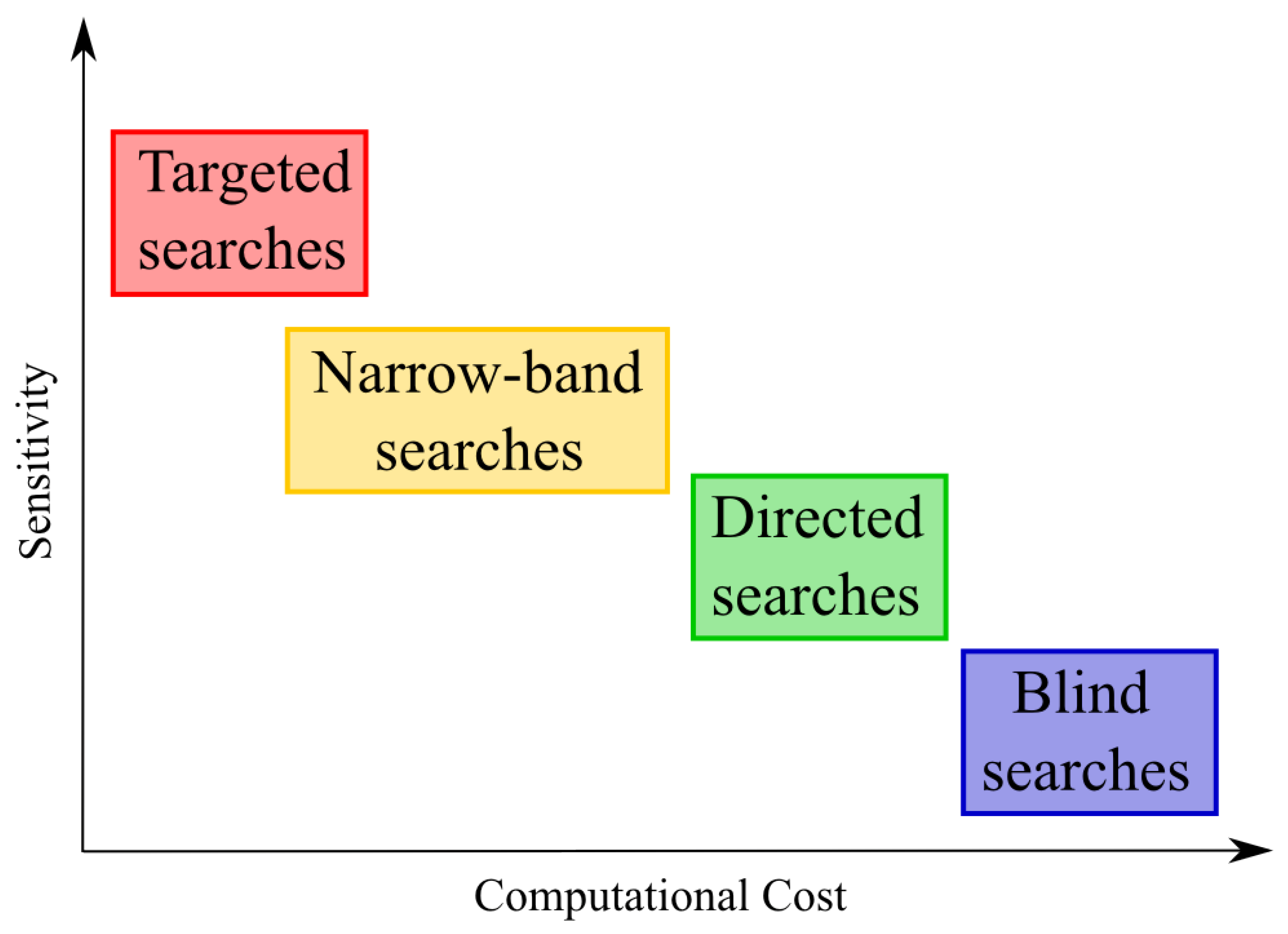
1.5. Methods and Strategies of CGWs Searches
- The -statistic method introduced in [13]. The -statistic is obtained by maximizing the likelihood function with respect to four unknown parameters of the simple CGW model of rotating NSs—CGW amplitude , initial phase of the wave , inclination angle of NS rotation axis with respect to the line of sight , and polarisation angle of the wave (which are henceforth called the extrinsic parameters). This leaves a function of only four remaining parameters: , , and (called the intrinsic parameters). Thus the dimension of the parameter space that we need to search decreases from 8 to 4. To reduce computational cost and improve method efficiency, the -statistic can be evaluated on the 4-dimensional optimal grid of the intrinsic parameters [117]. As was shown in Equation (20), strength of the signal depends on the observational time: on the one hand by increasing T one can expect a detection of weaker signals, on the other hand however, analysing long-duration data requires substantial computational resources, e.g., for Polgraw time-domain F-statistic pipeline7, computational cost for an all-sky search scales as . Promising strategies to solve this problem are hierarchical semi-coherent methods, in which data is broken into short segments. In the first stage, each segment is analysed with the -statistic method. In second stage, the short time segments results are combined incoherently using a certain algorithm. Several methods were proposed for the second stage: search for coincidences among candidates from short segments [118,119], stack-slide method [101,120,121], PowerFlux method [122,123] with the latest significant search sensitivity improvements for O1 data [124,125], global correlation coordinate method [126,127], Weave method [128,129]. Independently of the details, the main goal of the -statistic method is to find the maximum of function, and hence the parameters associated with the signal. Several optimisation procedures (such as optimal grid-based or non-derivative algorithms) were implemented in such analyses [130,131,132]. -statistic can be evaluated on the time-domain data [13,47,49,117,130,133] and the frequency-domain data [101,118,119,120,134,135]. The main difference between these two concepts is that in the time-domain the information is distributed across the entire data set, while the frequency-domain analysis focuses on the part of the data around the frequency at which the peak appears. The data is initially calibrated in the time-domain and to be used by the frequency-domain methods, usually it is converted with the Fourier Transform methods.
- The Hough transform [136,137] is a widely used method to detect patterns in images. It can be applied to detect the CGWs signals in specific representations of the data: on the sky [138], and in frequency-spin-down plane [139,140]. Both types of the Hough transform method, called SkyHough and FrequencyHough, are typically used for all-sky searches and are similar to the -statistic are matched-filtering type methods. Due to limited computational power, they require division of data into relatively short segments. Interesting application of the Hough transform to the unknown sources searches was introduced in [141]. This Generalised FrequencyHough algorithm is sensitive to the braking index n, a quantity that determines the frequency behaviour of an expected signal as a function of time. In general, the evolution (decrease) of rotational frequency is described aswhere K is a positive constant. Time derivative of the above equation provides the dependency of the braking index on measurable quantities (from EM observations, e.g., [142,143,144,145]), frequency and its higher derivatives:Value of the braking index reveals a spin-down mechanism: if the spin-down is triggered by the relativistic particle wind; , if the spin-down is dominated by dipole radiation (as in the case of dipolar EM field); if it is purely quadrupolar radiation (GWs emission in General Relativity); if the spin-down is due to the oscillations (lowest order r-modes, see Section 4 for further details). Some of the CGWs searches strategies assume that object is spinning-down only due to the gravitational radiation (), as it was mentioned with Equations (33) and (34), while Generalised FrequencyHough method does not assume any specific spin-down mechanism, but allows for its examination.
- The 5-vector method [146], in which detection of the signal is based on matching a filter to the signal + and × polarization Fourier components. The antenna response function depends on Earth sidereal angular frequency and results in a splitting of the signal power among five angular frequencies , and , where . This method is typically used for narrowband and targeted searches.
- The Band Sampled Data (BSD) method, is dedicated for the directed searches, or those assuming limited sky regions, such as the Galactic Centre [147]. The application of this method results in a gain in sensitivity at a fixed computational cost, as well as gain in robustness with respect to source parameter uncertainties and instrumental disturbances. From the cleaned, band-limited and down-sampled time series, collection of the overlapped short Fourier Transforms is produced. Then, the inverse Fourier Transform allows removing overlap, edge and windowing effects. Demodulation of the signal from the Doppler and spin-down effects can be done e.g., by using heterodyne technique (see below). While in the -statistic method one could manipulate with the search sensitivity by increasing the observation time, BSD method works in Fourier-domain and analogously can be improved by increasing length of frequency bands (for comparison: bandwidth in -statistic method is typically Hz and in BSD Hz).
- The time-domain heterodyne method [148] is a targeted search which uses the EM measurements of , and (model of the phase evolution, Equation (26), assumes ). The signal depends on four unknown parameters: , , and . Due to the Earth’s rotation, amplitude of the signal recorded by an interferometric detector is time-varying since the source moves through the antenna pattern (see Equations (8)–(10)). These variations, in the heterodyne method, are used to find characteristic frequency which is the instantaneous signal frequency, register at the detector. Additionally, frequency of the signal seen in the detector is affected due to the Earth motion. Second important step of the demodulation is to remove the Doppler shifts (correct signal time-of-arrival). A targeted search is performed with a simple Bayesian parameter estimation: first the data is heterodyned with an expected phase evolution and binned to short (e.g., 1 min) samples. Then, marginalisation over the unknown noise level is performed, assuming Gaussian and stationary noise over sufficiently long (e.g., of the order of 30 min) periods. 95% upper limit is defined, inferred by the analysis, in terms of a cumulative posterior, with uniform priors on orientation and strain amplitude. At the end the parameter estimation is done by numerical marginalisation. Effective and commonly used algorithm for the last marginalisation stage is called Markov Chain Monte Carlo [149,150], in which the parameter space is explored more efficiently and without spending much time in the areas with very low probability densities.
2. Elastic Deformations
3. Magnetic Field
4. Oscillations
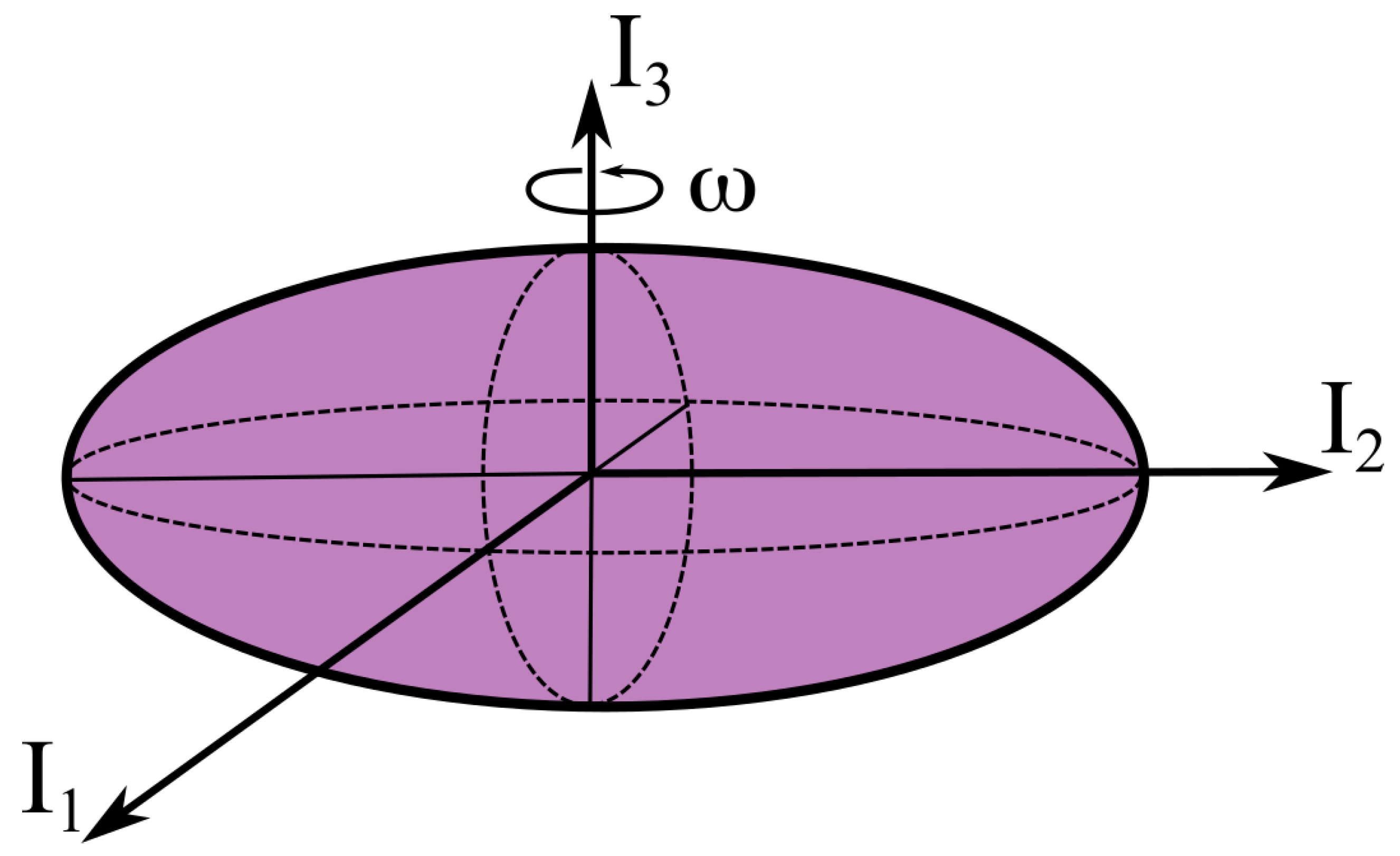
5. Free Precession
6. Summary
Funding
Acknowledgments
Conflicts of Interest
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin, Part 1. Available online: https://ui.adsabs.harvard.edu/abs/1916SPAW.......688E/abstract (accessed on 30 October 2019).
- Einstein, A. Über Gravitationswellen. Available online: https://ui.adsabs.harvard.edu/abs/1918SPAW.......154E/abstract (accessed on 30 October 2019).
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A. Analysis of Gravitational-Wave Data; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: Emission by the magnetic field induced distortion. Astron. Astrophys. 1996, 312, 675. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: San Francisco, CA, USA, 1973; Chapter 36. [Google Scholar]
- Prix, R. Gravitational Waves from Spinning Neutron Stars. In Neutron Stars and Pulsars; Becker, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 357. [Google Scholar]
- Jaranowski, P.; Królak, A. Optimal solution to the inverse problem for the gravitational wave signal of a coalescing compact binary. Phys. Rev. D 1994, 49, 1723. [Google Scholar] [CrossRef] [PubMed]
- Schutz, B.F.; Tinto, M. Antenna patterns of interferometric detectors of gravitational waves – I. Linearly polarized waves. Mon. Not. R. Astron. Soc. 1987, 224, 131. [Google Scholar] [CrossRef]
- Thorne, K.S. In 300 Years of Gravitation; Hawking, S.W., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1987; Chapter 9; p. 330. [Google Scholar]
- Jaranowski, P.; Królak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58, 063001. [Google Scholar] [CrossRef]
- Zimmerman, M.; Szedenits, E. Gravitational waves from rotating and precessing rigid bodies: Simple models and applications to pulsars. Phys. Rev. D 1979, 20, 351. [Google Scholar] [CrossRef]
- Paczyński, B. Gravitational Waves and the Evolution of Close Binaries. Acta Astron. 1967, 17, 287. [Google Scholar]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51. [Google Scholar] [CrossRef]
- Peters, P.C.; Mathews, J. Gravitational Radiation from Point Masses in a Keplerian Orbit. Phys. Rev. 1963, 131, 435. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Taylor, J.H. The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. Bin. Radio Pulsars Asp Conf. Ser. 2005, 328, 25. [Google Scholar]
- Taylor, J.H.; Weisberg, J.M. A new test of general relativity - Gravitational radiation and the binary pulsar PSR 1913+16. Astrophys. J. 1982, 253, 908–920. [Google Scholar] [CrossRef]
- Taylor, J.H.; Weisberg, J.M. Further experimental tests of relativistic gravity using the binary pulsar PSR 1913+16. Astrophys. J. 1989, 345, 434–450. [Google Scholar] [CrossRef]
- Weisberg, J.M.; Nice, D.J.; Taylor, J.H. Timing Measurements of the Relativistic Binary Pulsar PSR B1913+16. Astrophys. J. 2010, 722, 1030–1034. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quantum Grav. 2015, 32, 074001. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170608: Observation of a 19 Solar-mass Binary Black Hole Coalescence. Astrophys. J. Lett. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Estimating the Contribution of Dynamical Ejecta in the Kilonova Associated with GW170817. Astrophys. J. Lett. 2017, 850, L39. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. On the Progenitor of Binary Neutron Star Merger GW170817. Astrophys. J. Lett. 2017, 850, L40. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Post-merger Gravitational Waves from the Remnant of the Binary Neutron Star Merger GW170817. Astrophys. J. Lett. 2017, 851, L16. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Gravitational Waves from a Long-lived Remnant of the Binary Neutron Star Merger GW170817. Astrophys. J. 2019, 875, 160. [Google Scholar] [CrossRef]
- Harry, G.M. [LIGO Scientific Collaboration]. Advanced LIGO: The next generation of gravitational wave detectors. Class. Quantum Grav. 2010, 27, 084006. [Google Scholar] [CrossRef]
- Takahashi, R. [TAMA Collaboration]. Status of TAMA300. Class. Quantum Grav. 2004, 21, 5. [Google Scholar] [CrossRef]
- Willke, B.; Aufmuth, P.; Aulbert, C.; Babak, S.; Balasubramanian, R.; Barr, B.W.; Berukoff, S.; Bose, S.; Cagnoli, G.; Casey, M.M.; et al. The GEO 600 gravitational wave detector. Class. Quantum Grav. 2002, 19, 7. [Google Scholar] [CrossRef]
- Freise, A. [VIRGO Collaboration]. Status of VIRGO. Class. Quantum Grav. 2005, 22, S869–S880. [Google Scholar]
- Abramovici, A.; Althouse, W.E.; Drever, R.W.P.; Gursel, Y.; Kawamura, S.; Raab, F.J.; Shoemaker, D.; Sievers, L.; Spero, R.E.; Thorne, K.S.; et al. LIGO - The Laser Interferometer Gravitational-Wave Observatory. Science 1992, 256, 325. [Google Scholar] [CrossRef]
- Akatsu, T.; Ando, M.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Atsuta, S.; Awai, K.; Barton, M.A.; Cannon, K.; et al. The status of KAGRA underground cryogenic gravitational wave telescope. arXiv 2017, arXiv:1710.04823. [Google Scholar]
- Unnikrishnan, C.S. IndIGO and LIGO-India: Scope and Plans for Gravitational Wave Research and Precision Metrology in India. Int. J. Mod. Phys. D 2013, 22, 1341010. [Google Scholar] [CrossRef]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Ajith, P.; Allen, B.; Amaro-Seoane, P.; Andersson, N.; Aoudia, S.; Arun, K.; Astone, P.; et al. Scientific objectives of Einstein Telescope. Class. Quantum Grav. 2012, 29, 124013. [Google Scholar] [CrossRef]
- Moore, C.J.; Cole, R.H.; Berry, C.P.L. Gravitational-wave sensitivity curves. Class. Quantum Grav. 2015, 32, 015014. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. All-sky search for periodic gravitational waves in the O1 LIGO data. Phys. Rev. D 2017, 96, 062002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First Search for Nontensorial Gravitational Waves from Known Pulsars. Phys. Rev. Lett. 2018, 120, 031104. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data. Phys. Rev. D 2019, 100, 024004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Narrow-band search for gravitational waves from known pulsars using the second LIGO observing run. Phys. Rev. D 2019, 99, 122002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Upper Limits on the Stochastic Gravitational-Wave Background from Advanced LIGO’s First Observing Run. Phys. Rev. Lett. 2017, 118, 121101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Search for Tensor, Vector, and Scalar Polarizations in the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 201102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. All-sky search for short gravitational-wave bursts in the first Advanced LIGO run. Phys. Rev. D 2017, 95, 042003. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Search for transient gravitational wave signals associated with magnetar bursts during Advanced LIGO’s second observing run. arXiv 2019, arXiv:1902.01557. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of stars. Phys. Zs. Sowjetunion 1932, 1, 285. [Google Scholar]
- Yakovlev, D.G.; Haensel, P.; Baym, G.; Pethick, C.J. Lev Landau and the conception of neutron stars. Phys. Uspekhi 2013, 56, 289–295. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. On Super-novae. Proc. Natl. Acad. Sci. USA 1934, 20, 254–259. [Google Scholar] [CrossRef] [PubMed]
- Chadwick, J. The existence of a neutron. Proc. R. Soc. A 1932, 136, 692–708. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of Rapidly Pulsating Radio Source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Cole, T.W. Observations of some further Pulsed Radio Sources. Nature 1968, 218, 126–129. [Google Scholar]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1 Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 2. [Google Scholar] [CrossRef]
- Fortin, M.; Providência, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Gravitational-Wave Candidate Event Database. Available online: https://gracedb.ligo.org/superevents/S190425z/view (accessed on 26 April 2019).
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [PubMed]
- Burgio, G.F.; Drago, A.; Pagliara, G.; Schulze, H.-J.; Wei, J.-B. Has deconfined quark matter been detected during GW170817/AT2017gfo? arXiv 2018, arXiv:1803.09696. [Google Scholar]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, . A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef]
- Han, S.; Steiner, A.W. Tidal deformability with sharp phase transitions in binary neutron stars. Phys. Rev. D 2019, 99, 083014. [Google Scholar] [CrossRef]
- Lim, Y.; Holt, J.W. Neutron Star Tidal Deformabilities Constrained by Nuclear Theory and Experiment. Phys. Rev. Lett. 2018, 121, 062701. [Google Scholar] [CrossRef]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Montana, G.; Tolos, L.; Hanauske, M.; Rezzolla, L. Constraining twin stars with GW170817. Phys. Rev. D 2019, 99, 103009. [Google Scholar] [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [PubMed]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef]
- Raithel, C.; Özel, F.; Psaltis, D. Tidal Deformability from GW170817 as a Direct Probe of the Neutron Star Radius. Astrophys. J. Lett. 2018, 857, 2. [Google Scholar] [CrossRef]
- Sieniawska, M.; Turczański, W.; Bejger, M.; Zdunik, J.L. Tidal deformability and other global parameters of compact stars with strong phase transitions. Astron. Astrophys. 2019, 622, A174. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron star tidal Love numbers with gravitational wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Love, A.E.H. Some Problems of Geodynamics; Cambridge University Press: Cambridge, UK, 1911. [Google Scholar]
- Van Oeveren, E.D.; Friedman, J.L. Upper limit set by causality on the tidal deformability of a neutron star. Phys. Rev. D 2017, 95, 083014. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astrophys. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Camenzind, M. Compact Objects in Astrophysics White Dwarfs, Neutron Stars and Black Holes; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Narayan, R. The birthrate and initial spin period of single radio pulsars. Astrophys. J. 1987, 319, 162. [Google Scholar] [CrossRef]
- Lorimer, D.R. Binary and Millisecond Pulsars. Living Rev. Rel. 2005, 11, 8. [Google Scholar] [CrossRef]
- Cieślar, M.; Bulik, T.; Osłowski, S. Markov chain Monte Carlo population synthesis of single radio pulsars in the Galaxy. arXiv 2018, arXiv:1803.02397. [Google Scholar]
- Lorimer, D.R. High-Energy Emission from Pulsars and their Systems. In Astrophysics and Space Science Proceedings; Torres, D.F., Rea, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; p. 21. [Google Scholar]
- Popov, S.B.; Prokhorov, M.E. Population synthesis in astrophysics. Phys. Uspekhi 2007, 50, 1123. [Google Scholar] [CrossRef]
- Patruno, A.; Haskell, B.; Andersson, N. The Spin Distribution of Fast-spinning Neutron Stars in Low-mass X-Ray Binaries: Evidence for Two Subpopulations. Astrophys. J. 2017, 850, 106. [Google Scholar] [CrossRef]
- Haskell, B.; Zdunik, J.L.; Fortin, M.; Bejger, M.; Wijnands, R.; Patruno, A. Fundamental physics and the absence of sub-millisecond pulsars. Astron. Astrophys. 2018, 620, A69. [Google Scholar] [CrossRef]
- Chau, W.Y. Gravitational Radiation and the Oblique Rotator Model. Nature 1970, 228, 655. [Google Scholar] [CrossRef] [PubMed]
- Melosh, H.J. Estimate of the Gravitational Radiation from NP 0532. Nature 1969, 224, 781. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Gunn, J.E. On the Nature of Pulsars. I. Theory. Astrophys. J. 1969, 157, 1395. [Google Scholar] [CrossRef]
- Press, W.H.; Thorne, K.S. Gravitational-Wave Astronomy. Annu. Rev. Astron. Astrophys. 1972, 10, 335. [Google Scholar] [CrossRef]
- Zimmermann, M. Revised estimate of gravitational radiation from Crab and VELA pulsars. Nature 1978, 271, 524. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T.; Cutler, C.; Schutz, B.F. Searching for periodic sources with LIGO. Phys. Rev. D 1998, 57, 2101. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A. Data analysis of gravitational-wave signals from spinning neutron stars. III. Detection statistics and computational requirements. Phys. Rev. D 2000, 61, 062001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Prospects for Observing and Localizing Gravitational-Wave Transients with Advanced LIGO, Advanced Virgo and KAGRA. arXiv 2019, arXiv:1304.0670. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Papa, M.A.; Dergachev, V. Characterizing the sensitivity of isolated continuous gravitational wave searches to binary orbits. Phys. Rev. D 2019, 100, 024058. [Google Scholar] [CrossRef]
- Nieder, L.; Clark, C.J.; Bassa, C.G.; Wu, J.; Singh, A.; Donner, J.Y.; Allen, B.; Breton, R.P.; Dhillon, V.S.; Eggenstein, H.-B.; et al. Detection and Timing of Gamma-Ray Pulsations from the 707 Hz Pulsar J0952-0607. Astrophys. J. 2019, 883, 1. [Google Scholar] [CrossRef]
- Fesen, R.A.; Hammell, M.C.; Morse, J.; Chevalier, R.A.; Borkowski, K.J.; Dopita, M.A.; Gerardy, C.L.; Lawrence, S.S.; Raymond, J.C.; van den Bergh, S. The Expansion Asymmetry and Age of the Cassiopeia A Supernova Remnant. Astrophys. J. 2006, 645, 283. [Google Scholar] [CrossRef]
- Wette, K.; Owen, B.J.; Allen, B.; Ashley, M.; Betzwieser, J.; Christensen, N.; Creighton, T.D.; Dergachev, V.; Gholami, I.; Goetz, E.; et al. Searching for gravitational waves from Cassiopeia A with LIGO. Class. Quantum Grav. 2008, 25, 235011. [Google Scholar] [CrossRef]
- Abadie, J.; Abbott, B.P.; Abbott, R.; Abernathy, M.; Adams, C.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amador Ceron, E.; et al. First Search for Gravitational Waves from the Youngest Known Neutron Star. Astrophys. J. 2010, 722, 1504. [Google Scholar] [CrossRef]
- Ming, J.; Krishnan, B.; Papa, M.A.; Aulbert, C.; Fehrmann, H. Optimal directed searches for continuous gravitational waves. Phys. Rev. D 2016, 93, 064011. [Google Scholar] [CrossRef]
- Ming, J.; Papa, M.A.; Krishnan, B.; Prix, R.; Beer, C.; Zhu, S.J.; Eggenstein, H.-B.; Bock, O.; Machenschalk, B. Optimally setting up directed searches for continuous gravitational waves in Advanced LIGO O1 data. Phys. Rev. D 2018, 97, 024051. [Google Scholar] [CrossRef]
- Ming, J.; Papa, M.A.; Singh, A.; Ming, J.; Papa, M.A.; Singh, A.; Eggenstein, H.-B.; Zhu, S.J.; Dergachev, V.; Hu, Y.; et al. Results from an Einstein@Home search for continuous gravitational waves from Cassiopeia A, Vela Jr., and G347.3. Phys. Rev. D 2019, 100, 024063. [Google Scholar] [CrossRef]
- Zhu, S.J.; Papa, M.A.; Eggenstein, H.-B.; Prix, R.; Wette, K.; Allen, B.; Bock, O.; Keitel, D.; Krishnan, B.; Machenschalk, B.; et al. Einstein@Home search for continuous gravitational waves from Cassiopeia A. Phys. Rev. D 2016, 94, 082008. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Adams, C.; Adams, T.; et al. A directed search for continuous gravitational waves from the Galactic center. Phys. Rev. D 2013, 88, 102002. [Google Scholar] [CrossRef]
- Dergachev, V.; Papa, M.A.; Steltner, B.; Eggenstein, H.-B. Loosely coherent search in LIGO O1 data for continuous gravitational waves from Terzan 5 and the Galactic Center. Phys. Rev. D 2019, 99, 084048. [Google Scholar] [CrossRef]
- Walsh, S.; Pitkin, M.; Oliver, M.; D’Antonio, S.; Dergachev, V.; Królak, A.; Astone, P.; Bejger, M.; Di Giovanni, M.; Dorosh, O.; et al. Comparison of methods for the detection of gravitational waves from unknown neutron stars. Phys. Rev. D 2016, 94, 124010. [Google Scholar] [CrossRef]
- Dreissigacker, C.; Prix, R.; Wette, K. Fast and accurate sensitivity estimation for continuous-gravitational-wave searches. Phys. Rev. D 2018, 98, 084058. [Google Scholar] [CrossRef]
- Pisarski, A.; Jaranowski, P. Banks of templates for all-sky narrow-band searches of gravitational waves from spinning neutron stars. Class. Quantum Grav. 2015, 32, 145014. [Google Scholar] [CrossRef][Green Version]
- Abbott, B.P.; Abbott, R.; Adhikari, R.; Agresti, J.; Ajith, P.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Arain, M.; et al. Searches for periodic gravitational waves from unknown isolated sources and Scorpius X-1: Results from the second LIGO science run. Phys. Rev. D 2007, 76, 082001. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amin, R.; Anderson, D.P.; Anderson, S.B.; Anderson, W.G.; et al. Einstein@Home search for periodic gravitational waves in LIGO S4 data. Phys. Rev. D 2009, 79, 022001. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T. Searching for periodic sources with LIGO. II. Hierarchical searches. Phys. Rev. D 2000, 61, 082001. [Google Scholar] [CrossRef]
- Cutler, C.; Gholami, I.; Krishnan, B. Improved stack-slide searches for gravitational-wave pulsars. Phys. Rev. D 2005, 72, 042004. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Agresti, J.; Ajith, P.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Arain, M.; et al. All-sky search for periodic gravitational waves in LIGO S4 data. Phys. Rev. D 2008, 77, 022001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Amin, R.S.; Anderson, S.B.; Anderson, W.G.; Arain, M.A.; et al. All-Sky LIGO Search for Periodic Gravitational Waves in the Early Fifth-Science-Run Data. Phys. Rev. Lett. 2009, 102, 111102. [Google Scholar] [CrossRef] [PubMed]
- Dergachev, V.; Papa, M.A. Sensitivity Improvements in the Search for Periodic Gravitational Waves Using O1 LIGO Data. Phys. Rev. Lett. 2019, 123, 101101. [Google Scholar] [CrossRef] [PubMed]
- Dergachev, V.; Papa, M.A. Results from an extended Falcon all-sky survey for continuous gravitational waves. arXiv 2019, arXiv:1909.09619. [Google Scholar]
- Pletsch, H.J. Parameter-space correlations of the optimal statistic for continuous gravitational-wave detection. Phys. Rev. D 2008, 78, 102005. [Google Scholar] [CrossRef]
- Pletsch, H.J.; Allen, B. Exploiting Large-Scale Correlations to Detect Continuous Gravitational Waves. Phys. Rev. Lett. 2009, 103, 181102. [Google Scholar] [CrossRef]
- Walsh, S.; Wette, K.; Papa, M.A.; Prix, R. Optimizing the choice of analysis method for all-sky searches for continuous gravitational waves with Einstein@Home. Phys. Rev. D 2019, 99, 082004. [Google Scholar] [CrossRef]
- Wette, K.; Walsh, S.; Prix, R.; Papa, M.A. Implementing a semicoherent search for continuous gravitational waves using optimally constructed template banks. Phys. Rev. D 2018, 97, 123016. [Google Scholar] [CrossRef]
- Astone, P.; Borkowski, K.M.; Jaranowski, P.; Piętka, M.; Królak, A. Data analysis of gravitational-wave signals from spinning neutron stars. V. A narrow-band all-sky search. Phys. Rev. D 2010, 82, 022005. [Google Scholar] [CrossRef]
- Shaltev, M.; Prix, R. Fully coherent follow-up of continuous gravitational-wave candidates. Phys. Rev. D 2013, 87, 084057. [Google Scholar] [CrossRef]
- Sieniawska, M.; Bejger, M.; Królak, A. Follow-up procedure for gravitational wave searches from isolated neutron stars using the time-domain F-statistic method. Class. Quantum Grav. 2019, 36, 22. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; et al. Implementation of an F-statistic all-sky search for continuous gravitational waves in Virgo VSR1 data. Class. Quantum Grav. 2014, 31, 165014. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Adhikari, R.; Ageev, A.; Allen, B.; Amin, R.; Anderson, S.B.; Anderson, W.G.; Araya, M.; Armandula, H.; et al. Setting upper limits on the strength of periodic gravitational waves from PSR J1939+2134 using the first science data from the GEO 600 and LIGO detectors. Phys. Rev. D 2004, 69, 082004. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First low-frequency Einstein@Home all-sky search for continuous gravitational waves in Advanced LIGO data. Phys. Rev. D 2017, 96, 122004. [Google Scholar] [CrossRef]
- Hough, P.V.C. Machine analysis of bubble chamber pictures. In Proceedings of the International Conference on High Energy Accelerators and Instrumentation, Geneva, Switzerland, 14–19 September 1959. [Google Scholar]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. U.S. Patent US3069654A, 18 December 1962. [Google Scholar]
- Krishnan, B.; Sintes, A.M.; Papa, M.A.; Schutz, B.F.; Frasca, S.; Palomba, C. Hough transform search for continuous gravitational waves. Phys. Rev. D 2004, 70, 082001. [Google Scholar] [CrossRef]
- Antonucci, F.; Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C. Detection of periodic gravitational wave sources by Hough transform in the f versus skew6 dot f plane. Class. Quantum Grav. 2008, 25, 184015. [Google Scholar] [CrossRef]
- Astone, P.; Colla, A.; D’Antonio, S.; Frasca, S.; Palomba, C. Method for all-sky searches of continuous gravitational wave signals using the frequency-Hough transform. Phys. Rev. D 2014, 90, 042002. [Google Scholar] [CrossRef]
- Miller, A.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; La Rosa, I.; Leaci, P.; Mastrogiovanni, S.; Muciaccia, F.; Palomba, C.; et al. Method to search for long duration gravitational wave transients from isolated neutron stars using the generalized frequency-Hough transform. Phys. Rev. D 2018, 98, 102004. [Google Scholar] [CrossRef]
- Andersson, N.; Antonopoulou, D.; Espinoza, C.M.; Haskell, B.; Ho, W.C.G. The Enigmatic Spin Evolution of PSR J0537-6910: R-modes, Gravitational Waves, and the Case for Continued Timing. Astrophys. J. 2018, 864, 137. [Google Scholar] [CrossRef]
- Espinoza, C.M.; Lyne, A.G.; Kramer, M.; Manchester, R.N.; Kaspi, V.M. The Braking Index of PSR J1734-3333 and the Magnetar Population. Astrophys. J. Lett. 2011, 741, L13. [Google Scholar] [CrossRef]
- Hamil, O.Q.; Stone, J.R.; Urbanec, M.; Urbancova, G. Braking index of isolated pulsars. Phys. Rev. D 2015, 91, 063007. [Google Scholar] [CrossRef]
- Lasky, P.D.; Leris, C.; Rowlinson, A.; Glampedakis, K. The Braking Index of Millisecond Magnetars. Astrophys. J. Lett. 2017, 843, L1. [Google Scholar] [CrossRef]
- Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C. A method for detection of known sources of continuous gravitational wave signals in non-stationary data. Class. Quantum Grav. 2010, 27, 194016. [Google Scholar] [CrossRef]
- Piccinni, O.J.; Astone, P.; D’Antonio, S.; Frasca, S.; Intini, G.; Leaci, P.; Mastrogiovanni, S.; Miller, A.; Palomba, C.; Singhal, A. A new data analysis framework for the search of continuous gravitational wave signals. Class. Quantum Grav. 2019, 36, 015008. [Google Scholar] [CrossRef]
- Dupuis, R.; Woan, G. Bayesian estimation of pulsar parameters from gravitational wave data. Phys. Rev. D 2005, 72, 102002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Acernese, F.; Adhikari, R.; Ajith, P.; Allen, B.; Allen, G.; Alshourbagy, M.; Amin, R.S.; Anderson, S.B.; et al. Searches for Gravitational Waves from Known Pulsars with Science Run 5 LIGO Data. Astrophys. J. 2010, 713, 671–685. [Google Scholar] [CrossRef]
- Ashton, G.; Prix, R. Hierarchical multistage MCMC follow-up of continuous gravitational wave candidates. Phys. Rev. D 2018, 97, 103020. [Google Scholar] [CrossRef]
- Goetz, E.; Riles, K. An all-sky search algorithm for continuous gravitational waves from spinning neutron stars in binary systems. Class. Quantum Grav. 2011, 28, 21. [Google Scholar] [CrossRef]
- Meadors, G.D.; Goetz, E.; Riles, K.; Creighton, T.; Robinet, F. Searches for continuous gravitational waves from Scorpius X-1 and XTE J1751-305 in LIGO’s sixth science run. Phys. Rev. D 2017, 95, 042005. [Google Scholar] [CrossRef]
- Meadors, G.D.; Krishnan, B.; Papa, M.A.; Whelan, J.T.; Zhang, Y. Resampling to accelerate cross-correlation searches for continuous gravitational waves from binary systems. Phys. Rev. D 2018, 97, 044017. [Google Scholar] [CrossRef]
- Whelan, J.T.; Sundaresan, S.; Zhang, Y.; Peiris, P. Model-based cross-correlation search for gravitational waves from Scorpius X-1. Phys. Rev. D 2015, 91, 102005. [Google Scholar] [CrossRef]
- Suvorova, S.; Sun, L.; Melatos, A.; Evans, R.J. Hidden Markov model tracking of continuous gravitational waves from a neutron star with wandering spin. Phys. Rev. D 2016, 93, 123009. [Google Scholar] [CrossRef]
- Suvorova, S.; Clearwater, P.; Melatos, A.; Sun, L.; Moran, W.; Evans, R.J. Hidden Markov model tracking of continuous gravitational waves from a binary neutron star with wandering spin. II. Binary orbital phase tracking. Phys. Rev. D 2017, 96, 102006. [Google Scholar] [CrossRef]
- Leaci, P.; Astone, P.; D’Antonio, S.; Frasca, S.; Palomba, C.; Piccinni, O.; Mastrogiovanni, S. Novel directed search strategy to detect continuous gravitational waves from neutron stars in low- and high-eccentricity binary systems. Phys. Rev. D 2017, 95, 122001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Upper Limits on Gravitational Waves from Scorpius X-1 from a Model-based Cross-correlation Search in Advanced LIGO Data. Astrophys. J. 2017, 847, 1. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Searches for Gravitational Waves from Known Pulsars at Two Harmonics in 2015–2017 LIGO Data. Astrophys. J. 2019, 879, 10. [Google Scholar] [CrossRef]
- Bejger, M.; Haensel, P. Moments of inertia for neutron and strange stars: Limits derived for the Crab pulsar. Astron. Astrophys. 2002, 396, 917–921. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum elastic deformations of compact stars with exotic equations of state. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef]
- Ushomirsky, G.; Cutler, C.; Bildsten, L. Deformations of accreting neutron star crusts and gravitational wave emission. Mon. Not. R. Astron. Soc. 2000, 319, 902. [Google Scholar] [CrossRef]
- Chugunov, A.I.; Horowitz, C.J. Breaking stress of neutron star crust. Mon. Not. R. Astron. Soc. 2010, 407, L54–L58. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Kadau, K. The Breaking Strain of Neutron Star Crust and Gravitational Waves. Phys. Rev. Lett. 2009, 102, 191102. [Google Scholar] [CrossRef] [PubMed]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Ruderman, M. Neutron Star Crust Breaking and Magnetic Field Evolution. In Structure and Evolution of Neutron Stars; Pines, D., Tamagaki, R., Tsuruta, S., Eds.; Proc. Conf. SENS’90; Addison-Wesley: Redwood City, CA, USA, 1992; p. 353. [Google Scholar]
- Baym, G.; Chin, S. Can a Neutron Star Be a Giant MIT Bag? Phys. Lett. 1976, 62B, 241. [Google Scholar] [CrossRef]
- Chapline, G.; Nauenberg, M. Asymptotic freedom and the baryon-quark phase transition. Phys. Rev. D 1977, 16, 450. [Google Scholar] [CrossRef]
- Fechner, W.B.; Joss, P.C. Quark stars with ’realistic’ equations of state. Nature 1978, 274, 347. [Google Scholar] [CrossRef]
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. 1973, 47B, 365. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291. [Google Scholar] [CrossRef]
- Ivanenko, D.D.; Kurdgelaidze, D.F. Hypothesis concerning quark stars. Astrophysics 1965, 1, 251. [Google Scholar] [CrossRef]
- Keister, B.D.; Kisslinger, L.S. Free-quark phases in dense stars. Phys. Lett. 1976, 64B, 117. [Google Scholar] [CrossRef]
- Bodmer, A.R. Collapsed Nuclei. Phys. Rev. D 1971, 4, 1601. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L.; Schaefer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Madsen, J. How to Identify a Strange Star. Phys. Rev. Lett. 1998, 81, 3311. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272. [Google Scholar] [CrossRef]
- Weber, F. Strange Quark Matter and Compact Stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Xu, R.X. Solid Quark Stars? Astrophys. J. 2003, 596, L59. [Google Scholar] [CrossRef]
- Haskell, B.; Andersson, N.; Jones, D.I.; Samuelsson, L. Are Neutron Stars with Crystalline Color-Superconducting Cores Relevant for the LIGO Experiment? Phys. Rev. Lett. 2007, 99, 231101. [Google Scholar] [CrossRef] [PubMed]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Knippel, B.; Sedrakian, A. Gravitational radiation from crystalline color-superconducting hybrid stars. Phys. Rev. D 2009, 79, 083007. [Google Scholar] [CrossRef]
- Mannarelli, M.; Rajagopal, K.; Sharma, R. The strength of crystalline color superconductors. AIP Conf. Proc. 2007, 964, 264–271. [Google Scholar]
- Mannarelli, M.; Sharma, R. The rigidity of three flavor quark matter. Pos Confin. 2008, 8, 141. [Google Scholar]
- Knispel, B.; Allen, B. Blandford’s argument: The strongest continuous gravitational wave signal. Phys. Rev. D 2008, 78, 044031. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. First narrow-band search for continuous gravitational waves from known pulsars in advanced detector data. Phys. Rev. D 2017, 96, 122006. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Fermi, E. Problems of Gravitational Stability in the Presence of a Magnetic Field. Astrophys. J. 1953, 118, 116. [Google Scholar] [CrossRef]
- Jones, D.I.; Andersson, N. Gravitational waves from freely precessing neutron stars. Mon. Not. R. Astron. Soc. 2002, 331, 203. [Google Scholar] [CrossRef]
- Cutler, C. Gravitational waves from neutron stars with large toroidal B fields. Phys. Rev. D 2002, 66, 084025. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Continuous gravitational wave from magnetized white dwarfs and neutron stars: Possible missions for LISA, DECIGO, BBO, ET detectors. Mon. Not. R. Astron. Soc. 2019, 490, 2. [Google Scholar] [CrossRef]
- Haskell, B.; Samuelsson, L.; Glampedakis, K.; Andersson, N. Modelling magnetically deformed neutron stars. Mon. Not. R. Astron. Soc. 2008, 385, 531–542. [Google Scholar] [CrossRef]
- Gal’tsov, D.V.; Tsvetkov, V.P.; Tsirulev, A.N. Spectrum and polarization of the gravitational radiation of pulsars. Zh. Eksp. Teor. Fiz. 1984, 86, 809, English translation in Sov. Phys. JETP 1984, 59, 472. [Google Scholar]
- Gal’tsov, D.V.; Tsvetkov, V.P. On the gravitational radiation of an oblique rotator. Phys. Lett. 1984, 103A, 193. [Google Scholar] [CrossRef]
- Braithwaite, J.; Spruit, H.C. Evolution of the magnetic field in magnetars. Astron. Astrophys. 2006, 450, 1097. [Google Scholar] [CrossRef]
- Braithwaite, J. The stability of poloidal magnetic fields in rotating stars. Astron. Astrophys. 2007, 469, 275. [Google Scholar] [CrossRef]
- Wright, G.A.E. Pinch instabilities in magnetic stars. Mon. Not. R. Astron. Soc. 1973, 162, 339. [Google Scholar] [CrossRef]
- Braithwaite, J.; Nordlund, A. Stable magnetic fields in stellar interiors. Astron. Astrophys. 2006, 450, 1077. [Google Scholar] [CrossRef]
- Ciolfi, R.; Ferrari, V.; Gualtieri, L.; Pons, J.A. Relativistic models of magnetars: The twisted torus magnetic field configuration. Mon. Not. R. Astron. Soc. 2009, 397, 913. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Are there any stable magnetic fields in barotropic stars? Mon. Not. R. Astron. Soc. 2012, 424, 482. [Google Scholar] [CrossRef]
- Mastrano, A.; Melatos, A.; Reissenegger, A.; Akgün, T. Gravitational wave emission from a magnetically deformed non-barotropic neutron star. Mon. Not. R. Astron. Soc. 2011, 417, 2288. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Lasky, P.D. Gravitational Waves from Neutron Stars: A Review. Publ. Astron. Soc. Aust. 2015, 32, 34. [Google Scholar] [CrossRef]
- Dall’Osso, S.; Stella, L.; Palomba, C. Neutron star bulk viscosity, ’spin-flip’. Mon. Not. R. Astron. Soc. 2018, 480, 1353–1362. [Google Scholar] [CrossRef]
- Bildsten, L. Gravitational Radiation and Rotation of Accreting Neutron Stars. Astrophys. J. 1998, 501, L89. [Google Scholar] [CrossRef]
- Papaloizou, J.; Pringle, J.E. The dynamical stability of differentially rotating discs with constant specific angular momentum. Mon. Not. R. Astron. Soc. 1978, 184, 501. [Google Scholar] [CrossRef]
- Wagoner, R.V. Gravitational radiation from accreting neutron stars. Astrophys. J. 1984, 278, 345. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Morgan, E.H.; Muno, M.P.; Muno, M.P.; Galloway, D.K.; Wijnands, R.; van der Klis, M.; Markwardt, C.B. Nuclear-powered millisecond pulsars and the maximum spin frequency of neutron stars. Nature 2003, 424, 42. [Google Scholar] [CrossRef] [PubMed]
- Giacconi, R.; Gursky, H.; Paolini, F.R.; Rossi, B.B. Evidence for x Rays From Sources Outside the Solar System. Phys. Rev. Lett. 1962, 9, 439–443. [Google Scholar] [CrossRef]
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. Directed search for gravitational waves from Scorpius X-1 with initial LIGO data. Phys. Rev. D 2015, 91, 062008. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Search for gravitational waves from Scorpius X-1 in the second Advanced LIGO observing run with an improved hidden Markov model. arXiv 2019, arXiv:1906.12040. [Google Scholar]
- Rossby, C.G. Relation between variations in the intensity of the zonal circulation of the atmosphere and the displacements of the semi-permanent centers of action. J. Mar. Res. 1939, 2, 38. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Solutions of Two Problems in the Theory of Gravitational Radiation. Phys. Rev. Lett. 1970, 24, 611. [Google Scholar] [CrossRef]
- Friedman, J.L.; Schutz, B.F. Gravitational radiation instability in rotating stars. Astrophys. J. Lett. 1975, 199, L157. [Google Scholar] [CrossRef]
- Cunha, M.S.; Aerts, C.; Christensen-Dalsgaard, J.; Baglin, A.; Bigot, L.; Brown, T.M.; Catala, C.; Creevey, O.L.; Domiciano de Souza, A.; Eggenberger, P.; et al. Asteroseismology and interferometry. Astron. Astrophys. Rev. 2007, 14, 217–360. [Google Scholar] [CrossRef]
- Owen, B.J.; Lindblom, L.; Cutler, C.; Schutz, B.F.; Vecchio, A.; Andersson, N. Gravitational waves from hot young rapidly rotating neutron stars. Phys. Rev. D 1998, 58, 084020. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D.; Stergioulas, N. On the Relevance of the R-Mode Instability for Accreting Neutron Stars and White Dwarfs. Astrophys. J. 1999, 516, 307. [Google Scholar] [CrossRef]
- Bondarescu, R.; Teukolsky, S.A.; Wasserman, I. Spin evolution of accreting neutron stars: Nonlinear development of the r-mode instability. Phys. Rev. D 2007, 76, 064019. [Google Scholar] [CrossRef]
- Haskell, B. R-modes in neutron stars: Theory and observations. Int. J. Mod. Phys. E 2015, 24, 1541007. [Google Scholar] [CrossRef]
- Haskell, B.; Patruno, A. Are Gravitational Waves Spinning Down PSR J 1023+ 0038? Phys. Rev. Lett. 2017, 119, 161103. [Google Scholar] [CrossRef] [PubMed]
- Alpar, M.A.; Cheng, A.F.; Ruderman, M.A.; Shaham, J. A new class of radio pulsars. Nature 1982, 300, 728. [Google Scholar] [CrossRef]
- Levin, Y. Runaway Heating by R-Modes of Neutron Stars in Low-Mass X-Ray Binaries. Astrophys. J. 1999, 517, 328. [Google Scholar] [CrossRef]
- Spruit, H.C. Differential rotation and magnetic fields in stellar interiors. Astron. Astrophys. 1999, 349, 189. [Google Scholar]
- Heyl, J.S. Low-Mass X-Ray Binaries May Be Important Laser Interferometer Gravitational-Wave Observatory Sources After All. Astrophys. J. Lett. 2002, 574, L57. [Google Scholar] [CrossRef]
- Haskell, B.; Degenaar, N.; Ho, W.C.G. Constraining the physics of the r-mode instability in neutron stars with X-ray and ultraviolet observations. Mon. Not. R. Astron. Soc. 2012, 424, 93. [Google Scholar] [CrossRef]
- Alford, M.G.; Mahmoodifar, S.; Schwenzer, K. Viscous damping of r-modes: Small amplitude instability. Phys. Rev. D 2012, 85, 024007. [Google Scholar] [CrossRef]
- Glampedakis, K.; Andersson, N. Crust-core coupling in rotating neutron stars. Phys. Rev. D 2006, 74, 044040. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Andersson, N.; Haskell, B. Revealing the Physics of r Modes in Low-Mass X-Ray Binaries. Phys. Rev. Lett. 2011, 107, 101101. [Google Scholar] [CrossRef] [PubMed]
- Andersson, N.; Sidery, T.; Comer, G.L. Mutual friction in superfluid neutron stars. Mon. Not. R. Astron. Soc. 2006, 368, 162. [Google Scholar] [CrossRef]
- Haskell, B.; Andersson, N.; Passamonti, A. R-modes and mutual friction in rapidly rotating superfluid neutron stars. Mon. Not. R. Astron. Soc. 2009, 397, 1464. [Google Scholar] [CrossRef]
- Chugunov, A.I.; Gusakov, M.E.; Kantor, E.M. R-modes and neutron star recycling scenario. Mon. Not. R. Astron. Soc. 2017, 468, 291. [Google Scholar] [CrossRef]
- Wang, Y.-B.; Zhou, X.; Wang, N.; Liu, X.-W. The r-mode instability windows of strange stars. arxiv 2019, arXiv:1810.07264. [Google Scholar] [CrossRef]
- Kokkotas, K.; Schwenzer, K. R-mode astronomy. Eur. Phys. J. A 2016, 52, 38. [Google Scholar] [CrossRef]
- Idrisy, A.; Owen, B.J.; Jones, D.I. R-mode frequencies of slowly rotating relativistic neutron stars with realistic equations of state. Phys. Rev. D 2015, 91, 024001. [Google Scholar] [CrossRef]
- Jasiulek, M.; Chirenti, C. R-mode frequencies of rapidly and differentially rotating relativistic neutron stars. Phys. Rev. D 2017, 95, 064060. [Google Scholar] [CrossRef]
- Lockitch, K.H.; Friedman, J.L.; Andersson, N. Rotational modes of relativistic stars: Numerical results. Phys. Rev. D 2003, 68, 124010. [Google Scholar] [CrossRef]
- Pons, J.A.; Gualtieri, L.; Miralles, J.A.; Ferrari, V. Relativistic r modes and shear viscosity: Regularizing the continuous spectrum. Mon. Not. R. Astron. Soc. 2005, 363, 1. [Google Scholar] [CrossRef]
- Lindblom, L.; Mendell, G.; Owen, B.J. Second-order rotational effects on the r-modes of neutron stars. Phys. Rev. D 1999, 60, 064006. [Google Scholar] [CrossRef]
- Stavridis, A.; Passamonti, A.; Kokkotas, K. Nonradial oscillations of slowly and differentially rotating compact stars. Phys. Rev. D 2007, 75, 064019. [Google Scholar] [CrossRef]
- Bildsten, L.; Ushomirsky, G. Viscous Boundary-Layer Damping of R-Modes in Neutron Stars. Astrophys. J. Lett. 2000, 529, L33. [Google Scholar] [CrossRef]
- Levin, Y.; Ushomirsky, G. Crust–core coupling and r-mode damping in neutron stars: A toy model. Mon. Not. R. Astron. Soc. 2001, 324, 917. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints. Phys. Rep. 2007, 442, 109. [Google Scholar] [CrossRef]
- Arras, P.; Flanagan, E.E.; Morsink, S.M.; Schenk, A.K.; Teukolsky, S.A.; Wasserman, I. Saturation of the r-Mode Instability. Astrophys. J. 2003, 591, 2. [Google Scholar] [CrossRef]
- Alford, M.G.; Mahmoodifar, S.; Schwenzer, K. Large amplitude behavior of the bulk viscosity of dense matter. J. Phys. Nucl. Part. Phys. 2010, 37, 12. [Google Scholar] [CrossRef]
- Chatterjee, D.; Bandyopadhyay, D. Bulk viscosity of strange matter and r-modes in neutron stars. arXiv 2008, arXiv:0812.5021. [Google Scholar]
- Blaschke, D.; Bombaci, I.; Grigorian, H.; Poghosyan, G. Timing evolution of accreting strange stars. New Astron. 2002, 7, 107–112. [Google Scholar] [CrossRef][Green Version]
- Jaikumar, P.; Reddy, S.; Steiner, A.W. Strange Star Surface: A Crust with Nuggets. Phys. Rev. Lett. 2006, 96, 041101. [Google Scholar] [CrossRef]
- Mytidis, A.; Coughlin, M.; Whiting, B. Constraining the r-mode saturation amplitude from a hypothetical detection of r-mode gravitational waves from a newborn neutron star: Sensitivity study. Astrophys. J. 2015, 810, 27. [Google Scholar] [CrossRef]
- Lindblom, L.; Owen, B.J.; Morsink, S.M. Gravitational Radiation Instability in Hot Young Neutron Stars. Phys. Rev. Lett. 1998, 80, 4843. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. The r-mode instability in rotating neutron stars. Int. J. Mod. Phys. D 2001, 10, 381. [Google Scholar] [CrossRef]
- Andersson, N.; Haskell, B.; Comer, G.L. R-modes in low temperature colour-flavour-locked superconducting quark star. Phys. Rev. D 2010, 82, 023007. [Google Scholar] [CrossRef]
- Haskell, B.; Glampedakis, K.; Andersson, N. A new mechanism for saturating unstable r-modes in neutron stars. Mon. Not. R. Astron. Soc. 2014, 441, 1662. [Google Scholar] [CrossRef]
- Chugunov, A.I. Long-term evolution of CFS-unstable neutron stars and the role of differential rotation on short time-scales. Mon. Not. R. Astron. Soc. 2019, 482, 3045–3057. [Google Scholar] [CrossRef]
- Owen, B.J. How to adapt broad-band gravitational-wave searches for r-modes. Phys. Rev. D 2010, 82, 104002. [Google Scholar] [CrossRef]
- Alford, M.G.; Schwenzer, K. Gravitational Wave Emission and Spin-down of Young Pulsars. Astrophys. J. 2014, 781, 1. [Google Scholar] [CrossRef]
- Caride, S.; Inta, R.; Owen, B.J.; Rajbhandari, B. How to search for gravitational waves from r-modes of known pulsars. arXiv 2019, arXiv:1907.04946. [Google Scholar] [CrossRef]
- Ferrari, V.; Miniutti, G.; Pons, J.A. Gravitational waves from newly born, hot neutron stars. Mon. Not. R. Astron. Soc. 2003, 342, 629. [Google Scholar] [CrossRef]
- Dimmelmeier, H.; Font, J.A.; Müller, E. Relativistic simulations of rotational core collapse II. Collapse dynamics and gravitational radiation. Astron. Astrophys. 2002, 393, 523. [Google Scholar] [CrossRef]
- Friedman, J.L. Upper Limit on the Frequency of Pulsars. Phys. Rev. Lett. 1983, 51, 11, Erratum in Phys. Rev. Lett. 1983, 51, 718. [Google Scholar] [CrossRef]
- Ipser, J.R.; Lindblom, L. The oscillations of rapidly rotating Newtonian stellar models. II - Dissipative effects. Astrophys. J. 1991, 373, 213. [Google Scholar] [CrossRef]
- Page, D.; Prakash, M.; Lattimer, J.M.; Steiner, A.W. Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter. Phys. Rev. Lett. 2011, 106, 081101. [Google Scholar] [CrossRef]
- Shternin, P.S.; Yakovlev, D.G.; Heinke, C.O.; Ho, W.C.G.; Patnaude, D.J. Cooling neutron star in the Cassiopeia A supernova remnant: Evidence for superfluidity in the core. Mon. Not. R. Astron. Soc. 2011, 412, L108. [Google Scholar] [CrossRef]
- Passamonti, A.; Gaertig, E.; Kokkotas, K.D. Evolution of the f-mode instability in neutron stars and gravitational wave detectability. Phys. Rev. D 2013, 87, 084010. [Google Scholar] [CrossRef]
- Doneva, D.D.; Gaertig, E.; Kokkotas, K.D.; Krüger, C. Gravitational wave asteroseismology of fast rotating neutron stars with realistic equations of state. Phys. Rev. D 2013, 88, 044052. [Google Scholar] [CrossRef]
- Gaertig, E.; Glampedakis, K.; Kokkotas, K.D.; Zink, B. f-Mode Instability in Relativistic Neutron Stars. Phys. Rev. Lett. 2011, 107, 101102. [Google Scholar] [CrossRef]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D., Rea, N., Vidana, I., Eds.; Springer: Cham, Switzerland, 2018; p. 457. [Google Scholar]
- Kokkotas, K. Stellar pulsations and gravitational waves. Banach Cent. Publ. 1997, 41, 31–41. [Google Scholar] [CrossRef]
- Alpar, A.; Pines, D. Gravitational radiation from a solid-crust neutron star. Nature 1985, 314, 334. [Google Scholar] [CrossRef]
- Haskell, B.; Sedrakian, A. Superfluidity and Superconductivity in Neutron Stars. Astrophys. Space Sci. Libr. 2018, 457, 401–454. [Google Scholar]
- Sedrakian, A.; Wasserman, I.; Cordes, J.M. Precession of Isolated Neutron Stars. I. Effects of Imperfect Pinning. Astrophys. J. 1999, 524, 341–360. [Google Scholar] [CrossRef]
- Shaham, J. Free precession of neutron stars: Role of possible vortex pinning. Astrophys. J. 1977, 214, 251–260. [Google Scholar] [CrossRef]
- Wasserman, I. Precession of isolated neutron stars — II. Magnetic fields and type II superconductivity. Mon. Not. R. Astron. Soc. 2003, 341, 3. [Google Scholar] [CrossRef]
- Mestel, L.; Takhar, H.S. The internal Dynamics of the Oblique Rotator. Mon. Not. R. Astron. Soc. 1972, 156, 419. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Non-rigid precession of magnetic stars. Mon. Not. R. Astron. Soc. 2017, 467, 4343–4382. [Google Scholar] [CrossRef]
- Lander, S.K.; Jones, D.I. Neutron-star spindown and magnetic inclination-angle evolution. Mon. Not. R. Astron. Soc. 2018, 481, 4169–4193. [Google Scholar] [CrossRef]
- Bertotti, B.; Anile, A.M. Gravitational Slowing Down of Solid Spinning Bodies. Astron. Astrophys. 1973, 28, 429. [Google Scholar]
- Lamb, D.Q.; Lamb, F.K.; Pines, D.; Shaham, J. Neutron Star Wobble in Binary X-Ray Sources. Astrophys. J. Lett. 1975, 198, L21. [Google Scholar] [CrossRef]
- Van Den Broeck, C. The gravitational wave spectrum of non-axisymmetric, freely precessing neutron stars. Class. Quantum Grav. 2005, 22, 1825–1840. [Google Scholar] [CrossRef]
- Cutler, C.; Jones, D.I. Gravitational wave damping of neutron star wobble. Phys. Rev. D 2000, 63, 024002. [Google Scholar] [CrossRef]
- Akgün, T.; Link, B.; Wasserman, I. Precession of the isolated neutron star PSR B1828-11. Astron. Astrophys. 2006, 365, 2. [Google Scholar] [CrossRef]
- Stairs, I.H.; Lyne, A.G.; Shemar, S.L. Evidence for free precession in a pulsar. Nature 2000, 406, 484. [Google Scholar] [CrossRef] [PubMed]
- Cordes, J.M. Planets around Pulsars; Phillips, J.A., Thorsett, S.E., Kulkarni, S.R., Eds.; ASP Conf. Ser. 36; ASP: San Francisco, CA, USA, 1993; p. 43. [Google Scholar]
- Shabanova, T.V.; Lyne, A.G.; Urama, J.O. Evidence for Free Precession in the Pulsar B1642-03. Astrophys. J. 2001, 552, 321–325. [Google Scholar] [CrossRef]
- Pitkin, M.; Messenger, C.; Wright, L. Astrophysical calibration of gravitational-wave detectors. Phys. Rev. D 2016, 93, 06200. [Google Scholar] [CrossRef]
- Isi, M.; Pitkin, M.; Weinstein, A.J. Probing dynamical gravity with the polarization of continuous gravitational waves. Phys. Rev. D 2017, 96, 042001. [Google Scholar] [CrossRef]
| 1. | In Einstein’s theory, for weak gravitational fields, space-time can be described as a metric: , where is Minkowski metric and corresponds to (small) GW perturbation. In the TT gauge the perturbation is purely spatial , and traceless . From the Lorentz gauge condition one can imply that the spatial metric perturbation is transverse: . |
| 2. | |
| 3. | For the chronology of the events see [56]. |
| 4. | Note that the most precisely measured quantity from an inspiral phase is a so-called chirp mass: . Using Newton laws of motion, Newton universal law of gravitation, and Einstein quadrupole formula, one can see that depends only on GW frequency and its derivative —quantities determined directly from the observational data: . Information about the individual masses is taken from the waveforms filtering, including post-Newtonian expansion. That is why determination has the smallest errors, while estimations are model-dependent and generate relatively big errors, e.g., for the GW170817 event individual masses (for the low-spin priors) were estimated as: M and M, while chirp mass M [34,69]. |
| 5. | The ATNF Pulsar Database website: http://www.atnf.csiro.au/people/pulsar/psrcat/. |
| 6. | Of course, the whole picture is more complex when binary system is considered since in that case also the binary orbital parameters that additionally modulate the CGW signal have to be taken into account. In this review we focus only on the isolated NSs. Leverage of searches for CGWs signals from isolated objects, in order to identify and follow-up signals from NSs in binary systems were investigated in [104]. |
| 7. | Project repository: https://github.com/mbejger/polgraw-allsky. |
| 8. | Project webpage: http://einstein.phys.uwm.edu. |
| 9. | We consider here density perturbations, which affect the spherical shape of the star , where denotes spherical harmonics. The multipole moment of the perturbation along radius coordinate r is . Here we focus only on the lowest-order perturbation , consistent with , for which . Note that in this section we consider the simplest model, in which rotational and axes are aligned. In general they may be misaligned, producing additional CGW radiation at frequency, whose strength depends on the angle between rotational and axes and is maximal when they are perpendicular [7]. Such cases are consider in Section 3 and Section 5. Searches in the LVC data for the CGW radiation at both and were performed in the past [159]. |
| 10. | Note that in Equation (36) the function has a positive sign, which means that the poloidal magnetic field tends to distort a NS into an oblate shape. For a toroidal field the expression changes sign, making the NS shape prolate. |
| 11. | Whole energy of the mode is transferred to the NS spin-down and loss of the canonical angular momentum of the mode. |
| 12. | Unlike in the case of the elastic deformations, what was shown in Section 2, r-modes affect equation of motion , where is dimensionless amplitude and is the angular frequency in co-rotating frame. The only non-trivial solution is for , giving , what can be transferred to the angular frequency in the inertial frame: . Dividing this expression by gives . |
| 13. | When viscosity is dominated by normal matter, then the NS enters into a limit cycle of spin-up by accretion and spin-down by the r-mode. |
| 14. | The timescales discussed here are related to the polytrope and : the simplest illustrative model. General expressions of the timescales are [248]: ; , where is the shear viscosity factor; , where is the bulk viscosity factor. In principle all these timescales are sensitive to EOS due to the occurrence of density in the equations. |
| 15. | In the case of precession, general expression for the ellipticity is defined as , where moment-of-inertia tensor is given by and is the moment of inertia of the spherically symmetric density field . |



| Known Waveform | Unknown Waveform | |
|---|---|---|
| Long-lived | Rotating neutron stars | Stochastic background |
| (continuous) | ||
| Short-lived | Compact binaries coalescences | Supernovæ |
| ( s) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. https://doi.org/10.3390/universe5110217
Sieniawska M, Bejger M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe. 2019; 5(11):217. https://doi.org/10.3390/universe5110217
Chicago/Turabian StyleSieniawska, Magdalena, and Michał Bejger. 2019. "Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects" Universe 5, no. 11: 217. https://doi.org/10.3390/universe5110217
APA StyleSieniawska, M., & Bejger, M. (2019). Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe, 5(11), 217. https://doi.org/10.3390/universe5110217





