Dynamics of Electromagnetic Fields and Structure of Regular Rotating Electrically Charged Black Holes and Solitons in Nonlinear Electrodynamics Minimally Coupled to Gravity

Abstract

We study the dynamics of electromagnetic fields of regular rotating electrically charged black holes and solitons replacing naked singularities in nonlinear electrodynamics minimally coupled to gravity (NED-GR). They are related by electromagnetic and gravitational interactions and described by the axially symmetric NED-GR solutions asymptotically Kerr-Newman for a distant observer. Geometry is described by the metrics of the Kerr-Schild class specified by $T_t^t=T_r^r(p_r=-\rho )$ in the co-rotating frame. All regular axially symmetric solutions obtained from spherical solutions with the Newman-Janis algorithm belong to this class. The basic generic feature of all regular objects of this class, both electrically charged and electrically neutral, is the existence of two kinds of de Sitter vacuum interiors. We analyze the regular solutions to dynamical equations for electromagnetic fields and show which kind of a regular interior is favored by electromagnetic dynamics for NED-GR objects.

1. Introduction

The question of existence of astrophysical electrically charged black holes remains open and is actively studied in the literature. As early as in 1974 it was shown [1] that a black hole with the angular momentum J in an external magnetic field B captures charged particles up to acquiring the charge $q=2BJ$. Detailed investigation of mechanisms of charging a black hole in its interaction with a surrounding ionized cosmic plasma in the presence of a magnetic field has been done in the paper [2]. Self-consistent analysis in the frame of linear electrodynamics of accretions of collisionless charged fluid on a neutral black hole has shown that an acquired charge depends on the accretion velocity and is estimated within the range $0<q/m<0.99$ [3]. In Reference [4] the method has been proposed for establishing the fact that a black hole is charged, with using the process of reflection of an electromagnetic wave.

For electrically charged black holes a substantial enhancement of efficiency of extraction of a rotational energy was predicted for particles collisions near their event horizons [5,6,7,8] and in vicinities of naked singularities without horizons [9], for powering outflows from accretion disk-fed black holes [10,11,12,13] and for accelerating ultra-high energy cosmic rays [14]. Detailed calculations of gravitational radiation generated in direct collisions of black holes revealed also more substantial increasing energy output with increasing their charges than with increasing their angular momenta [15].

Electrically charged black holes can arise also in collisions of high energy particles [16,17], including the mass range where this process is dominated by the classical General Relativity [16,18,19,20].

In the linear electrodynamics coupled to gravity the fields of rotating electrically charged bodies are described by the Kerr-Newman solution to the source-free Einstein-Maxwell equations [21]

$$d{s}^2=-d{t}^2+\frac{\Sigma }{\Delta }d{r}^2+\Sigma d{\theta }^2+\frac{(2mr-q^2)}{\Sigma }{(dt-a{sin}^2\theta d\varphi )}^2+(r^2+a^2){sin}^2\theta d{\varphi }^2$$

(1)

where

$$\Sigma =r^2+a^2{cos}^2\theta ;\Delta =r^2-2mr+a^2+q^2,$$

(2)

and associated electromagnetic potential is $A_i=-\left(qr\right)/\Sigma [1;0,0,-a{sin}^2\theta ]$.

Detailed analysis of this solution has been presented by Carter who found that the parameter a coupled with the mass m gives the angular momentum $J=ma$ and coupled with the charge q gives an asymptotic magnetic momentum $\mu =qa$, so that the gyromagnetic ratio $q/m$ is the same as predicted for a spinning particle by the Dirac equation [22]. This suggested the classical image of the spinning electron visualized as a massive charged source of the Kerr-Newman fields [23,24,25] and motivated further studies towards a search for models of material sources for the Kerr-Newman fields.

Carter has also revealed the global causality violation in the Kerr-Newman geometry for the case of a charged spinning object without horizon, $a^2+q^2>m^2$. In this case there exist closed time-like curves which originate in the deep interior region where the vector $\partial /\partial \varphi$ is time-like but can extend over the whole manifold and cannot be removed by taking a covering space [22].

The source models involving screening or covering of the causally dangerous region can be classified as disk-like [23,26,27], shell-like [25,28], bag-like [24,29,30,31,32,33,34] and string-like [35,36]. The problem of matching the Kerr-Newman exterior to a rotating material source does not have a unique solution, since one is free to choose the boundary between the exterior and the interior [23].

The Kerr-Newman solution has been obtained from the spherical Reissner-Nordström solution with using the Newman-Janis algorithm [37]. As it was shown by Gürses and Gürsey [38], this algorithm belongs to the Trautman-Newman complex coordinate translations and works for the algebraically special metrics of the Kerr-Schild class [39] (written here in the units $c=G=1$)

$$d{s}^2=g\left(r\right)d{t}^2-\frac{d{r}^2}{g\left(r\right)}-r^{2}d{\Omega }^2;g\left(r\right)=1-\frac{2\mathcal{M}\left(r\right)}{r};\mathcal{M}\left(r\right)=4\pi {\int }_0^r\tilde{\rho }\left(x\right)x^{2}dx$$

(3)

which present the algebraically degenerated solutions to the Einstein equations [38,39]1

Most of presented in the literature regular charged black hole solutions [40,41,42,43,44,45,46,47,48,49,50] belong to the Kerr-Schild class (for a review see Reference [51]).

For the metrics (3) the source terms have the algebraic structure such that [52]

$$T_t^t=T_r^r(p_r=-\rho ).$$

(4)

Regular spherical solutions with stress-energy tensors from the class (4) satisfying the weak energy condition (WEC), which requires non-negative density as measured by any observer on a time-like curve, have obligatory de Sitter center $p=-\rho$ [52,53,54]. Regular solutions which describe electrically charged objects belong to this class automatically since for any gauge-invariant Lagrangian $\mathcal{L}\left(F\right)$ a stress-energy tensor of an electromagnetic field has the algebraic structure specified by (4) [47,55].

In the Boyer-Lindquist coordinates the regular axially symmetric metric reads [38]

$$d{s}^2=\frac{2f-\Sigma }{\Sigma }d{t}^2+\frac{\Sigma }{\Delta }d{r}^2+\Sigma d{\theta }^2-\frac{4af{sin}^2\theta }{\Sigma }dtd\varphi +\left(r^2+a^2+\frac{2f{a}^2{sin}^2\theta }{\Sigma }\right){sin}^2\theta d{\varphi }^2.$$

(5)

Here a is the specific angular momentum, the Lorentz signature is [- + + +], and

$$f\left(r\right)=r\mathcal{M}\left(r\right);\Delta =r^2+a^2-2f\left(r\right).$$

(6)

The Boyer-Lindquist coordinates $r,\theta ,\varphi$ are related with the Cartesian coordinates $x,y,z$ by $x^2+y^2=(r^2+a^2){sin}^2\theta ;z=rcos\theta$. The surfaces of constant r are the oblate confocal ellipsoids $r^4-(x^2+y^2+z^2-a^2)r^2-a^2{z}^2=0$ which degenerate, for $r=0$, to the equatorial disk [56]

$$x^2+y^2\le a^2,z=0,$$

(7)

centered on the symmetry axis and bounded by the ring $x^2+y^2=a^2,z=0$.

In the Kerr-Newman geometry $2f\left(r\right)=2mr-q^2$ and spacetime is singular on the ring. In regular geometries $2f\left(r\right)=2\mathcal{M}\left(r\right)r$, at approaching the disk $\mathcal{M}\left(r\right)\to 4\pi {\rho }_0{r}^3/3$ and $2f\left(r\right)\to 8\pi {\rho }_0{r}^4/3$ where ${\rho }_0=\tilde{\rho }(r=0)$ and tilde refers to a related spherical solution.. In the metric (5) $(2f\left(r\right)/\Sigma )-1\to 8\pi {\rho }_0{r}^2/3-1$ since $r^2/\Sigma \to 1$ in this limit [55]. In the dimensional units $2f\left(r\right)/\Sigma -1\to \Lambda r^2/3-1$ where $\Lambda =8\pi G{\rho }_0/c^2$ and the metric (5) represents the maximally symmetric de Sitter spacetime with the constant curvature, of the 1-st kind for $\Lambda >0$ and of the 2-nd kind for $\Lambda <0$ [57], the latter is frequently referred to as anti-de Sitter ([58] and references therein). In both cases on the disk the metric (5) reduces to $d{s}^2=-d{t}^2+(\Sigma /(r^2+a^2))d{r}^2+\Sigma d{\theta }^2+(r^2+a^2){sin}^2\theta d{\varphi }^2$ and represents the Minkowski metric in the ellipsoidal coordinates. It follows that the disk is intrinsically flat together with the ring and totally regular (for more details see Reference [55]). The de Sitter asymptotic with the positive density ($\Lambda >0$) for the considered class of regular metrics is fixed by imposing the weak energy condition on related spherical solutions. In this case the totally regular disk $r=0$ is filled with the de Sitter vacuum with the positive density $\tilde{\rho }(r=0)$.

The energy density component of a stress-energy tensor responsible for the metric (5) achieves the value $\rho =\tilde{\rho }(r=0)$ at approaching the disk in full consistency with the asymptotical behavior of the metric.

The anisotropic stress-energy tensors responsible for geometries with the Kerr-Schild metrics (5) can be written in the form [38]

$$T_{\mu \nu }=(\rho +p_{\perp })(u_{\mu }{u}_{\nu }-l_{\mu }{l}_{\nu })+p_{\perp }{g}_{\mu \nu }$$

(8)

in the orthonormal tetrad

$$u^{\mu }=\frac{1}{\sqrt{\pm \Delta \Sigma }}[(r^2+a^2){\delta }_0^{\mu }+a{\delta }_3^{\mu }],l^{\mu }=\sqrt{\frac{\pm \Delta }{\Sigma }}{\delta }_1^{\mu },n^{\mu }=\frac{1}{\sqrt{\Sigma }}{\delta }_2^{\mu },m^{\mu }=\frac{-1}{\sqrt{\Sigma }sin\theta }[a{sin}^2\theta {\delta }_0^{\mu }+{\delta }_3^{\mu }].$$

(9)

The sign plus refers to the R-regions outside the event horizon $r_{+}$ and inside the internal horizon $r_{-}$ (shown in Figure 1 Left) where the vector $u^{\mu }$ is time-like. The vectors $m^{\mu }$ and $n^{\mu }$ are space-like in all regions. The eigenvalues of the stress-energy tensor (8), calculated in the co-rotating references frame with the angular velocity $\omega \left(r\right)=u^{\varphi }/u^t=a/(r^2+a^2)$, are defined by

$$T_{\mu \nu }{u}^{\mu }{u}^{\nu }=\rho (r,\theta );T_{\mu \nu }{l}^{\mu }{l}^{\nu }=p_r=-\rho ;T_{\mu \nu }{n}^{\mu }{n}^{\nu }=T_{\mu \nu }{m}^{\mu }{m}^{\nu }=p_{\perp }(r,\theta ).$$

(10)

This gives [38]

$$\rho (r,\theta )=\frac{2(f^{\prime }r-f)}{{\Sigma }^2}=\frac{r^4}{{\Sigma }^2}\tilde{\rho }\left(r\right);p_{\perp }(r,\theta )=\frac{2(f^{\prime }r-f)-f^{″}\Sigma }{{\Sigma }^2}=\left(\frac{r^4}{{\Sigma }^2}-\frac{2r^2}{\Sigma }\right)\tilde{\rho }\left(r\right)-\frac{r^3}{2\Sigma }{\tilde{\rho }}^{\prime }\left(r\right).$$

(11)

The density and pressures are related by [59]

$$p_r(r,\theta )=-\rho ;p_{\perp }+\rho =\frac{r|{\tilde{\rho }}^{\prime }|}{2{\Sigma }^2}\mathcal{S}(r,z);\mathcal{S}(r,z)=r^4-z^2\frac{2a^2}{r|{\tilde{\rho }}^{\prime }|}(\tilde{\rho }-{\tilde{p}}_{\perp }).$$

(12)

The prime denotes the derivative with respect to r. $r^2/\Sigma \to 1$ as $z\to 0$ and $(p_{\perp }+\rho )\to -r{\tilde{\rho }}^{\prime }\left(r\right)/2$. For regular spherical solutions satisfying WEC regularity requires ${\tilde{\rho }}^{\prime }\le 0$ and $r{\tilde{\rho }}^{\prime }\left(r\right)\to 0$ as $r\to 0$ [54]. Equation of state on the disk reads thus $p=-\rho =-\tilde{\rho }(r=0)$ and describes the rotating de Sitter vacuum in the co-rotating frame [55].

The basic generic feature of all regular rotating compact objects of the Kerr-Schild class is the interior de Sitter vacuum disk (7) of the radius a [55,59]. The mass parameter m appearing in the Kerr-Newman limit is the finite positive mass, $m=\mathcal{M}(r\to \infty )$, generically related to the interior de Sitter vacuum and to breaking of the spacetime symmetry from the de Sitter group [54].

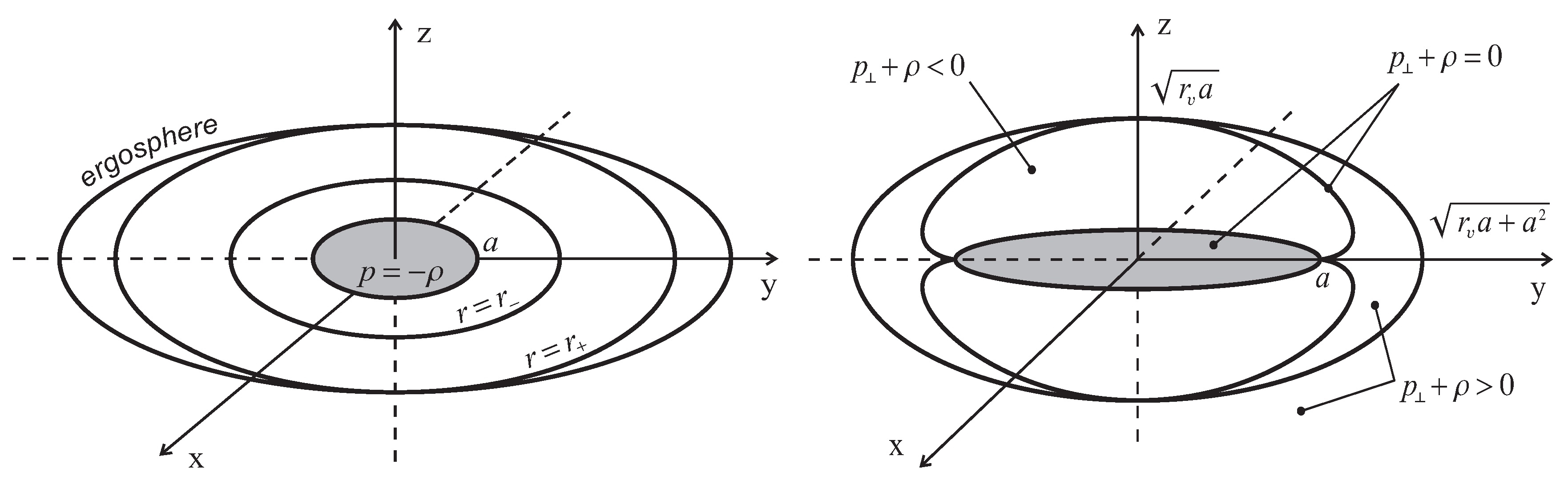
Spacetime of regular rotating objects of this class can have at most two horizons defined by $\Delta \left(r\right)=0$, and at most two ergospheres which are surfaces of a static limit $g_{tt}=0$ [59]. Extraction of a rotational energy is possible in ergoregions where $g_{tt}<0$ (see References [50,60,61] and references therein).

The basic relation for $p_{\perp }+\rho \ge 0$ in (12) implies a possibility of generic violation of the weak energy condition which is valid if and only if $\rho \ge 0$ and $p_k+\rho \ge 0$ [57]. The first of these two conditions is satisfied according to (4), so that satisfaction of WEC requires $p_{\perp }+\rho \ge 0$. As a result regular rotating compact objects can have two different kinds of interiors [51,59,62].

If a related spherical solution violates the dominant energy condition (DEC, which requires $\rho \ge p_k$ for any principal pressure [57]), the function $\mathcal{S}(r,z)$ in Equation (12) vanishes only at approaching the disk (7). In this (first) type of interior $p_{\perp }+\rho \ge 0$, WEC is satisfied for a rotating object and its interior is presented by the de Sitter vacuum disk $r=0$.

If a related spherical solution satisfies the dominant energy condition, $\tilde{\rho }\ge \widetilde{p_k}$ in (12), then there can exist an additional surface of the de Sitter vacuum, $\mathcal{S}$-surface defined by $p_{\perp }+\rho =0$, which contains the de Sitter disk as a bridge and represents the second type of interior [59,62]. In this case WEC is violated in the internal cavities between the $\mathcal{S}$-surface and the disk, which are filled thus with an anisotropic phantom fluid, $p_{\perp }=w_{\perp }\rho$ with $w_{\perp }<-1$ [62].

Two types of interior are shown in Figure 1 [62], where $r_v$ is a regularity parameter for the cases admitting the second type interior.

The first type interior is shown in Figure 1 Left [62], where we plotted also horizons, the event horizon $r=r_{+}$ and the internal horizon $r=r_{-}$ and the ergosphere defined by $g_{tt}=0$ in (5) which results in $r^2+a^2{cos}^2\theta -2f\left(r\right)=0$. The second type interior is shown in Figure 1 Right [62].

The main question addressed in the present paper is which of geometrically possible types of a regular interior is preferred by the electromagnetic fields dynamics.

Electrically charged regular objects related by electromagnetic and gravitational interactions are described in general setting by nonlinear electrodynamics coupled to gravity (NED-GR).

Nonlinear electrodynamics (NED) was proposed by Born and Infeld as intended to consider electromagnetic field and particles in the unique common framework of electromagnetic field and to obtain finite values for physical quantities [63].

NED theories appear as low-energy effective limits in certain models of string/M-theories [64,65,66]. The NED theories are nonlinear theories in the Minkowski spacetime, the NED Lagrangians are gauge and Lorentz invariant and depend on the scalar invariant F of the electromagnetic field with the potential $A_{\mu }$, $F=F_{\mu \nu }{F}^{\mu \nu }$, $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ and in the more general case depend also on the pseudoscalar invariant $G{=}^{★}{F}^{\mu \nu }{F}_{\mu \nu }$, ${}^{★}{F}^{\mu \nu }={\eta }^{\mu \nu \alpha \beta }{F}_{\alpha \beta }/2;{\eta }^{0123}=-1/\sqrt{-g}$. The Maxwell equations in the flat spacetime of NED theories are the same for $\mathcal{L}(F,G)$ and $\mathcal{L}\left(F\right)$ frames (see Reference [67] and references therein). In NED-GR theories geometry and dynamical equations for electromagnetic fields are also the same for both NED frames [45]. Therefore here we present the results obtained in the NED-GR Lagrange dynamics with the $\mathcal{L}\left(F\right)$ frame for electromagnetic fields (detailed analysis in Section 3).

Two basic points underlying the Born-Infeld program can be realized in NED-GR due to the crucial role of gravity for a compact object with a regular interior where fields tensions and energy are particularly high (a regular interior must somehow replace a singularity specified by the infinite curvature invariants). Source-free NED-GR equations admit the class of regular causally safe axially symmetric solutions asymptotically Kerr-Newman for a distant observer [55,59], which describe regular black holes and electromagnetic solitons - compact objects without horizons replacing naked singularities, representing spinning particles and defined as physical solitons in the spirit of the Coleman lumps [68] as non-singular non-dissipative objects keeping themselves together by their self-interaction.

For NED-GR regular electrically charged objects interior de Sitter vacuum provides a finite value for the self-interaction divergent for a point charge [47,55]. For spinning NED-GR objects regularity requires ${\mathcal{L}}_F\to \infty$ at approaching the disk and ${\mathcal{L}}_F$ determines the basic properties of nonlinear electromagnetic field as anisotropic ($p_r\ne p_{\perp }$) medium. On the disk this medium becomes isotropic ($p_r=p_{\perp }=-\rho =-\tilde{\rho }(r=0)$) and the de Sitter vacuum distributed on the disk has the properties of a perfect conductor and ideal diamagnetic due to ${\mathcal{L}}_F\to \infty$ [55] (detailed presentation in Section 2). The ring singularity is replaced with the superconducting ring current, which presents the electromagnetic non-dissipative source for a compact regular spinning electrically charged NED-GR object described by a regular asymptotically Kerr-Newman geometry [69] as well as an intrinsic source of its magnetic momentum [70].

In this paper we present the analysis of electromagnetic fields of regular spinning NED-GR objects. In Section 2 we analyze the solutions to the dynamical equations for electromagnetic field and the conditions of their existence. In Section 3 we show which type of a regular interior for NED-GR objects is favored by the electromagnetic fields dynamics. In Section 4 we summarize and discuss the results.

2. Electromagnetic Fields of Regular Spinning NED-GR Objects

Nonlinear electrodynamics minimally coupled to gravity is described by the action

$$\mathcal{I}=\frac{1}{16\pi }\int (R-\mathcal{L}\left(F\right))\sqrt{-g}{d}^{4}x$$

(13)

where R is the scalar curvature, and F is the scalar invariant of the electromagnetic field, $F=F_{\mu \nu }{F}^{\mu \nu }$, where $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the electromagnetic field.

The gauge-invariant electromagnetic Lagrangian $\mathcal{L}\left(F\right)$ should have the Maxwell limit, $\mathcal{L}\to F,{\mathcal{L}}_F\to 1$, where ${\mathcal{L}}_F=d\mathcal{L}/dF$, in the weak field regime as $r\to \infty$.

Variation with respect to $A^{\mu }$ and $g_{\mu \nu }$ yields the dynamical field equations

$${\nabla }_{\mu }\left({\mathcal{L}}_F{F}^{\mu \nu }\right)=0;$$

(14)

$${\nabla }_{\mu }{}^{*}{F}^{\mu \nu }=0;{}^{★}{F}^{\mu \nu }=\frac{1}{2}{\eta }^{\mu \nu \alpha \beta }{F}_{\alpha \beta };{\eta }^{0123}=-\frac{1}{\sqrt{-g}},$$

(15)

and the Einstein equations $G_{\mu \nu }=-8\pi G{T}_{\mu \nu }$ where the stress-energy tensor of an electromagnetic field is defined by Reference ([47] and references therein)

$$T_{\nu }^{\mu }=-2{\mathcal{L}}_F{F}_{\nu \alpha }{F}^{\mu \alpha }+\frac{1}{2}{\delta }_{\nu }^{\mu }\mathcal{L}$$

(16)

In terms of the 3-vectors defined as [55,71]

$$E_j=\left\{F_{j0}\right\};D^j=\left\{{\mathcal{L}}_F{F}^{0j}\right\};B^j=\left\{{}^{*}{F}^{j0}\right\};H_j=\left\{{\mathcal{L}}_F{}^{*}{F}_{0j}\right\};j=1,2,3$$

(17)

the field Equations (14) and (15) take the form of the source-free Maxwell equations

$$\nabla ·\mathbf{D}=0;\nabla \times \mathbf{H}=\frac{\partial \mathbf{D}}{\partial t};\nabla ·\mathbf{B}=0;\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}.$$

(18)

The electric induction $\mathbf{D}$ and the magnetic induction $\mathbf{B}$ are related with the electric and magnetic field intensities by

$$D^j={ϵ}_k^j{E}^k;B^j={\mu }_k^j{H}^k,$$

(19)

where ${ϵ}_j^k$ and ${\mu }_j^k$ are the tensors of the electric and magnetic permeability given by [55]

$${ϵ}_r^r=\frac{(r^2+a^2)}{\Delta }{\mathcal{L}}_F;{ϵ}_{\theta }^{\theta }={\mathcal{L}}_F;{\mu }_r^r=\frac{(r^2+a^2)}{\Delta {\mathcal{L}}_F};{\mu }_{\theta }^{\theta }=\frac{1}{{\mathcal{L}}_F}.$$

(20)

Non-zero field components compatible with the axial symmetry are $F_{01},F_{02},F_{13},F_{23}$. Standard formulae for 2-rank tensors $F_{\alpha \beta }=g_{\alpha \mu }{g}_{\beta \nu }{F}^{\mu \nu }$ and $F^{\alpha \beta }=g^{\alpha \mu }{g}^{\beta \nu }{F}_{\mu \nu }$ give in geometry with the metric (5) the relations

$$F_{31}=a{sin}^2\theta F_{10};a{F}_{23}=(r^2+a^2)F_{02}.$$

(21)

The field invariant reads

$$F=2\left(\frac{F_{20}^2}{a^2{sin}^2\theta }-F_{10}^2\right).$$

(22)

The relations of density and pressures with the electromagnetic field are given by [55]

$$\rho =\frac{1}{2}\mathcal{L}+2{\mathcal{L}}_F{F}_{10}^2;p_r=-\rho ;p_{\perp }=-\frac{1}{2}\mathcal{L}+2{\mathcal{L}}_F\frac{F_{20}^2}{a^2{sin}^2\theta }$$

(23)

and provide the tool for investigation of the weak energy condition

$$p_{\perp }+\rho =2{\mathcal{L}}_F\left(F_{10}^2+\frac{F_{20}^2}{a^2{sin}^2\theta }\right).$$

(24)

Equations (14) and (15) form the system of 4 equations for 2 independent field components

$$\frac{\partial }{\partial r}[(r^2+a^2)sin\theta {\mathcal{L}}_F{F}_{10}]+\frac{\partial }{\partial \theta }[sin\theta {\mathcal{L}}_F{F}_{20}]=0;$$

(25)

$$\frac{\partial }{\partial r}\left[\frac{1}{sin\theta }{\mathcal{L}}_F{F}_{31}\right]+\frac{\partial }{\partial \theta }\left[\frac{1}{(r^2+a^2)sin\theta }{\mathcal{L}}_F{F}_{32}\right]=0;$$

(26)

$$\frac{\partial F_{23}}{\partial r}+\frac{\partial F_{31}}{\partial \theta }=0;\frac{\partial F_{01}}{\partial \theta }+\frac{\partial F_{20}}{\partial r}=0.$$

(27)

Dynamical equations (14) are satisfied by the field functions [55,59]

$${\Sigma }^2\left({\mathcal{L}}_F{F}_{01}\right)=-q(r^2-a^2{cos}^2\theta );{\Sigma }^2\left({\mathcal{L}}_F{F}_{02}\right)=q{a}^{2}rsin2\theta ;$$

(28)

$${\Sigma }^2\left({\mathcal{L}}_F{F}_{31}\right)=aq{sin}^2\theta (r^2-a^2{cos}^2\theta );{\Sigma }^2\left({\mathcal{L}}_F{F}_{23}\right)=aqr(r^2+a^2)sin2\theta .$$

(29)

In the case ${\mathcal{L}}_F=1$, these functions satisfy also the dynamical Equations (15) and asymptotically coincide with the solutions to the Maxwell equations in the Kerr-Newman geometry [22,24].

The question is when the field components (28) and (29) are the solutions to the whole system of the dynamical Equations (14) and (15).

The functions (28) and (29) satisfy the equations

$$\frac{\partial \left({\mathcal{L}}_F{F}_{23}\right)}{\partial r}+\frac{\partial \left({\mathcal{L}}_F{F}_{31}\right)}{\partial \theta }=0;\frac{\partial \left({\mathcal{L}}_F{F}_{01}\right)}{\partial \theta }+\frac{\partial \left({\mathcal{L}}_F{F}_{20}\right)}{\partial r}=0.$$

(30)

It follows

$$\frac{\partial F_{23}}{\partial r}+\frac{\partial F_{31}}{\partial \theta }=-\frac{{\mathcal{L}}_{FF}}{{\mathcal{L}}_F}\left[F_{31}\frac{\partial F}{\partial \theta }+F_{23}\frac{\partial F}{\partial r}\right]$$

(31)

$$\frac{\partial F_{01}}{\partial \theta }+\frac{\partial F_{20}}{\partial r}=-\frac{{\mathcal{L}}_{FF}}{{\mathcal{L}}_F}\left[F_{01}\frac{\partial F}{\partial \theta }+F_{20}\frac{\partial F}{\partial r}\right].$$

(32)

Left sides vanish identically when right sides are zero. This defines the following cases when the functions (29) and (28) satisfy the whole dynamical system (25) and (27):

(A)${\mathcal{L}}_{FF}=0,{\mathcal{L}}_F\ne 0$, the Maxwell limit with ${\mathcal{L}}_F=const$;

(B)${\mathcal{L}}_F=\infty ,{\mathcal{L}}_{FF}\ne 0$, strongly nonlinear regime, which can be expected in a deep interior. According to (12), on the $\mathcal{S}$-surface including the disk $p_{\perp }+\rho =0$. From (24) it follows that $F_{10}^2=F_{20}^2/a^2{sin}^2\theta =0$ since ${\mathcal{L}}_F$ cannot be zero. As a result the Equation (23) gives

$$F_{10}^2=\frac{2\rho -\mathcal{L}}{4{\mathcal{L}}_{\mathcal{F}}}=0$$

(33)

on the $\mathcal{S}$-surface uncluding the disk, which is possible (for regular solutions with an arbitrary Lagrangian $\mathcal{L}$) only if ${\mathcal{L}}_F\to \infty$ there. The case (B) represents thus the natural realization of the underlying hypothesis of non-linearity replacing a singularity.

Another possibility is vanishing of the expression in the square brackets in Equations (31) and (32)

$$F_{31}\frac{\partial F}{\partial \theta }+F_{23}\frac{\partial F}{\partial r}=0;F_{01}\frac{\partial F}{\partial \theta }+F_{20}\frac{\partial F}{\partial r}=0.$$

(34)

Taking into account (21), we reduce this system to

$$a^2{sin}^2\theta F_{01}\frac{\partial F}{\partial \theta }+(r^2+a^2)F_{20}\frac{\partial F}{\partial r}=0;F_{01}\frac{\partial F}{\partial \theta }+F_{20}\frac{\partial F}{\partial r}=0.$$

(35)

It is the system of two algebraic equations for $F_{01}(\partial F/\partial \theta )$ and $F_{20}(\partial F/\partial r)$ with the determinant $Det=-\Sigma$. The solutions for $\Sigma \ne 0$ read $F_{01}(\partial F/\partial \theta )=0$, $F_{20}(\partial F/\partial r)=0$, and include two cases:

(C)$F_{10}=F_{20}=0$, zero fields regime.

(D)$\partial F/\partial r=0$ and $\partial F/\partial \theta =0$. This case needs detailed investigation of extrema of the field invariant F and will be presented in the next Section.

3. Electromagnetic Dynamics

Presented in the frame of the Lagrange dynamics regular spherically symmetric solutions with the non-zero electric charge [41,42,43,44,47] are typically found with using the alternative P-form of nonlinear electrodynamics obtained from the standard Lagrangian F-form by the Legendre transformation [72]. The F-P duality turns into the electric-magnetic duality in the Maxwell limit but in general case it connects different theories [45] which is manifested by branching of a Lagrangian in the F frame.

In the spherically symmetric case $F=-2q^2/{\mathcal{L}}_F^2{r}^4$ [45], which results in $F{\mathcal{L}}_F^2\to -\infty$ as $r\to 0$. The structure of stress-energy tensor implies $p_{\perp }+\rho =F{\mathcal{L}}_F$, regular solutions have obligatory de Sitter center where $p_{\perp }+\rho =0$ and hence $F{\mathcal{L}}_F=0$ [47]. Requirement of regularity demands thus ${\mathcal{L}}_F\to \infty$ and $F\to -0$ when $r\to 0$. The Maxwell limit implies $F\to -0$ as $r\to \infty$. Non-monotonic behavior of the invariant F leads inevitably to branching of a Lagrangian $\mathcal{L}\left(F\right)$ in the point where the invariant F achieves its minimum [45,47]. This problem requires the correct description of the Lagrange dynamics for regular electrically charged structures by the non-uniform variational problem with the action [73]

$$\mathcal{I}={\mathcal{I}}_{int}+{\mathcal{I}}_{ext}=\frac{1}{16\pi }\left[{\int }_{{\Omega }_{int}}(R-{\mathcal{L}}_{int}\left(F\right))\sqrt{-g}{d}^{4}x+{\int }_{{\Omega }_{ext}}(R-{\mathcal{L}}_{ext}\left(F\right))\sqrt{-g}{d}^{4}x\right].$$

(36)

Each part of the manifold, ${\Omega }_{int}$ and ${\Omega }_{ext}$, is confined by the space-like hypersurfaces $t=t_{in}$ and $t=t_{fin}$ and by the time-like 3-surface at infinity, where electromagnetic fields vanish in the Maxwell limit. Internal boundary between ${\Omega }_{int}$ and ${\Omega }_{ext}$ is defined as a time-like hypersurface ${\Sigma }_c$ at which the field invariant F achieves its extremum [73]. In the case of the minimal coupling variation in the action (36) results in the dynamical Equations (14) and (15) in both ${\Omega }_{int}$ and ${\Omega }_{ext}$ and in the standard boundary conditions on the surface ${\Sigma }_c$ [73]

$${\int }_{{\Sigma }_c}\left({\mathcal{L}}_{F\left(int\right)}{F}_{\mu \nu \left(int\right)}-{\mathcal{L}}_{F\left(ext\right)}{F}_{\mu \nu \left(ext\right)}\right)\sqrt{-g}\delta A^{\mu }d{\sigma }^{\nu }=0;{\mathcal{L}}_{int}-2{\mathcal{L}}_{F\left(int\right)}{F}_{int}={\mathcal{L}}_{ext}-2{\mathcal{L}}_{F\left(ext\right)}{F}_{ext}$$

(37)

In the axially symmetric case solutions (29) and (28) applied in (24) give on the $\mathcal{S}$-surface

$$(p_{\perp }+\rho )=\frac{2q^2}{{\mathcal{L}}_F{\Sigma }^2};{\mathcal{L}}_F^{2}F=-\frac{2q^2}{{\Sigma }^2}+\frac{16q^2{a}^2{r}^2{cos}^2\theta }{{\Sigma }^4}.$$

(38)

It follows that ${\mathcal{L}}_F{\Sigma }^2\to \infty$ and $F\to -0$ over the whole $\mathcal{S}$-surface. On the disk [55]

$${\mathcal{L}}_F=\frac{2q^2}{{\Sigma }^2(p_{\perp }+\rho )};F=-\frac{{\Sigma }^2{(p_{\perp }+\rho )}^2}{2q^2}.$$

(39)

We see that $F\to -0$ and, by virtue of (24) and (23), $\mathcal{L}\to 2\tilde{\rho }\left(0\right)$ as $r\to 0$. In the Maxwell weak field limit, ${\mathcal{L}}_F=1$, the above relations give $F\to -0$ and $\mathcal{L}\to 0$ as $r\to \infty$ with taking into account in (23) that $\rho \to 0$ for compact objects with the finite mass.

The de Sitter disk exists in all regular axially symmetric configurations. Two different kinds of a regular interior involve the existence or absence of the $\mathcal{S}$-surface. To investigate these cases we need information on behavior of electromagnetic field in the extrema of the invariant F.

Analysis of conditions for the extrema of the invariant F —According to the condition D from the previous Section, the dynamical Equations (14) and (15) are satisfied by the field functions (29) and (28). The field invariant (22) can be written thus as

$$F=\frac{2q^2}{L_F^2}\Phi (r,\theta );\Phi (r,\theta )=\frac{8a^2{r}^2{cos}^2\theta -{\Sigma }^2}{{\Sigma }^4},$$

(40)

which gives

$$\nabla F=2q^2\frac{L_F}{L_F^3+4q^2{L}_{FF}\Phi }\nabla \Phi .$$

(41)

It follows that $\nabla F=0$ when

(1)$L_F=\infty$; (2)$L_{FF}=\infty$ and $\Phi \ne 0$; (3) $\Phi \to \infty$; (4)$\nabla \Phi =0$.

The case (3) corresponds to the disk where $L_F\to \infty$ and $F\to -0$.

In the case (4), $\nabla \Phi =0$, derivatives are given by

$$\frac{\partial \Phi }{\partial r}=\frac{4r}{{\Sigma }^5}\left({\Sigma }^2-4a^2{cos}^2\theta (4r^2-\Sigma )\right),$$

(42)

$$\frac{\partial \Phi }{\partial \theta }=-\frac{4a^{2}sin\theta cos\theta }{{\Sigma }^5}\left({\Sigma }^2-4r^2(4a^2{cos}^2\theta -\Sigma )\right).$$

(43)

The system of two equations

$$\frac{4r}{{\Sigma }^5}\left({\Sigma }^2-4a^2{cos}^2\theta (4r^2-\Sigma )\right)=0;\frac{4a^{2}sin\theta cos\theta }{{\Sigma }^5}\left({\Sigma }^2-4r^2(4a^2{cos}^2\theta -\Sigma )\right)=0.$$

(44)

in the case $\Sigma \ne 0$ transforms to

$${\Sigma }^2-4a^2{cos}^2\theta (4r^2-\Sigma )=0;{\Sigma }^2-4r^2(4a^2{cos}^2\theta -\Sigma )=0.$$

(45)

Subtracting and summing these equations we obtain the equations

$$(r^2-a^2{cos}^2\theta )\Sigma =0;3{\Sigma }^2-16a^2{r}^2{cos}^2\theta =0$$

(46)

which show that the only solution to the system (44) is $r=0,\theta =\pi /2$, that is it does not have solutions in the case $\Sigma \ne 0$. The only case when $\nabla \Phi =0$ takes place on the disk.

The cases with the WEC violation—WEC can be violated when DEC is satisfied for a related spherical solution and the $\mathcal{S}$-surface can exist.

At approaching the disk (7), $F<0$, since the invariant F goes to $-0$ as $r\to 0$, and its first extremum is the minimum located somewhere between the disk and $\mathcal{S}$-surface where $F\to -0$ again. The field invariant is negative in this region, the derivative ${\mathcal{L}}_F$ should have to be negative too, by virtue of (24), and the Lagrangian, given by (23) as

$$\mathcal{L}=2\rho -4{\mathcal{L}}_F{F}_{10}^2$$

(47)

takes some positive value at the surface where a Lagrangian branches for the first time.

After the first minimum the invariant F achieves its second zero value, $F\to -0$ at the $\mathcal{S}$-surface where it has the maximum in accordance with the condition (1) for the existence of the extremum; the Lagrangian takes the value $\mathcal{L}=2\rho$ and branches for the second time. From the maximum at $F=-0$ the field invariant F goes to the minimum at a certain negative value where the Lagrangian takes some negative value and branches for the third time.

Another case concerns the possible vanishing of the invariant F suggested by its form (22), somewhere except the disk and $\mathcal{S}$-surface. At any other surface $F=0$ cannot be an extremum. Indeed, when $F=0$, the relation (24) takes the form $p_{\perp }+\rho =4{\mathcal{L}}_F{F}_{10}^2$, WEC is satisfied and ${\mathcal{L}}_F$ is finite, and none of the conditions (1)–(4) for the existence of extremum is fulfilled. It follows that an extremum in this case would have to exist at a certain positive value of the invariant F which should have to increase from the first minimum at $F_1<0$ to a maximum $F_3>0$ crossing $F_2=0$. At the point $F_2=0$, we have $F_{10}^2=F_{20}^2/\left(a^2{sin}^2\theta \right)=0$, the Lagrangian takes the value ${\mathcal{L}}_2=2\rho$ according to (47). Equation (23) gives the relation

$$\rho -p_{\perp }=\mathcal{L}-{\mathcal{L}}_{F}F.$$

(48)

For $F=0$ we have $\rho -p_{\perp }=2\rho$, DEC is satisfied, an $\mathcal{S}$-surface could exist and WEC violated.

Both above cases should have to be excluded because, according to (20) and (24), violation of the weak energy condition leads to negative values of the electric and magnetic permeability. For objects satisfying the basic requirement of electrodynamics of continued media (positivity of the electric permeability) [74], the cases of WEC violation rather can not be admitted.

The case when WEC is satisfied—In the case when a $\mathcal{S}$-surface does not exist, the field invariant vanishes only on the disk $r=0$ and at infinity as $r\to \infty$. In this case the Lagrangian branches only in the minimum of the invariant F, where $F\ne 0$ and ${\mathcal{L}}_{FF}$ breaks and changes the sign. Characteristic behavior in the Lagrange dynamics is shown in Figure 2.

Let us note that in this case also DEC is satisfied for the regular rotating NED-GR objects since an $\mathcal{S}$-surface does not exist and $p_{\perp }+\rho =0$ only on the disk. The general relation, following from (12)

$$\rho -p_{\perp }=\frac{r^2}{\Sigma }(\tilde{\rho }-{\tilde{p}}_{\perp })$$

(49)

gives on the disk $\rho -p_{\perp }=2\tilde{\rho }(r=0)$ since $p_{\perp }=-\rho$ and $r^2/\Sigma =1$ there.

The cases when DEC is satisfied also for a related spherical solution but not enough to lead to appearance of $\mathcal{S}$-surface, so that WEC is satisfied, put certain constraints on behavior of a spherical density profile. This question should be studied carefully for each particular case.

The structure of the electrically charged regular rotating black hole looks like it is shown in Figure 1 Left. The interior of the electromagnetic soliton looks similar but soliton does not have horizons. Its structure can include two or less ergospheres [59].

4. Summary and Discussion

Regular rotating electrically charged compact objects are described by regular axially symmetric solutions to the source-free NED-GR equations which for a distant observer asymptotically coincide with the Kerr-Newman solution. The source of their gravitational field is the stress-energy tensor of the nonlinear electromagnetic field itself. Geometry is described by the metrics of the Kerr-Schild class specified by $T_t^t=T_r^r(p_r=-\rho )$ in the co-rotating frame.

Axially symmetric metrics describing rotating objects originate from spherical metrics of the Kerr-Schild class generated by stress-energy tensors with the algebraic structure $T_t^t=T_r^r(p_r=-\rho )$. In most cases they are obtained with using the Newman-Janis algorithm which belongs to the Trautman-Newman complex coordinate translations and works for all spherical Kerr-Schild metrics. Rotating metrics can be obtained also in more general approach using the basic properties of the Kerr-Schild metrics [40].

The common generic feature of all regular rotating objects is the interior de Sitter vacuum disk $r=0$. Geometry allows also for the existence of an additional surface of the de Sitter vacuum, $\mathcal{S}$-surface, which includes the de Sitter disk as the bridge. In cavities between the $\mathcal{S}$-surface and the disk both WEC and DEC are violated (for a review see Reference [51]).

Dynamical equations for electromagnetic fields ${\nabla }_{\mu }\left({\mathcal{L}}_F{F}^{\mu \nu }\right)=0;{\nabla }_{\mu }{}^{*}{F}^{\mu \nu }=0$ have the form of the source-free Maxwell equations

$$\nabla ·\mathbf{D}=0;\nabla \times \mathbf{H}=\frac{\partial \mathbf{D}}{\partial t};\nabla ·\mathbf{B}=0;\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

where the electric and magnetic inductions and the field intensities $E_j=\left\{F_{j0}\right\};D^j=\left\{{\mathcal{L}}_F{F}^{0j}\right\};$ $B^j=\left\{{}^{*}{F}^{j0}\right\};H_j=\left\{{\mathcal{L}}_F{}^{*}{F}_{0j}\right\};j=1,2,3$, are related by the tensors of the electric and magnetic permeability [55]

$${ϵ}_r^r=\frac{(r^2+a^2)}{\Delta }{\mathcal{L}}_F;{ϵ}_{\theta }^{\theta }={\mathcal{L}}_F;{\mu }_r^r=\frac{(r^2+a^2)}{\Delta {\mathcal{L}}_F};{\mu }_{\theta }^{\theta }=\frac{1}{{\mathcal{L}}_F}.$$

Permeability tensors depend essentially on the Lagrangian derivative ${\mathcal{L}}_F$. Regularity requires ${\mathcal{L}}_F\to \infty$ at the $\mathcal{S}$-surface including the disk. As a result these surfaces have the properties of a perfect conductor and ideal diamagnetic.

For regular solutions the field invariant evolves from $F=-0$ as $r=0$ to $F=-0$ as $r\to \infty$. Its non-monotonic behavior results in inevitable branching of a Lagrangian. The number of branches depends on satisfaction or violation of energy conditions which require $p_{\perp }+\rho \ge 0$ (WEC) and $\rho -p_{\perp }\ge 0$ (DEC) where

$$p_{\perp }+\rho =2{\mathcal{L}}_F\left(F_{10}^2+\frac{F_{20}^2}{a^2{sin}^2\theta }\right);\rho -p_{\perp }=\mathcal{L}-{\mathcal{L}}_{F}F;F=2\left(\frac{F_{20}^2}{a^2{sin}^2\theta }-F_{10}^2\right).$$

Analysis of the regular solutions to the dynamical equations [55,59]

$${\Sigma }^2\left({\mathcal{L}}_F{F}_{01}\right)=-q(r^2-a^2{cos}^2\theta );{\Sigma }^2\left({\mathcal{L}}_F{F}_{02}\right)=q{a}^{2}rsin2\theta ;F_{31}=a{sin}^2\theta F_{10};a{F}_{23}=(r^2+a^2)F_{02}$$

distinguishes the first type of interior which contains the de Sitter vacuum disk without $\mathcal{S}$-surface as the only type of interior compatible with the standard requirement of electrodynamics of continued media (positivity of the electric permeability). In this case WEC and DEC are satisfied everywhere and the Lagrangian is branching only in the single minimum of the field invariant F. Typical behavior of a Lagrangian and its derivatives is shown in Figure 2. The source of the de Sitter vacuum on the disk is the nonlinear electromagnetic field in the vacuum state characterized by $p_r=p_{\perp }=-\rho$. The ring singularity of the Kerr-Newman geometry is replaced with the superconduction ring current which serves as the non-dissipative source of the external fields, Kerr-Newman for a distant observer [69] and of the intrinsic magnetic momentum for all regular electrically charged NED-GR objects described by the metrics of the Kerr-Schild class [70].

Electromagnetic dynamics distinguishes also the disk-like source models for the Kerr-Newman fields among all source models presented in the literature.

An open question concerns propagation of light in a nonlinear electromagnetic field. For NED theories in the Minkowski spacetime it has been shown that photons propagate along geodesics of the optical metrics on the background of electromagnetic fields; the proper character of these geodesics with respect to spacetime metric is ensured by imposing the causality conditions (see Reference [67] and references therein) obtained in the $\mathcal{L}(F,G)$ frame and violated in $\mathcal{L}\left(F\right)$ frame for some allowed background electromagnetic fields [67]. This point requires further careful investigation, especially in the NED-GR context involving strong gravitational fields.

Another open question concerns efficiency of energy extraction in physical processes involving NED-GR solitons with the de Sitter interiors which is highly facilitated by the absence of the event horizons. It is expected that NED-GR solitons (as well as neutral spinning solitons) can originate physical effects similar to those recently discovered for the Kerr-Newman braneworld naked singularities [9,12] where a special regime with the very large efficiency of accretion was revealed related to occurrence of an infinitely deep gravitational potential for circular geodesics governing the Keplerian accretion [12]. In this case the ultrahigh center-of-mass energy can be obtained in collisions of particles not only in the near-extreme spacetimes but also in spacetimes without event horizons; in addition, observers on the stable circular geodesics would register extremely blue-shifted radiation so that their ultrarelativistic orbiting motion in this special regime would provide an additional and substantial energy supply from the CMB radiation due to extremely large blue-shifting [9].

In the case of spinning solitons with the de Sitter interiors their observational signatures related to the eventual effects of this type will carry the information on the scale of the internal de Sitter vacuum. Currently we are working on geodesics around NED-GR and neutral spinning black holes and solitons and see promising possibilities related to behavior of potentials in the case of a soliton. In the case of a spherical soliton we found the existence of the special class of the isotropic geodesics corresponding to the stable photon circular orbits; the stable isotropic and time-like geodesics exist in the deep interiors of solitons, are specified by the critical values that depend on the basic parameters including those characterizing the interior de Sitter vacuum and can serve as a diagnostic tool in research of the spacetime structure in the interiors of the regular black holes and solitons [75].