Constraints on Microscopic and Phenomenological Equations of State of Dense Matter from GW170817
Abstract
1. Introduction
2. Equation of State for Neutron Star Matter
3. Results
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klahn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Nagar, A. Modeling the complete gravitational wave spectrum of neutron star mergers. Phys. Rev. Lett. 2015, 115, 091101. [Google Scholar] [CrossRef] [PubMed]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Dynamical mass ejection from the merger of asymmetric binary neutron stars: Radiation-hydrodynamics study in general relativity. Phys. Rev. D 2016, 93, 124046. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 9. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; et al. [LIGO Scientific Collaboration and Virgo Collaboration] GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Vidaña, I.; Logoteta, D.; Providência, C.; Polls, A.; Bombaci, I. Estimation of the effect of hyperonic three-body forces on the maximum mass of neutron stars. Europhys. Lett. 2011, 94, 11002. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G.F. Properties of the nuclear medium. Rep. Progr. Phys. 2012, 75, 026301. [Google Scholar] [CrossRef] [PubMed]
- Dutra, M.; Lourenço, O.; Martins, J.S.; Delfino, A.; Stone, J.R.; Stevenson, P.D. Skyrme interaction and nuclear matter constraints. Phys. Rev. C 2012, 85, 035201. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, D.F. A generalized equation of state for hot, dense matter. Nucl. Phys. 1991, 535, 331. [Google Scholar] [CrossRef]
- Schmidt, K.E.; Fantoni, S. A quantum Monte Carlo method for nucleon systems. Phys. Lett. B 1999, 446, 99. [Google Scholar] [CrossRef]
- Lonardoni, D.; Gandolfi, S.; Lynn, J.E.; Petrie, C.; Carlson, J.; Schmidt, K.E.; Schwenk, A. Auxiliary field diffusion Monte Carlo calculations of light and medium-mass nuclei with local chiral interactions. Phys. Rev. Lett. 2018, 97, 044318. [Google Scholar] [CrossRef]
- Carlson, J.; Gandolfi, S.; Pederiva, F.; Pieper, S.C.; Schiavilla, R.; Schmidt, K.E.; Wiringa, R.B. Quantum Monte Carlo methods for nuclear physics. Rev. Mod. Phys. 2015, 87, 1067. [Google Scholar] [CrossRef]
- Glendenning, N.K. (Ed.) Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: New York, NY, USA, 2000. [Google Scholar]
- Kalantar-Nayestanaki, N.; Epelbaum, E.; Messchendorp, J.S.; Nogga, A. Signatures of three-nucleon interactions in few-nucleon systems. Rep. Prog. Phys. 2012, 75, 016301. [Google Scholar] [CrossRef] [PubMed]
- Logoteta, D.; Vidaña, I.; Bombaci, I.; Kievsky, A. Comparative study of three-nucleon force models in nuclear matter. Phys. Rev. C 2015, 91, 064001. [Google Scholar] [CrossRef]
- Logoteta, I.; Bombaci, I.; Kievsky, A. Nuclear matter saturation with chiral three-nucleon interactions fitted to light nuclei properties. Phys. Lett. B 2016, 758, 449. [Google Scholar] [CrossRef]
- Logoteta, I.; Bombaci, I.; Kievsky, A. Nuclear matter properties from local chiral interactions with Δ isobar intermediate states. Phys. Rev. C 2016, 94, 064001. [Google Scholar] [CrossRef]
- Logoteta, I. Optimized chiral N2LO interactions in nuclear matter. Eur. Phys. J. A 2018, 54, 111. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, I. Equation of state of dense nuclear matter and neutron star structure from nuclear chiral interactions. Astron. Astrophys. 2018, 609, A128. [Google Scholar] [CrossRef]
- Logoteta, I.; Bombaci, I. Neutron star properties from optimized chiral nuclear interactions. Publi. Astron. Soc. Aust. 2018, 35, e035. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804. [Google Scholar] [CrossRef]
- Baldo, M.; Bombaci, I.; Burgio, G.F. Microscopic nuclear equation of state with three-body forces and neutron star structure. Astron. Astrophys. 1997, 328, 274. [Google Scholar]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2012, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Phenomenological lagrangians. Physica A 1979, 96, 327. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meissner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 501, 1. [Google Scholar] [CrossRef]
- Endrizzi, A.; Logoteta, D.; Giacomazzo, B.; Bombaci, I.; Ciolfi, R.; Kastaun, W. Effects of chiral effective field theory equation of state on binary neutron star mergers. Phys. Rev. D 2018, 98, 043015. [Google Scholar] [CrossRef]
- Kievsky, A.; Viviani, M.; Logoteta, D.; Bombaci, I.; Girlanda, L. Correlations imposed by the unitary limit between few-nucleon systems and compact stellar systems. Phys. Rev. Lett. 2018, 121, 072701. [Google Scholar] [CrossRef]
- Providência, C.; Rabhi, A. Interplay between the symmetry energy and the strangeness content of neutron stars. Phys. Rev. C 2013, 87, 055801. [Google Scholar] [CrossRef]
- Marczenko, M.; Blaschke, D.; Redlich, K.; Sasaki, C. Chiral symmetry restoration by parity doubling and the structure of neutron stars. Phys. Rev. D 2018, 98, 103021. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, D.; Vidaña, I.; Providência, C. Quark matter nucleation in neutron stars and astrophysical implications. Eur. Phys. J. A 2016, 52, 58. [Google Scholar] [CrossRef]
- Bombaci, I.; Logoteta, I. A link between measured neutron star masses and lattice QCD data. Mon. Not. R. Astron. Soc. Lett. 2013, L79, 433. [Google Scholar] [CrossRef]
- Logoteta, I.; Bombaci, I. Quark deconfinement transition in neutron stars with the field correlator method. Phys. Rev. D 2013, 88, 063001. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G. Effects of color superconductivity on the structure and formation of compact stars. Phys. Rev. D 2004, 69, 057505. [Google Scholar] [CrossRef]
- Lugones, G.; Bombaci, I. Deconfinement and color superconductivity in cold neutron stars. Phys. Rev. D 2005, 72, 065021. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I.; Providência, C.; Vidaña, I. Quark matter nucleation with a microscopic hadronic equation of state. Phys. Rev. C 2012, 85, 055807. [Google Scholar] [CrossRef]
- Dexheimer, V.; Steinheimer, J.; Negreiros, R.; Schramm, S. Hybrid stars in an SU(3) parity doublet model. Phys. Rev. C 2013, 87, 015804. [Google Scholar] [CrossRef]
- Logoteta, D.; Bombaci, I.; Providência, C.; Vidaña, I. Chiral model approach to quark matter nucleation in neutron stars. Phys. Rev. D 2012, 85, 023003. [Google Scholar] [CrossRef]
- Logoteta, D. Constraints on hybrid neutron stars equation of state from neutron stars merging. Eur. Phys. J. A 2019, 55, 133. [Google Scholar] [CrossRef]
- Tolman, R.C. (Ed.) Relativity, Thermodynamica and Cosmology; Oxford University Press: Oxford, UK, 1934. [Google Scholar]
- Oppenheimer, J.; Volkoff, G. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.L.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The Neutron star Interior Composition Explorer (NICER): Design and development. In Proceedings of the Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Edinburgh, UK, 26 June–1 July 2016; p. 99051H. [Google Scholar]
- Watts, A.L.; Yu, W.; Poutanen, J.; Zhang, S.; Bhattacharyya, S.; Bogdanov, S.; Ji, L.; Patruno, A.; Riley, T.E.; Bakala, P.; et al. Dense matter with eXTP. Sci. China Phys. Mech. Astron. 2019, 62, 29503. [Google Scholar] [CrossRef]
- Damour, T. Gravitational radiation and the motion of compact bodies. In Gravitational Radiation; Deruelle, N., Piran, T., Eds.; North-Holland: Amsterdam, The Netherlands, 1983; pp. 59–144. [Google Scholar]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A.; Villain, L. Measurability of the tidal polarizability of neutron stars in late-inspiral gravitational-wave signals. Phys. Rev. D 2012, 85, 123007. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Abbott, B.P.; et al. [LIGO Scientific Collaboration and Virgo Collaboration] Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar]
- Abbott, B.P.; et al. [LIGO Scientific Collaboration and Virgo Collaboration] GWTC-1: A gravitational-wave transient catalog of compact binary mergers observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar]
- Abbott, B.P.; et al. [LIGO Scientific Collaboration and Virgo Collaboration] GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal deformabilities and radii of neutron stars from the observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453 + 1559: A double neutron star system with large mass asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Effects of hyperons in binary neutron star mergers. Phys. Rev. Lett. 2011, 107, 211101. [Google Scholar] [CrossRef] [PubMed]
- Radice, D.; Bernuzzi, S.; Del Pozzo, W.; Ott, C.; Roberts, L.F. Probing extreme-density matter with gravitational wave observations of binary neutron star merger remnants. Astrophys. J. Lett. 2017, 842, 2. [Google Scholar] [CrossRef]
- De Pietri, R.; Drago, A.; Feo, A.; Pagliara, G.; Pasquali, M.; Traversi, S.; Wiktorowicz, G. Merger of Compact Stars in the Two-Families Scenario. Available online: https://arxiv.org/abs/1904.01545 (accessed on 24 September 2019).
- Radice, D.; Dai, L. Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 2018, 55, 50. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multi-Messenger Bayesian Parameter Inference of a Binary Neutron-Star Merger. Available online: https://arxiv.org/abs/1812.04803 (accessed on 24 September 2019).
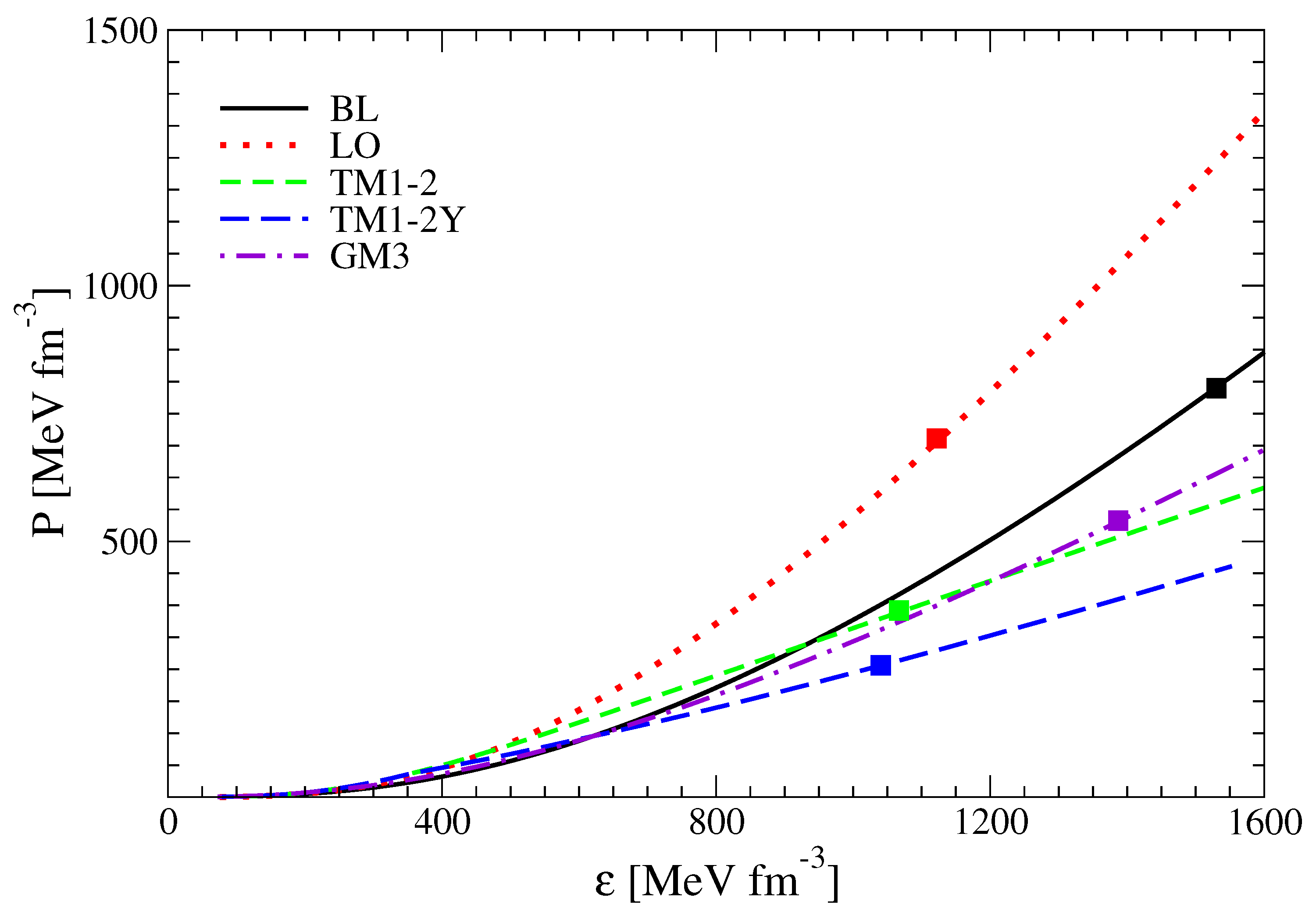
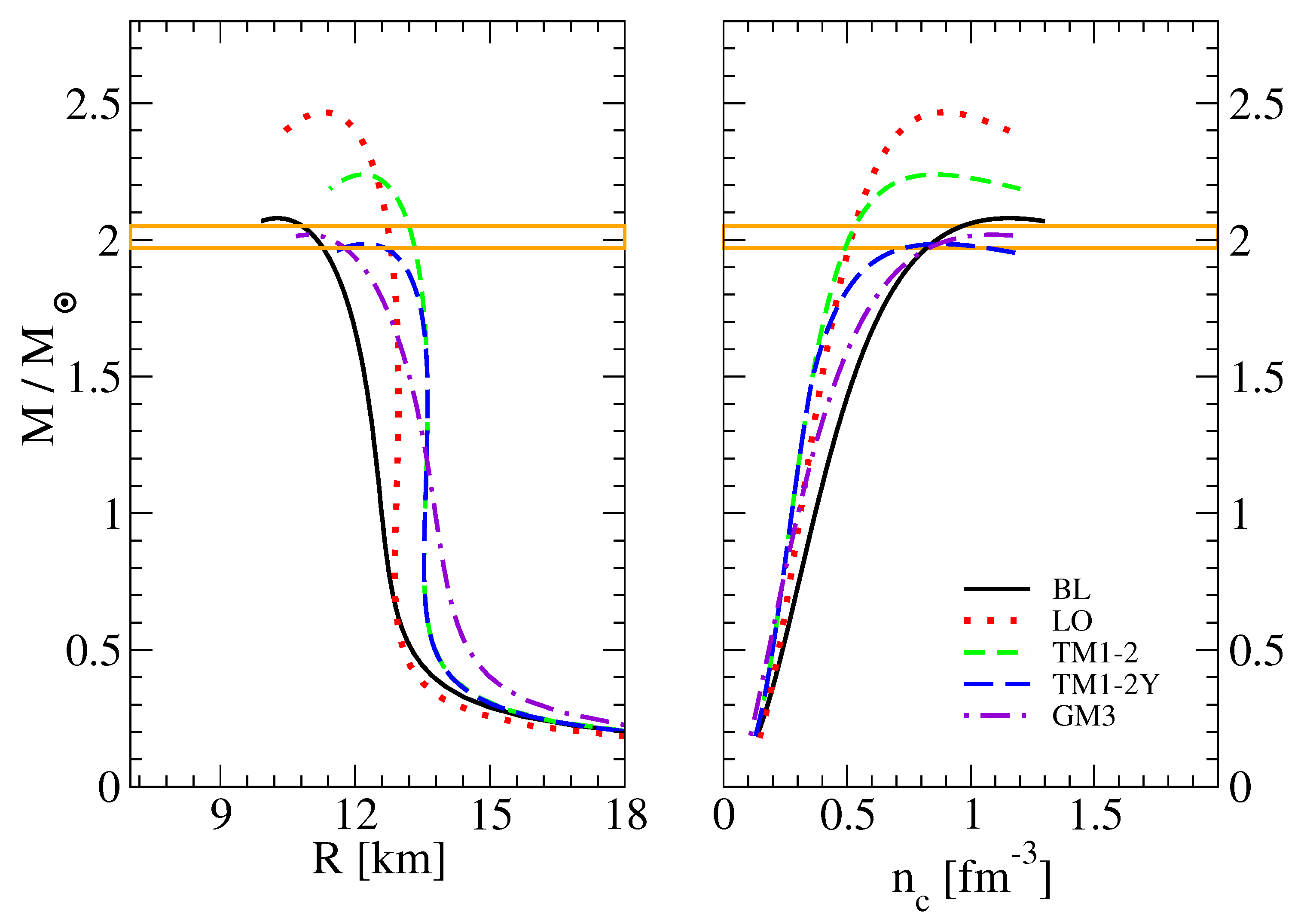
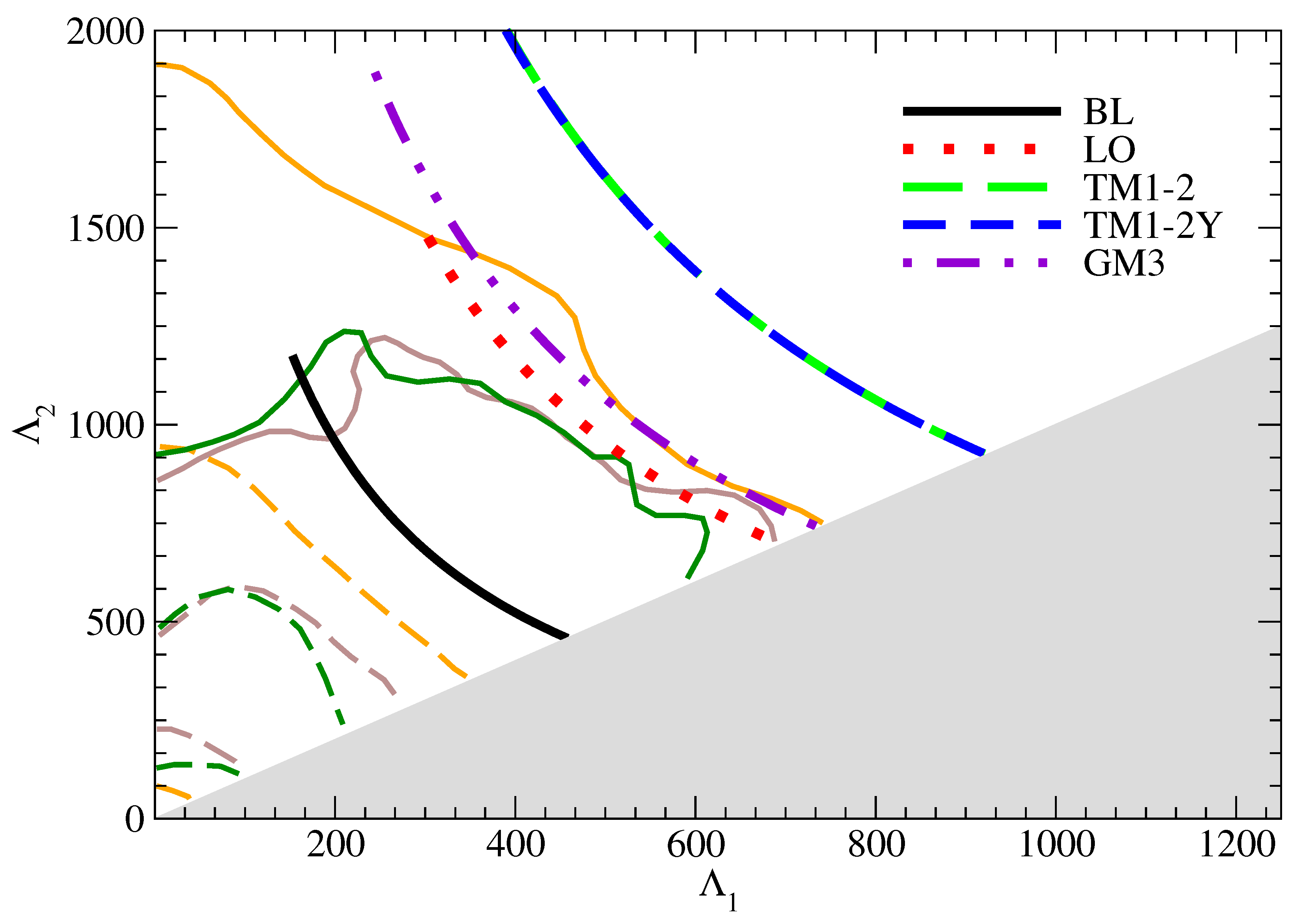
| Model | R [km] | [] | [] | |
|---|---|---|---|---|
| BL | 2.08 | 10.26 | 1.156 | 1535 |
| LO | 2.52 | 11.65 | 0.842 | 1129 |
| TM1-2 | 2.23 | 12.17 | 0.858 | 1064 |
| TM1-2Y | 1.98 | 12.23 | 0.877 | 1042 |
| GM3 | 2.01 | 10.97 | 1.088 | 1393 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Logoteta, D.; Bombaci, I. Constraints on Microscopic and Phenomenological Equations of State of Dense Matter from GW170817. Universe 2019, 5, 204. https://doi.org/10.3390/universe5100204
Logoteta D, Bombaci I. Constraints on Microscopic and Phenomenological Equations of State of Dense Matter from GW170817. Universe. 2019; 5(10):204. https://doi.org/10.3390/universe5100204
Chicago/Turabian StyleLogoteta, Domenico, and Ignazio Bombaci. 2019. "Constraints on Microscopic and Phenomenological Equations of State of Dense Matter from GW170817" Universe 5, no. 10: 204. https://doi.org/10.3390/universe5100204
APA StyleLogoteta, D., & Bombaci, I. (2019). Constraints on Microscopic and Phenomenological Equations of State of Dense Matter from GW170817. Universe, 5(10), 204. https://doi.org/10.3390/universe5100204






