Spontaneous CPT Violation and Quantum Anomalies in a Model for Matter–Antimatter Asymmetry in the Cosmos †
Abstract
1. Introduction
2. Spontaneous-CPT-Violation-Induced Leptogenesis
3. Microscopic String-Inspired Models
- First, we formulate the path integral, integrated over the KR field strength H.
- We insist on the preservation of the Bianchi identity (Equation (10)) at a quantum level, via the addition of appropriate counterterms (in a renormalisation group sense) order by order in perturbation theory. This guarantees the conservation of the “H-torsion charge” , which is implemented in the path-integral via a -functional constraint in the form and expressing the latter in terms of a (dimensionless) Lagrange multiplier field , which eventually will correspond to the dual KR axion field:where the second equality has been obtained by partial integration, upon assuming that the KR field strength dies out at spatial infinity.
- Integrating out the H-field in the path integral with the action in Equation (16), we obtain a path integral over the Lagrange multiplier field ,
4. KR axion Backgrounds, Anomalies and the Chiral Magnetic Effect
4.1. Chiral Anomalies and the Chiral Magnetic Effect
4.2. Non-Contribution of the KR Background to the Chiral Magnetic Effect
4.3. The Irrelevancy of Chern–Simons Terms for the Chiral Magnetic Effect
5. KR Axions and Anomalous Generation of Majorana Mass for the Right-Handed Neutrinos
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On the Anomalous Electroweak Baryon Number Nonconservation in the Early Universe. Phys. Lett. 1985, 155B, 36. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernandez, P.; Orloff, J.; Pene, O. Standard model CP violation and baryon asymmetry. Mod. Phys. Lett. A 1994, 9, 795. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernandez, P.; Orloff, J.; Pene, O.; Quimbay, C. Standard model CP violation and baryon asymmetry. Part 2: Finite temperature. Nucl. Phys. B 1994, 430, 382. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175. [Google Scholar] [CrossRef]
- Sakharov, A.D. Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe. Sov. Phys. Usp. 1991, 34, 392. [Google Scholar] [CrossRef]
- Buchmuller, W.; di Bari, P.; Plumacher, M. Leptogenesis for pedestrians. Ann. Phys. 2005, 315, 305. [Google Scholar] [CrossRef]
- Davidson, S.; Nardi, E.; Nir, Y. Leptogenesis. Phys. Rep. 2008, 466, 105. [Google Scholar] [CrossRef]
- Pilaftsis, A. The Little Review on Leptogenesis. J. Phys. Conf. Ser. 2009, 171, 012017. [Google Scholar] [CrossRef]
- Pilaftsis, A. Advances in Leptogenesis. J. Phys. Conf. Ser. 2013, 447, 012007. [Google Scholar] [CrossRef]
- Biondini, S.; Bodeker, D.; Brambilla, N.; Garny, M.; Ghiglieri, J.; Hohenegger, A.; Laine, M.; Mendizabal, S.; Millington, P.; Salvio, A.; et al. Status of rates and rate equations for thermal leptogenesis. Int. J. Mod. Phys. A 2018, 33, 1842004. [Google Scholar] [CrossRef]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Progress in electroweak baryogenesis. Ann. Rev. Nucl. Part. Sci. 1993, 43, 27. [Google Scholar] [CrossRef]
- Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 1999, 71, 1463. [Google Scholar] [CrossRef]
- Riotto, A.; Trodden, M. Recent progress in baryogenesis. Ann. Rev. Nucl. Part. Sci. 1999, 49, 35. [Google Scholar] [CrossRef]
- Buchmuller, W. Baryogenesis: 40 Years Later. arXiv, 2007; arXiv:0710.5857. [Google Scholar]
- Fukugita, M.; Yanagida, T. Baryogenesis without Grand Unification. Phys. Lett. B 1986, 174, 45. [Google Scholar] [CrossRef]
- Luty, M.A. Baryogenesis via leptogenesis. Phys. Rev. D 1992, 45, 455. [Google Scholar] [CrossRef]
- Pilaftsis, A. CP violation and baryogenesis due to heavy Majorana neutrinos. Phys. Rev. D 1997, 56, 5431. [Google Scholar] [CrossRef]
- Buchmuller, W.; Peccei, R.D.; Yanagida, T. Leptogenesis as the origin of matter. Ann. Rev. Nucl. Part. Sci. 2005, 55, 311. [Google Scholar] [CrossRef]
- Strumia, A. Baryogenesis via leptogenesis. In Particle Physics Beyond the Standard Model, Proceedings, Summer School on Theoretical Physics, 84th Session, Les Houches, France, 1–26 August 2005; Kazakov, D., Lavignac, S., Dalibard, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Shaposhnikov, M.; Tkachev, I. The nuMSM, inflation, and dark matter. Phys. Lett. B 2006, 639, 414. [Google Scholar] [CrossRef]
- Shaposhnikov, M. Neutrino masses, dark matter, baryon asymmetry and inflation can be explained at once. Subnucl. Ser. 2011, 47, 167. [Google Scholar] [CrossRef]
- Minkowski, P. μ → eγ at a rate of one out of 109 muon decays? Phys. Lett. B 1977, 67, 421. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Ramond, P.; Slansky, R. Supergravity; Freedman, D.Z., van Nieuwenhuizen, P., Eds.; North-Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Yanagida, T. Horizontal gauge symmetry and masses of neutrinos. In Proceedings of the Workshop on the Unified Theory and the Baryon Number in the Universe, Tsukuba, Japan, 13–14 February 1979. [Google Scholar]
- Sawada, O.; Sugamoto, A.; Mohapatra, R.N.; Senjanovic, G. Neutrino Mass and Spontaneous Parity Violation. Phys. Rev. Lett. 1980, 44, 912. [Google Scholar]
- Schechter, J.; Valle, J.W.F. Neutrino Masses in SU(2) × U(1) Theories. Phys. Rev. D 1980, 22, 2227. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.C.; Maltoni, M. Phenomenology with Massive Neutrinos. Phys. Rep. 2008, 460, 1. [Google Scholar] [CrossRef]
- Forero, D.V.; Tortola, M.; Valle, J.W.F. Global status of neutrino oscillation parameters after Neutrino-2012. Phys. Rev. D 2012, 86, 073012. [Google Scholar] [CrossRef]
- Streater, R.F.; Wightman, A.S. PCT, Spin and Statistics, and All That; Princeton University Press: Princeton, NJ, USA, 2000; 207p. [Google Scholar]
- Chaichian, M.; Dolgov, A.D.; Novikov, V.A.; Tureanu, A. CPT Violation Does Not Lead to Violation of Lorentz Invariance and Vice Versa. Phys. Lett. B 2011, 699, 177. [Google Scholar] [CrossRef]
- Chaichian, M.; Fujikawa, K.; Tureanu, A. Lorentz invariant CPT violation. Eur. Phys. J. C 2013, 73, 2349. [Google Scholar] [CrossRef]
- Arraut, I. The Quantum Yang Baxter conditions and the dispersion relations for the Nambu-Goldstone bosons. arXiv, 2016; arXiv:1611.05035. [Google Scholar]
- Arraut, I. Spontaneous symmetry breaking as a triangular relation between pairs of Goldstone bosons and the degenerate vacuum: Interactions of D-branes. arXiv, 2017; arXiv:1705.02218. [Google Scholar]
- Arraut, I. The origin of the mass of the Nambu?Goldstone bosons. Int. J. Mod. Phys. A 2018, 33, 1850041. [Google Scholar] [CrossRef]
- Greenberg, O.W. CPT violation implies violation of Lorentz invariance. Phys. Rev. Lett. 2002, 89, 231602. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Sarkar, S. CPT-Violating Leptogenesis induced by Gravitational Defects. Eur. Phys. J. C 2013, 73, 2359. [Google Scholar] [CrossRef]
- Ellis, J.; Mavromatos, N.E.; Sarkar, S. Environmental CPT Violation in an Expanding Universe in String Theory. Phys. Lett. B 2013, 725, 407. [Google Scholar] [CrossRef]
- de Cesare, M.; Mavromatos, N.E.; Sarkar, S. On the possibility of tree-level leptogenesis from Kalb? Ramond torsion background. Eur. Phys. J. C 2015, 75, 514. [Google Scholar] [CrossRef] [PubMed]
- Bossingham, T.; Mavromatos, N.E.; Sarkar, S. Leptogenesis from Heavy Right-Handed Neutrinos in CPT Violating Backgrounds. Eur. Phys. J. C 2018, 78, 113. [Google Scholar] [CrossRef]
- Bossingham, T.; Mavromatos, N.E.; Sarkar, S. The role of temperature dependent string-inspired CPT violating backgrounds in leptogenesis and the chiral magnetic effect. arXiv, 2018; arXiv:1810.13384. [Google Scholar]
- Colladay, D.; Kostelecky, V.A. Lorentz violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11. [Google Scholar] [CrossRef]
- Mavromatos, N.E. Theory overview of testing fundamental symmetries. Hyperfine Interact. 2014, 228, 7. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Lorentz-violating electrodynamics and the cosmic microwave background. Phys. Rev. Lett. 2007, 99, 011601. [Google Scholar] [CrossRef] [PubMed]
- Das, M.; Mohanty, S.; Prasanna, A.R. Constraints on background torsion from birefringence of CMB polarization. Int. J. Mod. Phys. D 2013, 22, 1350011. [Google Scholar] [CrossRef]
- Bertolami, O.; Colladay, D.; Kostelecky, V.A.; Potting, R. CPT violation and baryogenesis. Phys. Lett. B 1997, 395, 178. [Google Scholar] [CrossRef]
- Dolgov, A.D. CPT violation and particle-antiparticle asymmetry in cosmology. Phys. Atom. Nucl. 2010, 73, 588. [Google Scholar] [CrossRef]
- Ulmer, S.; Smorra, C.; Mooser, A.; Franke, K.; Nagahama, H.; Schneider, G.; Higuchi, T.; van Gorp, S.; Blaum, K.; Matsuda, Y.; et al. High-precision comparison of the antiproton-to-proton charge-to-mass ratio. Nature 2015, 524, 196. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory. Vol. 1: Introduction. In Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1987; 469p. [Google Scholar]
- Superstring Theory. Vol. 2: Loop Amplitudes, Anomalies and Phenomenology. In Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1987; 596p.
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Order alpha-prime (Two Loop) Equivalence of the String Equations of Motion and the Sigma Model Weyl Invariance Conditions: Dependence on the Dilaton and the Antisymmetric Tensor. Nucl. Phys. B 1987, 293, 385. [Google Scholar] [CrossRef]
- Bento, M.C.; Mavromatos, N.E. Ambiguities in the Low-energy Effective Actions of String Theories with the Inclusion of Antisymmetric Tensor and Dilaton Fields. Phys. Lett. B 1987, 190, 105. [Google Scholar] [CrossRef]
- Antoniadis, I.; Bachas, C.; Ellis, J.R.; Nanopoulos, D.V. An Expanding Universe in String Theory. Nucl. Phys. B 1989, 328, 117. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Rizos, J. Exact solutions and the cosmological constant problem in dilatonic domain wall higher curvature string gravity. Int. J. Mod. Phys. A 2003, 18, 57. [Google Scholar] [CrossRef]
- Mavromatos, N.E. String inspired higher curvature terms and the Randall-Sundrum scenario. Phys. Rev. D 2000, 62, 124004. [Google Scholar] [CrossRef]
- Duncan, M.J.; Kaloper, N.; Olive, K.A. Axion hair and dynamical torsion from anomalies. Nucl. Phys. B 1992, 387, 215. [Google Scholar] [CrossRef]
- Greenberg, O.W. Why is CPT fundamental? Found. Phys. 2006, 36, 1535. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Cota, R.; Barranco, J.; Delepine, D.; Khalil, S. Time-dependent Lepton Asymmetry with Primordial Magnetic Fields. PoS DSU 2012, 2012, 026. [Google Scholar] [CrossRef]
- Cota, R. Lepton Asymmetry with Primordial Magnetic Fields. J. Phys. Conf. Ser. 2013, 468, 012003. [Google Scholar] [CrossRef]
- Dvornikov, M.; Semikoz, V.B. Leptogenesis via hypermagnetic fields and baryon asymmetry. J. Cosmol. Astropart. Phys. 2012, 2012, 040, Erratum in 2012; 2012, E01. [Google Scholar] [CrossRef]
- Long, A.J.; Sabancilar, E.; Vachaspati, T. Leptogenesis and Primordial Magnetic Fields. J. Cosmol. Astropart. Phys. 2014, 2014, 036. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Reddy, S.; Sen, S. Energy Conservation and the Chiral Magnetic Effect. Phys. Rev. D 2017, 96, 016008. [Google Scholar] [CrossRef]
- Dvornikov, M. Chiral magnetic effect in the presence of an external axial-vector field. Phys. Rev. D 2018, 98, 036016. [Google Scholar] [CrossRef]
- Adler, S.L. Axial-Vector Vertex in Spinor Electrodynamics. Phys. Rev. 1969, 177, 2246. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0 → γγ in the σ-model. Nuovo Cim. A 1969, 60, 47. [Google Scholar]
- Hull, C.M. Anomalies, Ambiguities and Superstrings. Phys. Lett. 1986, 167B, 51. [Google Scholar] [CrossRef]
- Mavromatos, N.E. A Note on the Atiyah-singer Index Theorem for Manifolds With Totally Antisymmetric H Torsion. J. Phys. A 1988, 21, 2279. [Google Scholar] [CrossRef]
- Metlitski, M.A.; Zhitnitsky, A.R. Anomalous axion interactions and topological currents in dense matter. Phys. Rev. D 2005, 72, 045011. [Google Scholar] [CrossRef]
- Chandia, O.; Zanelli, J. Reply to “Comment on ‘Topological invariants, instantons, and the chiral anomaly on spaces with torsion’”. Phys. Rev. D 2001, 63, 048502. [Google Scholar] [CrossRef]
- Nieh, H.T.; Yan, M.L. Some comments on finite subgroups of SU(3). J. Math. Phys. 1982, 23, 373. [Google Scholar] [CrossRef]
- Dobado, A.; Maroto, A.L. The lepton anomaly in the presence of torsion. Phys. Rev. D 1996, 54, 5185. [Google Scholar] [CrossRef]
- Dvoeglazov, V.V. Photon and Poincare Group; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 1999; pp. 298–312. [Google Scholar]
- Alexander, S.H.S.; Peskin, M.E.; Sheikh-Jabbari, M.M. Leptogenesis from gravity waves in models of inflation. Phys. Rev. Lett. 2006, 96, 081301. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Pilaftsis, A. Anomalous Majorana Neutrino Masses from Torsionful Quantum Gravity. Phys. Rev. D 2012, 86, 124038. [Google Scholar] [CrossRef]
- Dvornikov, M. Impossibility of the strong magnetic fields generation in an electron-positron plasma. Phys. Rev. D 2014, 90, 041702. [Google Scholar] [CrossRef]
- Dvornikov, M.; Semikoz, V.B. Magnetic field instability in a neutron star driven by the electroweak electron-nucleon interaction versus the chiral magnetic effect. Phys. Rev. D 2015, 91, 061301. [Google Scholar] [CrossRef]
- Dolan, B.P. Chiral fermions and torsion in the early Universe. Class. Quant. Grav. 2010, 27, 095010, Erratum in Class. Quant. Grav. 2010, 27, 249801. [Google Scholar] [CrossRef]
- Balantsev, I.A.; Popov, Y.V.; Studenikin, A.I. On the problem of relativistic particles motion in strong magnetic field and dense matter. J. Phys. A 2011, 44, 255301. [Google Scholar] [CrossRef]
- Garcia de Andrade, L.C. Cosmological and astrophysical consequences from the magnetic dynamo equation in torsioned spacetime and teleparallel gravity. Class. Quant. Grav. 2016, 33, 025006. [Google Scholar] [CrossRef]
- Garcia de Andrade, L.C. Metric-torsion decay of non-adiabatic chiral helical magnetic fields against chiral dynamo action in bouncing cosmological models. Eur. Phys. J. C 2018, 78, 530. [Google Scholar] [CrossRef]
- Majumdar, P.; SenGupta, S. Parity violating gravitational coupling of electromagnetic fields. Class. Quant. Grav. 1999, 16, L89. [Google Scholar] [CrossRef]
- Kar, S.; Majumdar, P.; SenGupta, S.; Sur, S. Cosmic optical activity from an inhomogeneous Kalb-Ramond field. Class. Quant. Grav. 2002, 19, 677. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String Axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Cicoli, M.; Goodsell, M.; Ringwald, A. The type IIB string axiverse and its low-energy phenomenology. J. High Energy Phys. 2012, 2012, 146. [Google Scholar] [CrossRef]
- Donoghue, J.F. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874. [Google Scholar] [CrossRef]
- Perez, K.; Ng, K.C.Y.; Beacom, J.F.; Hersh, C.; Horiuchi, S.; Krivonos, R. Almost closing the nuMSM sterile neutrino dark matter window with NuSTAR. Phys. Rev. D 2017, 95, 123002. [Google Scholar] [CrossRef]
- Yunis, R.; Argüelles, C.R.; Mavromatos, N.E.; Moliné, A.; Krut, A.; Rueda, J.A.; Ruffini, R. New constraints on sterile neutrino dark matter from the Galactic Center. arXiv, 2018; arXiv:1810.05756. [Google Scholar]
| 1. | If the effects of CPTV manifested themselves only in mass differences between particles and antiparticles, then, under the natural assumptions [48], it has been argued that the dominant effects should come from the quarks; since the quark-antiquark mass differences are bounded from above by the current bounds on the proton-antiproton mass difference [49], the induced BAU, due to the corresponding differences in the thermal distribution functions (Equation (2)), turns out to be several orders of magnitude smaller than the observed value (Equation (1)). This result is reached [48] by applying the standard linear scaling of the quark mass with temperature in the range of validity of (1). |
| 2. | At high temperatures, above the spontaneous electroweak symmetry breaking, the charged Higgs fields do not decouple from the physical spectrum, and play an important role in leptogenesis. |
| 3. | There is a certain uncertainty related to the Taylor expansions used in our Padé analysis and to indicate this a range of numbers in brackets is given below. |
| 4. | In (Heterotic) string theory, in the presence of gauge and gravitational fields, the right-hand-side of Equation (9) is modified by appropriate (parity-violating) Chern–Simons three-forms. The right-hand side of the Bianchi identity (Equation (10)) becomes non-zero, a sign of gauge and gravitational anomalies [50,51]. We do not deal explicitly with such (higher derivative) terms here, as they are not directly relevant to our leptogenesis scenario. We briefly demonstrate, however, in Section 4, that their inclusion does not affect the chiral magnetic effect. |
| 5. | Par contrast, in [55], the Lorentz invariance violating constant background solution is argued to be an exact solution of bosonic string theory. |
| 6. | A chiral chemical potential has different values of the chemical potential for left and right chiral spinors. |
| 7. | We note that this is the complete form of the anomaly in our case, which is characterised by the conservation of the H-torsion charge (Equation (17)), at a quantum level. Indeed, as discussed in [73], for a generic torsion three form , with the vielbein one-form and the contorsion tensor, the righ- hand side of the anomaly (30) also contains the Nieh–Yan topological invariant density [74], . In our case, , and thus the Nieh–Yan invariant vanishes identically on account of the torsion charge conservation constraint (Equation (17)), which can be written as . |
| 8. | The reader should notice that there is no H-torsion contribution to the covariant four-divergence of a four-vector. |
| 9. | As already mentioned, this can also be understood from the fact [70,71] that the chiral anomaly is associated with the index of the Dirac operator for fermions, and the latter is not affected by torsion, as it is associated with the topological quantity , where is a compact target-space-time manifold without boundary, and we took into account that the torsion contributions to the gravitational part of the anomaly (Equation (31)) is a total differential. The latter property would also imply that one can appropriately redefine the axial current by such torsion dependent terms [75,76], to arrive at a new gauge and Lorentz-invariant axial current, whose anomaly equation is torsion free. |
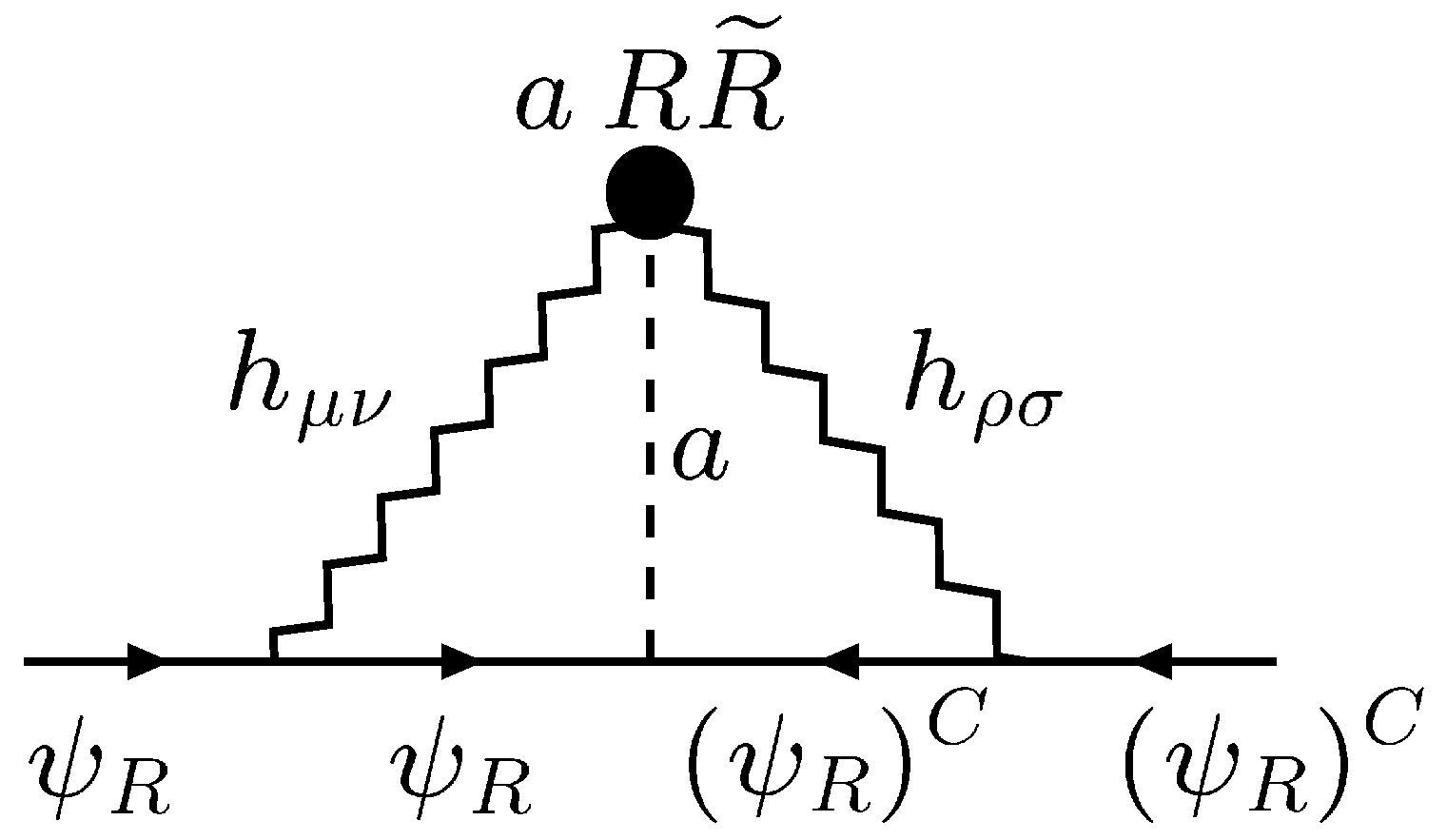
| 10. | In fact, it is only the gravitational-wave type fluctuations that contribute to the (torsion-free) Riemann-curvature-dependent part of the anomaly (Equation (30)), which can then lead to interesting scenarios for leptogenesis, different from our approach here [77]. Moreover, graviton fluctuations in the gravitational parts of the anomaly (Equation (30)) might play an important role in radiative Majorana mass generation for the right-handed neutrinos [78], as we review in Section 5. |
| 11. | We should stress that both the present and previous works of ours [41] pertain to cases in which the axial background is an independent field, e.g., the KR axion. We do not discuss here situations where the totally antisymmetric torsion is a chiral condensate of fermions. In such cases, as we remarked in [41], the free-fermion analysis of [67] needs to be modified to take proper account of the fermion self-interactions in Equation (18). For a discussion along those lines, and the potential role (in the early universe) of torsion arising from thermal condensates of massless chiral fermions, the reader is referred to Ref. [81]. |
| 12. | This model can be obtained from a string-inspired effective theory of the modified Kalb–Ramond H-field with CS terms, truncated to quadratic order in a derivative expansion, in a curved space-time with (non-duynamical) torsion , which appears in both the Riemann curvature and the fermion gravitational covariant derivative, and is coupled to the field via terms in the action [85,86]. This auxiliary torsion field can then be integrated exactly in the path integral, with the result that it obeys the constraint . Substituting back to the action, and taking the Minkowski flat space-time limit, leads then to the action (Equation (36)). |
| 13. | The overall minus sign is due to the fact that the three-dimensional Levi–Civita symbol is defined as: . |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mavromatos, N.E.; Sarkar, S. Spontaneous CPT Violation and Quantum Anomalies in a Model for Matter–Antimatter Asymmetry in the Cosmos. Universe 2019, 5, 5. https://doi.org/10.3390/universe5010005
Mavromatos NE, Sarkar S. Spontaneous CPT Violation and Quantum Anomalies in a Model for Matter–Antimatter Asymmetry in the Cosmos. Universe. 2019; 5(1):5. https://doi.org/10.3390/universe5010005
Chicago/Turabian StyleMavromatos, Nick E., and Sarben Sarkar. 2019. "Spontaneous CPT Violation and Quantum Anomalies in a Model for Matter–Antimatter Asymmetry in the Cosmos" Universe 5, no. 1: 5. https://doi.org/10.3390/universe5010005
APA StyleMavromatos, N. E., & Sarkar, S. (2019). Spontaneous CPT Violation and Quantum Anomalies in a Model for Matter–Antimatter Asymmetry in the Cosmos. Universe, 5(1), 5. https://doi.org/10.3390/universe5010005





