A Scale at 10 MeV, Gravitational Topological Vacuum, and Large Extra Dimensions
Abstract
1. Introduction
2. The MacDowell–Mansouri Formalism and the Bjorken–Zeldovich Scale
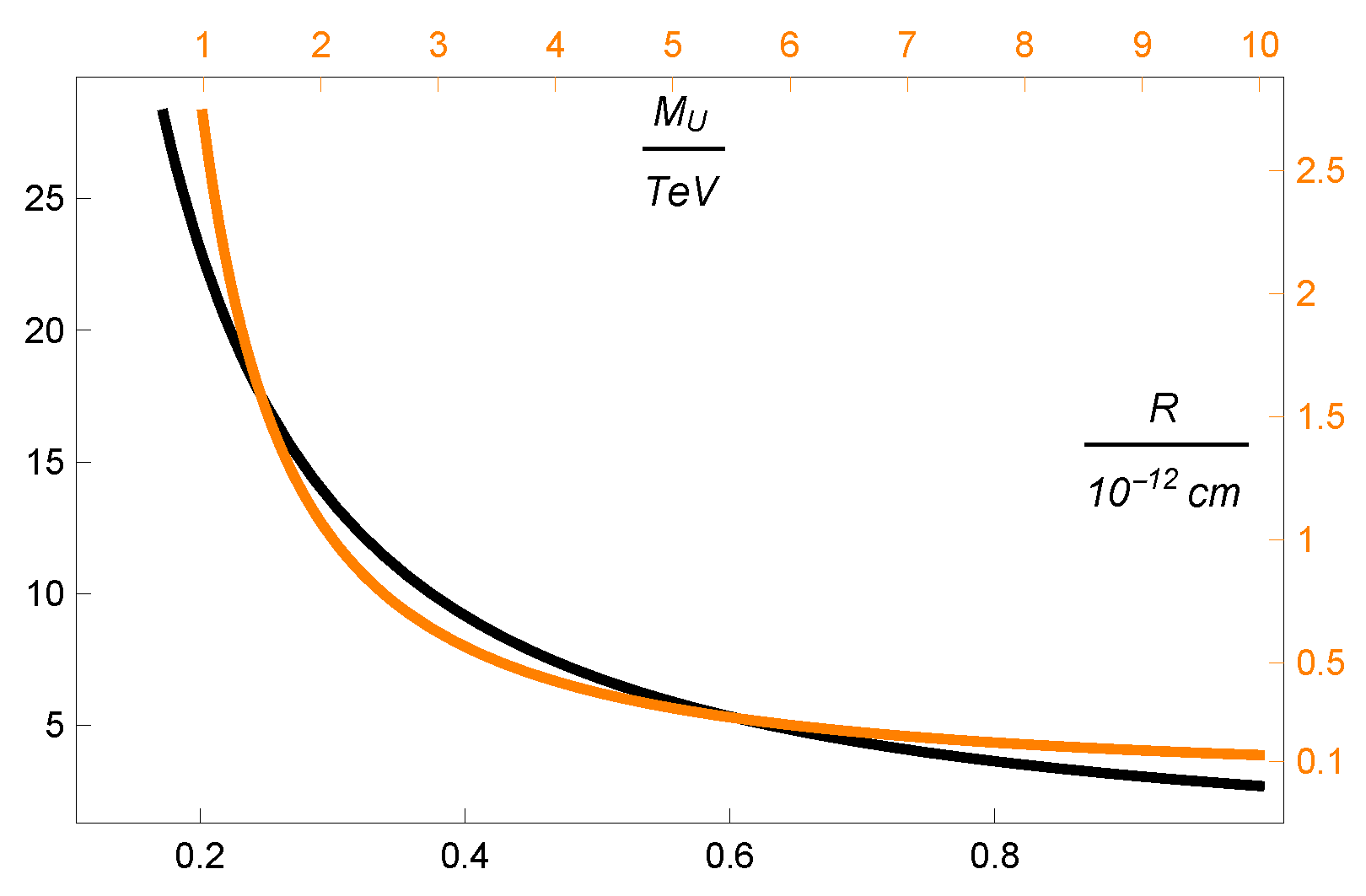
3. Bjorken–Zeldovich Scale from Large Extra Dimensions
4. A “See-Saw” Relation for the Small Cosmological Constant and the Neutrino Mass?
5. More on the Relevance in Cosmology
6. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Bjorken, J. Darkness: What comprises empty space? Annalen der Physik 2013, 525, A67–A79. [Google Scholar] [CrossRef]
- MacDowell, S.W.; Mansouri, F. Unified Geometric Theory of Gravity and Supergravity. Phys. Rev. Lett. 1977, 38, 739. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. Cosmological Constant and Elementary Particles. JETP Lett. 1967, 6, 316–317. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Krasinski, A. The Cosmological constant and the theory of elementary particles. Sov. Phys. Uspekhi 1968, 11, 381–393. [Google Scholar] [CrossRef]
- Freidel, L.; Starodubtsev, A. Quantum gravity in terms of topological observables. arXiv, 2005; arXiv:hep-th/0501191. [Google Scholar]
- Wise, D.K. MacDowell–Mansouri gravity and Cartan geometry. Class. Quantum Gravity 2010, 27, 155010. [Google Scholar] [CrossRef]
- Wise, D.K. Symmetric space Cartan connections and gravity in three and four dimensions. Symmetry Integr. Geom. 2009, 5, 080. [Google Scholar] [CrossRef]
- Randono, A. A Mesoscopic Quantum Gravity Effect. Gen. Relativ. Gravit. 2010, 42, 1909–1917. [Google Scholar] [CrossRef]
- Kodama, H. Specialization of Ashtekar’s Formalism to Bianchi Cosmology. Prog. Theor. Phys. 1988, 80, 1024. [Google Scholar] [CrossRef]
- Smolin, L. Quantum gravity with a positive cosmological constant. arXiv, 2002; arXiv:hep-th/0209079. [Google Scholar]
- Witten, E. A Note on the Chern–Simons and Kodama wave functions. arXiv, 2003; arXiv:gr-qc/0306083. [Google Scholar]
- Randono, A. Generalizing the Kodama state. I. Construction. arXiv, 2006; arXiv:gr-qc/0611073. [Google Scholar]
- Randono, A. Generalizing the Kodama state. II. Properties and physical interpretation. arXiv, 2006; arXiv:gr-qc/0611074. [Google Scholar]
- Rovelli, C. Loop quantum gravity: The first twenty five years. Class. Quantum Gravity 2011, 28, 153002. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pullin, J. The Overview Chapter in Loop Quantum Gravity: The First 30 Years. arXiv, 2017; arXiv:gr-qc/1703.07396. [Google Scholar]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Relat. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Polchinski, J. The Cosmological Constant and the String Landscape. In The Quantum Structure of Space and Time: Proceedings of the 23rd Solvay Conference on Physics, Brussels, Belgium, 1–3 December 2005; Cornell University Library: Ithaca, NY, USA, 2006; pp. 216–236. [Google Scholar]
- Padilla, A. Lectures on the Cosmological Constant Problem. arXiv, 2015; arXiv:hep-th/1502.05296. [Google Scholar]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Kaloper, N.; Sundrum, R. A Small cosmological constant from a large extra dimension. Phys. Lett. B 2000, 480, 193–199. [Google Scholar] [CrossRef]
- Antoniadis, I.; Dimopoulos, S.; Dvali, G.R. Millimeter range forces in superstring theories with weak scale compactification. Nucl. Phys. B 1998, 516, 70–82. [Google Scholar] [CrossRef]
- Accomando, E.; Antoniadis, I.; Benakli, K. Looking for TeV scale strings and extra dimensions. Nucl. Phys. B 2000, 579, 3–16. [Google Scholar] [CrossRef]
- Antoniadis, I.; Benakli, K.; Quiros, M. Direct collider signatures of large extra dimensions. Phys. Lett. B 1999, 460, 176–183. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the gravitational inverse-square law below the dark-energy length scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef] [PubMed]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Patrignani, C.; et al. [Particle Data Group]. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Pearson Education Inc.: London, UK, 2004. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Langacker, P. The Standard Model and Beyond; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Krasznahorkay, A.J.; Csatlós, M.; Csige, L.; Gácsi, Z.; Gulyás, J.; Hunyadi, M.; Kuti, I.; Nyakó, B.M.; Stuhl, L.; Timár, J.; et al. Observation of Anomalous Internal Pair Creation in 8Be: A Possible Indication of a Light, Neutral Boson. Phys. Rev. Lett. 2016, 116, 042501. [Google Scholar] [CrossRef] [PubMed]
- De Boer, F.W.N.; Fröhlich, O.; Stiebing, K.E.; Bethge, K.; Bokemeyer, H.; Balanda, A.; Buda, A.; Van Dantzig, R.; Elze, T.W.; Folger, H.; et al. A deviation in internal pair conversion. Phys. Lett. B 1996, 388, 235–240. [Google Scholar] [CrossRef]
- De Boer, F.W.N.; van Dantzig, R.; van Klinken, J.; Bethge, K.; Bokemeyer, H.; Buda, A.; Muller, K.A.; Stiebing, K.E. Excess in e+e− pairs near 9 MeV invariant mass. J. Phys. 1997, G23, L85–L96. [Google Scholar] [CrossRef]
- De Boer, F.W.N.; Bethge, K.; Bokemeyer, H.; van Dantzig, R.; van Klinken, J.; Mironov, V.; Muller, K.A.; Stiebing, K.E. Further search for a neutral boson with a mass around 9-MeV/c2. J. Phys. 2001, G27, L29. [Google Scholar] [CrossRef]
- De Boer, F. Anomalous internal pair conversion signaling elusive light neutral particles. AIP Conf. Proc. 2006, 802, 146–152. [Google Scholar]
- Krasznahorkay, A.; de Boer, F.W.N.; Csatlós, M.; Csige, L.; Gácsi, Z.; Gulyás, J.; Hunyadi, M.; Ketel, T.J.; van Klinken, J.; Krasznahorkay, A., Jr.; et al. e+e− pairs from a nuclear transition signaling an elusive light neutral boson. AIP Conf. Proc. 2005, 802, 236. [Google Scholar]
- Krasznahorkay, A.; Gacsi, Z.; Ketel, T.J.; van Klinken, J.; de Boer, F.W.N.; Gulyás, J.; Csige, L.; Krasznahorkay, A. Jr.; Hunyadi, M.; Vitez, A.; et al. Lepton pairs from a forbidden M0 transition: Signaling an elusive light neutral boson? Acta Phys. Polon. B 2006, 37, 239–244. [Google Scholar]
- De Boer, F.W.N.; Fields, C.A. A Re-evaluation of Evidence for Light Neutral Bosons in Nuclear Emulsions. Int. J. Mod. Phys. E 2011, 20, 1787–1803. [Google Scholar] [CrossRef]
- Wojtsekhowski, B.; Nikolenko, D.; Rachek, I. Searching for a new force at VEPP-3. arXiv, 2012; arXiv:hep-ex/1207.5089. [Google Scholar]
- Gulyas, J.; Ketel, T.J.; Krasznahorkay, A.J.; Csatlos, M.; Csige, L.; Gacsi, Z.; Hunyadi, M.; Krasznahorkay, A.; Vitez, A.; Tornyi, T.G. A pair spectrometer for measuring multipolarities of energetic nuclear transitions. Nucl. Instrum. Method. 2016, A808, 21–28. [Google Scholar] [CrossRef]
- Feng, J.L.; Fornal, B.; Galon, I.; Gardner, S.; Smolinsky, J.; Tait, T.M.P.; Tanedo, P. Protophobic Fifth-Force Interpretation of the Observed Anomaly in 8Be Nuclear Transitions. Phys. Rev. Lett. 2016, 117, 071803. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.L.; Fornal, B.; Galon, I.; Gardner, S.; Smolinsky, J.; Tait, T.M.P.; Tanedo, P. Particle Physics Models for the 17 MeV Anomaly in Beryllium Nuclear Decays. arXiv, 2016; arXiv:hep-ph/1608.03591. [Google Scholar] [CrossRef]
- Gninenko, S.N.; Krasnikov, N.V.; Kirsanov, M.M.; Kirpichnikov, D.V. Missing energy signature from invisible decays of dark photons at the CERN SPS. Phys. Rev. D 2016, 94, 095025. [Google Scholar] [CrossRef]
- Gu, P.H.; He, X.G. Realistic model for a fifth force explaining anomaly in 8Be∗ → 8Be e+e− Decay. Nucl. Phys. B 2017, 919, 209–217. [Google Scholar] [CrossRef]
- Jia, L.B.; Li, X.Q. The new interaction suggested by the anomalous 8Be transition sets a rigorous constraint on the mass range of dark matter. Eur. Phys. J. C 2016, 76, 706. [Google Scholar] [CrossRef]
- Kitahara, T.; Yamamoto, Y. Protophobic Light Vector Boson as a Mediator to the Dark Sector. Phys. Rev. D 2017, 95, 015008. [Google Scholar] [CrossRef]
- Ellwanger, U.; Moretti, S. Possible Explanation of the Electron Positron Anomaly at 17 MeV in 8Be Transitions Through a Light Pseudoscalar. J. High Energy Phys. 2016, 2016, 039. [Google Scholar] [CrossRef]
- Chen, C.S.; Lin, G.L.; Lin, Y.H.; Xu, F. The 17 MeV Anomaly in Beryllium Decays and U(1) Portal to Dark Matter. arXiv, 2016; arXiv:hep-ph/1609.07198. [Google Scholar]
- Neves, M.J.; Helayel-Neto, J.A. TeV- and MeV-physics out of an SU(2) × U(1) × U(1) model. arXiv, 2016; arXiv:hep-ph/1609.08471. [Google Scholar]
- Kahn, Y.; Krnjaic, G.; Mishra-Sharma, S.; Tait, T.M.P. Light Weakly Coupled Axial Forces: Models, Constraints, and Projections. arXiv, 2016; arXiv:hep-ph/1609.09072. [Google Scholar] [CrossRef]
- Fayet, P. The light U boson as the mediator of a new force, coupled to a combination of Q, B, L and dark matter. Eur. Phys. J. C 2017, 77, 53. [Google Scholar] [CrossRef]
- Neves, M.J.; Helayel-Neto, J.A. A Unified Hidden-Sector-Electroweak Model, Paraphotons and the X-Boson. arXiv, 2016; arXiv:hep-ph/1611.07974. [Google Scholar]
- Kozaczuk, J.; Morrissey, D.E.; Stroberg, S.R. Light Axial Vectors, Nuclear Transitions, and the 8Be Anomaly. arXiv, 2016; arXiv:hep-ph/1612.01525. [Google Scholar]
- Chiang, C.W.; Tseng, P.Y. Probing a dark photon using rare leptonic kaon and pion decays. Phys. Lett. B 2017, 767, 289–294. [Google Scholar] [CrossRef]
- Krasnikov, N.V. The muon (g − 2) anomaly and a new light vector boson. arXiv, 2017; arXiv:hep-ph/1702.04596. [Google Scholar]
- Araki, T.; Hoshino, S.; Ota, T.; Sato, J.; Shimomura, T. Detecting the Lμ − Lτ gauge boson at Belle II. Phys. Rev. D 2017, 95, 055006. [Google Scholar] [CrossRef]
- Benavides, R.; Munoz, L.A.; Ponce, W.A.; Rodriguez, O.; Rojas, E. Minimal non-universal EW extensions of the Standard Model: A chiral multi-parameter solution. arXiv, 2016; arXiv:hep-ph/1612.07660. [Google Scholar]
- Neves, M.J. The protophobic X-boson unified to the quantum electrodynamics. arXiv, 2017; arXiv:hep-ph/1704.02491. [Google Scholar]
- Delle Rose, L.; Khalil, S.; Moretti, S. Explanation of the 17 MeV Atomki Anomaly in a U(1)′-Extended 2-Higgs Doublet Model. arXiv, 2017; arXiv:hep-ph/1704.03436. [Google Scholar] [CrossRef]
- Csaki, C. TASI lectures on extra dimensions and branes. From fields to strings: Circumnavigating theoretical physics. Ian Kogan memorial collection (3 volume set). arXiv, 2004; arXiv:hep-ph/0404096. [Google Scholar]
- Rizzo, T.G. Introduction to Extra Dimensions. AIP Conf. Proc. 2010, 1256, 27–50. [Google Scholar]
- Roy, A. Search for Dark Matter and Large Extra Dimensions in the Photon + MET Final State in pp Collisions at = 13 TeV. Springer Proc. Phys. 2018, 203, 205–208. [Google Scholar]
- Ghosh, S. Large Extra Dimensions Search in the Photon + MET Final State in pp Collisions at = 13 TeV at CMS in LHC. Springer Proc. Phys. 2018, 203, 745–747. [Google Scholar]
- Sirunyan, A.M.; et al. [The CMS Collaboration]. Search for new physics in the monophoton final state in proton-proton collisions at = 13 TeV. J. High Energy Phys. 2017, 2017, 73. [Google Scholar] [CrossRef]
- Banks, T. SUSY breaking, cosmology, vacuum selection and the cosmological constant in string theory. In Proceedings of the ITP Workshop on SUSY Phenomena and SUSY GUTS Santa Barbara, California, CA, USA, 7–9 December 1995. [Google Scholar]
- Cohen, A.G.; Kaplan, D.B.; Nelson, A.E. Effective field theory, black holes, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 4971–4974. [Google Scholar] [CrossRef]
- Kim, J.E. Model dependent axion as quintessence with almost massless hidden sector quarks. J. High Energy Phys. 2000, 2000, 016. [Google Scholar] [CrossRef]
- Kiritsis, E. Supergravity, D-brane probes and thermal superYang–Mills: A Comparison. J. High Energy Phys. 1999, 1999, 010. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Hall, L.J.; Kolda, C.F.; Murayama, H. A New perspective on cosmic coincidence problems. Phys. Rev. Lett. 2000, 85, 4434–4437. [Google Scholar] [CrossRef] [PubMed]
- Banks, T. Cosmological breaking of supersymmetry? Int. J. Mod. Phys. A 2001, 16, 910–921. [Google Scholar] [CrossRef]
- Chang, L.N.; Minic, D.; Okamura, N.; Takeuchi, T. The Effect of the minimal length uncertainty relation on the density of states and the cosmological constant problem. Phys. Rev. D 2002, 65, 125028. [Google Scholar] [CrossRef]
- Chang, L.N.; Minic, D.; Okamura, N.; Takeuchi, T. Exact solution of the harmonic oscillator in arbitrary dimensions with minimal length uncertainty relations. Phys. Rev. D 2002, 65, 125027. [Google Scholar] [CrossRef]
- Barr, S.M.; Seckel, D. The Cosmological constant, false vacua, and axions. Phys. Rev. D 2001, 64, 123513. [Google Scholar] [CrossRef]
- Berglund, P.; Hubsch, T.; Minic, D. Relating the cosmological constant and supersymmetry breaking in warped compactifications of IIB string theory. Phys. Rev. D 2003, 67, 041901. [Google Scholar] [CrossRef]
- Hsu, S.D.H.; Zee, A. A Speculative relation between the cosmological constant and the Planck mass. Mod. Phys. Lett. A 2005, 20, 2699–2704. [Google Scholar] [CrossRef]
- Urban, F.R.; Zhitnitsky, A.R. The Cosmological constant from the ghost: A Toy model. Phys. Rev. D 2009, 80, 063001. [Google Scholar] [CrossRef]
- Urban, F.R.; Zhitnitsky, A.R. The cosmological constant from the QCD Veneziano ghost. Phys. Lett. B 2010, 688, 9–12. [Google Scholar] [CrossRef]
- Urban, F.R.; Zhitnitsky, A.R. The QCD nature of Dark Energy. Nucl. Phys. B 2010, 835, 135–173. [Google Scholar] [CrossRef]
- Chang, L.N.; Minic, D.; Takeuchi, T. Quantum Gravity, Dynamical Energy-Momentum Space and Vacuum Energy. Mod. Phys. Lett. A 2010, 25, 2947–2954. [Google Scholar] [CrossRef]
- Chang, L.N.; Lewis, Z.; Minic, D.; Takeuchi, T. On the Minimal Length Uncertainty Relation and the Foundations of String Theory. Adv. High Energy Phys. 2011, 2011, 493514. [Google Scholar] [CrossRef]
- Garretson, W.D.; Carlson, E.D. Could there be something rather than nothing? Phys. Lett. B 1993, 315, 232–238. [Google Scholar] [CrossRef]
- Lisi, A.G. An Exceptionally Simple Theory of Everything. arXiv, 2007; arXiv:hep-th/0711.0770. [Google Scholar]
- Nesti, F.; Percacci, R. Chirality in unified theories of gravity. Phys. Rev. D 2010, 81, 025010. [Google Scholar] [CrossRef]
- Lisi, A.G.; Smolin, L.; Speziale, S. Unification of gravity, gauge fields, and Higgs bosons. J. Phys. A 2010, 43, 445401–445408. [Google Scholar] [CrossRef]
- Ne’eman, Y. Irreducible Gauge Theory of a Consolidated Weinberg-Salam Model. Phys. Lett. B 1979, 81, 190–194. [Google Scholar] [CrossRef]
- Fairlie, D.B. Higgs’ Fields and the Determination of the Weinberg Angle. Phys. Lett. B 1979, 82, 97–100. [Google Scholar] [CrossRef]
- Fairlie, D.B. Two Consistent Calculations of the Weinberg Angle. J. Phys. G 1979, 5, L55. [Google Scholar] [CrossRef]
- Ne’eman, Y.; Sternberg, S. Superconnections and internal supersymmetry dynamics. Proc. Natl. Acad. Sci. USA 1990, 87, 7875–7877. [Google Scholar] [CrossRef] [PubMed]
- Ne’eman, Y.; Sternberg, S.; Fairlie, D. Superconnections for electroweak su(2/1) and extensions, and the mass of the Higgs. Phys. Rep. 2005, 406, 303–377. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Connes, A. Noncommutative Geometry as a Framework for Unification of all Fundamental Interactions including Gravity. Part I. Fortsch. Phys. 2010, 58, 553–600. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Connes, A. Resilience of the Spectral Standard Model. J. High Energy Phys. 2012, 2012, 104. [Google Scholar] [CrossRef]
- Chamseddine, A.H.; Connes, A.; van Suijlekom, W.D. Beyond the Spectral Standard Model: Emergence of Pati-Salam Unification. J. High Energy Phys. 2013, 2013, 132. [Google Scholar] [CrossRef]
- Aydemir, U.; Minic, D.; Takeuchi, T. The Higgs Mass and the Emergence of New Physics. Phys. Lett. B 2013, 724, 301–305. [Google Scholar] [CrossRef]
- Aydemir, U.; Minic, D.; Sun, C.; Takeuchi, T. Higgs mass, superconnections, and the TeV-scale left-right symmetric model. Phys. Rev. D 2015, 91, 045020. [Google Scholar] [CrossRef]
- Schwarz, J.H. Physical States and Pomeron Poles in the Dual Pion Model. Nucl. Phys. B 1972, 46, 61–74. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J.H. Dual Field Theory of Quarks and Gluons. Phys. Lett. B 1975, 57, 463–466. [Google Scholar] [CrossRef]
- Candelas, P.; Horowitz, G.T.; Strominger, A.; Witten, E. Vacuum Configurations for Superstrings. Nucl. Phys. B 1985, 258, 46–74. [Google Scholar] [CrossRef]
- Han, T.; Lykken, J.D.; Zhang, R.J. On Kaluza–Klein states from large extra dimensions. Phys. Rev. D 1999, 59, 105006. [Google Scholar] [CrossRef]
| 1 | Recently, the Atomki group in Hungary reported an anomaly in the Be nuclear decay by internal formation at an invariant mass MeV, with a statistical significance of 6.8 [33]. See also Refs. [34,35,36,37,38,39,40,41,42] for the previous studies relevant to this observation. The observation has ignited interest in the high energy physics community to suggest explanations, some of which consider a hidden sector at around this energy scale whose effects have so far remained unnoticed [43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. |
| 2 | |
| 3 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydemir, U. A Scale at 10 MeV, Gravitational Topological Vacuum, and Large Extra Dimensions. Universe 2018, 4, 80. https://doi.org/10.3390/universe4070080
Aydemir U. A Scale at 10 MeV, Gravitational Topological Vacuum, and Large Extra Dimensions. Universe. 2018; 4(7):80. https://doi.org/10.3390/universe4070080
Chicago/Turabian StyleAydemir, Ufuk. 2018. "A Scale at 10 MeV, Gravitational Topological Vacuum, and Large Extra Dimensions" Universe 4, no. 7: 80. https://doi.org/10.3390/universe4070080
APA StyleAydemir, U. (2018). A Scale at 10 MeV, Gravitational Topological Vacuum, and Large Extra Dimensions. Universe, 4(7), 80. https://doi.org/10.3390/universe4070080



