Abstract
We compute the principal non-radial oscillation mode frequencies of Neutron Stars described with a Skyrme-like Equation of State (EoS), taking into account the possibility of neutron and proton superfluidity. Using the CompOSE database and interpolation routines to obtain the needed thermodynamic quantities, we solve the fluid oscillation equations numerically in the background of a fully relativistic star, and identify imprints of the superfluid state. Though these modes cannot be observed with current technology, increased sensitivity of future Gravitational-Wave Observatories could allow us to observe these oscillations and potentially constrain or refine models of dense matter relevant to the interior of neutron stars.
1. Introduction
The Laser Interferometer Gravitational-Wave Observatory (LIGO) recently detected gravitational waves emitted from the merger of two neutron stars, heralding a new era of compact star physics [1]. As the sensitivity of gravitational wave detectors increases, we may expect to directly observe the gravitational waves even from isolated neutron stars. Neutron star oscillations allow us to probe the nature of ultra-dense nuclear matter, since the equation of state (EoS) plays a central role in determining the spectrum of oscillation modes. Thus, in the event that actual oscillation modes can be observed, comparison to theoretical templates based on models of dense matter can help to refine or constrain the EoS. For calculating the spectrum of oscillation modes theoretically, we require tabulated EoS from realistic microscopic models of dense matter. The CompOSE database [2] provides an array of such models with thermodynamically consistent interpolation. In these proceedings, we report results from a calculation of the spectrum of non-radial oscillation modes of neutron stars based on Skyrme-like EoS in the CompOSE database, and compare the results to the polytropic equation of state. We also consider the effects of superfluidity in neutron stars on the oscillation modes, using the same family of EoS. After establishing the background structure of the neutron star in Section 2, we present the main equations and numerical results from solving the oscillation equations in Section 3, including the extension to superfluidity. In Section 4, we summarize our findings and comment on further extensions of this work in Section 5.
2. EoS Models and Superfluid Neutron Star Structure
One of the simplest models of a neutron star assumes a polytropic equation of state with polytropic index n and a proportionality constant K. In this work, we choose and km in G = c = 1 units, which simplifies the numerics of the Tolman-Oppenheimer-Volkov (TOV) equations for the mass and radius of the neutron star. There is a limitation of the polytrope: the structure of such a star in General Relativity can only provide a maximum mass of about 1.2 . We therefore employ Newtonian structure equations for the polytrope, in which case, for , the mass is independent of the radius [3]. This allows us to study the model for stars as heavy as 2 while keeping the radius fixed at a canonical value (e.g., 10 km). We emphasize that the polytropic equation of state is only used here as a simple model for a rough estimate of the non-radial oscillation spectra of neutron stars, and the Skyrme-like model [4,5] is used for more realistic calculations. For the latter case, the CompOSE database provides appropriate tables of thermodynamic quantities based on the baryon number density within the star. While the structure of the star can be solved from the standard TOV equations using the energy and pressure alone, finding the oscillation modes for the normal and superfluid cases requires knowing the chemical potentials and densities of the neutrons, protons, and electrons in the star from center to surface. The CompOSE database provides these for various EoS along with consistent interpolation routines. From this database, we choose three Skyrme models with interaction parameters provided by the KDE0, KDE0v1 and the SK255 dataset, as calculated by Agrawal [4,6]. We refer to these three sets of parameters as Skyrme Model A, B and C respectively. These interaction parameters can be thought of as specifying a nucleon energy density [7]
where , , and refer to neutron, proton, and baryon number densities respectively; the are based on these densities; and the and are specific to the interaction.
A neutron star may be considered to have three major regions: the outer crust, the inner crust, and the core. In the outer crust, the density ranges from to . This part of the star consists mostly of nuclei and electrons. The inner crust ranges from to . Here, the temperature is below the critical temperature for neutron pairing, and a neutron superfluid can form. The core of the neutron star has densities greater than , and consists of both neutrons and protons in a superfluid state, with electrons present to satisfy charge neutrality. For this work, we adopt a simplified two-layer model of core and inner crust, applying a Skyrme effective force model to describe the nucleon-nucleon interactions. This is similar to previous works such as [8], where the fluid below a certain critical density is treated as normal (i.e, the inner crust), and above the critical density is treated as a superfluid (i.e, the core). In a more complete treatment, the location of fluid and superfluid regions would be determined by a profile of the density-dependent critical temperature ; however, we limit ourselves to a calculation. It is important to state the possible consequences of this assumption on our results. It is known that non-zero temperatures can shift the frequency of the superfluid mode by approximately (5–10)%, without affecting the non-superfluid modes [9]. This is because the entrainment matrix depends on the critical temperature profile of the superfluids through its density dependence. We choose a simpler form of entrainment that applies only at . Studying the temperature effects requires models of the critical temperature which are currently not available within the EoS models we use, but this would certainly be interesting to explore with a self-consistent finite temperature model of the neutron star. Although entropy entrainment does not arise in the case of zero temperature [10], entrainment in the cores of superfluid neutron stars between neutrons and protons can still arise at due to the Andreev-Bashkin effect [11], which is encoded in the terms in the set of equations in Section 3.2 below.
The plots in Figure 1 and Figure 2 show the run of interior variables such as pressure and density in the star for one of the Skyrme EoS (Model A), as well as the mass-radius curves for all three of the Skymre models.
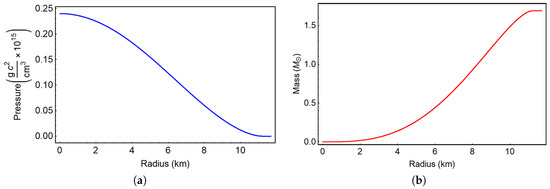
Figure 1.
(a): Pressure vs. radial distance and (b): enclosed mass vs. radial distance for the Skyrme (Model A) equation of state. These curves both correspond to the same star with a central density of 1.102 g/cm, which yields a mass of 1.69 and radius of 11.68 km.
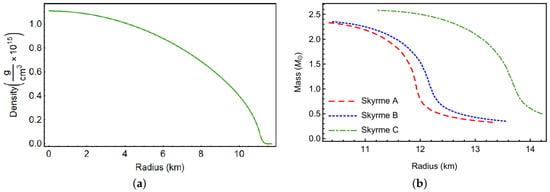
Figure 2.
(a): Density profile vs. radius of the Skyrme (Model A) equation of state, with a central density of 1.102 g/cm, corresponding to a mass of 1.69 and radius of 11.68 km. The density decrease is not smooth near the surface of the star. This feature requires special care in the solution of the oscillation equations. (b): Mass-radius curves for the Skyrme A, B, and C models. All three models can support a maximum mass of more than 2 .
3. Fluid Oscillation Equations
3.1. Normal Fluid
We assume the neutron and proton fluids to be ideal in nature, neglecting dissipative effects due to viscous drag, which is negligible for a superfluid at . This is the case for cold neutron stars with K. However, there can still be dissipation and damping of various oscillation modes due to mutual friction and other microscopic processes such as electron-electron scattering that dominate the shear viscosity when both neutrons and protons are superfluid [12]. Previous works [13] lead us to believe that these effects are not expected to change the real part of the frequency, which is the quantity calculated in this work. For the case of the polytropic EoS, we use a coupled system of differential equations for the radial displacement and pressure perturbation of the fluid [14] to find the oscillation modes of the star. For the polytrope, the stellar structure and the fluid perturbation equations are being described in Newtonian gravity, for the reason explained in Section 2. The structure of the star for the Skyrme models will be treated in General Relativity, although we still employ Newtonian hydrodynamics for the oscillation equations. It is convenient to use the Dziembowski parameterization [14], with non-dimensional variables to efficiently solve for the oscillation eigenfrequencies. The relevant equations in the Cowling approximation, which neglects the back-reaction of the fluid perturbations on the gravitational potential, are:
where are related respectively to the perturbations in the radial component of the fluid motion and the fluid pressure; V, U, and A are derived from logarithmic derivatives of the pressure, mass, and density; l is an angular momentum parameter, is a combination of the mass and radius of the star, and is the normalized frequency of oscillation. For the Skyrme models with superfluidity, we employ a more complicated system of equations given in Section 3.2 that can be applied to the entrained neutron and proton superfluids.
In Figure 3 below, we compare the f- and p-modes for the polytropic EoS and the Skyrme (Model A) EoS. While we have only taken one fixed configuration (, km) for the polytrope, the f- and p-mode frequencies for larger n values are even higher [15]. A larger value of K for the same n would make the star less compact and lower the mode frequencies. In any case, the Newtonian polytrope is meant to provide a rough estimate only. The f-modes scale with the mean density in both cases. The p-modes scale with the compactness rather than the mean density, though a general increase with mean density is still evident since increased compactness leads to increased mean density. It follows that the oscillation frequencies of the realistic models is lower than the polytrope with our chosen value of K, since these stars are less compact and less dense on average than the polytrope. The modes for the polytrope would be lower if the structure was computed in General Relativity, but as previously mentioned, this cannot meet the observational constraint of at least 2 maximum mass. The X-axis range is different for the two figures, since we spanned the same mass range for the two EoS, which leads to different ranges for the mean density. The data in the right panel of Figure 3 is for Skyrme Model A.
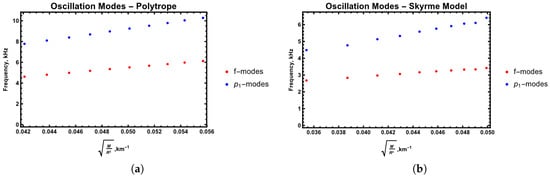
Figure 3.
The trend of f- and p-modes with the square root of the mean density of the neutron star, given a polytropic equation of state (a) and a Skyrme (Model A) equation of state (b).
3.2. Oscillation Equations: Extension to Superfluidity
Since both neutron and proton fluids can undergo pairing, the extension to superfluidity leads to the following equations for determining the oscillation modes, as given in [16]
where the matrix components (, , ) and the parameter are based on the particle densities and and the nucleon effective masses and ; the Q matrix components (, , ) are derivatives of the particle chemical potentials with respect to the particle densities; and g is the gravitational field. As mentioned before, entrainment is included through . All other parameters take the same definitions as in the normal fluid.
We determine the effective masses self-consistently from the Skyrme EoS model, following Chamel’s theoretical treatment of superfluidity [7]. The effective masses and all other required thermodynamic quantities are consistently determined at each grid point in the star using inbuilt interpolation routines in CompOSE. It is important to note that the effective masses are included self-consistently in the calculation of the oscillation spectrum. Though the extension to superfluidity is ultimately straightforward, we find that a minimal fraction of normal fluid is needed to tame the discontinuities in the density profile near the surface of the star, which otherwise cause numerical problems. This is particularly the case for Model A (KDE0 interaction), suggesting that either the model or the interpolation routine needs to be further investigated at low densities. For this work, we confine our calculations to the case of a superfluid core surrounded by a normal envelope with a transition density at nearly half the radius of the star.
4. Results
In this section, we present our numerical results and summarize the main findings from our work. In Table 1, we show the oscillation mode frequencies for neutron stars of mass {1.4, 1.8, 2.2} with normal fluid and superfluid components.

Table 1.
Mode Frequency in kHz ().
The polytropic model has only a normal component, while the Skyrme EoS admits both normal and superfluid components. For the latter case, the numbers in brackets are the mode frequencies if only the normal component exists in the star, showing that these modes (f and p) remain approximately unchanged even in the presence of superfluidity. The last row is the frequency of the superfluid mode. Similar to previous works with other EoS [8,16], we find that the modes of the two-fluid star support f- and p-modes that are very close to the corresponding normal fluid star, with the addition of one or two superfluid modes, the lower one of which is intermediate between the f and p modes and is denoted by “s" in Table 1. The superfluid mode frequency also decreases with decreasing compactness, though no simple scaling with global stellar properties as for normal fluid modes could be determined. It is likely that the superfluid mode is quite sensitive to the details of the EoS such as the effective masses, and the superfluid fraction, which must ideally be determined by the critical temperature profile in the star. The systematic thoeretical study of the superfluid modes with variable superfluid fraction, EoS models and including non-zero temperature certainly deserves more study. Nevertheless, even in our simple framework, the appearance of these distinct modes in the spectrum indicating superfluidity in the cores of neutron stars is an exciting observational possibility for gravitational wave detectors of increased sensitivity. At this stage, it is useful to summarize the main new developments in this work:
- The appearance of a new superfluid mode, while leaving the frequencies of the normal modes almost unchanged, was already noted in [8], but they used a much older EoS [17] based on the Walecka model. We have used the Skyrme EoS which obeys modern constraints from isospin diffusion data and the slope of the symmetry energy. In addition, we employ neutron and proton effective masses that are obtained consistently within the model [7]. This was not the case, for e.g., in all other previous computations of the superfluid oscillation modes [8,16]. This is an important point since the entrainment matrix depends on the effective masses, and different models for the density dependent effective mass yield different numerical values for the modes [8]. In this way, our results are based on an EoS that is built from a unified treatment of terrestrial nuclear experiments and the astrophysics of compact stars, and our results are more consistent from a quantitative standpoint.
- We have reported the mode frequencies for a 1.8 and 2 configuration, which is a new result since earlier works [8,16] that considered configurations of 1.4 predate the discovery of the presently observed heaviest neutron star.
- We demonstrate the utility of the CompOSE database in using modern EoS for studies of neutron star oscillations and gravitational waves. The EoS models taken from CompOSE calculate the nucleon effective masses consistently, which is important in superfluid mode calculations. This database also provides easy-to-use interpolation routines that are necessary since the computational grid for the oscillation equations requires more points than are typically provided in tabulated EoS. Readers interested in using the CompOSE repository for compact star and supernova studies may consult the manual [18] or write to the authors of this manuscript.
5. Future Work
The results presented here are part of an ongoing, more systematic study of the effects of superfluidity in dense matter on the oscillation modes of compact stars. We made some approximations for the structure of the neutron star that can, and should be improved upon. For example, the EoS models adopted here assume that the interior consists primarily of nucleons, with the addition of electrons to satisfy charge neutrality. If hyperons are included, the entrainment matrix must be modified [19] and this will affect the superfluid modes. The normal fluid modes will also change, since the addition of hyperons softens the EoS at high density, making the star more compact. We expect, as shown in previous studies with polytropic models [20], that with increasing compactness (i.e., decreasing ), the f and p-mode frequencies will also increase. We are currently working on extensions to include quark matter, which has a relativistic dispersion and additional neutrality conditions. In such a case, the superfluid equations become more complicated: instead of dealing with the two species of nucleon, one would likely have to account for the entrainment between up, down and possibly strange quarks. Thus, not only does the equation of state have to be modified, but the fluid equations must be altered as well. The non-radial oscillations of a superconducting quark fluid have been recently discussed in [21], although its superfluid modes have not been calculated. Further improvements such as extending the analysis to finite temperature and including viscous dissipation that damps the oscillation modes are needed to provide a more complete picture of the spectrum and damping times of oscillations in a neutron star. As shown in this work, the CompOSE database can serve as a useful repository for studies in this direction.
Acknowledgments
P. J. gratefully acknowledges support from the U.S. National Science Foundation as P. I. of Grant No. PHY 1608959. R. M. was supported as a graduate student by the same grant.
Author Contributions
R. M. and P. J. performed the calculations. R. M. also made the figures, P. J. drafted the paper and T. K. provided critical input via CompOSE data and interpretation of results. All three authors approved the final version to be published.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EoS | equation of state |
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- CompStar Online Supernovae Equations of State. Available online: https://compose.obspm.fr/ (accessed on 6 March 2018).
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover Publications, Incorporated: Mineola, NY, USA, 1967; ISBN 13: 9780486604138. [Google Scholar]
- Agrawal, B.K.; Shlomo, S.; Kim Au, V. Determination of the parameters of a Skyrme type effective interaction using the simulated annealing approach. Phys. Rev. C 2005, 72, 014310. [Google Scholar] [CrossRef]
- Gulminelli, F.; Raduta, A.R. Unified treatment of subsaturation stellar matter at zero and finite temperature. Phys. Rev. C 2015, 92, 055803. [Google Scholar] [CrossRef]
- Agrawal, B.K.; Shlomo, S.; Kim Au, V. Nuclear matter incompressibility coefficient in relativistic and nonrelativistic microscopic models. Phys. Rev. C 2003, 68, 031304. [Google Scholar] [CrossRef]
- Chamel, N. Two-fluid models of superfluid neutron star cores. Mon. Not. R. Astron. Soc. 2008, 388, 737–752. [Google Scholar] [CrossRef]
- Lindblom, L.; Mendell, G. The oscillations of superfluid neutron stars. Astrophys. J. 1994, 421, 689–704. [Google Scholar]
- Gualtieri, L.; Kantor, E.M.; Gusakov, M.E.; Chugunov, A.I. Quasinormal modes of superfluid neutron stars. Phys. Rev. D 2014, 90, 024010. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Entropy entrainment and dissipation in superfluid Helium. Int. J. Mod. Phys. D 2011, 20, 1215. [Google Scholar] [CrossRef]
- Andreev, A.F.; Bashkin, E.P. Three-velocity hydrodynamics of superfluid solutions. Sov. Phys. J. Exp. Theor. Phys. 1976, 42, 164. [Google Scholar]
- Andersson, N.; Comer, G.L.; Glampedakis, K. How viscous is a superfluid neutron star core? Nucl. Phys. A 2005, 763, 212–229. [Google Scholar] [CrossRef]
- Lindblom, L.; Mendell, G. R-modes in superfluid neutron stars. Phys. Rev. D 2000, 61, 104003. [Google Scholar] [CrossRef]
- Mcdermott, P.N.; Van Horn, H.M.; Hansen, C.J. Nonradial oscillations of neutron stars. Astrophys. J. 1988, 325, 725–748. [Google Scholar] [CrossRef]
- Asbell, J.L. Non-Radial Fluid Pulsation Modes of Compact Stars. Master’s Thesis, California State University, Long Beach, CA, USA, 2016. [Google Scholar]
- Lee, U. Nonradial oscillations of neutron stars with the superfluid core. Astron. Astrophys. 1995, 303, 515–525. [Google Scholar]
- Serot, B.D. A relativistic nuclear field theory with π and ρ mesons. Phys. Lett. B 1979, 86, 146–150. [Google Scholar] [CrossRef]
- Typel, S.; Oertel, M.; Klähn, T. CompOSE CompStar online supernova equations of state; harmonising the concert of nuclear physics and astrophysics compose.obspm.fr. Phys. Part. Nucl. 1979, 46, 633–664. [Google Scholar] [CrossRef]
- Gusakov, M.E.; Kantor, M.; Haensel, P. The relativistic entrainment matrix of a superfluid nucleon-hyperon mixture at zero temperature. Phys. Rev. C 2009, 79, 055806. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. Pulsation modes for increasingly relativistic polytropes. Mon. Not. R. Astron. Soc. 1998, 297, 493–496. [Google Scholar] [CrossRef]
- Flores, C.V.; Lugones, G. Constraining color flavor locked strange stars in the gravitational wave era. Phys. Rev. C 2017, 95, 025808. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).