The Pierre Auger Observatory: Review of Latest Results and Perspectives
Abstract
1. Introduction
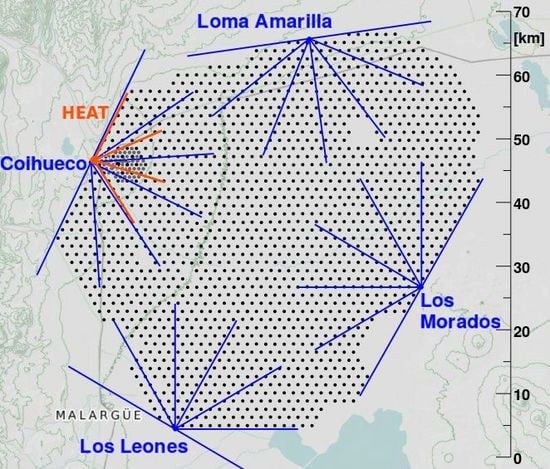
2. The Pierre Auger Observatory
3. Results
3.1. High Energy Cosmic Ray Spectra
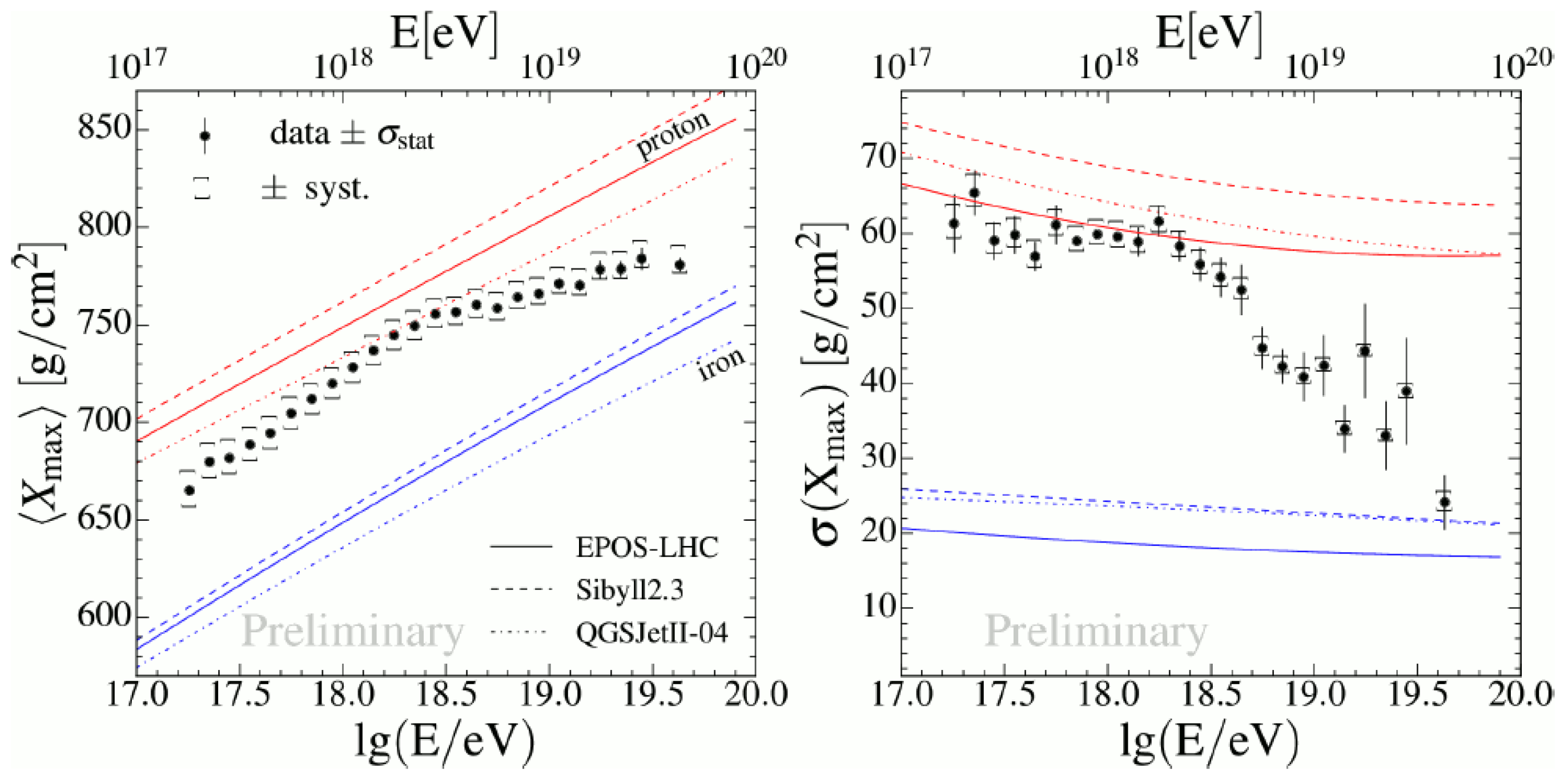
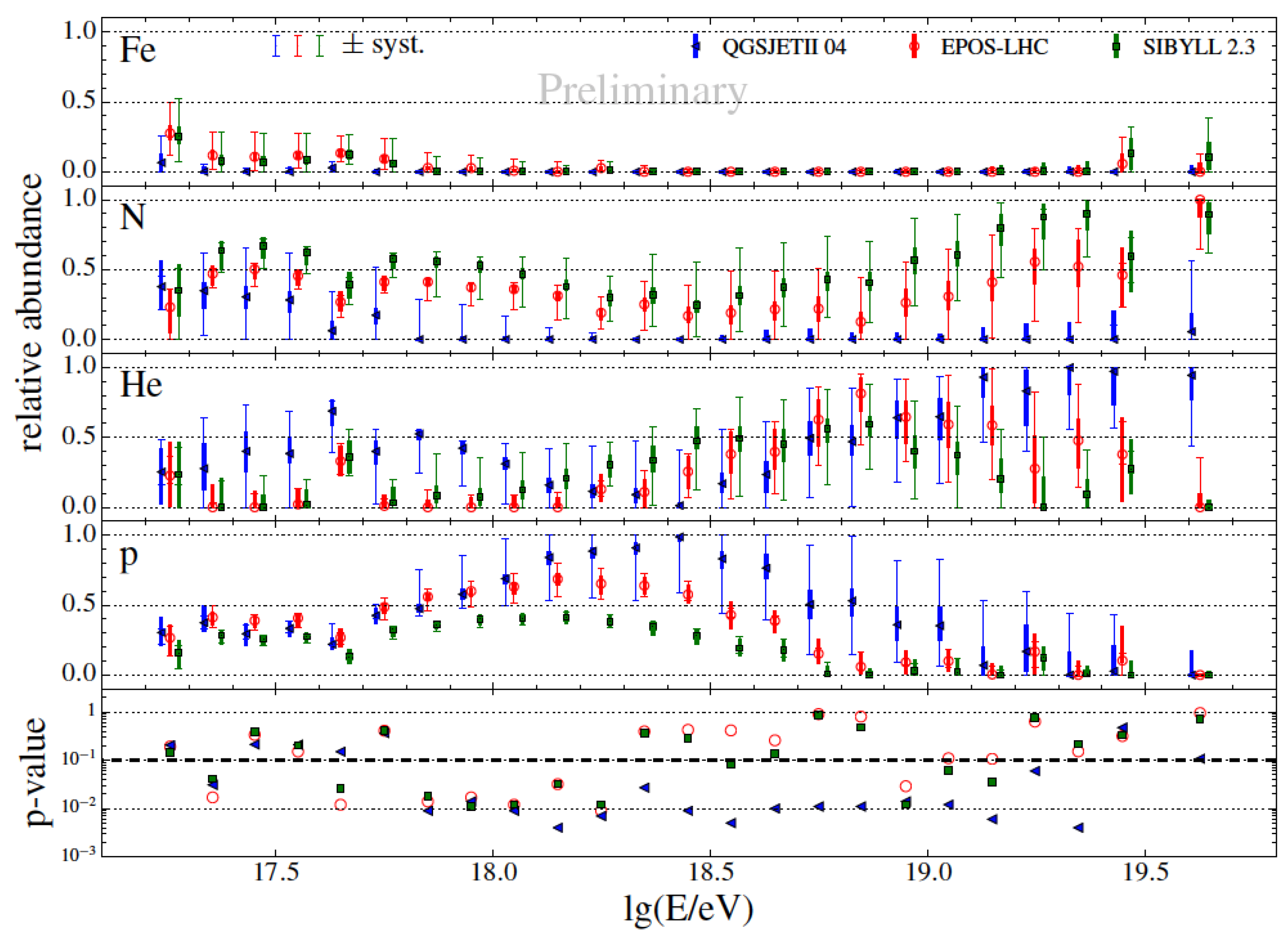
3.2. Composition
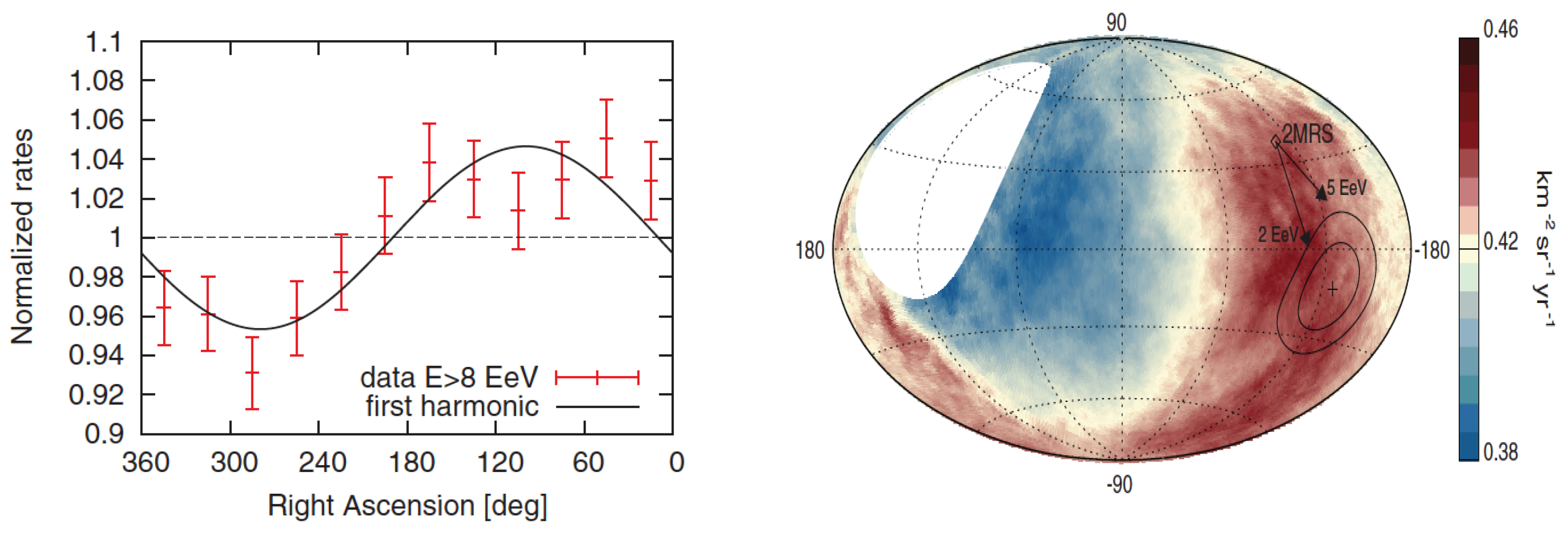
3.3. Anisotropy
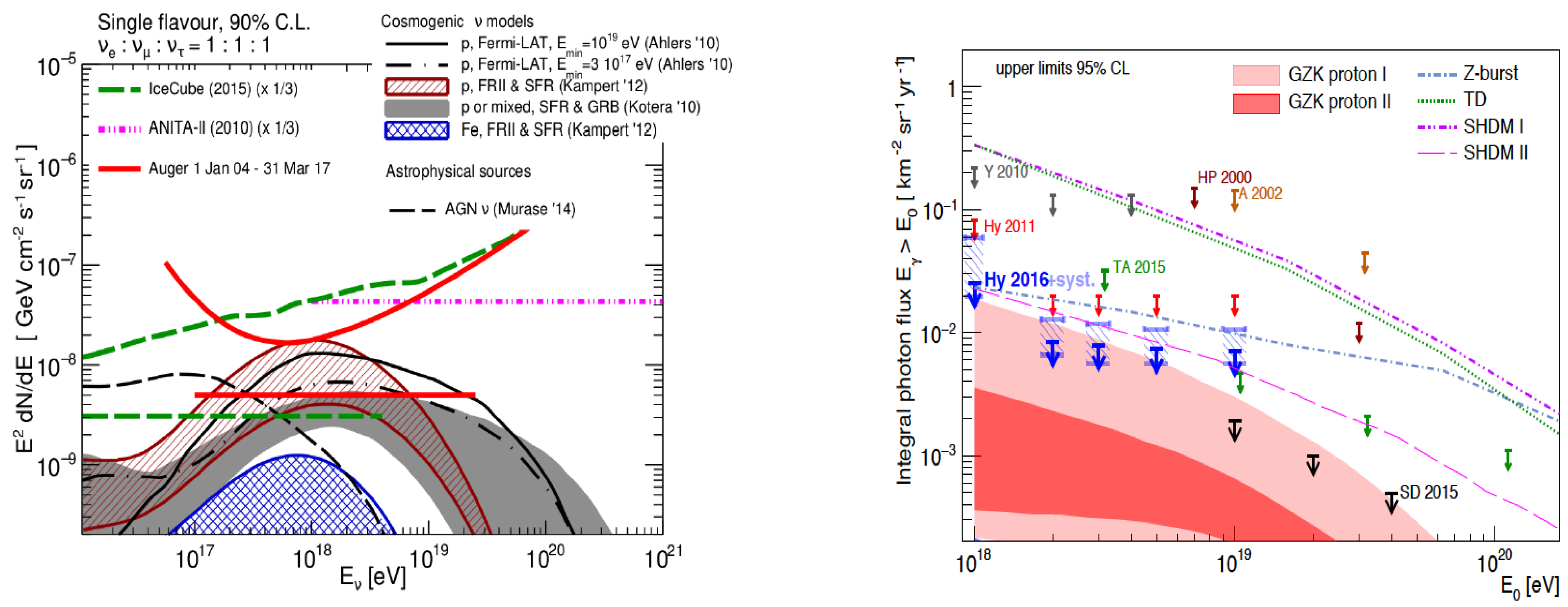
3.4. Photons and Neutrinos
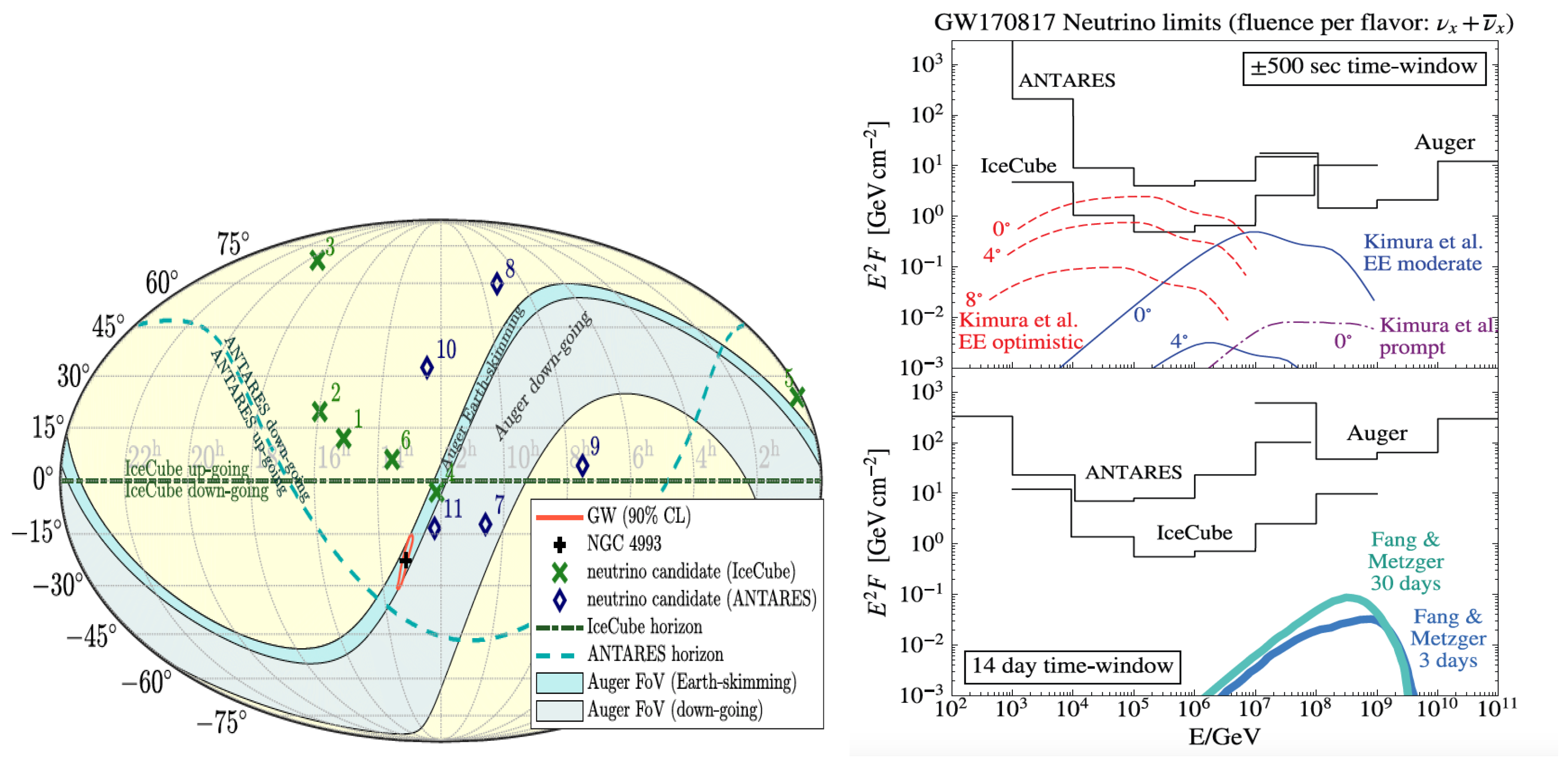
3.5. Multi-Messenger Astronomy
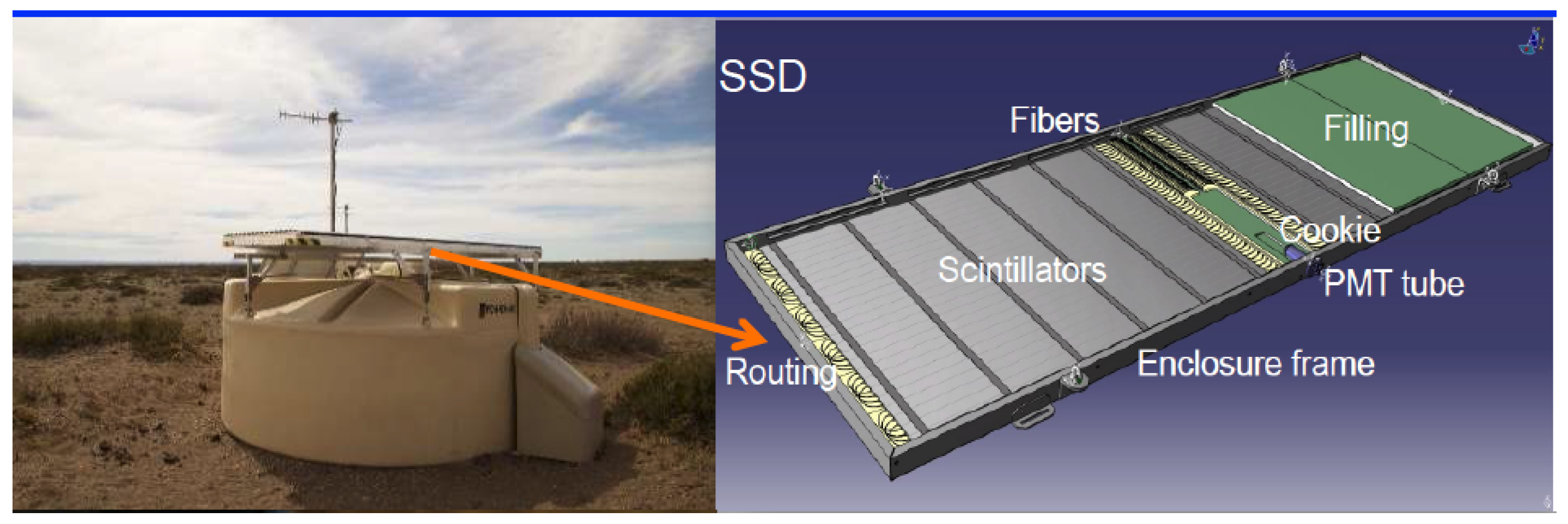
3.6. Auger Prime
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Linsley, J. Evidence for a Primary Cosmic-Ray Particle with Energy 1020 eV. Phys. Rev. Lett. 1963, 10, 146–148. [Google Scholar] [CrossRef]
- Aad, G. et al. [The ATLAS Collaboration] Luminosity determination in pp collisions at = 7 TeV using the ATLAS detector at the LHC. Eur. Phys. J. C 2011, 71, 1630. [Google Scholar] [CrossRef]
- Linsley, J. Spectra, anisotropies and composition of cosmic rays above 1000 GeV. In Proceedings of the 18th International Cosmic Ray Conference, Bangalore, India, 22 August–3 September 1983; Volume 12, p. 144. [Google Scholar]
- Abraham, J. et al. [Pierre Auger Collaboration] Properties and performance of the prototype instrument for the Pierre Auger Observatory. Nucl. Instrum. Methods 2004, A523, 50–95. [Google Scholar]
- Aab, A. et al. [The Pierre Auger Collaboration] The Pierre Auger Cosmic Ray Observatory. Nuclear Instrum. Methods Phys. Res. A 2015, 798, 172–213. [Google Scholar] [CrossRef]
- Abraham, J. et al. [The Pierre Auger Collaboration] Trigger and Aperture of the Surface Detector Array of the Pierre Auger Observatory. Nucl. Instrum. Methods A 2010, 613, 29–39. [Google Scholar] [CrossRef]
- Abreu, P. et al. [The Pierre Auger Collaboration] Antennas for the Detection of Radio Emission Pulses from Cosmic-Ray induced Air Showers at the Pierre Auger Observatory. J. Instrum. 2012, 437, P10011. [Google Scholar]
- Hillas, A.M.; Hollows, J.D.; Hunter, H.W.; Marsde, D.J. Calculations on the particle and energy-loss densities in extensive air showers at large axial distances. Acta Phys. Acad. Sci. Hung. 1970, 29 (Suppl. 3), 533. [Google Scholar]
- Newton, D.; Knapp, J.; Watson, A.A. The optimum distance at which to determine the size of a giant air shower. Astropart. Phys. 2007, 26, 414–419. [Google Scholar] [CrossRef]
- Abraham, J. et al. [The Pierre Auger Collaboration] Observation of the suppression of the flux of cosmic rays above 4 × 1019 eV. Phys. Rev. Lett. 2008, 101, 061101. [Google Scholar]
- Aab, A. et al. [The Pierre Auger Collaboration] Reconstruction of inclined air showers detected with the Pierre Auger Observator. J. Cosmol. Astropart. Phys. 2014, 2014, 16. [Google Scholar]
- Fenu, F. et al. [The Pierre Auger Collaboration] The cosmic ray energy spectrum measured using the Pierre Auger Observatory. In Proceedings of the 35th International Cosmic Ray Conference 2017 (ICRC 2017), Busan, Korea, 12–20 July 2017; Volume 486. [Google Scholar]
- Abraham, J. et al. [The Pierre Auger Collaboration] Measurement of the energy spectrum of cosmic rays above 1018 eV using the Pierre Auger Observatory. Phys. Lett. B 2010, 685, 239–246. [Google Scholar] [CrossRef]
- Verzi, V. The Energy Scale of the Pierre Auger Observatory. In Proceedings of the 33rd International Cosmic Ray Conference (ICRC 2013), Rio de Janeiro, Brazil, 2–9 July 2013. [Google Scholar]
- Berezinsky, V.S.; Gazizov, A.Z.; Grigorieva, S.I. On astrophysical solution to ultra high energy cosmic rays. Phys. Rev. D 2006, 74, 043005. [Google Scholar] [CrossRef]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuz’min, V.A. Upper limit of the spectrum of cosmic rays. J. Exp. Theor. Phys. Lett. 1966, 4, 78–80. [Google Scholar]
- Bellido, J. et al. [The Pierre Auger Collaboration] Depth of maximum of air-shower profiles at the Pierre Auger Observatory: Measurements above 1017.2 eV and Composition Implications. In Proceedings of the 35th International Cosmic Ray Conference 2017 (ICRC 2017), Busan, Korea, 12–20 July 2017; Volume 506. [Google Scholar]
- Matthews, J. A Heitler model of extensive air showers. Astropart. Phys. 2005, 22, 387–397. [Google Scholar] [CrossRef]
- Aab, A. et al. [The Pierre Auger Collaboration] Depth of maximum of air-shower profiles at the Pierre Auger Observatory. I. Measurements at energies above 1017.8 eV. Phys. Rev. D 2014, 90, 122005. [Google Scholar] [CrossRef]
- Aab, A. et al. [The Pierre Auger Collaboration] The Pierre Auger Observatory: Contributions to the 35th International Cosmic Ray Conference (ICRC 2017). arXiv, 2017; arXiv:1708.06592. [Google Scholar]
- Aab, A. et al. [The Pierre Auger Collaboration] Depth of maximum of air-shower profiles at the Pierre Auger Observatory. II. Composition implications. Phys. Rev. D 2014, 90, 122006. [Google Scholar] [CrossRef]
- Bergmann, T.; Engel, R.; Heck, D.; Kalmykov, N.N.; Ostapchenko, S.; Pierog, T.; Thouw, T.; Werner, K. One-dimensional Hybrid Approach to Extensive Air Shower Simulation. Astropart. Phys. 2007, 26, 420–432. [Google Scholar] [CrossRef]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: I. QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar] [CrossRef]
- Riehn, F.; Engel, R.; Fedynitch, A.; Gaisser, T.K.; Stanev, T. A new version of the event generator Sibyll. In Proceedings of the 34th International Cosmic Ray Conference (ICRC 2015), The Hague, The Netherlands, 30 July–6 August 2015; p. 558. [Google Scholar]
- Blaess, S.; Bellido, J.; Dawson, D. Reducing the model dependence in the cosmic ray composition interpretation of Xmax distributions. In Proceedings of the 35th International Cosmic Ray Conference 2017 (ICRC 2017), Busan, Korea, 12–20 July 2017; p. 490. [Google Scholar]
- Abreu, P. et al. [The Pierre Auger Collaboration] Search for First Harmonic Modulation in the Right Ascension Distribution of Cosmic Rays Detected at the Pierre Auger Observatory. Astropart. Phys. 2011, 34, 627–639. [Google Scholar] [CrossRef]
- Abraham, J. et al. [The Pierre Auger Collaboration] Correlation of the highest-energy cosmic rays with the positions of nearby active galactic nuclei. Astropart. Phys. 2008, 29, 188–204. [Google Scholar] [CrossRef]
- Aartsen, A. et al. [The Pierre Auger Collaboration] Search for correlations between the arrival directions of IceCube neutrino events and ultra high-energy cosmic rays detected by the Pierre Auger Observatory and the Telescope Array. J. Cosmol. Astropart. Phys. 2016, 2016, 037. [Google Scholar] [CrossRef]
- Aab, A. et al. [The Pierre Auger Collaboration] Observation of a Large-scale Anisotropy in the Arrival Directions of Cosmic Rays above 8·1018 eV. Science 2017, 357, 1266–1270. [Google Scholar] [CrossRef] [PubMed]
- Erdoğdu, P. The dipole anisotropy of the 2 Micron All-Sky Redshift Survey. Mon. Not. R. Astron. Soc. 2006, 368, 1515–1526. [Google Scholar] [CrossRef]
- Jansson, R.; Farrar, G.R. A New Model of the Galactic Magnetic Field. Astrophys. J. 2012, 757, 14. [Google Scholar] [CrossRef]
- Beresinsky, V.S.; Zatsepin, G.T. Cosmic rays at ultra high energies (neutrino?). Phys. Lett. B 1969, 28, 423–424. [Google Scholar] [CrossRef]
- Fargion, D. Discovering Ultra High Energy Neutrinos by Horizontal and Upward tau Air-Showers: Evidences in Terrestrial Gamma Flashes? Astrophys. J. 2002, 570, 909. [Google Scholar] [CrossRef]
- Bertou, X.; Billoir, P.; Deligny, O.; Lachaud, C.; Letessier-Selvon, A. Tau Neutrinos in the Auger Observatory: A New Window to UHECR Sources. Astropart. Phys. 2002, 17, 183–193. [Google Scholar] [CrossRef]
- Zas, E. et al. [The Pierre Auger Collaboration] Searches for neutrino fluxes in the EeV regime with the Pierre Auger Observatory. Proc. Sci. 2018, 972, 64–71. [Google Scholar]
- Bleve, C. et al. [The Pierre Auger Collaboration] Updates on the neutrino and photon limits from the Pierre Auger Observatory. Proc. Sci. 2015, 236, 1103. [Google Scholar]
- Niechciol, M. et al. [The Pierre Auger Collaboration] Diffuse and targeted searches for ultra high-energy photons using the hybrid detector of the Pierre Auger Observatory. Proc. Sci. 2018, 301, 517. [Google Scholar]
- Aab, A. et al. [The Pierre Auger Collaboration] Search for photons with energies above 1018 eV using the hybrid detector of the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2017, 2017, 9. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Aab, A. et al. [The Virgo Collaboration] Ultra high-energy neutrino follow-up of gravitational wave events GW150914 and GW151226 with the Pierre Auger Observatory. Phys. Rev. D 2016, 94, 122007. [Google Scholar] [CrossRef]
- Albert, A. et al. [LIGO Scientific Collaboration and Virgo Collaboration] Search for High-energy Neutrinos from Binary Neutron Star Merger GW170817 with ANTARES, IceCube, and the Pierre Auger Observatory. Astrophys. J. 2017, 850, L35. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration; Virgo Collaboration; Fermi GBM; INTEGRAL; IceCube Collaboration; AstroSat Cadmium Zinc Telluride Imager Team; IPN Collaboration; The Insight-HXMT Collaboration; ANTARES Collaboration; The Swift Collaboration; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Kimura, S.S.; Murase, K.; Mészáros, P.; Kiuchi, K. High-energy Neutrino Emission from Short Gamma-Ray Bursts: Prospects for Coincident Detection with Gravitational Waves. Astrophys. J. Lett. 2017, 848, L4. [Google Scholar] [CrossRef]
- Aab, A. et al. [The Pierre Auger Collaboration] The Pierre Auger Observatory Upgrade—Preliminary Design Report. arXiv, 2016; arXiv:1604.03637. [Google Scholar]
- Martello, D. et al. [The Pierre Auger Collaboration] The Pierre Auger Observatory Upgrade. Proc. Sci. 2017, 383, 02003. [Google Scholar]
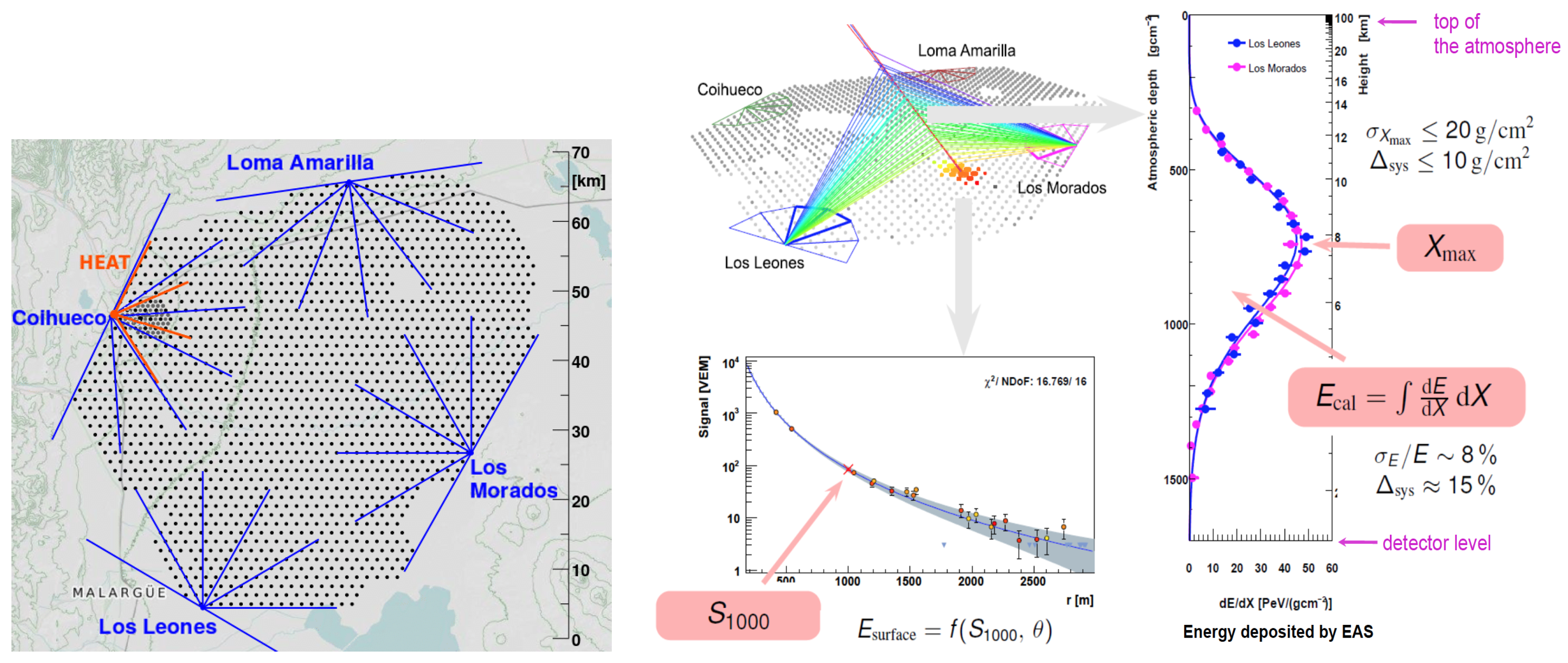
| 1 | The SD only samples the properties of an air shower at a limited number of points at different distances from the shower axis. To avoid the large fluctuations in the signal integrated over all distances caused by fluctuations in the shower development, Hillas [8] proposed to use the signal at a given distance to classify the size of the shower. In [9], it has been shown that for the Auger array spacing (1.5 km), the optimum distance to minimize this experimental error is ∼1000 m. Therefore, the observable that we use to relate to the primary energy will be the signal size at 1000 m e.g., . |
| 2 | We fitted the flux with a power law allowing for a break in the spectral index at and a suppression of the flux at ultrahigh energies . |
| 3 | This connection assumes the Heitler model of EAS [19]. |

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Góra, D.; For the Pierre Auger Collaboration. The Pierre Auger Observatory: Review of Latest Results and Perspectives. Universe 2018, 4, 128. https://doi.org/10.3390/universe4110128
Góra D, For the Pierre Auger Collaboration. The Pierre Auger Observatory: Review of Latest Results and Perspectives. Universe. 2018; 4(11):128. https://doi.org/10.3390/universe4110128
Chicago/Turabian StyleGóra, Dariusz, and For the Pierre Auger Collaboration. 2018. "The Pierre Auger Observatory: Review of Latest Results and Perspectives" Universe 4, no. 11: 128. https://doi.org/10.3390/universe4110128
APA StyleGóra, D., & For the Pierre Auger Collaboration. (2018). The Pierre Auger Observatory: Review of Latest Results and Perspectives. Universe, 4(11), 128. https://doi.org/10.3390/universe4110128