Abstract
We review that in no-scale models in perturbative string theory, flat, homogeneous and isotropic cosmological evolutions found at the quantum level can enter into “quantum no-scale regimes” (QNSRs). When this is the case, the quantum effective potential is dominated by the classical kinetic energies of the no-scale modulus, dilaton and moduli not involved in the supersymmetry breaking. As a result, the evolutions approach the classical ones, where the no-scale structure is exact. When the one-loop potential is positive, a global attractor mechanism forces the initially expanding solutions to enter the QNSR describing a flat, ever-expanding universe. On the contrary, when the potential can reach negative values, the internal moduli induce in most cases some kind of instability of the growing universe. The latter stops expanding and eventually collapses, unless the initial conditions are tuned in a tiny region of the phase space. Finally, in QNSR, no gauge instability takes place, regardless of the details of the potential.
1. Introduction
In quantum field theory, what is considered classically is a flat and static universe, with arbitrary particle content. Quantum corrections of the associated fields are then computed, without wondering whether the particle content imposes constraints for the flat universe to be stable. In fact, for spacetime to remain (nearly) flat and static in the presence of gravity, the minima of the quantum potential should (nearly) vanish, a fact that is obviously satisfied, but of limited phenomenological interest when supersymmetry is exact. On the contrary, when supersymmetry is spontaneously broken, one may look for models at weak string coupling where the one-loop potential (nearly) vanishes, [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18].1 Additional conditions should then be imposed for loop corrections up to some higher order to be (nearly) vanishing, as well [19,20,21]. If such models with realistic particle content would exist, selecting them may necessitate some version of the anthropic principle.
In the present paper, we follow a different approach, where the one-loop effective potential is generic. In this case, the quantum potential energy appears as a source term to be added in the classical Einstein equations. The static universe being no longer a solution, we look for the flat, homogeneous and isotropic cosmological evolutions. This is done in the framework of the initially maximally-supersymmetric heterotic string in d dimensions, where all supersymmetries are spontaneously broken by a stringy version [22,23,24,25,26] of the Scherk–Schwarz mechanism [27]. In this framework, analytic derivations can be done explicitly, allowing us to address two questions [28,29]:
(i) Under which conditions does a flat expanding universe keep on growing? A direct consequence of Einstein equations is that a sufficient condition for this to arise in a perturbative regime is to have . It turns out that in the heterotic setup we analyze, the universe can also be ever-expanding when . However, the presence of moduli fields often induces some kind of “instability”: most of the initially growing universes stop expanding and eventually collapse into Big Crunches. This happens unless the initial conditions are tuned in a tiny region of the phase space. These observations may suggest that spectra leading to positive quantum potentials are way more natural to describe flat expanding spacetimes.
(ii) What are the properties of these flat, expanding universes? In the stringy Scherk–Schwarz mechanism, the supersymmetry breaking scale is a field, for some constant , that parameterizes at the tree level a flat direction of a classical potential . As a result, is referred as the “no-scale modulus”, and the classical model is said to be a “no-scale model” [30,31,32,33]. In the cosmological evolutions, we find at the quantum level the classical kinetic energies of of the dilaton and of moduli fields to be characterized to dominate over and the kinetic energies of the remaining moduli. As a result, the expanding solutions approach asymptotically those found classically, when the one-loop potential is not taken into account, or alternatively when vanishes (up to exponentially suppressed terms). In other words, the no-scale structure present at the classical level and broken by quantum effects is restored cosmologically. For this reason, we will say that the universe enters dynamically into the “quantum no-scale regime” (QNSR). Moreover, we will see that no Higgs-like instability occurs in such a regime, whether moduli sit at minima, maxima, saddle points or actually anywhere in moduli space.
2. Toy Model
The positive thing in considering a reduced set of degrees of freedom is that solving exactly the equations of motions at one-loop is possible. To be specific, we consider the heterotic string with the classical background:
where the size of is of the order of the string scale. A coordinate-dependent compactification [22,23,24,25,26] along the n circles of radii is implemented, which is the counterpart in string theory of the Scherk–Schwarz mechanism in supergravity [27]. The radii are chosen large (compared to one) for the supersymmetry breaking scale to be lower than the string scale,
This restriction ensures that no Hagedorn instability can occur and allows a great simplification of the expression of the one-loop effective potential. The latter, defined in terms of the partition function Z, takes the following form [1,2,3,4,5,6]:
where are the numbers of massless bosons and fermions.2 The dominant contribution of this expression arises from the towers of Kaluza–Klein (KK) modes associated with the large supersymmetry-breaking circles. In fact, is a function of the complex structures , we will treat in this section as constants. The contributions of all other string states are exponentially suppressed and will be neglected from now on. At one-loop order, the effective action involves the classical kinetic terms of and of the dilaton , as well as the potential.3 In the Einstein frame, we obtain:
where we have introduced canonical scalars and . The former is the no-scale modulus, which is related to the supersymmetry-breaking scale measured in this frame, while is an “orthonormal” combination of fields,
In our notations, is the Ricci curvature, is the Einstein constant and the potential becomes:
Ignoring higher order corrections in string coupling, the field configurations that make extremal this action are relevant when compatible with weak coupling.
Being interested in homogeneous and isotropic cosmological evolutions in flat space, we consider the scalar fields , and metric ansatz, where t is cosmic time. If is a free field, it turns out that the proportionality of and leads to the existence of a second free field, which involves the no-scale modulus. Integrating once their equations of motion, we obtain:
where and are constants. These results can be used in the equation obtained by varying S with respect to a,
where , to obtain a second order differential equation in the scale factor only. The latter can be solved when by defining a new (dimensionless) time variable , in terms of which Equation (8) becomes:
Finally, it is convenient to determine the second integration constant of the no-scale modulus by using the Friedmann equation, which takes an algebraic form in terms of ,
In the following, we present the cosmological solution found for arbitrary , for which a critical value turns out to be [28]:
2.1. Supercritical Case,
The degree two polynomial has no real root. Due to the Friedmann Equation (10), this case arises only in models where . Moreover, no classical limit exists, and the evolutions are thus intrinsically of a quantum nature. The scale factor, which involves an integration constant , is found to be:
and is shown in Figure 1i. The arrow indicates the direction of the evolution when t increases and .
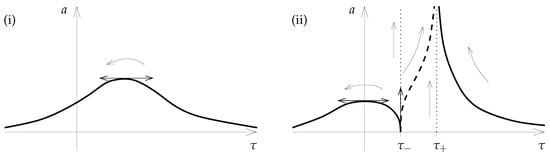
Figure 1.
Qualitative behaviors of , (i) in the supercritical and (ii) subcritical cases. The arrows indicate the directions of the evolutions for increasing cosmic time t, when . Solid and dashed curves correspond to no-scale models with and , respectively. Dotted lines describe the classical trajectories.
Translating the limits in cosmic time, the scale factor behaves as , for some constants . In these limits, the evolution describes a Big Bang and a Big Crunch, where the universe is dominated by the total energy of M, i.e., kinetic plus quantum potential,
The one-loop potential is also responsible for stopping the expansion of the universe, since we have at the maximum of a. In fact, the evolution can be trusted far enough from the Big Bang and the Big Crunch, for several reasons: First, all kinetic energies must be bounded by the string scale, a fact that is guaranteed as far as is not too low. Second, the string coupling must remain weak, which imposes a limitation on the range of , since we have , as . To conclude on the supercritical case, the generation of negative quantum potentials allows new universes to exist (they have no classical counterparts), however “unstable” in the sense that the potentials are also responsible for their collapses.
For completeness, we signal that the case is somehow “infinitely supercritical” when . It requires and yields an evolution qualitatively similar to the above one. When , the maximum of the scale factor is formally sent to infinity, and the trajectories become monotonic.
2.2. Subcritical Case,
The polynomial has two distinct real roots,
From Equation (10), we see that there is no restriction on the massless spectrum of the models:
- When , the range of allowed time is .
- When , is constrained to be identically equal to or .
- When , two branches of solutions are allowed, namely and .
Let us first describe the case . In the literature, the models with massless spectra satisfying this condition are sometimes referred to as “super no-scale models”. This follows from the fact that at the points in moduli space associated with the classical backgrounds, the one-loop effective potential is extremal (with respect to all internal space moduli), vanishes and is degenerate for an arbitrary value of the no-scale modulus.4 Thus, when the extremum is a minimum, the exact classical no-scale structure is promoted to the one-loop level.4 When the one-loop effective potential does not contribute at all in the action S, one should in principle add the one-loop corrections to the kinetic terms of and . However, once marginal deformations associated with the internal space are taken into account, as is done in Section 3, is not identically vanishing even when . Thus, the present case where the potential is formally absent does not need to be considered in very much detail, and we only present the limit behaviors of the one-loop evolutions. In the perturbative regime, they can be found easily by extremizing the classical action. For , we find the expanding (or contracting, by time reversal) behaviors:
which imply in particular:
It can be checked that for the evolution , an interval of exists such that as , which yields a consistent perturbative expanding universe. Similarly, for , the Big Crunch behavior is also perturbative in some finite range of [28].
In generic models, where , the scale factor and supersymmetry breaking scale evolutions are found to be:
where can be expressed in terms of , and . As announced before and shown in Figure 1ii, the expression of admits two branches when (in solid lines), while for , a unique branch exists (in dashed line). The classical trajectories are also plotted (in dotted lines). Some remarks are in order:
- All trajectories start and/or end with a Big Bang or Big Crunch.
- The behavior of the solutions as , which exists when , is identical to that found in the supercritical case.
- More interesting is the fact that all solutions approach and/or , i.e., the classical evolutions, which are also the limit behaviors found in the super no-scale case . To be specific, when , we have:which shows that the no-scale structure is restored during the cosmological evolution. By definition, we will say that the universe enters “quantum no-scale regimes”, which are characterized by the no-scale modulus becoming free.
- The conditions for the QNSRs to be compatible with string weak coupling are identical to those found in the classical case.
- When , the initially expanding solutions are always attracted to the ever-expanding QNSR . However, in the models where , only one out of the two branches describes this behavior, while the second branch yields initially expanding universes sentenced to collapse. These two drastically different histories are somehow on equal footing, depending on the choice of initial conditions for , greater than or lower than . This very fact turns out to be amended when the dynamics of other moduli fields is included, as will be seen in the next section.
- The supersymmetry breaking scale admits a non-trivial dynamics. In the branch , where the potential is negative, Equation (17) shows that when the universe expands (), M decreases. Thus, the no-scale modulus climbs its exponential potential. In addition, when varies between and , M climbs and then descends its positive potential, when the integration constant satisfies (see also [34]). Around the maximum of M, the cosmological evolution may accelerate, but with at most an e-fold number of order one, thus not describing a substantial inflation.
For completeness, we mention that the critical case, namely , for which the polynomial admits a double root , is qualitatively similar to the subcritical one, up to the fact that it applies only to models where .
3. Including Moduli Fields
Having defined the QNSRs in a toy model, our aim is to show how they are affected by the dynamics of marginal deformations [29]. Compactifying the heterotic string on , the Narain moduli space:
can be parameterized by the internal metric and antisymmetric tensor G, B, as well as Y-fields. They can be split into constant backgrounds and y-deformations,
where is the Wilson line of the j-th Cartan along . For simplicity, we implement the coordinate-dependent compactification along the direction, . As a result, the supersymmetry breaking scale in the -model frame is . As before, we take the direction to be large, while the size of the remaining compact coordinates is of the order of the string scale.
Once we take into account marginal deformations, and are not strictly speaking integer constant. This is due to the fact that they interpolate between distinct integer values valid in different regions of moduli space. Choosing an initial background where no non-zero mass scale exists below , the one-loop effective potential in Equation (6) now involves and , which are functions of the y-deformations. Taylor expanding, one obtains [5,6,29]:
where () is times the sum of the (charges)2 of all massless bosons (fermions) of the undeformed background, with respect to the j-th Cartan . As a result, Wilson lines may be massive, massless or tachyonic. To analyze all cases, we need to consider backgrounds with factors of arbitrary signs. Let us first remind that in the most standard implementations of the Scherk–Schwarz mechanism, the massless bosonic (fermionic) fields in the dimension are periodic (antiperiodic) along . As a result, denoting and the momentum and fermionic number of the descendent modes in d dimensions, the generalized momentum along is:
where is the winding number along , . In this formula, the ellipses stand for irrelevant contributions involving the Y-fields. When the background is chosen so that is an even integer, the lightest bosons are massless at , while the lightest fermions have a KKmass. However, when is an odd integer, the role of bosons and fermions is reversed: the lightest bosons have a KK mass at , while the lightest fermions are massless.
As an example to be given in great detail until the end of this paper, consider the matrix for , with ,
When and supersymmetry is recovered in dimensions, two vector multiplets with are massless when b is even and the y-deformations vanish. As a result, the Cartan gauge symmetry arising from the direction is enhanced to . When is finite, the fermionic parts of these vector multiplets acquire a mass , the gauge symmetry remains valid and we end up with a mass coefficient . However, finite allows the other interesting case where b is odd. In this case, the fermionic parts of the vector multiplets are massless, the gauge symmetry becomes and the mass coefficient is . In fact, freezing for simplicity the degrees of freedom:
the one-loop effective potential for arbitrary , and turns out to be, in the -model frame,
In this result, characterizes how the non-Cartan fields are massive. When they are heavy, , all of the second line of is exponentially suppressed, as follows from the function . On the contrary, when , the potential has a simple U-shape, with a minimum at , when b is even and . Moreover, the potential is one-periodic in , and the second line evolves essentially as . Consistently, changing b even to b odd amounts to shifting . Note that since there are only two combinations and z of Wilson lines on which the potential depends, the latter admits a flat direction [29].
3.1. Small Wilson Line Deformations
In order to show the existence of QNSRs in the presence of dynamical Wilson lines, it is enough to consider the case of small deformations, , , . At quadratic order in y’s, the one-loop effective action to be considered is:
The ellipses stand for higher order corrections in Wilson lines we neglect for the time being, , and the potential is:
After deriving the equations of motion, evolutions describing flat, homogeneous and isotropic ever-expanding universes or Big Bangs are sought, with the one-loop potential dominated in the Friedmann equation:
In the above ansatz, is a constant to be determined by consistency. We find the following:
- The simplest behavior to derive is that of the scale factor, , which is a consequence of the negligible potential.
- As can be seen from the action S, the Wilson lines and have non-trivial friction terms. Moreover, the positive or negative mass term of turns out to be irrelevant in the limits (28), so that:An important remark then follows. In the Friedmann equation,the l.h.s. behaves as , while in the r.h.s., the kinetic energies of and yield a contribution , and the potential is dominated. For consistency, we assume that , where is a constant to be determined. Under this assumption, one obtains that and converge to arbitrary constants, which are small in the present paragraph. Note that even when its mass term is negative, does not automatically develop a large expectation value, which would drastically destabilize the initial background.
- has a positive or negative mass term, irrelevant in the limits we consider. As a result, one obtains:where is an integration constant. Due to the fact that , with , we have . This shows that even if has a logarithmic behavior, it is effectively attracted to the extremum of the potential at . In other words, whether the potential has a minimum at (when b is even) or a maximum (when b is odd), the theory is always approaching the configuration where effectively vanishes.
- and couple to the kinetic and mass terms of Wilson lines. However, in the regimes we are interested in, they are becoming free,where , are constants.
- From the above relations, the coefficients and can be determined in terms of and . The result for is that found in the toy model, Equation (16), up to the change in the expression of r given in Equation (14). As a result, the subcritical region for which QNSRs exist, which is a segment in the previous section, becomes a disk of radius one, as shown in Figure 2.
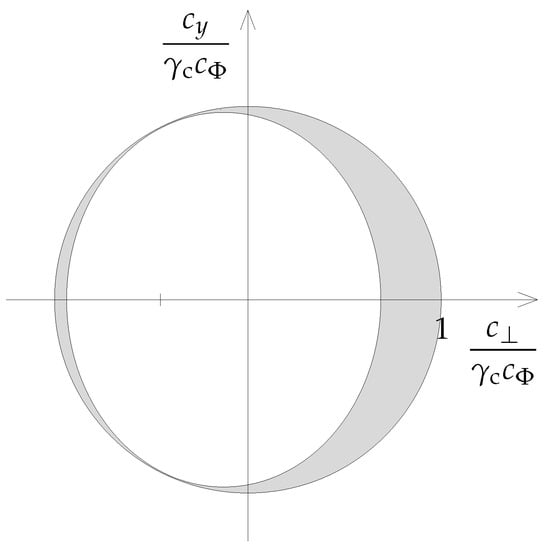 Figure 2. The points of the disk of radius one that yield quantum no-scale regimes (QNSRs) and sit in the left and right shaded crescents, respectively.However, the additional condition arising from the dynamics of and amounts to restricting to the shaded regions: the left and right crescents yield QNSRs and , respectively.
Figure 2. The points of the disk of radius one that yield quantum no-scale regimes (QNSRs) and sit in the left and right shaded crescents, respectively.However, the additional condition arising from the dynamics of and amounts to restricting to the shaded regions: the left and right crescents yield QNSRs and , respectively. - Due to this restriction to the shaded domains, the QNSR turns out to always be perturbative. The one is also perturbative, except in the neighborhood of the tips of the right crescent [28].
This concludes the proof that QNSRs exist even when the dynamics of internal moduli fields is taken into account. However, it is important to stress that in Figure 2, the left crescent is actually much smaller than that we have drawn. Its width along the horizontal axis is between and , for . However, one should not conclude that to be reached; QNSRs always imply some kind of fine tuning, as explained in the following.
3.2. Numerical Simulations
To analyze whether global attractor mechanisms avoid the need to tune integration constants or initial conditions for the QNSR to be reached, we consider computer simulations. For this purpose, restricting to the spacetime dimension , we simulate numerically the quantities:
which are expected to converge to constants , , . In fact, we have checked that if starts in the left thin shell of Figure 2 and that the initial velocities are low, the above quantities do freeze. Moreover, the climbing of M when its potential is negative, as well as the non-destabilization of the background when and sit at maxima are confirmed.
On the contrary, if the trajectory of starts outside the shell and/or the initial velocities are high, the scalars y are expected to explore large distances in moduli space. Thus, we are forced to simulate , , , and using the exact kinetic terms and the full potential in Equation (25). For simplicity, we have kept in this analysis, which implies to be a flat direction. We find that when for some values of , the initially expanding flat universes stop growing and then collapse, unless the trajectories sit in the tiny shell. As a result, the presence of Wilson lines implies the set of initial conditions that yield ever-expending universes to be drastically reduced, as compared to as in the toy model. On the contrary, when for all , the point is always attracted towards the shell, inside of which it eventually stops. Recalling that in the QNSR, we consider the scale factor satisfies , Figure 3i shows the trajectory and convergence of to a constant.
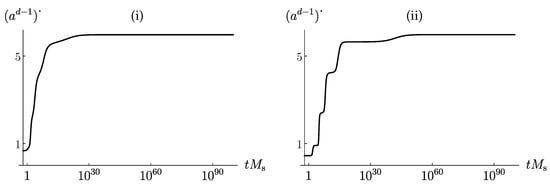
Figure 3.
(i) Convergence of towards a constant, signaling the entrance of the universe in QNSR. (ii) When the initial velocities of the Wilson lines are small, the final convergence is reached after successive approximate QNSRs.
Figure 3ii represents the curve obtained when the initial velocities and approach zero. A surprising structure of a plateau appears, which can be understood as follows:
- (1)
- When the initial time-derivatives of the Wilson lines are small, we are essentially back to the toy model, where we have shown that when , the universe is always attracted to a QNSR. Thus, converges to its first plateau.
- (2)
- However, at this stage, the value of is in most cases negative (we do not a priori sit in the tiny shell). As a result, the kinetic energies of and end up dominating in the Friedmann equation (see the remark below Equation (10)) and destabilize the above “approximate” QNSR. Since:leaves the plateau from above.
- (3)
- However, we have shown analytically that the domination of the kinetic energies of and cannot last forever (there is no such asymptotic solution). Therefore, these moduli have to release this energy to the rest of the system, and the latter is back to the conditions mentioned in Point .
- (4)
- The process is repeated until becomes positive, i.e., the representative point of the system stops in the shell, so that the universe stays in QNSR for good.
4. Conclusions
We have shown that the flat cosmological evolutions found at the quantum level in generic no-scale models can be identical, asymptotically, to those found classically. This means that the no-scale structure broken by quantum effects can be restored during the evolution. We have seen in an example that global attractor mechanisms can make the entrance into the QNSR unavoidable when . On the contrary, when the potential can reach negative values, the QNSR is only reached when the initial conditions are chosen in a tiny region of the phase space.
In QNSR, the universe is dominated by the kinetic energies of the supersymmetry-breaking scale M, of the dilaton and of the Wilson lines , where are not directions involved in the Scherk–Schwarz mechanism. On the contrary, the effective potential and the kinetic energies of the Wilson lines having indices in Scherk–Schwarz directions are negligible.
Finally, the scalars are effectively attracted towards the extrema of the effective potential, which are not necessarily minima, while the remaining moduli freeze at arbitrary values.
Funding
This research was partially funded by the Royal Society International Cost Share Award.
Acknowledgments
This work is based on works done in collaboration with T. Coudarchet and C. Fleming [28,29]. I am grateful to Steve Abel, Carlo Angelantonj, Keith Dienes, Emilian Dudas, Sergio Ferrara, Lucien Heurtier, Alexandros Kahagias and Costas Kounnas for fruitful discussions.
Conflicts of Interest
The author declare no conflict of interest.
References
- Itoyama, H.; Taylor, T.R. Supersymmetry restoration in the compactified O(16) × O(16)′ heterotic string theory. Phys. Lett. B 1987, 186, 129–133. [Google Scholar] [CrossRef]
- Abel, S.; Dienes, K.R.; Mavroudi, E. Towards a non-supersymmetric string phenomenology. Phys. Rev. D 2015, 91, 126014. [Google Scholar] [CrossRef]
- Abel, S.; Dienes, K.R.; Mavroudi, E. GUT precursors and entwined SUSY: The phenomenology of stable nonsupersymmetric strings. Phys. Rev. D 2018, 97, 126017. [Google Scholar] [CrossRef]
- Florakis, I.; Rizos, J. Chiral heterotic strings with positive cosmological constant. Nucl. Phys. B 2016, 913, 495–533. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H. Super no-scale models in string theory. Nucl. Phys. B 2016, 913, 593–626. [Google Scholar] [CrossRef]
- Kounnas, C.; Partouche, H. = 2 → 0 super no-scale models and moduli quantum stability. Nucl. Phys. B 2017, 919, 41–73. [Google Scholar] [CrossRef]
- Kachru, S.; Kumar, J.; Silverstein, E. Vacuum energy cancellation in a non-supersymmetric string. Phys. Rev. D 1999, 59, 106004. [Google Scholar] [CrossRef]
- Shiu, G.; Tye, S.H.H. Bose-Fermi degeneracy and duality in non-supersymmetric strings. Nucl. Phys. B 1999, 542, 45–72. [Google Scholar] [CrossRef]
- Harvey, J.A. String duality and non-supersymmetric strings. Phys. Rev. D 1999, 59, 026002. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Gorlich, L. Orientifolds of non-supersymmetric asymmetric orbifolds. Nucl. Phys. B 1999, 551, 601–616. [Google Scholar] [CrossRef]
- Angelantonj, C.; Antoniadis, I.; Forger, K. Non-supersymmetric type I strings with zero vacuum energy. Nucl. Phys. B 1999, 555, 116–134. [Google Scholar] [CrossRef]
- Angelantonj, C.; Cardella, M. Vanishing perturbative vacuum energy in nonsupersymmetric orientifolds. Phys. Lett. B 2004, 595, 505–512. [Google Scholar] [CrossRef]
- Satoh, Y.; Sugawara, Y.; Wada, T. Non-supersymmetric asymmetric orbifolds with vanishing cosmological constant. J. High Energy Phys. 2016, 2016, 184. [Google Scholar] [CrossRef]
- Sugawara, Y.; Wada, T. More on non-supersymmetric asymmetric orbifolds with vanishing cosmological constant. J. High Energy Phys. 2016, 2016, 28. [Google Scholar] [CrossRef]
- Groot Nibbelink, S.; Loukas, O.; Mütter, A.; Parr, E.; Vaudrevange, P.K.S. Tension between a vanishing cosmological constant and non-supersymmetric heterotic orbifolds. arXiv, 2017; arXiv:1710.09237. [Google Scholar]
- Faraggi, A.E.; Tsulaia, M. On the low energy spectra of the nonsupersymmetric heterotic string theories. Eur. Phys. J. C 2008, 54, 495–500. [Google Scholar] [CrossRef]
- Faraggi, A.E.; Tsulaia, M. Interpolations among NAHE-based supersymmetric and nonsupersymmetric string vacua. Phys. Lett. B 2010, 683, 314–320. [Google Scholar] [CrossRef]
- Ashfaque, J.M.; Athanasopoulos, P.; Faraggi, A.E.; Sonmez, H. Non-tachyonic semi-realistic non-supersymmetric heterotic string vacua. Eur. Phys. J. C 2016, 76, 208. [Google Scholar] [CrossRef]
- Abel, S.; Stewart, R.J. On exponential suppression of the cosmological constant in non-SUSY strings at two loops and beyond. Phys. Rev. D 2017, 96, 106013. [Google Scholar] [CrossRef]
- Aoki, K.; D’Hoker, E.; Phong, D.H. Two-loop superstrings on orbifold compactifications. Nucl. Phys. B 2004, 688, 3–69. [Google Scholar] [CrossRef]
- Iengo, R.; Zhu, C.J. Evidence for nonvanishing cosmological constant in nonSUSY superstring models. J. High Energy Phys. 2000, 2000. [Google Scholar] [CrossRef]
- Rohm, R. Spontaneous supersymmetry breaking in supersymmetric string theories. Nucl. Phys. B 1984, 237, 553–572. [Google Scholar] [CrossRef]
- Kounnas, C.; Porrati, M. Spontaneous supersymmetry breaking in string theory. Nucl. Phys. B 1988, 310, 355. [Google Scholar] [CrossRef]
- Ferrara, S.; Kounnas, C.; Porrati, M. Superstring solutions with spontaneously broken four-dimensional supersymmetry. Nucl. Phys. B 1988, 304, 500–512. [Google Scholar] [CrossRef]
- Ferrara, S.; Kounnas, C.; Porrati, M.; Zwirner, F. Superstrings with spontaneously broken supersymmetry and their effective theories. Nucl. Phys. B 1989, 318, 75–105. [Google Scholar] [CrossRef]
- Kounnas, C.; Rostand, B. Coordinate-dependent compactifications and discrete symmetries. Nucl. Phys. B 1990, 341, 641–665. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J.H. Spontaneous breaking of supersymmetry through dimensional reduction. Phys. Lett. B 1979, 82, 60–64. [Google Scholar] [CrossRef]
- Coudarchet, T.; Fleming, C.; Partouche, H. Quantum no-scale regimes in string theory. Nucl. Phys. B 2018, 930, 235–254. [Google Scholar] [CrossRef]
- Coudarchet, T.; Partouche, H. Quantum no-scale regimes and moduli dynamics. Nucl. Phys. B 2018, 933, 134–184. [Google Scholar] [CrossRef]
- Cremmer, E.; Ferrara, S.; Kounnas, C.; Nanopoulos, D.V. Naturally vanishing cosmological constant in = 1 supergravity. Phys. Lett. B 1983, 133, 61–66. [Google Scholar] [CrossRef]
- Ellis, J.R.; Kounnas, C.; Nanopoulos, D.V. Phenomenological SU(1, 1) supergravity. Nucl. Phys. B 1984, 241, 406–428. [Google Scholar] [CrossRef]
- Ellis, J.R.; Lahanas, A.B.; Nanopoulos, D.V.; Tamvakis, K. No-scale supersymmetric standard model. Phys. Lett. B 1984, 134, 429–435. [Google Scholar] [CrossRef]
- Ellis, J.R.; Kounnas, C.; Nanopoulos, D.V. No scale supersymmetric GUTs. Nucl. Phys. B 1984, 247, 373–395. [Google Scholar] [CrossRef]
- Dudas, E.; Kitazawa, N.; Sagnotti, A. On climbing scalars in string theory. Phys. Lett. B 2011, 694, 80–88. [Google Scholar] [CrossRef]
| 1 | In the framework described in the core of this review, “nearly vanishes” means exponentially suppressed in , where is the string scale and the supersymmetry breaking scale measured in the -model frame. |
| 2 | As usual, is the genus-one Teichmüller parameter and the fundamental domain of . |
| 3 | When does not vanish identically, it is a source for the kinetic energies. Adding one-loop corrections to the kinetic terms would effectively modify the solutions at second order in string coupling. |
| 4 | Up to exponentially suppressed terms. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).