Solar Neutrinos Spectroscopy with Borexino Phase-II

Abstract

Solar neutrinos have played a central role in the discovery of the neutrino oscillation mechanism. They still are proving to be a unique tool to help investigate the fusion reactions that power stars and further probe basic neutrino properties. The Borexino neutrino observatory has been operationally acquiring data at Laboratori Nazionali del Gran Sasso in Italy since 2007. Its main goal is the real-time study of low energy neutrinos (solar or originated elsewhere, such as geo-neutrinos). The latest analysis of experimental data, taken during the so-called Borexino Phase-II (2011-present), will be showcased in this talk—yielding new high-precision, simultaneous wide band flux measurements of the four main solar neutrino components belonging to the “pp” fusion chain (pp, pep, ${}^7$Be, ${}^8$B), as well as upper limits on the remaining two solar neutrino fluxes (CNO and hep).

1. Solar Neutrinos Production and Detection

Electron neutrinos (${\nu }_e$) are copiously produced in stars by thermonuclear fusion of protons. Solar neutrinos emitted by our star provide a direct and unique tool to infer properties of the interior of the Sun. The main contribution to the solar luminosity comes from reactions belonging to the pp chain that account for ∼99% while the remaining ∼1% is due to the CNO cycle. In the Sun the CNO cycle plays a sub-dominant role but it becomes dominant in massive stars [1,2]. The effort to develop a model able to reproduce accurately the physical characteristics of the Sun, the spectra and the fluxes of the produced neutrino components, was initiated by John Bahcall in the mid-1960s. This model in now called the Standard Solar Model (SSM) [3]. 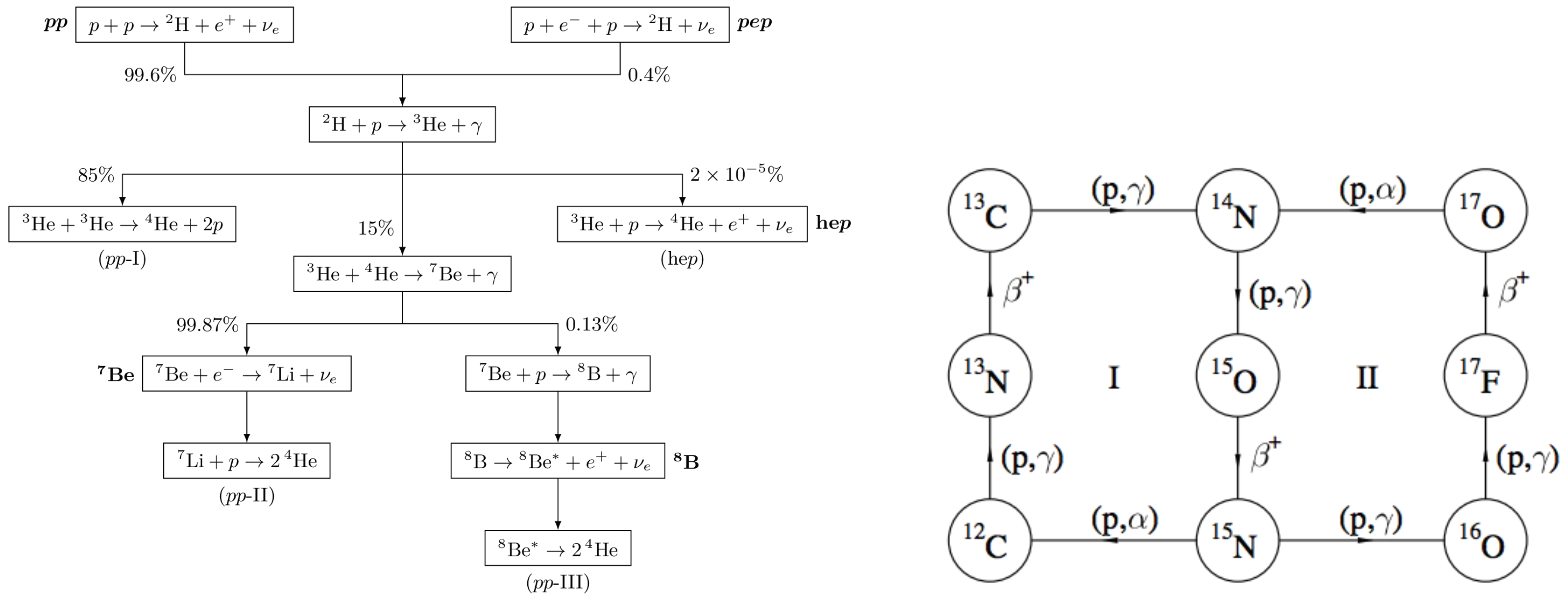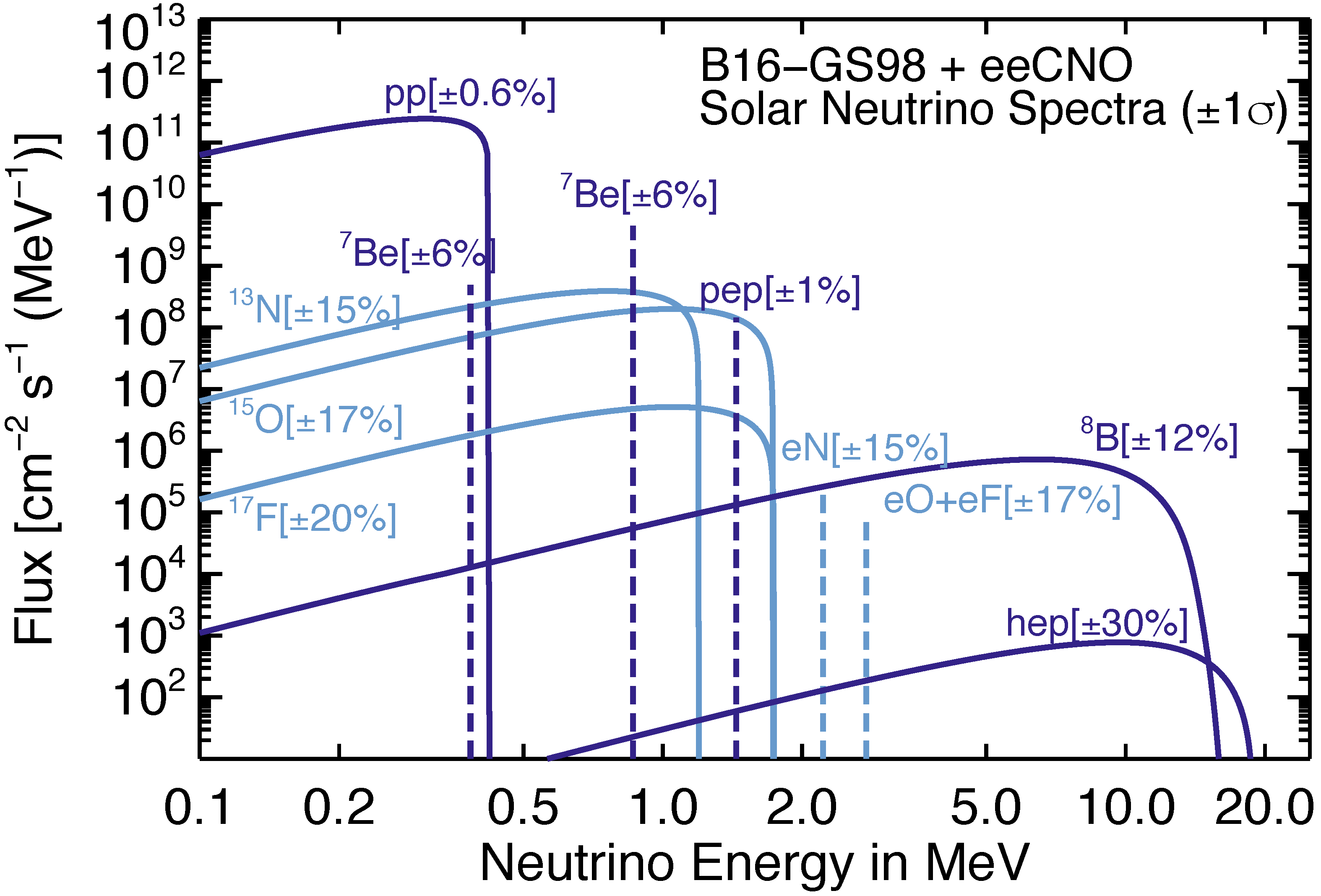Figure 1 shows the pp chain with the relative branching percentages and the CNO bi-cycle; the corresponding neutrino fluxes are plotted in Figure 2. The spectrum is dominated by the low-energy ${\nu }_e$s coming from the pp reaction, and extend up to ∼18.8 MeV, the maximum energy reached by the hep neutrinos. Beside the continuous spectra there are two mono-energetic lines from ${}^7$Be $\nu$’s (E${}_{\nu }$ = 0.384 MeV with a BR of ∼10% and 0.862 MeV with a BR of ∼90%) and one mono-energetic line from pep$\nu$’s (E${}_{\nu }$ = 1.44 MeV). Neutrinos emitted from the CNO cycle are expected to have a continuous energy spectrum extending up to 1.74 MeV.

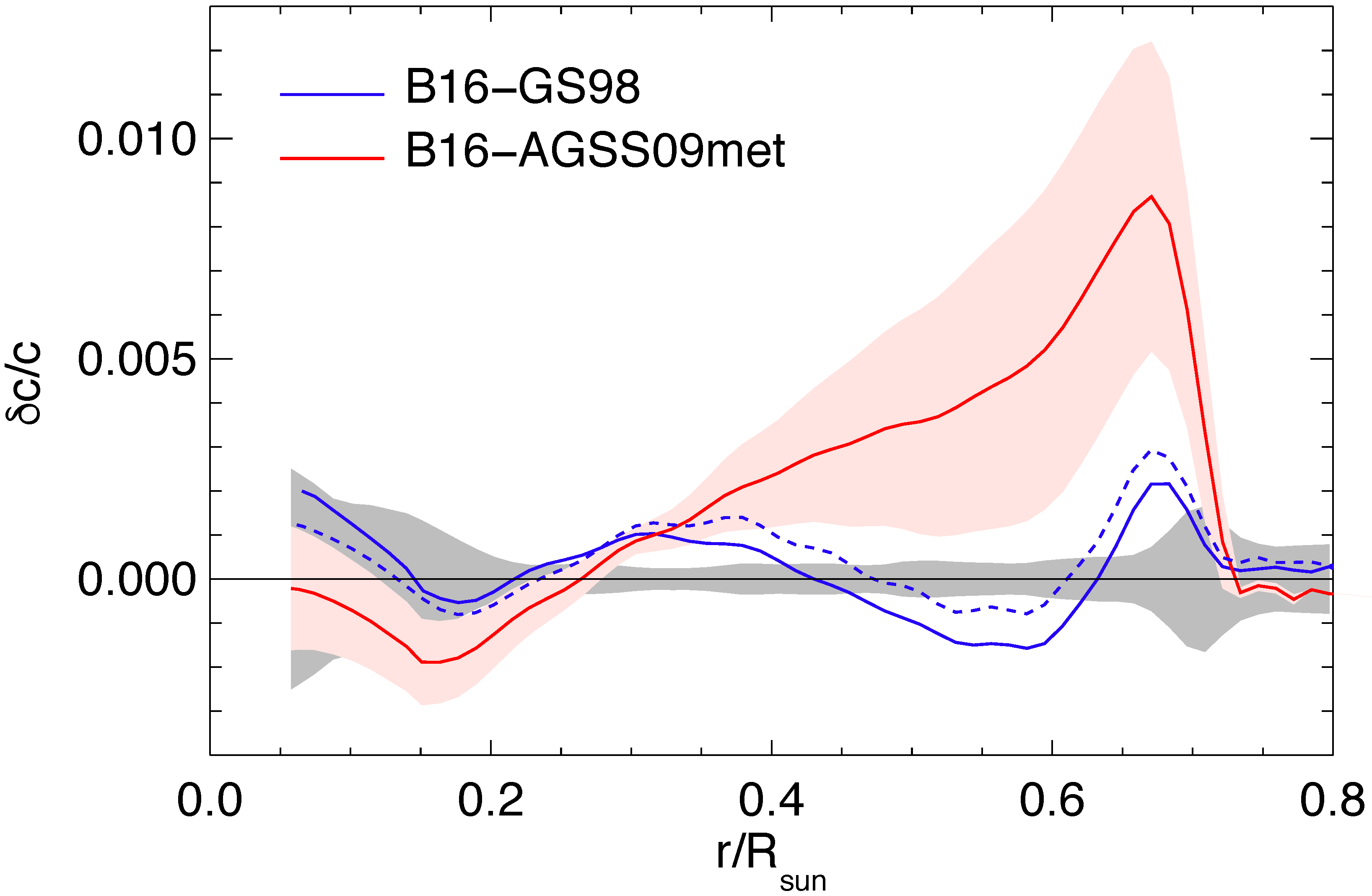
In recent years, previous excellent agreement between the SSM and helioseismology (that is, the science that studies the interior of the Sun by looking at its vibration modes) has been seriously compromised due to a downward revision of the heavy-element content at the solar surface from (Z/X) = 0.0229 [5] to (Z/X) = 0.0165 [6]. This profound discrepancy between the SSM and helioseismology is now called the Solar Metallicity Problem (see Figure 3). To fix this puzzle would imply either to revise the physical inputs of the SSM or to modify the core abundances, in particular those of C,N,O.

A completely new revision of the abundances of almost all elements in the solar photosphere with a three-dimensional hydrodynamical model has been done in 2009 [7]. The new results gave a solar abundance (Z/X) = 0.0178. The three different sets (GS98 [5], AGS05 [6] and AGSS09 [7]) of solar abundances have been used in [8] originating two main different SSM variants: the low metallicity and the high metallicity SSMs.

To settle the low (LZ) versus high (HZ) metallicity problem it is important to experimentally measure the ${}^7$Be, ${}^8$B or CNO neutrino fluxes, which are sensitive to the solar metallicity. The difference between the two metallicities is ∼9% for ${}^7$Be, ∼18% for ${}^8$B and almost 40% for CNO (see

Table 1. Model and solar neutrino fluxes. Units are: ${10}^{10}$ (pp), ${10}^9{(}^7\mathrm{Be})$, ${10}^8(\mathrm{pep},{}^{13}\mathrm{N},{}^{15}\mathrm{O})$, ${10}^6({}^8\mathrm{B}{,}^{17}\mathrm{F})$ and ${10}^3\left(\mathrm{hep}\right)$${\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$. Table adopted from [4].

Flux	B16-GS98	B16-AGSS09met
$\Phi \left(\mathrm{pp}\right)$	$5.98(1\pm 0.006)$	$6.03(1\pm 0.005)$
$\Phi \left(\mathrm{pep}\right)$	$1.44(1\pm 0.01)$	$1.46(1\pm 0.009)$
$\Phi \left(\mathrm{hep}\right)$	$7.98(1\pm 0.30)$	$8.25(1\pm 0.30)$
$\Phi \left({}^7\mathrm{Be}\right)$	$4.93(1\pm 0.06)$	$4.50(1\pm 0.06)$
$\Phi \left({}^8\mathrm{B}\right)$	$5.46(1\pm 0.12)$	$4.50(1\pm 0.12)$
$\Phi \left({}^{13}\mathrm{N}\right)$	$2.78(1\pm 0.15)$	$2.04(1\pm 0.14)$
$\Phi \left({}^{15}\mathrm{O}\right)$	$2.05(1\pm 0.17)$	$1.44(1\pm 0.16)$
$\Phi \left({}^{17}\mathrm{F}\right)$	$5.29(1\pm 0.20)$	$3.26(1\pm 0.18)$

) [4].

The first solar neutrino detector was built at the end of the 1960s in the Homestake mine in South Dakota To detect solar neutrinos. The deficit in detected neutrinos, about one third compared to the expected value form the SSM, was the start of the so called Solar Neutrino Problem (SNP) [9,10,11,12].

The detector consisted of a large tank filled with 615 metric tonnes of liquid perchloroethylene ${\mathrm{C}}_2{\mathrm{Cl}}_4$, suitable to detect ${}^7$Be and ${}^8$B $\nu$s, and a small signal from the CNO and pep solar neutrinos, via the reaction ${\nu }_e+{}^{37}\mathrm{Cl}\to {}^{37}\mathrm{Ar}+e^{-}$ with an energy threshold of $E_{th}=814\mathrm{keV}$.

At the beginning of the 1980s Kamiokande, a large water Čerenkov detector of about 3000 metric tonnes, was built in Japan [13]. Kamiokande was a real time neutrino detector looking for the Čerenkov light produced by the electrons scattered by an impinging neutrino, mainly via the reaction ${\nu }_x+e^{-}\to {\nu }_x+e^{-}$. The energy threshold of the reaction was $E_{th}=7.5\mathrm{MeV}$ and, therefore, only ${}^8$B and hep neutrinos were detected. At the beginning of the 1990s a larger version of the detector was built, Super-Kamiokande, a 50,000 metric tonne pure water detector with the energy threshold lowered to $E_{th}=5.5\mathrm{MeV}$ [14]. Both Kamiokande and Super-Kamiokande detected about half of the neutrinos foreseen by the SSM.

The SNP was also confirmed by two new radiochemical experiments with a very low energy threshold of $E_{th}=233\mathrm{keV}$, via the reaction ${\nu }_e+{}^{71}\mathrm{Ga}\to {}^{71}\mathrm{Ge}+e^{-}$. The Soviet-American Gallium Experiment (SAGE), used more than 50 metric tons of metallic gallium [15], while the Gallex experiment at the Gran Sasso Underground Laboratories (LNGS), employed 30 metric tonnes of natural gallium [16,17] (After the end of GALLEX, the Gallium Neutrino Observatory or GNO, started in April 1998). Both detectors were calibrated with an artificial neutrino source. They looked for a less model-dependent component of neutrino spectra and hence more robust to test the hypothesis that fusion of hydrogen powers the Sun. Both experiments measured a smaller neutrino signal, by about $60\%$, than predicted by the SSM (for an historical introduction see for instance [18]).

At the turn of the century, the advent of the heavy water-based Sudbury Neutrino Observatory (SNO) experiment was able to measure simultaneously three different interaction channels; the elastic scattering ${\nu }_x+e^{-}\to {\nu }_x+e^{-}$, the charged current ${\nu }_e+d\to e^{-}+p^{+}+p^{+}$, that is sensitive only to electronic neutrinos and the neutral current ${\nu }_x+d\to {\nu }_x+p^{+}+n$, receiving contributions from all active flavors. SNO proved that the measured total neutrino flux detected via neutral current interactions was in good agreement with the theoretical predictions of the SSM. Only a fraction of these neutrinos had conserved their flavor during their travel from the core of the Sun to the Earth [19,20,21].

The two oscillation parameters that lead solar neutrino oscillations are $\Delta m_{12}^2$ and ${\theta }_{12}$ of the PMNS mixing matrix. Up to a few MeV, the ${\nu }_e$ survival probabilities are described by vacuum oscillations, but at energies above some MeV, matter effects enhance the conversion ${\nu }_e\to {\nu }_{\mu ,\tau }$, leading to a further suppression of the ${\nu }_e$ rate detected on Earth. This matter enhancement effect was first proposed by Wolfenstein and then reprised by Mikheyev and Smirnov, it is now called MSW effect [22,23]. It consists in the transformation of one neutrino species (flavor) into another one in a medium with varying density. Electron neutrinos have different interactions with matter compared to muon or tau neutrinos flavours. In particular, electron neutrinos can have both charged current and neutral current elastic scattering with electrons, while muon or tau neutrinos have only neutral current interactions with electrons. The Large Mixing Angle (LMA) MSW effect provides the solution of the long standing Solar Neutrino Problem. The MSW-LMA oscillation scenario is confirmed by all the solar neutrino experiments both for vacuum and matter-dominated regimes. The vacuum-matter transition region (from ∼1 to ∼5 MeV), however, remains to be explored and might hold evidence for non-standard neutrino interactions (NSI).

2. Borexino Detector

To explore the whole neutrino spectrum it has been necessary to build a real time detector with an energy threshold as low as possible. The Borexino experiment was conceived mainly to detect the mono-energetic beryllium line, but it succeeded in measuring all the solar neutrino components from the pp cycle.

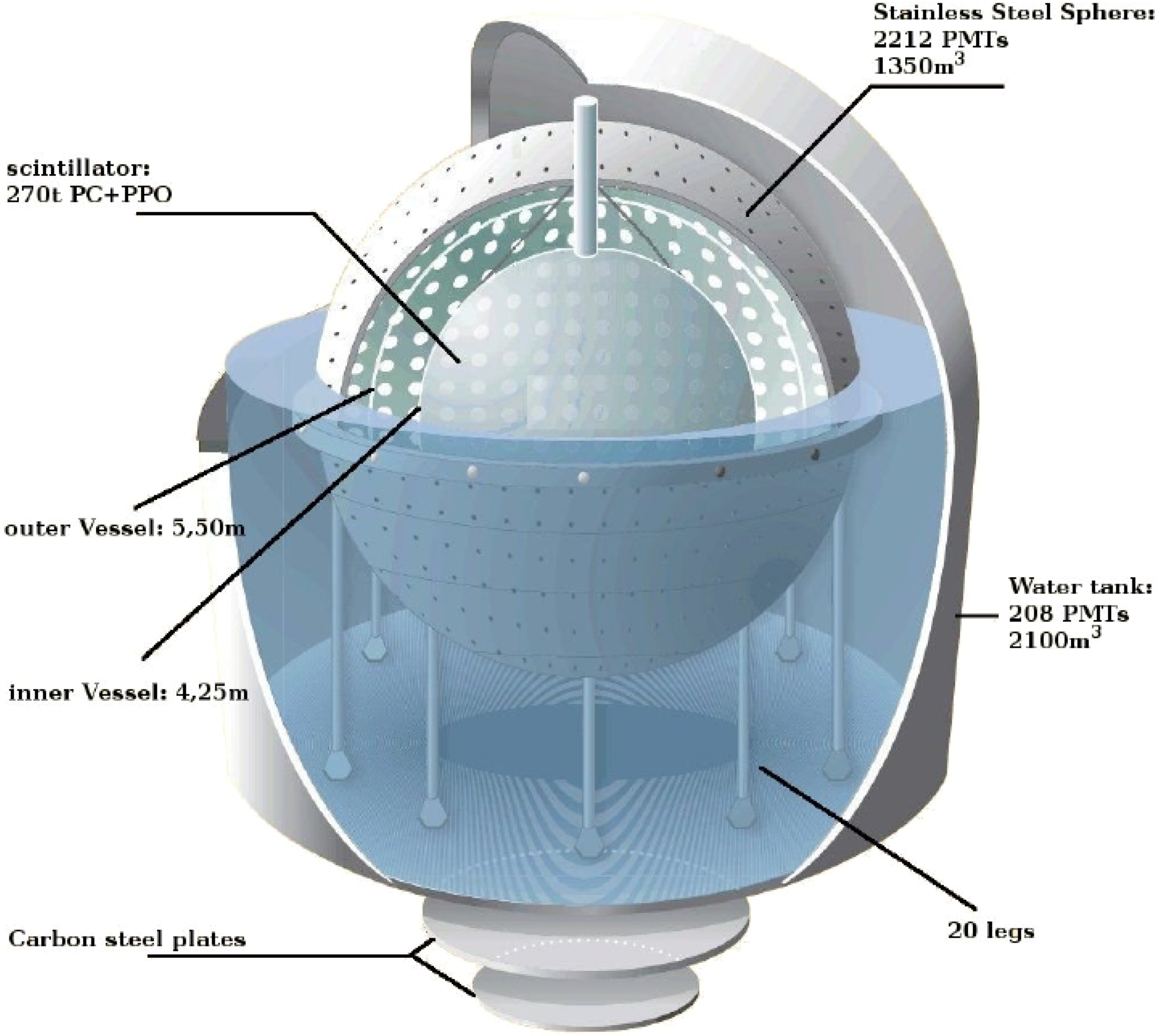
The Borexino detector is located at the Gran Sasso National Laboratories (LNGS) in central Italy, at a depth of ∼1.4 km of rock, equivalent to 3800 m of water. The flux of cosmic muons which cross the rock shielding and reach the underground halls is ∼1.2 $\mathsf{\mu }$m${}^{-2}$h${}^{-1}$. Figure 4 shows a 3D sketch of the detector [24].

The active mass is composed by 278 tonnes of pseudocumene which is doped with 1.5 g/l of PPO, in order to enhance the scintillator properties, and it is contained in an 8.5 m diameter nylon Inner Vessel with a thickness of 125 $\mathsf{\mu }$m. The Inner Vessel is surrounded by two concentric pseudocumene buffers doped with a light quencher (DMP). A Stainless Steel Sphere (SSS) with a diameter of 13.7 m contains the scintillator and buffers. In turn this sphere is enclosed in a dome-shaped Water Tank containing 2100 tons of ultra-pure water as an additional shield.

The light created by the scintillator is detected by 2212 8″ PhotoMultiplier Tubes (PMTs) distributed on the inner surface of the Stainless Steel Sphere. Into the Water Tank 208 8″ PMTs detect the Čerenkov light radiated by cosmic muons. The principle of neutrino detection is based on elastic scattering on electrons in the target material ${\nu }_x+e^{-}\to {\nu }_x+e^{-}$.

The light yield of the scintillator is ∼10${}^4$ photons per MeV, corresponding to ∼500 detected photoelectrons per MeV. The fast time response of ∼3 ns allows the reconstruction of the events’ position by means of a time-of-flight technique; the precision in position reconstruction is within ∼10 cm at 1 MeV. Thanks to the position reconstruction it is possible to define a fiducial volume between 75 and 150 tonnes depending on the analysis type.

The light created by the scattered electron is emitted isotropically; thus it is impossible to distinguish the light generated by the signal from the one produced by beta and gamma rays emitted by radioactive isotopes. In order to reach a signal to noise ratio of the order of one, the ${}^{238}$U and ${}^{232}$Th content must be reduced to a level of ${10}^{-16}g\left(U\right)/g$ corresponding to about one count per day (cpd) in 100 tonnes.

Several techniques have been applied to reduce the radioisotope content in the scintillator such as distillation, water extraction and nitrogen stripping [25].

Borexino began data taking in 2007. The $PhaseI$ dataset was obtained between May 2007 and May 2010. The uncertainty in the energy scale between 200 keV and 2000 keV has been determined at 1.5% precision, using multiple $\gamma$-ray sources. The position reconstruction algorithm has been tuned with the help of a $Rn$ source located in 184 positions in the active volume with a steerable arm. The obtained error on the fiducial volume is (−1.3% + 0.5%).

To correctly model external gamma backgrounds, high energy $\gamma$-ray sources (${}^{208}$Tl from a ${}^{228}$Th source) were placed outside the Stainless Steel Sphere.

3. First Simultaneous Precision Spectroscopy of pp, ${}^7$Be, and pep

The first simultaneous precision spectroscopy of pp, ${}^7$Be, and pep is based on an exposure of 1291.51 days × 71.3 t with data collected between 14 December 2011 to 21 May 2016. This second phase (Borexino $PhaseII$) started after an extensive purification campaign consisting of six cycles of closed-loop water extraction, during which the radioactive contaminants were significantly reduced to: ${}^{238}$U < 9.4 × 10${}^{-20}$ g/g (95% C.L.), ${}^{232}$Th < 5.7 × 10${}^{-19}$ g/g (95% C.L.), ${}^{85}$Kr, reduced by a factor ∼4.6, and ${}^{210}$Bi, reduced by a factor ∼2.3

For each event, the energy, the position and the pulse shape are reconstructed by exploiting the number of detected photons and their detection times. The energy resolution is ∼50 keV at 1 MeV. The hardware energy threshold is $N_p$ > 20, (total number of triggered PMTs) which corresponds to ∼50 keV [26]. Events are selected removing internal (external) muons [27] and applying a 300 (2) ms veto to suppress cosmogenic backgrounds. These vetos led to a total dead-time of about 1.5%.

The ${}^{214}$Bi-${}^{214}$Po fast coincidences from the ${}^{238}$U chain and unphysical noise events are removed; the fraction of good events removed is ∼0.1% and it is estimated using MonteCarlo (MC) simulations [28] and calibration data [29].

A Fiducial Volume (FV) cut is defined in order to reduce background from sources external to the scintillator in particular from the nylon vessel, from the SSS, and from PMTs. Thanks to this FV the innermost region of the scintillator is selected (71.3 t), contained within the radius R < 2.8 m and the vertical coordinate −1.8 < z < 2.2 m.

After these cuts the main background is due to radioactive isotopes in the scintillator itself: ${}^{14}$C (${\beta }^{-}$ decay, Q = 156 keV), ${}^{210}$Po ($\alpha$ decay, E = 5.3 MeV quenched by a factor ∼10), ${}^{85}$Kr (${\beta }^{-}$ decay, Q = 687 keV), and ${}^{210}$Bi (${\beta }^{-}$ decay, Q = 1160 keV) from ${}^{210}$Pb. An additional background is also due to the pile-up of uncorrelated events coming mostly from ${}^{14}$C, external background, and ${}^{210}$Po [28,30]. Other important contributions to the background are the residual external background, mainly due to $\gamma$’s from the decay of ${}^{208}$Tl, ${}^{214}$Bi, and ${}^{40}$K and the cosmogenic isotope ${}^{11}$C (${\beta }^{+}$ decay, $\tau$ = 29.4 min) that is continuously produced by muons through spallation on ${}^{12}$C. The Collaboration has developed a method called Three-Fold Coincidence (TFC) by which it it possible to tag events correlated in space and time with a muon and a neutron (${}^{11}$C is often produced together with one or even a burst of neutrons). Furthermore, in order to better disentangle ${}^{11}$C events, a $e^{+}/e^{-}$ pulse-shape discrimination is applied [26,31]. The TFC algorithm has (92 ± 4)% ${}^{11}$C-tagging efficiency.

To extract the interaction rates of the solar neutrinos and the background species we maximize a binned likelihood function (through a multivariate approach) built as the product of 4 different factors; the TFC-subtracted energy spectrum, the TFC-tagged energy spectrum, the PS-${\mathcal{L}}_{\mathrm{PR}}$ and the radial distributions of the events.

In the fit procedure the neutrinos signal and the background reference spectral shapes are obtained with two complementary strategies; a first one based on the analytical description of the detector response function, and a second one fully based on MC simulations.

The interaction rates of pp, ${}^7$Be, and pep neutrinos are obtained from the fit together with the decay rates of ${}^{85}$Kr, ${}^{210}$Po, ${}^{210}$Bi, ${}^{11}$C, and external backgrounds due to $\gamma$ rays from ${}^{208}$Tl, ${}^{214}$Bi, and ${}^{40}$K.

Because the degeneracy between the CNO $\nu$ and the ${}^{210}$Bi spectral shapes we have constrained the CNO $\nu$ interaction rate to the HZ-SSM predictions, including MSW-LMA oscillations to 4.92 ± 0.55 cpd/100 t [4,32], (3.52 ± 0.37 cpd/100 t in case of LZ-SSM). The contribution of ${}^8$B $\nu$’s has been fixed to the HZ-metallicity rate 0.46 cpd/100 t.

Table 2. Borexino Phase-II results on pp, ${}^7$Be (862 +384 keV), pep and CNO solar $\nu$’s: interaction rates and fluxes inferred assuming the MSW-LMA oscillation parameters [32]. The first error is the statistical derived by profiling the likelihood under Wilk’s approximation. The interval extracted is coherent with the expectation from the toy-MC. The second error is the systematic uncertainty. Different contributions to the systematic error are detailed in Table 4. The result on pep $\nu$’s depends on whether we assume HZ or LZ metallicity for CNO $\nu$’s. The remaining columns show the theoretical interaction rates and fluxes predicted by the Standard Solar Model under the high (HZ) and low (LZ) metallicity assumptions [4]. Table from [33].

Solar $\mathit{\nu }$	Borexino Experimental Results		B16(GS98)-HZ		B16(AGSS09)-LZ
	Rate	Flux	Rate	Flux	Rate	Flux
	[cpd/100 t]	$\left[{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$	[cpd/100 t]	$\left[{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$	[cpd/100 t]	$\left[{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}\right]$
pp	$134\pm 10{}_{-10}^{+6}$	$(6.1\pm 0.5{}_{-0.5}^{+0.3})\times {10}^{10}$	$131.1\pm 1.4$	$5.98(1\pm 0.006)\times {10}^{10}$	$132.2\pm 1.4$	$6.03(1\pm 0.005)\times {10}^{10}$
${}^7\mathrm{Be}$	$48.3\pm 1.1{}_{-0.7}^{+0.4}$	$(4.99\pm 0.11{}_{-0.88}^{+0.06})\times {10}^9$	$47.9\pm 2.8$	$4.93(1\pm 0.06)\times {10}^9$	$43.7\pm 2.5$	$4.50(1\pm 0.06)\times {10}^9$
pep (HZ)	$2.43\pm 0.36{}_{-0.22}^{+0.15}$	$(1.27\pm 0.19{}_{-0.12}^{+0.08})\times {10}^8$	$2.74\pm 0.04$	$1.44(1\pm 0.009)\times {10}^8$	$2.78\pm 0.04$	$1.46(1\pm 0.009)\times {10}^8$
pep (LZ)	$2.65\pm 0.36{}_{-0.24}^{+0.15}$	$(1.39\pm 0.19{}_{-0.13}^{+0.08})\times {10}^8$	$2.74\pm 0.04$	$1.44(1\pm 0.009)\times {10}^8$	$2.78\pm 0.04$	$1.46(1\pm 0.009)\times {10}^8$
$\mathrm{CNO}$	$<8.1(95\%\mathrm{C}.\mathrm{L}.)$	$<7.9\times {10}^8(95\%\mathrm{C}.\mathrm{L}.)$	$4.92\pm 0.55$	$4.88(1\pm 0.11)\times {10}^8$	$3.52\pm 0.37$	$3.51(1\pm 0.10)\times {10}^8$

summarizes the interaction rates of solar neutrinos while in

Table 3. Best estimates for the total rates of the background species included in the fit with statistical and systematic uncertainties added in quadrature. Table from [33].

Background	Rate [cpd/100 t]
${}^{14}$C [Bq/100 t]	$40.0\pm 2.0$
${}^{85}$Kr	$6.8\pm 1.8$
${}^{210}$Bi	$17.5\pm 1.9$
${}^{11}$C	$26.8\pm 0.2$
${}^{210}$Po	$260.0\pm 3.0$
Ext. ${}^{40}$K	$1.0\pm 0.6$
Ext. ${}^{214}$Bi	$1.9\pm 0.3$
Ext. ${}^{208}$Tl	$3.3\pm 0.1$

are reported the decay rates of background species, both rates are obtained by averaging the results of the analytical and MC approaches.

The ${}^7$Be solar $\nu$ flux is the sum of the two mono-energetic lines at 384 and 862 keV. The uncertainty in this flux has been reduced by the greatest amount.

To extract the pep neutrino flux we constrain the CNO one. With our sensitivity the ${}^7$Be and pp $\nu$ interaction rates are not affected by the hypothesis on CNO (i.e., $\nu$’s HZ hypothesis vs LZ hypothesis). However, the pep $\nu$ interaction rate depends on it, being 0.22 cpd/100 t higher if the LZ hypothesis is assumed.

The absence of the pep reaction is rejected for both the HZ and LZ assumptions with high confidence in this new analysis.

The $e^{-}$ recoil spectrum induced by CNO neutrinos and the ${}^{210}$Bi spectrum are degenerate and this makes impossible to disentangle the two contributions with the spectral fit. Due to this spectrum degeneracy, it is only possible to provide an upper limit on the CNO neutrinos contribution, and in order to extract this number, we have further to break the correlation between the CNO and pep contributions. We exploit the theoretically well known pp and pep flux ratio in order to indirectly constraint the pep $\nu$’s contribution.

It is possible to combine the Borexino results on pp and ${}^7$Be $\nu$ fluxes in order to measure experimentally the ratio $\mathcal{R}$ between the rates of the ${}^3$He-${}^4$He and the ${}^3$He-${}^3$He reactions occurring within the pp chain [34]. The value of $\mathcal{R}$ tell us the competition between the two primary modes of terminating the pp chain and for this reason represent a valuable probe of solar fusion. In first approximation we can neglect the pep and ${}^8$B $\nu$ contribution and $\mathcal{R}$ can be written as 2 $\Phi$(${}^7$Be)/$[\Phi$(pp)-$\Phi$(${}^7$Be)]. The measured value is in agreement with the predicted values for $\mathcal{R}$ = 0.180 ± 0.011 (HZ) and 0.161 ± 0.010 (LZ) [4].

4. Improved Measurement of ${}^8$B Solar Neutrinos with 1.5 kt·y Exposure

Concerning the ${}^8$B analysis the energy threshold is set at 1650 p.e., which correspond to 3.2 MeV electron energy. The analysis is based on data collected between January 2008 and December 2016 and corresponds to 2062.4 live days of data. Data collected during detector operations such as scintillator purification and calibrations are omitted. The dataset is split into a low energy range (LE), with [1650, 2950] p.e., including events from natural radioactivity, and a high energy range (HE), with [2950, 8500] p.e. This high energy region is dominated by external $\gamma$-rays following neutron capture processes on the SSS. Results from the HE sample use data from the entire active volume, while the LE sample requires a spatial cut to remove the top layer of scintillator (the motivation is due to the presence of PPO from the scintillator leak in the upper buffer fluid volume).

The High Energy data sample is fitted with only two components, the ${}^8$B neutrinos and the external component from neutron captures, while the Low Energy sample requires three additional fit components, all due to ${}^{208}$Tl that is present in the bulk dissolved in the scintillator, at the surface intrinsic to the nylon vessel, and from emanation diffused from the nylon vessel into the outer edge of scintillator.

5. $P_{ee}$ and ${}^7$Be and ${}^8$B $\nu$ Reduced Fluxes

We can write the electron neutrino survival probability as function of the neutrino energy. The value for flavor conversion parameters from the MSW-LMA solution are ($\Delta$m${}_{12}^2$ = 7.50 × 10${}^{-5}$ eV${}^2$, tan${}^2{\theta }_{12}$ = 0.441, and tan${}^2{\theta }_{13}$ = 0.022 [32]). For the ${}^8$B neutrino source both the high-Z B16(GS98) SSM and the low-Z B16(AGSS09met) SSM are assumed [4,5,7]. 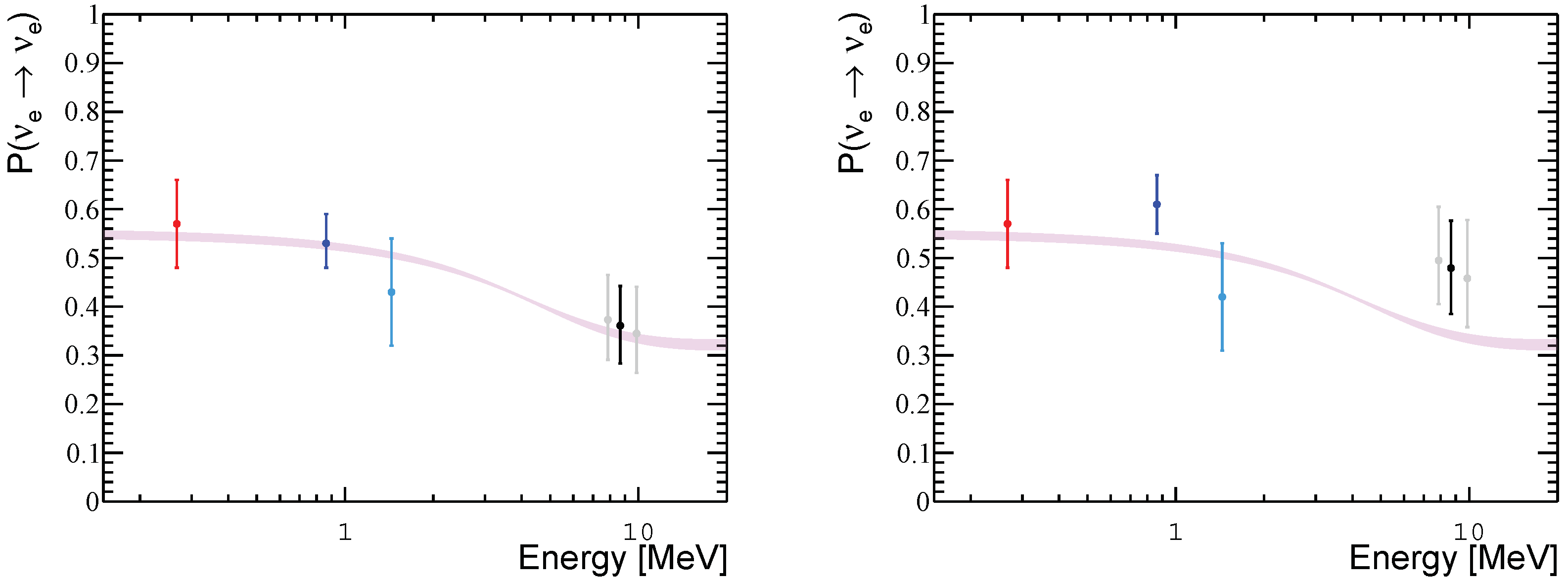As seen from Figure 5 dots represent the Borexino results from pp (red), ${}^7$Be (blue), pep (azure), ${}^8$B neutrino measurements are in black for the LE+HE range, and grey for the separate sub-ranges. For the non mono-energetic pp and ${}^8$B dots are set at the mean energy of detected neutrinos, weighted on the detection range in electron recoil energy. The error bars include experimental and theoretical uncertainties.

6. Toward the Measurement of CNO Solar Neutrinos

CNO neutrinos have never been directly detected; according to astrophysical models, the CNO cycle is responsible for about 1% of the solar neutrino luminosity and it is the main mechanism of energy generation in massive stars. The Borexino Collaboration has recently concentrated all its activities on the investigation of the CNO flux, the only remaining component of the solar neutrino flux which has not yet been measured. The measurement of CNO neutrinos will allow to complete the SSM and could solve for the Solar Metallicity Problem.

The measurement of the CNO flux is very challenging because the low rate expected in Borexino (about 5 cpd/100 t for the high metallicity or about 2 cpd/100 t for the low metallicity) and it is almost degenerate with the ${}^{210}$Bi beta spectrum. Furthermore it is on the same region of the pep $\nu$s (but the correlation pp-pep can help).

To extract the CNO $\nu$ signal the strategy identified by the Collaboration stands on two approaches. The first one exploits the link between ${}^{210}$Bi and ${}^{210}$Po in order to determine the level of ${}^{210}$Bi with the required precision, while a second one would consist in an another purification campaign of the scintillator, in order to further reduce the ${}^{210}$Bi content.

Since the end of 2015, the detector is surrounded by a thick layer of rock wool and the dome of Borexino is equipped with a water coil able to provide heat to compensate the seasonal heat exchanges with the surrounding environment that have been seen to trigger fluid mixing in the IV scintillator and, with it, out-of-equilibrium ${}^{210}$Po migration towards the FV.

Thank to these measures the thermal stabilization of the scintillator is close to being achieved. The upper part of the IV shows stable, low background levels with the ${}^{210}$Po decay rate following a nearly exponential behavior.

A thermally stable scintillator would allow to follow the ${}^{210}$Po decay and, from this, to constrain the ${}^{210}$Bi rate to a precision level that would consequently allow for attempting the measurement of the CNO neutrino flux.

7. Conclusions

In this talk I reported the measurements of the first complete study of the solar pp-chain and of its different terminations by means of neutrino detection in the Borexino detector with a uniform data analysis procedure.

Thanks to these measurements it is possible to probe our understanding of solar physics assuming the validity of the neutrino oscillation mechanism or, alternatively, to test the MSW-LMA paradigm assuming Standard Solar Model flux predictions.

The Borexino detector provides the most precise measurement of the $P_{ee}$ survival probability in the low-energy region, where flavor conversion took place in vacuum. The results obtained by Borexino for the $P_{ee}$ survival probability at higher energy, where flavor conversion is dominated by matter effects, are in good agreement with the SuperKamiokande and SNO measurements.

I also presented the derivation for the first time of the ratio $\mathcal{R}$ between the ${}^3$He-${}^4$He and the ${}^3$He-${}^3$He fusion rates. The value obtained is in agreement with the most up-to-date predicted values by the SSM.

The results obtained by Borexino are compatible with the predictions of both high Z and low Z of the SSM. However, the ${}^7$Be and ${}^8$B solar neutrino fluxes measured by Borexino provide an interesting hint in favor of the high metallicity SSM.

The next goal of the Borexino Collaboration is to attempt the measurement of the, never been detected, CNO neutrinos.