Ions, Protons, and Photons as Signatures of Monopoles
Abstract
1. Introduction
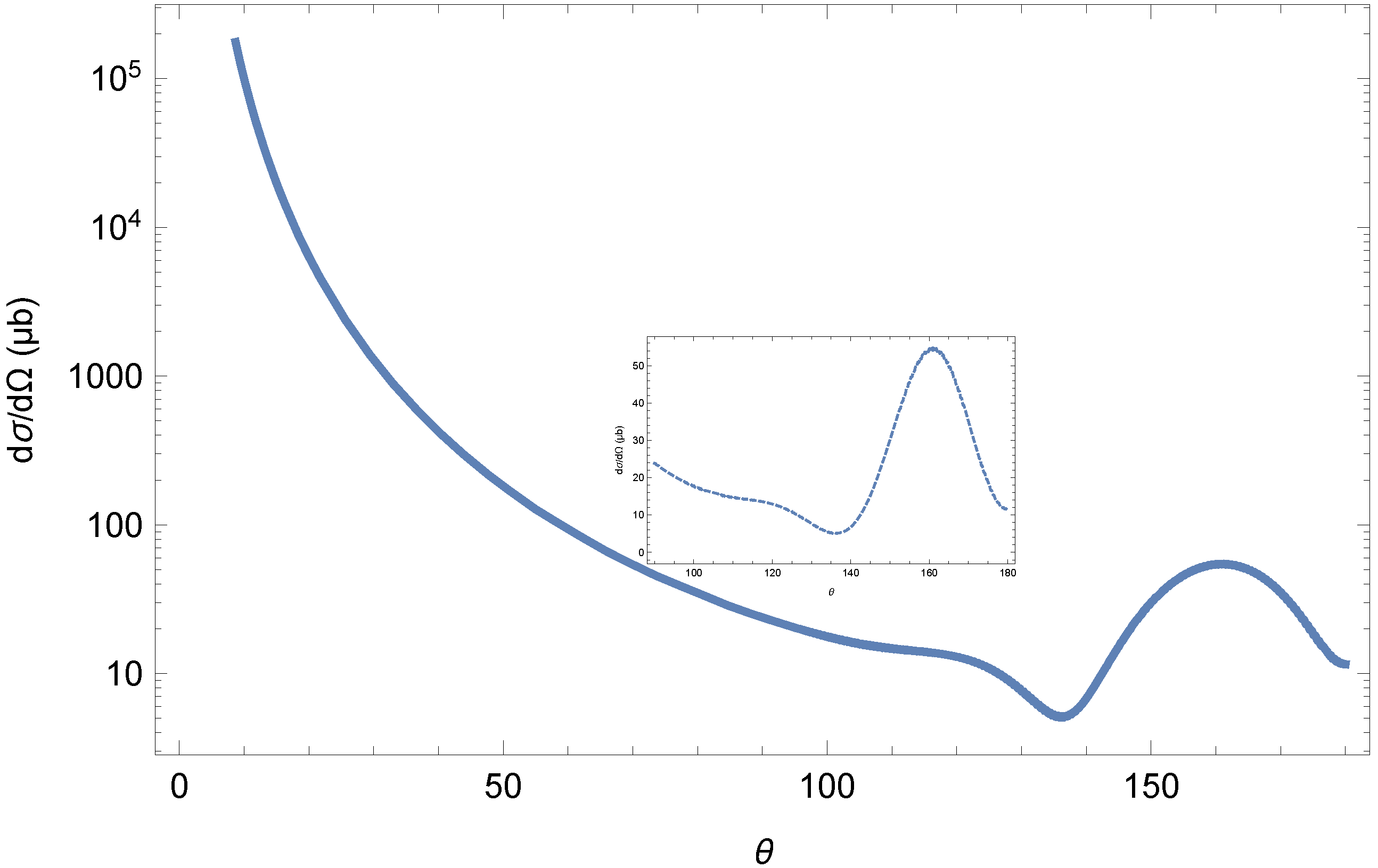
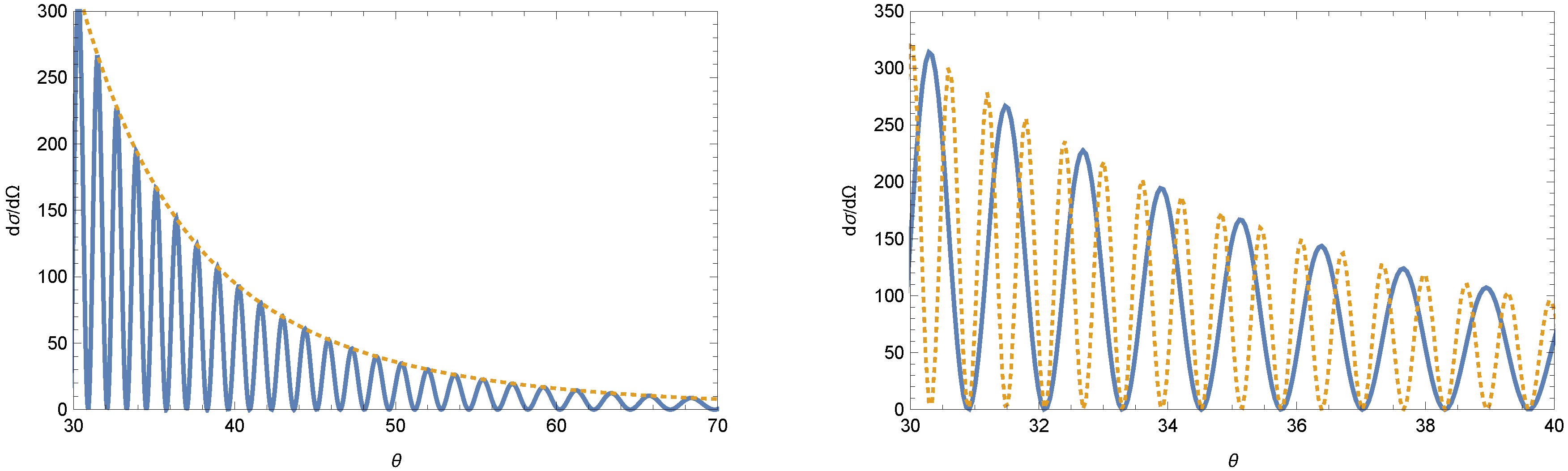
2. Ion Scattering off Bound Monopoles
2.1. Scattering of a Charged Spin Particle Using a Spinless Magnetic Monopole
2.2. Backscattering Spectrography
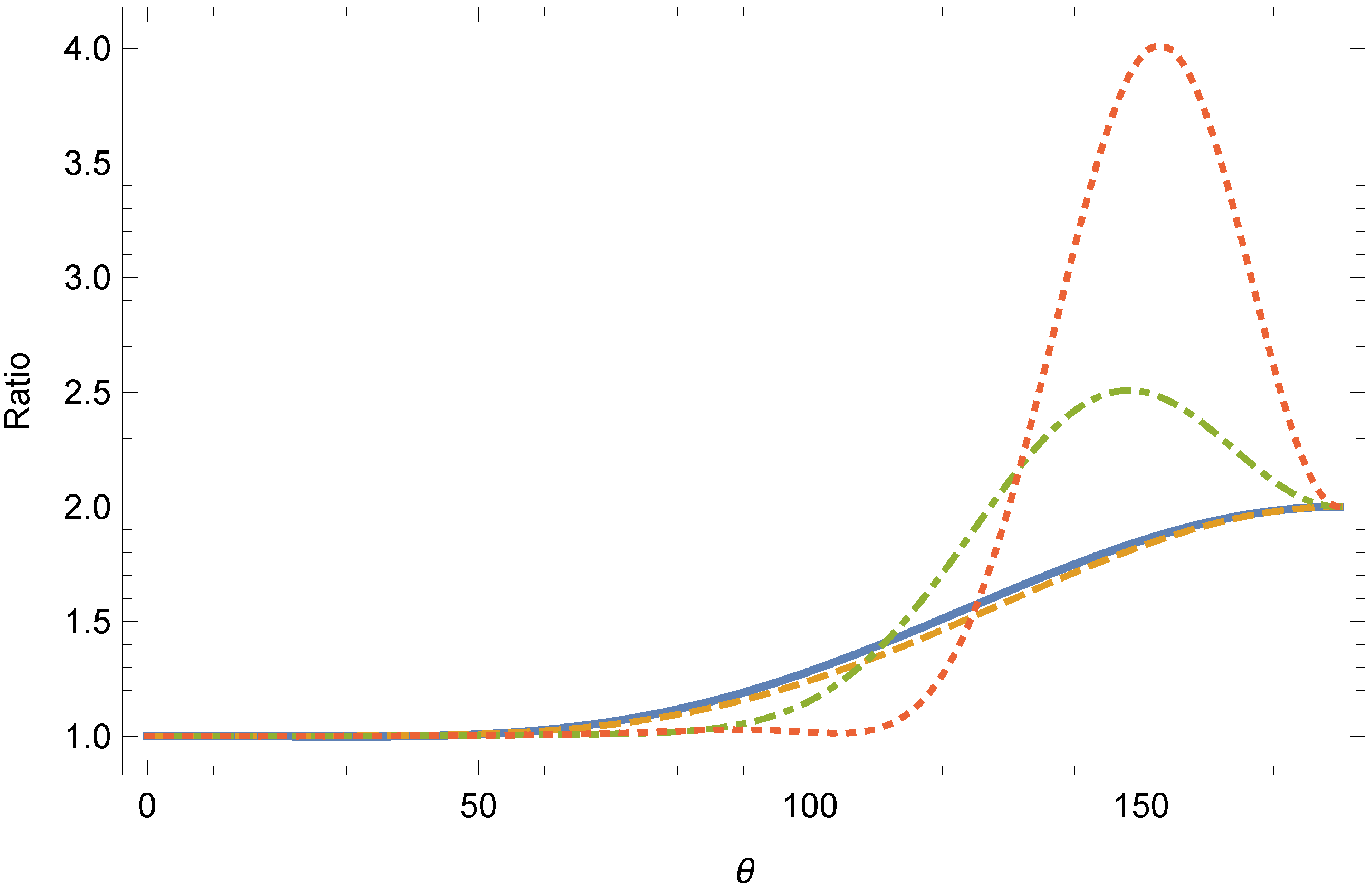
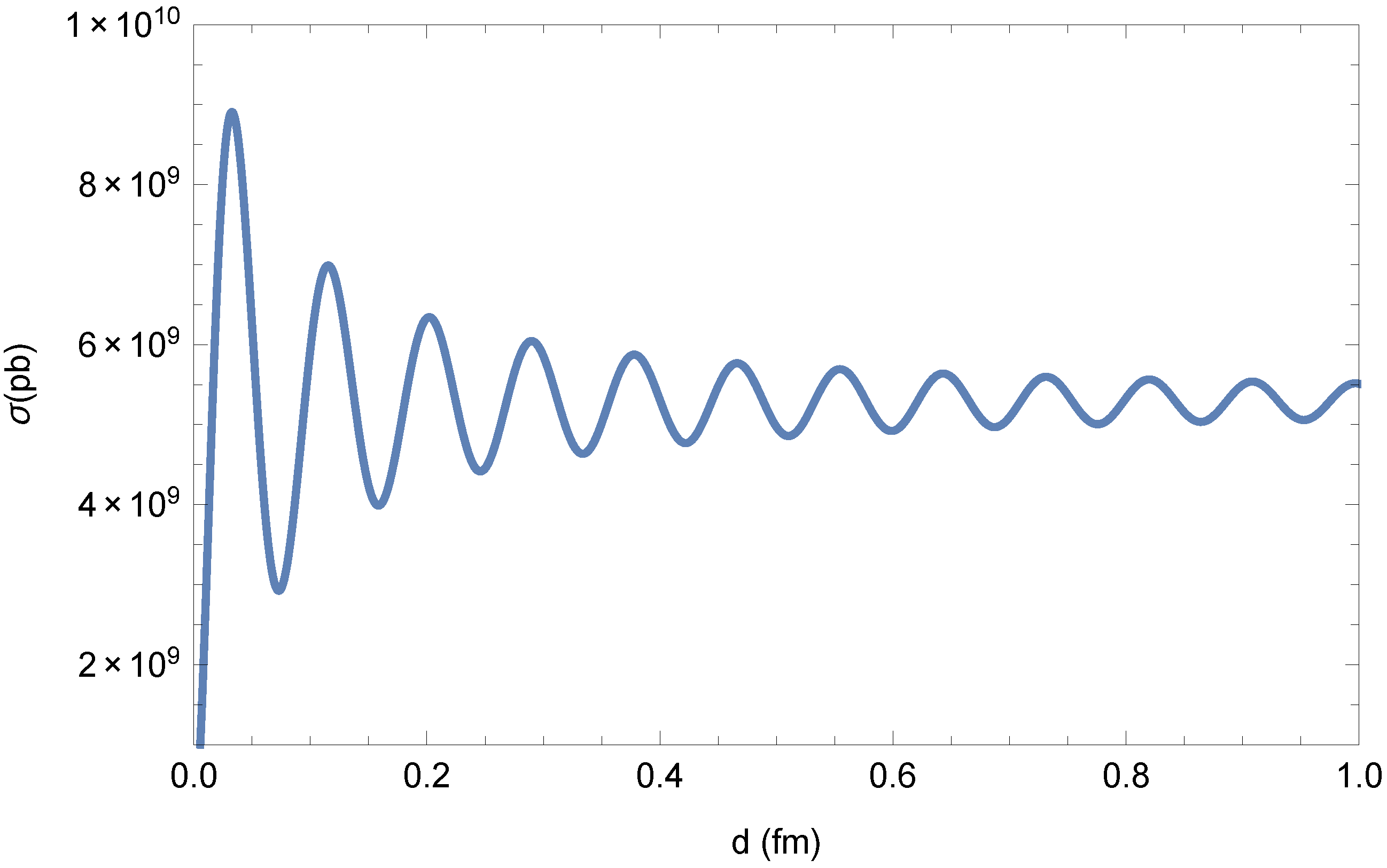
3. Ion and Proton Scattering on Monopole–Antimonopole Pairs
Scattering of Charged Particles by a Magnetic Dipole
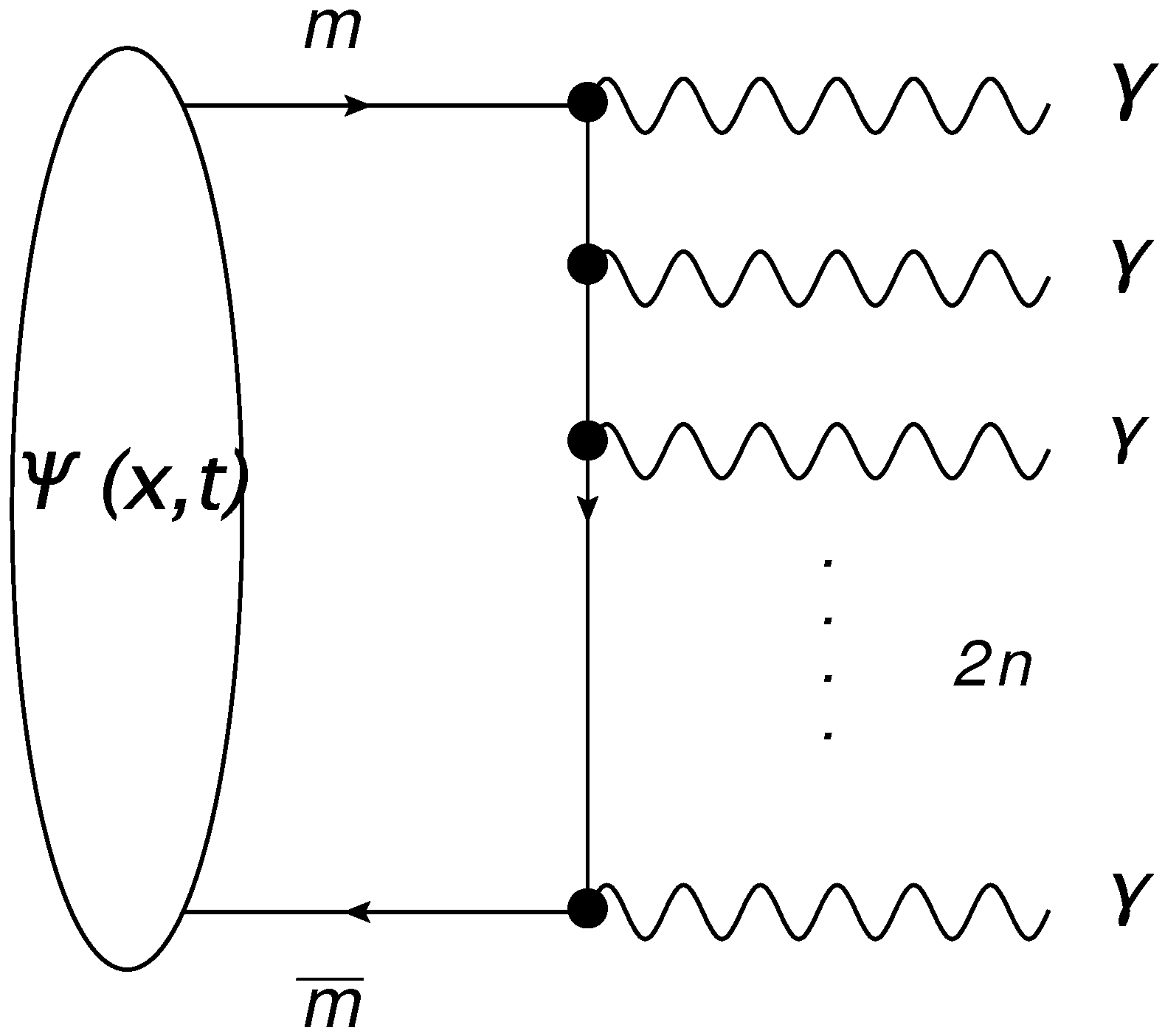
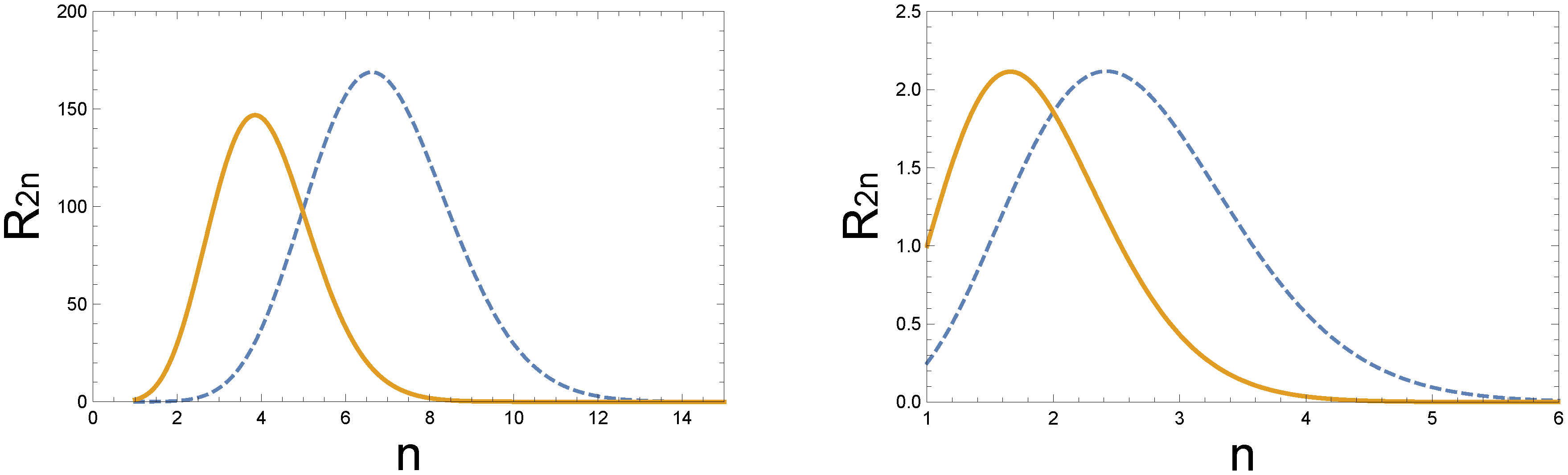
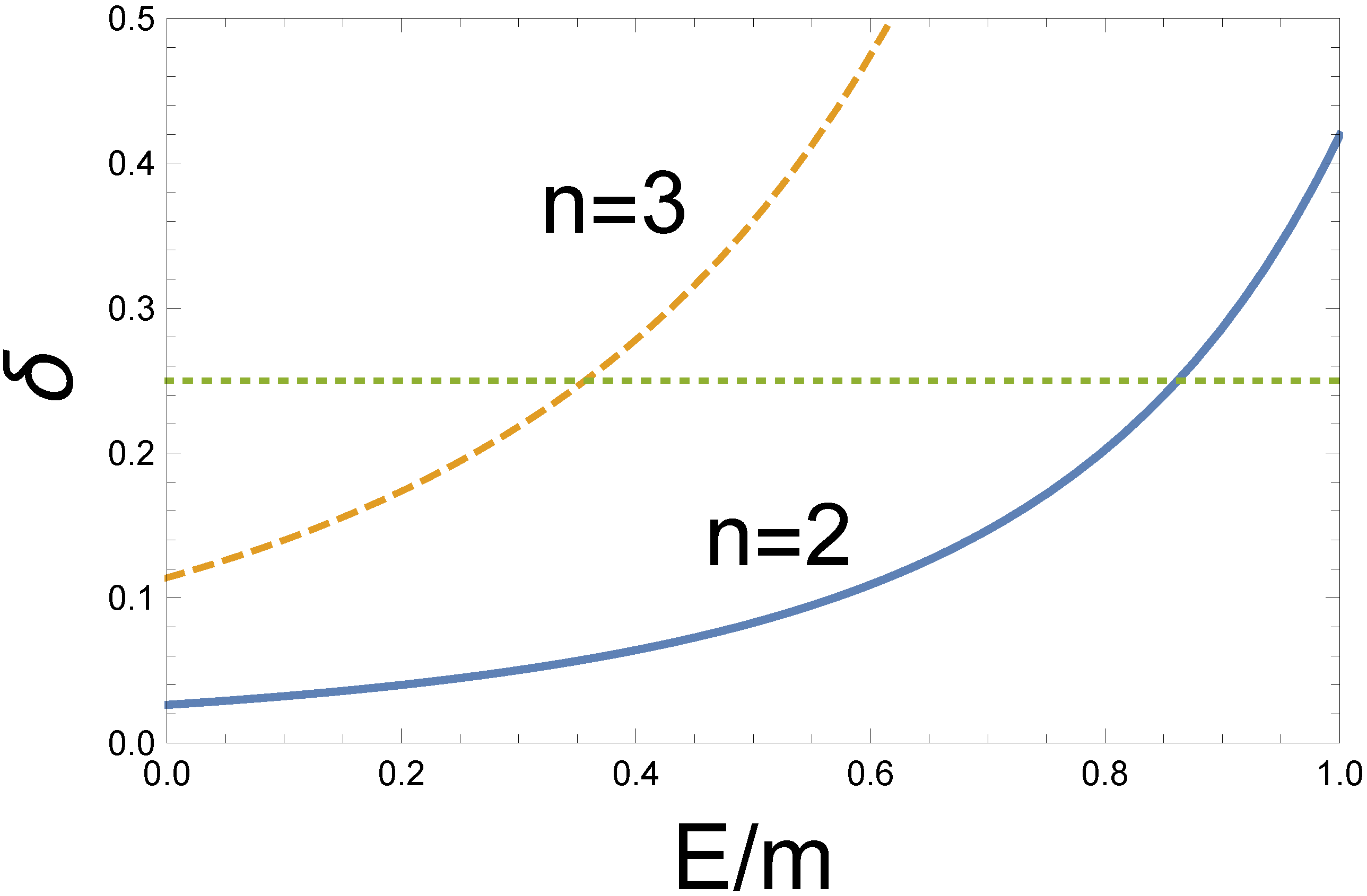
4. Monopole–Antimonopole Disintegration into Many Photons
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Dirac, P.A.M. Quantised singularities in the electromagnetic field. Proc. R. Soc. Lond. A 1931, 133, 60–72. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Theory of magnetic poles. Phys. Rev. 1948, 74, 817. [Google Scholar] [CrossRef]
- Milton, K.A. Theoretical and experimental status of magnetic monopoles. Rep. Prog. Phys. 2006, 69, 1637. [Google Scholar] [CrossRef]
- Abulencia, A.; Acosta, D.; Adelman, J.; Affolder, T.; Akimoto, T.; Albrow, M.G.; Ambrose, D.; Amerio, S.; Amidei, D.; Anastassov, A.; et al. Direct search for Dirac magnetic monopoles in collisions at = 1.96 TeV. Phys. Rev. Lett. 2006, 96, 201801. [Google Scholar] [CrossRef] [PubMed]
- Fairbairn, M.; Kraan, A.C.; Milstead, D.A.; Sjostrand, T.; Skands, P.Z.; Sloan, T. Stable massive particles at colliders. Phys. Rep. 2007, 438, 1–63. [Google Scholar] [CrossRef]
- Bbiendi, G.; Ainsley, C.; Åkesson, P.F.; Alexander, G.; Anagnostou, G.; Anderson, K.J.; Asai, S.; Axen, D.; Bailey, I.; Barberio, E.; et al. Search for Dirac magnetic monopoles in e+e- collisions with the OPAL detector at LEP2. Phys. Lett. B 2008, 663, 37–42. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for magnetic monopoles in = 7 TeV pp collisions with the ATLAS detector. Phys. Rev. Lett. 2012, 109, 261803. [Google Scholar] [CrossRef] [PubMed]
- ATLAS Collaboration. Search for magnetic monopoles and stable particles with high electric charges in 8 TeV pp collisions with the ATLAS detector. Phys. Rev. D 2016, 93, 052009. [Google Scholar] [CrossRef]
- Lenz, T. Searches for long-lived and highly-ionizing particles at the CMS and ATLAS experiments. PoS LHCP 2016, 2016, 104–113. [Google Scholar]
- Acharya, B.; Alexandre, J.; Bernabéu, J.; Campbell, M.; Cecchini, S.; Chwastowski, J.; De Montigny, D.; Derendarz, A.; De Roeck, J.R.; Ellis, M.; et al. The Physics Programme of the MoEDAL Experiment at the LHC. Int. J. Mod. Phys. A 2014, 29, 1430050. [Google Scholar] [CrossRef]
- Acharya, B.; Alexandre, J.; Bendtz, K.; Benes, P.; Bernabéu, J.; Campbell, M.; Cecchini, S.; Chwastowski, J.; Chatterjee, A.; de Montigny, M.; et al. Search for magnetic monopoles with the MoEDAL prototype trapping detector in 8 TeV proton-proton collisions at the LHC. J. High Energy Phys. 2016, 2016, 67. [Google Scholar] [CrossRef]
- Acharya, B.; Alexandre, J.; Baines, S.; Benes, P.; Bergmann, B.; Bernabéu, J.; Branzas, H.; Campbell, M.; Caramete, L.; Cecchini, S.; et al. Search for Magnetic Monopoles with the MoEDAL Forward Trapping Detector in 13 TeV Proton-Proton Collisions at the LHC. Phys. Rev. Lett. 2017, 118, 061801. [Google Scholar] [CrossRef] [PubMed]
- Acharya, B.; Alexandre, J.; Baines, S.; Benes, P.; Bergmann, B.; Bernabéu, J.; Branzas, H.; Campbell, M.; Caramete, L.; Cecchini, S.; et al. Search for magnetic monopoles with the MoEDAL forward trapping detector in 2.11 fb−1 of 13 TeV proton-proton collisions at the LHC. Phys. Lett. B 2018, 782, 510–516. [Google Scholar] [CrossRef]
- Vento, V. Ion scattering on monopoles. arXiv, 2018; arXiv:1809.04504. [Google Scholar]
- Fanchiotti, H.; Garcia Canal, C.A.; Vento, V. Multiphoton annihilation of monopolium. Int. J. Mod. Phys. A 2017, 32, 1750202. [Google Scholar] [CrossRef]
- Kazama, Y.; Yang, C.N.; Goldhaber, A.S. Scattering of a Dirac Particle with Charge Ze by a Fixed Magnetic Monopole. Phys. Rev. D 1977, 15, 2287. [Google Scholar] [CrossRef]
- Wu, T.T.; Yang, C.N. Dirac Monopole Without Strings: Monopole Harmonics. Nucl. Phys. B 1976, 107, 365–380. [Google Scholar] [CrossRef]
- Feldman, L.C.; Mayer, J.W. Fundamentals of Surface and Thin Film Analysis; North-Holland: New York, NY, USA, 1986. [Google Scholar]
- Orava, R.; Vento, V. Can we use the proton beam at LHC to detect monopoles? Unpublished work. 2018. [Google Scholar]
- McNulty, R. Central Exclusive Production at LHCb. arXiv, 2017; arXiv:1711.06668. [Google Scholar]
- Epele, L.N.; Fanchiotti, H.; Canal, C.A.G.; Mitsou, V.A.; Vento, V. Looking for magnetic monopoles at LHC with diphoton events. Eur. Phys. J. Plus 2012, 127, 60. [Google Scholar] [CrossRef]
- Weinberg, S. Lectures in Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Parzen, G. On the Scattering Theory of the Dirac Equation. Phys. Rev. 1950, 80, 261. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Khlopov, M.Y. On The Concentration Of Relic Magnetic Monopoles in the Universe. Phys. Lett. B 1978, 79, 239–241. [Google Scholar] [CrossRef]
- Hill, C.T. Monopolonium. Nucl. Phys. B 1983, 224, 469–490. [Google Scholar] [CrossRef]
- Vento, V. Hidden Dirac Monopoles. Int. J. Mod. Phys. A 2008, 23, 4023–4037. [Google Scholar] [CrossRef]
- Epele, L.N.; Fanchiotti, H.; Garcia Canal, C.A.; Vento, V. Monopolium: The Key to monopoles. Eur. Phys. J. C 2008, 56, 87–95. [Google Scholar] [CrossRef]
- Epele, L.N.; Fanchiotti, H.; Garcia Canal, C.A.; Vento, V. Can the 750 GeV enhancement be a signal of light magnetic monopoles? arXiv, 2016; arXiv:1607.05592. [Google Scholar]
- Barrie, N.D.; Sugamoto, A.; Yamashita, K. Construction of a model of monopolium and its search via multiphoton channels at LHC. Prog. Theor. Exp. Phys. 2016, 2016, 113B02. [Google Scholar] [CrossRef]
- Penin, A.A. High order QED corrections in physics of positronium. Int. J. Mod. Phys. A 2004, 19, 3897–3904. [Google Scholar] [CrossRef]
- Lepage, G.P.; Mackenzie, P.B.; Streng, K.H.; Zerwas, P.M. Multi-Photon Decays of Positronium. Phys. Rev. A 1983, 28, 3090. [Google Scholar] [CrossRef]
- Khriplovich, I.B.; Yelkhovsky, A.S. On the radiative corrections to the positronium decay rate. Phys. Lett. B 1990, 246, 520–522. [Google Scholar] [CrossRef]
- Czarnecki, A.; Karshenboim, S.G. Decays of positronium. arXiv, 1999; arXiv:hep-ph/9911410. [Google Scholar]
- Adkins, G.S.; Pfahl, E.D. Order-a radiative correction to the rate for parapositronium decay to four photons. Phys. ReV. D 1998, 59, R915. [Google Scholar] [CrossRef]
- Billoire, A.; Lacaze, R.; Morel, A.; Navelet, H. The OZI Rule Violating Radiative Decays of the Heavy Pseudoscalars. Phys. Lett. 1978, 78, 140–143. [Google Scholar] [CrossRef]
- Muta, T.; Niuya, T. Nonplanar Four Jets in Quarkonium Decays as a Probe for Three Gluon Coupling. Prog. Theor. Phys. 1982, 68, 1735–1748. [Google Scholar] [CrossRef]
- Zwanziger, D. Local Lagrangian quantum field theory of electric and magnetic charges. Phys. Rev. D 1971, 3, 880. [Google Scholar] [CrossRef]
- Patrizii, L.; Spurio, M. Status of Searches for Magnetic Monopoles. Annu. Rev. Nucl. Part. Sci. 2015, 65, 279–302. [Google Scholar] [CrossRef]
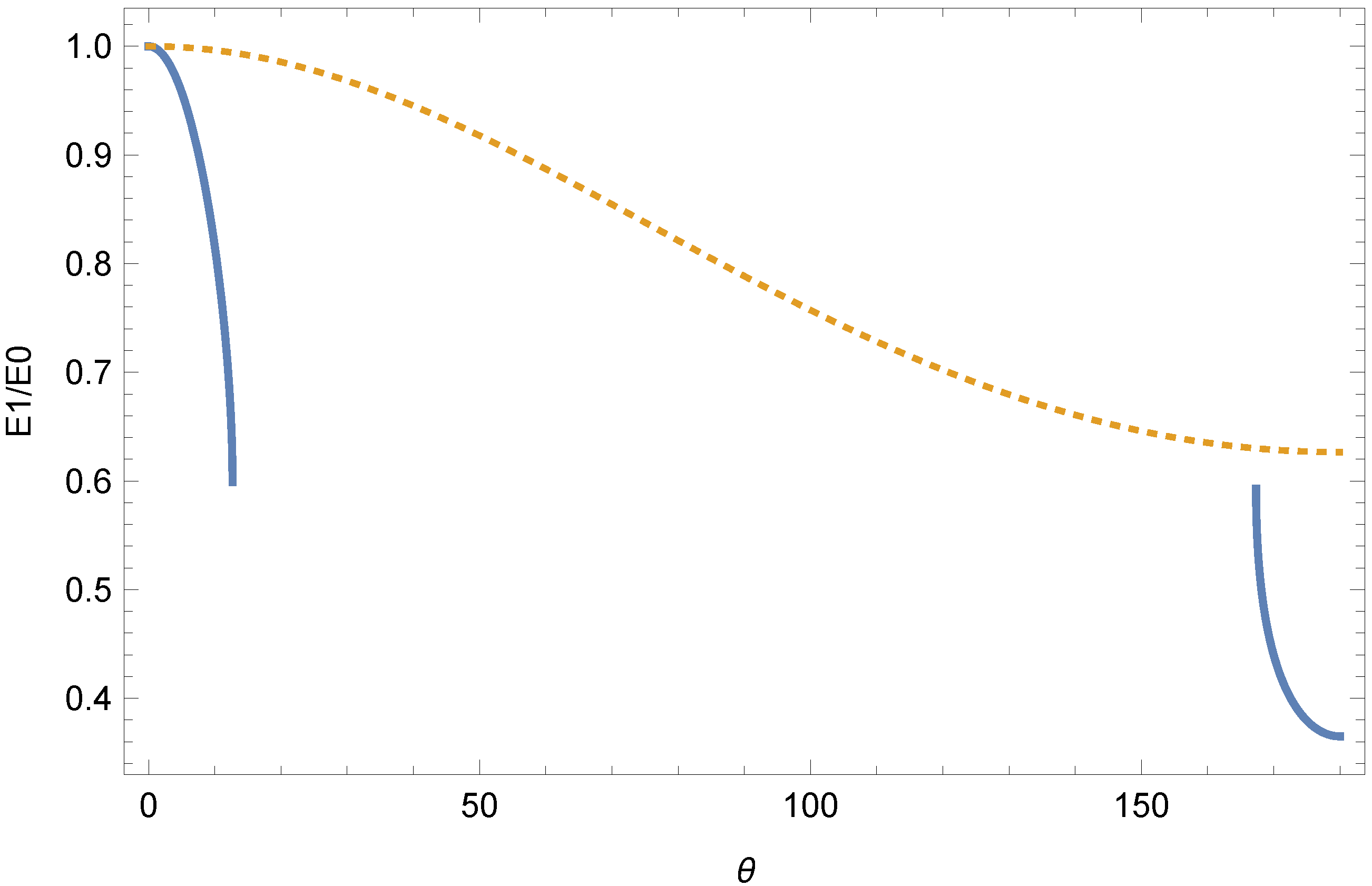

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vento, V. Ions, Protons, and Photons as Signatures of Monopoles. Universe 2018, 4, 117. https://doi.org/10.3390/universe4110117
Vento V. Ions, Protons, and Photons as Signatures of Monopoles. Universe. 2018; 4(11):117. https://doi.org/10.3390/universe4110117
Chicago/Turabian StyleVento, Vicente. 2018. "Ions, Protons, and Photons as Signatures of Monopoles" Universe 4, no. 11: 117. https://doi.org/10.3390/universe4110117
APA StyleVento, V. (2018). Ions, Protons, and Photons as Signatures of Monopoles. Universe, 4(11), 117. https://doi.org/10.3390/universe4110117




