Lévy Femtoscopy with PHENIX at RHIC
Abstract
:1. Introduction
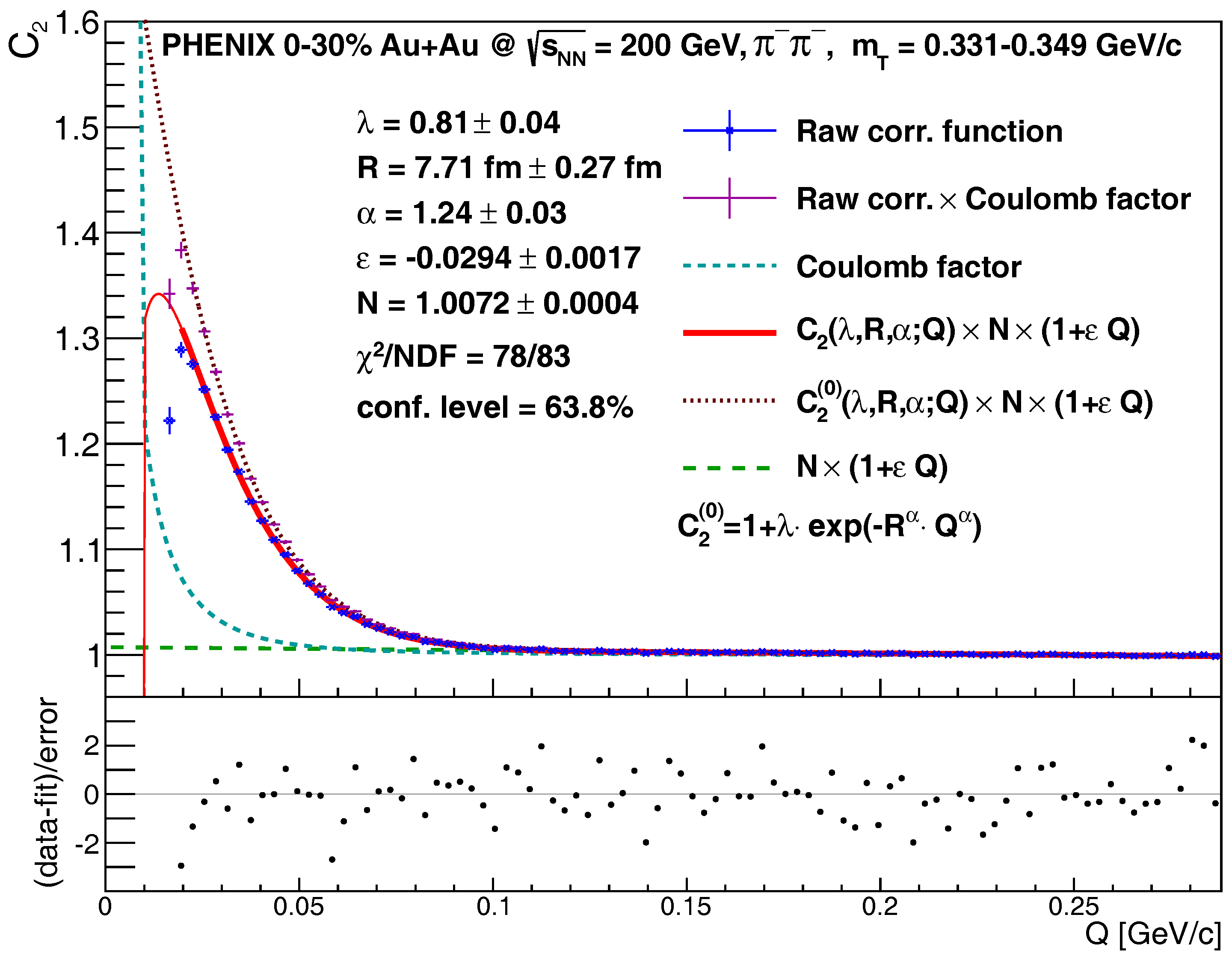
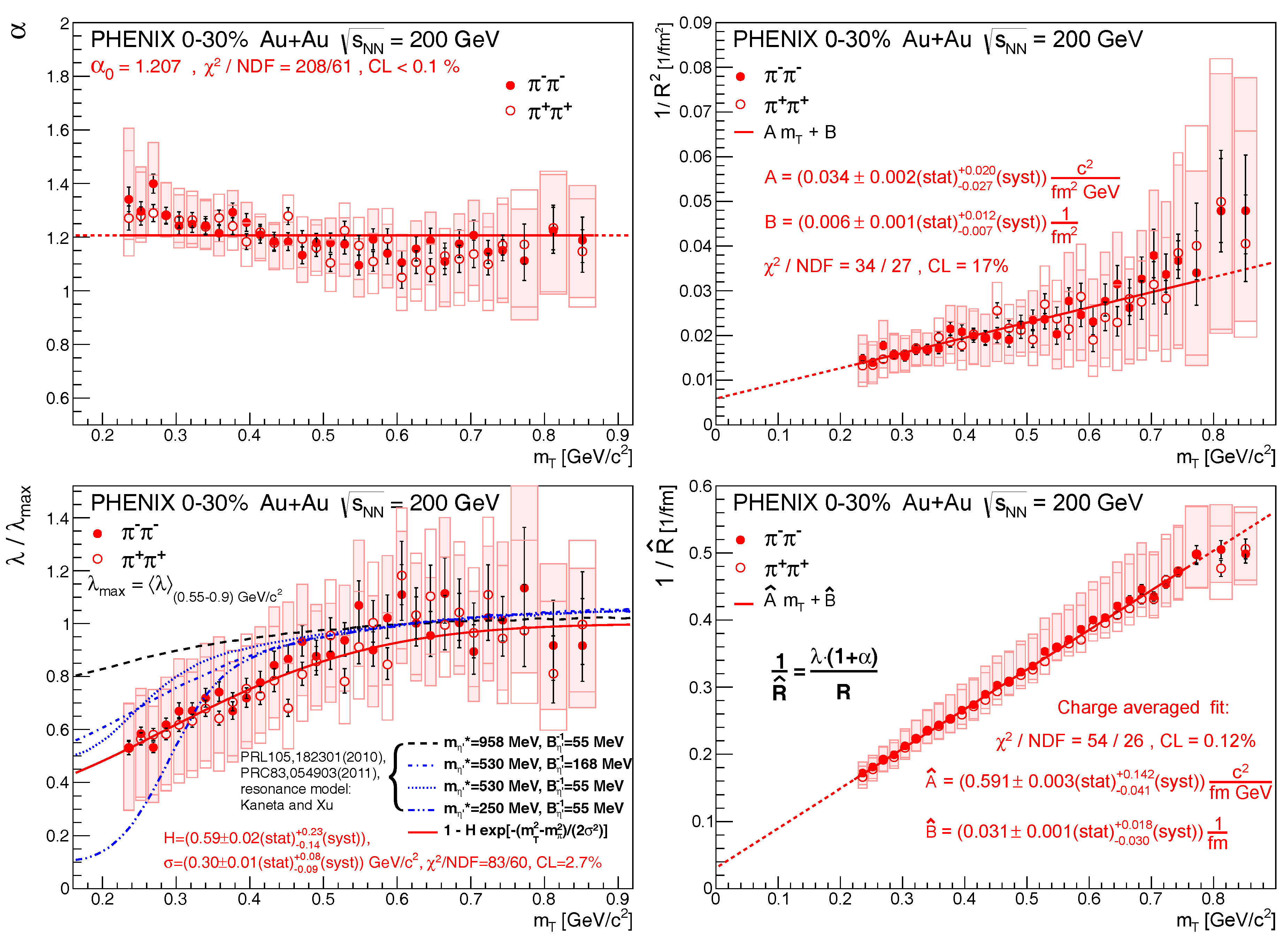
2. Results
Acknowledgments
Conflicts of Interest
References
- Adcox, K.; Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Becker, B.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Hanbury Brown, R.; Twiss, R.Q. A Test of a new type of stellar interferometer on Sirius. Nature 1956, 178, 1046–1048. [Google Scholar] [CrossRef]
- Goldhaber, G.; Fowler, W.B.; Goldhaber, S.; Hoang, T.F. Pion-pion correlations in antiproton annihilation events. Phys. Rev. Lett. 1959, 3, 181–183. [Google Scholar] [CrossRef]
- Goldhaber, G.; Goldhaber, S.; Lee, W.Y.; Pais, A. Influence of Bose-Einstein statistics on the antiproton proton annihilation process. Phys. Rev. 1960, 120, 300–312. [Google Scholar] [CrossRef]
- Yano, F.B.; Koonin, S.E. Determining Pion Source Parameters in Relativistic Heavy Ion Collisions. Phys. Lett. B 1978, 78, 556–559. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Bose-Einstein correlations of charged pion pairs in Au + Au collisions at s(NN)**(1/2) = 200 GeV. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef] [PubMed]
- Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; Armendariz, R.; Aronson, S.H.; et al. Kaon interferometric probes of space-time evolution in Au + Au collisions at s(NN)**(1/2) = 200 GeV. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Makhlin, A.N.; Sinyukov, Y.M. The hydrodynamics of hadron matter under a pion interferometric microscope. Z. Phys. C 1988, 39, 69–73. [Google Scholar] [CrossRef]
- Csörgő, T.; Lörstad, B. Bose-Einstein Correlations for Three-Dimensionally Expanding, Cylindrically Symmetric, Finite Systems. Phys. Rev. C 1996, 54, 1390–1403. [Google Scholar] [CrossRef]
- Adare, A.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Alexander, J.; Alfred, M.; Al-Ta’ani, H.; Angerami, A.; Aoki, K.; et al. Lévy-stable two-pion Bose-Einstein correlations in GeV Au+Au collisions. arXiv, 2017; arXiv:1709.05649. [Google Scholar]
- Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; Armendariz, R.; Aronson, S.H.; et al. Source breakup dynamics in Au + Au Collisions at s(NN)**(1/2) = 200 GeV via three-dimensional two-pion source imaging. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Evidence for a long-range component in the pion emission source in Au + Au collisions at s(NN)**(1/2) = 200 GeV. Phys. Rev. Lett. 2007, 98. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Barkai, E.; Klafter, J. Anomalous Diffusion and Relaxation Close to Thermal Equilibrium: A Fractional Fokker-Planck Equation Approach. Phys. Rev. Lett. 1999, 82, 3563–3567. [Google Scholar] [CrossRef]
- Csörgő, T.; Hegyi, S.; Zajc, W.A. Bose-Einstein correlations for Levy stable source distributions. Eur. Phys. J. C 2004, 36, 67–78. [Google Scholar] [CrossRef]
- Csanád, M.; Csörgő, T.; Nagy, M. Anomalous diffusion of pions at RHIC. Braz. J. Phys. 2007, 37, 1002–1013. [Google Scholar] [CrossRef]
- Csörgő, T. Correlation Probes of a QCD Critical Point. arXiv, 2008; arXiv:0903.0669. [Google Scholar]
- El-Showk, S.; Paulos, M.F.; Poland, D.; Rychkov, S.; Simmons-Duffin, D.; Vichi, A. Solving the 3D Ising Model with the Conformal Bootstrap II. c-Minimization and Precise Critical Exponents. J. Stat. Phys. 2014, 157, 869–914. [Google Scholar] [CrossRef]
- Rieger, H. Critical behavior of the three-dimensional random-field Ising model: Two-exponent scaling and discontinuous transition. Phys. Rev. B 1995, 52, 6659–6667. [Google Scholar] [CrossRef]
- Halasz, M.A.; Jackson, A.D.; Shrock, R.E.; Stephanov, M.A.; Verbaarschot, J.J.M. On the phase diagram of QCD. Phys. Rev. D 1998, 58. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Signatures of the tricritical point in QCD. Phys. Rev. Lett. 1998, 81, 4816–4819. [Google Scholar] [CrossRef]
- Vance, S.E.; Csörgő, T.; Kharzeev, D. Partial U(A)(1) restoration from Bose-Einstein correlations. Phys. Rev. Lett. 1998, 81, 2205–2208. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Kharzeev, D.; McLerran, L.D. The Return of the prodigal Goldstone boson. Phys. Rev. D 1996, 53, 5028–5033. [Google Scholar] [CrossRef]
- Novák, T.; Csörgő, T.; Eggers, H.C.; de Kock, M. Model independent analysis of nearly Lévy correlations. Acta Phys. Pol. Suppl. 2016, 9, 289. [Google Scholar] [CrossRef]
- Kincses, D. PHENIX results on Lévy analysis of Bose-Einstein correlation functions. Acta Phys. Pol. Suppl. 2017, 10, 627–632. [Google Scholar]
- Vértesi, R.; Csörgő, T.; Sziklai, J. Significant in-medium η’ mass reduction in GeV Au + Au collisions at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C 2011, 83. [Google Scholar] [CrossRef]
- Kaneta, M.; Xu, N. Centrality dependence of chemical freeze-out in Au + Au collisions at RHIC (QM2004 proceedings). arXiv, 2004; arXiv:nucl-th/0405068. [Google Scholar]
| 1. |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csanád, M. Lévy Femtoscopy with PHENIX at RHIC. Universe 2017, 3, 85. https://doi.org/10.3390/universe3040085
Csanád M. Lévy Femtoscopy with PHENIX at RHIC. Universe. 2017; 3(4):85. https://doi.org/10.3390/universe3040085
Chicago/Turabian StyleCsanád, Máté. 2017. "Lévy Femtoscopy with PHENIX at RHIC" Universe 3, no. 4: 85. https://doi.org/10.3390/universe3040085
APA StyleCsanád, M. (2017). Lévy Femtoscopy with PHENIX at RHIC. Universe, 3(4), 85. https://doi.org/10.3390/universe3040085





