Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations
Abstract
:1. Introduction
2. Matter under Extreme Conditions
3. Phases of QCD Matter
3.1. The Role of the QCD Ground State
3.2. Strongly Interacting Quark–Gluon Plasma
3.3. QCD at High Temperatures and Vanishing Chemical Potentials
3.3.1. Softest Point in the EoS of Deconfined QCD Matter
3.3.2. Testing the Properties of the Medium with Infinitely Heavy Static Test Charges
3.4. QCD at High Temperatures and Non-Zero Chemical Potentials
4. Study of Hot and Dense Nuclear Matter Using Nuclear Collisions
4.1. Heavy Ion Accelerators
4.2. Heavy Ion Collisions as a Source of Strong Electromagnetic Fields
Quark–Gluon Plasma in a Strong Magnetic Field
4.3. Transport Models
4.3.1. Elements of Relativistic Hydrodynamics
4.3.2. Blast Wave Parametrization
4.4. Initial State Description of Nuclear and Hadronic Interactions
4.4.1. Glauber Model
4.4.2. QCD Scattering in the Dipole Picture: Initial-State Energy Loss and Shadowing
4.4.3. Color Glass Condensate
4.4.4. Other Initial State Models
5. Experimental Signatures of Deconfined QCD Matter
5.1. Bulk Observables
5.2. Hard Probes
5.2.1. High- Hadrons and Jets
5.2.2. Quarkonia
5.3. Penetrating Probes
6. New Developments
6.1. Search for the Critical Point of QCD Phase Diagram
6.2. Collectivity in Small Systems
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Collins, J.C.; Perry, M.J. Superdense Matter: Neutrons or Asymptotically Free Quarks? Phys. Rev. Lett. 1975, 34, 1353. [Google Scholar] [CrossRef]
- Cabibbo, N.; Parisi, G. Exponential hadronic spectrum and quark liberation. Phys. Lett. B 1975, 59, 67–69. [Google Scholar] [CrossRef]
- Gell-Mann, M. A Schematic Model of Baryons and Mesons. Phys. Lett. 1964, 8, 214–215. [Google Scholar] [CrossRef]
- Zweig, G. An SU(3) Model for Strong Interaction Symmetry and Its Breaking. Version 1. CERN-TH-401. Available online: http://inspirehep.net/record/11881/files/CM-P00042883.pdf (accessed on 17 January 2017).
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. B 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Nambu, Y. The Confinement of Quarks. Sci. Am. 1976, 235, 48–70. [Google Scholar] [CrossRef]
- Yagi, K.; Hatsuda, T.; Miake, Y. Quark-Gluon Plasma: From Big Bang to Little Bang (Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology); Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Schmidt, H.R.; Schukraft, J. The Physics of ultrarelativistic heavy ion collisions. J. Phys. G 1993, 19, 1705–1795. [Google Scholar] [CrossRef]
- Stock, R. Nucleus-Nucleus Collisions and the QCD Matter Phase Diagram. In Landolt-Börnstein—Group I Elementary Particles, Nuclei and Atoms, Vol. 21A, Chapter 7; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Schukraft, J.; Stock, R. Toward the Limits of Matter: Ultra-Relativistic Nuclear Collisions at CERN; World Scientific: Singapore, 2015. [Google Scholar]
- Heinz, U.W.; Jacob, M. Evidence for a New State of Matter: An Assessment of the Results from the CERN Lead Beam Program; Theoretical Physics Division: Geneva, Switzerland, 2000. [Google Scholar]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Becker, B.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Adcox, K.; Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Gyulassy, M.; McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30–63. [Google Scholar] [CrossRef]
- Kapusta, J.; Müller, B.; Rafelski, J. Quark-Gluon Plasma: Theoretical Foundations. An Annotated Reprint Collection; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Csernai, L.P. Introduction to Relativistic Heavy Ion Collisions; Wiley: Chichester, UK, 1994. [Google Scholar]
- Letessier, J.; Rafelski, J. Hadrons and Quark-Gluon Plasma; Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Vogt, R. Ultrarelativistic Heavy-Ion Collisions; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Florkowski, W. Phenomenology of Ultra-Relativistic Heavy-Ion Collisions; World Scientific: Singapore, 2010. [Google Scholar]
- Rak, J.; Tannenbaum, M.J. High pT Physics in the Heavy Ion Era; Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Braun-Munzinger, P.; Stachel, J. The quest for the quark-gluon plasma. Nature 2007, 448, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Shuryak, E. Physics of Strongly coupled Quark-Gluon Plasma. Prog. Part. Nucl. Phys. 2009, 62, 48–101. [Google Scholar] [CrossRef]
- Sarkar, S.; Satz, H.; Sinha, B. The physics of the quark-gluon plasma. Lect. Notes Phys. 2010, 785, 1–369. [Google Scholar]
- Florkowski, W. Basic phenomenology for relativistic heavy-ion collisions. Acta Phys. Pol. B 2014, 45, 2329–2354. [Google Scholar] [CrossRef]
- Roland, G.; Safarik, K.; Steinberg, P. Heavy-ion collisions at the LHC. Prog. Part. Nucl. Phys. 2014, 77, 70–127. [Google Scholar] [CrossRef]
- Nouicer, R. New State of Nuclear Matter: Nearly Perfect Fluid of Quarks and Gluons in Heavy Ion Collisions at RHIC Energies. Eur. Phys. J. Plus 2016, 131, 70. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High-Temperature Hydrodynamics Phenomena; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar]
- Fortov, V.I. Extreme States of Matter on Earth and in the Cosmos; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of stars. Physik. Zeits. Sowjetunion 1932, 1, 285–288. [Google Scholar]
- Zeldovich, Y.B. The equation of state at ultrahigh densities and its relativistic limitations. J. Exp. Theor. Phys. 1962, 14, 1143–1147. [Google Scholar]
- Baym, G.; Chin, S.A. Can a neutron star be a giant MIT bag? Phys. Lett. B 1976, 62, 241–244. [Google Scholar] [CrossRef]
- Gamow, G. Expanding universe and the origin of elements. Phys. Rev. 1946, 70, 572–573. [Google Scholar] [CrossRef]
- Penzias, A.A.; Wilson, R.W. A Measurement of excess antenna temperature at 4080-Mc/s. Astrophys. J. 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Sakharov, A.D. Maximum temperature of thermal radiation. JETP Lett. 1966, 3, 288–289. [Google Scholar]
- Huang, K.; Weinberg, S. Ultimate temperature and the early universe. Phys. Rev. Lett. 1970, 25, 895–897. [Google Scholar] [CrossRef]
- Hagedorn, R. Statistical thermodynamics of strong interactions at high-energies. Nuovo Cim. Suppl. 1965, 3, 147–186. [Google Scholar]
- Rafelski, J. Melting Hadrons, Boiling Quarks—From Hagedorn Temperature to Ultra-Relativistic Heavy-Ion Collisions at CERN: With a Tribute to Rolf Hagedorn; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Majumder, A.; Muller, B. Hadron mass spectrum from lattice QCD. Phys. Rev. Lett. 2010, 105, 252002. [Google Scholar] [CrossRef] [PubMed]
- Zeldovich, Y.B. The hot model of the universe and the elementary particles. Acta Phys. Hung. 1967, 22, 51–58. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. Hot model of Universe. Sov. Phys. Uspechi 1967, 9, 602–617. [Google Scholar] [CrossRef]
- Linde, A.D. Phase Transitions in Gauge Theories and Cosmology. Rep. Prog. Phys. 1979, 42, 389–437. [Google Scholar] [CrossRef]
- Bailin, D.; Love, A. Cosmology in Gauge Field Theory and String Theory; IOP: Bristol, UK, 2004. [Google Scholar]
- Boyanovsky, D.; de Vega, H.J.; Schwarz, D.J. Phase transitions in the early and the present universe. Ann. Rev. Nucl. Part. Sci. 2006, 56, 441–500. [Google Scholar] [CrossRef]
- Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 1999, 71, 1463–1500. [Google Scholar] [CrossRef]
- Kajantie, K.; Laine, M.; Rummukainen, K.; Shaposhnikov, M.E. Is there a hot electroweak phase transition at m(H) larger or equal to m(W)? Phys. Rev. Lett. 1996, 77, 2887–2890. [Google Scholar] [CrossRef] [PubMed]
- Susskind, L. Lattice Models of Quark Confinement at High Temperature. Phys. Rev. D 1979, 20, 2610–2618. [Google Scholar] [CrossRef]
- Petreczky, P. Lattice QCD at non-zero temperature. J. Phys. G 2012, 39, 093002. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, T.; Buchoff, M.I.; Christ, N.H.; Ding, H.-T.; Gupta, R.; Jung, C.; Karsch, F.; Lin, Z.; Mawhinney, R.; McGlynn, G.; et al. QCD Phase Transition with Chiral Quarks and Physical Quark Masses. Phys. Rev. Lett. 2014, 113, 082001. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.; Christ, N.H.; Datta, S.; van der Heide, J.; Jung, C.; Karsch, F.; Kaczmarek, O.; Laermann, E.; Mawhinney, R.D.; Miao, C.; et al. QCD equation of state with almost physical quark masses. Phys. Rev. D 2008, 77, 014511. [Google Scholar] [CrossRef]
- Rischke, D. The Quark-Gluon Plasma in Equilibrium. Prog. Part. Nucl. Phys. 2004, 52, 197–296. [Google Scholar] [CrossRef]
- McLerran, L.; Pisarski, R.D. Phases of Dense Quarks at Large N_c. Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barnby, L.S.; Baumgart, S.; et al. An Experimental Exploration of the QCD Phase Diagram: The Search for the Critical Point and the Onset of De-confinement. arXiv, 2010; arXiv:1007.2613. [Google Scholar]
- Itoh, N. Concept of quark matter was mentioned as early as 1970 by Itoh in the context of neutron stars. Prog. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Shuryak, E.V. Theory of Hadronic Plasma. Sov. Phys. JETP 1978, 47, 212–219. [Google Scholar]
- Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017–1059. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Koch, V.; Schäfer, T.; Stachel, J. Properties of hot and dense matter from relativistic heavy ion collisions. Phys. Rep. 2016, 621, 76–126. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Wambach, J. The Phase Diagram of Strongly-Interacting Matter. Rev. Mod. Phys. 2009, 81, 1031–1050. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rept. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Bailin, D.; Love, A. Superfluidity and Superconductivity in Relativistic Fermion Systems. Phys. Rep. 1984, 107, 325–385. [Google Scholar] [CrossRef]
- Buballa, M.; Hosek, J.; Oertel, M. Anisotropic admixture in color superconducting quark matter. Phys. Rev. Lett. 2003, 90, 182002. [Google Scholar] [CrossRef] [PubMed]
- Alford, M.G.; Rajagopal, K.; Wilczek, F. Color flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef]
- Becker, W. Neutron Stars and Pulsars; Springer: Berlin, Germany, 2009. [Google Scholar]
- Migdal, A.B. Pion Fields in Nuclear Matter. Rev. Mod. Phys. 1978, 50, 107–172. [Google Scholar] [CrossRef]
- D’Enterria, D.; Ballintijn, M.; Bedjidian, M.; Hofman, D.; Kodolova, O.; Loizides, C.; Lokthin, I.P.; Lourenço, C.; Mironov, C.; et al. CMS physics technical design report: Addendum on high density QCD with heavy ions. J. Phys. G 2007, 34, 2307. [Google Scholar]
- Water Structure and Science. Available online: http://www1.lsbu.ac.uk/water/water_phase_diagram.html (accessed on 17 January 2017).
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics. Theoretical Foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics: Applications. Nucl. Phys. B 1979, 147, 448–518. [Google Scholar] [CrossRef]
- Schäfer, T.; Shuryak, E.V. Instantons in QCD. Rev. Mod. Phys. 1998, 70, 323–426. [Google Scholar] [CrossRef]
- Diakonov, D. Instantons at work. Prog. Part. Nucl. Phys. 2003, 51, 173–222. [Google Scholar] [CrossRef]
- Diakonov, D. Topology and confinement. Nucl. Phys. Proc. Suppl. 2009, 195, 5–45. [Google Scholar] [CrossRef]
- Belavin, A.A.; Polyakov, A.M.; Schwartz, A.S.; Tyupkin, Y.S. Pseudoparticle Solutions of the Yang-Mills Equations. Phys. Lett. B 1975, 59, 85–87. [Google Scholar] [CrossRef]
- Vainshtein, A.I.; Zakharov, V.I.; Novikov, V.A.; Shifman, M.A. ABC’s of Instantons. Sov. Phys. Usp. 1982, 25, 195–215. [Google Scholar] [CrossRef]
- Matinyan, S.G.; Savvidy, G.K. Vacuum Polarization Induced by the Intense Gauge Field. Nucl. Phys. B 1978, 134, 539–545. [Google Scholar] [CrossRef]
- Pasechnik, R. Quantum Yang–Mills Dark Energy. Universe 2016, 2, 4. [Google Scholar] [CrossRef]
- Pasechnik, R.; Beylin, V.; Vereshkov, G. Dark Energy from graviton-mediated interactions in the QCD vacuum. J. Cosmol. Astropart. Phys. 2013, 1306, 11. [Google Scholar] [CrossRef]
- Pasechnik, R.; Beylin, V.; Vereshkov, G. Possible compensation of the QCD vacuum contribution to the dark energy. Phys. Rev. D 2013, 88, 023509. [Google Scholar] [CrossRef]
- Pasechnik, R.; Prokhorov, G.; Teryaev, O. Mirror QCD and Cosmological Constant. arXiv, 2016; arXiv:1609.09249. [Google Scholar]
- Pagels, H.; Tomboulis, E. Vacuum of the Quantum Yang-Mills Theory and Magnetostatics. Nucl. Phys. B 1978, 143, 485–502. [Google Scholar] [CrossRef]
- Prokhorov, G.; Pasechnik, R.; Vereshkov, G. Dynamics of wave fluctuations in the homogeneous Yang-Mills condensate. J. High Energy Phys. 2014, 2014, 3. [Google Scholar]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality dependence of π, K, p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Two- and three-pion quantum statistics correlations in Pb-Pb collisions at = 2.76 TeV at the CERN Large Hadron Collider. Phys. Rev. C 2014, 89, 024911. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Multipion Bose-Einstein correlations in pp, p-Pb, and Pb-Pb collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2016, 93, 054908. [Google Scholar] [CrossRef]
- Petrán, M.; Letessier, J.; Petráček, V.; Rafelski, J. Hadron production and quark-gluon plasma hadronization in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 034907. [Google Scholar] [CrossRef]
- Csorgo, T.; Csernai, L.P. Quark-gluon plasma freezeout from a supercooled state? Phys. Lett. B 1994, 333, 494–499. [Google Scholar] [CrossRef]
- Shuryak, E. Heavy Ion Collisions: Achievements and Challenges. arXiv, 2014; arXiv:1412.8393. [Google Scholar]
- Blaizot, J.P.; Gelis, F.; Liao, J.F.; McLerran, L.; Venugopalan, R. Bose-Einstein Condensation and Thermalization of the Quark Gluon Plasma. Nucl. Phys. A 2012, 873, 68–80. [Google Scholar] [CrossRef]
- Begun, V.; Florkowski, W.; Rybczynski, M. Explanation of hadron transverse-momentum spectra in heavy-ion collisions at = 2.76 TeV within chemical non-equilibrium statistical hadronization model. Phys. Rev. C 2014, 90, 014906. [Google Scholar] [CrossRef]
- Begun, V.; Florkowski, W.; Rybczynski, M. Transverse-momentum spectra of strange particles produced in Pb+Pb collisions at = 2.76 TeV in the chemical non-equilibrium model. Phys. Rev. C 2014, 90, 054912. [Google Scholar] [CrossRef]
- Begun, V.; Florkowski, W. Bose-Einstein condensation of pions in heavy-ion collisions at the CERN Large Hadron Collider (LHC) energies. Phys. Rev. C 2015, 91, 054909. [Google Scholar] [CrossRef]
- Begun, V. Fluctuations as a test of chemical non-equilibrium at the LHC. Phys. Rev. C 2016, 94, 054904. [Google Scholar] [CrossRef]
- Plumer, M.; Raha, S.; Weiner, R.M. How Free Is The Quark-Gluon-Plasma? Nucl. Phys. A 1984, 418, 549C–557C. [Google Scholar] [CrossRef]
- Rischke, D.H.; Gorenstein, M.I.; Schafer, A.; Stoecker, H.; Greiner, W. Nonperturbative effects in the SU(3) gluon plasma. Phys. Lett. B 1992, 278, 19–23. [Google Scholar] [CrossRef]
- Bannur, V.M. Equation of state for a nonideal quark gluon plasma. Phys. Lett. B 1995, 362, 7–10. [Google Scholar] [CrossRef]
- Thoma, M.H. The quark–gluon plasma liquid. J. Phys. G 2005, 31, L7–L11. [Google Scholar] [CrossRef]
- Bannur, V.M. Strongly coupled quark gluon plasma (SCQGP). J. Phys. G 2006, 32, 993–1002. [Google Scholar] [CrossRef]
- Bonitz, M.; Henning, C.; Block, D. Complex plasmas: A laboratory for strong correlations. Rep. Prog. Phys. 2010, 73, 066501. [Google Scholar] [CrossRef]
- Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008, 80, 1215–1274. [Google Scholar] [CrossRef]
- Cao, C.; Elliott, E.; Joseph, J.; Wu, H.; Petricka, J.; Schäfer, T.; Thomas, J.E. Universal Quantum Viscosity in a Unitary Fermi Gas. Science 2011, 331, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.V.; Steinberg, P. What black holes teach about strongly coupled particles. Phys. Today 2010, 63, 29–33. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef] [PubMed]
- Schafer, T.; Teaney, D. Nearly Perfect Fluidity: From Cold Atomic Gases to Hot Quark Gluon Plasmas. Rep. Prog. Phys. 2009, 72, 126001. [Google Scholar] [CrossRef]
- Thomas, J.E. The nearly perfect Fermi gas. Phys. Today 2010, 63, 34–37. [Google Scholar] [CrossRef]
- Gupta, S. Analyticity and the phase diagram of QCD. Phys. Lett. B 2004, 588, 136–144. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; Laermann, E.; et al. Equation of state in ( 2+1 )-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1; Pergamon Press: London, UK, 1980. [Google Scholar]
- Shuryak, E.V.; Zhirov, O.V. Is the explosion of a quark-gluon plasma found? Phys. Lett. B 1986, 171, 99–102. [Google Scholar] [CrossRef]
- Hung, C.M.; Shuryak, E.V. Hydrodynamics near the QCD phase transition: Looking for the longest-lived fireball. Phys. Rev. Lett. 1995, 75, 4003. [Google Scholar] [CrossRef] [PubMed]
- Matsui, T.; Satz, H. J/ψ Suppression by Quark-Gluon Plasma Formation. Phys. Lett. B 1986, 178, 416–422. [Google Scholar] [CrossRef]
- Brambilla, N.; Eidelman, S.; Heltsley, B.K.; Vogt, R.; Bodwin, G.T.; Eichten, E.; Frawley, A.D.; Meyer, A.B.; Mitchell, R.E.; Papadimitriou, V.; et al. Heavy quarkonium: Progress, puzzles, and opportunities. Eur. Phys. J. C 2011, 71, 1534. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Katz, S.D.; Pásztor, A.; Szabó, K.K.; Török, C. Static Q pair free energy and screening masses from correlators of Polyakov loops: continuum extrapolated lattice results at the QCD physical point. J. High Energy Phys. 2015, 1504, 138. [Google Scholar] [CrossRef]
- Bazavov, A.; Petreczky, P.; Velytsky, A. Quarkonium at Finite Temperature. In Quark-gluon Plasma 4; World Scientific Publishing Company: Singapore, 2009. [Google Scholar]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Ding, H.T.; Karsch, F.; Mukherjee, S. Thermodynamics of strong-interaction matter from Lattice QCD. Int. J. Mod. Phys. E 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Scheid, W.; Muller, H.; Greiner, W. Nuclear Shock Waves in Heavy-Ion Collisions. Phys. Rev. Lett. 1974, 32, 741. [Google Scholar] [CrossRef]
- Sobel, M.I.; Bethe, H.A.; Siemens, P.J.; Bondorf, J.P. Shock waves in colliding nuclei. Nucl. Phys. A 1975, 251, 502–529. [Google Scholar] [CrossRef]
- Chapline, G.F.; Johnson, M.H.; Teller, E.; Weiss, M.S. Highly excited nuclear matter. Phys. Rev. D 1973, 8, 4302. [Google Scholar] [CrossRef]
- Nagamiya, S.; Gyulassy, M. High-energy Nuclear Collisions. Adv. Nucl. Phys. 1984, 13, 201–315. [Google Scholar] [CrossRef]
- Stock, R. Particle Production In High-Energy Nucleus Nucleus Collisions. Phys. Rep. 1986, 135, 259–315. [Google Scholar] [CrossRef]
- Lee, T.D.; Wick, G.C. Vacuum Stability and Vacuum Excitation in a Spin 0 Field Theory. Phys. Rev. D 1974, 9, 2291–2316. [Google Scholar] [CrossRef]
- Harrison, M.; Peggs, S.G.; Roser, T. The RHIC accelerator. Ann. Rev. Nucl. Part. Sci. 2002, 52, 425–469. [Google Scholar] [CrossRef]
- Evans, L.; Bryant, P. LHC Machine. J. Instrum. 2008, 3, S08001. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Jamel, A.; et al. Transverse energy production and charged-particle multiplicity at midrapidity in various systems from = 7.7 to 200 GeV. Phys. Rev. C 2016, 93, 024901. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Measurement of the pseudorapidity and centrality dependence of the transverse energy density in PbPb collisions at = 2.76 TeV. Phys. Rev. Lett. 2012, 109, 152303. [Google Scholar] [CrossRef] [PubMed]
- Mitchelll, J.T. Transverse Energy Measurements from the Beam Energy Scan in PHENIX. Nucl. Phys. A 2016, 956, 842–845. [Google Scholar] [CrossRef]
- Fischer, W.; Baltz, A.J.; Blaskiewicz, M.; Gassner, D.; Drees, K.A.; Luo, Y.; Minty, M.; Thieberger, P.; Wilinski, M.; Pshenichnov, I.A. Measurement of the total cross section of uranium-uranium collisions at = 192.8 GeV. Phys. Rev. C 2014, 89, 014906. [Google Scholar] [CrossRef]
- Fermi, E. On the Theory of the impact between atoms and electrically charged particles. Z. Phys. 1924, 29, 315–327. [Google Scholar] [CrossRef]
- Von Weizsacker, C.F. Radiation emitted in collisions of very fast electrons. Z. Phys. 1934, 88, 612–625. [Google Scholar]
- Williams, E.J. Nature of the high-energy particles of penetrating radiation and status of ionization and radiation formulae. Phys. Rev. 1934, 45, 729–730. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Baur, G.; Hencken, K.; Trautmann, D.; Sadovsky, S.; Kharlov, Y. Coherent gamma gamma and gamma-A interactions in very peripheral collisions at relativistic ion colliders. Phys. Rep. 2002, 364, 359–450. [Google Scholar] [CrossRef]
- Bertulani, C.A.; Klein, S.R.; Nystrand, J. Physics of ultra-peripheral nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2005, 55, 271–310. [Google Scholar] [CrossRef]
- Baltz, A.J.; Baur, G.; d’Enterria, D.; Frankfurt, L.; Gelis, F.; Guzey, V.; Hencken, K.; Kharlov, Y.; Klasen, M.; Klein, S.R. The Physics of Ultraperipheral Collisions at the LHC. Phys. Rep. 2008, 458, 1–171. [Google Scholar] [CrossRef]
- Klein, S.R. Ultra-peripheral Collisions at RHIC: An Experimental Overview. In Proceedings of the Initial States 2014 Conference, Napa, CA, USA, 3–7 December 2014.
- Tuchin, K. Particle production in strong electromagnetic fields in relativistic heavy-ion collisions. Adv. High Energy Phys. 2013, 2013, 490495. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Duncan, R.C.; Thompson, C. Magnetars. Sci. Am. 2003, 288N2, 24. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The effects of topological charge change in heavy ion collisions: ’Event by event P and CP violation. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef]
- Ding, H.-T.; Francis, A.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Soeldner, W. Thermal dilepton rate and electrical conductivity: An analysis of vector current correlation functions in quenched lattice QCD. Phys. Rev. D 2011, 83, 034504. [Google Scholar] [CrossRef]
- Aarts, G.; Allton, C.; Amato, A.; Giudice, P.; Hands, S.; Skullerud, J.I. Electrical conductivity of the quark-gluon plasma across the deconfinement transition. Phys. Rev. Lett. 2013, 111, 172001. [Google Scholar]
- Aarts, G.; Allton, C.; Amato, A.; Giudice, P.; Hands, S.; Skullerud, J.I. Electrical conductivity and charge diffusion in thermal QCD from the lattice. J. High Energy Phys. 2015, 1502, 186. [Google Scholar] [CrossRef]
- Filip, P. Decay of Resonaces in Strong Magnetic Field. J. Phys. Conf. Ser. 2015, 636, 012013. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; Liao, J.; Voloshin, S.A.; Wang, G. Chiral magnetic and vortical effects in high-energy nuclear collisions—A status report. Prog. Part. Nucl. Phys. 2016, 88, 1–28. [Google Scholar] [CrossRef]
- Gursoy, U.; Kharzeev, D.; Rajagopal, K. Magnetohydrodynamics, charged currents and directed flow in heavy ion collisions. Phys. Rev. C 2014, 89, 054905. [Google Scholar] [CrossRef]
- Kharzeev, D.; Pisarski, R.D.; Tytgat, M.H.G. Possibility of spontaneous parity violation in hot QCD. Phys. Rev. Lett. 1998, 81, 512–515. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Azimuthal Charged-Particle Correlations and Possible Local Strong Parity Violation. Phys. Rev. Lett. 2009, 103, 251601. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.C.; et al. Observation of charge asymmetry dependence of pion elliptic flow and the possible chiral magnetic wave in heavy-ion collisions. Phys. Rev. Lett. 2015, 114, 252302. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Beam-energy dependence of charge separation along the magnetic field in Au+Au collisions at RHIC. Phys. Rev. Lett. 2014, 113, 052302. [Google Scholar] [CrossRef] [PubMed]
- Abelev, B.; Adam, J.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; Ahammed, Z.; et al. Charge separation relative to the reaction plane in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2013, 110, 012301. [Google Scholar] [CrossRef] [PubMed]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Ero, J.; et al. Observation of charge-dependent azimuthal correlations in pPb collisions and its implication for the search for the chiral magnetic effect. arXiv, 2016; arXiv:1610.00263. [Google Scholar]
- Schlichting, S.; Pratt, S. Charge conservation at energies available at the BNL Relativistic Heavy Ion Collider and contributions to local parity violation observables. Phys. Rev. C 2011, 83, 014913. [Google Scholar] [CrossRef]
- Skokov, V.; Sorensen, P.; Koch, V.; Schlichting, S.; Thomas, J.; Voloshin, S.; Wang, G.; Yee, H.U. Chiral Magnetic Effect Task Force Report. arXiv, 2016; arXiv:1608.00982. [Google Scholar]
- Becattini, F.; Karpenko, I.; Lisa, M.; Upsal, I.; Voloshin, S. Global Hyperon Polarization at Local Thermodynamic Equilibrium with Vorticity, Magnetic Field and Feed-dow. arXiv, 2016; arXiv:1608.00982. [Google Scholar]
- Aichelin, J. ’Quantum’ molecular dynamics: A Dynamical microscopic n body approach to investigate fragment formation and the nuclear equation of state in heavy ion collisions. Phys. Rep. 1991, 202, 233–360. [Google Scholar] [CrossRef]
- Werner, K. Strings, pomerons, and the venus model of hadronic interactions at ultrarelativistic energies. Phys. Rep. 1993, 232, 87–299. [Google Scholar] [CrossRef]
- Gyulassy, M.; Wang, X.N. HIJING 1.0: A Monte Carlo program for parton and particle production in high-energy hadronic and nuclear collisions. Comput. Phys. Commun. 1994, 83, 307–331. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Humanic, T.J. Constraining a simple hadronization model of relativistic heavy ion collisions using hadronic observables. Phys. Rev. C 1998, 57, 866–876. [Google Scholar] [CrossRef]
- Lin, Z.W.; Ko, C.M.; Li, B.A.; Zhang, B.; Pal, S. A Multi-phase transport model for relativistic heavy ion collisions. Phys. Rev. C 2005, 72, 064901. [Google Scholar] [CrossRef]
- Xu, H.J.; Li, Z.; Song, H. High-order flow harmonics of identified hadrons in 2.76A TeV Pb + Pb collisions. Phys. Rev. C 2016, 93, 064905. [Google Scholar] [CrossRef]
- Roesler, S.; Engel, R.; Ranft, J. The Monte Carlo Event Generator DPMJET-III. In Proceedings of the Monte Carlo 2000, Lisbon, Portugal, 23–26 October 2000.
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Akamatsu, Y.; Inutsuka, S.I.; Nonaka, C.; Takamoto, M. A new scheme of causal viscous hydrodynamics for relativistic heavy-ion collisions: A Riemann solver for quark-gluon plasma. J. Comput. Phys. 2014, 256, 34–54. [Google Scholar] [CrossRef]
- Bozek, P.; Wyskiel-Piekarska, I. Particle spectra in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2012, 85, 064915. [Google Scholar] [CrossRef]
- De Souza, R.D.; Koide, T.; Kodama, T. Hydrodynamic Approaches in Relativistic Heavy Ion Reactions. Prog. Part. Nucl. Phys. 2016, 86, 35–85. [Google Scholar] [CrossRef]
- Kolb, P.F.; Sollfrank, J.; Heinz, U.W. Anisotropic transverse flow and the quark hadron phase transition. Phys. Rev. C 2000, 62, 054909. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Malinina, L.V.; Petrushanko, S.V.; Snigirev, A.M.; Arsene, I.; Tywoniuk, K. Heavy ion event generator HYDJET++ (HYDrodynamics plus JETs). Comput. Phys. Commun. 2009, 180, 779–799. [Google Scholar] [CrossRef]
- Hirano, T.; Huovinen, P.; Murase, K.; Nara, Y. Integrated Dynamical Approach to Relativistic Heavy Ion Collisions. Prog. Part. Nucl. Phys. 2013, 70, 108–158. [Google Scholar] [CrossRef]
- Shen, C.; Qiu, Z.; Song, H.; Bernhard, J.; Bass, S.; Heinz, U. The iEBE-VISHNU code package for relativistic heavy-ion collisions. Comput. Phys. Commun. 2016, 199, 61–85. [Google Scholar] [CrossRef]
- Abelev, B.B.; Adam, J.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Multiplicity Dependence of Pion, Kaon, Proton and Lambda Production in p-Pb Collisions at = 5.02 TeV. Phys. Lett. B 2014, 728, 25–38. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Amirikas, R.; Aphecetche, L.; Aronson, S.H.; Averbeck, R.; et al. Identified charged particle spectra and yields in Au+Au collisions at S(NN)**1/2 = 200-GeV. Phys. Rev. C 2004, 69, 034909. [Google Scholar] [CrossRef]
- Nonaka, C.; Bass, S.A. Space-time evolution of bulk QCD matter. Phys. Rev. C 2007, 75, 014902. [Google Scholar] [CrossRef]
- Muller, B. Quark matter ’99—Theoretical summary: What next? Nucl. Phys. A 1999, 661, 272–281. [Google Scholar] [CrossRef]
- Kittel, W.; De Wolf, E.A. Soft Multihadron Dynamics; World Scientific: Singapore, 2005. [Google Scholar]
- Landau, L.D. On the multiparticle production in high-energy collisions. Izv. Akad. Nauk Ser. Fiz. 1953, 17, 51. [Google Scholar]
- Weiner, R.M. Experiment and Theory in Computations of the He Atom Ground State. Int. J. Mod. Phys. E 2006, 15, 37–56. [Google Scholar] [CrossRef]
- Heinz, U.W. Early collective expansion: Relativistic hydrodynamics and the transport properties of QCD matter. In Landolt-Bornstein; Springer: Berlin, Germany, 2010; Volume 23, pp. 240–292. [Google Scholar]
- Stöcker, H.; Greiner, W. High-Energy Heavy Ion Collisions: Probing The Equation Of State Of Highly Excited Hadronic Matter. Phys. Rep. 1986, 137, 277–392. [Google Scholar] [CrossRef]
- Hirano, T.; van der Kolk, N.; Bilandzic, A. Hydrodynamics and Flow. Lect. Notes Phys. 2010, 785, 139–178. [Google Scholar]
- Gale, C.; Jeon, S.; Schenke, B. Hydrodynamic Modeling of Heavy-Ion Collisions. Int. J. Mod. Phys. A 2013, 28, 1340011. [Google Scholar] [CrossRef]
- Jaiswal, A.; Roy, V. Relativistic hydrodynamics in heavy-ion collisions: General aspects and recent developments. Adv. High Energy Phys. 2016, 2016, 9623034. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of irreversible processes. 3. Relativistic theory of the simple fluid. Phys. Rev. 1940, 58, 919–924. [Google Scholar] [CrossRef]
- Nakamura, A.; Sakai, S. Transport coefficients of gluon plasma. Phys. Rev. Lett. 2005, 94, 072305. [Google Scholar] [CrossRef] [PubMed]
- Karsch, F.; Kharzeev, D.; Tuchin, K. Universal properties of bulk viscosity near the QCD phase transition. Phys. Lett. B 2008, 663, 217–221. [Google Scholar] [CrossRef]
- Muronga, A. Causal theories of dissipative relativistic fluid dynamics for nuclear collisions. Phys. Rev. C 2004, 69, 034903. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Stability and causality in dissipative relativistic fluids. Ann. Phys. 1983, 151, 466–496. [Google Scholar] [CrossRef]
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Systematic Measurements of Identified Particle Spectra in pp, d+ Au and Au+Au Collisions from STAR. Phys. Rev. C 2009, 79, 034909. [Google Scholar] [CrossRef]
- Siemens, P.J.; Rasmussen, J.O. Evidence for a blast wave from compress nuclear matter. Phys. Rev. Lett. 1979, 42, 880–887. [Google Scholar] [CrossRef]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200-A/GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef]
- Retiere, F.; Lisa, M.A. Observable implications of geometrical and dynamical aspects of freeze out in heavy ion collisions. Phys. Rev. C 2004, 70, 044907. [Google Scholar] [CrossRef]
- Cooper, F.; Frye, G. Comment on the Single Particle Distribution in the Hydrodynamic and Statistical Thermodynamic Models of Multiparticle Production. Phys. Rev. D 1974, 10, 186–189. [Google Scholar] [CrossRef]
- Kumar, L. Systematics of Kinetic Freeze-out Properties in High Energy Collisions from STAR. Nucl. Phys. A 2014, 931, 1114–1119. [Google Scholar] [CrossRef]
- Sjostrand, T.; Mrenna, S.; Skands, P.Z. A Brief Introduction to PYTHIA 8.1. Comput. Phys. Commun. 2008, 178, 852–867. [Google Scholar] [CrossRef]
- Baier, R.; Mueller, A.H.; Schiff, D.; Son, D.T. ’Bottom up’ thermalization in heavy ion collisions. Phys. Lett. B 2001, 502, 51–58. [Google Scholar] [CrossRef]
- Xu, Z.; Greiner, C. Thermalization of gluons in ultrarelativistic heavy ion collisions by including three-body interactions in a parton cascade. Phys. Rev. C 2005, 71, 064901. [Google Scholar] [CrossRef]
- Kurkela, A.; Moore, G.D. Thermalization in Weakly Coupled Nonabelian Plasmas. J. High Energy Phys. 2011, 1112, 44. [Google Scholar] [CrossRef]
- Romatschke, P. Do Nuclear Collisions Create a Locally Equilibrated Quark-Gluon Plasma? Eur. Phys. J. C 2016, 77, 21. [Google Scholar] [CrossRef]
- Broniowski, W.; Chojnacki, M.; Florkowski, W.; Kisiel, A. Uniform Description of Soft Observables in Heavy-Ion Collisions at = 200 GeV. Phys. Rev. Lett. 2008, 101, 022301. [Google Scholar] [CrossRef] [PubMed]
- Petersen, H.; Coleman-Smith, C.; Bass, S.A.; Wolpert, R. Constraining the initial state granularity with bulk observables in Au+Au collisions at = 200 GeV. J. Phys. G 2011, 38, 045102. [Google Scholar] [CrossRef]
- Heinz, U.; Moreland, J.S. Energy dependent growth of the nucleon and hydrodynamic initial conditions. Phys. Rev. C 2011, 84, 054905. [Google Scholar]
- Noronha-Hostler, J.; Betz, B.; Noronha, J.; Gyulassy, M. Event-by-event hydrodynamics + jet energy loss: A solution to the RAA ⊗ v2 puzzle. Phys. Rev. Lett. 2016, 116, 252301. [Google Scholar] [CrossRef] [PubMed]
- Glauber, R.J. Cross-sections in deuterium at high-energies. Phys. Rev. 1955, 100, 242–248. [Google Scholar] [CrossRef]
- Czyz, W.; Maximon, L.C. High-energy, small angle elastic scattering of strongly interacting composite particles. Ann. Phys. 1969, 52, 59–121. [Google Scholar] [CrossRef]
- Glauber, R.J.; Matthiae, G. High-energy scattering of protons by nuclei. Nucl. Phys. B 1970, 21, 135–157. [Google Scholar] [CrossRef]
- Glauber, R.J. Quantum Optics and Heavy Ion Physics. Nucl. Phys. A 2006, 774, 3–13. [Google Scholar] [CrossRef]
- Joachain, C.J.; Quigg, C. Multiple scattering expansions in several particle dynamics. Rev. Mod. Phys. 1974, 46, 279–324. [Google Scholar] [CrossRef]
- Franco, V.; Varma, G.K. Collisions Between Composite Particles at Medium and High-Energies. Phys. Rev. C 1978, 18, 349–370. [Google Scholar] [CrossRef]
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Broniowski, W.; Rybczynski, M.; Bozek, P. GLISSANDO: Glauber initial-state simulation and more. Comput. Phys. Commun. 2009, 180, 69–83. [Google Scholar] [CrossRef]
- Loizides, C.; Nagle, J.; Steinberg, P. Improved version of the PHOBOS Glauber Monte Carlo. SoftwareX 2015, 1, 13–18. [Google Scholar] [CrossRef]
- Abreu, M.C.; Alessandro, B.; Alexa, C.; Arnaldi, R.; Atayan, M.; Baglin, C.; Baldit, A.; Bedjidian, M.; Beole, S.; Boldea, V. The Dependence of the anomalous J/psi suppression on the number of participant nucleons. Phys. Lett. B 2001, 521, 195–203. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Measurement of Z boson Production in Pb+Pb Collisions at = 2.76 TeV with the ATLAS Detector. Phys. Rev. Lett. 2013, 110, 022301. [Google Scholar] [CrossRef] [PubMed]
- Gribov, V.N. A Reggeon Diagram Technique. Sov. Phys. JETP 1968, 26, 414–422. [Google Scholar]
- Gribov, V.N. Glauber corrections and the interaction between high-energy hadrons and nuclei. Sov. Phys. JETP 1969, 29, 483–487. [Google Scholar]
- Abramovsky, V.A.; Gribov, V.N.; Kancheli, O.V. Character of Inclusive Spectra and Fluctuations Produced in Inelastic Processes by Multi-Pomeron Exchange. Yad. Fiz. 1973, 18, 595–616. [Google Scholar]
- Braun, V.M.; Shabelski, Y.M. Multiple Scattering Theory for Inelastic Processes. Int. J. Mod. Phys. A 1988, 3, 2417–2501. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton based Gribov-Regge theory. Phys. Rep. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: I. QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar] [CrossRef]
- Pasechnik, R.; Enberg, R.; Ingelman, G. QCD rescattering mechanism for diffractive deep inelastic scattering. Phys. Rev. D 2010, 82, 054036. [Google Scholar] [CrossRef]
- Pasechnik, R.; Enberg, R.; Ingelman, G. Diffractive deep inelastic scattering from multiple soft gluon exchange in QCD. Phys. Lett. B 2011, 695, 189–193. [Google Scholar] [CrossRef]
- Nemchik, J.; Petracek, V.; Potashnikova, I.K.; Sumbera, M. Nuclear suppression at large forward rapidities in d-Au collisions at relativistic and ultrarelativistic energies. Phys. Rev. C 2008, 78, 025213. [Google Scholar] [CrossRef]
- Loizides, C. Glauber modeling of high-energy nuclear collisions at the subnucleon level. Phys. Rev. C 2016, 94, 024914. [Google Scholar] [CrossRef]
- Nikolaev, N.N.; Zakharov, B.G. The triple-pomeron regime and structure function of the pomeron in diffractive deep inelastic scattering at very smallx. Phys. C 1994, 64, 631–652. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Lapidus, L.I.; Zamolodchikov, A.B. Dynamics Of Color In Hadron Diffraction On Nuclei. JETP Lett. 1981, 33, 595–597. [Google Scholar]
- Nikolaev, N.N.; Zakharov, B.G. The Pomeron in diffractive deep inelastic scattering. J. Exp. Theor. Phys. 1994, 78, 598–618. [Google Scholar]
- Kopeliovich, B.Z. Proceedings of the International Workshop XXIII on Gross Properties of Nuclei and Nuclear Excitations, Hirschegg, Austria, 1995; Feldmeyer, H., Norenberg, W., Eds.; Gesellschaft Schwerionenforschung: Darmstadt, Germany, 1995. [Google Scholar]
- Brodsky, S.J.; Hebecker, A.; Quack, E. The Drell-Yan process and factorization in impact parameter space. Phys. Rev. D 1997, 55, 2584–2590. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Schafer, A.; Tarasov, A.V. Bremsstrahlung of a quark propagating through a nucleus. Phys. Rev. C 1999, 59, 1609–1619. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Schafer, A.; Tarasov, A.V. The color dipole picture of the Drell-Yan process. Phys. Lett. B 2001, 503, 91–98. [Google Scholar] [CrossRef]
- Nikolaev, N.N.; Piller, G.; Zakharov, B.G. Quantum coherence in heavy flavor production on nuclei. Z. Phys. A 1996, 354, 99–105. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Tarasov, A.V. Gluon shadowing and heavy flavor production off nuclei. Nucl. Phys. A 2002, 710, 180–217. [Google Scholar] [CrossRef]
- Bertsch, G.; Brodsky, S.J.; Goldhaber, A.S.; Gunion, J.F. Diffractive Excitation in Quantum Chromodynamics. Phys. Rev. Lett. 1981, 47, 297. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Mueller, A. Using nuclei to probe hadronization in QCD. Phys. Lett. B 1988, 206, 685–690. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation effects in deep inelastic scattering at low Q2 and its ... and its implications on diffraction. Phys. Rev. D 1998, 59, 014017. [Google Scholar] [CrossRef]
- Bartels, J.; Golec-Biernat, K.; Kowalski, H. Modification of the saturation model: Dokshitzer-Gribov-Lipatov- Altarelli-Parisi evolution. Phys. Rev. D 2002, 66, 014001. [Google Scholar] [CrossRef]
- Kowalski, H.; Motyka, L.; Watt, G. Exclusive diffractive processes at HERA within the dipole picture. Phys. Rev. D 2006, 74, 074016. [Google Scholar] [CrossRef]
- Watt, G.; Kowalski, H. Impact parameter dependent colour glass condensate dipole model. Phys. Rev. D 2008, 78, 014016. [Google Scholar] [CrossRef]
- Rezaeian, A.H.; Siddikov, M.; van de Klundert, M.; Venugopalan, R. NΣc and NΣb resonances in the quark-delocalization color-screening model. Phys. Rev. D 2013, 87, 034002. [Google Scholar] [CrossRef]
- Iancu, E.; Itakura, K.; Munier, S. Saturation and BFKL dynamics in the HERA data at small-x. Phys. Lett. B 2004, 590, 199–208. [Google Scholar] [CrossRef]
- Kharzeev, D.; Kovchegov, Y.V.; Tuchin, K. Nuclear modification factor in image collisions: Onset of suppression in the color glass condensate. Phys. Lett. B 2004, 599, 23–31. [Google Scholar] [CrossRef]
- Kharzeev, D.; Kovchegov, Y.V.; Tuchin, K. The color glass condensate and hadron production in the forward region. Nucl. Phys. A 2006, 765, 464–482. [Google Scholar]
- Boer, D.; Utermann, A.; Wessels, E. Geometric Scaling at RHIC and LHC. Phys. Rev. D 2008, 77, 054014. [Google Scholar] [CrossRef]
- Soyez, G. Saturation QCD predictions with heavy quarks at HERA. Phys. Lett. B 2007, 655, 32–38. [Google Scholar] [CrossRef]
- Kowalski, H.; Teaney, D. Impact parameter dipole saturation model. Phys. Rev. D 2003, 68, 114005. [Google Scholar] [CrossRef]
- Rezaeian, A.; Schmidt, I. Impact-parameter dependent color glass condensate dipole model and new combined HERA data. Phys. Rev. D 2013, 88, 074016. [Google Scholar] [CrossRef]
- Basso, E.; Goncalves, V.P.; Nemchik, J.; Pasechnik, R.; Sumbera, M. Drell-Yan phenomenology in the color dipole picture revisited. Phys. Rev. D 2016, 93, 034023. [Google Scholar] [CrossRef]
- Basso, E.; Goncalves, V.P.; Krelina, M.; Nemchik, J.; Pasechnik, R. Nuclear effects in Drell-Yan pair production in high-energy pA collisions. Phys. Rev. D 2016, 93, 094027. [Google Scholar] [CrossRef]
- Basso, E.; Goncalves, V.P.; Krelina, M.; Nemchik, J.; Pasechnik, R. Drell-Yan process in pA collisions: The exact treatment of coherence effects. Phys. Rev. D 2016, 94, 114009. [Google Scholar]
- Kopeliovich, B.Z.; Nemchik, J.; Potashnikova, I.K.; Johnson, M.B.; Schmidt, I. Breakdown of QCD factorization at large Feynman x. Phys. Rev. C 2005, 72, 054606. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Nemchik, J.; Potashnikova, I.K.; Schmidt, I. Energy conservation in high-pT nuclear reactions. Int. J. Mod. Phys. E 2014, 23, 1430006. [Google Scholar] [CrossRef]
- Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; et al. Centrality Dependence of π 0 and η Production at Large Transverse Momentum in s N N = 200 GeV d+ Au Collisions. Phys. Rev. Lett. 2007, 98, 172302. [Google Scholar] [CrossRef]
- Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; Aronson, S.H.; et al. Measurement of Direct Photons in Au+Au Collisions at √sNN = 200 GeV. Phys. Rev. Lett. 2012, 109, 152302. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, T. Measurement of electro-magnetic radiation at RHIC-PHENIX. Nucl. Phys. A 2008, 805, 355–360. [Google Scholar] [CrossRef]
- Landau, L.D.; Pomeranchuk, I. Limits of applicability of the theory of bremsstrahlung electrons and pair production at high-energies. Dokl. Akad. Nauk Ser. Fiz. 1953, 92, 535–536. [Google Scholar]
- Landau, L.D.; Pomeranchuk, I. Electron cascade process at very high-energies. Dokl. Akad. Nauk Ser. Fiz. 1953, 92, 735–738. [Google Scholar]
- Migdal, A.B. Bremsstrahlung and pair production in condensed media at high-energies. Phys. Rev. 1956, 103, 1811–1820. [Google Scholar] [CrossRef]
- Baier, R.; Shiff, D.; Zakharov, B.G. Energy loss in perturbative QCD. Ann. Rev. Nucl. Part. Sci. 2000, 50, 37–69. [Google Scholar] [CrossRef]
- Gyulassy, M.; Wang, X.-N. Multiple collisions and induced gluon Bremsstrahlung in QCD. Nucl. Phys. B 1994, 420, 583–614. [Google Scholar] [CrossRef]
- Wang, X.-N.; Gyulassy, M.; Plumer, M. Landau-Pomeranchuk-Migdal effect in QCD and radiative energy loss in a quark-gluon plasma. Phys. Rev. D 1995, 51, 3436–3446. [Google Scholar] [CrossRef]
- Wiedemann, U.A.; Gyulassy, M. Transverse momentum dependence of the Landau-Pomeranchuk-Migdal effect. Nucl. Phys. B 1999, 560, 345–382. [Google Scholar] [CrossRef]
- Zakharov, B.G. Applicability of the eikonal approximation for calculation of the probability of passage of ultrarelativistic positronium through matter. Sov. J. Nucl. Phys. 1987, 46, 92–95. [Google Scholar]
- Zakharov, B.G. Radiative energy loss of high-energy quarks in finite-size nuclear matter and quark-gluon plasma. J. Exp. Theor. Phys. Lett. 1997, 65, 615–620. [Google Scholar] [CrossRef]
- Zakharov, B.G. Transverse Spectra of Radiation Processes in Medium. J. Exp. Theor. Phys. Lett. 1999, 70, 176–182. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Schiff, D. Angular dependence of the radiative gluon spectrum and the energy loss of hard jets in QCD media. Phys. Rev. C 1999, 60, 064902. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Schiff, D. Induced Gluon Radiation in a QCD Medium. Phys. Lett. B 1995, 345, 277–286. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Peigne, S.; Schiff, D. The Landau-Pomeranchuk-Migdal effect in QED. Nucl. Phys. B 1996, 478, 577–597. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Schiff, D. Medium-induced radiative energy loss; equivalence between the BDMPS and Zakharov formalisms. Nucl. Phys. B 1998, 531, 403–425. [Google Scholar] [CrossRef]
- Nemchik, J.; Pasechnik, R.; Potashnikova, I. A heuristic description of high- pT hadron production in heavy ion collisions. Eur. Phys. J. C 2015, 75, 95. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Schaefer, A.; Tarasov, A.V. Nonperturbative Effects in Gluon Radiation and Photoproduction of Quark Pairs. Phys. Rev. D 2000, 62, 054022. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Nemchik, J.; Schaefer, A. Color transparency versus quantum coherence in electroproduction of vector mesons off nuclei. Phys. Rev. C 2002, 65, 035201. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Nemchik, J.; Potashnikova, I.K.; Schmidt, I. Gluon Shadowing in DIS off Nuclei. J. Phys. G 2008, 35, 115010. [Google Scholar] [CrossRef]
- Gribov, L.V.; Levin, E.M.; Ryskin, M.G. Semihard Processes In QCD. Phys. Rep. 1983, 100, 1–150. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L. Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e- Annihilation by Perturbation Theory in Quantum Chromodynamics. Sov. Phys. JETP 1977, 46, 641–653. [Google Scholar]
- Gribov, V.N.; Lipatov, L.N. Deep inelastic e p scattering in perturbation theory. Sov. J. Nucl. Phys. 1972, 15, 438–450. [Google Scholar]
- Altarelli, G.; Parisi, G. Asymptotic Freedom in Parton Language. Nucl. Phys. B 1977, 126, 298–318. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 1994, 49, 3352–3355. [Google Scholar] [CrossRef]
- Jalilian-Marian, J.; Kovchegov, Y.V. Saturation physics and deuteron gold collisions at RHIC. Prog. Part. Nucl. Phys. 2006, 56, 104–231. [Google Scholar] [CrossRef]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef]
- Kharzeev, D.; Levin, E.; Nardi, M. Color glass condensate at the LHC: Hadron multiplicities in pp, pA and AA collisions. Nucl. Phys. A 2005, 747, 609–629. [Google Scholar] [CrossRef]
- Jalilian-Marian, J.; Kovner, A.; Leonidov, A.; Weigert, H. The BFKL equation from the Wilson renormalization group. Nucl. Phys. B 1997, 504, 415–431. [Google Scholar] [CrossRef]
- Jalilian-Marian, J.; Kovner, A.; Leonidov, A.; Weigert, H. The Wilson renormalization group for low x physics: Towards the high density regime. Phys. Rev. D 1998, 59, 014014. [Google Scholar] [CrossRef]
- Kovner, A.; Milhano, J.G.; Weigert, H. Relating different approaches to nonlinear QCD evolution at finite gluon density. Phys. Rev. D 2000, 62, 114005. [Google Scholar] [CrossRef]
- Weigert, H. Unitarity at small Bjorken x. Nucl. Phys. A 2002, 703, 823–860. [Google Scholar] [CrossRef]
- Iancu, E.; Leonidov, A.; McLerran, L.D. Nonlinear gluon evolution in the color glass condensate. 1. Nucl. Phys. A 2001, 692, 583–645. [Google Scholar] [CrossRef]
- Ferreiro, E.; Iancu, E.; Leonidov, A.; McLerran, L. Nonlinear gluon evolution in the color glass condensate. 2. Nucl. Phys. A 2002, 703, 489–538. [Google Scholar] [CrossRef]
- Golec-Biernat, K.J.; Wusthoff, M. Saturation in diffractive deep inelastic scattering. Phys. Rev. D 1999, 60, 114023. [Google Scholar] [CrossRef]
- Caola, F.; Forte, S. Geometric Scaling from GLAP evolution. Phys. Rev. Lett. 2008, 101, 022001. [Google Scholar] [CrossRef] [PubMed]
- Kharzeev, D.; Levin, E.; Nardi, M. The Onset of classical QCD dynamics in relativistic heavy ion collisions. Phys. Rev. C 2005, 71, 054903. [Google Scholar] [CrossRef]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Fluctuating Glasma initial conditions and flow in heavy ion collisions. Phys. Rev. Lett. 2012, 108, 252301. [Google Scholar] [CrossRef] [PubMed]
- Drescher, H.-J.; Nara, Y. Effects of fluctuations on the initial eccentricity from the Color Glass Condensate in heavy ion collisions. Phys. Rev. C 2007, 75, 034905. [Google Scholar] [CrossRef]
- Hirano, T.; Huovinen, P.; Nara, Y. Elliptic flow in Pb+Pb collisions at = 2.76 TeV: Hybrid model assessment of the first data. Phys. Rev. C 2011, 84, 011901. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z. Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef] [PubMed]
- Pang, L.; Wang, Q.; Wang, X.N. Effects of initial flow velocity fluctuation in event-by-event (3+1)D hydrodynamics. Phys. Rev. C 2012, 86, 024911. [Google Scholar] [CrossRef]
- Bhalerao, R.S.; Jaiswal, A.; Pal, S. Collective flow in event-by-event partonic transport plus hydrodynamics hybrid approach. Phys. Rev. C 2015, 92, 014903. [Google Scholar] [CrossRef]
- Paatelainen, R.; Eskola, K.J.; Niemi, H.; Tuominen, K. Fluid dynamics with saturated minijet initial conditions in ultrarelativistic heavy-ion collisions. Phys. Lett. B 2014, 731, 126–130. [Google Scholar] [CrossRef]
- Niemi, H.; Eskola, K.J.; Paatelainen, R. Event-by-event fluctuations in a perturbative QCD + saturation + hydrodynamics model: Determining QCD matter shear viscosity in ultrarelativistic heavy-ion collisions. Phys. Rev. C 2016, 93, 024907. [Google Scholar] [CrossRef]
- Moreland, J.S.; Bernhard, J.E.; Bass, S.A. Alternative ansatz to wounded nucleon and binary collision scaling in high-energy nuclear collisions. Phys. Rev. C 2015, 92, 011901. [Google Scholar] [CrossRef]
- Bielcikova, J. Jets and correlations in heavy-ion collisions. In Proceedings of the 2015 European Physical Society Conference on High Energy Physics, Vienna, Austria, 22–29 July 2015.
- Andronic, A.; Arleo, F.; Arnaldi, R.; Beraudo, A.; Bruna, E.; Caffarri, D.; del Valle, Z.C.; Contreras, J.G.; Dahms, T.; Dainese, A.; et al. Heavy-flavour and quarkonium production in the LHC era: From proton-proton to heavy-ion collisions. Eur. Phys. J. C 2016, 76, 107. [Google Scholar] [CrossRef] [PubMed]
- Rafelski, J.; Muller, B. Strangeness Production in the Quark-Gluon Plasma. Phys. Rev. Lett. 1982, 48, 1066. [Google Scholar] [CrossRef]
- Koch, P.; Muller, B.; Rafelski, J. Strangeness in Relativistic Heavy Ion Collisions. Phys. Rep. 1986, 142, 167–262. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions: The Hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 2009, 673, 142–145. [Google Scholar] [CrossRef]
- Teaney, D.; Lauret, J.; Shuryak, E.V. Flow at the SPS and RHIC as a quark gluon plasma signature. Phys. Rev. Lett. 2001, 86, 4783–4786. [Google Scholar] [CrossRef] [PubMed]
- Modeling Relativistic Heavy-Ion Collisions. Available online: https://www.phy.duke.edu/modeling-relativistic-heavy-ion-collisions (accessed on 17 January 2017).
- Tribedy, P.; Venugopalan, R. QCD saturation at the LHC: Comparisons of models to p + p and A + A data and predictions for p + Pb collisions. Phys. Lett. B 2012, 710, 125–133. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Measurement of the centrality dependence of the charged particle pseudorapidity distribution in lead-lead collisions at = 2.76 TeV with the ATLAS detector. Phys. Lett. B 2012, 710, 363–382. [Google Scholar] [CrossRef]
- Ollitrault, J.Y. Anisotropy as a signature of transverse collective flow. Phys. Rev. D 1992, 46, 229–245. [Google Scholar] [CrossRef]
- Poskanzer, A.M.; Voloshin, S.A. Methods for analyzing anisotropic flow in relativistic nuclear collisions. Phys. Rev. C 1998, 58, 1671–1678. [Google Scholar] [CrossRef]
- Manly, S. System size, energy and pseudorapidity dependence of directed and elliptic flow at RHIC. Nucl. Phys. A 2006, 774, 523–526. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; et al. Higher harmonic anisotropic flow measurements of charged particles in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2011, 107, 032301. [Google Scholar] [CrossRef] [PubMed]
- Venema, L.B.; Braak, H.; Löhner, H.; Raschke, A.E.; Siemssen, R.H.; Šumbera, M.; Wilschut, H.W.; Berg, F.D.; Kühn, W.; Metag, V.; et al. Azimuthal asymmetry of neutral pion emission in Au+Au reactions at 1 GeV/nucleon. Phys. Rev. Lett. 1993, 71, 835–838. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Aparin, A.; Arkhipkin, D.; Aschenauer, E.C.; Attri, A.; et al. Beam Energy Dependence of the Third Harmonic of Azimuthal Correlations in Au+Au Collisions at RHIC. Phys. Rev. Lett. 2016, 116, 112302. [Google Scholar] [CrossRef] [PubMed]
- Gale, C.; Jeon, S.; Schenke, B.; Tribedy, P.; Venugopalan, R. Event-by-event anisotropic flow in heavy-ion collisions from combined Yang-Mills and viscous fluid dynamics. Phys. Rev. Lett. 2013, 110, 012302. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M. Measurement of the distributions of event-by-event flow harmonics in lead-lead collisions at = 2.76 TeV with the ATLAS detector at the LHC. J. High Energy Phys. 2013, 1311, 183. [Google Scholar] [CrossRef]
- Qiu, Z.; Heinz, U. Hydrodynamic event-plane correlations in Pb+Pb collisions at = 2.76A TeV. Phys. Lett. B 2012, 717, 261–265. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; Abouzeid, O.; Abramowicz, H.; et al. Measurement of event-plane correlations in = 2.76 TeV lead-lead collisions with the ATLAS detector. Phys. Rev. C 2014, 90, 024905. [Google Scholar] [CrossRef]
- Qian, J.; Heinz, U. Hydrodynamic flow amplitude correlations in event-by-event fluctuating heavy-ion collisions. Phys. Rev. C 2016, 94, 024910. [Google Scholar] [CrossRef]
- Giacalone, G.; Yan, L.; Noronha-Hostler, J.; Ollitrault, J.Y. Symmetric cumulants and event-plane correlations in Pb + Pb collisions. Phys. Rev. C 2016, 94, 014906. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdesselam, A.; Abdinov, O.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Measurement of the correlation between flow harmonics of different order in lead-lead collisions at = 2.76 TeV with the ATLAS detector. Phys. Rev. C 2015, 92, 034903. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; et al. Correlated event-by-event fluctuations of flow harmonics in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. Lett. 2016, 117, 182301. [Google Scholar]
- Wheaton, S.; Cleymans, J. THERMUS: A Thermal model package for ROOT. Comput. Phys. Commun. 2009, 180, 84–106. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Multi-strange baryon production at mid-rapidity in Pb-Pb collisions at = 2.76 TeV. Phys. Lett. B 2014, 728, 216–227. [Google Scholar] [CrossRef]
- Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Multi-strange baryon production in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2016, 758, 389–401. [Google Scholar]
- Bjorken, J.D. Energy Loss of Energetic Partons in Quark-Gluon Plasma: Possible Extinction of High p(t) Jets in Hadron-Hadron Collisions. Available online: http://lss.fnal.gov/archive/1982/pub/Pub-82-059-T.pdf (accessed on 17 January 2017).
- Appel, D.A. Jets as a Probe of Quark-Gluon Plasmas. Phys. Rev. D 1986, 33, 717–722. [Google Scholar] [CrossRef]
- Gyulassy, M.; Plumer, M. Jet Quenching in Dense Matter, The quenching of hard jets in ultrarelativistic nuclear collisions is estimated emphasizing its sensitivity to possible changes in the energy loss mechanism in a quark-gluon plasma. Phys. Lett. B 1990, 243, 432–438. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Charged-Particle Nuclear Modification Factors in PbPb and pPb Collisions at = 5.02 TeV. arXiv, 2016; arXiv:1611.01664. [Google Scholar]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Anderson, M.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J. Direct Observation of Dijets in Central Au+Au Collisions at = 200 GeV. Phys. Rev. Lett. 2006, 97, 162301. [Google Scholar] [CrossRef] [PubMed]
- D’Enterria, D. Perturbative probes of QCD matter at the Large Hadron Collider. In Proceedings of the 6th International Conference on Quarks and Nuclear Physics, Palaiseau, Paris, France, 16–20 April 2012.
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M. Studies of jet quenching using isolated-photon+jet correlations in PbPb and pp collisions at = 2.76 TeV. Phys. Lett. B 2013, 718, 773–794. [Google Scholar] [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Peigne, S.; Schiff, D. Radiative energy loss and p(T) broadening of high-energy partons in nuclei. Nucl. Phys. B 1997, 484, 265–282. [Google Scholar] [CrossRef]
- Caron-Huot, S. O(g) plasma effects in jet quenching. Phys. Rev. D 2009, 79, 065039. [Google Scholar] [CrossRef]
- Laine, M. A non-perturbative contribution to jet quenching. Eur. Phys. J. C 2012, 72, 2233. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Mehtar-Tani, Y. Renormalization of the jet-quenching parameter. Nucl. Phys. A 2014, 929, 202–229. [Google Scholar] [CrossRef]
- Panero, M.; Rummukainen, K.; Schfer, A. Lattice Study of the Jet Quenching Parameter. Phys. Rev. Lett. 2014, 112, 162001. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Rajagopal, K.; Wiedemann, U.A. Calculating the jet quenching parameter from AdS/CFT. Phys. Rev. Lett. 2006, 97, 182301. [Google Scholar] [CrossRef] [PubMed]
- Svetitsky, B. Diffusion of charmed quarks in the quark-gluon plasma. Phys. Rev. D 1988, 37, 2484. [Google Scholar] [CrossRef]
- Young, C.; Shuryak, E. Charmonium in strongly coupled quark-gluon plasma. Phys. Rev. C 2009, 79, 034907. [Google Scholar] [CrossRef]
- Petreczky, P.; Young, C. Sequential Bottomonium Production at High Temperatures. arXiv, 2016; arXiv:1606.08421. [Google Scholar]
- Digal, S.; Petreczky, P.; Satz, H. Quarkonium feed down and sequential suppression. Phys. Rev. D 2001, 64, 094015. [Google Scholar] [CrossRef]
- CMS Collaboration. Strong Suppression of Υ Excited States in PbPb Collisions at √sNN = 5.02 TeV; CMS-PAS-HIN-16-008; CMS Collaboration: Cessy, France, 2016. [Google Scholar]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of sequential Upsilon suppression in PbPb collisions. Phys. Rev. Lett. 2012, 109, 222301. [Google Scholar] [CrossRef] [PubMed]
- Shuryak, E.V. Quark-Gluon Plasma and Hadronic Production of Leptons, Photons and Psions. Phys. Lett. B 1978, 78, 150–153. [Google Scholar] [CrossRef]
- Feinberg, E.L. Direct Production of Photons and Dileptons in Thermodynamical Models of Multiple Hadron Production. Nuovo Cim. A 1976, 34, 391–412. [Google Scholar]
- Domokos, G.; Goldman, J.I. Quark-matter diagnostics. Phys. Rev. D 1981, 23, 203. [Google Scholar] [CrossRef]
- Stankus, P. Direct photon production in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2005, 55, 517–554. [Google Scholar] [CrossRef]
- Aggarwal, M.M.; Agnihotri, A.; Ahammed, Z.; Angelis, A.L.S.; Antonenko, V.; Arefiev, V.; Astakhov, V.; Avdeitchikov, V.; Awes, T.C.; Baba, P.V.K.S.; et al. Observation of direct photons in central 158-A-GeV Pb-208 + Pb-208 collisions. Phys. Rev. Lett. 2000, 85, 3595. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, M.M.; Aggarwal, M.M.; Agnihotri, A.; Ahammed, Z.; Angelis, A.L.S.; Antonenko, V.; Areev, V.; Astakhov, V.; Avdeitchikov, V.; Awes, T.C.; Baba, P.V.K.S.; et al. Direct Photon Production in 158-A-GeV Pb-208 + Pb-208 Collisions. Phys. Rev. Lett. 2000, 85, 3595–3599. [Google Scholar] [CrossRef] [PubMed]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Enhanced Production of Direct Photons in Au+Au Collisions at = 200 GeV and Implications for the Initial Temperature. Phys. Rev. Lett. 2010, 104, 132301. [Google Scholar] [CrossRef] [PubMed]
- Adam, J.; Adamova, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; Aiola, S.; Akindinov, A. Direct photon production in Pb-Pb collisions at = 2.76 TeV. Phys. Lett. B 2016, 754, 235–248. [Google Scholar] [CrossRef]
- Sumbera, M. Soft Physics at RHIC. EPJ Web. Conf. 2012, 28, 03006. [Google Scholar] [CrossRef]
- Sumbera, M. Results from STAR Beam Energy Scan Program. Acta Phys. Pol. Supp. 2013, 6, 429–436. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Al-Ta’ani, H.; Angerami, A.; et al. Measurement of higher cumulants of net-charge multiplicity distributions in Au+Au collisions at = 7.7 − 200 GeV. Phys. Rev. C 2016, 93, 011901. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Signatures of the tricritical point in QCD. Phys. Rev. Lett. 1998, 81, 4816–4819. [Google Scholar] [CrossRef]
- Asakawa, M.; Kitazawa, M. Fluctuations of conserved charges in relativistic heavy ion collisions: An introduction. Prog. Part. Nucl. Phys. 2016, 90, 299–342. [Google Scholar] [CrossRef]
- Lacey, R.A. Indications for a Critical End Point in the Phase Diagram for Hot and Dense Nuclear Matter. Phys. Rev. Lett. 2015, 114, 142301. [Google Scholar] [CrossRef] [PubMed]
- Gavai, R.V.; Gupta, S. Lattice QCD predictions for shapes of event distributions along the freezeout curve in heavy-ion collisions. Phys. Lett. B 2011, 696, 459–463. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Energy Dependence of Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2014, 112, 032302. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Alford, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barnby, L.S.; et al. Higher Moments of Net-proton Multiplicity Distributions at RHIC. Phys. Rev. Lett. 2010, 105, 022302. [Google Scholar] [CrossRef] [PubMed]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Alford, J.; Anson, C.D.; Aparin, A.; Arkhipkin, D.; et al. Beam energy dependence of moments of the net-charge multiplicity distributions in Au+Au collisions at RHIC. Phys. Rev. Lett. 2014, 113, 092301. [Google Scholar] [CrossRef] [PubMed]
- Luo, X. Energy Dependence of Moments of Net-Proton and Net-Charge Multiplicity Distributions at STAR. In Proceedings of the 9th International Workshop on Critical Point and Onset of Deconfinement, Bielefeld, Germany, 17–21 November 2014.
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC. J. High Energy Phys. 2010, 1009, 91. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Measurement of long-range near-side two-particle angular correlations in pp collisions at = 13 TeV. Phys. Rev. Lett. 2016, 116, 172302. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdinov, O.; Aben, R.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; Abreu, R.; et al. Observation of Long-Range Elliptic Azimuthal Anisotropies in = 13 and 2.76 TeV pp Collisions with the ATLAS Detector. Phys. Rev. Lett. 2016, 116, 172301. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Observation of Associated Near-Side and Away-Side Long-Range Correlations in = 5.02 TeV Proton-Lead Collisions with the ATLAS Detector. Phys. Rev. Lett. 2013, 110, 182302. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of long-range near-side angular correlations in proton-lead collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Friedl, M.; Frühwirth, R.; Ghete, V.M.; et al. Evidence for Collective Multiparticle Correlations in p-Pb Collisions. Phys. Rev. Lett. 2015, 115, 012301. [Google Scholar] [CrossRef] [PubMed]
- Abelev, B.; Adam, J.; Adamova, D.; Adare, A.M.; Aggarwal, M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Long-range angular correlations on the near and away side in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2013, 719, 29–41. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Ta’ani, H.; Andrews, K.R. Measurements of elliptic and triangular flow in high-multiplicity 3He+Au collisions at = 200 GeV. Phys. Rev. Lett. 2015, 115, 142301. [Google Scholar] [CrossRef] [PubMed]
- Orjuela Koop, J.D.; Adare, A.; McGlinchey, D.; Nagle, J.L. Azimuthal anisotropy relative to the participant plane from a multiphase transport model in central p + Au , d + Au , and 3He + Au collisions at = 200 GeV. Phys. Rev. C 2015, 92, 054903. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Balewski, J.; Barannikova, O.; Barnby, L.S.; Baudot, J.; et al. Long range rapidity correlations and jet production in high energy nuclear collisions. Phys. Rev. C 2009, 80, 064912. [Google Scholar] [CrossRef]
- Alver, B.; Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Busza, W.; Carroll, A.; et al. High transverse momentum triggered correlations over a large pseudorapidity acceptance in Au+Au collisions at s(NN)**1/2 = 200 GeV. Phys. Rev. Lett. 2010, 104, 062301. [Google Scholar] [CrossRef] [PubMed]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; et al. Harmonic decomposition of two-particle angular correlations in Pb-Pb collisions at = 2.76 TeV. Phys. Lett. B 2012, 708, 249–264. [Google Scholar] [CrossRef]
- Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alakhverdyants, A.V.; Alekseev, I.; Alford, J.; Anderson, B.D.; Anson, C.D.; Arkhipkin, D.; Averichev, G.S.; et al. System size and energy dependence of near-side di-hadron correlations. Phys. Rev. C 2012, 85, 014903. [Google Scholar] [CrossRef]
- Voloshin, S.A. Two particle rapidity, transverse momentum, and azimuthal correlations in relativistic nuclear collisions and transverse radial expansion. Nucl. Phys. A 2005, 749, 287–290. [Google Scholar] [CrossRef]
- Rezaeian, A.H. Photon-jet ridge at RHIC and the LHC. Phys. Rev. D 2016, 93, 094030. [Google Scholar] [CrossRef]
- Dusling, K.; Tribedy, P.; Venugopalan, R. Energy dependence of the ridge in high multiplicity proton-proton collisions. Phys. Rev. D 2016, 93, 014034. [Google Scholar] [CrossRef]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; Abolins, M.; et al. Measurement with the ATLAS detector of multi-particle azimuthal correlations in p+Pb collisions at = 5.02 TeV. Phys. Lett. B 2013, 725, 60–78. [Google Scholar]
- Abelev, B.; Adam, J.; Adamová, D.; Adaredu, A.M.; Aggarwalcc, M.M.; Rinellaag, G.A.; Ci, M.A.; Agocsdt, A.G.; Agostinelliy, A.; Ahammed, Z. Long-range angular correlations of ß, K and p in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2013, 726, 164–177. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agostinelli, A.; Agrawal, N.; Ahammed, Z.; Ahmad, N.; et al. Multiparticle azimuthal correlations in p -Pb and Pb-Pb collisions at the CERN Large Hadron Collider. Phys. Rev. C 2014, 90, 054901. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Long-range two-particle correlations of strange hadrons with charged particles in pPb and PbPb collisions at LHC energies. Phys. Lett. B 2015, 742, 200–224. [Google Scholar] [CrossRef]
- Hirono, Y.; Shuryak, E. Femtoscopic signature of strong radial flow in high-multiplicity pp collisions. Phys. Rev. C 2015, 91, 054915. [Google Scholar] [CrossRef]
- Bozek, P.; Broniowski, W. Correlations from hydrodynamic flow in p-Pb collisions. Phys. Lett. B 2013, 718, 1557. [Google Scholar] [CrossRef]
- Bozek, P.; Broniowski, W.; Torrieri, G. Mass hierarchy in identified particle distributions in proton-lead collisions. Phys. Rev. Lett. 2013, 111, 172303. [Google Scholar] [CrossRef] [PubMed]
- Werner, K.; Bleicher, M.; Guiot, B.; Karpenko, I.; Pierog, T. Evidence for Flow from Hydrodynamic Simulations of p-Pb Collisions at 5.02 TeV from ν2 Mass Splitting. Phys. Rev. Lett. 2014, 112, 232301. [Google Scholar] [CrossRef] [PubMed]
- Romatschke, P. Light-Heavy Ion Collisions: A window into pre-equilibrium QCD dynamics? Eur. Phys. J. C 2015, 75, 305. [Google Scholar] [CrossRef]
- Niemi, H. Recent developments in hydrodynamics and collectivity in small systems. In Proceedings of the European Physical Society Conference on High Energy Physics (EPS-HEP2015), Vienna, Austria, 22–29 July 2015.
- Koblesky, T. Collectivity in Small QCD Systems. In Proceedings of the CIPANP2015 Conference, Vail, CO, USA, 19–24 May 2015.
- Schenke, B.; Venugopalan, R. Eccentric protons? Sensitivity of flow to system size and shape in p+p, p+Pb and Pb+Pb collisions. Phys. Rev. Lett. 2014, 113, 102301. [Google Scholar] [CrossRef] [PubMed]
- Bzdak, A.; Ma, G.L. Elliptic and triangular flow in p+Pb and peripheral Pb+Pb collisions from parton scatterings. Phys. Rev. Lett. 2014, 113, 252301. [Google Scholar] [CrossRef] [PubMed]
- Bozek, P.; Bzdak, A.; Ma, G.L. Rapidity dependence of elliptic and triangular flow in proton–nucleus collisions from collective dynamics. Phys. Lett. B 2015, 748, 301–305. [Google Scholar] [CrossRef]
- Antinori, F.; Becattini, F.; Braun-Munzinger, P.; Chujo, T.; Hamagaki, H.; Harris, J.; Heinz, U.; Hippolyte, B.; Hirano, T.; Jacak, B.; et al. Thoughts on Heavy-Ion Physics in the High Luminosity Era: The Soft Sector. arXiv, 2016; arXiv:1604.03310. [Google Scholar]
- Bala, R.; Bautista, I.; Bielcikova, J.; Ortiz, A. Heavy-ion physics at the LHC: Review of Run I results. Int. J. Mod. Phys. E 2016, 25, 1642006. [Google Scholar] [CrossRef]
- Sinyukov, Y.M.; Akkelin, S.V.; Karpenko, I.A.; Shapoval, V.M. Femtoscopic and Nonfemtoscopic Two-Particle Correlations in A + A and p + p Collisions at RHIC and LHC Energies. Adv. High Energy Phys. 2013, 2013, 198928. [Google Scholar] [CrossRef]
- Lisa, M. Timescales in heavy ion collisions. Acta Phys. Pol. B 2016, 47, 1847–1855. [Google Scholar] [CrossRef]
- 1.The string picture of hadrons also makes it possible to explain the transition from a hadronic to a QGP state of matter at finite temperature T as a phase transition from the ordered state to the disordered state (see Ref. [9], p. 44). With T approaching the critical temperature of deconfinement , the effective string tension decreases, and q and attached to its end points lose their correlation.
- 2.For a representative collection of papers tracing the development of theoretical ideas on the QCD deconfining phase transition before nineties , see Ref. [19].
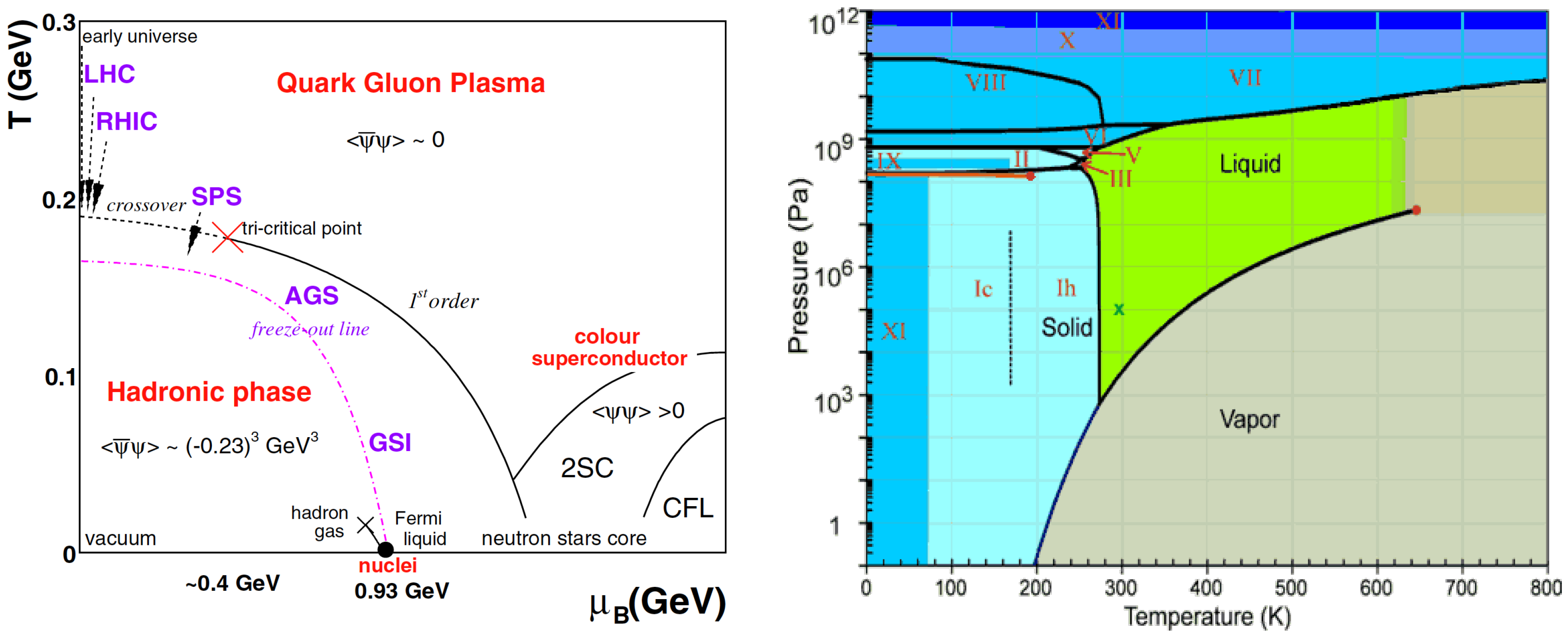
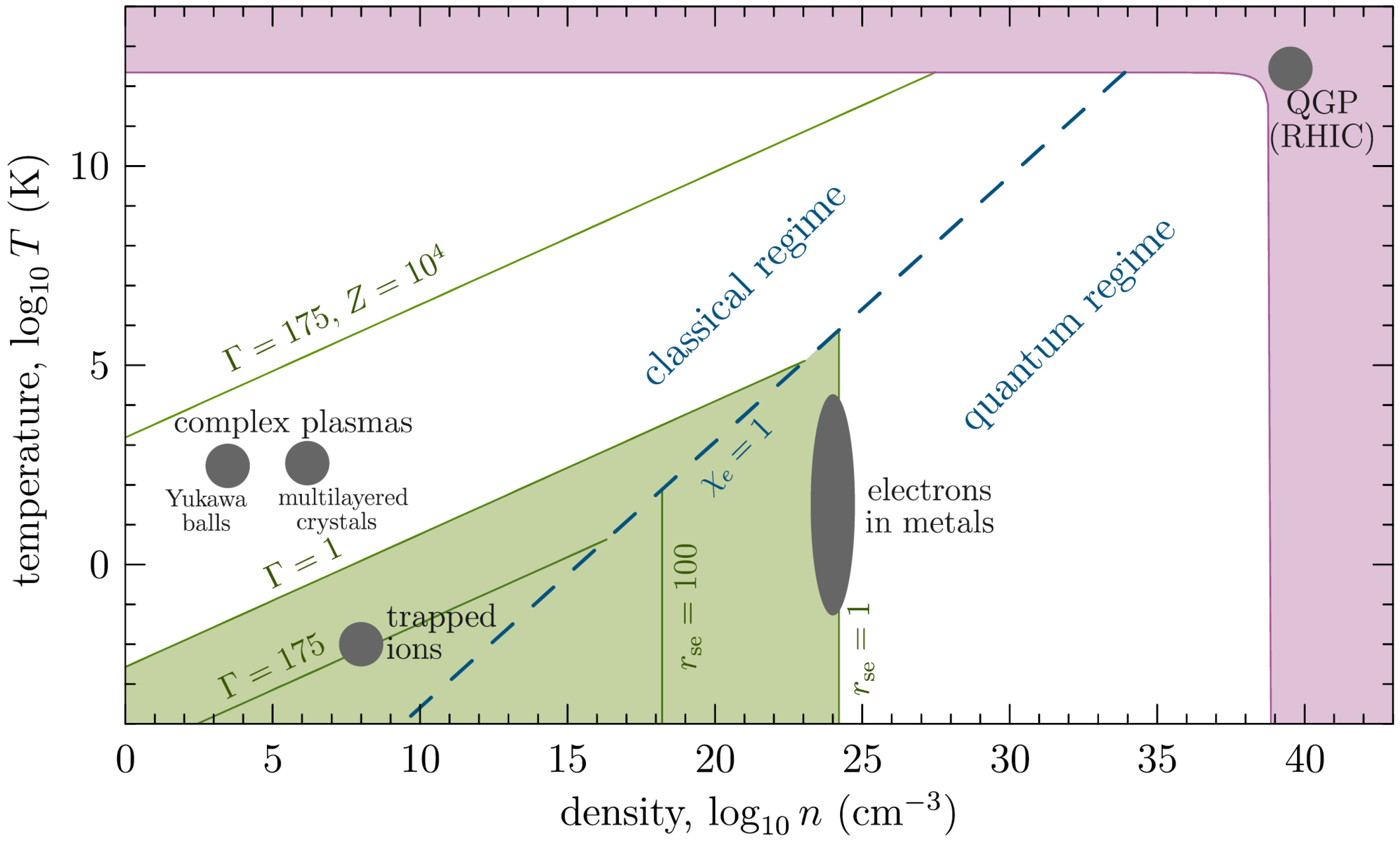
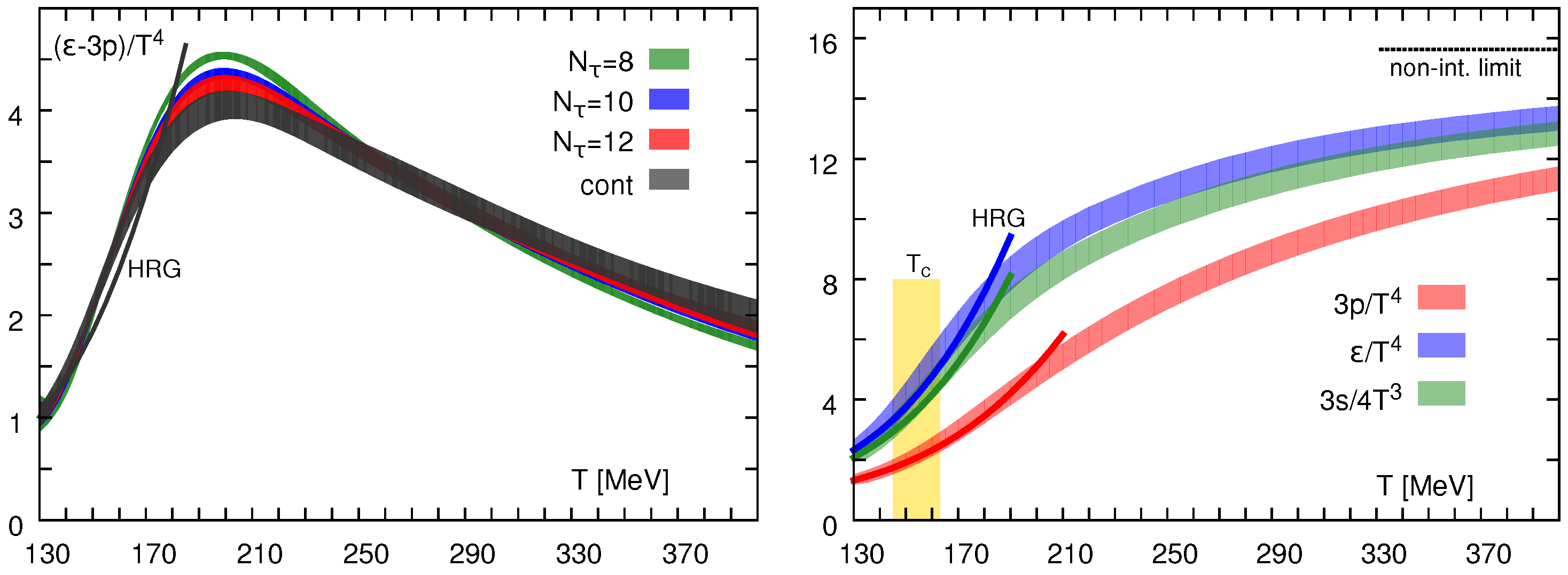
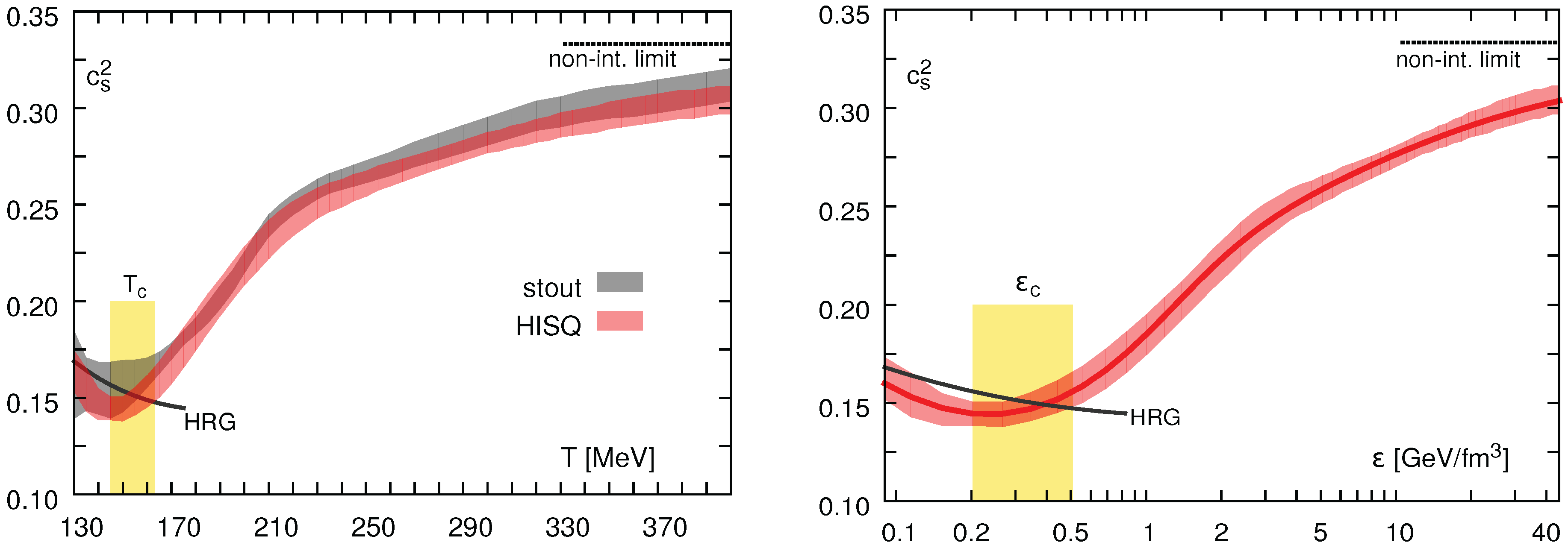
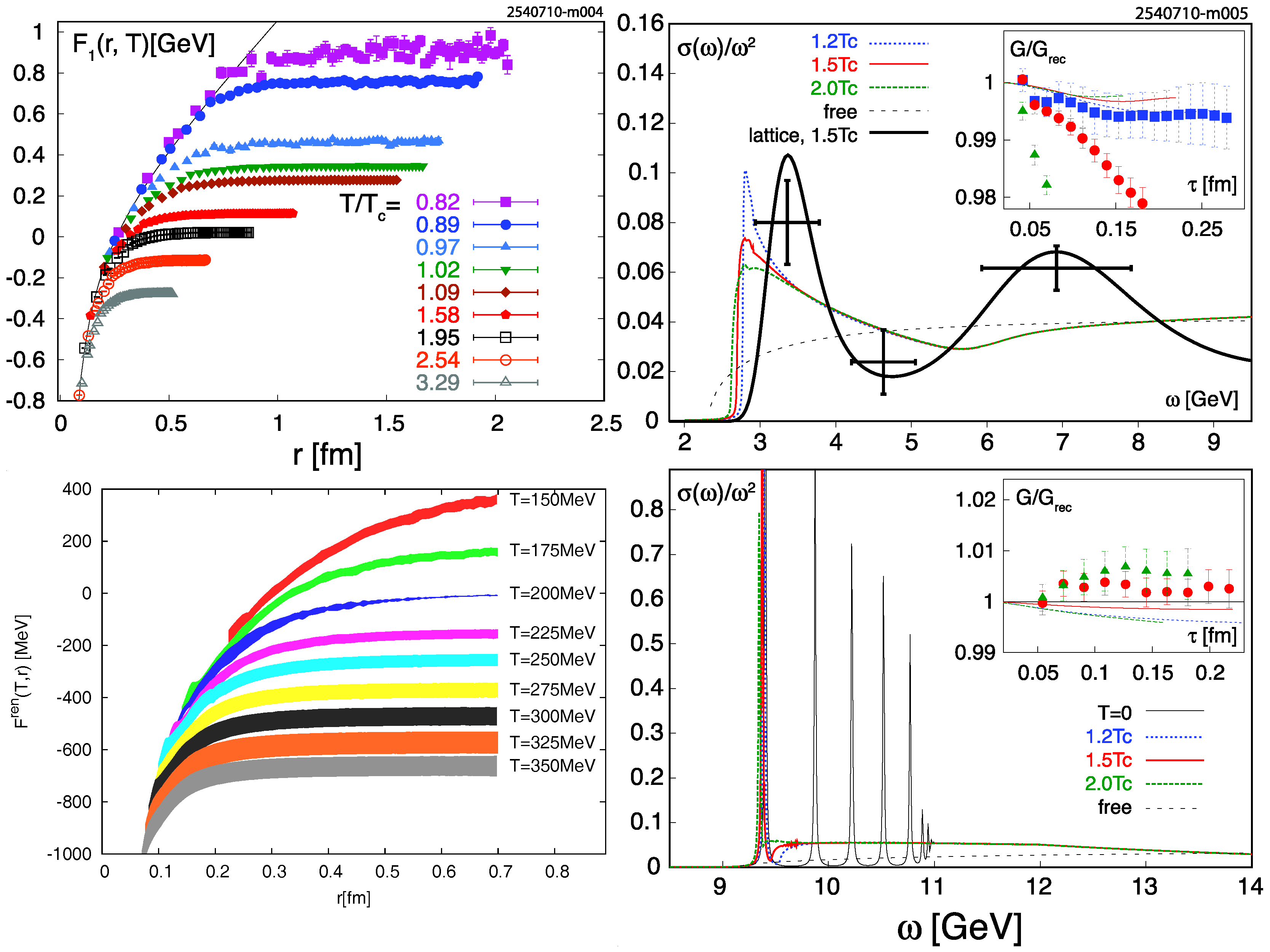
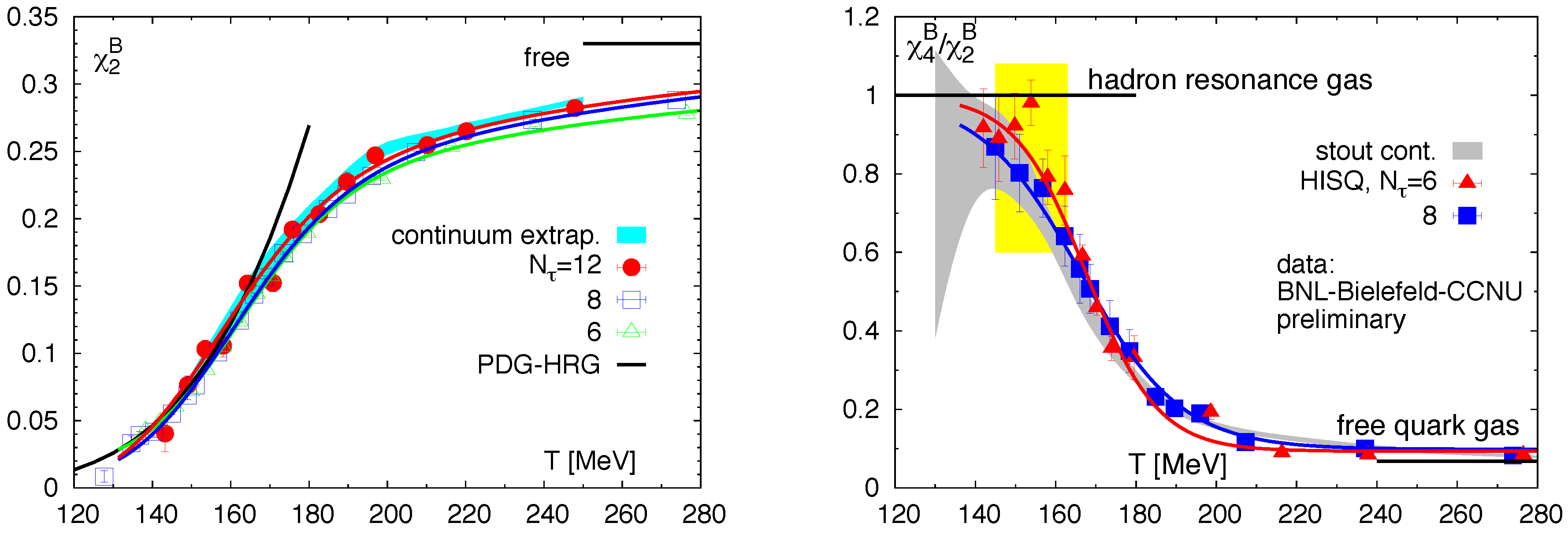
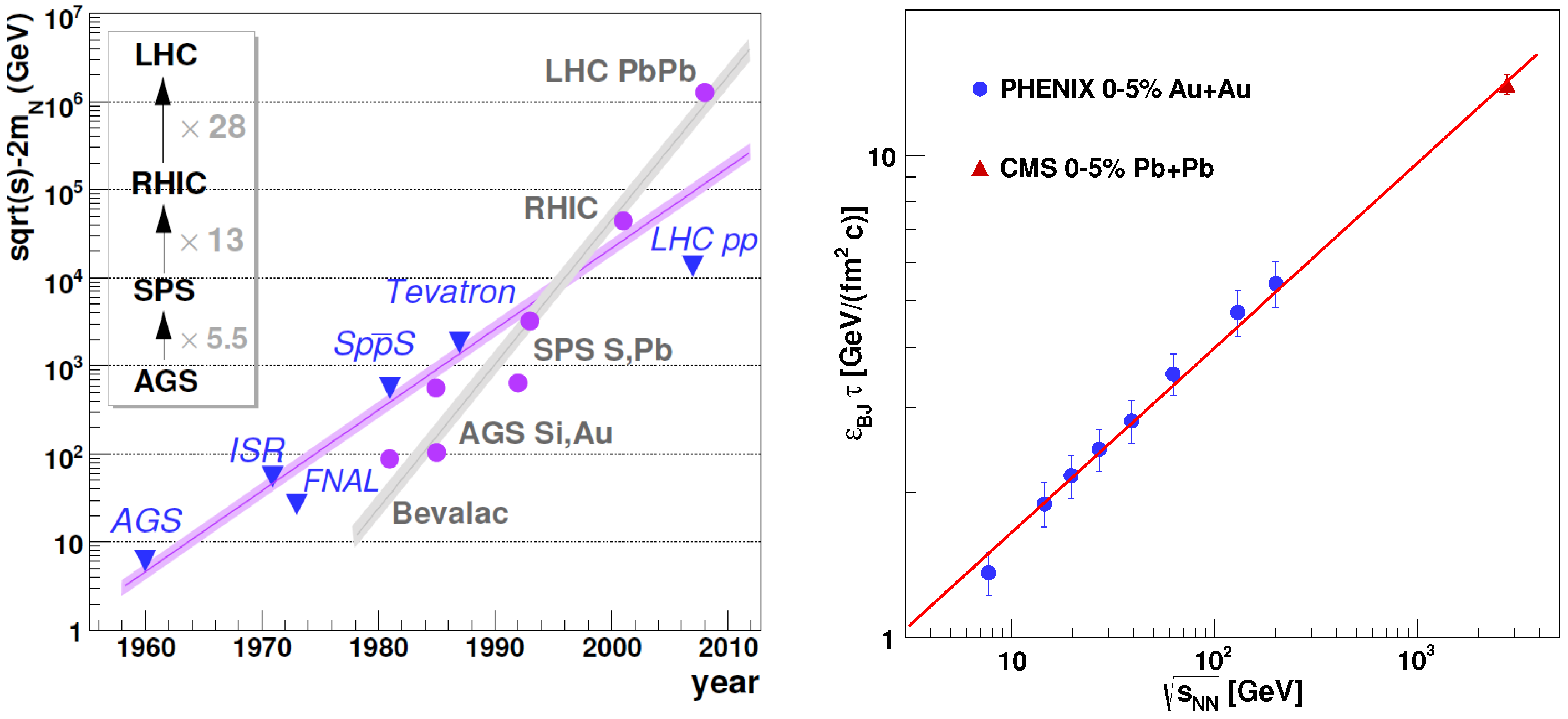
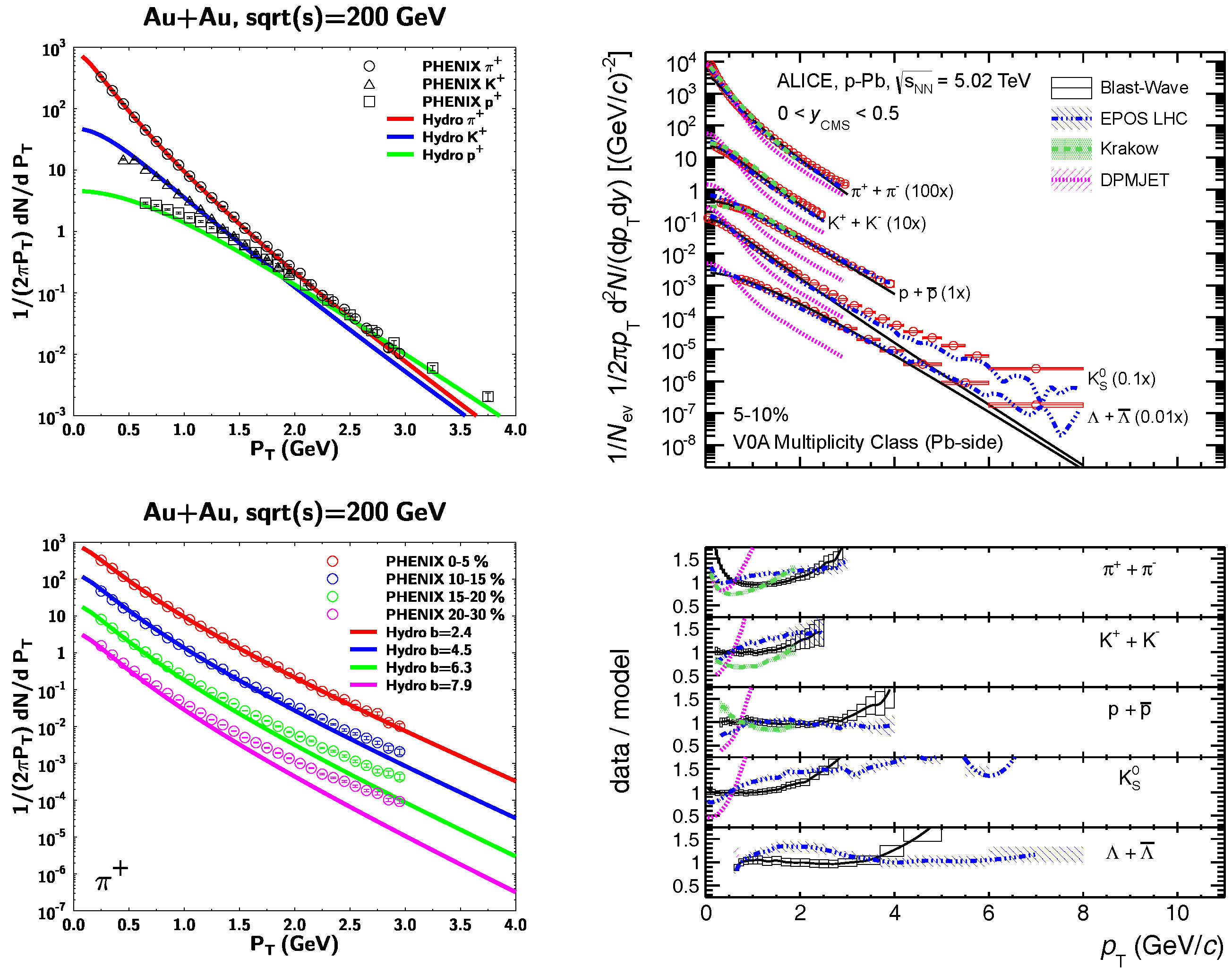
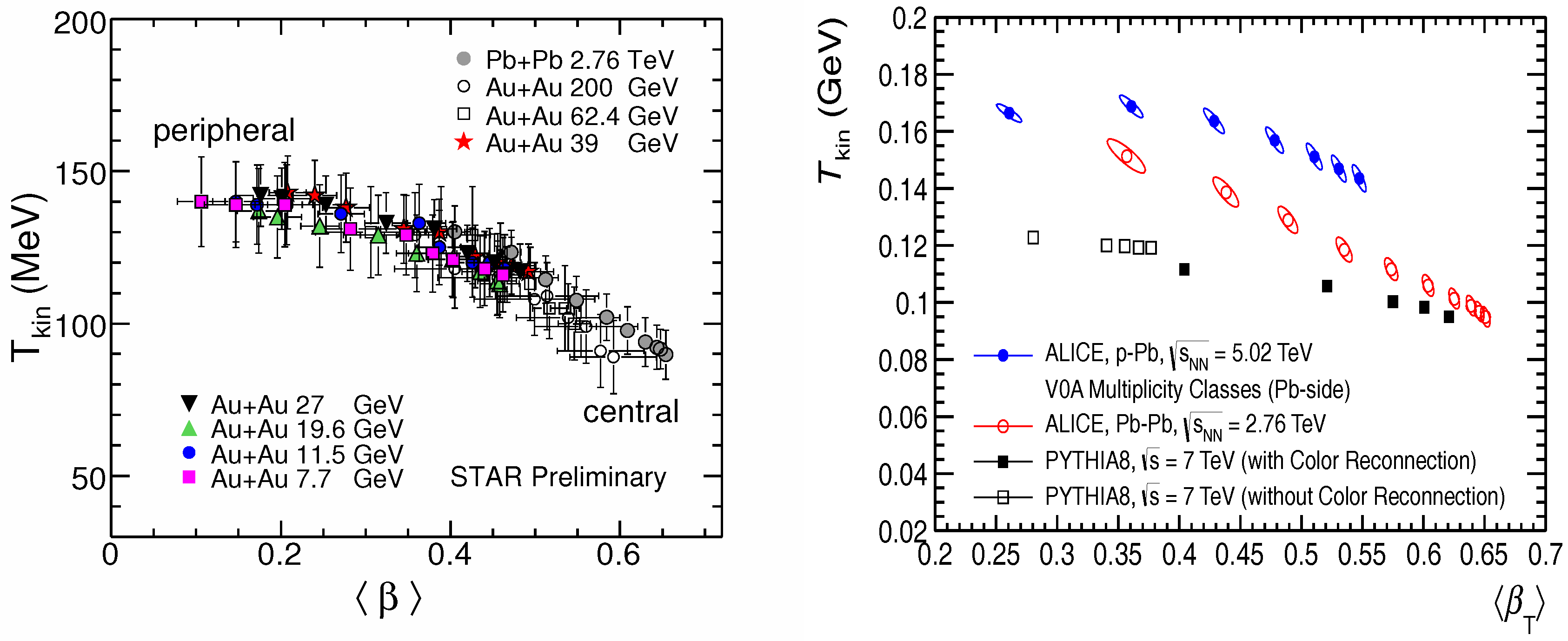
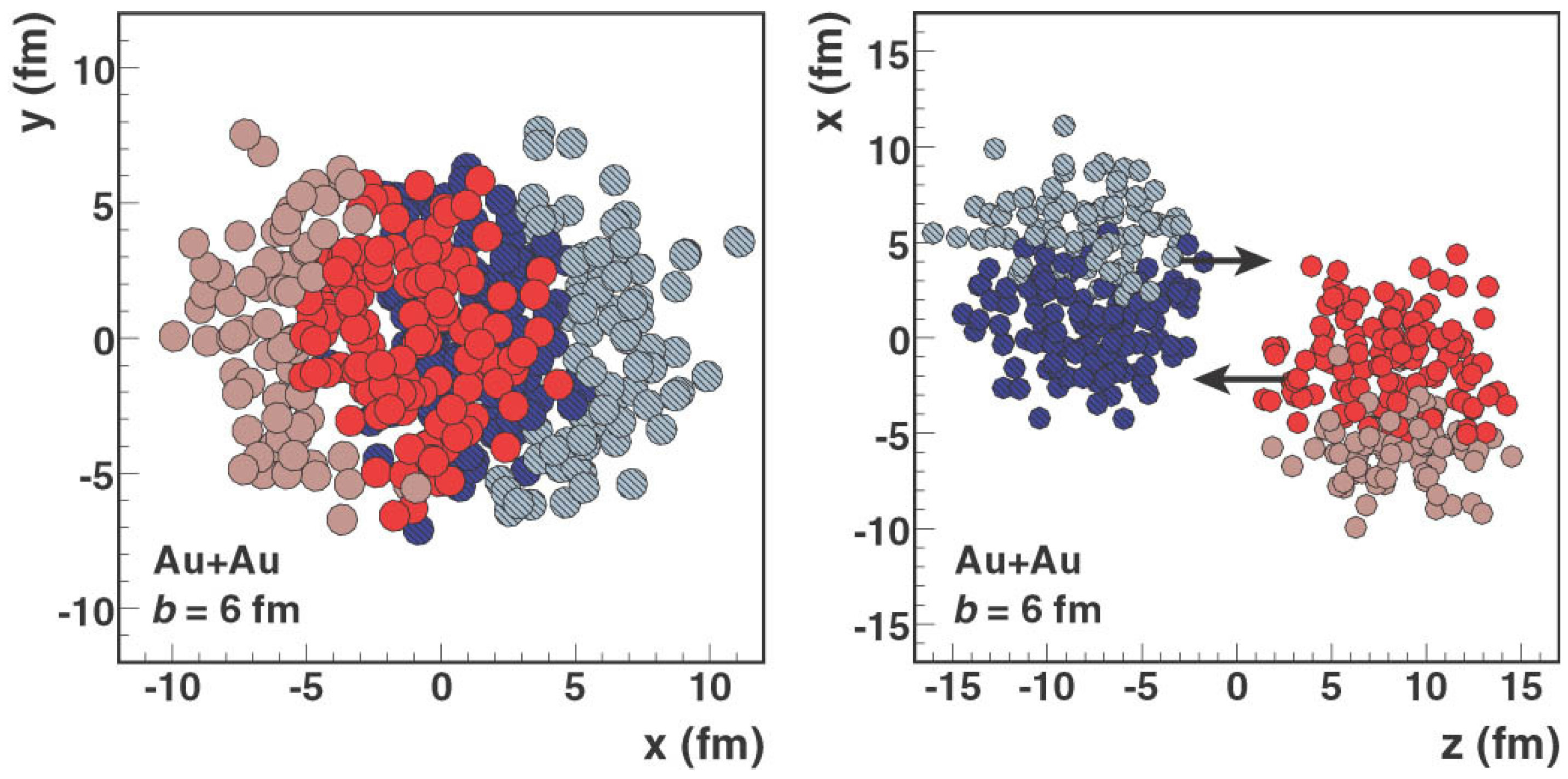
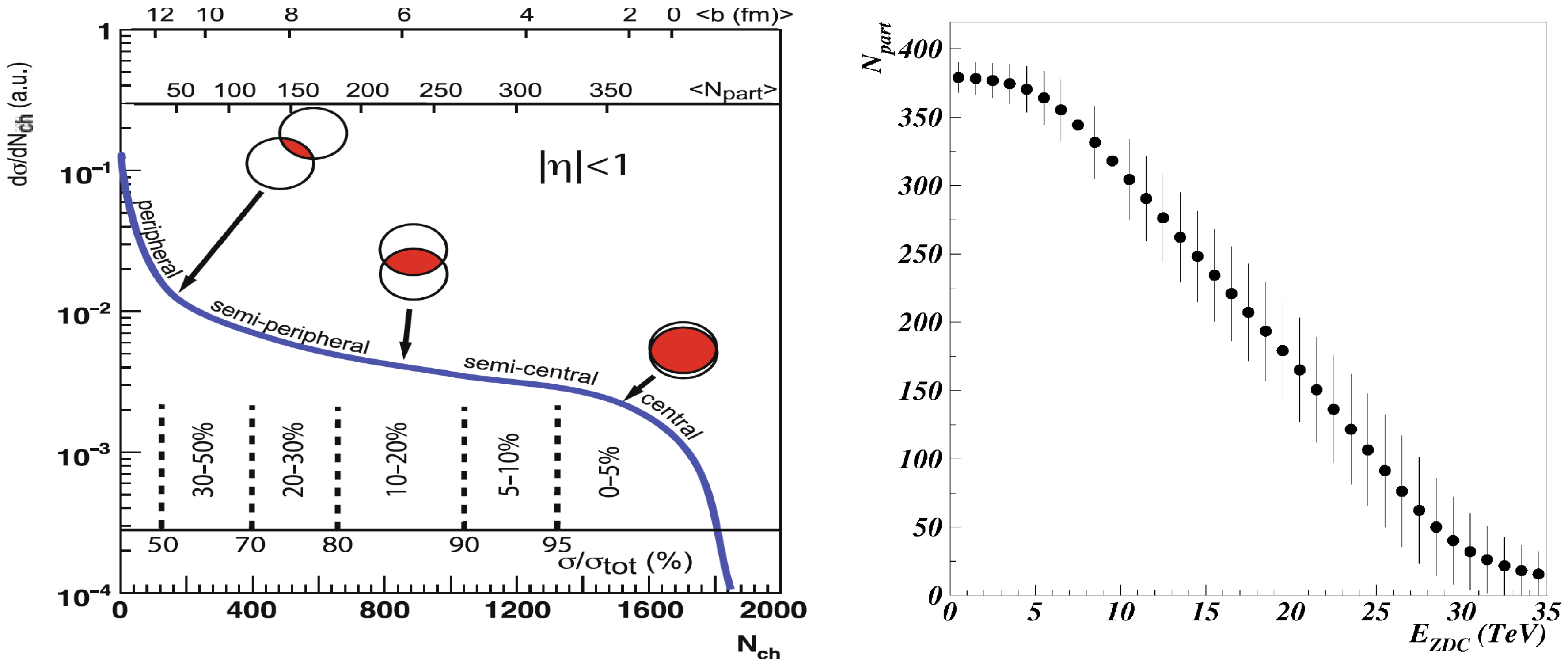

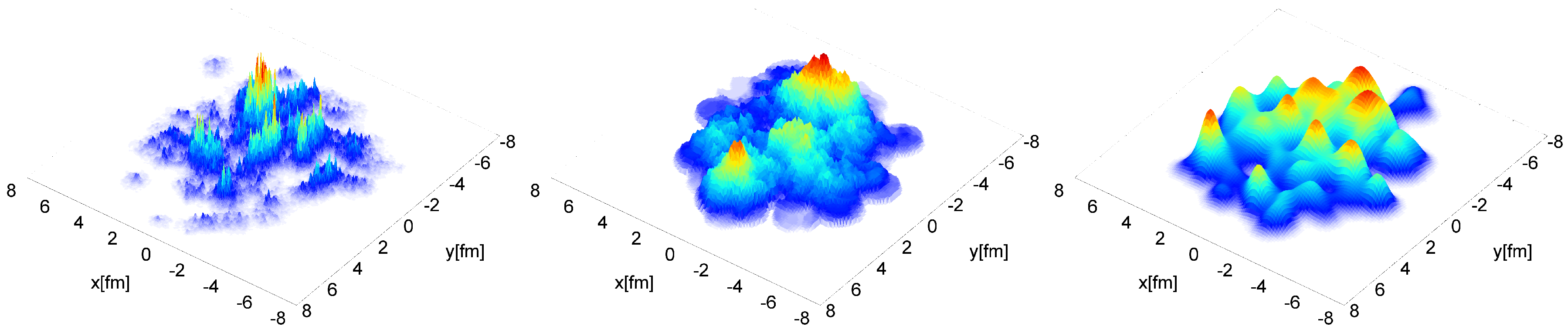
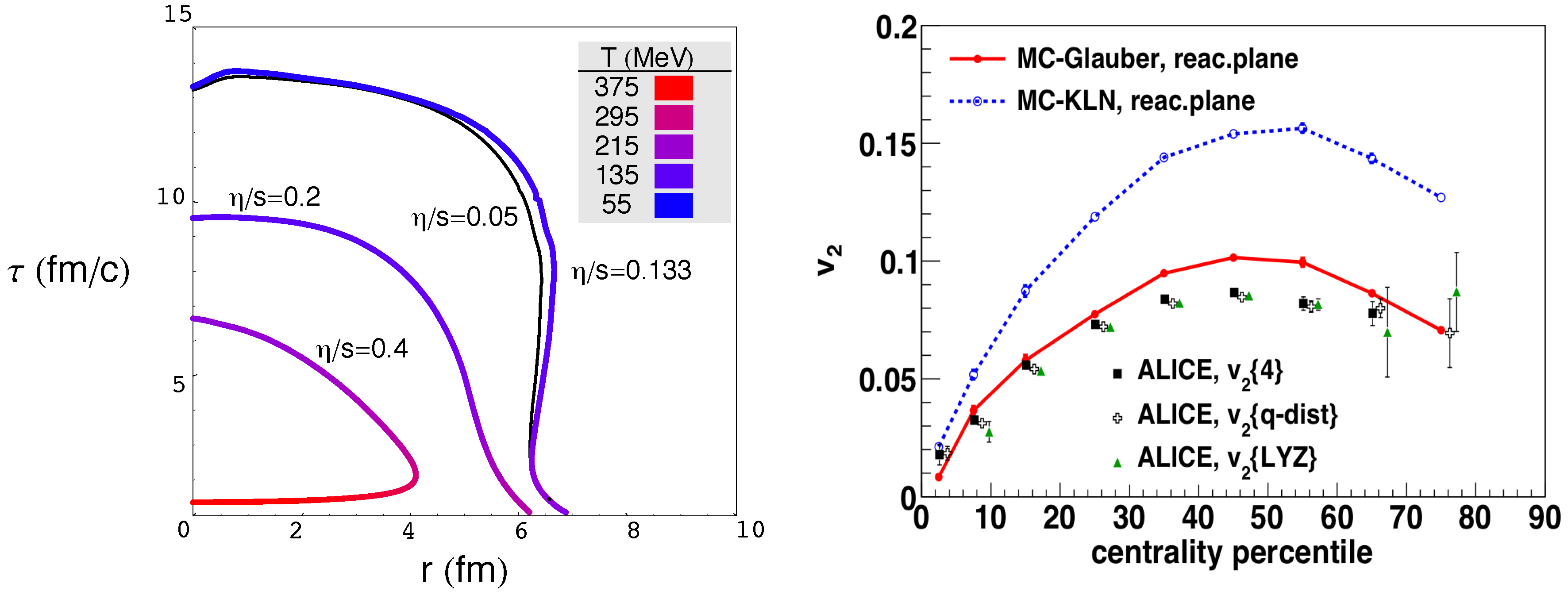
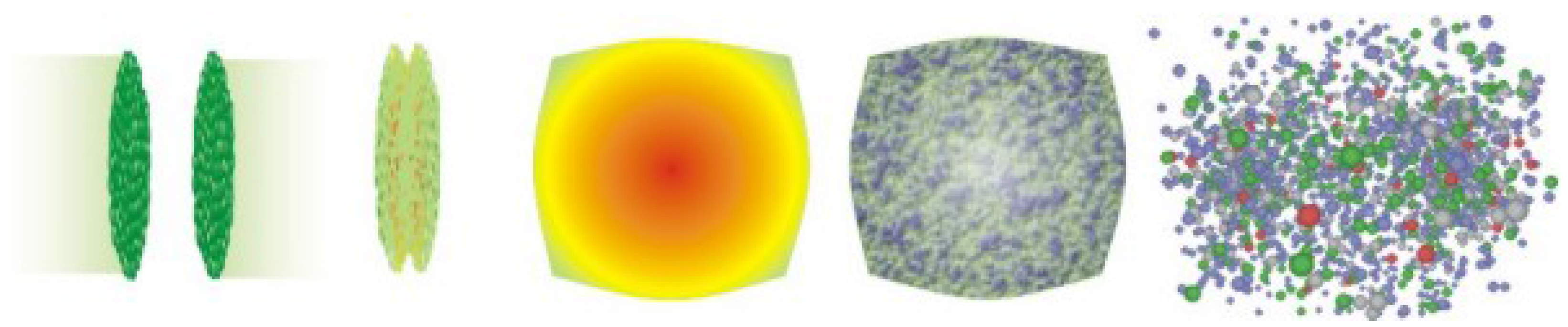
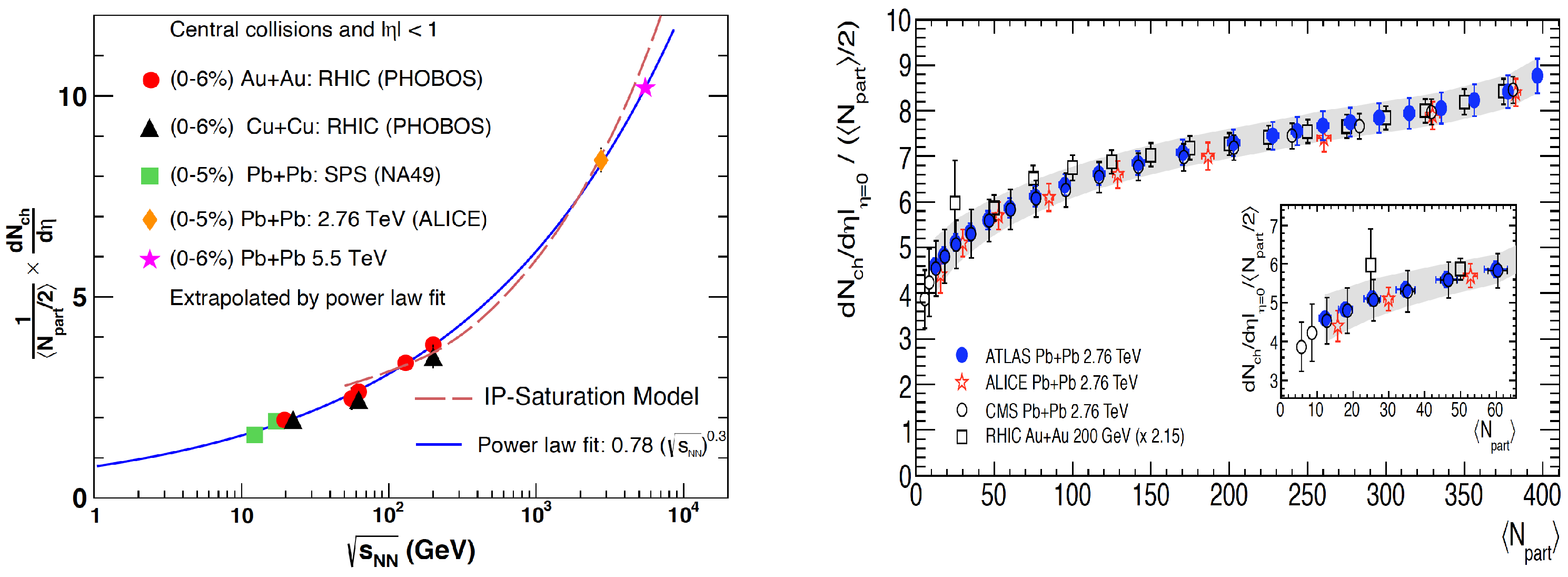
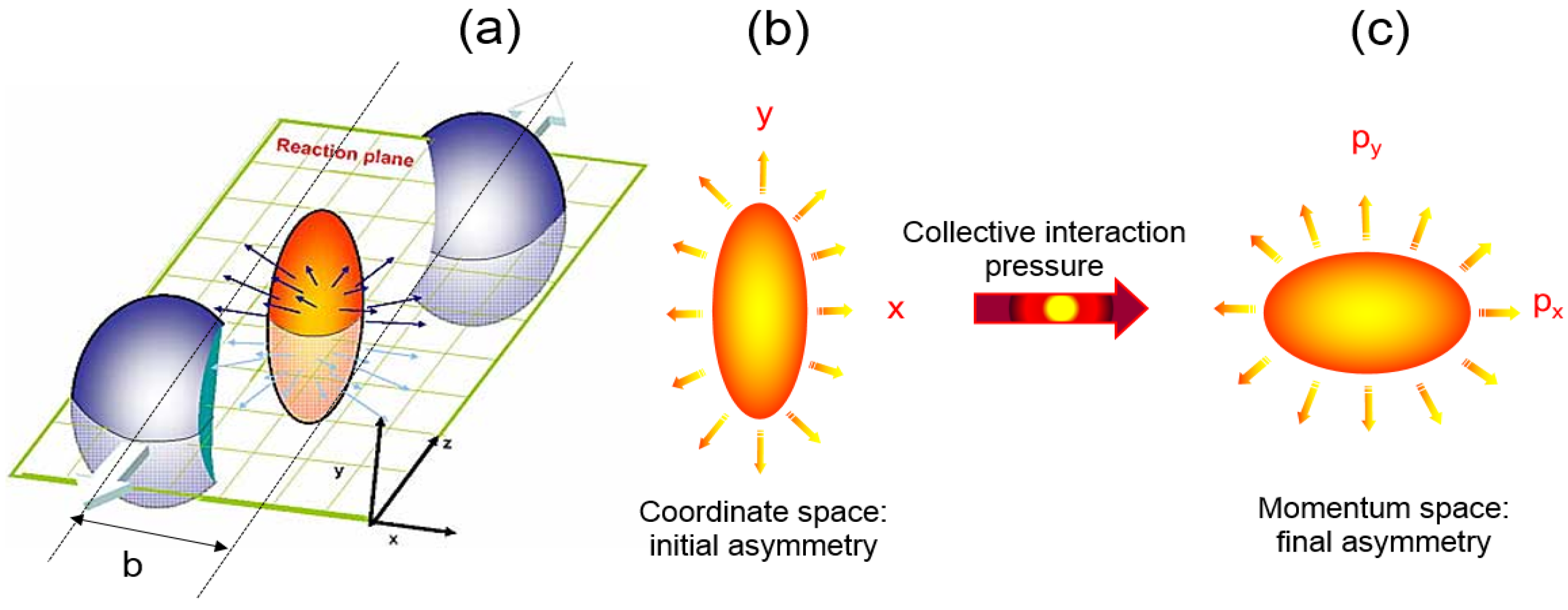
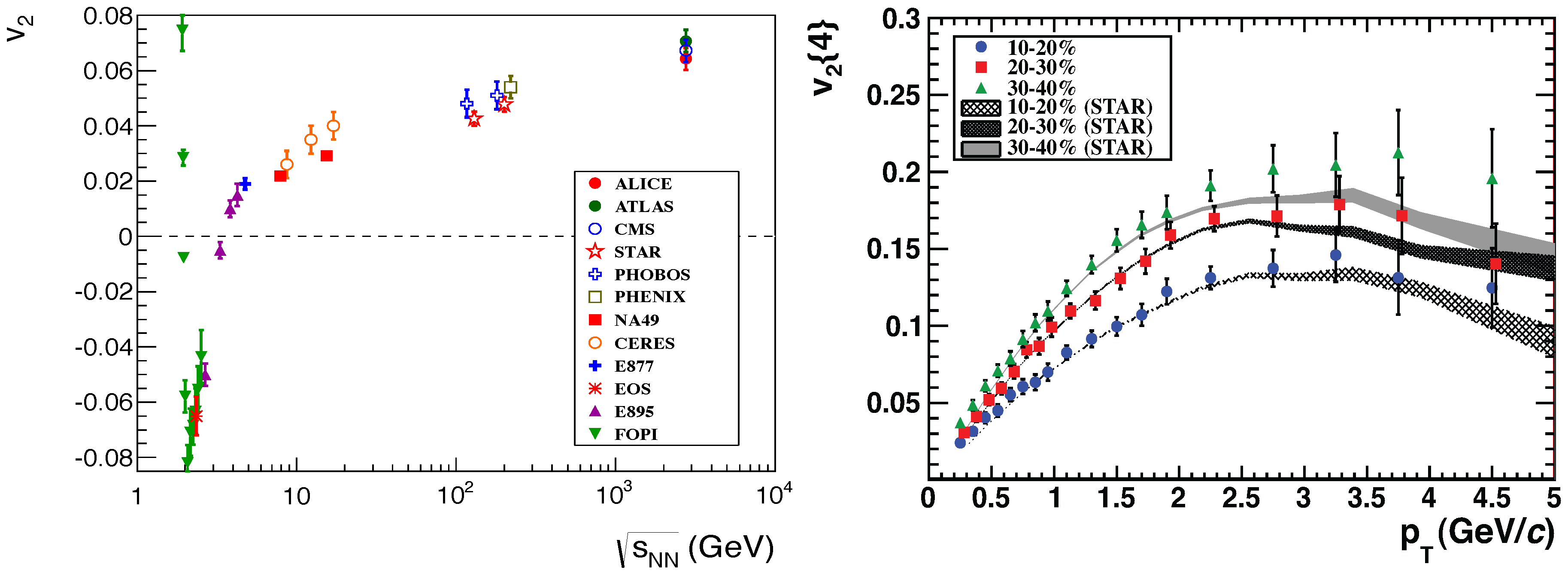
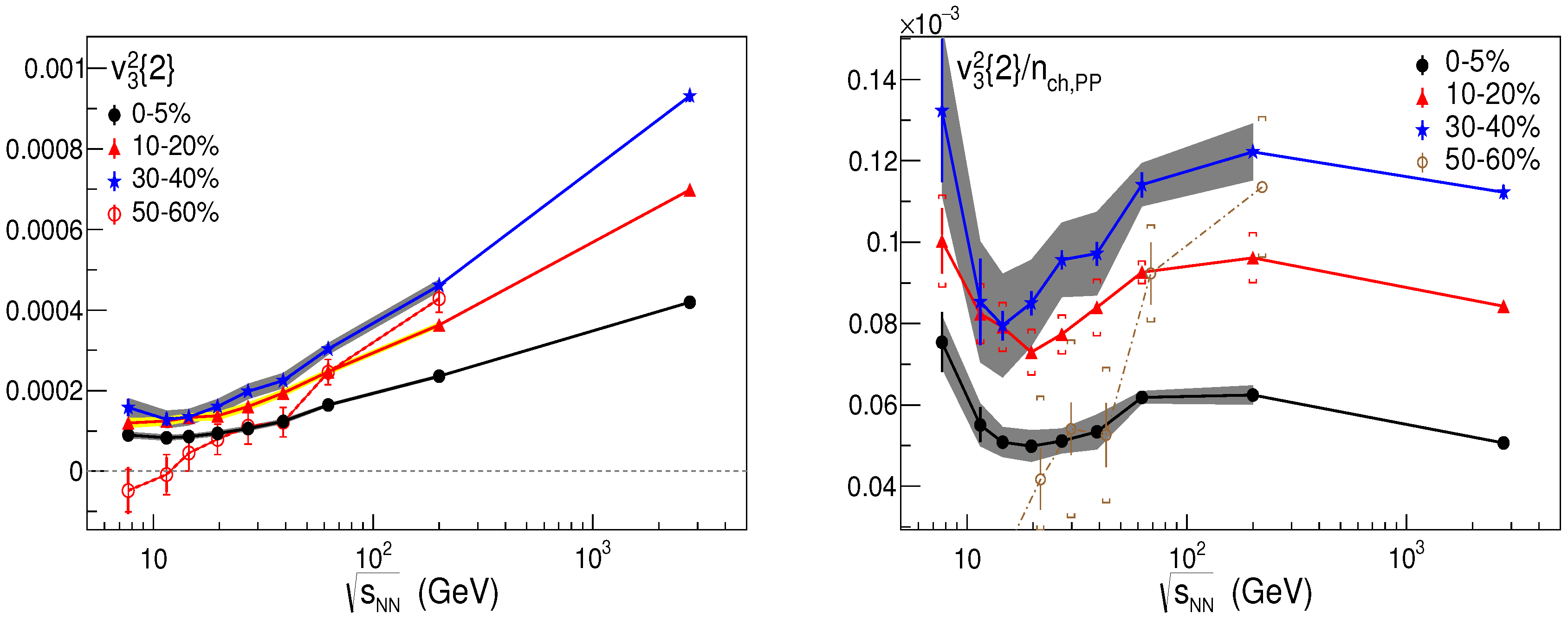
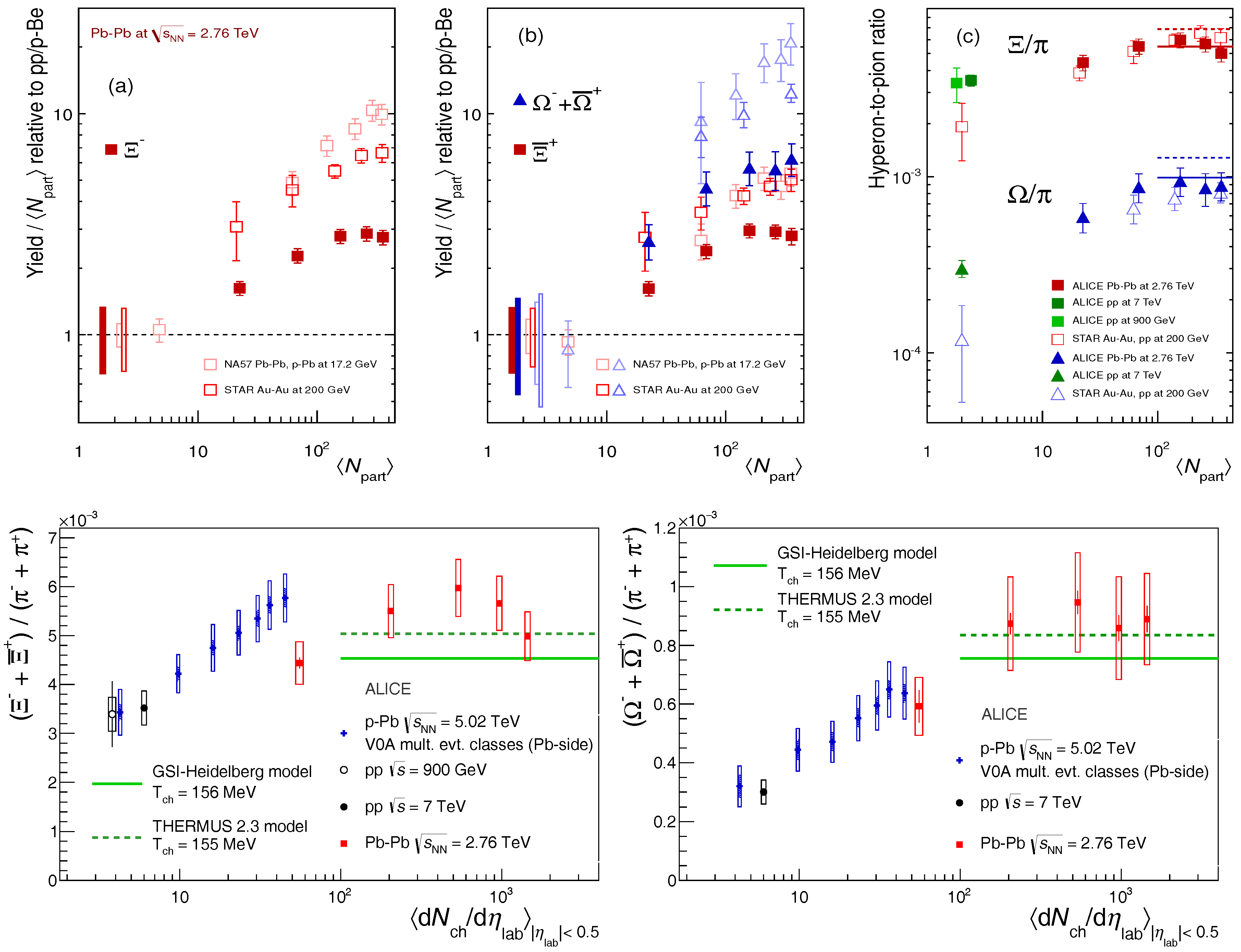
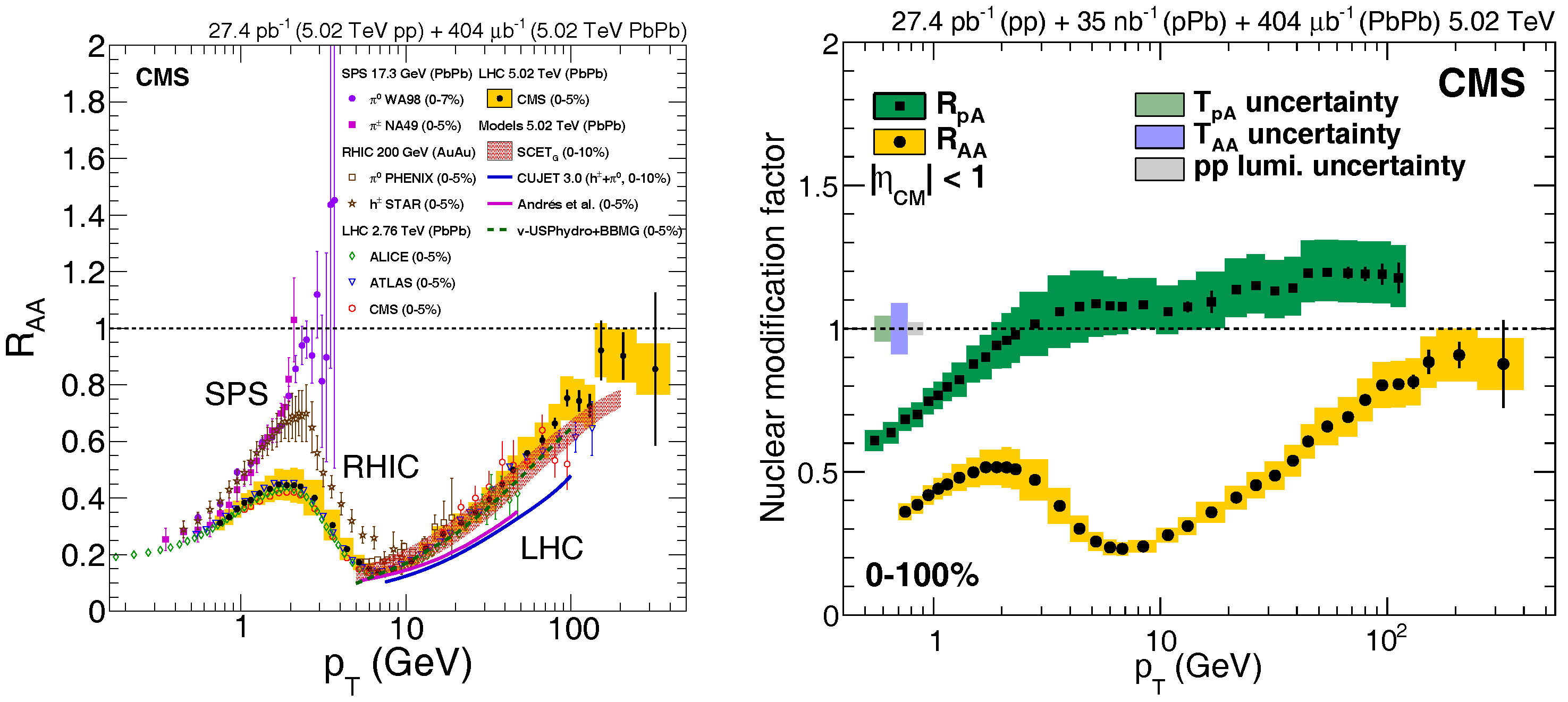
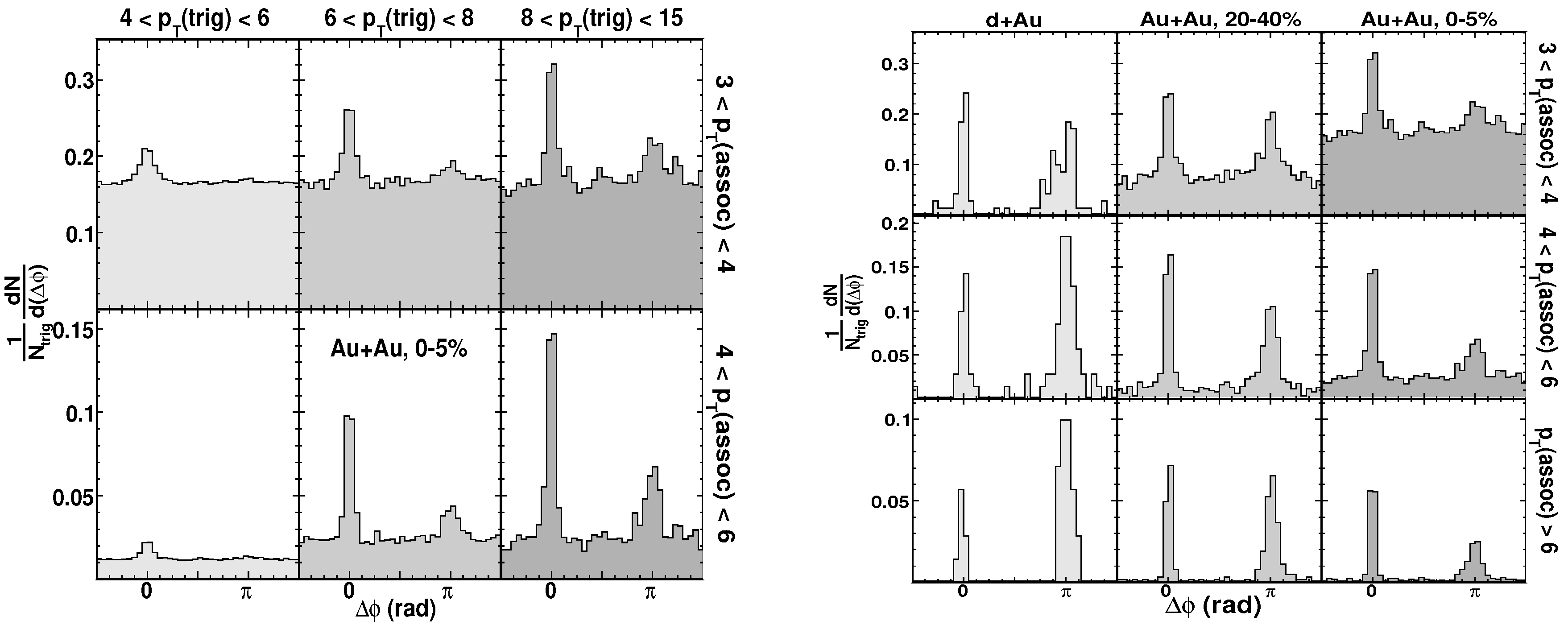
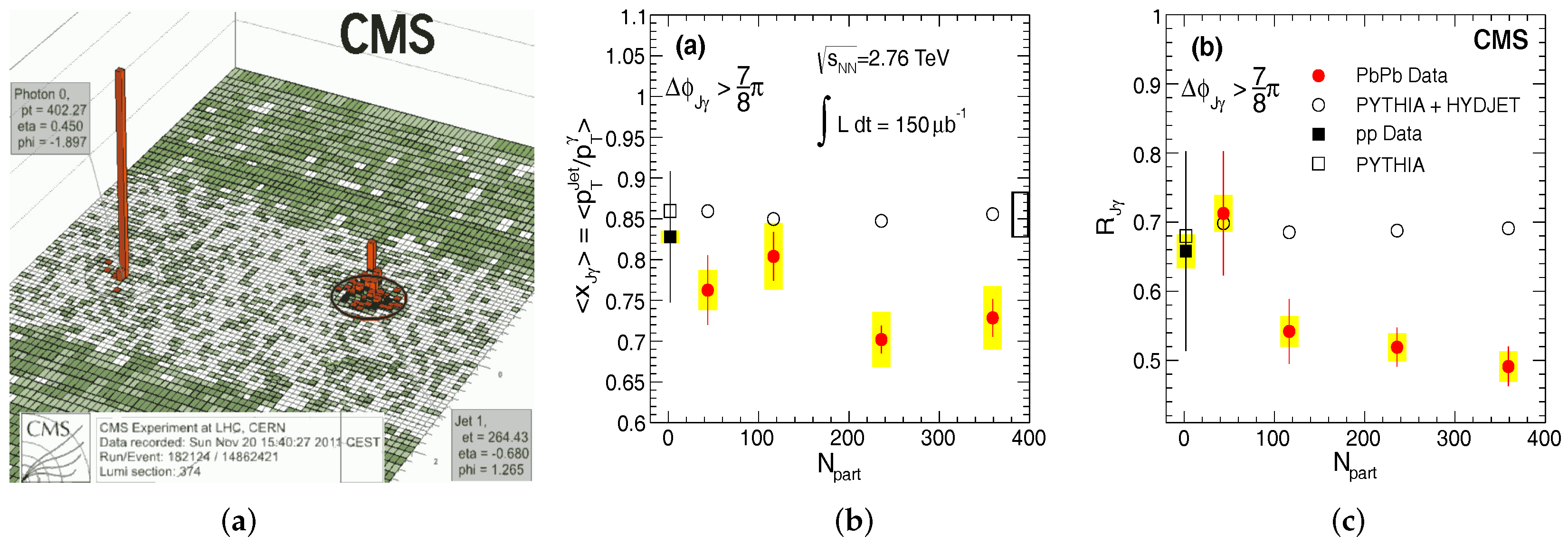
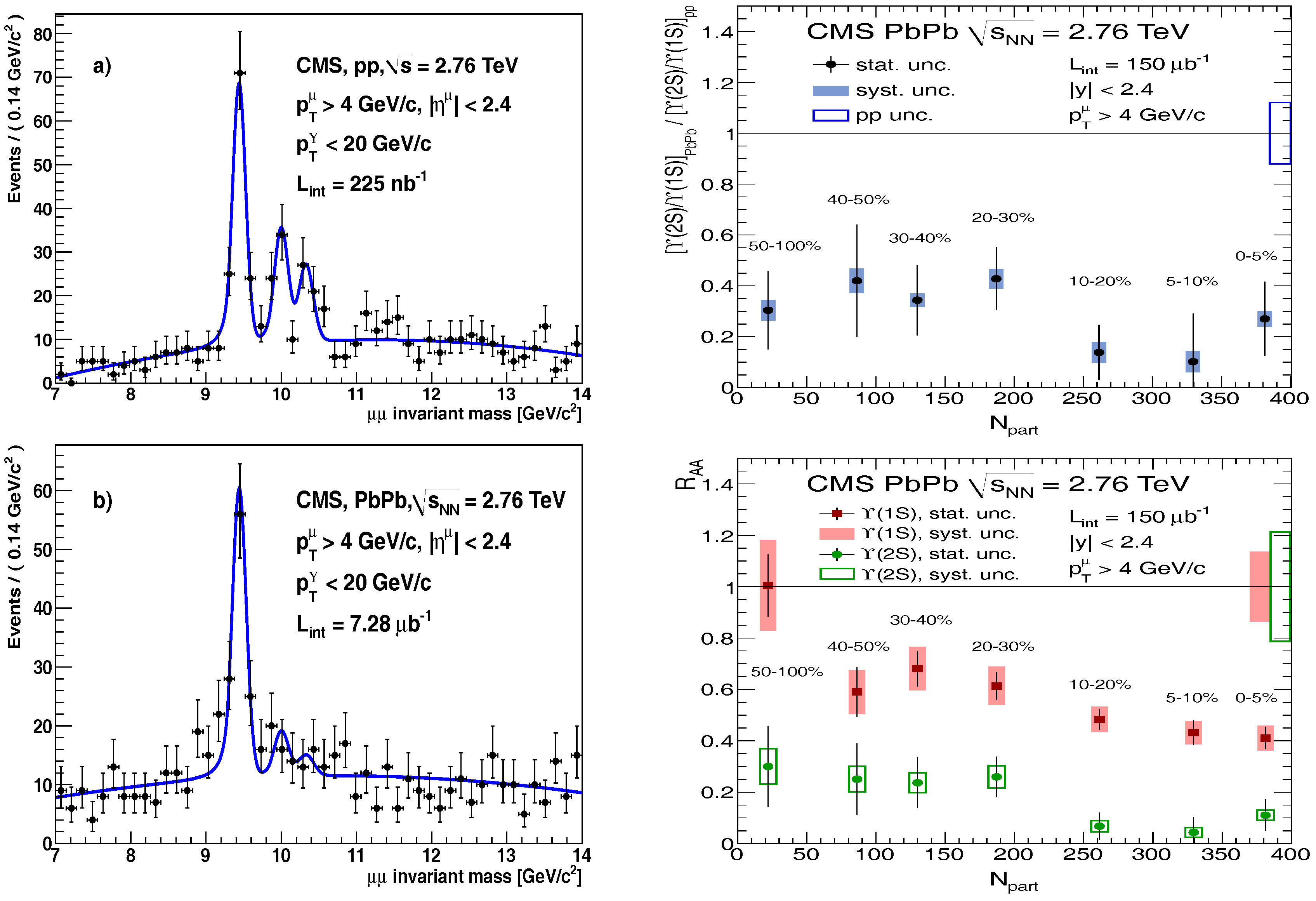
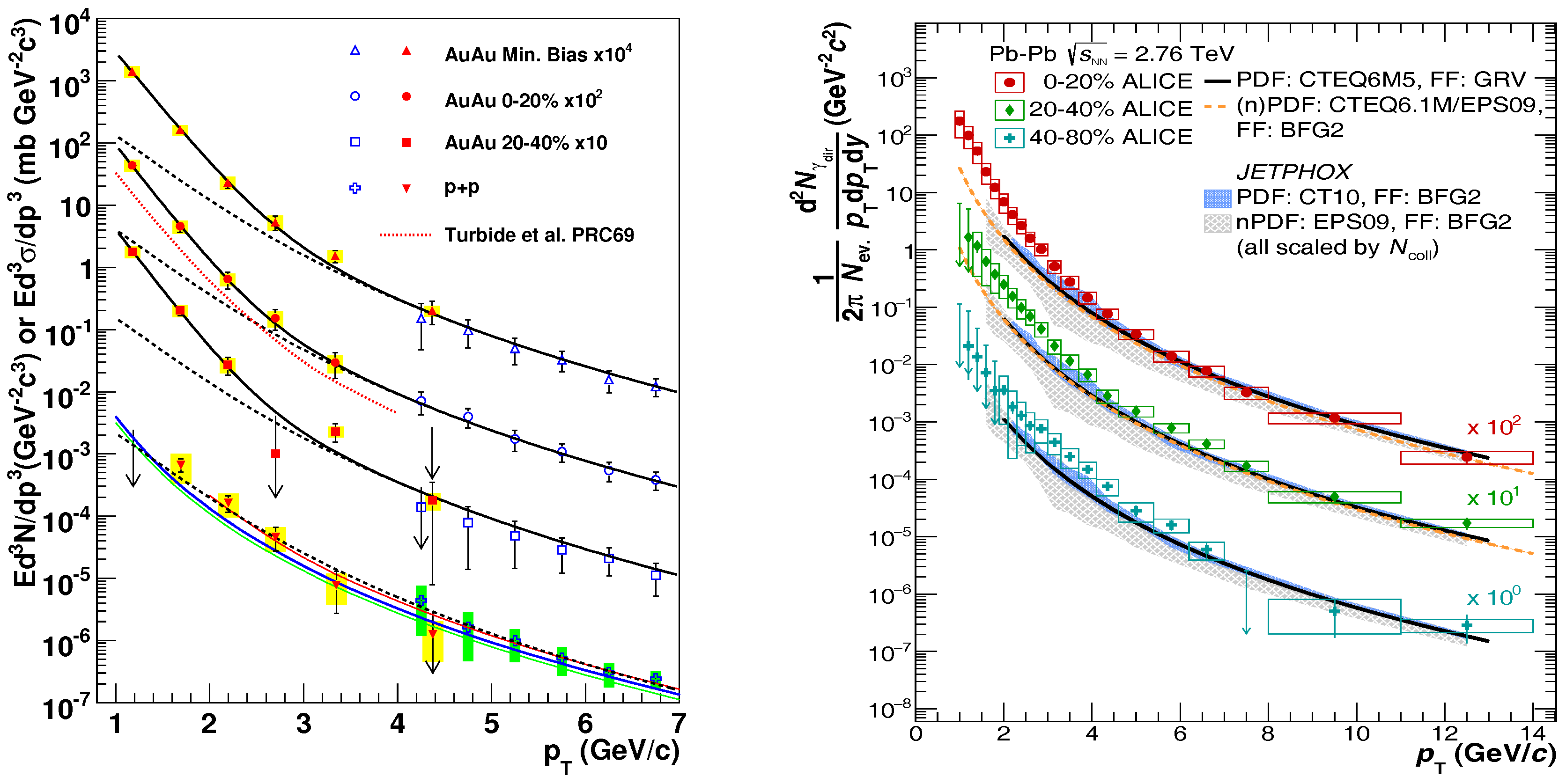
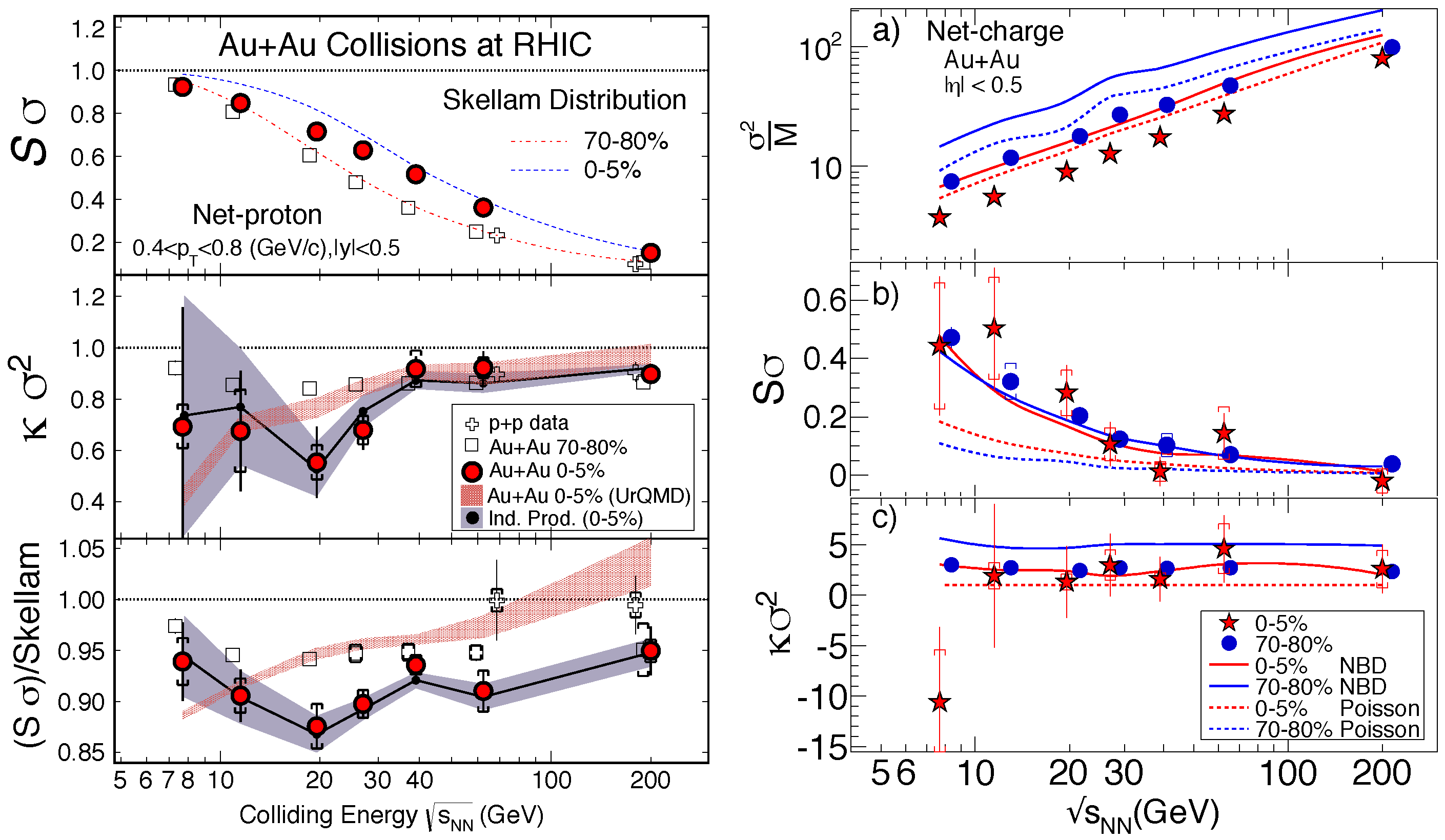
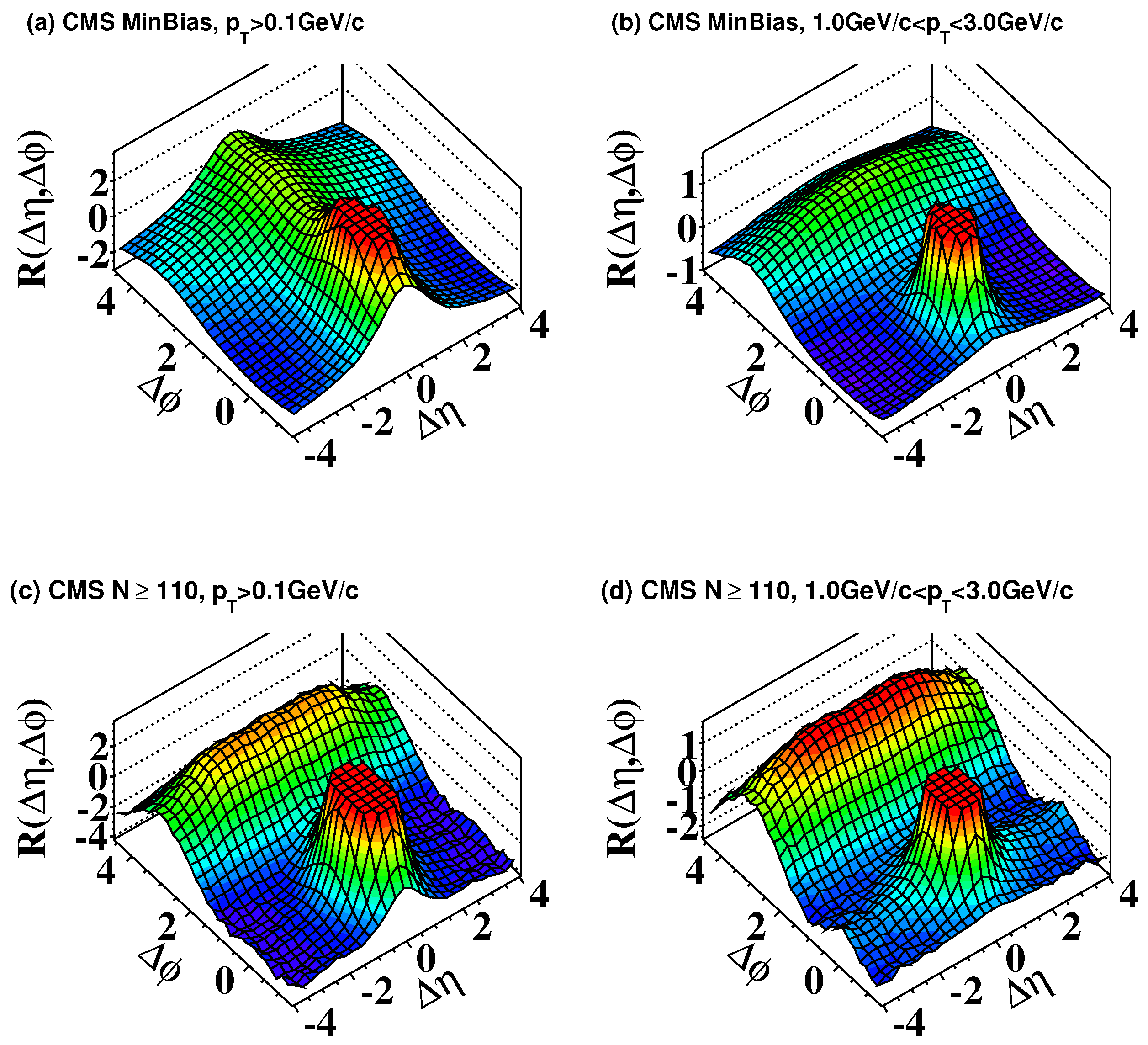
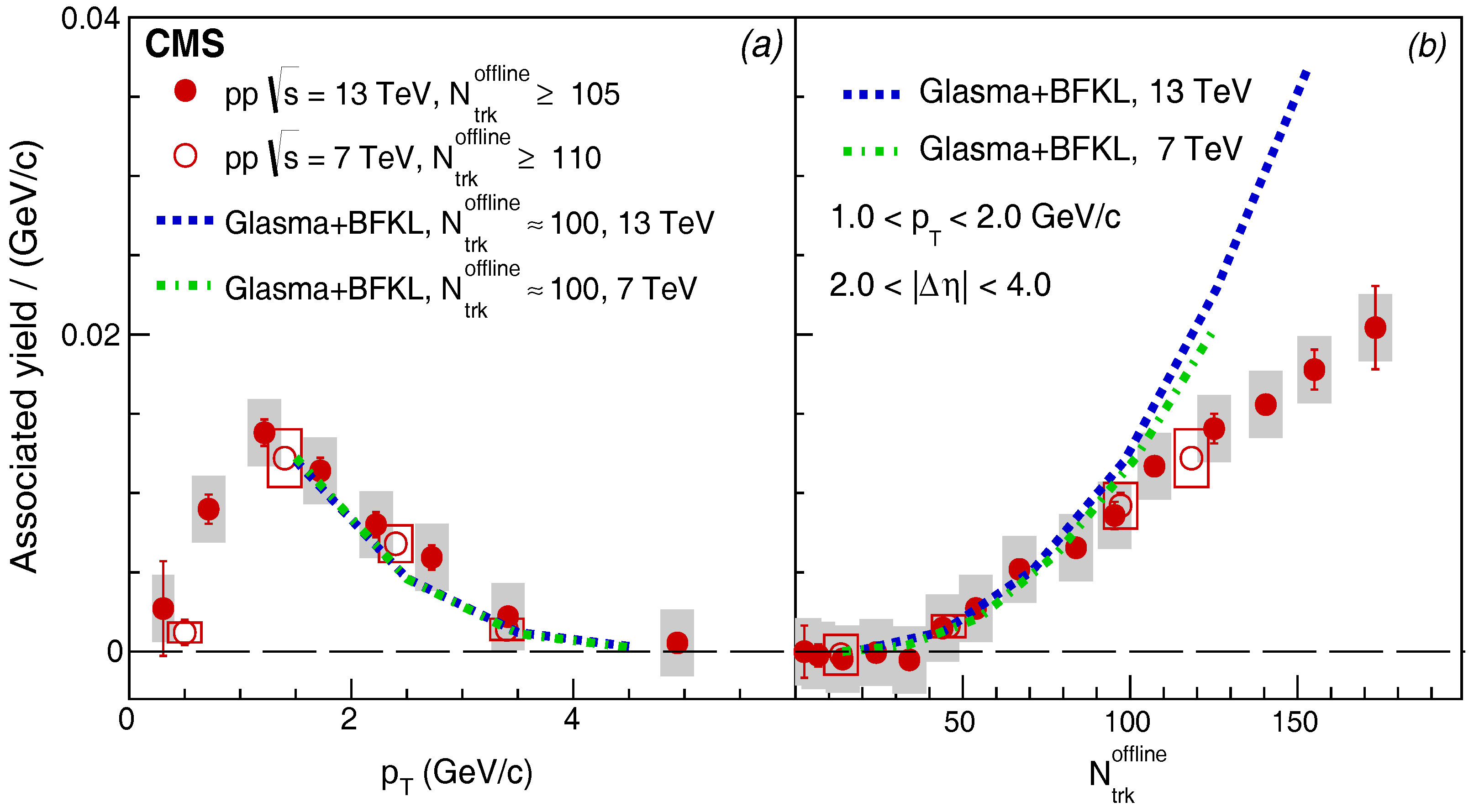
| Fluid | p [Pa] | T [K] | η [Pa·s] | ||
|---|---|---|---|---|---|
| HO | 0.1 | 370 | 85 | 8.2 | |
| He | 0.1 | 2.0 | 0.5 | 1.9 | |
| HO | 22.6 | 650 | 32 | 2.0 | |
| He | 0.22 | 5.1 | 1.7 | 0.7 | |
| Li () | 12 | 23 | ≤1.7 × | ≤1 | ≤0.5 |
| QGP | 88 | 2 | ≤5 × | ≤0.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pasechnik, R.; Šumbera, M. Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations. Universe 2017, 3, 7. https://doi.org/10.3390/universe3010007
Pasechnik R, Šumbera M. Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations. Universe. 2017; 3(1):7. https://doi.org/10.3390/universe3010007
Chicago/Turabian StylePasechnik, Roman, and Michal Šumbera. 2017. "Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations" Universe 3, no. 1: 7. https://doi.org/10.3390/universe3010007
APA StylePasechnik, R., & Šumbera, M. (2017). Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations. Universe, 3(1), 7. https://doi.org/10.3390/universe3010007






