Abstract
Results from the Relativistic Heavy Ion Colloder (RHIC) and the Large Hadron Collider (LHC) experiments show that in relativistic heavy ion collisions, a new state of matter, a strongly interacting perfect fluid, is created. Accelerating, exact and explicit solutions of relativistic hydrodynamics allow for a simple and natural description of this medium. A finite rapidity distribution arises from these solutions, leading to an advanced estimate of the initial energy density of high energy collisions. These solutions can be utilized to describe various aspects of proton–proton collisions, as originally suggested by Landau. We show that an advanced estimate based on hydrodynamics yields an initial energy density in and 8 TeV proton–proton (p–p) collisions at the LHC on the same order as the critical energy density from lattice Quantum Chromodynamics (QCD). The advanced estimate yields a corresponding initial temperature that is around the critical temperature from QCD and the Hagedorn temperature. The multiplicity dependence of the estimated initial energy density suggests that in high multiplicity p–p collisions at the LHC, there is large enough initial energy density to create a non-hadronic perfect fluid.
Keywords:
quark–gluon plasma; hydrodynamics; pseudorapidity distribution; initial state; energy density; Bjorken estimate PACS:
25.75.-q; 25.75.Nq; 13.85.-t
1. Introduction
The first years of data taking in the experiments at the Relativistic Heavy Ion Collider (RHIC) resulted in the discovery of a new state of matter produced in GeV gold–gold (Au+Au) collisions [1,2,3,4], the so-called strongly coupled quark–gluon plasma (sQGP), the “perfect liquid of quarks”: it consists of deconfined quarks, but behaves like an almost perfect fluid (contrary to the expectations that predicted a gas-like state).
The RHIC experiments achieved the following “milestones” [5,6,7,8,9,10,11] among others in discovering and characterizing this new state of matter. The opaqueness to energetic partons is because a new state of matter is present. This matter behaves collectively and contains deconfined quarks. Its viscosity to entropy ratio is the lowest of any known substance, and its initial temperature is at least twice the Hagedorn temperature [12], the upper limiting temperature for the description of matter based exclusively on hadronic states. This Hagedorn temperature is found in a phenomenological manner based on just the number of hadronic states as a function of mass, however, it is important to note that lattice QCD calculations also predict a quark deconfinement transition around the same temperature, approximately 170 MeV [13,14,15]. The LHC heavy ion experiments also confirmed the existence of this new state of matter (see e.g., References [16,17,18,19]), meaning that at collision energies that are two orders of magnitude higher, the created matter behaves very similarly, an intriguing result in itself.
The interest in relativistic hydrodynamics grew in past years mainly due to the above described discovery of the nearly perfect fluidity of the experimentally created sQGP, and the success of hydro models in describing the experimental data. One of the most interesting open questions is perhaps whether collectivity also exists in smaller systems, such as proton–nucleus (p–A) or even p–p collisions. Hydrodynamics can be successfully applied in describing systems of vastly different sizes (such as the expansion of the Universe and high energy particle and nuclear collisions), as the fundamental equations contain no internal scale. Hydrodynamical models utilize locally thermal distributions and apply the local conservation of energy, momentum, and sometimes a conserved charge or entropy. Models based on hydrodynamics aim to describe the space-time picture of heavy-ion collisions and infer the relation between experimental observables and the initial conditions. The equations of hydrodynamics are highly nonlinear, so they are frequently solved via simulations, where suitable initial conditions have to be assumed, and the equations of hydrodynamics are then solved numerically, see details for example in the recent reviews of References [20,21]. Besides these efforts, there is also an interest in models where exact, explicit and parametric solutions of the hydrodynamical equations are used, and where the initial state may be inferred directly from matching the parameters of the solution to the data. Several famous hydrodynamical solutions were developed to describe high energy collisions [22,23,24], but also advanced relativistic solutions were found in the last decade [25,26,27,28,29,30,31,32], when a revival of this sub-field was seen.
While it is customary to describe the medium created in heavy ion collisions with hydrodynamic models, proton–proton collisions are frequently considered to form a system that might be too small for thermalization, or that might be not hot or dense enough to create a supercritical (non-hadronic) medium. Energy densities in GeV p–p collisions are likely below this limit. It is however an interesting question, how high energy densities can be reached in p–p collisions at the LHC with and higher collision energies, as at sufficiently high energy densities, the degrees of freedom may allow for a collective description of the system.
We recall here that the application of hydrodynamical expansion to data analysis in high energy p–p collisions is not an unprecedented or new idea, as Landau worked out hydrodynamics for p–p collisions [33], and Bjorken also notes this possibility in his paper [24] describing his energy density estimate. It is also noteworthy that Hama and Padula assumed [34] the formation of an ideal fluid of massless quarks and gluons in p–p collisions at CERN Intersecting Storage Rings (ISR) energies of = 53–126 GeV. Alexopoulos et al. used Bjorken’s estimate to determine the initial energy density of ∼ GeV/fm at the Tevatron in = 1.8 TeV p+ collisions in the E735 experiment [35], while Lévai and Müller argued [36], that the transverse momentum spectra of pions and baryons indicate the creation of a fluid-like quark–gluon plasma in the same experiment at the same Tevatron energies. However, these earlier works considered the quark–gluon plasma as an ideal gas of massless quarks and gluons, while the RHIC experiments pointed to a nearly perfect fluid of quarks where the speed of sound () is measured to be [6] that is significantly different from that of a massless ideal gas of quarks and gluons, characterized by a . More recently, Wong used Landau hydrodynamics to predict multiplicities and rapidity densities in proton–proton collisions [37]. Furthermore, Shuryak and Zahed proposed [38] the application of hydrodynamics for high multiplicity p–p and p–A collisions at CERN LHC. The ridge effect [39,40], i.e., long range azimuthal correlations were observed in high multiplicity p–p and p–A as well as in heavy ion reactions, which also points toward similarities in collectivity, and perhaps the applicability of hydrodynamics can be extended to these systems.
In this paper, we apply the hydrodynamical solution of References [26,27] to describe the pseudorapidity distribution in p–p collisions at and 8 TeV and use the results of these hydrodynamical fits to estimate the initial energy density in these reactions.
2. Rapidity Distributions from Hydrodynamics
Equations of hydrodynamics can be described by the continuity of conserved charges and that of the energy-momentum-tensor:
with n being a conserved charge, and T is the energy-momentum tensor. In the case of a perfect fluid, the latter can be expressed as
where is the velocity field, ϵ is the energy density and p the pressure, and this tensor is equal to diag() in the locally comoving frame, where . An Equation of State (EoS) is needed to close the above set of equations, and for that, is frequently utilized with a constant κ value. Furthermore, the temperature T may be defined as , or if there are no conserved charges, the relation (with σ being the entropy density) may be utilized. Note that if κ is a constant, independent of the temperature, then it is simply connected to the speed of sound () as . An analytic hydrodynamical solution is a functional form of ϵ, p, T, and n, which solves the above equations. The solution is explicit if these fields are explicitly expressed as a function of space-time coordinates .
Let us utilize the Rindler-coordinates, where is a coordinate proper-time, the space-time rapidity. With these, we can discuss the solution detailed in References [26,27,28,41] as:
where subscript f denotes quantities at the freeze-out, while λ controls the acceleration. If , there is no acceleration and (if the expansion is one-dimensional) we get back the accelerationless Hwa–Bjorken solution of Reference [23,24]. For , we obtain several classes of accelerating solutions, described in References [26,27,28,41]. For example, 1 + 1 dimensional hydrodynamical solutions are obtained for any real value of λ, for the special EoS of . Also (with d being the number of dimensions) solutions can be obtained with , other possibilities are summarized in the above references. We will use the 1 + 1 dimensional solution, as this can be applied well to describe the longitudinal dynamics of the system, and to estimate the initial energy density based on final state observables, similarly to the original paper of Bjorken [24]. Even though this solution is valid with the EoS of , we will later see that we can make a simple additional correction to make up for this shortcoming of the given solution. Also note that in Reference [28], an exact 1+1 dimensional solution was also given for fluctuating initial conditions, so in this case the case is solved for arbitrary initial conditions. This also allowed the confirmation of the stability of the solutions.
To apply the above solutions of hydrodynamics, one has to calculate hadron momentum distributions. In order to do so, one has to utilize a freeze-out condition. Let us define as the freeze-out temperature at , and the freeze-out hypersurface shall be pseudo-orthogonal to the velocity field, i.e., where is the vector-measure of the freeze-out hypersurface. In the case of the above discussed solution, the equation of the hypersurface will be . Using this, one may calculate rapidity distribution (with N being then the total number of hadrons (or that of charged hadrons), and the rapidity). This was performed in References [26,27,28,41], and the approximate analytic result is:
with containing the acceleration parameter λ, m is the average mass of the hadrons to be described (typically this is very close to the pion mass) and is a normalization parameter, to be determined by fit to the data. Note that here we defined the four-momentum components as . The rapidity distribution is approximately Gaussian with the width of , where m is the mass of the particles for which we calculate the rapidity density. At , the width becomes infinity and the distribution becomes flat, as in the Bjorken limit (corresponding to the Hwa–Bjorken solution), where the solution becomes boost invariant. Note that fluctuating initial conditions in our case would result in fluctuations of the measured rapidity densities. However, if the fitted data are smooth, the final state fluctuations are averaged out, so the initial condition can be taken as a smooth distribution as well.
It is important to observe that in order to describe the majority of experimental data, besides rapidity distributions, pseudorapidity distributions (with pseudorapidity defined as ) have to be calculated as well [26,27,28,41]. This can be done by using an average transverse momentum () value and making a transformation from pseudorapidity η to rapidity y. The double differential particle number distributions are connected as
thus, then we obtain
with being the (rapidity dependent) average transverse momentum of these particles. The value of latter can be estimated from the effective temperature () of hadron spectra, e.g., using the Buda–Lund model [42,43], that indicates a behavior observed already in GeV h+p collisions at the EHS/NA22 Collaboration [44], and is a generic property of three-dimensional, finite, exact hydrodynamical solutions with directional Hubble flows [25,45,46]. These findings can be summarized as:
and here , and are model parameters describing the central temperature, the average transverse flow and the rapidity distribution width, all at the freeze-out. These can be extracted from model comparisons, and here we made the simplification of using just the first formula of the above equations and using and σ as the only model parameters, where the first was fixed to a value of 170 MeV, while the second was determined by the fits.
3. Energy Density Estimation
In this section, we recapitulate how this model can be used for improving the famous energy density estimation made by Bjorken [24]. Let us look at the thin transverse slab at mid-rapidity, at the coordinate proper-time of the thermalization , which is in fact the initial time of a possible hydro type of evolution. This thin slab is illustrated by Figure 2 of Reference [24]. The size of this slab is estimated by the radius R of the colliding hadrons or nuclei, then the initial volume is , with being the longitudinal size, while is the space-time rapidity width at , as detailed in References [26,27,28,41]. The energy contained in this volume is , where is the number of particles and is their average energy near . In the special case of the accelerationless, boost-invariant Hwa–Bjorken flow, equals to the the freeze-out width of the same slab, , as illustrated by Figure 4.2 of Reference [47]. Furthermore, due to boost-invariance, symbolically. With this, Bjorken concludes on the initial energy density for a boost invariant solution:
However, in the case of an accelerating solution, the latter two assumptions do not hold, hence one arrives at a correction to take into account the acceleration effects on the energy density estimation, as discussed e.g., in Reference [28]. This correction can be calculated from the partial derivatives
Thus, for the hydrodynamical solutions where the acceleration parameter is . the initial energy density is given by a corrected estimation as
Here, is the Bjorken estimation, which is recovered if is flat (i.e., ), but for , both correction factors are bigger than 1. These correction factors take into account the work done by the pressure on the surface of a finite and accelerating, hot fireball. Hence, the initial energy densities are under-estimated by the Bjorken formula, if the measured distributions are not constant, but have a finite width. In References [26,27,28,41], we performed fits to pseudo-rapidity distribution data of the RHIC BRAHMS experiment, published in Reference [48], and these fits indicate that GeV/fm in GeV Au+Au collisions at the RHIC.
The above corrections are exact results derived in details for a special EoS of [28]. However, the relation of the pressure to the energy density is obviously EoS dependent. As of today, no simple, exact, analytic solutions of the equations of relativistic hydrodynamics are known that utilize other EoS values. However, as proposed in References [41,47], the effects of a non-ideal EoS can be estimated with a conjecture. Any result about the EoS dependent initial energy density shall fulfill the following simple requirements:
- It has to reproduce the EoS-independent Bjorken estimate for .
- It has to reproduce the exact result of Equation (12) for any λ, in the limit.
- It has to follow known hydro behavior for corresponding to exact solutions valid for any (temperature independent) EoS, see e.g., References [45,49], where behavior is found, assuming a fluid volume proportional to τ.
- It should approximately reproduce the results of numerical hydro calculations; most importantly, the additional correction for should increase the initial energy density.
By the principle of Occam’s razor, we then arrive at
This conjecture satisfies the previously mentioned consistency requirement. It goes back to the initial energy density of Bjorken in the exactly solvable special case (for any ), and it also gives the correct energy density for for the exactly solvable special case. Furthermore, this estimate was cross-checked against numerical solutions of relativistic hydrodynamics, that reproduce rapidity distributions. For example, Reference [50], using various EoS versions, obtains 55 GeV/fm in 200 GeV Au+Au collisions for 0.4 fm or approximately 35–40 GeV/fm at 0.55 fm. Evaluation of these values for fm/c (assuming three-dimensional expansion and an EoS value valid at high temperatures) we obtain ≈20 GeV/fm initial energy density, which is similar to the value of 15 GeV/fm that is obtained from our conjectured formula in Reference [41,47].
>From basic considerations [24], as well as from lattice QCD calculations [14], it follows that the critical energy density, needed to form a non-hadronic medium is around 1 GeV/fm. From the lattice QCD calculations, one gets (in units), and even with a conservative estimate of MeV, one gets GeV/fm. Thus, initial energy densities above this value indicate the formation of a non-hadronic medium, which, in case of RHIC Au+Au collisions at 200 GeV/nucleon collision energy, is confirmed by the observations of the RHIC White Papers [1,2,3,4]. It is however an interesting question, as already addressed in the introduction, whether a non-hadronic medium may also be formed in small systems, such as p–p collisions. The RHIC energies are most probably not high enough for that, so let us investigate LHC p–p collisions in the next section.
4. Initial Energy Densities in 7 and 8 TeV LHC p–p Collisions
Now we utilize the Bjorken estimate, first to calculate the initial energy density in 7 TeV p–p collisions. For that, we need to estimate the quantities indicated in Equation (10). The average transverse momentum in TeV p–p collisions is GeV [51], which corresponds to GeV at midrapidity (assuming that most of these particles are pions).
It is a non-trivial question, how to estimate the initial transverse area in p–p collisions, because the geometrical area relates to the total, elastic, inelastic and differential cross-sections in an involved and non-trivial manner. In the case of the collisions of large heavy ions, the initial overlap area is evaluated based on nuclear density profiles, for example using the relation where is proportional to the atomic number of the given nucleus. Basically, these relations that determine the nuclear geometry were obtained from the analysis of the differential cross-sections of elastic electron-ion [52] and elastic proton–nucleus data [53]. Similarly, to get a reliable estimate of the initial transverse area in p–p collisions, we should rely on the analysis of elastic p–p scattering data.
Our analysis is based on Equations (117–119) and (124–126) of Reference [54], that show that both for a grey disc and for a Gaussian scattering density profile, and , where A measures the “greyness" of the proton. Thus, the geometrical area actually can be estimated as
We have cross-checked these estimates by evaluating the geometrical area from B, the slope of a differential elastic scattering cross-section at zero momentum transfer, as we may also use the relation [54]. We found that, within errors, both methods yield the same estimate for the initial geometry of p–p collisions. Based on the results of References [55,56], we have conservatively estimated fm.
Furthermore, the formation time, , may conservatively be assumed to be 1 fm, as was done in Bjorken’s paper as well. The only remaining parameter is the multiplicity or (pseudo)rapidity density at midrapidity. As measured by the LHC experiments, the charged particle pseudorapidity density at midrapidity is found to be at the LHC ALICE experiment [51], while at LHC CMS experiment [57], but in some multiplicity classes it may reach values of 25–30 (see Table I. of Reference [58]). We will take the average of the first two values. The total multiplicity is then 3/2× the charged particle multiplicity. Substituting all of the above mentioned values to Equation (10), one gets:
which is below the critical value.
Let us now make an advanced estimate of the initial energy density. Such an estimate may be based on TOTEM pseudorapidity density data, as these reach out to large enough η values so that the acceleration parameter can be determined. Fits to TOTEM data were performed via Equation (4), as shown in Figure 1. The fit resulted in the acceleration parameter , where the systematic error is based on the point-to-point systematic error of the data points. The fit also determined the normalization parameter to be 7.45 (with a systematic uncertainty of approximately 3%, contributing to the initial energy estimate), and the conversion parameter σ to be 0.8, with an uncertainty contributing to the initial energy density mainly through the value of λ. We can now use the λ value to make a realistic estimation of the initial energy density.
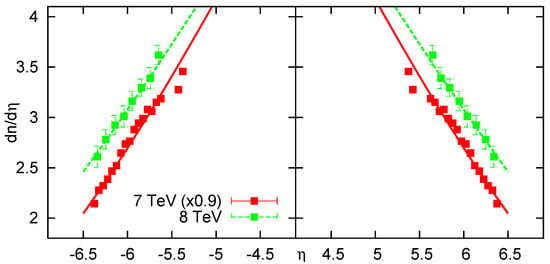
Figure 1.
Charged particle distributions from the LHC TOTEM experiment, fitted with the result of the relativistic hydro solution described in this paper.
Assuming (this is a quite realistic value, at least no harder EoS is expected at LHC, as similar EoS was found at the RHIC as well [14,59,60]), one only needs a value. As shown in Equation (3), temperature is proportional to . >From this, . Thus, if the freeze-out temperature is MeV, then an initial temperature of MeV (needed in order to form a strongly interacting quark gluon plasma) corresponds to being 5–6 times , for and . Even if and λ are higher, seems to be a rather conservative value. With this, one gets a correction factor of 1.262, thus the corrected initial energy density estimate is
which is still below the critical value. The and dependence of the correction factor is shown in Figure 2.
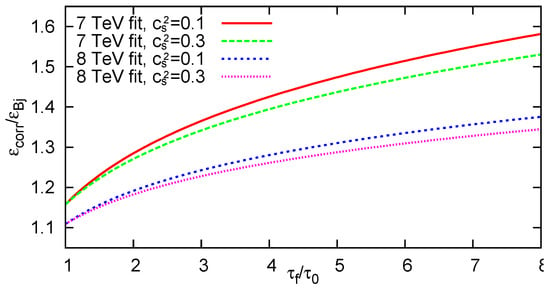
Figure 2.
The correction factor as a function of freeze-out time versus thermalization time (). At a reasonable value of 2, the correction factor is around 25%.
Note that the average p–p multiplicity was used here, so this value represents an average energy density in p–p collisions below the critical value of 1 GeV/fm (cf. Reference [61] where a possible cross-over starting at was conjectured). Based on Table I. of Reference [58], much larger multiplicities have been reached however. The energy density results for these multiplicities are shown in Figure 3. It is clear from this plot, that even for the original Bjorken estimate, supercritical energy densities may have been reached in high multiplicity events, roughly above a charged particle multiplicity of 12. The corrected estimate gives supercritical values for charged particle multiplicities of 9. We also calculated the initial temperature based on the relationship, assuming that 175 MeV corresponds to 1 GeV/fm approximately. This is also shown in the left panel of Figure 3, as well as the reachable pressure values. It is known that temperature of 300–600 MeV may have been reached in 200 GeV central Au+Au collisions of the RHIC [7]. Initial temperature values in 7 TeV p–p seem to be lower than that; 300 MeV can be reached in events with a multiplicity of . However, a temperature of 200 MeV may already be reached in events with a multiplicity of 16.
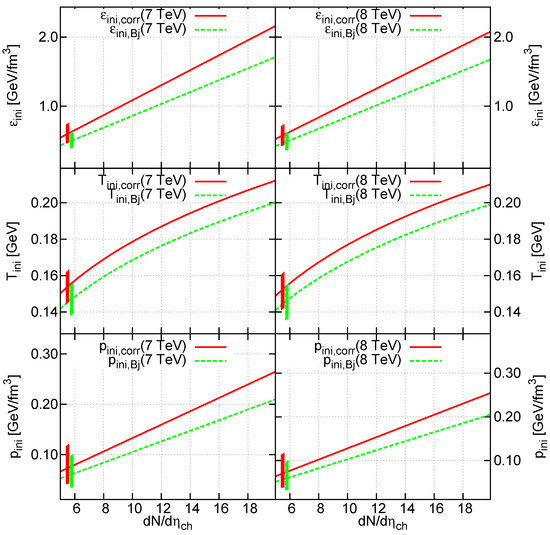
Figure 3.
Initial energy density (based on Table 1), temperature and pressure (based on the relationship) at 7 TeV (left) and 8 TeV (right), is indicated as a function of central charged particle multiplicity density. The Bjorken-estimate (dashed curve) is above the critical energy density of 1 GeV/fm if the multiplicity is larger than 12. Corrected initial energy density (solid curve) is above the critical value if multiplicity is larger than 9. Boxes (parallelograms) show systematic uncertainty (estimated from the 7 TeV case).
Now let us estimate what happens at TeV. As for the Bjorken-estimate, we need the change in charged particle multiplicity, average transverse energy and transverse size. CMS indicates for a non-single diffractive enhanced data sample in Reference [62], while is given in Reference [63]. The average of the two values is in good agreement with the approximate s dependence of of as estimated in Reference [62]. Average transverse momentum s dependence is estimated as in Reference [51], which means a 1.53% increase in . Transverse size can be estimated based on the measurement of References [64], mb, which means a 3.8% increase in area compared to 7 TeV, and fm Based on Equation (10); this altogether means a 2.4% increase in , i.e.,
which is again below the critical value. We also fitted data from TOTEM [62] as shown in Figure 1. We obtained in this case. This corresponds to a correction factor of 1.240, similarly to Equation (16). Finally, we arrive at
This value is based on the average multiplicity in TeV collisions. However, at a fixed multiplicity, there is almost no difference between the two collision energies: average transverse energy increases by 1.5%, but the transverse size also increases by 2.4%. This means a roughly 1% decrease, which is much smaller than the systematic uncertainties in this estimate—to be discussed in the next section. We plot the multiplicity dependence of , and for the 8 TeV case in the right panel of Figure 3. We may again observe that supercritical values are reached for multiplicities higher than 10 in the case of the corrected estimate; but even Bjorken’s estimate yields supercriticality if .
5. Uncertainty of the Estimate
Different sources of uncertainties are detailed in Table 1. The most important one comes from at midrapidity. From Figure 3, it is clear that for the Bjorken-estimate, energy density is above the critical value of 1 GeV/fm if the multiplicity is larger than 12, while in the case of the corrected initial energy density, is needed. Taking all sources of uncertainties into account, the final result for the energy density corresponding to mean multiplicity density at 7 TeV is
and the main systematic error comes from the estimation of the ratio . In the 8 TeV case, the estimate yields a somewhat larger number (0.644 versus 0.640 GeV/fm), but the uncertainties are somewhat higher due to extrapolations to 8 TeV.

Table 1.
Sources of statistical and systematic errors for the 7 TeV estimate.
An important source of systematic uncertainty is the use of the given hydrodynamic solution. This uncertainty may be estimated by using other hydrodynamic models that contain acceleration: the Landau model [22], the Bialas–Peschanski model [65], or numeric models of hydrodynamics, however, in the current paper we focus on the analytic results that can improve on Bjorken’s famous initial energy density estimate. Let us also note that we describe the measured pseudorapidity distributions by suitably choosing i.e., fitting the initial conditions. With this, we predict only a moderate correction to the Bjorken estimate of the initial energy density. However, in the case of numerical solutions, one has to assume a distribution of initial conditions, and one cannot directly determine the initial conditions from the data. A more detailed, or a numerical hydrodynamical investigation is outside the scope of the present manuscript, however we can cross-check these results by fitting the simultaneously taken CMS and TOTEM pseudorapidity density data with the same model, to investigate the stability of our initial energy density estimate from the details of pseudorapidity density at midrapidity.
6. Improved Initial Energy Density Using Combined TOTEM+CMS Data
Fit to TOTEM data was shown in Section 4 and in particular in Figure 1. This shows an advanced estimate and reaches out to a large η region. However, it may seem necessary to put more attention on the central η region and perform fits on a combined central+forward η region. Thus, in this section, we present distributions of charged particles from combined TOTEM+CMS datasets. In the left panel of Figure 4, a fit to such combined data at 7 TeV [51,66] is shown.
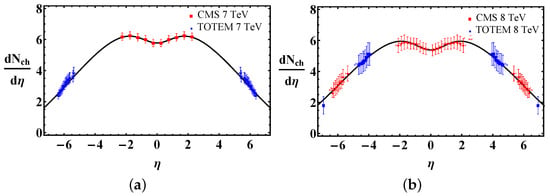
Figure 4.
(a) Charged particle distributions from CMS [51] and TOTEM [66] at 7 TeV fitted with the result of our relativistic hydrodynamical solution described in this paper, with ; (b) Charged particle distributions from CMS and TOTEM 8 TeV data of Reference [62,67] fitted with our results, with .
This fit to TOTEM+CMS data [51,66] yields an initial flow acceleration parameter for 7 TeV p–p collisions. As seen from the terms on the right hand side in Equation (13), the corrected initial energy density depends on the acceleration parameter λ, the driving force for the hydrodynamic expansion or the pressure gradients and volume element expansion. The obtained correction factor is 1.273, thus the advanced hydrodynamic estimate is
Here, we stress that compared to the estimate from fitting TOTEM only, the difference is less than 1%, which is quite reasonable. The fit in the right panel of Figure 4 shows the hydrodynamic distribution and charged particle in 8 TeV pp collision measured by TOTEM and CMS [62] (including TOTEM data measured in collisions with a displaced interaction vertex [67]). The resulting acceleration parameter is ; this corresponds to a correction factor of 1.235 and a final result of corrected initial energy density from the advanced estimate
which differs from the previous estimate based on only TOTEM data by less than 0.5%.
7. Summary
We have shown that based on an accelerating hydro solution and data of the TOTEM and CMS experiments at CERN LHC, the advanced estimate of the initial energy density yields a value that is below the critical value of 1 GeV/fm, but is not inconsistent with a supercritical state in high multiplicity 7 and 8 TeV proton–proton collisions. The energy density is proportional to the measured multiplicity, and so in high-multiplicity events, initial energy densities several times the critical energy density of 1 GeV/fm have been reached. It means that an important and necessary condition is satisfied for the formation of a non-hadronic medium in high multiplicity () 7 and 8 TeV p–p collisions at CERN LHC, however, the exploration of additional signatures (radial and elliptic flow; volume or mean multiplicity dependence of the signatures of the nearly perfect fluid in p–p collisions; scaling of the Bose–Einstein correlation radii with transverse mass; and possible direct photon signal and low-mass dilepton enhancement) and their multiplicity dependence can be a subject of detailed experimental investigation even in p–p collisions at the LHC. It is also important to note that even the measurement of a differential elastic scattering cross-section has implications regarding this estimate.
The main result of our study indicates that the initial energy density is apparently large enough in high multiplicity p–p collisions at the = 7 and 8 TeV LHC energies to create a strongly interacting quark–gluon plasma, so a transition with increasing multiplicity is expected, as far as hydrodynamical phenomena are considered. Since in RHIC p–p collisions, multiplicities are a factor of almost 10 smaller [68], high enough initial energy densities are most probably not reached there. However, that does not necessarily mean that no collectivity is found in those systems. As for p–A collisions and similar, intermediate size systems, the situation is more close to nucleus–nucleus collisions, as indicated by Reference [69].
Probably the most important implication of our study is the need for an electron–proton and electron–nucleus collider: as far as we know, only in lepton induced proton and heavy ion reactions can one be certain that a hydrodynamically evolving medium is not created even at the TeV energy range. The results of lepton–hadron and lepton–nucleus interactions thus will define very clearly the particle physics background to possible collective effects. For example, recently, azimuthal correlations were observed in high multiplicity p–p and p–A as well as in heavy ion reactions (the ridge effect [39,40]), whose origin is currently not entirely clear. If such a ridge effect appears also in e+p and e+A collisions, then this effect is most likely not of a hydrodynamical origin, while if it does not appear in e+p and e+A collisions in the same multiplicity range as in p–p and p–A reactions, than the ridge is more likely a hydrodynamical effect.
If, indeed, a strongly interacting non-hadronic medium is formed in high multiplicity p–p collisions, then purely the jet suppression in heavy ion collisions does not reveal the true nature of these systems: the proper measure would be energy loss per unit length (as proposed in Reference [70]), which may be quite similar in these systems, even if the total suppression is different.
We are looking forward to measurements unveiling the nature of the matter created in proton–proton collisions. In experimental p–p data, one should look for the enhancement of the photon to pion ratio in high multiplicity events (as compared to low multiplicity ones) [71], for a hydrodynamic scaling of Bose–Einstein correlation radii or that of azimuthal asymmetry [6], or even the enhancement of low mass dileptons [9].
Acknowledgments
The authors thank the important discussions to Simone Giani, Paolo Guibellino, Federico Antinori, Michael Tannenbaum, Péter Lévai, Sandra S. Padula, Endel Lippmaa and Renato Campanini. We acknowledge the support of the Hungarian OTKA grant NK-101438 and of the bilateral Chinese-Hungarian governmental project, TeT 12CN-1-2012-0016. T. Cs. gratefully acknowledges partial support from the Ch. Simonyi Foundation. M. Cs. was supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.
Author Contributions
M. Cs. performed the fits to TOTEM data and the calculations based on these fits. T. Cs. and M. Cs. wrote Section 1, Section 2, Section 3, Section 4 , Section 5 and Section 7 of the manuscript. Z-F. J. and C-B. Y. performed fits to combined TOTEM and CMS data and wrote Section 6. All authors worked on finalization of the text of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Adcox, K.; Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Jamel, A.; Alexander, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Baia, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Back, B.B.; Baker, M.D.; Ballintijn, M.; Barton, D.S.; Becker, B.; Betts, R.R.; Bickley, A.A.; Bindel, R.; Budzanowski, A.; Busza, W.; et al. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Energy loss and flow of heavy quarks in Au+Au collisions at s(NN)**(1/2) = 200-GeV. Phys. Rev. Lett. 2007, 98, 172301. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Zolin, L. Scaling properties of azimuthal anisotropy in Au+Au and Cu+Cu collisions at s(NN)**(1/2) = 200-GeV. Phys. Rev. Lett. 2007, 98, 162301. [Google Scholar] [CrossRef] [PubMed]
- Adare, A.; Afanasiev, S.; Aidala, C.; Zolin, L. Enhanced production of direct photons in Au+Au collisions at GeV and implications for the initial temperature. Phys. Rev. Lett. 2010, 104, 132301. [Google Scholar] [CrossRef] [PubMed]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aramaki, Y.; Atomssa, E.T.; et al. Observation of direct-photon collective flow in GeV Au+Au collisions. Phys. Rev. Lett. 2012, 109, 122302. [Google Scholar] [CrossRef] [PubMed]
- Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; Armendariz, R.; Aronson, S.H.; et al. Enhancement of the dielectron continuum in s(NN)**(1/2) = 200-geV Au+Au collisions. arXiv, 2007; arXiv:0706.3034. [Google Scholar]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aramaki, Y.; Atomssa, E.T.; et al. Elliptic and hexadecapole flow of charged hadrons in Au+Au collisions at GeV. Phys. Rev. Lett. 2010, 105, 062301. [Google Scholar] [CrossRef] [PubMed]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aramaki, Y.; Atomssa, E.T.; et al. Measurements of Higher-Order Flow Harmonics in Au+Au Collisions at GeV. Phys. Rev. Lett. 2011, 107, 252301. [Google Scholar] [CrossRef] [PubMed]
- Hagedorn, R. Statistical thermodynamics of strong interactions at high- energies. Nuovo Cim. Suppl. 1965, 3, 147–186. [Google Scholar]
- Aoki, Y.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The QCD transition temperature: Results with physical masses in the continuum limit. Phys. Lett. B 2006, 643, 46–54. [Google Scholar] [CrossRef]
- Borsányi, S.; Endrodi, G.; Fodor, Z.; Jakovac, A.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. The QCD equation of state with dynamical quarks. J. High Energy Phys. 2010, 11, 077. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Aamodt, K.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; Ahmad, N.; et al. Suppression of Charged Particle Production at Large Transverse Momentum in Central Pb–Pb Collisions at TeV. Phys. Lett. B 2011, 696, 30–39. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Abrahantes Quintana, A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Aguilar Salazar, S.; Ahammed, Z.; et al. Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Study of high-pT charged particle suppression in PbPb compared to pp collisions at TeV. Eur. Phys. J. C 2012, 72, 1945. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Measurement of the elliptic anisotropy of charged particles produced in PbPb collisions at nucleon-nucleon center-of-mass energy = 2.76 TeV. Phys. Rev. C 2013, 87, 014902. [Google Scholar] [CrossRef]
- Derradi de Souza, R.; Koide, T.; Kodama, T. Hydrodynamic Approaches in Relativistic Heavy Ion Reactions. Prog. Part. Nucl. Phys. 2016, 86, 35–85. [Google Scholar] [CrossRef]
- Huovinen, P. Hydrodynamics at RHIC and LHC: What have we learned? Int. J. Mod. Phys. E 2013, 22, 1330029. [Google Scholar] [CrossRef]
- Landau, L.D. On the multiparticle production in high-energy collisions. Izv. Akad. Nauk SSSR Ser. Fiz. 1953, 17, 51–64. [Google Scholar]
- Hwa, R.C. Statistical Description of Hadron Constituents as a Basis for the Fluid Model of High-Energy Collisions. Phys. Rev. D 1974, 10, 2260. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Csörgő, T.; Csernai, L.P.; Hama, Y.; Kodama, T. Simple solutions of relativistic hydrodynamics for systems with ellipsoidal symmetry. Acta Phys. Hung. A 2004, 21, 73–84. [Google Scholar] [CrossRef]
- Csörgő, T.; Nagy, M.I.; Csanád, M. A New Family of Simple Solutions of Perfect Fluid Hydrodynamics. Phys. Lett. B 2008, 663, 306–311. [Google Scholar] [CrossRef]
- Csörgő, T.; Nagy, M.; Csanád, M. Accelerating Solutions of Perfect Fluid Hydrodynamics for Initial Energy Density and Life-Time Measurements in Heavy Ion Collisions. Braz. J. Phys. 2007, 37, 723–725. [Google Scholar] [CrossRef]
- Nagy, M.I.; Csörgő, T.; Csanád, M. Detailed description of accelerating, simple solutions of relativistic perfect fluid hydrodynamics. Phys. Rev. C 2008, 77, 024908. [Google Scholar] [CrossRef]
- Csanád, M.; Nagy, M.; Lökös, S. Exact solutions of relativistic perfect fluid hydrodynamics for a QCD equation of state. Eur. Phys. J. A 2012, 48, 173. [Google Scholar] [CrossRef]
- Borshch, M.S.; Zhdanov, V.I. Exact Solutions of the Equations of Relativistic Hydrodynamics Representing Potential Flows. Symmetry Integr. Geom. Methods Appl. 2007, 3, 116. [Google Scholar] [CrossRef]
- Pratt, S. A co-moving coordinate system for relativistic hydrodynamics. Phys. Rev. C 2007, 75, 024907. [Google Scholar] [CrossRef]
- Csanád, M.; Szabó, A. Multipole solution of hydrodynamics and higher order harmonics. Phys. Rev. C 2014, 90, 054911. [Google Scholar] [CrossRef]
- Belenkij, S.Z.; Landau, L.D. Hydrodynamic theory of multiple production of particles. Nuovo Cim. Suppl. 1956, 3S10, 15–31. [Google Scholar] [CrossRef]
- Hama, Y.; Padula, S.S. Bose-Einstein correlation of particles produced by expanding sources. Phys. Rev. D 1988, 37, 3237–3245. [Google Scholar] [CrossRef]
- Alexopoulos, T.; Anderson, E.; Bujak, A.; Carmony, D.; Erwin, A.; Gutay, L.J.; Hirsch, A.S.; Nelson, K.S.; Porile, N.T.; Oh, S.H.; et al. Evidence for hadronic deconfinement in anti-p - p collisions at 1.8-TeV. Phys. Lett. B 2002, 528, 43–48. [Google Scholar] [CrossRef]
- Lévai, P.; Müller, B. Transverse baryon flow as possible evidence for a quark - gluon plasma phase. Phys. Rev. Lett. 1991, 67, 1519–1522. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.Y. Landau Hydrodynamics Revisited. Phys. Rev. C 2008, 78, 054902. [Google Scholar] [CrossRef]
- Shuryak, E.; Zahed, I. High Multiplicity pp and pA Collisions: Hydrodynamics at its Edge and Stringy Black Hole. Phys. Rev. C 2013, 88, 044915. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Observation of long-range near-side angular correlations in proton-lead collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- Padula, S.S. Long-range dihadron correlations in high multiplicity p p and PbPb with CMS. In Proceedings of the 7th Workshop on Particle Correlations and Femtoscopy (WPCF 2011), Tokyo, Japan, 20–24 September 2011.
- Csörgő, T.; Nagy, M.; Csanád, M. New exact solutions of relativistic hydrodynamics. J. Phys. G Nucl. Part. Phys. 2008, 35, 104128. [Google Scholar] [CrossRef]
- Csörgő, T.; Lörstad, B. Bose-Einstein Correlations for Three-Dimensionally Expanding, Cylindrically Symmetric, Finite Systems. Phys. Rev. C 1996, 54, 1390–1403. [Google Scholar] [CrossRef]
- Csanád, M.; Csörgő, T.; Lörstad, B. Buda-Lund hydro model for ellipsoidally symmetric fireballs and the elliptic flow at RHIC. Nucl. Phys. A 2004, 742, 80–94. [Google Scholar] [CrossRef]
- Agababyan, N.M.; Atayan, M.R.; Csörgő, T.; de Wolf, E.A.; Dziunikowska, K.; Endler, A.M.F.; Garutchava, Z.S.; Gulkanyan, H.R.; Hakobyan, R.S.; Karamyan, J.K.; et al. Estimation of hydrodynamical model parameters from the invariant spectrum and the Bose-Einstein correlations of pi- mesons produced in (pi+/K+) p interactions at 250- GeV/c. Phys. Lett. B 1998, 422, 359–368. [Google Scholar] [CrossRef]
- Csörgő, T.; Akkelin, S.V.; Hama, Y.; Lukács, B.; Sinyukov, Y.M. Observables and initial conditions for self-similar ellipsoidal flows. Phys. Rev. C 2003, 67, 034904. [Google Scholar] [CrossRef]
- Csanád, M.; Vargyas, M. Observables from a solution of 1+3 dimensional relativistic hydrodynamics. Eur. Phys. J. A 2010, 44, 473–478. [Google Scholar] [CrossRef]
- Nagy, M. Exact solutions of hydrodynamics and their applications in heavy-ion physics. Ph.D. Thesis (in Hungarian), Wigner Research Centre for Physics, Budapest, Hungary, December 2012. [Google Scholar]
- Bearden, I.G.; Beavis, D.; Besliu, C.; Blyakhman, Y.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Pseudorapidity distributions of charged particles from Au + Au collisions at the maximum RHIC energy. Phys. Rev. Lett. 2002, 88, 202301. [Google Scholar] [CrossRef] [PubMed]
- Csörgő, T.; Grassi, F.; Hama, Y.; Kodama, T. Simple solutions of relativistic hydrodynamics for longitudinally and cylindrically expanding systems. Phys. Lett. B 2003, 565, 107–115. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. (3+1)D hydrodynamic simulation of relativistic heavy-ion collisions. Phys. Rev. C 2010, 82, 014903. [Google Scholar] [CrossRef]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Transverse-momentum and pseudorapidity distributions of charged hadrons in pp collisions at sqrt(s) = 7 TeV. Phys. Rev. Lett. 2010, 105, 022002. [Google Scholar] [CrossRef] [PubMed]
- Hofstadter, R. Electron scattering and nuclear structure. Rev. Mod. Phys. 1956, 28, 214–254. [Google Scholar] [CrossRef]
- Glauber, R.J.; Matthiae, G. High-energy scattering of protons by nuclei. Nucl. Phys. B 1970, 21, 135–157. [Google Scholar] [CrossRef]
- Block, M.M. Hadronic forward scattering: Predictions for the Large Hadron Collider and cosmic rays. Phys. Rept. 2006, 436, 71–215. [Google Scholar] [CrossRef]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bozzo, M.; Brücken, E.; Buzzo, A.; et al. Proton-proton elastic scattering at the LHC energy of s** (1/2) = 7-TeV. Europhys. Lett. 2011, 95, 41001. [Google Scholar]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bozzo, M.; Brücken, E.; Buzzo, A.; et al. Luminosity-independent measurements of total, elastic and inelastic cross-sections at TeV. Europhys. Lett. 2013, 101, 21004. [Google Scholar]
- Aamodt, K.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; Ahmad, N.; et al. Charged-particle multiplicity measurement in proton-proton collisions at sqrt(s) = 7 TeV with ALICE at LHC. Eur. Phys. J. C 2010, 68, 345–354. [Google Scholar] [CrossRef]
- Aamodt, K.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; Ahmad, N.; et al. Femtoscopy of pp collisions at sqrts=0.9 and 7 TeV at the LHC with two-pion Bose-Einstein correlations. Phys. Rev. D 2011, 84, 112004. [Google Scholar] [CrossRef]
- Lacey, R.A.; Ajitanand, N.N.; Alexander, J.M.; Chung, P.; Holzmann, W.G.; Issah, M.; Taranenko, A.; Danielewicz, P.; Stocker, H. Has the QCD critical point been signaled by observations at RHIC? Phys. Rev. Lett. 2007, 98, 092301. [Google Scholar] [CrossRef] [PubMed]
- Csanád, M.; Májer, I. Equation of state and initial temperature of quark gluon plasma at RHIC. Cent. Eur. J. Phys. 2012, 10, 850–857. [Google Scholar] [CrossRef]
- Campanini, R.; Ferri, G.; Ferri, G. Experimental equation of state in proton-proton and proton-antiproton collisions and phase transition to quark gluon plasma. Phys. Lett. B 2011, 703, 237–245. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; et al. Measurement of pseudorapidity distributions of charged particles in proton-proton collisions at TeV by the CMS and TOTEM experiments. Eur. Phys. J. C 2014, 74, 3053. [Google Scholar] [CrossRef]
- Adam, J.; Adamova, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmed, I.; Ahn, S.U.; et al. Charged-particle multiplicities in proton-proton collisions at to 8 TeV. arXiv, 2015; arXiv:1509.07541. [Google Scholar]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bozzo, M.; Brücken, E.; Buzzo, A.; et al. Luminosity-Independent Measurement of the Proton-Proton Total Cross Section at TeV. Phys. Rev. Lett. 2013, 111, 012001. [Google Scholar] [CrossRef] [PubMed]
- Bialas, A.; Janik, R.A.; Peschanski, R.B. Unified description of Bjorken and Landau 1+1 hydrodynamics. Phys. Rev. C 2007, 76, 054901. [Google Scholar] [CrossRef]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bozzo, M.; Brücken, E.; Buzzo, A.; et al. Measurement of the forward charged particle pseudorapidity density in pp collisions at TeV with the TOTEM experiment. Europhys. Lett. 2012, 98, 31002. [Google Scholar]
- Antchev, G.; Aspell, P.; Atanassov, I.; Avati, V.; Baechler, J.; Berardi, V.; Berretti, M.; Bozzo, M.; Brücken, E.; Buzzo, A.; et al. Measurement of the forward charged particle pseudorapidity density in pp collisions at TeV using a displaced interaction point. Eur. Phys. J. C 2015, 75, 126. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Identified charged hadron production in p + p collisions at and 62.4 GeV. Phys. Rev. C 2011, 83, 064903. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Al-Jamel, A.; Aoki, K.; Aphecetche, L.; et al. Transverse energy production and charged-particle multiplicity at midrapidity in various systems from to 200 GeV. Phys. Rev. C 2016, 93, 024901. [Google Scholar] [CrossRef]
- Csörgő, T. Critical Opalescence: An Optical Signature for a QCD Critical Point. In Proceedings of the 5th International Workshop on Critical Point and Onset of Deconfinement (CPOD 2009), Brookhaven, NY, USA, 8–12 June 2009.
- Tannenbaum, M.J.; Weiner, R.M. Comments on ’Observation of Long-Range, Near-Side Angular Correlations in Proton-Proton Collisions at the LHC’ by the CMS collaboration. arXiv, 2010; arXiv:1010.0964. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).