Quark Deconfinement in Rotating Neutron Stars
Abstract
:1. Introduction
2. Models for the Nuclear Equations of State
2.1. Hadronic Matter
2.2. Deconfined Quark Phase
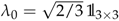 . The currents and are given by
. The currents and are given by
2.3. Quark-Hadron Mixed Phase
3. Treatment of Rotating Neutron Stars in General Relativity Theory
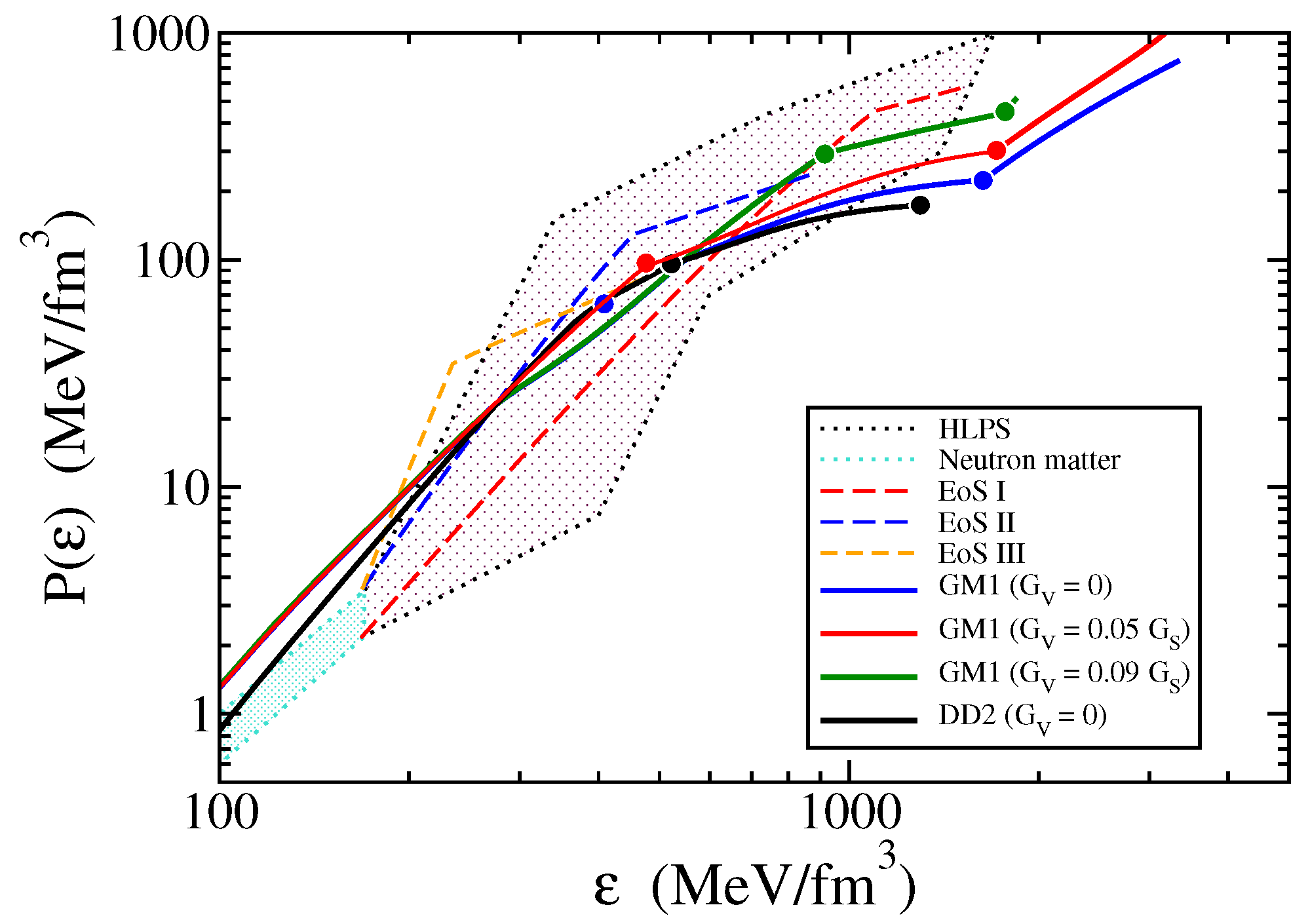
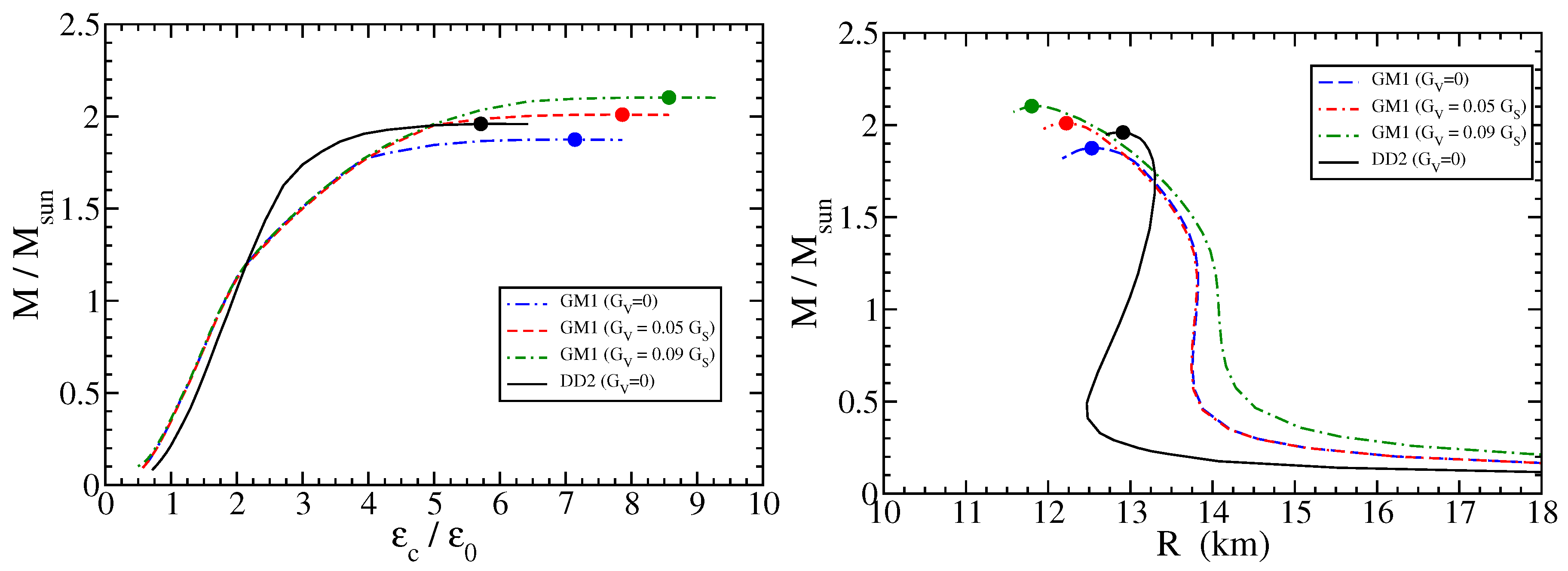
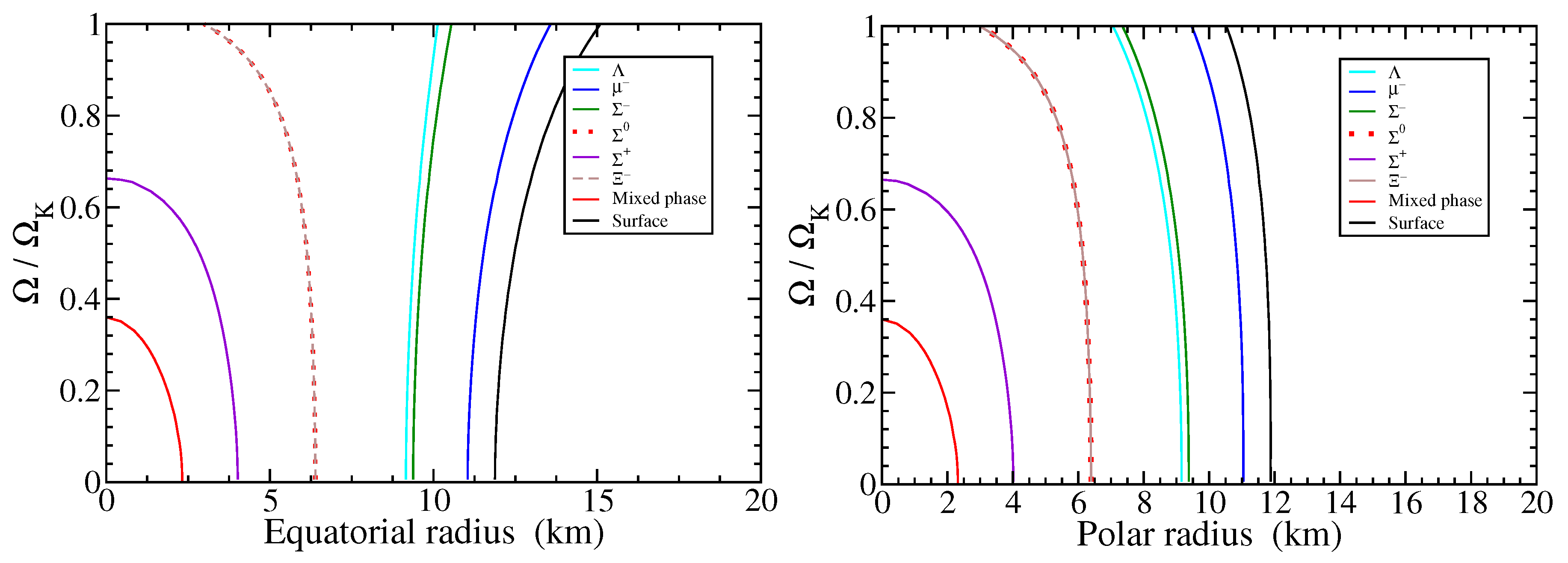
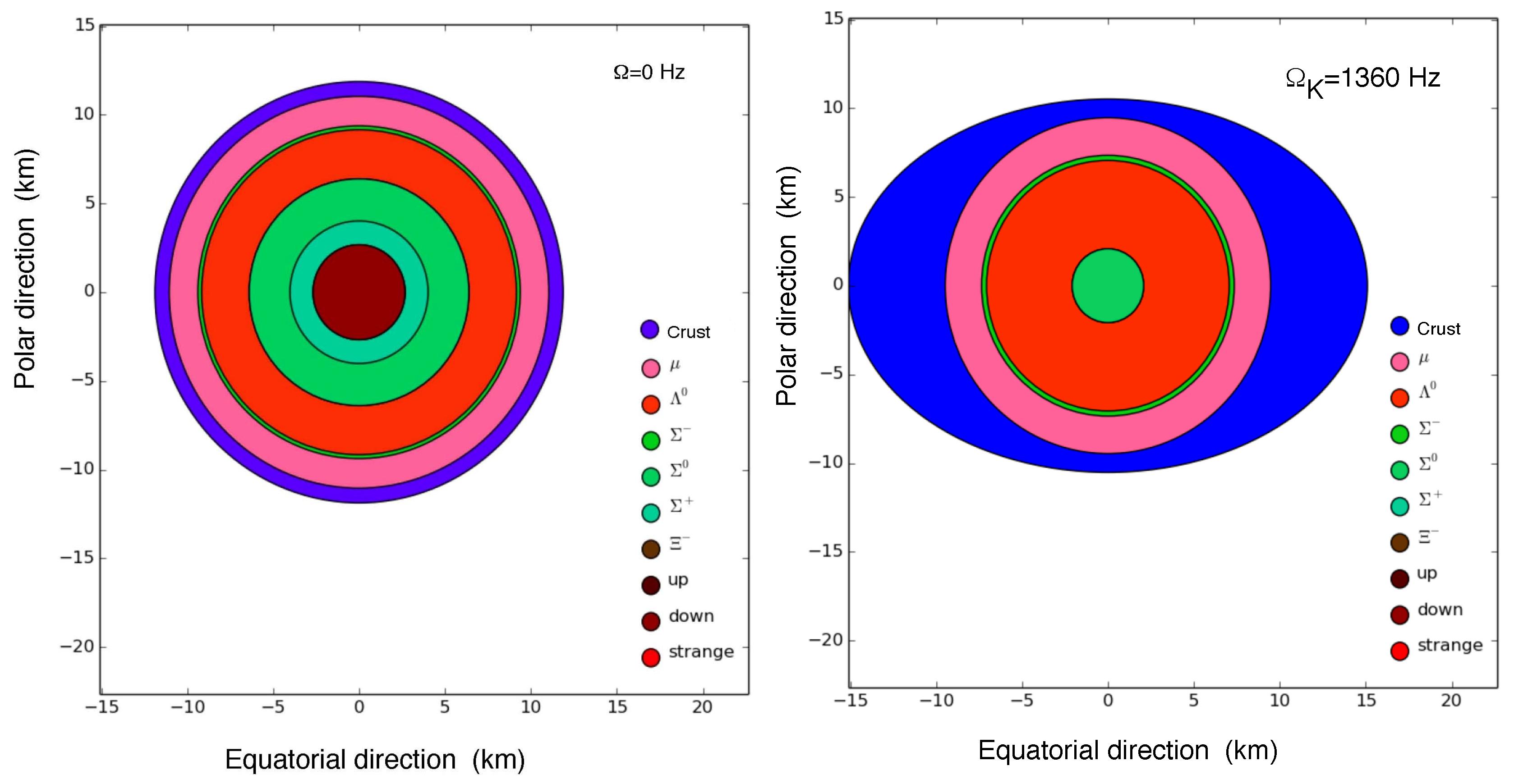
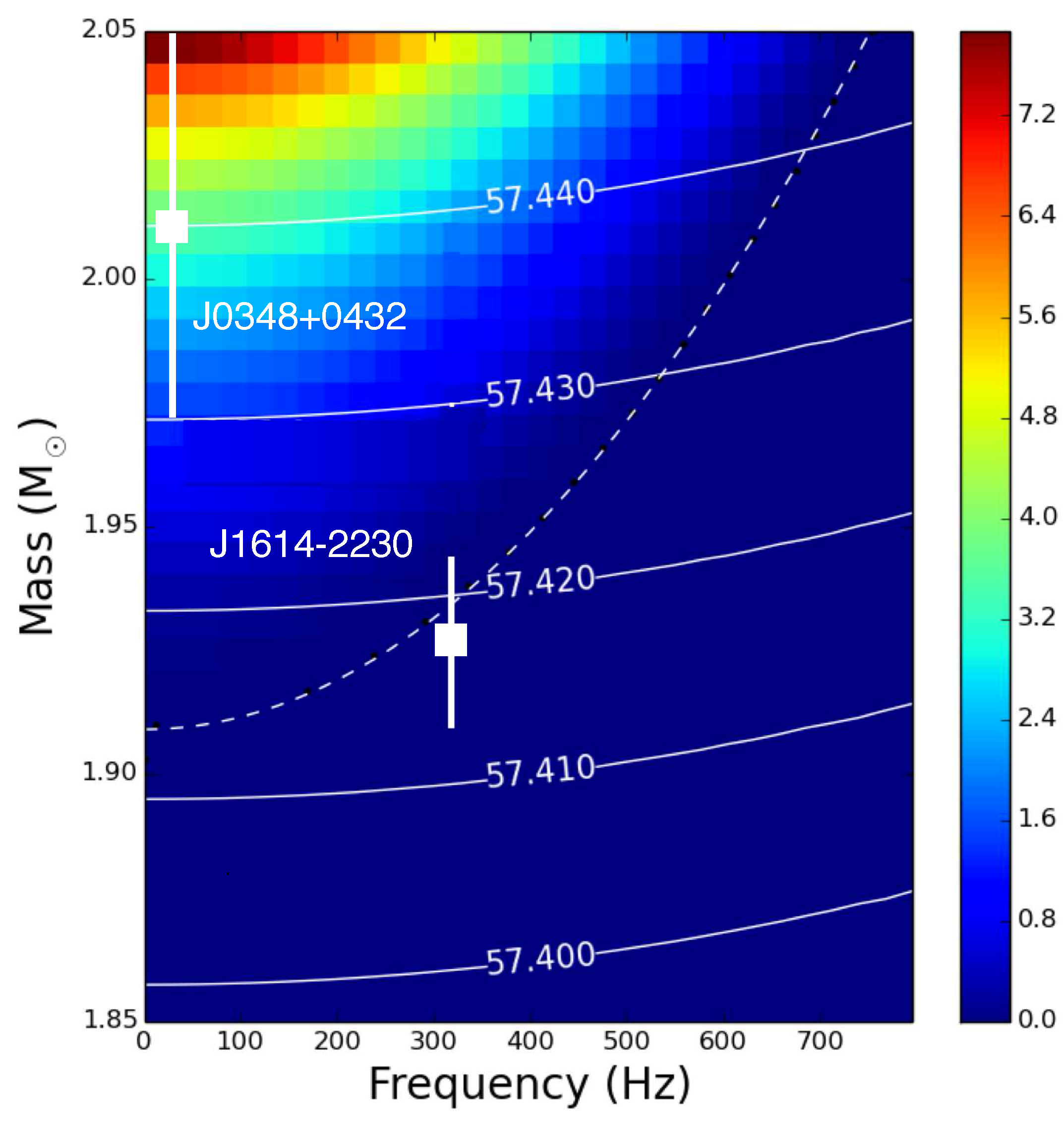
4. Results
5. Discussion and Summary
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Friman, B.; Höhne, C.; Knoll, J.; Leupold, S.; Randrup, J.; Rapp, R.; Senger, P. (Eds.) The CBM Physics Book; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 814.
- Blaschke, D.; Aichelin, J.; Bratkovskaya, E.; Friese, V.; Gazdzicki, M.; Randrup, J.; Rogachevsky, O.; Teryaev, O.; Toneev, V. Topical Issue on Exploring Strongly Interacting Matter at High Densities—NICA White Paper. Eur. Phys. J. A 2016, 52, 267. [Google Scholar] [CrossRef]
- Bass, S.; Caines, H.; Cole, B.A.; Dunlop, J.; Hemmick, T.K.; Morrison, D.; Putschke, J.; Salur, S.; Schenke, B.; Solz, R.A.; et al. Hot and Dense QCD Matter. Community White Paper. Available online: http://www.bnl.gov/npp/ (accessed on 10 October 2016).
- Glendenning, N.K. Compact Stars, Nuclear Physics, Particle Physics, and General Relativity, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; High Energy Physics, Cosmology and Gravitation Series; IOP Publishing: Bristol, UK, 1999. [Google Scholar]
- Baldo, M.; Burgio, F. Microscopic Theory of the Nuclear Equation of State and Neutron Star Structure. In Physics Of Neutron Star Interiors; Blaschke, D., Glendenning, N.K., Sedrakian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 578, pp. 1–29. [Google Scholar]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef]
- Weber, F. Strange Quark Matter and Compact Stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Page, D.; Reddy, S. Dense Matter in Compact Stars: Theoretical Developments and Observational Constraints. Ann. Rev. Nucl. Part. Sci. 2006, 56, 327–374. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.H.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Sedrakian, A. The physics of dense hadronic matter and compact. stars. Prog. Part. Nucl. Phys. 2007, 58, 168–246. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Sandin, F.; Fuchs, C.H.; Faessler, A.; Grigorian, H.; Röpke, G.; Trümper, J. Modern compact star observations and the quark matter equation of state. Phys. Lett. B 2007, 654, 170–176. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Becker, W. (Ed.) Neutron Stars and Pulsars, Astrophysics and Space Science Library; Springer: New York, NY, USA, 2009; Volume 357.
- Grigorian, H.; Blaschke, D.; Aguilera, D.N. Hybrid stars with color superconductivity within a nonlocal chiral quark model. Phys. Rev. C 2004, 69, 065802. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Gómez Dumm, D.; Grunfeld, A.G.; Klähn, T.; Scoccola, N.N. Hybrid stars within a covariant, nonlocal chiral quark model. Phys. Rev. C 2007, 75, 065804. [Google Scholar] [CrossRef]
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Pei, S.; Weber, F. Signal of Quark Deconfinement in the Timing Structure of Pulsar Spin-Down. Phys. Rev. Lett. 1997, 79, 1603–1606. [Google Scholar] [CrossRef]
- Chubarian, E.; Grigorian, H.; Poghosyan, G.; Blaschke, D. Deconfinement transition in rotating compact stars. Astron. Astrophys. 2000, 357, 968–976. [Google Scholar]
- Glendenning, N.K.; Weber, F. Signal of Quark Deconfinement in Millisecond Pulsars and Reconfinement in Accreting X-ray Neutron Stars. In Physics Of Neutron Star Interiors; Blaschke, D., Glendenning, N.K., Sedrakian, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 578, pp. 305–332. [Google Scholar]
- Glendenning, N.K.; Weber, F. Phase Transition and Spin Clustering of Neutron Stars in X-Ray Binaries. Astrophys. J. 2001, 559, 119–122. [Google Scholar] [CrossRef]
- Poghosyan, G.; Grigorian, H.; Blaschke, D. Population Clustering as a Signal for Deconfinement in Accreting Compact Stars. Astrophys. J. 2001, 551, 73–76. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astron. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. ATNF Pulsar Catalogue: Version 1.53. 2005. Available online: http://www.atnf.csiro.au/research/pulsar/psrcat/ (accessed on 23 September 2015).
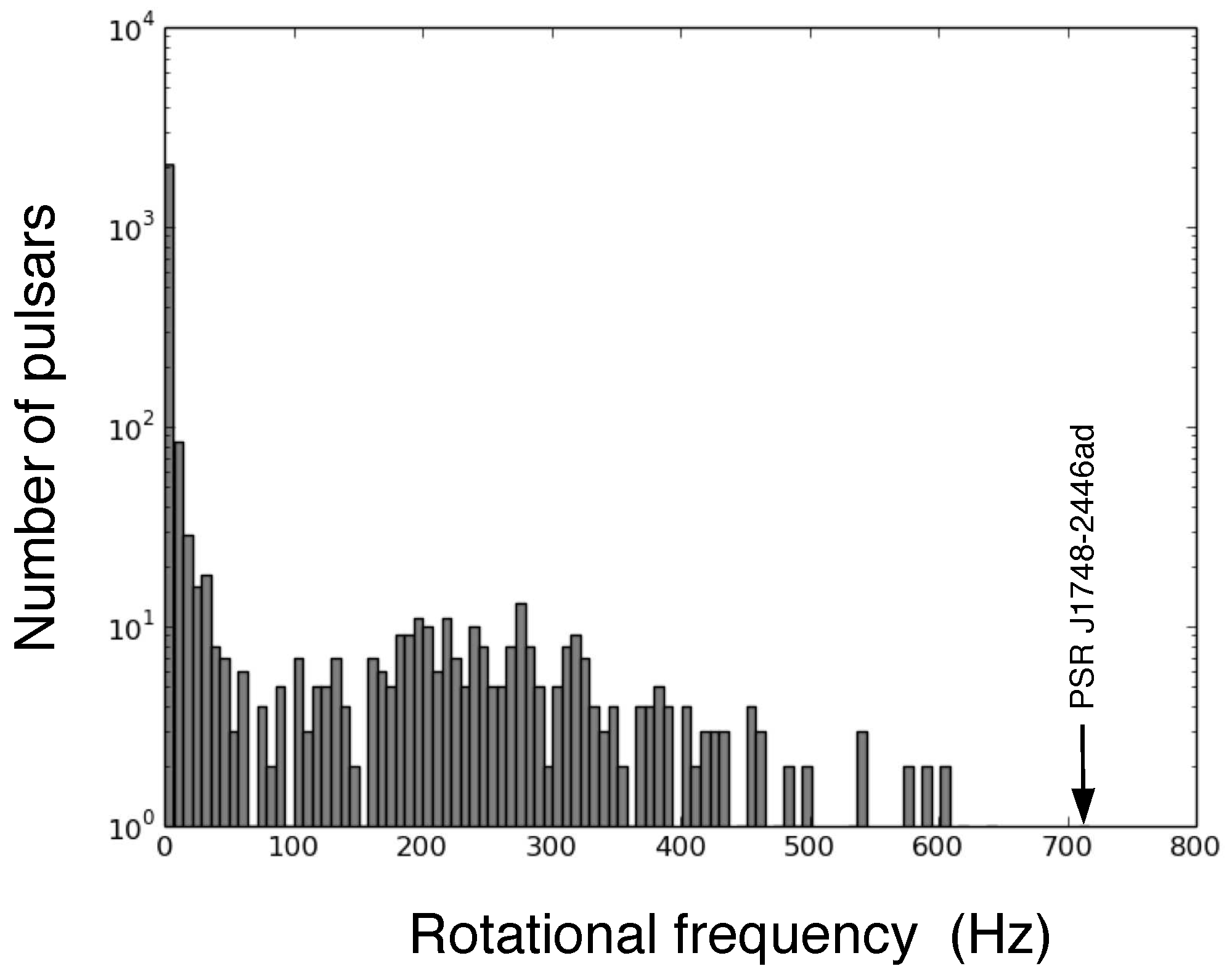
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A Radio Pulsar Spinning at 716 Hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef] [PubMed]
- Walecka, J.D. A theory of highly condensed matter. Ann. Phys. 1974, 83, 491–531. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Boguta, J.; Rafelski, J. Thomas Fermi model of finite nuclei. Phys. Lett. 1977, 71, 22–26. [Google Scholar] [CrossRef]
- Boguta, J.; Stöcker, H. Systematics of nuclear matter properties in a non-linear relativistic field theory. Phys. Lett. 1983, 120, 289–293. [Google Scholar] [CrossRef]
- Shlomo, S.; Kolomietz, V.M.; Coló, G. Deducing the nuclear-matter incompressibility coefficient from data on isoscalar compression modes. Eur. Phys. J. A 2006, 30, 23–30. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Krüger, T.; Tews, I.; Hebeler, K.; Schwenk, A. Neutron matter from chiral effective field theory interactions. Phys. Rev. C 2013, 88, 025802. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Moszkowski, S.A. Reconciliation of neutron-star masses and binding of the Λ in hypernuclei. Phys. Rev. Lett. 1991, 67, 2414–2417. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Ropke, G.; Klähn, T.; Blaschke, D.; Wolter, H.H. Composition and thermodynamics of nuclear matter with light clusters. Phys. Rev. C 2010, 81, 015803. [Google Scholar] [CrossRef]
- Brockmann, R.; Toki, H. Relativistic density-dependent Hartree approach for finite nuclei. Phys. Rev. Lett. 1992, 68, 3408–3411. [Google Scholar] [CrossRef] [PubMed]
- Lenske, H.; Fuchs, C.H. Rearrangement in the density dependent relativistic field theory of nucle. Phys. Lett. B 1995, 345, 355–360. [Google Scholar] [CrossRef]
- Hofmann, F.; Keil, C.M.; Lenske, H. Application of the density dependent hadron field theory to neutron star matter. Phys. Rev. C 2001, 64, 025804. [Google Scholar] [CrossRef]
- Fuchs, C.H.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C 1995, 52, 3043. [Google Scholar] [CrossRef]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Klevansky, S.P. The Nambu—Jona-Lasinio model of quantum chromodynamics. Rev. Mod. Phys. 1992, 64, 649–708. [Google Scholar] [CrossRef]
- Vogl, U.; Weise, W. The Nambu and Jona-Lasinio model: Its implications for Hadrons and Nuclei. Prog. Part. Nucl. Phys. 1991, 27, 195–272. [Google Scholar] [CrossRef]
- Buballa, M. NJL-model analysis of dense quark matter. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark-hybrid matter in the cores of massive neutron stars. Phys. Rev. D 2013, 87, 023001. [Google Scholar] [CrossRef]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Contrera, G.A.; Gomez Dumm, D.; Scoccola, N.N. Nonlocal SU(3) chiral quark models at finite temperature: The role of the Polyakov loop. Phys. Lett. B 2008, 661, 113–117. [Google Scholar] [CrossRef]
- Contrera, G.A.; Gomez Dumm, D.; Scoccola, N.N. Meson properties at finite temperature in a three flavor nonlocal chiral quark model with Polyakov loop. Phys. Rev. D 2010, 81, 054005. [Google Scholar] [CrossRef]
- Sasaki, C.; Friman, B.; Redlich, K. Quark Number Fluctuations in a Chiral Model at Finite Baryon Chemical Potential. Phys. Rev. D 2007, 75, 054026. [Google Scholar] [CrossRef]
- Fukushima, K. Phase diagrams in the three-flavor Nambu-Jona-Lasinio model with the Polyakov loop. Phys. Rev. D 2008, 77, 114028, Erratum in 2008, 78, 039902. [Google Scholar] [CrossRef]
- Bratovic, N.M.; Hatsuda, T.; Weise, W. Role of Vector Interaction and Axial Anomaly in the PNJL Modeling of the QCD Phase Diagram. Phys. Lett. B 2013, 719, 131–135. [Google Scholar] [CrossRef]
- Glendenning, N.K. First-order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 1274–1287. [Google Scholar] [CrossRef]
- Glendenning, N.K. Phase transitions and crystalline structures in neutron star cores. Phys. Rep. 2001, 342, 393–447. [Google Scholar] [CrossRef]
- Bonanno, L.; Sedrakian, A. Composition and stability of hybrid stars with hyperons and quark color-superconductivity. Astron. Astrophys. 2012, 539, A16. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron-quark crossover and massive hybrid stars with strangeness. Astrophys. J. 2013, 764, 12. [Google Scholar] [CrossRef]
- Masuda, K.; Hatsuda, T.; Takatsuka, T. Hadron–quark crossover and massive hybrid stars. Prog. Theor. Exp. Phys. 2013, 7, 073D01. [Google Scholar] [CrossRef]
- Lenzi, C.H.; Lugones, G. Hybrid Stars in the Light of the Massive Pulsar PSR J1614-2230. Astrophys. J. 2012, 759, 57. [Google Scholar] [CrossRef]
- Ranea-Sandoval, I.F.; Han, S.; Orsaria, M.O.; Contrera, G.A.; Weber, F.; Alford, M.G. Constant-sound-speed parametrization for Nambu–Jona-Lasinio models of quark matter in hybrid stars. Phys. Rev. C 2016, 93, 045812. [Google Scholar] [CrossRef]
- Contrera, G.A.; Orsaria, M.; Ranea-Sandoval, I.F.; Weber, F. Hybrid Stars in the Framework of different NJL Models. arXiv 2016. [Google Scholar]
- Voskresensky, D.N.; Yasuhira, M.; Tatsumi, T. Charge screening in hadron–quark mixed phase. Phys. Lett. B 2002, 541, 93–100. [Google Scholar] [CrossRef]
- Yasutake, N.; Lastowiecki, R.; Benic, S.; Blaschke, D.; Maruyama, T.; Tatsumi, T. Finite-size effects at the hadron-quark transition and heavy hybrid stars. Phys. Rev. C 2014, 89, 065803. [Google Scholar] [CrossRef]
- Palhares, L.F.; Fraga, E.S. Droplets in the cold and dense linear sigma model with quarks. Phys. Rev. D 2010, 82, 125018. [Google Scholar] [CrossRef]
- Pinto, M.B.; Koch, V.; Randrup, J. Surface tension of quark matter in a geometrical approach. Phys. Rev. C 2012, 86, 025203. [Google Scholar] [CrossRef]
- Mintz, B.W.; Stiele, R.; Ramos, R.O.; Schaffner-Bielich, J. Phase diagram and surface tension in the three-flavor Polyakov-quark-meson model. Phys. Rev. D 2013, 87, 036004. [Google Scholar] [CrossRef]
- Spinella, W.M.; Weber, F.; Contrera, G.A.; Orsaria, M.G. Neutrino emissivity in the quark-hadron mixed phase of neutron stars. Eur. Phys. J. A 2016, 52, 61. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Kurkela, A.; Fraga, E.S.; Schaffner-Bielich, J.; Vuorinen, A. Constraining neutron star matter with Quantum Chromodynamics. Astrophys. J. 2014, 789, 127. [Google Scholar] [CrossRef]
- Friedman, J.L.; Ipser, J.R.; Parker, L. Rapidly rotating neutron star models. Astrophys. J. 1986, 304, 115–139. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M.; Masak, D.; Yahil, A. Rapidly rotating pulsars and the equation of state. Astrophys. J. 1990, 355, 241–254. [Google Scholar] [CrossRef]
- Salgado, M.; Bonazzola, S.; Gourgoulhon, E.; Haensel, P. High precision rotating netron star models 1: Analysis of neutron star properties. Astron. Astrophys. 1994, 291, 155–170. [Google Scholar]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly rotating polytropes in general relativity. Astrophys. J. 1994, 422, 227–242. [Google Scholar] [CrossRef]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly rotating neutron stars in general relativity: Realistic equations of state. Astrophys. J. 1994, 424, 823–845. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Weber, F. Nuclear solid crust on rotating strange quark stars. Astrophys. J. 1992, 400, 647–658. [Google Scholar] [CrossRef]
- Glendenning, N.K. Limiting rotational period of neutron stars. Phys. Rev. D 1992, 46, 4161–4168. [Google Scholar] [CrossRef]
- Backer, D.C.; Kulkarni, S.R.; Heiles, C.; Davis, M.M.; Goss, W.M. A millisecond pulsar. Nature 1982, 300, 615–618. [Google Scholar] [CrossRef]
- Fruchter, A.S.; Stinebring, D.R.; Taylor, J.H. A millisecond pulsar in an eclipsing binary. Nature 1988, 333, 237–239. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Hartle, J.B.; Thorne, K.S. Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars. Astrophys. J. 1968, 153, 807–834. [Google Scholar] [CrossRef]
- Weber, F.; Glendenning, N.K. Application of the improved Hartle method for the construction of general relativistic rotating neutron star models. Astrophys. J. 1992, 390, 541–549. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ranson, S.M.; Roberts, M.S.E.; Hessels, J.W.T. Shapiro delay measurement of a two solar mass neutron star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, E.; Pennucci, T.T.; Ellis, J.A.; Stairs, I.H.; Nice, D.J.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Crowter, K.; Dolch, T.; et al. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Lynch, R.S.; Boyles, J.; Ransom, S.M.; Stairs, I.H.; Lorimer, D.R.; McLaughlin, M.A.; Hessels, J.W.T.; Kaspi, V.M.; Kondratiev, V.I.; Archibald, A.M. The Green Bank Telescope 350 MHz drift-scan survey II: data analysis and the timing of 10 new pulsars, including a relativistic binary. Astrophys. J. 2013, 763, 81. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Stejner, M.; Weber, F.; Madsen, J. Signature of deconfinement with spin-down compression in cooling hybrid stars. Astrophys. J. 2009, 694, 1019–1033. [Google Scholar] [CrossRef]
| Nuclear Matter Property | Units | GM1 | DD2 |
|---|---|---|---|
| fm | 0.153 | 0.149 | |
| E/N | MeV | ||
| K | MeV | 300 | 243 |
| 0.70 | 0.56 | ||
| MeV | 32.5 | 32.7 | |
| L | MeV | 91.96 | 55.04 |
| EoS | a () | c () |
|---|---|---|
| GM1 () | ||
| GM1 () | ||
| DD2 () |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mellinger, R.D.; Weber, F.; Spinella, W.; Contrera, G.A.; Orsaria, M.G. Quark Deconfinement in Rotating Neutron Stars. Universe 2017, 3, 5. https://doi.org/10.3390/universe3010005
Mellinger RD, Weber F, Spinella W, Contrera GA, Orsaria MG. Quark Deconfinement in Rotating Neutron Stars. Universe. 2017; 3(1):5. https://doi.org/10.3390/universe3010005
Chicago/Turabian StyleMellinger, Richard D., Fridolin Weber, William Spinella, Gustavo A. Contrera, and Milva G. Orsaria. 2017. "Quark Deconfinement in Rotating Neutron Stars" Universe 3, no. 1: 5. https://doi.org/10.3390/universe3010005
APA StyleMellinger, R. D., Weber, F., Spinella, W., Contrera, G. A., & Orsaria, M. G. (2017). Quark Deconfinement in Rotating Neutron Stars. Universe, 3(1), 5. https://doi.org/10.3390/universe3010005







