Strategies to Ascertain the Sign of the Spatial Curvature

Abstract

The second law of thermodynamics, in the presence of gravity, is known to hold at small scales, as in the case of black holes and self-gravitating radiation spheres. Using the Friedmann–Lemaître–Robertson–Walker metric and the history of the Hubble factor, we argue that this law also holds at cosmological scales. Based on this, we study the connection between the deceleration parameter and the spatial curvature of the metric, ${\mathsf{\Omega }}_k$, and set limits on the latter, valid for any homogeneous and isotropic cosmological model. Likewise, we devise strategies to determine the sign of the spatial curvature index k. Finally, assuming the lambda cold dark matter model is correct, we find that the acceleration of the cosmic expansion is increasing today.

1. Introduction

The validity of the second law of thermodynamics for systems dominated by gravity should not be taken for granted. Gravity is a long-ranged interaction while the formulation of the second is based on the observation of ordinary systems, i.e., those dominated by short-ranged interactions. In actual fact, its validity for the former systems was studied only recently, notably in the case of black holes and self-gravitating radiation spheres. In the former case, Bekenstein demonstrated that the black-hole entropy, in addition to the entropy of the black-hole exterior, never decreases [1,2]. In the latter, it was shown that the static stable configurations of a sphere of self-gravitating radiation are those that maximize the radiation entropy [3,4]. Both instances correspond to small scale systems. Although different authors assumed it to be in order to constrain the evolution of cosmological models (see, e.g., [5] and references therein), as far as we know, the validity of the said law at large (i.e., cosmic) scales has not been explored as yet. The main purpose of this work is to fill this gap. Our study analysis rests on the simplest realistic large-scale space-time metric, namely, the Friedmann–Lemaître–Robertson–Walker (FLRW) one alongside a selected set of observational data about the history of cosmic expansion.

Homogeneous and isotropic universe models are usually described by the FLRW metric

$$d{s}^2=-c^2\mathrm{d}{t}^2+a^2\left(t\right)\left\{\frac{\mathrm{d}{r}^2}{1-k{r}^2}+r^2\left(\mathrm{d}{\theta }^2+{sin}^2\theta \mathrm{d}{\varphi }^2\right)\right\},$$

(1)

coupled to the sources of the gravitational field. This metric relies on the cosmological principle [6,7,8] whose validity, at large scales, has not been contradicted thus far [9] and it looks rather robust [10,11,12]. The curvature index, k, is either $0,+1$, or $-1$ depending on whether the spatial part of the metric is flat, positively curved (closed), or negatively curved (hyperbolic), respectively.

This constant index, like the scale factor $a\left(t\right)$, is not a directly observable quantity. In principle, however, it can be determined through the knowledge of the dimensionless, fractional curvature density, ${\mathsf{\Omega }}_k\equiv -k/\left(a^2{H}^2\right)$, which is accessible to observation, albeit indirectly. As usual, $H=c\mathrm{d}lna/\mathrm{d}t$ denotes the Hubble factor. Current measurements of ${\mathsf{\Omega }}_k$ only indicate that its present absolute value is small ($\mid {\mathsf{\Omega }}_{k0}\mid$ ≲ 10${}^{-3}$ [13,14]). Note that this constraint was obtained under the assumption that the universe is accurately described by the ΛCDM model. Thus the sign of k remains unknown.

The aim of this research is fourfold: (i) To determine whether the second law of thermodynamics is fulfilled at cosmological scales and; if so, (ii) constrain ${\mathsf{\Omega }}_k$ as much as possible and (iii) determine the sign of k; finally, (iv) to derive a thermodynamic constraint relating the present value of the deceleration and jerk parameters. For the first three objectives, neither a cosmological model nor theory of gravity will be assumed. We shall just use the FLRW metric, the history $H\left(z\right)$ of the Hubble factor and the second law of thermodynamics. For the fourth objective, we will assume Einstein gravity and the ΛCDM model. As is customary, a subindex zero attached to any quantity means that the latter should be evaluated at present time.

2. Cosmological Consequences of the Second Law

Given the strong connection between gravity and thermodynamics [1,2,15,16,17], it is natural to expect that the universe behaves as a normal thermodynamic system; it therefore must tend to a state of maximum entropy in the long run [18,19].

For comoving observers, FLRW models entail “normal”, “trapped” and “anti-trapped” regions. In the first one, the expansion of outgoing null geodesic congruences, normal to the spatial two-sphere of radius $\tilde{r}(=ra\left(t\right))$ centered at the origin (i.e., at the position of the observer), is positive, and negative for ingoing null geodesic congruences. In the trapped region, both kind of geodesic congruences have negative expansion. By contrast, in the anti-trapped region the expansion of both congruences is positive. The boundary hyper-surface of the space-time anti-trapped region is called the apparent horizon; its radius is ${\tilde{r}}_{\mathcal{A}}={[{(H/c)}^2+k{a}^{-2}]}^{-1/2}$. Since the observer has no information about what might be going on beyond the horizon, the latter has an entropy, namely: $S_{\mathcal{A}}=k_B\pi {\tilde{r}}_{\mathcal{A}}^2/{\ell }_{\mathrm{pl}}^2$, where ${\ell }_{\mathrm{pl}}$ is Planck’s length. For details, see [20]. (Bear in mind that $\tilde{r}$ and H have dimensions of length and length${}^{-1}$, respectively, k of length${}^{-2}$, and a is dimensionless.)

A rather reasonable assumption concerning the entropy of the observable universe is that it is dominated by the entropy of the cosmic horizon. In the current universe, the entropy of the horizon exceeds that of supermassive black holes, stellar black holes, relic neutrinos and CMB photons by 18, 25, 33 and 33 orders of magnitude, respectively [21]. There are several possible choices for the cosmic horizon: the particle horizon, the event horizon, the apparent horizon and the Hubble horizon. Given that the first one does not exist for accelerating universes and the second only exists if the universe accelerates forever in the future, we take the apparent horizon, which, on the one hand, always exists, both for ever-expanding and ever-contracting universes, and, on the other hand, by contrast to the other mentioned possibilities, the laws of thermodynamics are fulfilled on it [22]. The Hubble horizon is a particular case of the apparent horizon when $k=0$.

To support the above claim that the entropy of the horizon dominates over the entropy of any form of energy inside the horizon, especially at late times, we shall consider the entropy of pressureless matter. The latter is given by $S_m=k_{B}n{V}_k$ [23], with $n=n_0{a}^{-3}$, being $n_0$ the present number density of matter particles, and

$$V_k=2\pi a^2\left[\sqrt{\mid k\mid }a{sin}^{-1}\left(\sqrt{\mid k\mid }{a}^{-1}{\tilde{r}}_{\mathcal{A}}\right)-k{\tilde{r}}_{\mathcal{A}}^{2}H\right]$$

(2)

the volume enclosed by the apparent horizon for $k=+1$ and $-1$ (for the flat case, $V_{k=0}=(4\pi /3){\tilde{r}}_{\mathcal{A}}^3$). For $k=-1$ one follows $S_m(a\gg 1)\to 2k_B{n}_0\pi a^{-1}{\tilde{r}}_{\mathcal{A}}^{2}H$. Hence, when $a\gg 1$ the ratio $S_{\mathcal{A}}/S_m$ results proportional to $a/H$. For $k=+1$ one has $S_m(a\gg 1)\to 2k_B{n}_0{a}^{-1}\left(1-\sqrt{1-{\tilde{r}}_{\mathcal{A}}^2{a}^{-1}}\right)$, hence

$$\frac{S_{\mathcal{A}}}{S_m}\propto \frac{a{\tilde{r}}_{\mathcal{A}}^2}{1-\sqrt{1-\frac{{\tilde{r}}_{\mathcal{A}}^2}{a}}}.$$

Accordingly, in all three cases ($k=0,+1,-1$) the entropy of the horizon overwhelms that of the matter inside it, especially at late times.

Recalling that $S_{\mathcal{A}}\propto \mathcal{A}$ with $\mathcal{A}=4\pi {(H^2+k{a}^{-2})}^{-1}$ the area of the horizon (henceforward we set $c=1$), the second law of thermodynamics $S_{\mathcal{A}}^{\prime }\ge 0$ leads to

$${\mathcal{A}}^{\prime }=-\frac{{\mathcal{A}}^2}{2\pi }\left(H{H}^{\prime }-\frac{k}{a^3}\right)\ge 0\Rightarrow H{H}^{\prime }\le \frac{k}{a^3},$$

(3)

where the prime means $d/da$.

The second inequality tells us that if $H^{\prime }$ is or has been positive at any stage of cosmic expansion (excluding, possibly, the pre-Planckian era), then $k=+1$ and that, in principle, any sign of k is compatible with $H^{\prime }<0$. Multiplying the said inequality by $-a{H}^{-2}$ produces $-a{H}^{\prime }/H\ge {\mathsf{\Omega }}_k$, which can be recast in terms of the redshift as

$$(1+z)\frac{dlnH}{dz}\ge {\mathsf{\Omega }}_k.$$

(4)

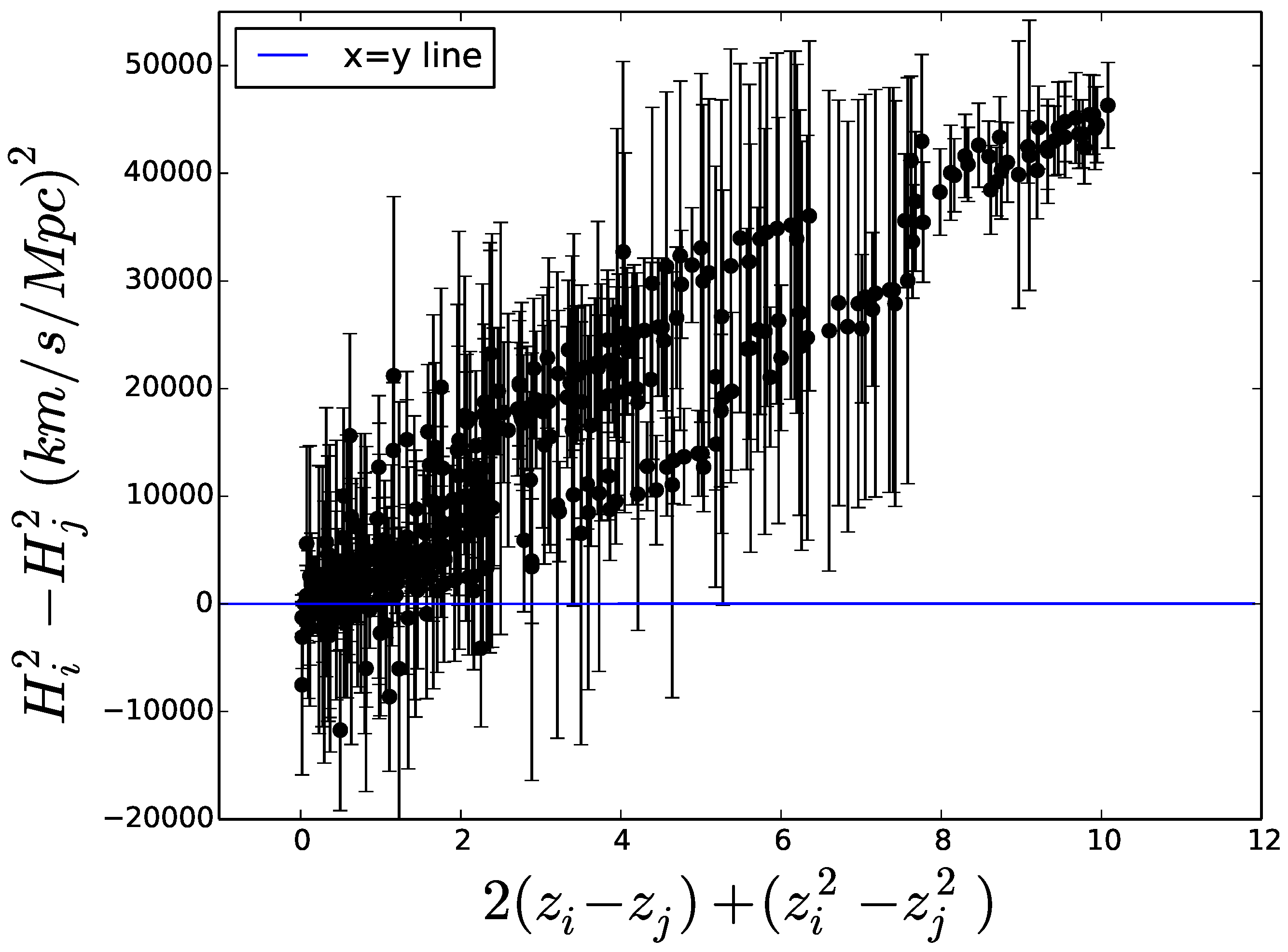
Thus, if $dH/dz>0$ for all $z\ge 0$, then both $k=+1$ and $k=0$ are consistent with the second law of thermodynamics at large scales. However, given the present ample uncertainties in the observational data regarding the Hubble history, if k were $-1$, then the said law could break down at cosmic scales. To explore this, we set $k=-1$ in Equation (4) and integrate the resulting expression in the interval $z_1\le z\le z_2$ to get

$$H_2^2-H_1^2\ge 2(z_2-z_1)+(z_2^2-z_1^2).$$

(5)

Therefore, if this relationship failed for whatever pair of points ($z_i$, $H_i$), with $i=1,2$, it should mean that the choice $k=-1$ would not be consistent with the second law at the said scales.

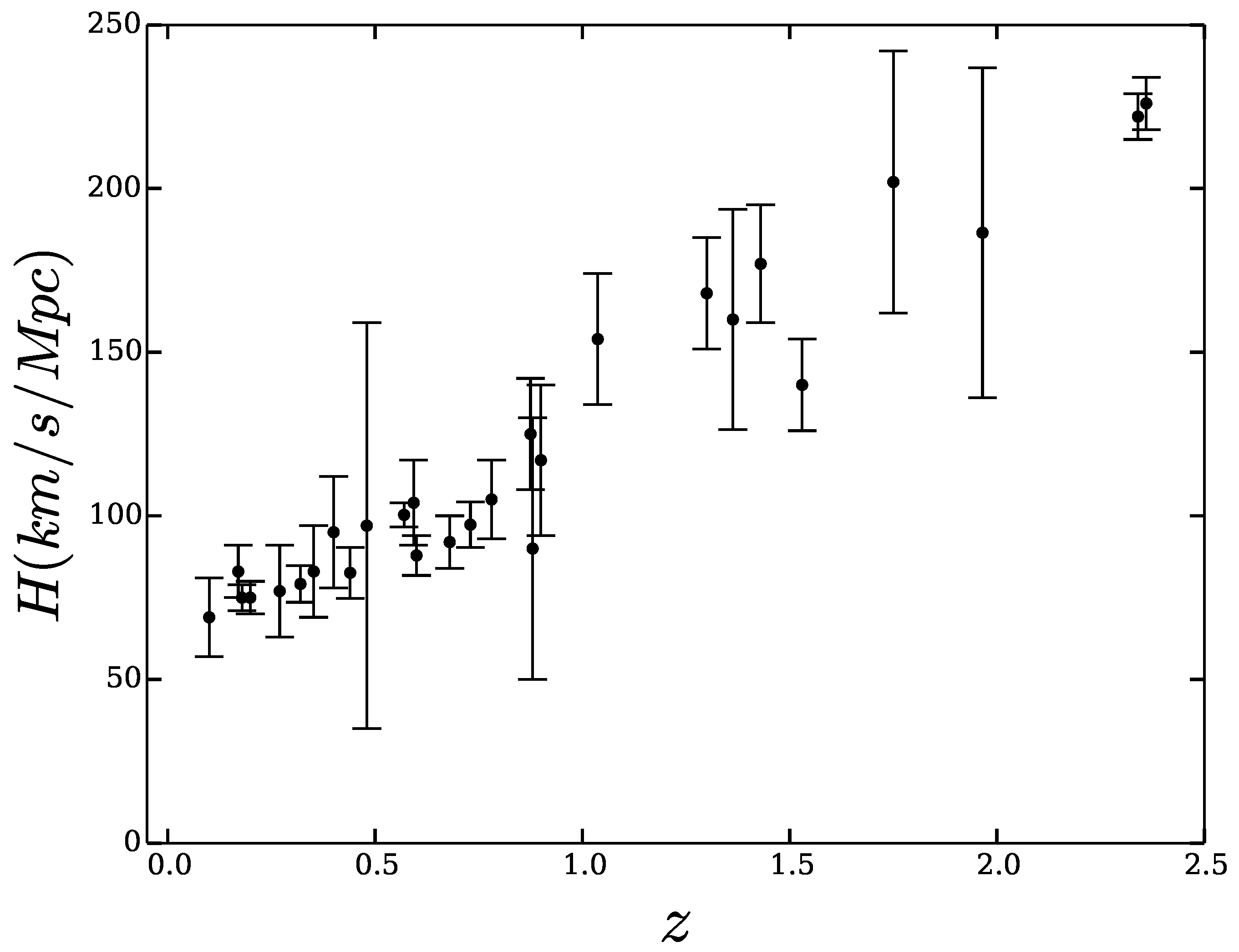
We use Equation (5) alongside the 28 experimental data H vs. z, in the interval $0.1\le z\le 2.36$, with their $1\sigma$ error bars, compiled by Farook et al. [24] and listed in Table 1 (see also Figure 1) for the reader convenience, to draw Figure 2. The latter suggests that, given the experimental uncertainties, the possibility $k=-1$ also appears compatible with the inequality $S_{\mathcal{A}}^{\prime }\ge 0$. While wider compilations of $H\left(z\right)$ are available, we believe this one is preferable because it does not include any obviously correlated data, nor does it contain older, less reliable data, some with much weight from anomalously small error bars.

Table 1. Hubble Parameter vs. Redshift Data.

z	$\mathit{H}\left(\mathit{z}\right)$ (km·s${}^{-1}$·Mpc${}^{-1}$)	Reference
$0.100$	$69\pm 12$	[26]
$0.170$	$83\pm 8$	[26]
$0.179$	$75\pm 4$	[27]
$0.199$	$75\pm 5$	[27]
$0.270$	$77\pm 14$	[26]
$0.320$	$79.2\pm 5.6$	[28]
$0.352$	$83\pm 14$	[27]
$0.400$	$95\pm 17$	[26]
$0.440$	$82.6\pm 7.8$	[29]
$0.480$	$97\pm 62$	[30]
$0.570$	$100.3\pm 3.7$	[28]
$0.593$	$104\pm 13$	[27]
$0.600$	$87.9\pm 6.1$	[29]
$0.680$	$92\pm 8$	[27]
$0.730$	$97.3\pm 7$	[29]
$0.781$	$105\pm 12$	[27]
$0.875$	$125\pm 17$	[27]
$0.880$	$90\pm 40$	[30]
$0.900$	$117\pm 23$	[26]
$1.037$	$154\pm 20$	[27]
$1.300$	$168\pm 17$	[26]
$1.363$	$160\pm 33.6$	[31]
$1.430$	$177\pm 18$	[26]
$1.530$	$140\pm 14$	[26]
$1.750$	$202\pm 40$	[26]
$1.965$	$186.5\pm 50.4$	[31]
$2.340$	$222\pm 7$	[32]
$2.360$	$226\pm 8$	[33]

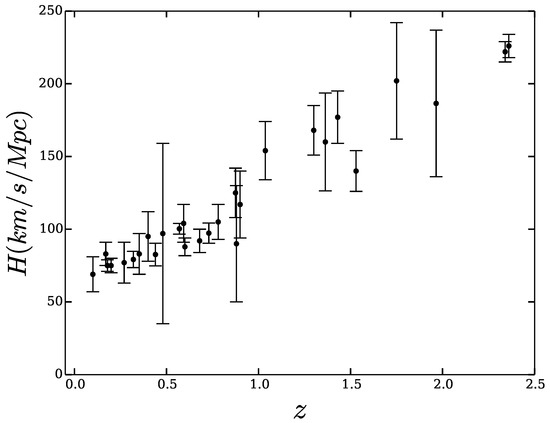
Figure 1. 28 $H\left(z\right)$ data points with their $1\sigma$ uncertainty.

Figure 2. Left-hand side vs. right-hand side of Equation (5) for all possible $i>j$ combinations of the data shown in Table 1. The error bars denote $1\sigma$ confidence level.

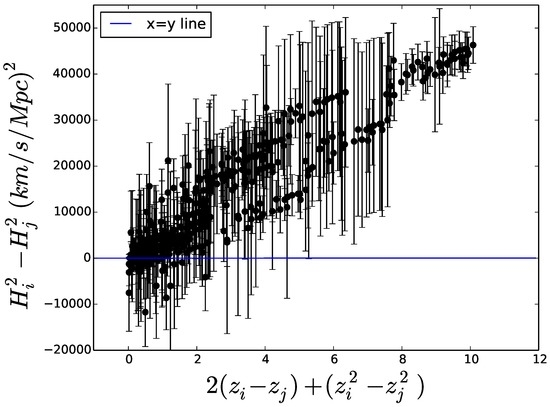
Equation (4) can alternatively be written as

$$1+q\ge {\mathsf{\Omega }}_k,$$

(6)

where $q=-\ddot{a}/\left(a{H}^2\right)$ is the dimensionless deceleration parameter. The last equation, like (4), imposes an upper bound (that depends on redshift) on ${\mathsf{\Omega }}_k$. In the radiation dominated era $q$ was close to 1; a result that, in spite of having been derived for spatially flat universes described by general relativity, should hold irrespective of the sign of the curvature and the gravity theory employed. Notice that even a mild deviation of $q\simeq 1$ at that time would conflict with the observational results about the primordial nucleosynthesis of light elements [25]. This suggests an easily verifiable test on modified gravity theories, namely, that they should be consistent with the bound ${\mathsf{\Omega }}_k\le 2$ at the radiation era. However, if general relativity is the right theory of gravity, the first Friedmann equation implies the stronger bound ${\mathsf{\Omega }}_k<1$ at all epochs. Nevertheless, even if one uses general relativity, Equation (6) might provide a useful bound when $q<0$.

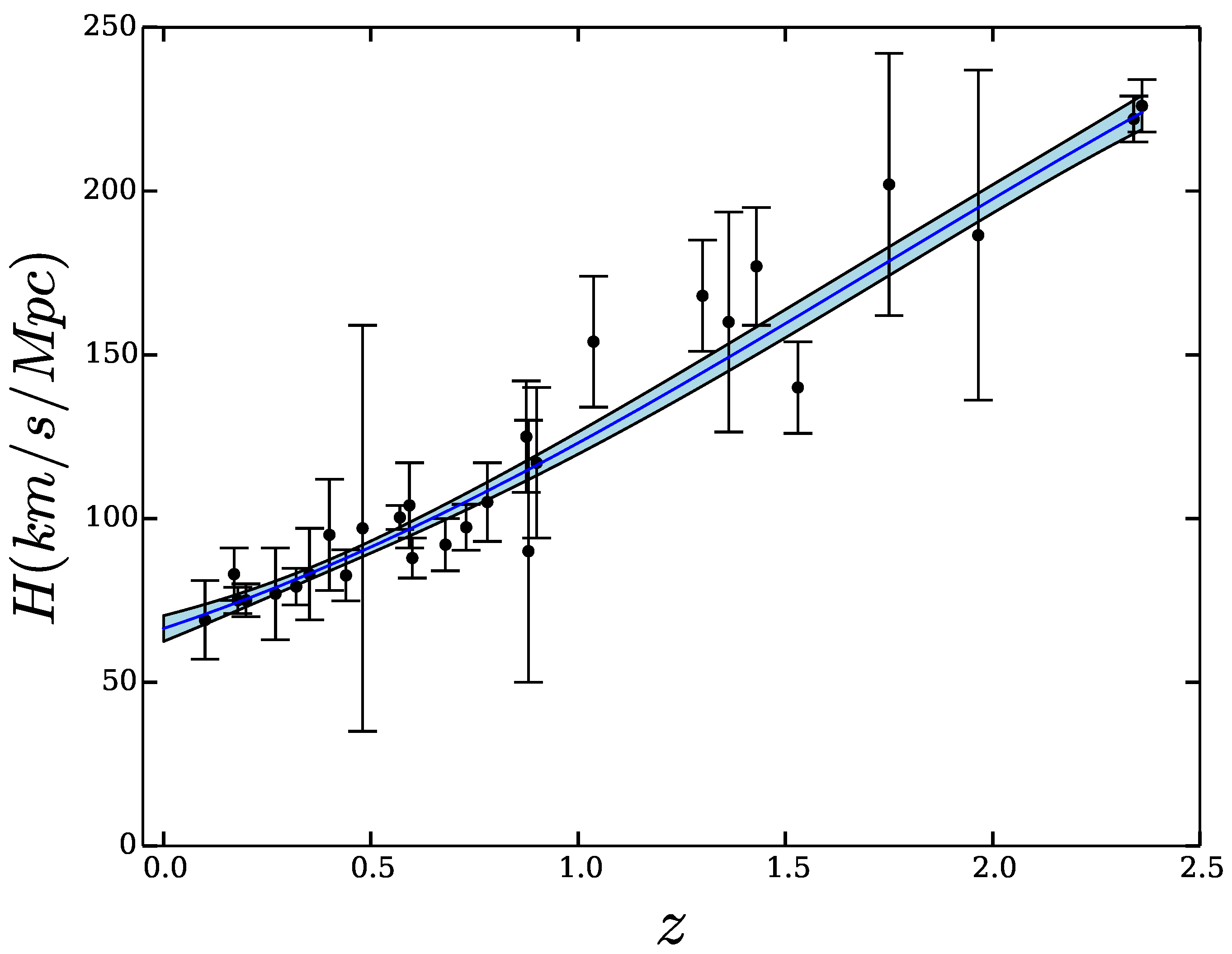
We can draw further consequences from the thermodynamic bound (6). To this end, we first apply the model independent Gaussian process (GP) introduced by Seikel et al. [34] to smooth the 28 observational $H\left(z\right)$ data depicted in Figure 1. Figure 3 shows the outcome.

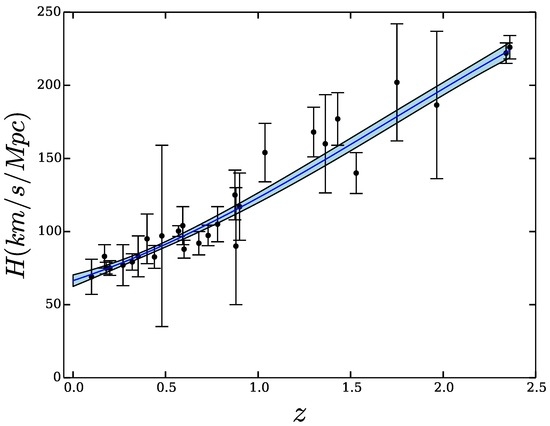
Figure 3. Gaussian process reconstruction of the history of the Hubble factor from the raw $H\left(z\right)$ data depicted in Figure 1, as well as here for convenience of the reader. The blue shaded region shows the $1\sigma$ uncertainty.

Inspection of the latter suggests that $dH/dz\ge 0$ in the redshift range be considered. If this gets confirmed by future $H\left(z\right)$ data of much higher quality, any sign of the curvature scalar index k will be consistent with the second law of thermodynamics. The following analysis, based on the smoothed data shown in Figure 3, allows the quantification of the gap between $1+q$ and ${\mathsf{\Omega }}_k$.

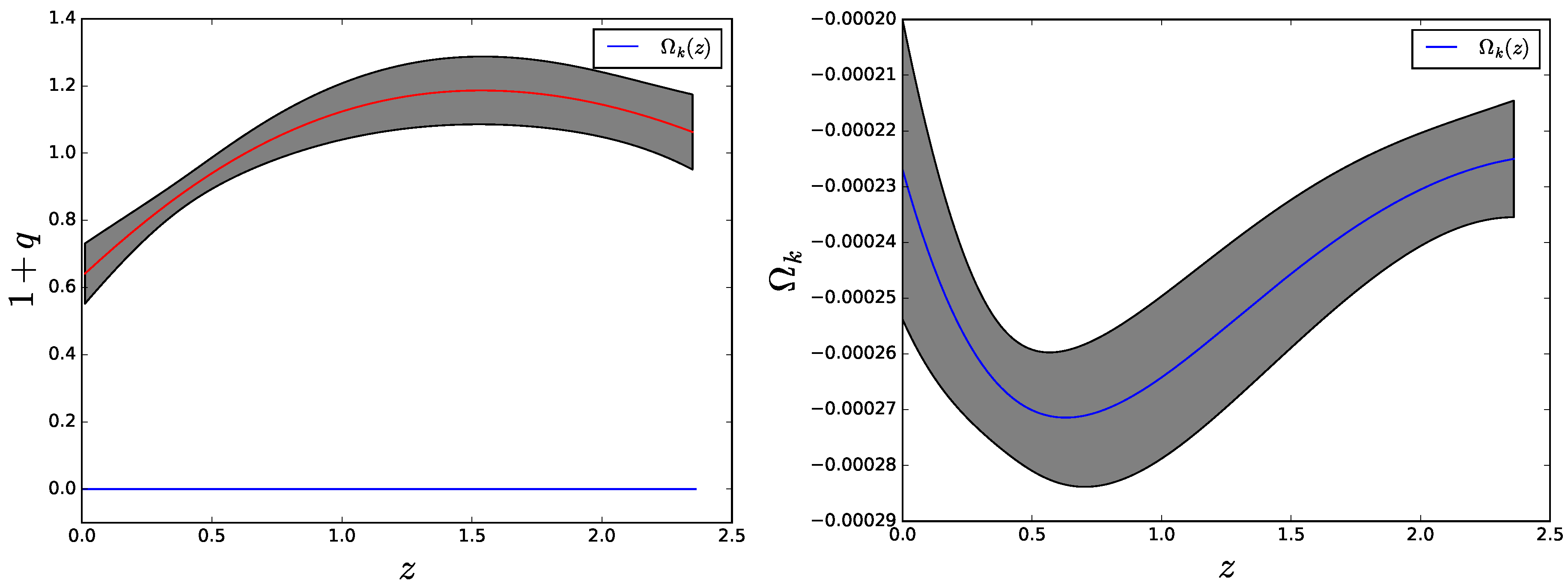
The quantity $1+q$ alongside its $1\sigma$, uncertainty is obtained by computing the quantity in the left-hand side of (4) using the smoothed $H\left(z\right)$ data, and similarly ${\mathsf{\Omega }}_k$ by computing $-k{(1+z)}^2/H^2\left(z\right)$ using the same data. Figure 4 and Figure 5 summarize the results for $k=+1$ and $-1$, respectively. It is apparent that, whatever the sign of k, the second law is fulfilled by a generous margin. Likewise, inspection of the left panels of the aforesaid figures indicates that ${\mathsf{\Omega }}_{k0}\le 0.64$. Obviously, this upper bound is much more loose than the one obtained in [14] ($6.5\times {10}^{-3}\le {\mathsf{\Omega }}_{k0}\le -6.6\times {10}^{-3}$), but the latter is based on a particular (though so far successful) cosmological model—the ΛCDM—that rests on a number of assumptions, some of which can be justified only a posteriori. By contrast, this other rests just on the FLRW metric and the second law of thermodynamics. Combining the readings on the vertical axes of the right panels of the same figures yields the constraint $2\times {10}^{-4}\le {\mathsf{\Omega }}_{k0}\le -2.6\times {10}^{-4}$.

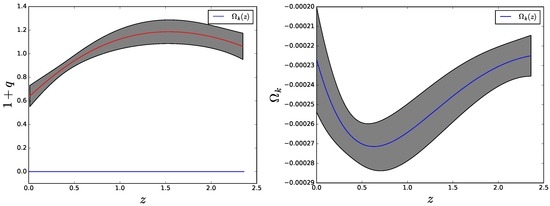
Figure 4. Left panel: $1+q$ vs. redshift after smoothing the 28 $H\left(z\right)$ data as depicted in Figure 3. Also shown is ${\mathsf{\Omega }}_k$ for $k=+1$. Clearly, the latter is practically zero. Right panel: Zoom of ${\mathsf{\Omega }}_k$ and its $1\sigma$ uncertainty interval.

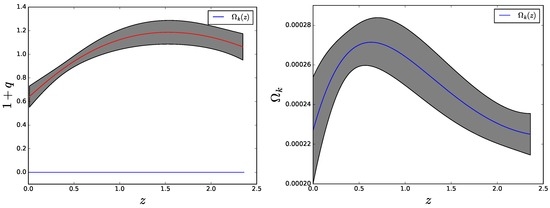
Figure 5. Same as Figure 4 but for $k=-1$.

Regrettably, as hinted above, the quality of the available sets of $H\left(z\right)$ data is not good enough to directly constrain ${\mathsf{\Omega }}_k$ into a small range, much less to discriminate the sign of k. One has to apply some smoothing procedure to the data of the Hubble history (the GP process in our case) to downsize the error bars and thus obtain a tighter constraint. However, one should not be fully confident about the outcome since the said procedure, though efficient, is not exempt of potential shortcomings.

Nevertheless, the situation is expected to improve greatly in the not so distant future thanks to the Sandage–Loeb (SL) test [35,36] based on the Mc-Vittie formula [37]

$$H\left(z_s\right)=H_0[1+z_s\left(t_0\right)]-\frac{\Delta z_s}{\Delta t_0}$$

(7)

that governs the drift of the redshift. Here, $z_s$ stands for the redshift of the source (e.g., quasar, globular cluster, HI region, ...). With the use of high precision spectrographs, such as CODEX [38], and extremely large telescopes, as the ELT [39], the SL test will provide us accurate $H\left(z\right)$ data sets at different redshift intervals. These data will be free of any assumption whatsoever about the spatial curvature, gravity theory or cosmological model.

Observational data in the $0<z<1.0$ interval will be provided by the square kilometer array (SKA) radio-telescope [40], likewise the wide radio-sky survey PARKES will scan 21-cm radio-sources [41] as well as the experiment CHIME in the $0.8<z<2.5$ interval [42]. To collect a useful sample of $H\left(z\right)$ data will take between one and four decades, approximately. Details can be found in References [43,44].

If the data revealed that, in some redshift, interval H decreased with increasing z, it would immediately imply $k=+1$. On the contrary, if H always increased in every z interval, the application of (4) would require more effort, but in any case it will (hopefully) permit one to discern the sign of k.

If the above strategy would fail, for instance if the data would indicate different signs for ${\mathsf{\Omega }}_k$ in separate intervals, it would mean either that the second law of thermodynamics does fail at large scales or that the FLRW metric should not be trusted after all.

3. The Jerk Parameter

By expanding the scale factor in terms of its successive derivatives we can write

$$a\left(t\right)=a_0\left\{1+H_0(t-t_0)-\frac{1}{2}{q}_0{H}_0^2{(t-t_0)}^2+\frac{1}{6}{j}_0{H}_0^3{(t-t_0)}^3+\frac{1}{24}{s}_0{H}_0^4{(t-t_0)}^4+\mathcal{O}\left({[t-t_0]}^5\right)\right\},$$

(8)

where $j=\stackrel{⃛}{a}/\left(a{H}^3\right)$ and $s={\left(a{H}^4\right)}^{-1}{d}^{4}a/d{t}^4$ are the dimensionless jerk and snap parameters, respectively.

Here, we shall focus on the current value of the jerk parameter of a universe dominated by pressureless matter and the cosmological constant (subindexes m and Λ, respectively). Thus far, we did not specialize to any cosmological model nor theory of gravity. In what follows, to constrain the theoretical value of $j_0$, we adopt general relativity and the ΛCDM model because they are the simplest theory and model, respectively, that comply, at least at the background level, with the observational data [14]. In this model, the Hubble factor, as well as the deceleration and jerk parameters, read in terms of the redshift

$$H\left(z\right)=H_0\sqrt{{\mathsf{\Omega }}_{m0}{(1+z)}^3+{\mathsf{\Omega }}_{\mathsf{\Lambda }0}+{\mathsf{\Omega }}_{k0}{(1+z)}^2},$$

(9)

$$q\left(z\right)=\frac{1}{2}\frac{{\mathsf{\Omega }}_{m0}{(1+z)}^3-2{\mathsf{\Omega }}_{\mathsf{\Lambda }0}}{{\mathsf{\Omega }}_{m0}{(1+z)}^3+{\mathsf{\Omega }}_{\mathsf{\Lambda }0}+{\mathsf{\Omega }}_{k0}{(1+z)}^2},$$

(10)

$$j\left(z\right)=1-\frac{{\mathsf{\Omega }}_{k0}{(1+z)}^2}{{\mathsf{\Omega }}_{m0}{(1+z)}^3+{\mathsf{\Omega }}_{\mathsf{\Lambda }0}+{\mathsf{\Omega }}_{k0}{(1+z)}^2},$$

(11)

where the various ${\mathsf{\Omega }}_{i0}$, with $i=m,\mathsf{\Lambda }$, and k, stand for the current values of the fractional energy densities.

Bearing in mind the Friedmann constraint ${\mathsf{\Omega }}_m+{\mathsf{\Omega }}_{\mathsf{\Lambda }}+{\mathsf{\Omega }}_k=1$ we readily get

$$j_0=1-{\mathsf{\Omega }}_{k0}$$

(12)

from Equation (11). Thereby if future accurate measurements show that $j_0$ deviates from unity, we will know that our universe (modulo the FLRW metric and the ΛCDM are correct) is not spatially flat, and the deviation will coincide with minus the present value of the spatial curvature. Unfortunately, current measurements of $j_0$ come along only with great latitude, $-7.6\le j_0\le 8.5$ [45]. However, this wide observational uncertainty gets substantially reduced after combining (12) with Equation (6), specialized to the ΛCDM model. It readily yields $q_0+j_0\ge 0$. For instance, using the experimental constraint on $q_0$ of Daly et al. [46], $q_0=-0.48\pm 0.11$, we find (within $1\sigma$)

$$j_0\ge 0.37.$$

(13)

The simple fact that, observationally, $q_0$ is negative [24,46,47,48], renders $j_0$ positive in the said model; i.e., cosmic acceleration should be increasing nowadays.

4. Concluding Remarks

The validity of the second law, in the presence of gravity, is well supported at small scales by the thermodynamics of astrophysical-sized collapsed objects, in particular of black holes [1,2], and of self-gravitating radiation spheres [3,4] but, to the best of our knowledge, this law had not been tested at cosmological scales thus far. Here, assuming the correctness of the FLRW metric at large scales and using the history of the Hubble factor—see Equations (4) and (5) and Figure 2—we found that the second law likely holds at these scales as well. However, due to the sizable error bars of the $H\left(z\right)$ data, the thermodynamic constraint on $\mid {\mathsf{\Omega }}_{k0}\mid$ is rather loose. As we have shown, the situation greatly improves by applying the GP procedure of Reference [34] to these data. Then, $\mid {\mathsf{\Omega }}_{k0}\mid \sim {10}^{-4}$—see the right-hand panel of Figure 4 and Figure 5. However, although the procedure rests on very reasonable assumptions, these are hard to test. On the other hand, we could not determine the sign of k. Nevertheless, we suggested that by means of Mc Vittie formula, Equation (7) of the drift of the redshift [37] and the use of advanced telescopes and spectrographs that will be in service soon, it will be possible to obtain accurate $H\left(z\right)$ data capable of discerning it. Further, in the context of the ΛCDM model, we demonstrated a very simple relationship, Equation (12), between the present value of the jerk parameter and ${\mathsf{\Omega }}_{k0}$. Finally, we showed that the second law drastically reduces the ample uncertainty about the current value of the jerk and using current constraints on $q_0$ sets a lower bound on it.