General Relativity and Cosmology: Unsolved Questions and Future Directions
Abstract
:1. Perspective
2. A Brief History
From Aristotle to Einstein
3. The Development of General Relativity
3.1. From Special to General Relativity
3.2. The Formalism of General Relativity
- The Strong Equivalence Principle: The laws of physics take the same form in a freely-falling reference frame as in Special Relativity
- The Weak Equivalence Principle: An observer in freefall should experience no gravitational field. That is to say, an observer cannot determine from a local experiment whether the his laboratory is being accelerated by a rocket of static at the surface of a gravitating body. Gravity is erased up to tidal forces, which are determined by the size of the laboratory and its distance to the centre of the gravitational attraction.
- it agrees with experiment
- it describes gravity entirely in terms of geometry
- it is free of any “prior geometry”
In 4 spacetime dimensions, the only divergence-free symmetric rank-2 tensor constructed solely from the metric g and its derivatives up to second differential order, and preserving diffeomorphism invariance, is the Einstein tensor plus a cosmological term.
3.3. Newtonian Nostalgia: The First Wave of Alternative Theories
3.4. Self-Consistency, Completeness, and Agreement with Experiment
3.5. Metric Theories and Quantum Gravity
3.6. The Gauge Approach and Non-Metric Theories
4. Why Consider Alternative Theories?
5. From General Relativity to Standard Cosmology
5.1. Cosmological Expansion and Evolution Histories
5.2. Matter (Dust)
5.3. Radiation
6. The Components and Geometry of the Universe and Cosmic Expansion
7. The Hot Big Bang
7.1. The Cosmic Microwave Background
7.2. Matter-Radiation Equality
7.3. Neutrinos
8. Inflation: The Second Wave of Alternative Theories
- The Horizon Problem
- The Flatness Problem
- The Monopole Problem
Hot Big Bang Plus Inflation
- The Horizon Problem. Solution: the entire universe evolved out of the same causally-connected region.
- The Flatness Problem. Solution: any initial curvature is diluted by the inflationary epoch and driven to zero.
- The Monopole Problem. Solution: the rapid expansion of the universe drastically reduces the predicted density of magnetic monopoles, if they exist.
9. The First Unknown Component: Dark Matter
10. The Second Unknown: Dark Energy and the New Wave Alternative Theories
11. The Evolution of Large-Scale Structure
11.1. Evolution on Small Scales
11.2. Growth oF Perturbations in the Presence of Dark Energy
11.3. The Power Spectrum of Matter
11.3.1. Nonlinear Evolution
11.3.2. The Primordial Perturbations
12. How Do We Test General Relativity?
13. Cosmological Tests
- (1)
- A theory of gravitational interactions.
- (2)
- A description of the matter in the universe and the non-gravitational interactions such as electromagnetic emissions.
- (3)
- A hypothesis on the symmetry.
- (4)
- A hypothesis on the topology, or the global structure of the universe.
13.1. Testing the Description of Matter and Non-Gravitational Interactions
13.2. Testing the Assumption of Symmetry
13.3. Testing the Gravitational Interactions
- Tests of the consistency between the expansion history and the growth of structure. A discrepancy in the equation of state parameter of dark energy w, inferred from the two approaches can indicate a breakdown of the GR-based smooth dark energy cosmological paradigm.
- Detailed measurements of the linear growth factor across different scales and redshifts.
- Comparison of the cosmological mass distribution inferred from different probes, especially redshift space distortions and lensing.
14. Possible Modifications of GR and Cosmological Implications
14.1. Weak and Strong-Field Regimes
14.2. Small and Large Distances
14.3. Low and High Accelerations
14.4. Low and High Curvature
14.5. Cosmological Probes
15. The Nature of Dark Energy and the Implications for General Relativity
- (1)
- there is some new kind of component in the universe, or
- (2)
- there is some new property of gravity.
16. The Current Status of General Relativity
17. Future Developments
17.1. Plausible Conclusions from Incomplete Information
- (1)
- Parameter inference (estimation). We assume that a model M is true, and we select a prior for the parameters θ, or the .
- (2)
- Model comparison. There are several possible models . We find the relative plausibility of each in the light of the data D, that is we calculate the ratio .
- (3)
- Model averaging. There is no clear evidence for a best model. We find the inference on the parameters which accounts for the model uncertainty.
17.2. Experimental Progress
17.3. Theoretical and Computational Progress
17.4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AU | Astronomical Unit |
| CDM | Cold Dark Matter |
| CMB | Cosmic Microwave Background |
| EEP | Einstein Equivalence Principle |
| ECKS | Einstein-Cartan-Kibble-Sciama |
| eV | electronvolt |
| FLRW | Friedmann-Lemaître-Robertson-Walker |
| GR | General Relativity |
| Gy | Gigayear ( years) |
| ΛCDM | Λ Cold Dark Matter |
| LLI | Local Lorentz invariance |
| LLR | Lunar laser ranging |
| LPI | Local position invariance |
| Mpc | Megaparsec |
| PPN | Parameterised post-Newtonian |
| SR | Special Relativity |
| TeV | teraelectronvolt ( electronvolts) |
References
- Feynman, R.; Leighton, R.B.; Sands, M.L. The Feynman Lectures on Physics; Addison-Wesley: Redwood City, CA, USA, 1989; Volume 2. [Google Scholar]
- Gauthier-Lafaye, F.; Holliger, P.; Blanc, P.L. Natural fission reactors in the Franceville basin, Gabon: A review of the conditions and results of a “critical event” in a geologic system. Geochim. Cosmochim. Acta 1996, 60, 4831–4852. [Google Scholar] [CrossRef]
- Einstein, A. Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. Sitzungsber. Preuss. Akad. Wiss. 1915, 1915, 831–839. (In German) [Google Scholar]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A Determination of the deflection of light by the sun’s gravitational field, from observations made at the total eclipse of 29 May 1919. Philos. Trans. R. Soc. Lond. Ser. A 1920, 220, 291–333. [Google Scholar] [CrossRef]
- Will, C.M. The 1919 measurement of the deflection of light. Class. Quantum Gravity 2015, 32, 124001. [Google Scholar] [CrossRef]
- Coles, P. Einstein, Eddington and the 1919 Eclipse. In Historical Development of Modern Cosmology; Martínez, V.J., Trimble, V., Pons-Bordería, M.J., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2001; Volume 252, p. 21. [Google Scholar]
- Popper, K.R. Logik der Forschung; Mohr Siebeck: Tübingen, Germany, 1934. [Google Scholar]
- Lahav, O.; Massimi, M. Dark energy, paradigm shifts, and the role of evidence. Astron. Geophys. 2014, 55, 3.12–3.15. [Google Scholar] [CrossRef]
- Ellis, G.F.R. Cosmology and verifiability. Q. J. R. Astron. Soc. 1975, 16, 245–264. [Google Scholar]
- Crombie, A.C. Quantification in medieval physics. Isis 1961, 52, 143–160. [Google Scholar] [CrossRef]
- Bennett, J. Early modern mathematical instruments. Isis 2011, 102, 697–705. [Google Scholar] [CrossRef] [PubMed]
- Franklin, A. Principle of inertia in the middle ages. Am. J. Phys. 1976, 44, 529–543. [Google Scholar] [CrossRef]
- Sorabji, R. Matter, Space and Motion: Theories in Antiquity and Their Sequel; Duckworth: London, UK, 1988. [Google Scholar]
- Cushing, J.T. Philosophical Concepts in Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Grant, E. Scientific Thought in Fourteenth-Century Paris: Jean Buridan and Nicole Oresme. Ann. N. Y. Acad. Sci. 1978, 314, 105–126. [Google Scholar] [CrossRef]
- Babb, J. Mathematical concepts and proofs from nicole oresme: Using the History of calculus to teach mathematics. Sci. Educ. 2005, 14, 443–456. [Google Scholar] [CrossRef]
- Transtrum, M.K.; Machta, B.B.; Brown, K.S.; Daniels, B.C.; Myers, C.R.; Sethna, J.P. Perspective: Sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 2015, 143, 010901. [Google Scholar] [CrossRef] [PubMed]
- Galilei, G. Sidereus Nuncius Magna, Longeque Admirabilia Spectacula Pandens; Tommaso Baglioni: Venice, Italy, 1610. [Google Scholar]
- Perryman, M. The history of astrometry. Eur. Phys. J. H 2012, 37, 745–792. [Google Scholar] [CrossRef]
- Newton, I. Philosophiae Naturalis Principia Mathematica, 1st ed.; Joseph Streater: London, UK, 1687. [Google Scholar]
- De Maupertuis, P.L.M. Les Loix du mouvement et du repos déduites d’un principe metaphysique. In Histoire de l’Académie Royale des Sciences et des Belles Lettres; Académie Royale des Sciences et des Belles Lettres de Berlin: Berlin, Germany, 1746. [Google Scholar]
- Euler, L. Réfléxions sur quelques loix générales de la nature qui s’observent dans les effets des forces quelconques. Acad. R. Sci. Berl. 1750, 4, 189–218. [Google Scholar]
- Lagrange, L. Méchanique Analytique; Chez La Veuve Desaint: Paris, France, 1788. [Google Scholar]
- Hamilton, W.R. On a general method in dynamics. Philos. Trans. R. Soc. Lond. 1834, 124, 247–308. [Google Scholar] [CrossRef]
- Hamilton, W.R. Second essay on a general method in dynamics. Philos. Trans. R. Soc. Lond. 1835, 125, 95–144. [Google Scholar] [CrossRef]
- Galle, J.G. Account of the discovery of Le Verrier’s planet Neptune, at Berlin, Sept. 23, 1846. Mon. Not. R. Astron. Soc. 1846, 7, 153. [Google Scholar]
- Danjon, A. Le centenaire de la découverte de Neptune. Ciel Terre 1946, 62, 369. [Google Scholar]
- Lexell, A.J. Recherches sur la nouvelle planete, decouverte par M. Herschel & nominee Georgium Sidus. Acta Acad. Sci. Imp. Petropolitanae 1783, 1, 303–329. [Google Scholar]
- Sheehan, W. News from Front (of the Solar System): The problem with Mercury, the Vulcan hypothesis, and General Relativity’s first astronomical triumph. In Proceedings of the 227th AAS Meeting, Kissimmee, FL, USA, 4–8 January 2016; Volume 227.
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Poincaré, H. Thorie Mathématique de la Lumiére; Carré & C. Naud: Paris, France, 1889. [Google Scholar]
- Maxwell, J.C. A dynamical theory of the electromagnetic field. Philos. Trans. R. Soc. Lond. 1865, 155, 489–512. [Google Scholar] [CrossRef]
- Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. (Germany) 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Einstein, A. Über den Einfluss der Schwerkraft auf die Ausbreitung des Lichtes. Ann. Phys. (Germany) 1911, 35, 898–908. [Google Scholar] [CrossRef]
- Einstein, A. Lichtgeschwindigkeit und Statik des Gravitationsfeldes. Ann. Phys. (Germany) 1912, 38, 355–369. [Google Scholar] [CrossRef]
- Einstein, A. Theorie des statischen Gravitationsfeldes. Ann. Phys. (Germany) 1912, 38, 443–458. [Google Scholar] [CrossRef]
- Einstein, A.; Grossmann, M. Entwurf einer verallgemeinerten Relativitätstheorie und eine Theorie der Gravitation. I. Physikalischer Teil von A. Einstein II. Mathematischer Teil von M. Grossmann. Z. Math. Phys. 1913, 62, 225–244 and 245–261. [Google Scholar]
- Le Verrier, U. Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète. C. R. Hebd. Séances L’Acad. Sci. 1859, 49, 379–383. [Google Scholar]
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 4. [Google Scholar] [CrossRef]
- Fierz, M.; Pauli, W. Relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. R. Soc. Lond. 1939, 173, 211–232. [Google Scholar] [CrossRef]
- Schild, A. Time. Tex. Q. 1960, 3, 42–62. [Google Scholar]
- Schild, A. Gravitational Theories of the Whitehead type and the principle of equivalence. In Evidence for Gravitational Theories; Møller, C., Ed.; Academic Press: New York, NY, USA, 1962. [Google Scholar]
- Schild, A. Lectures on General Relativity Theory. In Relativity Theory and Astrophysics: I, Relativity and Cosmology: II, Galactic Structure: III, Stellar Structure; Ehlers, J., Ed.; American Mathematical Society: Providence, RI, USA, 1967. [Google Scholar]
- Riemann, B. Bernhard Riemann’s Gesammelte mathematische Werke und wissenschaftlicher Nachlass, 1st ed.; Weber, H., Ed.; Teubner: Leipzig, Germany, 1876. [Google Scholar]
- Riemann, B. Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. Abh. Kön. Ges. Wiss. Gött. 1868, 13, 133–150. [Google Scholar]
- Einstein, A. Die Feldgleichungen der Gravitation. Sitzungsber. Preuss. Akad. Wiss. 1915, 1915, 844–847. (In German) [Google Scholar]
- Einstein, A. Zur Allgemeinen Relativitätstheorie. Sitzungsber. Preuss. Akad. Wiss. 1915, 1915, 799–801. (In German) [Google Scholar]
- Ni, W.T. Theoretical Frameworks for Testing Relativistic Gravity. IV. A Compendium of Metric Theories of Gravity and Their Post-Newtonian Limits. Astrophys. J. 1972, 176, 769–796. [Google Scholar] [CrossRef]
- Thorne, K.S.; Ni, W.T.; Will, C.M. Theoretical frameworks for testing relativistic gravity: A review. In Proceedings of the Conference on Experimental Tests of Gravitational Theories, Pasadena, CA, USA, 11–13 November 1970; pp. 10–31.
- Lovelock, D. The uniqueness of the Einstein field equations in a four-dimensional space. Arch. Ration. Mech. Anal. 1969, 33, 54–70. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein Tensor and Its Generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Lovelock, D. The Four-Dimensionality of Space and the Einstein Tensor. J. Math. Phys. 1972, 13, 874–876. [Google Scholar] [CrossRef]
- Cartan, E. Sur les équations de la gravitation d’Einstein. J. Math. Pures Appl. 1922, 1, 141–204. [Google Scholar]
- Anderson, J.L. Principles of Relativity Physics; Academic Press: New York, NY, USA, 1967. [Google Scholar]
- Norton, J.D. General covariance, gauge theories and the Kretschmann objection. In Symmetries in Physics: Philosophical Reflections; Brading, K.A., Castellani, E., Eds.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kretschmann, E. Über den physikalischen Sinn der Relativitätspostulate, A. Einsteins neue und seine ursprungliche Relativitätstheorie. Ann. Phys. (Germany) 1917, 53, 575–614. [Google Scholar] [CrossRef]
- Nordstrøm, G. Zur Theorie der Gravitation vom Standpunkt des Relativitäsprinzip. Ann. Phys. (Germany) 1913, 42, 533–554. [Google Scholar] [CrossRef]
- Einstein, A.; Fokker, A.D. The North current gravitation theory from the viewpoint of absolute differential calculus. Ann. Phys. (Germany) 1914, 44, 321–328. [Google Scholar] [CrossRef]
- Whitehead, A.N. The Principle of Relativity; Cambridge University Press: Cambridge, UK, 1922. [Google Scholar]
- Will, C.M. Relativistic gravity in the solar system, II: Anisotropy in the Newtonian gravitational constant. Astrophys. J. 1971, 169, 141–156. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Matter, electricity and gravitation in flat spacetime. Proc. Natl. Acad. Sci. USA 1943, 29, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Jordan, P. Zum gegenwärtigen Stand der Diracschen kosmologischen Hypothesen. Z. Phys. 1959, 157, 112–121. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Dicke, R.H. Mach’s principle and invariance under transformation of units. Phys. Rev. 1962, 125, 2163–2167. [Google Scholar] [CrossRef]
- Will, C.M. Theory and Experiment in Gravitational Physics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Psaltis, D. Constraining Brans-Dicke Gravity with Accreting Millisecond Pulsars in Ultracompact Binaries. Astrophys. J. 2008, 688, 1282–1287. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Avilez, A.; Skordis, C. Cosmological Constraints on Brans-Dicke Theory. Phys. Rev. Lett. 2014, 113, 011101. [Google Scholar] [CrossRef] [PubMed]
- Ooba, J.; Ichiki, K.; Chiba, T.; Sugiyama, N. Planck constraints on scalar-tensor cosmology and the variation of the gravitational constant. Phys. Rev. D 2016, 93, 122002. [Google Scholar] [CrossRef]
- Bull, P. Extending Cosmological Tests of General Relativity with the Square Kilometre Array. Astrophys. J. 2016, 817, 26. [Google Scholar] [CrossRef]
- Damour, T.; Nordtvedt, K. General relativity as a cosmological attractor of tensor-scalar theories. Phys. Rev. Lett. 1993, 70, 2217–2219. [Google Scholar] [CrossRef] [PubMed]
- Damour, T.; Nordtvedt, K. Tensor-scalar cosmological models and their relaxation toward general relativity. Phys. Rev. D 1993, 48, 3436–3450. [Google Scholar] [CrossRef]
- Kustaanheimo, P. Route dependence of the gravitational redshift. Phys. Lett. 1966, 23, 75–77. [Google Scholar] [CrossRef]
- Kustaanheimo, P.E.; Nuotio, V.S. Relativistic Theories of Gravitation I: The One-Body Problem; University of Helsinki: Helsinki, Finland, 1967; unpublished. [Google Scholar]
- Einstein, A. Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsber. Preuss. Akad. Wiss. 1916, 1916 Pt 1, 688–696. (In German) [Google Scholar]
- Kumar, D.; Soni, V. Single particle Schrödinger equation with gravitational self-interaction. Phys. Lett. A 2000, 271, 157–166. [Google Scholar] [CrossRef]
- Deser, S. Gravity from self-interaction redux. Gen. Relativ. Gravit. 2010, 42, 641–646. [Google Scholar] [CrossRef]
- Hertz, H. Untersuchungen über die Ausbreitung der Elektrischen Kraft; J.A. Barth: Leipzig, Germany, 1894. [Google Scholar]
- Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Ann. Phys. (Germany) 1905, 17, 132–148. [Google Scholar] [CrossRef]
- LIGO Collaboration. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar]
- Yang, C.L.; Mills, R.L. Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 1954, 96, 191–195. [Google Scholar] [CrossRef]
- Yang, C.L.; Mills, R.L. Isotopic Spin Conservation and a Generalized Gauge Invariance. Phys. Rev. 1954, 95, 631. [Google Scholar]
- Weyl, H. Gravitation und Elektrizität. In Das Relativitätsprinzip; J. A. Barth: Leipzig, Germany, 1918. [Google Scholar]
- Weyl, H. Raum-Zeit-Materie; Springer: Berlin, Germany, 1918. [Google Scholar]
- Christoffel, E.B. Über die Transformation der homogenen Differentialausdrücke zweiten Grades. J. Reine Angew. Math. 1869, 70, 46–70. [Google Scholar] [CrossRef]
- Goenner, H.F.M. On the History of Unified Field Theories. Living Rev. Relativ. 2004, 7, 2. [Google Scholar] [CrossRef]
- Smiciklas, M.; Brown, J.M.; Cheuk, L.W.; Smullin, S.J.; Romalis, M.V. New test of local lorentz invariance using a 21Ne-Rb-K comagnetometer. Phys. Rev. Lett. 2011, 107, 171604. [Google Scholar] [CrossRef] [PubMed]
- Peck, S.K.; Kim, D.K.; Stein, D.; Orbaker, D.; Foss, A.; Hummon, M.T.; Hunter, L.R. Limits on local Lorentz invariance in mercury and cesium. Phys. Rev. A 2012, 86, 012109. [Google Scholar] [CrossRef]
- Hohensee, M.A.; Leefer, N.; Budker, D.; Harabati, C.; Dzuba, V.A.; Flambaum, V.V. Limits on violations of lorentz symmetry and the einstein equivalence principle using radio-frequency spectroscopy of atomic dysprosium. Phys. Rev. Lett. 2013, 111, 050401. [Google Scholar] [CrossRef] [PubMed]
- Utiyama, R. Invariant theoretical interpretation of interaction. Phys. Rev. 1956, 101, 1597–1607. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Lorentz invariance and the gravitational field. J. Math. Phys. 1961, 2, 212–221. [Google Scholar] [CrossRef]
- Carmeli, M.; Malin, S. Reformulation of general relativity as a gauge theory. Ann. Phys. (Germany) 1977, 103, 208–232. [Google Scholar] [CrossRef]
- Ivanenko, D.; Sardanashvily, G. The gauge treatment of gravity. Phys. Rep. 1983, 94, 1–45. [Google Scholar] [CrossRef]
- Sardanashvily, G.; Zakharov, O. Gauge Gravitation Theory; World Scientific: Singapore, 1992. [Google Scholar]
- Jackson, J.D.; Okun, L.B. Historical roots of gauge invariance. Rev. Mod. Phys. 2001, 73, 663–680. [Google Scholar] [CrossRef]
- Sardanashvily, G. Classical gauge theory of gravity. Theor. Math. Phys. 2002, 132, 1163–1171. [Google Scholar] [CrossRef]
- Cartan, É. Sur une généralisation de la notion de courboure de Riemann et les espaces à torsion. C. R. Acad. Sci. (Paris) 1922, 174, 593–595. [Google Scholar]
- Cartan, É. Sur les variétés à connexion affine et la théorie de la relativité généralisée (première partie). Ann. Sci. École Norm. Super. 1923, 40, 325–412. [Google Scholar]
- Cartan, É. Sur les variétés à connexion affine et la théorie de la relativité généralisée (suite). Ann. Sci. École Norm. Super. 1924, 41, 1–25. [Google Scholar]
- Cartan, É. Sur les variétés à connexion affine et la théorie de la relativité généralisée (deuxième partie). Ann. Sci. École Norm. Super. 1925, 42, 17–88. [Google Scholar]
- Weyl, H. A remark on the coupling of gravitation and electron. Phys. Rev. 1950, 77, 699–701. [Google Scholar] [CrossRef]
- Sciama, D. The physical structure of general relativity. Rev. Mod. Phys. 1964, 36, 1103. [Google Scholar] [CrossRef]
- Weyssenhoff, J.; Raabe, A. Relativistic Dynamics of spin-fluids and spin-particles. Acta Phys. Pol. 1947, 9, 7–18. [Google Scholar]
- Costa de Beauregard, O. Translational inertial spin effect. Phys. Rev. 1963, 129, 466–471. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Théorie des Corps déformables; Hermann: Paris, France, 1909. [Google Scholar]
- Puetzfeld, D.; Obukhov, Y.N. Prospects of detecting spacetime torsion. Int. J. Mod. Phys. D 2014, 23, 1442004. [Google Scholar] [CrossRef]
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Lasenby, A.N.; Doran, C.J.; Gull, S.F. Cosmological consequences of a flat-space theory of gravity. In Clifford Algebras and Their Applications in Mathematical Physics; Brackx, F., Delanghe, R., Serras, H., Eds.; Kluwer: Dordrecht, The Netherlands, 1993; p. 387. [Google Scholar]
- Lasenby, A.N.; Doran, C.J.; Gull, S.F. Grassmann calculus, pseudoclassical mechanics and geometric algebra. J. Math. Phys. 1993, 34, 3683–3712. [Google Scholar] [CrossRef]
- Lasenby, A.N.; Doran, C.J.L.; Gull, S.F. A multivector derivative approach to Lagrangian field theory. Found. Phys. 1993, 23, 1295–1327. [Google Scholar] [CrossRef]
- Lasenby, A.N.; Doran, C.J.L.; Gull, S.F. 2-spinors, twistors and supersymmetry in the spacetime algebra. In Spinors, Twistors, Clifford Algebras and Quantum Deformations; Oziewicz, Z., Jancewicz, B., Borowiec, A., Eds.; Kluwer: Dordrecht, The Netherlands, 1993; p. 233. [Google Scholar]
- Lasenby, A.N.; Doran, C.J.L.; Gull, S.F. Astrophysical and cosmological consequences of a gauge theory of gravity. In Current Topics in Astrofundamental Physics; Sánchez, N., Zichichi, A., Eds.; World Scientific: Singapore, 1995; p. 359. [Google Scholar]
- Lasenby, A.N.; Doran, C.J.; Gull, S.F. Gravity, gauge theories and geometric algebra. Philos. Trans. R. Soc. Lond. 1998, A356, 487–582. [Google Scholar] [CrossRef]
- Carmeli, M.; Leibowitz, E.; Nissani, N. Gravitation: SL(2,ℂ) Gauge Theory and Conservation Laws; World Scientific: Singapore, 1990. [Google Scholar]
- Mukunda, N. An elementary introduction to the gauge theory approach to gravity. In Gravitation, Gauge Theories and the Early Universe; Iyer, B.R., Mukunda, N., Vishvershwara, C.V., Eds.; Kluwer: Dordrecht, The Netherlands, 1989. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing general relativity with present and future astrophysical observations. Class. Quantum Gravity 2015, 32, 243001. [Google Scholar] [CrossRef]
- Poincaré, H. L’état actuel et l’avenir de la physique mathématique. Bull. Sci. Math. 1904, 2, 302–324. [Google Scholar]
- Kaluza, T. Zum Unitätsproblem in der Physik; Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin): Berlin, Germany, 1921; pp. 966–972. [Google Scholar]
- Klein, O. Quantentheorie und fünfdimensionale Relativitätstheorie. Z. Phys. 1926, 37, 895–906. [Google Scholar] [CrossRef]
- Milne, E.A. Kinematic Relativity; A Sequel to Relativity, Gravitation and World Structure; Clarendon Press: Oxford, UK, 1948. [Google Scholar]
- Thiry, Y. Sur la régularité des champs gravitationels et électromagnétiques dans les théories unitaires. C. R. Hebd. Séances Acad. Sci. 1948, 226, 1881–1882. [Google Scholar]
- Belinfante, F.; Swihart, J. Phenomenological linear theory of gravitation: Part I. Classical mechanics. Ann. Phys. (Germany) 1957, 1, 168–195. [Google Scholar] [CrossRef]
- Will, C.M.; Nordtvedt, K., Jr. Conservation laws and preferred frames in relativistic gravity. I. Preferred-frame theories and an extended PPN formalism. Astrophys. J. 1972, 177, 757–774. [Google Scholar] [CrossRef]
- Barker, B.M. General scalar-tensor theory of gravity with constant G. Astrophys. J. 1978, 219, 5–11. [Google Scholar] [CrossRef]
- Rosen, N. A bi-metric theory of gravitation. Gen. Relativ. Gravitat. 1973, 4, 435–447. [Google Scholar] [CrossRef]
- Rosen, N. A bi-metric theory of gravitation. II. Gen. Relativ. Gravitat. 1975, 6, 259–268. [Google Scholar] [CrossRef]
- Rastall, P. A theory of gravity. Can. J. Phys. 1976, 54, 66–75. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–389. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the newtonian dynamics—Implications for galaxy systems. Astrophys. J. 1983, 270, 384–415. [Google Scholar] [CrossRef]
- Dvali, G.; Gabadadze, G.; Porrati, M. 4D gravity on a brane in 5D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Seifert, M.D. Stability of spherically symmetric solutions in modified theories of gravity. Phys. Rev. D 2007, 76, 064002. [Google Scholar] [CrossRef]
- Reyes, R.; Mandelbaum, R.; Seljak, U.; Baldauf, T.; Gunn, J.E.; Lombriser, L.; Smith, R.E. Confirmation of general relativity on large scales from weak lensing and galaxy velocities. Nature 2010, 464, 256–258. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitzungsber. Preuss. Akad. Wiss. 1917, 1917, 142–152. [Google Scholar]
- Friedmann, A. Über die Krümmung des Raumes. Z. Phys. 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Friedmann, A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Hubble, E. A relation between distance and radial velocity among extra-galactic nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Lemaître, G. Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Ann. Soc. Sci. Brux. 1927, A47, 49–59. [Google Scholar]
- Robertson, H.P. Kinematics and world structure. Astrophys. J. 1935, 82, 248–301. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and world structure II. Astrophys. J. 1936, 83, 187–201. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and world structure III. Astrophys. J. 1936, 83, 257–271. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s theory of world-structure. Proc. Lond. Math. Soc. 1937, 42, 90–127. [Google Scholar] [CrossRef]
- Ellis, G.F.R.; Stoeger, W. Horizons in inflationary universes. Class. Quantum Gravity 1988, 5, 207–220. [Google Scholar] [CrossRef]
- Einstein, A.; de Sitter, W. On the relation between the expansion and the mean density of the universe. Proc. Natl. Acad. Sci. USA 1932, 18, 213–214. [Google Scholar] [CrossRef] [PubMed]
- Adams, F.C.; Laughlin, G. A dying universe: The long-term fate and evolution of astrophysical objects. Rev. Mod. Phys. 1997, 69, 337–372. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy: Dark energy with w < −1 causes a cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [PubMed]
- Planck Collaboration. Planck 2015 Results. XIII. Cosmological Parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Alpher, R.A.; Bethe, H.; Gamow, G. The origin of chemical elements. Phys. Rev. 1948, 73, 803–804. [Google Scholar] [CrossRef]
- Alpher, R.A.; Herman, R. Evolution of the universe. Nature 1948, 162, 774–775. [Google Scholar] [CrossRef]
- Gamow, G. The evolution of the universe. Nature 1948, 162, 680–682. [Google Scholar] [CrossRef] [PubMed]
- Gamow, G. The origin of elements and the separation of galaxies. Phys. Rev. 1948, 74, 505–506. [Google Scholar] [CrossRef]
- Penzias, A.A.; Wilson, R.W. A measurement of excess antenna temperature at 4080 Mc/s. Astrophys. J. 1965, 142, 419–421. [Google Scholar] [CrossRef]
- Christenson, J.H.; Cronin, J.W.; Fitch, V.L.; Turlay, R. Evidence for the 2π decay of the meson. Phys. Rev. Lett. 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Sakharov, A.D. Violation of CP invariance, c asymmetry, and baryon asymmetry of the universe. JETP Lett. 1967, 5, 24–27. [Google Scholar]
- Kuzmin, V.A. CP-noninvariance and baryon asymmetry of the universe. J. Exp. Theor. Phys. Lett. 1970, 12, 228–230. [Google Scholar]
- Khlopov, M. Cosmological reflection of particle symmetry. Symmetry 2016, 8, 81. [Google Scholar] [CrossRef]
- Fixsen, D.J. The temperature of the cosmic microwave background. Astrophys. J. 2009, 707, 916–920. [Google Scholar] [CrossRef]
- Dunkley, J.; Komatsu, E.; Nolta, M.R.; Spergel, D.N.; Larson, D.; Hinshaw, G.; Page, L.; Bennett, C.L.; Gold, B.; Jarosik, N.; et al. Five-year Wilkinson Microwave Anisotropy Probe observations: Likelihoods and parameters from the WMAP data. Astrophys. J. Suppl. 2009, 180, 306–329. [Google Scholar] [CrossRef]
- Hannestad, S. Primordial neutrinos. Annu. Rev. Nucl. Part. Sci. 2006, 56, 137–161. [Google Scholar] [CrossRef]
- Lesgourgues, J.; Pastor, S. Massive neutrinos and cosmology. Phys. Rep. 2006, 429, 307–379. [Google Scholar] [CrossRef]
- Lesgourgues, J.; Pastor, S. Neutrino cosmology and Planck. New J. Phys. 2014, 16, 065002. [Google Scholar] [CrossRef]
- lgarøy, Ø.; Lahav, O. Neutrino masses from cosmological probes. New J. Phys. 2005, 7, 61. [Google Scholar]
- Abazajian, K.; Fuller, G.M.; Patel, M. Sterile neutrino hot, warm, and cold Dark Matter. Phys. Rev. D 2001, 64, 023501. [Google Scholar] [CrossRef]
- Boyarsky, A.; Ruchayskiy, O.; Shaposhnikov, M. The role of sterile neutrinos in cosmology and astrophysics. Annu. Rev. Nucl. Part. Sci. 2009, 59, 191–214. [Google Scholar] [CrossRef]
- Mangano, G.; Miele, G.; Pastor, S.; Peloso, M. A precision calculation of the effective number of cosmological neutrinos. Phys. Lett. B 2002, 534, 8–16. [Google Scholar] [CrossRef]
- Feeney, S.M.; Peiris, H.V.; Verde, L. Is there evidence for additional neutrino species from cosmology? J. Cosmol. Astropart. Phys. 2013, 4, 036. [Google Scholar] [CrossRef]
- Olive, K.; Group, P.D. Review of particle physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Primack, J.R.; Gross, M.A.K. Hot Dark Matter in cosmology. In Current Aspects of Neutrino Physics; Caldwell, D.O., Ed.; Springer: Berlin, Germany, 2001; pp. 287–308. [Google Scholar]
- Gerstein, G.; Zel’dovich, Y.B. Rest mass of the muonic neutrino and cosmology (English translation). Lett. J. Exp. Theor. Phys. 1966, 4, 120–122. [Google Scholar]
- Marx, G.; Szalay, A.S. Cosmological limit on the neutretto rest mass. In Proceedings of the Neutrino 72, Balatonfured, Hungary, 11–17 June 1972; Volume 1, p. 123.
- Cowsik, R.; McClelland, J. An upper limit on the neutrino rest mass. Phys. Rev. Lett. 1972, 29, 669–670. [Google Scholar] [CrossRef]
- Szalay, A.S.; Marx, G. Neutrino rest mass from cosmology. Astron. Astrophys. 1976, 49, 437–441. [Google Scholar]
- Tegmark, M.; Eisenstein, D.J.; Strauss, M.A.; Weinberg, D.H.; Blanton, M.R.; Frieman, J.A.; Fukugita, M.; Gunn, J.E.; Hamilton, A.J.S.; Knapp, G.R.; et al. Cosmological constraints from the SDSS luminous red galaxies. Phys. Rev. D 2006, 74, 123507. [Google Scholar] [CrossRef]
- Shiraishi, M.; Ichikawa, K.; Ichiki, K.; Sugiyama, N.; Yamaguchi, M. Constraints on neutrino masses from WMAP5 and BBN in the lepton asymmetric universe. J. Cosmol. Astropart. Phys. 2009, 7, 5. [Google Scholar] [CrossRef] [PubMed]
- Tereno, I.; Schimd, C.; Uzan, J.P.; Kilbinger, M.; Vincent, F.H.; Fu, L. CFHTLS weak-lensing constraints on the neutrino masses. Astron. Astrophys. 2009, 500, 657–665. [Google Scholar] [CrossRef]
- Ichiki, K.; Takada, M.; Takahashi, T. Constraints on neutrino masses from weak lensing. Phys. Rev. D 2009, 79, 023520. [Google Scholar] [CrossRef]
- Xia, J.Q.; Granett, B.R.; Viel, M.; Bird, S.; Guzzo, L.; Haehnelt, M.G.; Coupon, J.; McCracken, H.J.; Mellier, Y. Constraints on massive neutrinos from the CFHTLS angular power spectrum. J. Cosmol. Astropart. Phys. 2012, 6, 010. [Google Scholar] [CrossRef]
- Olive, K.A. Inflation. Phys. Rep. 1990, 190, 307–403. [Google Scholar] [CrossRef]
- Guth, A.H. (Ed.) The Inflationary Universe. The Quest for a New Theory of Cosmic Origins; Addison-Wesley: Reading, MA, USA, 1997.
- Peacock, J.A. Cosmological Physics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Uzan, J.P. Inflation in the standard cosmological model. C. R. Phys. 2015, 16, 875–890. [Google Scholar] [CrossRef]
- Misner, C.W. Mixmaster universe. Phys. Rev. Lett. 1969, 22, 1071–1074. [Google Scholar] [CrossRef]
- Belinskij, V.A.; Khalatnikov, I.M.; Lifshits, E.M. Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 1970, 19, 525–573. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. Sov. J. Exp. Theor. Phys. Lett. 1979, 30, 682–685. [Google Scholar]
- ’t Hooft, G. Magnetic monopoles in unified gauge theories. Nucl. Phys. B 1974, 79, 276–284. [Google Scholar] [CrossRef]
- Preskill, J. Magnetic monopoles. Annu. Rev. Nucl. Part. Sci. 1984, 34, 461–530. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Khlopov, M.Y. On the concentration of relic monopoles in the universe. Phys. Lett. B 1979, 79, 239–241. [Google Scholar] [CrossRef]
- Preskill, J.P. Cosmological production of superheavy magnetic monopoles. Phys. Rev. Lett. 1979, 43, 1365–1368. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A. Inflation and Quantum Cosmology; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Lidsey, J.E.; Liddle, A.R.; Kolb, E.W.; Copeland, E.J.; Barreiro, T.; Abney, M. Reconstructing the inflaton potential—An overview. Rev. Mod. Phys. 1997, 69, 373–410. [Google Scholar] [CrossRef]
- Sato, K. Cosmological baryon-number domain structure and the first order phase transition of a vacuum. Phys. Lett. B 1981, 99, 66–70. [Google Scholar] [CrossRef]
- Einhorn, M.B.; Sato, K. Monopole production in the very early universe in a first-order phase transition. Nucl. Phys. B 1981, 180, 385–404. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G.V. Energy of vacuum and the large-scale structure of the universe. Zhurnal Eksper. Teor. Fiz. 1982, 83, 475–487. [Google Scholar]
- Mukhanov, V.F.; Chibisov, G.V. Quantum fluctuations and a nonsingular universe. Sov. J. Exp. Theor. Phys. Lett. 1981, 33, 532–535. [Google Scholar]
- Guth, A.H.; Pi, S.Y. Fluctuations in the new inflationary universe. Phys. Rev. Lett. 1982, 49, 1110–1113. [Google Scholar] [CrossRef]
- Hawking, S.W. The development of irregularities in a single bubble inflationary universe. Phys. Lett. B 1982, 115, 295–297. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Steinhardt, P.J.; Turner, M.S. Spontaneous creation of almost scale-free density perturbations in an inflationary universe. Phys. Rev. D 1983, 28, 679–693. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 Results. XX. Constraints on Inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Liddle, A.R.; Lyth, D.H. COBE, gravitational waves, inflation and extended inflation. Phys. Lett. B 1992, 291, 391–398. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. The cold Dark Matter density perturbation. Phys. Rep. 1993, 231, 1–105. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Dodelson, S. Modern Cosmology; Academic Press: New York, NY, USA, 2003. [Google Scholar]
- Kosowsky, A.; Turner, M.S. CBR anisotropy and the running of the scalar spectral index. Phys. Rev. D 1995, 52, 1739–1743. [Google Scholar] [CrossRef]
- Smoot, G.F.; Bennett, C.L.; Kogut, A.; Wright, E.L.; Aymon, J.; Boggess, N.W.; Cheng, E.S.; de Amici, G.; Gulkis, S.; Hauser, M.G.; et al. Structure in the COBE differential microwave radiometer first-year maps. Astrophys. J. 1992, 396, L1–L5. [Google Scholar] [CrossRef]
- Fixsen, D.J.; Cheng, E.S.; Cottingham, D.A.; Eplee, R.E., Jr.; Isaacman, R.B.; Mather, J.C.; Meyer, S.S.; Noerdlinger, P.D.; Shafer, R.A.; Weiss, R.; et al. Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument. Astrophys. J. 1994, 420, 445–449. [Google Scholar] [CrossRef]
- Dwek, E.; Arendt, R.G.; Hauser, M.G.; Fixsen, D.; Kelsall, T.; Leisawitz, D.; Pei, Y.C.; Wright, E.L.; Mather, J.C.; Moseley, S.H.; et al. The COBE diffuse infrared background experiment search for the cosmic infrared background. IV. Cosmological implications. Astrophys. J. 1998, 508, 106–122. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Peiris, H.V.; Komatsu, E.; Verde, L.; Spergel, D.N.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; Limon, M.; et al. First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Implications for inflation. Astrophys. J. Suppl. 2003, 148, 213–231. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; et al. Three-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Implications for cosmology. Astrophys. J. Suppl. 2007, 170, 377–408. [Google Scholar] [CrossRef]
- Komatsu, E.; Dunkley, J.; Nolta, M.R.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Limon, M.; Page, L.; et al. Five-year Wilkinson Microwave Anisotropy Probe observations: Cosmological interpretation. Astrophys. J. Suppl. 2009, 180, 330–376. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Planck Collaboration. Planck 2013 results. XXII. Constraints on inflation. Astron. Astrophys. 2014, 571, A22. [Google Scholar]
- BICEP2 Collaboration. Detection of B-mode polarization at degree angular scales by BICEP2. Phys. Rev. Lett. 2014, 112, 241101. [Google Scholar]
- Planck Collaboration. Planck intermediate results XXX. The angular power spectrum of polarized dust emission at intermediate and high Galactic latitudes. Astron. Astrophys. 2016, 586, A133. [Google Scholar]
- Huang, Z.; Verde, L.; Vernizzi, F. Constraining inflation with future galaxy redshift surveys. J. Cosmol. Astropart. Phys. 2012, 4, 005. [Google Scholar] [CrossRef] [PubMed]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Relativ. 2013, 16, 6. [Google Scholar] [CrossRef]
- Namikawa, T.; Yamauchi, D.; Sherwin, B.; Nagata, R. Delensing cosmic microwave background B modes with the Square Kilometre Array Radio Continuum Survey. Phys. Rev. D 2016, 93, 043527. [Google Scholar] [CrossRef]
- Kapteyn, J.C. First attempt at a theory of the arrangement and motion of the sidereal system. Astrophys. J. 1922, 55, 302–328. [Google Scholar] [CrossRef]
- Oort, J.H. The force exerted by the stellar system in the direction perpendicular to the galactic plane and some related problems. Bull. Astron. Inst. Neth. 1932, 6, 249–287. [Google Scholar]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217–246. [Google Scholar] [CrossRef]
- Freese, K. Review of observational evidence for Dark Matter in the universe and in upcoming searches for dark stars. In Proceedings of the Dark Energy and Dark Matter: Observations, Experiments and Theories, Lyons, France, 7–11 July 2008; Volume 36, pp. 113–126.
- Kahn, F.D.; Woltjer, L. Intergalactic matter and the galaxy. Astrophys. J. 1959, 130, 705–717. [Google Scholar] [CrossRef]
- Roberts, M.S.; Rots, A.H. Comparison of rotation curves of different galaxy types. Astron. Astrophys. 1973, 26, 483–485. [Google Scholar]
- Einasto, J.; Kaasik, A.; Saar, E. Dynamic evidence on massive coronas of galaxies. Nature 1974, 250, 309–310. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E.; Yahil, A. The size and mass of galaxies, and the mass of the universe. Astrophys. J. 1974, 193, L1–L4. [Google Scholar] [CrossRef]
- Rubin, V.C.; Thonnard, N.; Ford, W.K., Jr. Extended rotation curves of high-luminosity spiral galaxies. IV—Systematic dynamical properties, SA through SC. Astrophys. J. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The structure of cold Dark Matter halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Fukugita, M.; Hogan, C.J.; Peebles, P.J.E. The cosmic baryon budget. Astrophys. J. 1998, 503, 518–530. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a cosmological model and angular variations of the microwave background. Astrophys. J. 1967, 147, 73–90. [Google Scholar] [CrossRef]
- Eisenstein, D.J. Dark energy and cosmic sound. New Astron. Rev. 2005, 49, 360–365. [Google Scholar] [CrossRef]
- Bassett, B.; Hlozek, R. Baryon acoustic oscillations. In Dark Energy: Observational and Theoretical Approaches; Ruiz-Lapuente, P., Ed.; Cambridge University Press: Cambridge, UK, 2010; p. 246. [Google Scholar]
- Schneider, P. Weak gravitational lensing. In Gravitational Lensing: Strong, Weak and Micro, Saas-Fee Advanced Courses 33; Schneider, P., Kochanek, C.S., Wambsganss, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; p. 269. [Google Scholar]
- Bacon, D.J.; Réfrégier, A.R.; Ellis, R.S. Detection of weak gravitational lensing by large-scale structure. Mon. Not. R. Astron. Soc. 2000, 318, 625–640. [Google Scholar] [CrossRef]
- Kaiser, N. A new shear estimator for weak-lensing observations. Astrophys. J. 2000, 537, 555–577. [Google Scholar] [CrossRef]
- Van Waerbeke, L.; Mellier, Y.; Erben, T.; Cuillandre, J.C.; Bernardeau, F.; Maoli, R.; Bertin, E.; Mc Cracken, H.J.; Le Fèvre, O.; Fort, B.; et al. Detection of correlated galaxy ellipticities from CFHT data: First evidence for gravitational lensing by large-scale structures. Astron. Astrophys. 2000, 358, 30–44. [Google Scholar]
- Wittman, D.M.; Tyson, J.A.; Kirkman, D.; Dell’Antonio, I.; Bernstein, G. Detection of weak gravitational lensing distortions of distant galaxies by cosmic Dark Matter at large scales. Nature 2000, 405, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Bertone, G.; Hooper, D.; Silk, J. Particle Dark Matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Salati, P. The bestiary of Dark Matter species. In Proceedings of the Dark Energy and Dark Matter: Observations, Experiments and Theories, Lyons, France, 7–11 July 2008; Volume 36, pp. 175–186.
- Garrett, K.; Dūda, G. Dark matter: A primer. Adv. Astron. 2011, 2011, 968283. [Google Scholar] [CrossRef]
- Kappl, R.; Winkler, M.W. New limits on Dark Matter from Super-Kamiokande. Nucl. Phys. B 2011, 850, 505–521. [Google Scholar] [CrossRef]
- Arina, C.; Hamann, J.; Wong, Y.Y.Y. A Bayesian view of the current status of Dark Matter direct searches. J. Cosmol. Astropart. Phys. 2011, 9, 022. [Google Scholar] [CrossRef]
- Porter, T.A.; Johnson, R.P.; Graham, P.W. Dark matter searches with astroparticle data. Annu. Rev. Astron. Astrophys. 2011, 49, 155–194. [Google Scholar] [CrossRef]
- Calore, F.; de Romeri, V.; Donato, F. Conservative upper limits on WIMP annihilation cross section from Fermi-LAT γ rays. Phys. Rev. D 2012, 85, 023004. [Google Scholar]
- Klasen, M.; Pohl, M.; Sigl, G. Indirect and direct search for Dark Matter. Prog. Part. Nucl. Phys. 2015, 85, 1–32. [Google Scholar] [CrossRef]
- Mayet, F.; Green, A.M.; Battat, J.B.R.; Billard, J.; Bozorgnia, N.; Gelmini, G.B.; Gondolo, P.; Kavanagh, B.J.; Lee, S.K.; Loomba, D.; et al. A review of the discovery reach of directional Dark Matter detection. Phys. Rep. 2016, 627, 1–49. [Google Scholar] [CrossRef]
- Jungman, G.; Kamionkowski, M.; Griest, K. Supersymmetric Dark Matter. Phys. Rep. 1996, 267, 195–373. [Google Scholar] [CrossRef]
- IceCube Collaboration. Search for Dark Matter annihilations in the Sun with the 79-string IceCube detector. Phys. Rev. Lett. 2013, 110, 131302. [Google Scholar]
- Aguirre, A.; Schaye, J.; Quataert, E. Problems for modified Newtonian dynamics in clusters and the Lyα forest? Astrophys. J. 2001, 561, 550–558. [Google Scholar] [CrossRef]
- Pointecouteau, E.; Silk, J. New constraints on modified Newtonian dynamics from galaxy clusters. Mon. Not. R. Astron. Soc. 2005, 364, 654–658. [Google Scholar] [CrossRef]
- Contaldi, C.R.; Wiseman, T.; Withers, B. TeVeS gets caught on caustics. Phys. Rev. D 2008, 78, 044034. [Google Scholar] [CrossRef]
- Lue, A.; Starkman, G.D. Squeezing MOND into a cosmological scenario. Phys. Rev. Lett. 2004, 92, 131102. [Google Scholar] [CrossRef] [PubMed]
- Dodelson, S. The real problem with MOND. Int. J. Mod. Phys. D 2011, 20, 2749–2753. [Google Scholar] [CrossRef]
- Ferreras, I.; Mavromatos, N.E.; Sakellariadou, M.; Yusaf, M.F. Confronting MOND and TeVeS with strong gravitational lensing over galactic scales: An extended survey. Phys. Rev. D 2012, 86, 083507. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A direct empirical proof of the existence of Dark Matter. Astrophys. J. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Peebles, P.J.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Slipher, V.M. Nebulae. Proc. Am. Philos. Soc. 1917, 56, 403–409. [Google Scholar]
- Paal, G.; Horvath, I.; Lukacs, B. Inflation and compactification from galaxy redshifts? Astrophys. Space Sci. 1992, 191, 107–124. [Google Scholar] [CrossRef]
- Krauss, L.M. The end of the age problem, and the case for a cosmological constant revisited. Astrophys. J. 1998, 501, 461–466. [Google Scholar] [CrossRef]
- Räsänen, S. Structure formation as an alternative to dark energy and modified gravity. In Proceedings of the Dark Energy and Dark Matter: Observations, Experiments and Theories, Lyons, France, 7–11 July 2008; Volume 36, pp. 63–74.
- Blasone, M.; Capolupo, A.; Capozziello, S.; Carloni, S.; Vitiello, G. Neutrino mixing contribution to the cosmological constant. Phys. Lett. A 2004, 323, 182–189. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Vitiello, G. Neutrino mixing as a source of dark energy. Phys. Lett. A 2007, 363, 53–56. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. The supernova cosmology project. Measurements of Omega and Lambda from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A. The case for a positive cosmological Λ-term. Int. J. Mod. Phys. D 2000, 9, 373–443. [Google Scholar] [CrossRef]
- Turner, M.S. Dark Matter and Dark Energy in the universe. In The Third Stromlo Symposium: The Galactic Halo; Gibson, B.K., Axelrod, R.S., Putman, M.E., Eds.; Astronomical Society of the Pacific Conference Series; The Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; Volume 165, p. 431. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the baryon acoustic peak in the large-scale correlation function of SDSS luminous red galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Astier, P.; Pain, R. Observational evidence of the accelerated expansion of the universe. C. R. Phys. 2012, 13, 521–538. [Google Scholar] [CrossRef]
- Enqvist, K. Lemaitre Tolman Bondi model and accelerating expansion. Gen. Relativ. Gravit. 2008, 40, 451–466. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; de Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Durrer, R.; Maartens, R. Dark energy and dark gravity: Theory overview. Gen. Relativ. Gravit. 2008, 40, 301–328. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
- Chevallier, M.; Polarski, D. Accelerating Universes with scaling Dark Matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linden, S.; Virey, J.M. Test of the Chevallier-Polarski-Linder parametrization for rapid dark energy equation of state transitions. Phys. Rev. D 2008, 78, 023526. [Google Scholar] [CrossRef]
- Wang, Y.; Freese, K. Probing dark energy using its density instead of its equation of state. Phys. Lett. B 2006, 632, 449–452. [Google Scholar] [CrossRef]
- Johri, V.B.; Rath, P.K. Parametrization of the dark energy equation of state. Int. J. Mod. Phys. D 2007, 16, 1581–1591. [Google Scholar] [CrossRef]
- Avelino, P.P.; Martins, C.J.A.P.; Nunes, N.J.; Olive, K.A. Reconstructing the dark energy equation of state with varying couplings. Phys. Rev. D 2006, 74, 083508. [Google Scholar] [CrossRef]
- Scherrer, R.J. Mapping the Chevallier-Polarski-Linder parametrization onto physical dark energy models. Phys. Rev. D 2015, 92, 043001. [Google Scholar] [CrossRef]
- Chongchitnan, S.; King, L. Imprints of dynamical dark energy on weak-lensing measurements. Mon. Not. R. Astron. Soc. 2010, 407, 1989–1997. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D. Confronting dark energy models mimicking ΛCDM epoch with observational constraints: Future cosmological perturbations decay or future Rip? Phys. Lett. B 2013, 718, 1194–1202. [Google Scholar] [CrossRef]
- Debono, I. Bayesian model selection for dark energy using weak lensing forecasts. Mon. Not. R. Astron. Soc. 2014, 437, 887–897. [Google Scholar] [CrossRef]
- Bardeen, J.M. Gauge-invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882–1905. [Google Scholar] [CrossRef]
- Lifshitz, E.M. On the gravitational stability of the expanding universe. J. Phys. (USSR) 1946, 46, 587–602. [Google Scholar]
- Bartelmann, M.; Schneider, P. Weak gravitational lensing. Phys. Rep. 2001, 340, 291–472. [Google Scholar] [CrossRef]
- Jeans, J.H. The stability of a spherical nebula. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1902, 199, 1–53. [Google Scholar] [CrossRef]
- Silk, J. Cosmic black-body radiation and galaxy formation. Astrophys. J. 1968, 151, 459–471. [Google Scholar] [CrossRef]
- Bond, J.R.; Efstathiou, G.; Silk, J. Massive neutrinos and the large-scale structure of the universe. Phys. Rev. Lett. 1980, 45, 1980–1984. [Google Scholar] [CrossRef]
- Silk, J.; Mamon, G.A. The current status of galaxy formation. Res. Astron. Astrophys. 2012, 12, 917–946. [Google Scholar] [CrossRef]
- Linder, E.V.; Jenkins, A. Cosmic structure growth and dark energy. Mon. Not. R. Astron. Soc. 2003, 346, 573–583. [Google Scholar] [CrossRef]
- Bernardeau, F.; Colombi, S.; Gaztañaga, E.; Scoccimarro, R. Large-scale structure of the Universe and cosmological perturbation theory. Phys. Rep. 2002, 367, 1–248. [Google Scholar] [CrossRef]
- Percival, W.J. Cosmological structure formation in a homogeneous dark energy background. Astron. Astrophys. 2005, 443, 819–830. [Google Scholar] [CrossRef]
- Hamilton, A.J.S.; Kumar, P.; Lu, E.; Matthews, A. Reconstructing the primordial spectrum of fluctuations of the universe from the observed nonlinear clustering of galaxies. Astrophys. J. 1991, 374, L1–L4. [Google Scholar] [CrossRef]
- Jain, B.; Mo, H.J.; White, S.D.M. The evolution of correlation functions and power spectra in gravitational clustering. Mon. Not. R. Astron. Soc. 1995, 276, L25–L29. [Google Scholar]
- Peacock, J.A.; Dodds, S.J. Non-linear evolution of cosmological power spectra. Mon. Not. R. Astron. Soc. 1996, 280, L19–L26. [Google Scholar] [CrossRef]
- Smith, R.E.; Peacock, J.A.; Jenkins, A.; White, S.D.M.; Frenk, C.S.; Pearce, F.R.; Thomas, P.A.; Efstathiou, G.; Couchman, H.M.P. Stable clustering, the halo model and non-linear cosmological power spectra. Mon. Not. R. Astron. Soc. 2003, 341, 1311–1332. [Google Scholar] [CrossRef]
- Seljak, U. Analytic model for galaxy and Dark Matter clustering. Mon. Not. R. Astron. Soc. 2000, 318, 203–213. [Google Scholar] [CrossRef]
- Peacock, J.A.; Smith, R.E. Halo occupation numbers and galaxy bias. Mon. Not. R. Astron. Soc. 2000, 318, 1144–1156. [Google Scholar] [CrossRef]
- Huterer, D.; Takada, M. Calibrating the nonlinear matter power spectrum: Requirements for future weak lensing surveys. Astropart. Phys. 2005, 23, 369–376. [Google Scholar] [CrossRef]
- Van Daalen, M.P.; Schaye, J.; Booth, C.M.; Dalla Vecchia, C. The effects of galaxy formation on the matter power spectrum: A challenge for precision cosmology. Mon. Not. R. Astron. Soc. 2011, 415, 3649–3665. [Google Scholar] [CrossRef]
- Semboloni, E.; Hoekstra, H.; Schaye, J.; van Daalen, M.P.; McCarthy, I.G. Quantifying the effect of baryon physics on weak lensing tomography. Mon. Not. R. Astron. Soc. 2011, 417, 2020–2035. [Google Scholar] [CrossRef]
- Bird, S.; Viel, M.; Haehnelt, M.G. Massive neutrinos and the non-linear matter power spectrum. Mon. Not. R. Astron. Soc. 2012, 420, 2551–2561. [Google Scholar] [CrossRef]
- Hearin, A.P.; Zentner, A.R.; Ma, Z. General requirements on matter power spectrum predictions for cosmology with weak lensing tomography. J. Cosmol. Astropart. Phys. 2012, 4, 034. [Google Scholar] [CrossRef]
- Takahashi, R.; Sato, M.; Nishimichi, T.; Taruya, A.; Oguri, M. Revising the halofit model for the nonlinear matter power spectrum. Astrophys. J. 2012, 761, 152. [Google Scholar] [CrossRef]
- Villaescusa-Navarro, F.; Viel, M.; Datta, K.K.; Choudhury, T.R. Modeling the neutral hydrogen distribution in the post-reionization Universe: Intensity mapping. J. Cosmol. Astropart. Phys. 2014, 9, 050. [Google Scholar] [CrossRef]
- Bentivegna, E.; Bruni, M. Effects of nonlinear inhomogeneity on the cosmic expansion with numerical relativity. Phys. Rev. Lett. 2016, 116, 251302. [Google Scholar] [CrossRef] [PubMed]
- Mertens, J.B.; Giblin, J.T.; Starkman, G.D. Integration of inhomogeneous cosmological spacetimes in the BSSN formalism. Phys. Rev. D 2016, 93, 124059. [Google Scholar] [CrossRef]
- Giblin, J.T.; Mertens, J.B.; Starkman, G.D. Departures from the Friedmann-Lemaitre-Robertston-Walker cosmological model in an inhomogeneous universe: A numerical examination. Phys. Rev. Lett. 2016, 116, 251301. [Google Scholar] [CrossRef] [PubMed]
- Harrison, E.R. Fluctuations at the threshold of classical cosmology. Phys. Rev. D 1970, 1, 2726–2730. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. A hypothesis, unifying the structure and the entropy of the Universe. Mon. Not. R. Astron. Soc. 1972, 160, 1–3. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval adiabatic perturbation in an expanding universe. Astrophys. J. 1970, 162, 815–836. [Google Scholar] [CrossRef]
- Mukherjee, P.; Wang, Y. Model-independent reconstruction of the primordial power spectrum from Wilkinson Microwave Anistropy Probe data. Astrophys. J. 2003, 599, 1–6. [Google Scholar] [CrossRef]
- Trotta, R. Forecasting the Bayes factor of a future observation. Mon. Not. R. Astron. Soc. 2007, 378, 819–824. [Google Scholar] [CrossRef]
- Trotta, R. Applications of Bayesian model selection to cosmological parameters. Mon. Not. R. Astron. Soc. 2007, 378, 72–82. [Google Scholar] [CrossRef]
- Bridges, M.; Feroz, F.; Hobson, M.P.; Lasenby, A.N. Bayesian optimal reconstruction of the primordial power spectrum. Mon. Not. R. Astron. Soc. 2009, 400, 1075–1084. [Google Scholar] [CrossRef]
- Vázquez, J.A.; Bridges, M.; Hobson, M.P.; Lasenby, A.N. Model selection applied to reconstruction of the Primordial Power Spectrum. J. Cosmol. Astropart. Phys. 2012, 6, 006. [Google Scholar] [CrossRef] [PubMed]
- Hoyle, C.D.; Kapner, D.J.; Heckel, B.R.; Adelberger, E.G.; Gundlach, J.H.; Schmidt, U.; Swanson, H.E. Submillimeter tests of the gravitational inverse-square law. Phys. Rev. D 2004, 70, 042004. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the gravitational inverse-square law below the dark-energy length scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef] [PubMed]
- Baker, T.; Psaltis, D.; Skordis, C. Linking tests of gravity on all scales: From the strong-field regime to cosmology. Astrophys. J. 2015, 802, 63. [Google Scholar] [CrossRef]
- Eddington, A.S. The Mathematical Theory of Relativity; Cambridge University Press: Cambridge, UK, 1923. [Google Scholar]
- Shapiro, I.I. Solar system tests of general relativity: Recent results and present plans. In General Relativity and Gravitation, 1989; Ashby, N., Bartlett, D.F., Wyss, W., Eds.; Cambridge University Press: Cambridge, UK, 2005; p. 313. [Google Scholar]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Progress in lunar laser ranging tests of relativistic gravity. Phys. Rev. Lett. 2004, 93, 261101. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Lunar laser ranging tests of the equivalence principle with the Earth and Moon. Int. J. Mod. Phys. D 2009, 18, 1129–1175. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Davis, J.L.; Lebach, D.E.; Gregory, J.S. Measurement of the solar gravitational deflection of radio waves using geodetic very-long-baseline interferometry data, 1979–1999. Phys. Rev. Lett. 2004, 92, 121101. [Google Scholar] [CrossRef] [PubMed]
- Pitjeva, E.V.; Pitjev, N.P. Relativistic effects and Dark Matter in the Solar system from observations of planets and spacecraft. Mon. Not. R. Astron. Soc. 2013, 432, 3431–3437. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Kuchynka, P.; Manche, H.; Desvignes, G.; Gastineau, M.; Cognard, I.; Theureau, G. The INPOP10a planetary ephemeris and its applications in fundamental physics. Celest. Mech. Dyn. Astron. 2011, 111, 363–385. [Google Scholar] [CrossRef]
- Iorio, L.; Lichtenegger, H.I.M.; Ruggiero, M.L.; Corda, C. Phenomenology of the Lense-Thirring effect in the solar system. Astrophys. Space Sci. 2011, 331, 351–395. [Google Scholar] [CrossRef]
- Hughes, V.W.; Robinson, H.G.; Beltran-Lopez, V. Upper Limit for the anisotropy of inertial mass from nuclear resonance experiments. Phys. Rev. Lett. 1960, 4, 342–344. [Google Scholar] [CrossRef]
- Drever, R.W.P. A search for anisotropy of inertial mass using a free precession technique. Philos. Mag. 1961, 6, 683–687. [Google Scholar] [CrossRef]
- Allmendinger, F.; Heil, W.; Karpuk, S.; Kilian, W.; Scharth, A.; Schmidt, U.; Schnabel, A.; Sobolev, Y.; Tullney, K. New limit on Lorentz-invariance- and CPT-violating neutron spin interactions using a free-spin-precession He3-Xe129 comagnetometer. Phys. Rev. Lett. 2014, 112, 110801. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.G.; Turyshev, S.G.; Boggs, D.H. Lunar laser ranging tests of the equivalence principle. Class. Quantum Gravity 2012, 29, 184004. [Google Scholar] [CrossRef]
- Delva, P.; Hees, A.; Bertone, S.; Richard, E.; Wolf, P. Test of the gravitational redshift with stable clocks in eccentric orbits: Application to Galileo satellites 5 and 6. Class. Quantum Gravity 2015, 32, 232003. [Google Scholar] [CrossRef]
- Iorio, L. Gravitational anomalies in the solar system? Int. J. Mod. Phys. D 2015, 24, 1530015. [Google Scholar] [CrossRef]
- Uzan, J.P. Varying constants, gravitation and cosmology. Living Rev. Relativ. 2011, 14, 2. [Google Scholar] [CrossRef]
- Flambaum, V.V. Variation of the fundamental constants: Theory and observations. Int. J. Mod. Phys. A 2007, 22, 4937–4950. [Google Scholar] [CrossRef]
- Lea, S.N. Limits to time variation of fundamental constants from comparisons of atomic frequency standards. Rep. Prog. Phys. 2007, 70, 1473–1523. [Google Scholar] [CrossRef]
- Rich, J. Which fundamental constants for cosmic microwave background and baryon-acoustic oscillation? Astron. Astrophys. 2015, 584, A69. [Google Scholar] [CrossRef]
- Barrow, J.D.; Sandvik, H.B.; Magueijo, J.A. Behavior of varying-alpha cosmologies. Phys. Rev. D 2002, 65, 063504. [Google Scholar] [CrossRef]
- Barrow, J.D.; Graham, A.A.H. General dynamics of varying-alpha universes. Phys. Rev. D 2013, 88, 103513. [Google Scholar] [CrossRef]
- Fujii, Y.; Iwamoto, A.; Fukahori, T.; Ohnuki, T.; Nakagawa, M.; Hidaka, H.; Oura, Y.; Möller, P. The nuclear interaction at Oklo 2 billion years ago. Nucl. Phys. B 2000, 573, 377–401. [Google Scholar] [CrossRef]
- Uzan, J.P. The fundamental constants and their variation: Observational and theoretical status. Rev. Mod. Phys. 2003, 75, 403–455. [Google Scholar] [CrossRef]
- Lamoreaux, S.K.; Torgerson, J.R. Neutron moderation in the Oklo natural reactor and the time variation of α. Phys. Rev. D 2004, 69, 121701. [Google Scholar] [CrossRef]
- Khatri, R.; Wandelt, B.D. 21-cm radiation: A new probe of variation in the fine-structure constant. Phys. Rev. Lett. 2007, 98, 111301. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, M.; Ichikawa, K.; Nagata, R.; Yokoyama, J. Constraining the time variation of the coupling constants from cosmic microwave background: Effect of ΛQCD. J. Cosmol. Astropart. Phys. 2010, 2010, 030. [Google Scholar] [CrossRef]
- Martins, C.J.A.P.; Menegoni, E.; Galli, S.; Mangano, G.; Melchiorri, A. Varying couplings in the early universe: Correlated variations of α and G. Phys. Rev. D 2010, 82, 023532. [Google Scholar]
- Anderson, J.D.; Schubert, G.; Trimble, V.; Feldman, M.R. Measurements of Newton’s gravitational constant and the length of day. Europhys. Lett. 2015, 110, 10002. [Google Scholar] [CrossRef]
- Pitkin, M. Comment on “Measurements of Newton’s gravitational constant and the length of day”. Europhys. Lett. 2015, 111, 30002. [Google Scholar] [CrossRef]
- Anderson, J.D.; Schubert, G.; Trimble, V.; Feldman, M.R. Reply to the comment by M. Pitkin. Europhys. Lett. 2015, 111, 30003. [Google Scholar] [CrossRef]
- Iorio, L. Does Newton’s gravitational constant vary sinusoidally with time? Orbital motions say no. Class. Quantum Gravity 2016, 33, 045004. [Google Scholar] [CrossRef]
- Feldman, M.R.; Anderson, J.D.; Schubert, G.; Trimble, V.; Kopeikin, S.M.; Lämmerzahl, C. Deep space experiment to measure G. Class. Quantum Gravity 2016, 33, 125013. [Google Scholar] [CrossRef]
- Lahav, O. Observational tests of FRW world models. Class. Quantum Gravity 2002, 19, 3517–3526. [Google Scholar] [CrossRef]
- Hansen, F.K.; Banday, A.J.; Górski, K.M. Testing the cosmological principle of isotropy: Local power-spectrum estimates of the WMAP data. Mon. Not. R. Astron. Soc. 2004, 354, 641–665. [Google Scholar] [CrossRef]
- Schwarz, D.J.; Bacon, D.; Chen, S.; Clarkson, C.; Huterer, D.; Kunz, M.; Maartens, R.; Raccanelli, A.; Rubart, M.; Starck, J.L. Testing foundations of modern cosmology with SKA all-sky surveys. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2014; p. 32.
- Segre, M. Galileo, Viviani and the tower of Pisa. Stud. Hist. Philos. Sci. Part A 1989, 20, 435–451. [Google Scholar] [CrossRef]
- Eötvos, R. Über die Anziehung der Erde auf Verschiedene Substanzen. Math. Naturwissenschaft. Ber. Ung. 1890, 8, 65–68. [Google Scholar]
- Gundlach, J.H.; Smith, G.L.; Adelberger, E.G.; Heckel, B.R.; Swanson, H.E. Short-range test of the equivalence principle. Phys. Rev. Lett. 1997, 78, 2523–2526. [Google Scholar] [CrossRef]
- Schlamminger, S.; Choi, K.Y.; Wagner, T.A.; Gundlach, J.H.; Adelberger, E.G. Test of the equivalence principle using a rotating torsion balance. Phys. Rev. Lett. 2008, 100, 041101. [Google Scholar] [CrossRef] [PubMed]
- Adelberger, E.; Gundlach, J.; Heckel, B.; Hoedl, S.; Schlamminger, S. Torsion balance experiments: A low-energy frontier of particle physics. Prog. Part. Nucl. Phys. 2009, 62, 102–134. [Google Scholar] [CrossRef]
- Wagner, T.A.; Schlamminger, S.; Gundlach, J.H.; Adelberger, E.G. Torsion-balance tests of the weak equivalence principle. Class. Quantum Gravity 2012, 29, 184002. [Google Scholar] [CrossRef]
- Dickey, J.O.; Bender, P.L.; Faller, J.E.; Newhall, X.X.; Ricklefs, R.L.; Ries, J.G.; Shelus, P.J.; Veillet, C.; Whipple, A.L.; Wiant, J.R.; et al. Lunar Laser ranging: A continuing legacy of the Apollo program. Science 1994, 265, 482–490. [Google Scholar] [CrossRef] [PubMed]
- Murphy, T.W. Lunar laser ranging: The millimeter challenge. Rep. Prog. Phys. 2013, 76, 076901. [Google Scholar] [CrossRef] [PubMed]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Appleby, G.; Rodríguez, J.; Altamimi, Z. Assessment of the accuracy of global geodetic satellite laser ranging observations and estimated impact on ITRF scale: Estimation of systematic errors in LAGEOS observations 1993–2014. J. Geod. 2016. [Google Scholar] [CrossRef]
- Degnan, J.J. Laser transponders for high-accuracy interplanetary laser ranging and time transfer. In Lasers, Clocks and Drag-Free Control: Exploration of Relativistic Gravity in Space; Dittus, H., Lammerzahl, C., Turyshev, S.G., Eds.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 2008; Volume 349, p. 231. [Google Scholar]
- Iorio, L. Effects of standard and modified gravity on interplanetary ranges. Int. J. Mod. Phys. D 2011, 20, 181–232. [Google Scholar] [CrossRef]
- Dirkx, D.; Noomen, R.; Visser, P.N.A.M.; Bauer, S.; Vermeersen, L.L.A. Comparative analysis of one- and two-way planetary laser ranging concepts. Planet. Space Sci. 2015, 117, 159–176. [Google Scholar] [CrossRef]
- Smith, D.; Zuber, M.; Sun, X.; Neumann, G.; Cavanaugh, J.; McGarry, J.; Zagwodzki, T. Two-way laser link over interplanetary distance. Science 2006, 311, 53. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Birnbaum, K.M.; Hemmati, H. Active laser ranging over planetary distances with millimeter accuracy. Appl. Phys. Lett. 2013, 102, 241107. [Google Scholar] [CrossRef]
- Margot, J.L.; Giorgini, J.D. Probing general relativity with radar astrometry in the inner solar system. Proc. Int. Astron. Union 2010, 261, 183–188. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Manche, H.; Gastineau, M. Tests of GR with INPOP15a Planetary Ephemerides: Estimations of Possible Supplementary Advances of Perihelia for Mercury and Saturn. 2016; arXiv:1601.00947. [Google Scholar]
- Iorio, L. The Solar Lense-Thirring Effect: Perspectives for a Future Measurement. 2016; arXiv:1601.01382. [Google Scholar]
- Anderson, J.D.; Laing, P.A.; Lau, E.L.; Liu, A.S.; Nieto, M.M.; Turyshev, S.G. Study of the anomalous acceleration of Pioneer 10 and 11. Phys. Rev. D 2002, 65, 082004. [Google Scholar] [CrossRef]
- Nieto, M.M.; Anderson, J.D. Using early data to illuminate the Pioneer anomaly. Class. Quantum Gravity 2005, 22, 5343–5354. [Google Scholar] [CrossRef]
- Turyshev, S.G.; Toth, V.T. The pioneer anomaly. Living Rev. Relativ. 2010, 13, 4. [Google Scholar] [CrossRef]
- Nieto, M.M. New Horizons and the onset of the Pioneer anomaly. Phys. Lett. B 2008, 659, 483–485. [Google Scholar] [CrossRef]
- Iorio, L. Perspectives on effectively constraining the location of a massive trans-Plutonian object with the New Horizons spacecraft: A sensitivity analysis. Celest. Mech. Dyn. Astron. 2013, 116, 357–366. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L.; Radicella, N.; Saridakis, E.N. Constraining the Schwarzschild-de Sitter solution in models of modified gravity. Phys. Dark Universe 2016, 13, 111–120. [Google Scholar] [CrossRef]
- Damour, T.; Taylor, J.H. Strong-field tests of relativistic gravity and binary pulsars. Phys. Rev. D 1992, 45, 1840–1868. [Google Scholar] [CrossRef]
- Lyne, A.G.; Burgay, M.; Kramer, M.; Possenti, A.; Manchester, R.N.; Camilo, F.; McLaughlin, M.A.; Lorimer, D.R.; D’Amico, N.; Joshi, B.C.; et al. A double-pulsar system: A rare laboratory for relativistic gravity and plasma physics. Science 2004, 303, 1153–1157. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M.; Wex, N. The double pulsar system: A unique laboratory for gravity. Class. Quantum Gravity 2009, 26, 073001. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The baryonic tully-fisher relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef] [PubMed]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational phenomenology and relativistic extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef]
- Adams, F.C.; Laughlin, G. Relativistic effects in extrasolar planetary systems. Int. J. Mod. Phys. D 2006, 15, 2133–2140. [Google Scholar] [CrossRef]
- Adams, F.C.; Laughlin, G. Effects of secular interactions in extrasolar planetary systems. Astrophys. J. 2006, 649, 992–1003. [Google Scholar] [CrossRef]
- Adams, F.C.; Laughlin, G. Long-term evolution of close planets including the effects of secular interactions. Astrophys. J. 2006, 649, 1004–1009. [Google Scholar] [CrossRef]
- Iorio, L. Are we far from testing general relativity with the transitting extrasolar planet HD 209458b ‘Osiris’? New Astron. 2006, 11, 490–494. [Google Scholar] [CrossRef]
- Jordán, A.; Bakos, G.Á. Observability of the general relativistic precession of periastra in exoplanets. Astrophys. J. 2008, 685, 543–552. [Google Scholar] [CrossRef]
- Pál, A.; Kocsis, B. Periastron precession measurements in transiting extrasolar planetary systems at the level of general relativity. Mon. Not. R. Astron. Soc. 2008, 389, 191–198. [Google Scholar] [CrossRef]
- Iorio, L. Classical and relativistic node precessional effects in WASP-33b and perspectives for detecting them. Astrophys. Space Sci. 2011, 331, 485–496. [Google Scholar] [CrossRef]
- Iorio, L. Classical and relativistic long-term time variations of some observables for transiting exoplanets. Mon. Not. R. Astron. Soc. 2011, 411, 167–183. [Google Scholar] [CrossRef]
- Iorio, L. Accurate characterization of the stellar and orbital parameters of the exoplanetary system WASP-33 b from orbital dynamics. Mon. Not. R. Astron. Soc. 2016, 455, 207–213. [Google Scholar] [CrossRef]
- Iorio, L. Post-Keplerian corrections to the orbital periods of a two-body system and their measurability. Mon. Not. R. Astron. Soc. 2016, 460, 2445–2452. [Google Scholar] [CrossRef]
- Henry, R.C. Kretschmann scalar for a kerr-newman black hole. Astrophys. J. 2000, 535, 350–353. [Google Scholar] [CrossRef]
- Will, C.M. Focus Issue: Gravity Probe B. Class. Quantum Gravity 2015, 32, 220301. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B test of general relativity. Class. Quantum Gravity 2015, 32, 224001. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Psaltis, D. Probes and tests of strong-field gravity with observations in the electromagnetic spectrum. Living Rev. Relativ. 2008, 11, 9. [Google Scholar] [CrossRef]
- Psaltis, D. Two approaches to testing general relativity in the strong-field regime. J. Phys. Conf. Ser. 2009, 189, 012033. [Google Scholar] [CrossRef]
- Johannsen, T. Testing general relativity in the strong-field regime with observations of black holes in the electromagnetic spectrum. Publ. Astron. Soc. Pac. 2012, 124, 1133–1134. [Google Scholar] [CrossRef]
- Kramer, M. Precision tests of theories of gravity using pulsars. In Thirteenth Marcel Grossmann Meeting: On Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories; Rosquist, K., Ed.; World Scientific: Singapore, 2015; pp. 315–332. [Google Scholar]
- Weisberg, J.M.; Taylor, J.H. The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. Astron. Soc. Pac. Conf. Ser. 2005, 328, 25–32. [Google Scholar]
- Bailes, M.; Ord, S.M.; Knight, H.S.; Hotan, A.W. Self-consistency of relativistic observables with general relativity in the white dwarf-neutron star binary PSR J1141-6545. Astrophys. J. 2003, 595, L49–L52. [Google Scholar] [CrossRef]
- Stairs, I.H.; Thorsett, S.E.; Taylor, J.H.; Wolszczan, A. Studies of the relativistic binary pulsar PSR B1534+12. I. Timing analysis. Astrophys. J. 2002, 581, 501–508. [Google Scholar] [CrossRef]
- Kramer, M.; Lorimer, D.R.; Lyne, A.G.; McLaughlin, M.; Burgay, M.; D’Amico, N.; Possenti, A.; Camilo, F.; Freire, P.C.C.; Joshi, B.C.; et al. Testing GR with the double pulsar: Recent results. In Proceedings of the 22nd Texas Symposium on Relativistic Astrophysics, Stanford, CA, USA, 13–17 December 2004; pp. 142–148.
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; McLaughlin, M.A.; Lyne, A.G.; Ferdman, R.D.; Burgay, M.; Lorimer, D.R.; Possenti, A.; D’Amico, N.; et al. Tests of general relativity from timing the double pulsar. Science 2006, 314, 97–102. [Google Scholar] [CrossRef] [PubMed]
- Desai, S.; Kahya, E.O. Galactic one-way Shapiro delay to PSR B1937+21. Mod. Phys. Lett. A 2016, 31, 1650083. [Google Scholar] [CrossRef]
- Huang, Y.; Weisberg, J.M. Timing the relativistic binary pulsar PSR B1913+16. In Proceedings of the 228th American Astronomical Society Meeting, San Diego, CA, USA, 12–16 June 2016.
- Iorio, L. Prospects for measuring the moment of inertia of pulsar J0737-3039A. New Astron. 2009, 14, 40–43. [Google Scholar] [CrossRef]
- Kehl, M.S.; Wex, N.; Kramer, M.; Liu, K. Future Measurements of the Lense-Thirring Effect in the Double Pulsar. 2016; arXiv:1605.00408. [Google Scholar]
- Iorio, L. Constraints from orbital motions around the Earth of the environmental fifth-force hypothesis for the OPERA superluminal neutrino phenomenology. J. High Energy Phys. 2012, 5, 73. [Google Scholar] [CrossRef]
- Deng, X.M.; Xie, Y. Yukawa effects on the clock onboard a drag-free satellite. Mon. Not. R. Astron. Soc. 2013, 431, 3236–3239. [Google Scholar] [CrossRef]
- Li, Z.W.; Yuan, S.F.; Lu, C.; Xie, Y. New upper limits on deviation from the inverse-square law of gravity in the solar system: A Yukawa parameterization. Res. Astron. Astrophys. 2014, 14, 139–143. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef] [PubMed]
- Tully, R.B.; Fisher, J.R. A new method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Dunsby, P.; Goheer, N.; Osano, B.; Uzan, J.P. How close can an inhomogeneous universe mimic the concordance model? J. Cosmol. Astropart. Phys. 2010, 6, 017. [Google Scholar] [CrossRef]
- Uzan, J.P.; Bernardeau, F. Lensing at cosmological scales: A test of higher dimensional gravity. Phys. Rev. D 2001, 64, 083004. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton Series in Physics: Princeton, NJ, USA, 1980. [Google Scholar]
- Rich, J. Fundamentals of Cosmology; Springer: Berlin, Germany, 2001. [Google Scholar]
- Uzan, J.P. The acceleration of the universe and the physics behind it. Gen. Relativ. Gravit. 2007, 39, 307–342. [Google Scholar] [CrossRef]
- Uzan, J.P. Tests of general relativity on astrophysical scales. Gen. Relativ. Gravit. 2010, 42, 2219–2246. [Google Scholar] [CrossRef]
- Lue, A.; Scoccimarro, R.; Starkman, G.D. Probing Newton’s constant on vast scales: Dvali-Gabadadze-Porrati gravity, cosmic acceleration, and large scale structure. Phys. Rev. D 2004, 69, 124015. [Google Scholar] [CrossRef]
- Song, Y.S. Large scale structure formation of the normal branch in the DGP brane world model. Phys. Rev. D 2008, 77, 124031. [Google Scholar] [CrossRef]
- Benabed, K.; Bernardeau, F. Testing quintessence models with large-scale structure growth. Phys. Rev. D 2001, 64, 083501. [Google Scholar] [CrossRef]
- Koivisto, T.; Mota, D.F. Gauss-Bonnet quintessence: Background evolution, large scale structure, and cosmological constraints. Phys. Rev. D 2007, 75, 023518. [Google Scholar] [CrossRef]
- Tsujikawa, S. Quintessence: A review. Class. Quantum Gravity 2013, 30, 214003. [Google Scholar] [CrossRef]
- Baldi, M.; Pettorino, V.; Amendola, L.; Wetterich, C. Oscillating non-linear large-scale structures in growing neutrino quintessence. Mon. Not. R. Astron. Soc. 2011, 418, 214–229. [Google Scholar] [CrossRef]
- Koivisto, T.S.; Saridakis, E.N.; Tamanini, N. Scalar-fluid theories: Cosmological perturbations and large-scale structure. J. Cosmol. Astropart. Phys. 2015, 2015, 047. [Google Scholar] [CrossRef]
- Schimd, C.; Uzan, J.P.; Riazuelo, A. Weak lensing in scalar-tensor theories of gravity. Phys. Rev. D 2005, 71, 083512. [Google Scholar] [CrossRef]
- Rodríguez-Meza, M.A. Power spectrum of large-scale structure cosmological models in the framework of scalar-tensor theories. J. Phys. Conf. Ser. 2010, 229, 012063. [Google Scholar] [CrossRef]
- Goenner, H. Some remarks on the genesis of scalar-tensor theories. Gen. Relativ. Gravit. 2012, 44, 2077–2097. [Google Scholar] [CrossRef]
- Takushima, Y.; Terukina, A.; Yamamoto, K. Bispectrum of cosmological density perturbations in the most general second-order scalar-tensor theory. Phys. Rev. D 2014, 89, 104007. [Google Scholar] [CrossRef]
- Dossett, J.N.; Ishak, M.; Parkinson, D.; Davis, T.M. Constraints and tensions in testing general relativity from Planck and CFHTLenS data including intrinsic alignment systematics. Phys. Rev. D 2015, 92, 023003. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological hints of modified gravity? Phys. Rev. D 2016, 93, 023513. [Google Scholar] [CrossRef]
- Hu, B.; Liguori, M.; Bartolo, N.; Matarrese, S. Parametrized modified gravity constraints after Planck. Phys. Rev. D 2013, 88, 123514. [Google Scholar] [CrossRef]
- Pettorino, V. Testing modified gravity with Planck: The case of coupled dark energy. Phys. Rev. D 2013, 88, 063519. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 Results. XIV. Dark Energy and Modified Gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar]
- Räsänen, S. Dark energy from back-reaction. J. Cosmol. Astropart. Phys. 2004, 2, 003. [Google Scholar]
- Wiltshire, D.L. Gravitational energy as dark energy: Towards concordance cosmology without Lambda. In Proceedings of the Dark Energy and Dark Matter: Observations, Experiments and Theories, Lyons, France, 7–11 July 2008; Volume 36, pp. 91–98.
- Räsänen, S. Backreaction: Directions of progress. Class. Quantum Gravity 2011, 28, 164008. [Google Scholar] [CrossRef]
- Buchert, T.; Carfora, M.; Ellis, G.F.R.; Kolb, E.W.; MacCallum, M.A.H.; Ostrowski, J.J.; Räsänen, S.; Roukema, B.F.; Andersson, L.; Coley, A.A.; et al. Is there proof that backreaction of inhomogeneities is irrelevant in cosmology? Class. Quantum Gravity 2015, 32, 215021. [Google Scholar] [CrossRef]
- Räsänen, S.; Bolejko, K.; Finoguenov, A. New test of the Friedmann-Lemaître-Robertson-Walker metric using the distance sum rule. Phys. Rev. Lett. 2015, 115, 101301. [Google Scholar] [CrossRef] [PubMed]
- Räsänen, S.; Väliviita, J.; Kosonen, V. Testing distance duality with CMB anisotropies. J. Cosmol. Astropart. Phys. 2016, 4, 050. [Google Scholar] [CrossRef]
- Boehm, C.; Räsänen, S. Violation of the FRW consistency condition as a signature of backreaction. J. Cosmol. Astropart. Phys. 2013, 9, 003. [Google Scholar] [CrossRef] [PubMed]
- Buchert, T. On average properties of inhomogeneous fluids in general relativity: Dust cosmologies. Gen. Relativ. Gravit. 2000, 32, 105–126. [Google Scholar] [CrossRef]
- Buchert, T. Dark Energy from structure: A status report. Gen. Relativ. Gravit. 2008, 40, 467–527. [Google Scholar] [CrossRef]
- Banks, T. Supersymmetry breaking and the cosmological constant. Int. J. Mod. Phy. A 2014, 29, 1430010. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S. Supersymmetric unification without low energy supersymmetry and signatures for fine-tuning at the LHC. J. High Energy Phys. 2005, 6, 073. [Google Scholar] [CrossRef]
- Susskind, L. The anthropic landscape of string theory. In Universe or Multiverse? Carr, B., Ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bauer, F.; Solà, J.; Štefancić, H. Dynamically avoiding fine-tuning the cosmological constant: The “Relaxed Universe”. J. Cosmol. Astropart. Phys. 2010, 12, 029. [Google Scholar] [CrossRef]
- Bombelli, L.; Lee, J.; Meyer, D.; Sorkin, R.D. Space-time as a causal set. Phys. Rev. Lett. 1987, 59, 521–524. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.; Dodelson, S.; Greene, P.B.; Sorkin, R. Everpresent Λ. Phys. Rev. D 2004, 69, 103523. [Google Scholar]
- Weinberg, S. Anthropic bound on the cosmological constant. Phys. Rev. Lett. 1987, 59, 2607–2610. [Google Scholar] [CrossRef] [PubMed]
- Garriga, J.; Linde, A.; Vilenkin, A. Dark energy equation of state and anthropic selection. Phys. Rev. D 2004, 69, 063521. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- de Putter, R.; Linder, E.V. Kinetic k-essence and quintessence. Astropart. Phys. 2007, 28, 263–272. [Google Scholar] [CrossRef]
- Durrer, R.; Maartens, R. Dark Energy and Modified Gravity. In Dark Energy: Observational and Theoretical Approaches; Ruiz-Lapuente, P., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 48–91. [Google Scholar]
- Deffayet, C.; Dvali, G.; Gabadadze, G. Accelerated universe from gravity leaking to extra dimensions. Phys. Rev. D 2002, 65, 044023. [Google Scholar] [CrossRef]
- Amendola, L.; Polarski, D.; Tsujikawa, S. Are f(R) Dark Energy Models Cosmologically Viable? Phys. Rev. Lett. 2007, 98, 131302. [Google Scholar] [CrossRef] [PubMed]
- Turyshev, S.G.; Toth, V.T.; Kinsella, G.; Lee, S.C.; Lok, S.M.; Ellis, J. Support for the thermal origin of the pioneer anomaly. Phys. Rev. Lett. 2012, 108, 241101. [Google Scholar] [CrossRef] [PubMed]
- Adler, C.G.; Coulter, B.L. Galileo and the Tower of Pisa experiment. Am. J. Phys. 1978, 46, 199–201. [Google Scholar] [CrossRef]
- Bergé, J.; Touboul, P.; Rodrigues, M.; The MICROSCOPE Team. Status of MICROSCOPE, a mission to test the Equivalence Principle in space. J. Phys. Conf. Ser. 2015, 610, 012009. [Google Scholar] [CrossRef]
- Overduin, J.; Everitt, F.; Worden, P.; Mester, J. STEP and fundamental physics. Class. Quantum Gravity 2012, 29, 184012. [Google Scholar] [CrossRef]
- Nobili, A.M.; Comandi, G.L.; Doravari, S.; Bramanti, D.; Kumar, R.; Maccarrone, F.; Polacco, E.; Turyshev, S.G.; Shao, M.; Lipa, J.; et al. “Galileo Galilei” (GG) a small satellite to test the equivalence principle of Galileo, Newton and Einstein. Exp. Astron. 2009, 23, 689–710. [Google Scholar] [CrossRef]
- Muller, H.; Peters, A.; Chu, S. A precision measurement of the gravitational redshift by the interference of matter waves. Nature 2010, 463, 926–929. [Google Scholar] [CrossRef] [PubMed]
- Bardeen, J.M.; Petterson, J.A. The lense-thirring effect and accretion disks around kerr black holes. Astrophys. J. 1975, 195, L65. [Google Scholar] [CrossRef]
- Pound, R.V.; Rebka, G.A. Apparent weight of photons. Phys. Rev. Lett. 1960, 4, 337–341. [Google Scholar] [CrossRef]
- Turyshev, S.G.; Yu, N.; Toth, V.T. General relativistic observables for the ACES experiment. Phys. Rev. D 2016, 93, 045027. [Google Scholar] [CrossRef]
- Vessot, R.F.C.; Levine, M.W.; Mattison, E.M.; Blomberg, E.L.; Hoffman, T.E.; Nystrom, G.U.; Farrel, B.F.; Decher, R.; Eby, P.B.; Baugher, C.R. Test of relativistic gravitation with a space-borne hydrogen maser. Phys. Rev. Lett. 1980, 45, 2081–2084. [Google Scholar] [CrossRef]
- Schiller, S.; Tino, G.M.; Gill, P.; Salomon, C.; Sterr, U.; Peik, E.; Nevsky, A.; Görlitz, A.; Svehla, D.; Ferrari, G.; et al. Einstein Gravity Explorer—A medium-class fundamental physics mission. Exp. Astron. 2009, 23, 573–610. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340, 448. [Google Scholar] [CrossRef] [PubMed]
- Iorio, L. Constraining the preferred-frame α1, α2 parameters from solar system planetary precessions. Int. J. Mod. Phys. D 2014, 23, 1450006. [Google Scholar] [CrossRef]
- Fienga, A.; Laskar, J.; Exertier, P.; Manche, H.; Gastineau, M. Numerical estimation of the sensitivity of INPOP planetary ephemerides to general relativity parameters. Celest. Mech. Dyn. Astron. 2015, 123, 325–349. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Debra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Conklin, J.W.; Heifetz, M.I.; Keiser, G.M.; Silbergleit, A.S.; Holmes, T.; Kolodziejczak, J.; et al. Gravity Probe B: Final results of a space experiment to test general relativity. Phys. Rev. Lett. 2011, 106, 221101. [Google Scholar] [CrossRef] [PubMed]
- Kramer, M. Pulsars as probes of gravity and fundamental physics. Int. J. Mod. Phys. D 2016, 25, 1630029. [Google Scholar] [CrossRef]
- Bertotti, B.; Ciufolini, I.; Bender, P.L. New test of general relativity—Measurement of de Sitter geodetic precession rate for lunar perigee. Phys. Rev. Lett. 1987, 58, 1062–1065. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, I.I.; Reasenberg, R.D.; Chandler, J.F.; Babcock, R.W. Measurement of the de Sitter precession of the moon—A relativistic three-body effect. Phys. Rev. Lett. 1988, 61, 2643–2646. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.G.; Newhall, X.X.; Dickey, J.O. Relativity parameters determined from lunar laser ranging. Phys. Rev. D 1996, 53, 6730–6739. [Google Scholar] [CrossRef] [PubMed]
- Merkowitz, S.M. Tests of gravity using lunar laser ranging. Living Rev. Relativ. 2010, 13, 7. [Google Scholar] [CrossRef]
- Martini, M.; Dell’Agnello, S.; Currie, D.; Delle Monache, G.O.; Vittori, R.; Berardi, S.; Boni, A.; Cantone, C.; Ciocci, E.; Lops, C.; et al. Moonlight: A new lunar laser ranging retroreflector and the lunar geodetic precession. Acta Polytech. 2013, 53, 745–750. [Google Scholar] [CrossRef]
- Kramer, M. Determination of the geometry of the PSR B1913 + 16 System by geodetic precession. Astrophys. J. 1998, 509, 856–860. [Google Scholar] [CrossRef]
- Breton, R.P.; Kaspi, V.M.; Kramer, M.; McLaughlin, M.A.; Lyutikov, M.; Ransom, S.M.; Stairs, I.H.; Ferdman, R.D.; Camilo, F.; Possenti, A. Relativistic spin precession in the double pulsar. Science 2008, 321, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Lucchesi, D.M.; Anselmo, L.; Bassan, M.; Pardini, C.; Peron, R.; Pucacco, G.; Visco, M. Testing the gravitational interaction in the field of the Earth via satellite laser ranging and the Laser Ranged Satellites Experiment (LARASE). Class. Quantum Gravity 2015, 32, 155012. [Google Scholar] [CrossRef]
- Ingram, A.; van der Klis, M.; Middleton, M.; Done, C.; Altamirano, D.; Heil, L.; Uttley, P.; Axelsson, M. A quasi-periodic modulation of the iron line centroid energy in the black hole binary H 1743-322. Mon. Not. R. Astron. Soc. 2016, 461, 1967–1980. [Google Scholar] [CrossRef]
- Bosi, F.; Cella, G.; di Virgilio, A.; Ortolan, A.; Porzio, A.; Solimeno, S.; Cerdonio, M.; Zendri, J.P.; Allegrini, M.; Belfi, J.; et al. Measuring gravitomagnetic effects by a multi-ring-laser gyroscope. Phys. Rev. D 2011, 84, 122002. [Google Scholar] [CrossRef]
- Stone, N.; Loeb, A. Observing lense-thirring precession in tidal disruption flares. Phys. Rev. Lett. 2012, 108, 061302. [Google Scholar] [CrossRef] [PubMed]
- Franchini, A.; Lodato, G.; Facchini, S. Lense-Thirring precession around supermassive black holes during tidal disruption events. Mon. Not. R. Astron. Soc. 2016, 455, 1946–1956. [Google Scholar] [CrossRef]
- Martynov, D.V.; Hall, E.D.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Adams, C.; Adhikari, R.X.; Anderson, R.A.; Anderson, S.B.; Arai, K.; et al. Sensitivity of the advanced LIGO detectors at the beginning of gravitational wave astronomy. Phys. Rev. D 2016, 93, 112004. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration. GW151226: Observation of gravitational waves from a 22-solar-mass binary black hole coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar]
- Johannsen, T. Sgr A* and general relativity. Class. Quantum Gravity 2016, 33, 113001. [Google Scholar] [CrossRef]
- Soffel, M.; Wirrer, R.; Schastok, J.; Ruder, H.; Schneider, M. Relativistic effects in the motion of artificial satellites: The oblateness of the central body I. Celest. Mech. 1987, 42, 81–89. [Google Scholar] [CrossRef]
- Heimberger, J.; Soffel, M.; Ruder, H. Relativistic effects in the motion of artificial satellites: The oblateness of the central body II. Celest. Mech. Dyn. Astron. 1989, 47, 205–217. [Google Scholar] [CrossRef]
- Soffel, M. Relativity in Astrometry, Celestial Mechanics and Geodesy; Springer-Verlag: Berlin, Germany, 1989. [Google Scholar]
- Iorio, L. Post-Newtonian direct and mixed orbital effects due to the oblateness of the central body. Int. J. Mod. Phys. D 2015, 24, 1550067. [Google Scholar] [CrossRef]
- Iorio, L. A possible new test of general relativity with Juno. Class. Quantum Gravity 2013, 30, 195011. [Google Scholar] [CrossRef]
- Starkman, G.D.; Trotta, R.; Vaudrevange, P.M. The virtues of frugality—Why cosmological observers should release their data slowly. Mon. Not. R. Astron. Soc. 2010, 401, L15–L18. [Google Scholar] [CrossRef]
- Domcke, V.; Pieroni, M.; Binétruy, P. Primordial gravitational waves for universality classes of pseudoscalar inflation. J. Cosmol. Astropart. Phys. 2016, 6, 031. [Google Scholar] [CrossRef]
- Ito, A.; Soda, J. MHz gravitational waves from short-term anisotropic inflation. J. Cosmol. Astropart. Phys. 2016, 4, 035. [Google Scholar] [CrossRef]
- Fidler, C.; Pettinari, G.W.; Beneke, M.; Crittenden, R.; Koyama, K.; Wands, D. The intrinsic B-mode polarisation of the Cosmic Microwave Background. J. Cosmol. Astropart. Phys. 2014, 7, 011. [Google Scholar] [CrossRef]
- Namikawa, T.; Nagata, R. Non-Gaussian structure of B-mode polarization after delensing. J. Cosmol. Astropart. Phys. 2015, 10, 004. [Google Scholar] [CrossRef] [PubMed]
- Abazajian, K.N.; Arnold, K.; Austermann, J.; Benson, B.A.; Bischoff, C.; Bock, J.; Bond, J.R.; Borrill, J.; Calabrese, E.; Carlstrom, J.E.; et al. Neutrino physics from the cosmic microwave background and large scale structure. Astropart. Phys. 2015, 63, 66–80. [Google Scholar] [CrossRef]
- Trotta, R. Bayes in the sky: Bayesian inference and model selection in cosmology. Contemp. Phys. 2008, 49, 71–104. [Google Scholar] [CrossRef]
- Hobson, M.P.; Jaffe, A.H.; Liddle, A.R.; Mukeherjee, P.; Parkinson, D. Bayesian Methods in Cosmology; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Liddle, A.R. How many cosmological parameters? Mon. Not. R. Astron. Soc. 2004, 351, L49–L53. [Google Scholar] [CrossRef]
- Metcalf, R.B.; Silk, J. On breaking cosmic degeneracy. Astrophys. J. 1998, 492, L1–L4. [Google Scholar] [CrossRef]
- Debono, I.; Rassat, A.; Réfrégier, A.; Amara, A.; Kitching, T.D. Weak lensing forecasts for dark energy, neutrinos and initial conditions. Mon. Not. R. Astron. Soc. 2010, 404, 110–119. [Google Scholar] [CrossRef]
- Howlett, C.; Lewis, A.; Hall, A.; Challinor, A. CMB power spectrum parameter degeneracies in the era of precision cosmology. J. Cosmol. Astropart. Phys. 2012, 4, 027. [Google Scholar] [CrossRef]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the cosmological standard model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Jaffe, A. H0 and odds on cosmology. Astrophys. J. 1996, 471, 24. [Google Scholar] [CrossRef]
- Mukherjee, P.; Parkinson, D.; Liddle, A.R. A nested sampling algorithm for cosmological model selection. Astrophys. J. 2006, 638, L51–L54. [Google Scholar] [CrossRef]
- Kilbinger, M.; Wraith, D.; Robert, C.P.; Benabed, K.; Cappé, O.; Cardoso, J.F.; Fort, G.; Prunet, S.; Bouchet, F.R. Bayesian model comparison in cosmology with Population Monte Carlo. Mon. Not. R. Astron. Soc. 2010, 405, 2381–2390. [Google Scholar] [CrossRef]
- Wraith, D.; Kilbinger, M.; Benabed, K.; Cappé, O.; Cardoso, J.; Fort, G.; Prunet, S.; Robert, C.P. Estimation of cosmological parameters using adaptive importance sampling. Phys. Rev. D 2009, 80, 023507. [Google Scholar] [CrossRef]
- Del Pozzo, W.; Veitch, J.; Vecchio, A. Testing general relativity using Bayesian model selection: Applications to observations of gravitational waves from compact binary systems. Phys. Rev. D 2011, 83, 082002. [Google Scholar] [CrossRef]
- Ellis, G.F.R. Dark Matter and Dark Energy Proposals: Maintaining Cosmology as a True Science; EAS Publications Series; European Astronomical Society: Versoix, Switzerland, 2009; Volume 36, pp. 325–336. [Google Scholar]
- Ellis, G.F.R. Issues in the Philosophy of Cosmology. In Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Handbook of the Philosophy of Science; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1183–1285. [Google Scholar]
- Jackman, S. Bayesian Analysis for the Social Sciences; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Niemack, M.D.; Ade, P.A.R.; Aguirre, J.; Barrientos, F.; Beall, J.A.; Bond, J.R.; Britton, J.; Cho, H.M.; Das, S.; Devlin, M.J.; et al. ACTPol: A polarization-sensitive receiver for the Atacama Cosmology Telescope. Proc. SPIE 2010, 7741, 77411S. [Google Scholar]
- Beynon, E.; Bacon, D.J.; Koyama, K. Weak lensing predictions for modified gravities at non-linear scales. Mon. Not. R. Astron. Soc. 2010, 403, 353–362. [Google Scholar] [CrossRef]
- Harnois-Déraps, J.; Munshi, D.; Valageas, P.; van Waerbeke, L.; Brax, P.; Coles, P.; Rizzo, L. Testing modified gravity with cosmic shear. Mon. Not. R. Astron. Soc. 2015, 454, 2722–2735. [Google Scholar] [CrossRef]
- Carlstrom, J.E.; CMB-S4 Collaboration. The next generation ground-based CMB experiment, CMB-S4. In Proceedings of the 228th AAS Meeting, San Diego, CA, USA, 12–16 June 2016.
- Santos, M.; Bull, P.; Alonso, D.; Camera, S.; Ferreira, P.; Bernardi, G.; Maartens, R.; Viel, M.; Villaescusa-Navarro, F.; Abdalla, F.B.; et al. Cosmology from a SKA HI intensity mapping survey. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2014.
- Hall, A.; Bonvin, C.; Challinor, A. Testing general relativity with 21-cm intensity mapping. Phys. Rev. D 2013, 87, 064026. [Google Scholar] [CrossRef]
- Lahav, O.; Suto, Y. Measuring our Universe from Galaxy Redshift Surveys. Living Rev. Relativ. 2004, 7, 8. [Google Scholar] [CrossRef]
- Dupé, F.X.; Rassat, A.; Starck, J.L.; Fadili, M.J. Measuring the integrated Sachs-Wolfe effect. Astron. Astrophys. 2011, 534, A51. [Google Scholar] [CrossRef]
- Stabenau, H.F.; Jain, B. N-body simulations of alternative gravity models. Phys. Rev. D 2006, 74, 084007. [Google Scholar] [CrossRef]
- Adamek, J.; Daverio, D.; Durrer, R.; Kunz, M. General relativistic N-body simulations in the weak field limit. Phys. Rev. D 2013, 88, 103527. [Google Scholar]
- He, J.H.; Li, B.; Hawken, A.J. Effective Dark Matter power spectra in f(R) gravity. Phys. Rev. D 2015, 92, 103508. [Google Scholar] [CrossRef]
- Winther, H.A.; Schmidt, F.; Barreira, A.; Arnold, C.; Bose, S.; Llinares, C.; Baldi, M.; Falck, B.; Hellwing, W.A.; Koyama, K.; et al. Modified gravity N-body code comparison project. Mon. Not. R. Astron. Soc. 2015, 454, 4208–4234. [Google Scholar] [CrossRef]
- Eingorn, M. First-order cosmological perturbations engendered by point-like masses. Astrophys. J. 2016, 825, 84. [Google Scholar] [CrossRef]
- Hahn, O.; Paranjape, A. General Relativistic “Screening” in Cosmological Simulations. 2016; arXiv:1602.07699. [Google Scholar]
- Kamdar, H.M.; Turk, M.J.; Brunner, R.J. Machine learning and cosmological simulations—I. Semi-analytical models. Mon. Not. R. Astron. Soc. 2016, 455, 642–658. [Google Scholar] [CrossRef]
- Kamdar, H.M.; Turk, M.J.; Brunner, R.J. Machine learning and cosmological simulations—II. Hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2016, 457, 1162–1179. [Google Scholar] [CrossRef]
- Smoot, G.F. See Saw Inflation/Dark Matter/Dark Energy/Baryogenesis. 2014; arXiv:1405.2776. [Google Scholar]
- Rickles, D. A “Second Superstring Revolution” and the Future of String Theory. In A Brief History of String Theory: From Dual Models to M-Theory; Springer: Berlin, Germany, 2014; pp. 207–242. [Google Scholar]
- Maartens, R.; Koyama, K. Brane-world gravity. Living Rev. Relativ. 2010, 13, 5. [Google Scholar] [CrossRef]
- Woodard, R.P. How far are we from the quantum theory of gravity? Rep. Prog. Phys. 2009, 72, 126002. [Google Scholar] [CrossRef]
- Norris, R.P. Data challenges for next-generation radio telescopes. In Proceedings of the Sixth IEEE International Conference on eScience, Brisbane, Australia, 7–10 December 2010; pp. 21–24.
- Planck Collaboration. Planck 2015 Results. II. Low Frequency Instrument Data Processing. Astron. Astrophys. 2016, 594, A2. [Google Scholar]
- Planck Collaboration. Planck 2015 Results. VIII. High Frequency Instrument Data Processing: Calibration and Maps. Astron. Astrophys. 2016, 594, A8. [Google Scholar]
- Jurić, M.; Kantor, J.; Lim, K.; Lupton, R.H.; Dubois-Felsmann, G.; Jenness, T.; Axelrod, T.S.; Aleksić, J.; Allsman, R.A.; AlSayyad, Y.; et al. The LSST Data Management System. 2015; arXiv:1512.07914. [Google Scholar]
- Desai, S.; Mohr, J.J.; Henderson, R.; Kümmel, M.; Paech, K.; Wetzstein, M. CosmoDM and its application to Pan-STARRS data. J. Instrum. 2015, 10, C06014. [Google Scholar] [CrossRef]
- Dodson, R.; Vinsen, K.; Wu, C.; Popping, A.; Meyer, M.; Wicenec, A.; Quinn, P.; van Gorkom, J.; Momjian, E. Imaging SKA-scale data in three different computing environments. Astron. Comput. 2016, 14, 8–22. [Google Scholar] [CrossRef]
- Arviset, C.; González, J.; Gutiérrez, R.; Hernández, J.; Salgado, J.; Segovia, J.C. The Gaia archive: VO in action in the big data era. In Proceedings of the International Symposium Dedicated to the 50th Anniversary of the Markarian Survey and the 10th Anniversary of the Armenian Virtual Observatory, Byurakan, Armenia, 5–8 October 2015; Volume 505, p. 218.
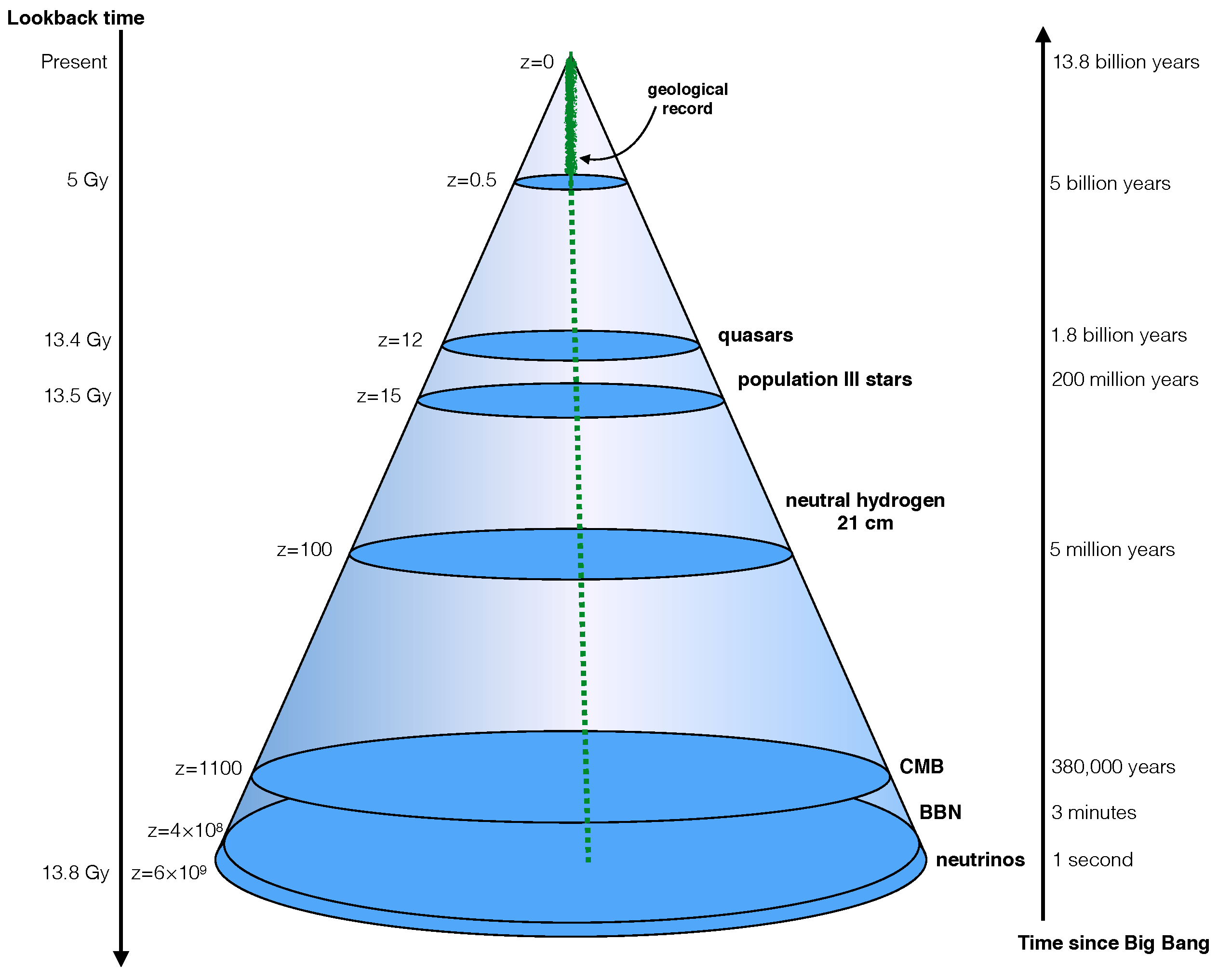
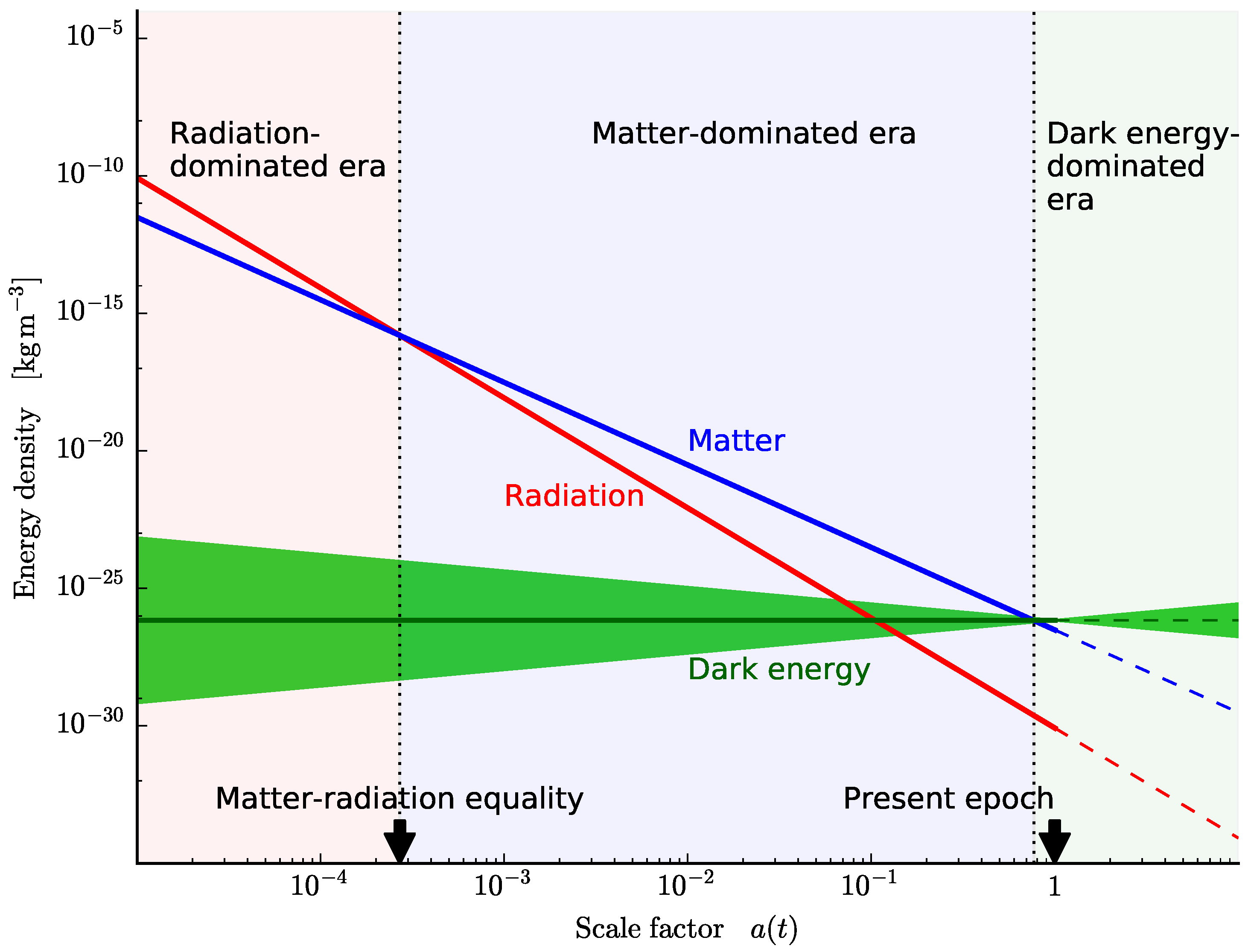
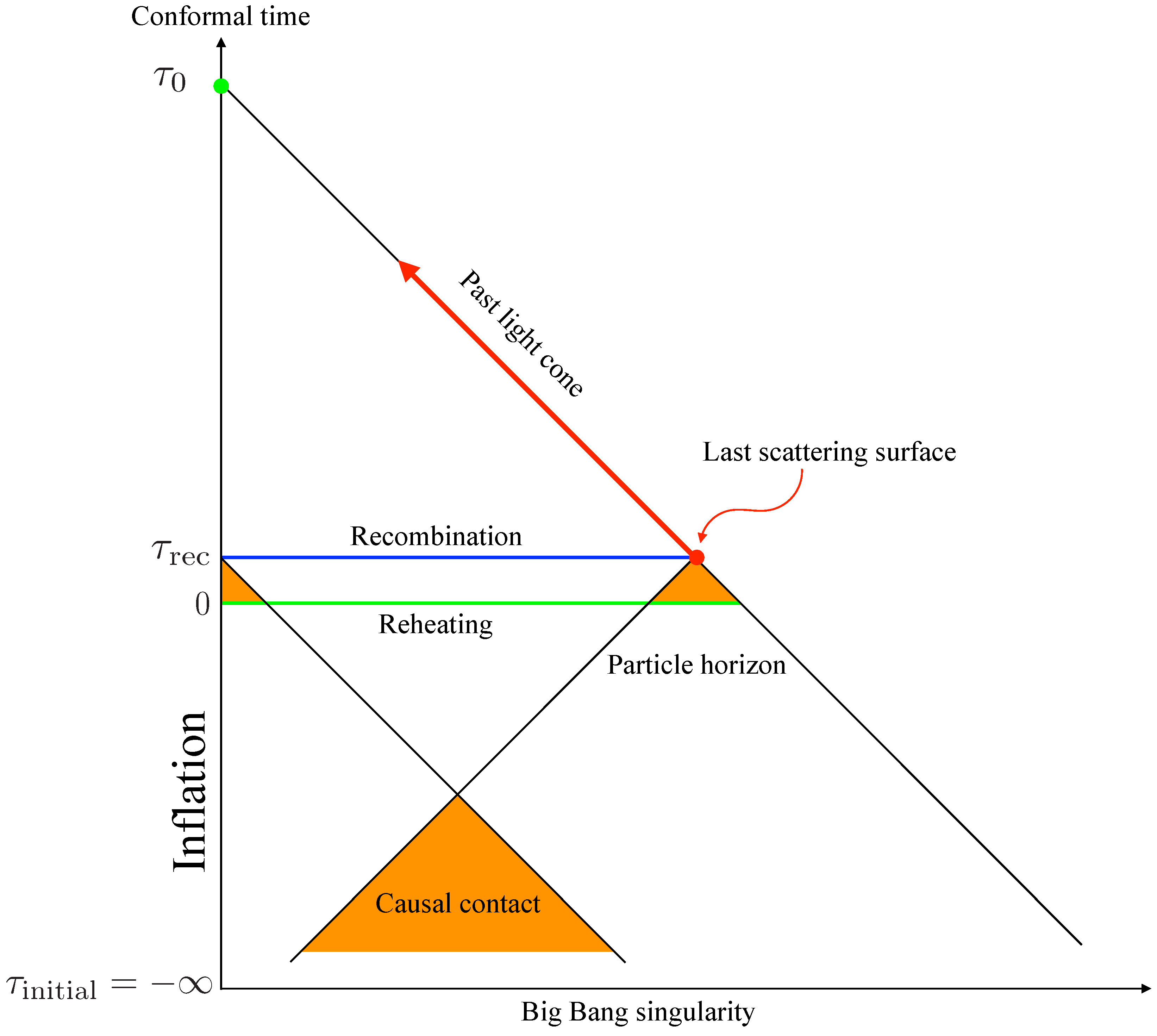
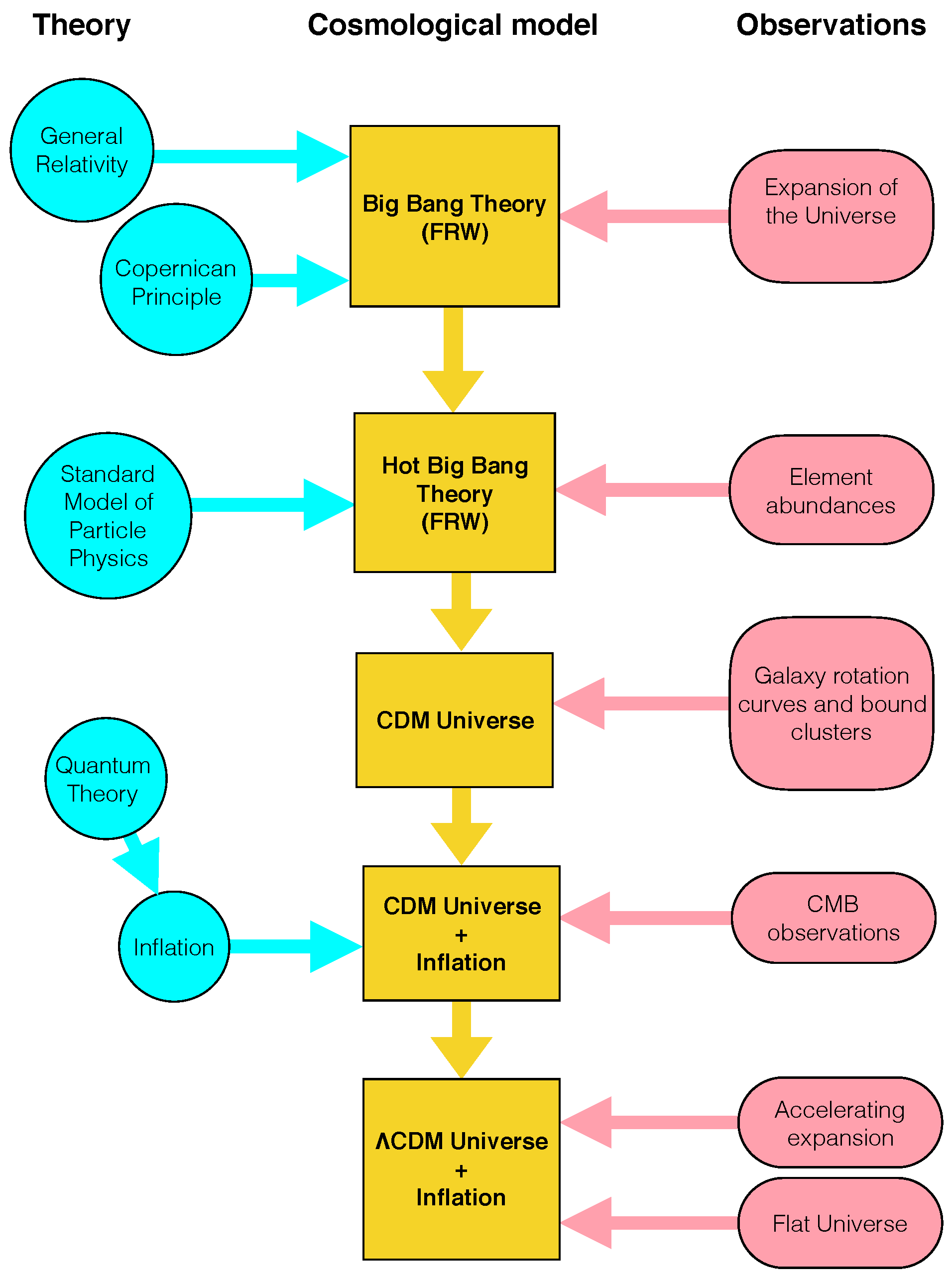
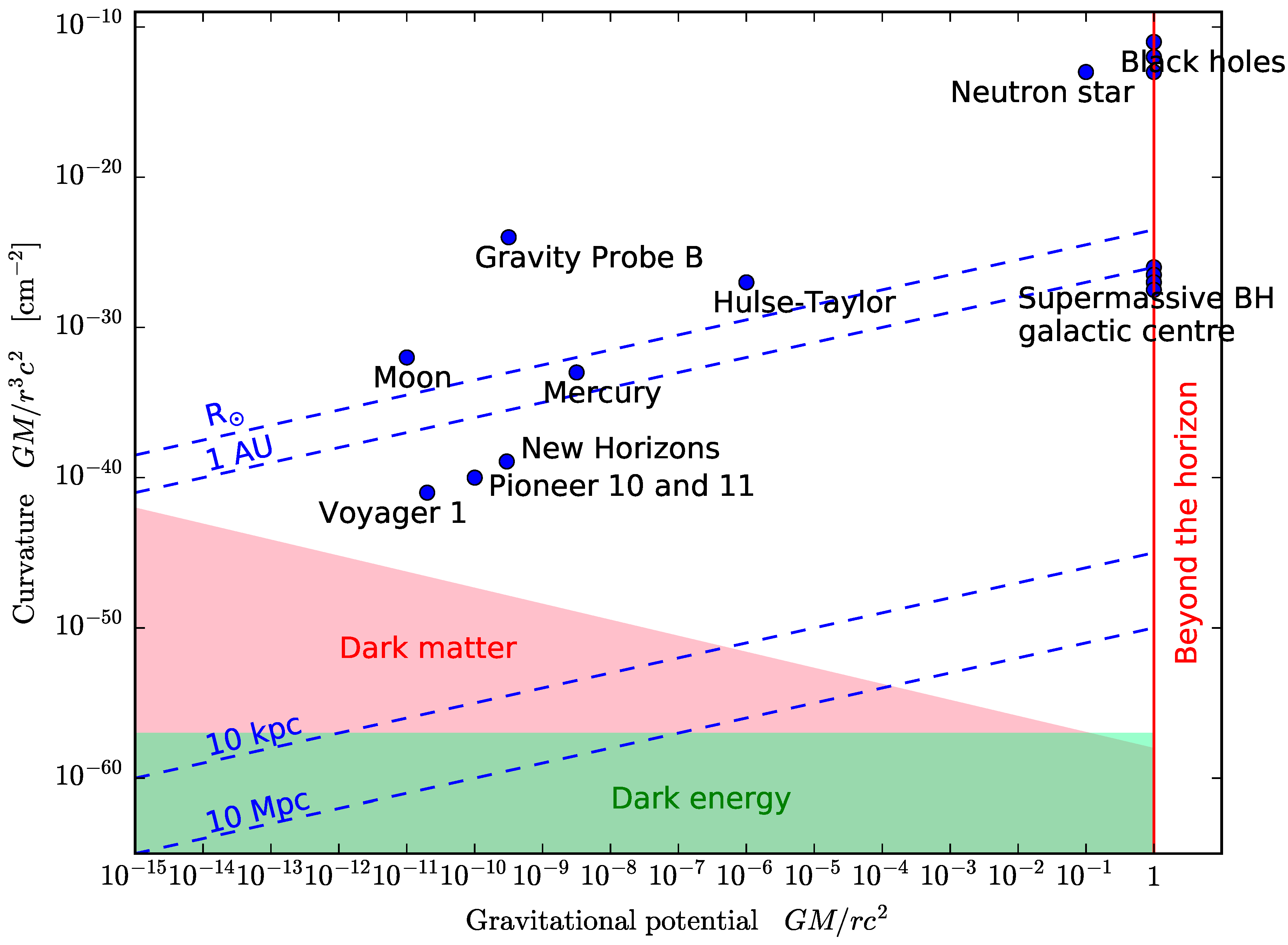
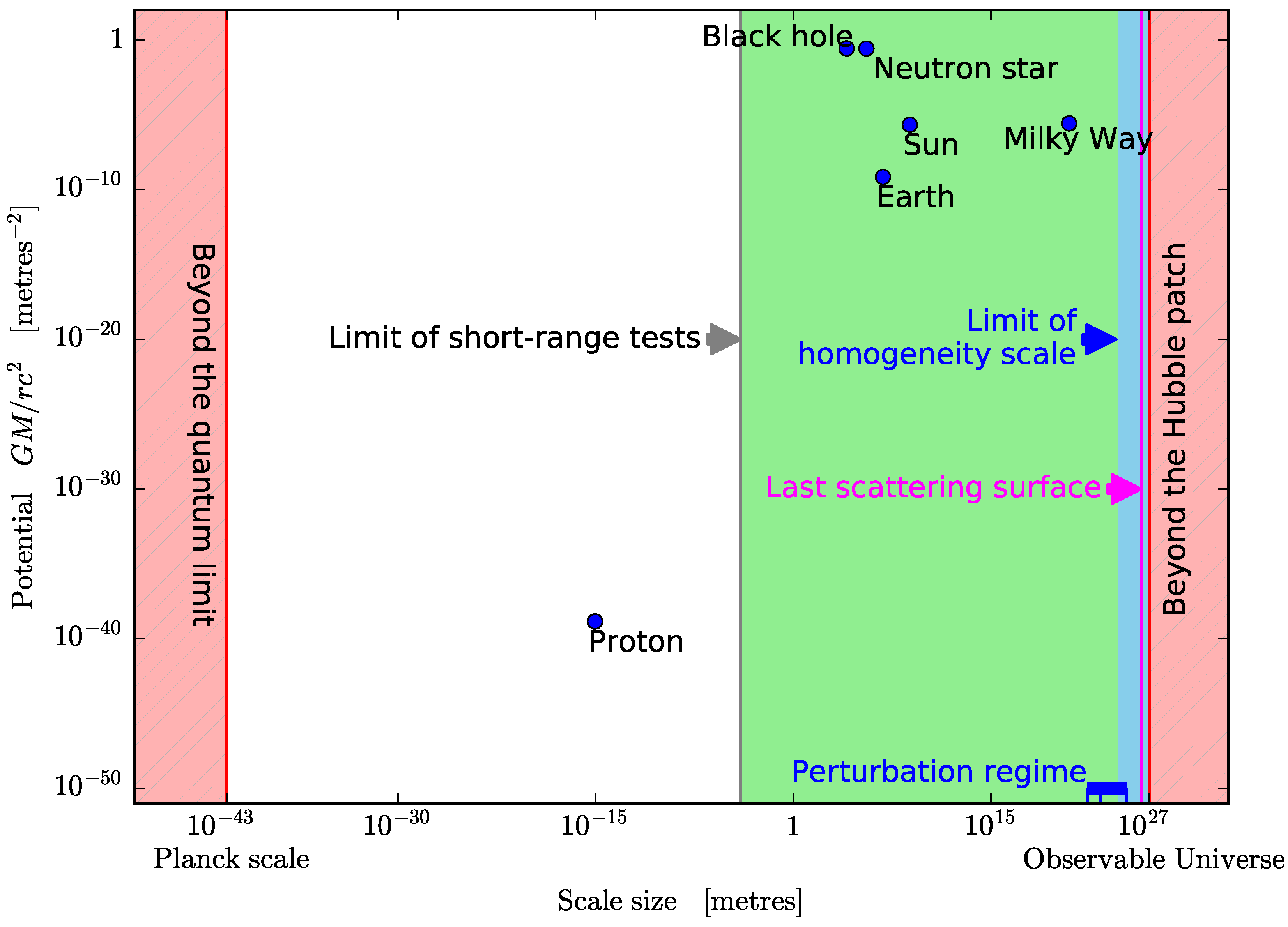
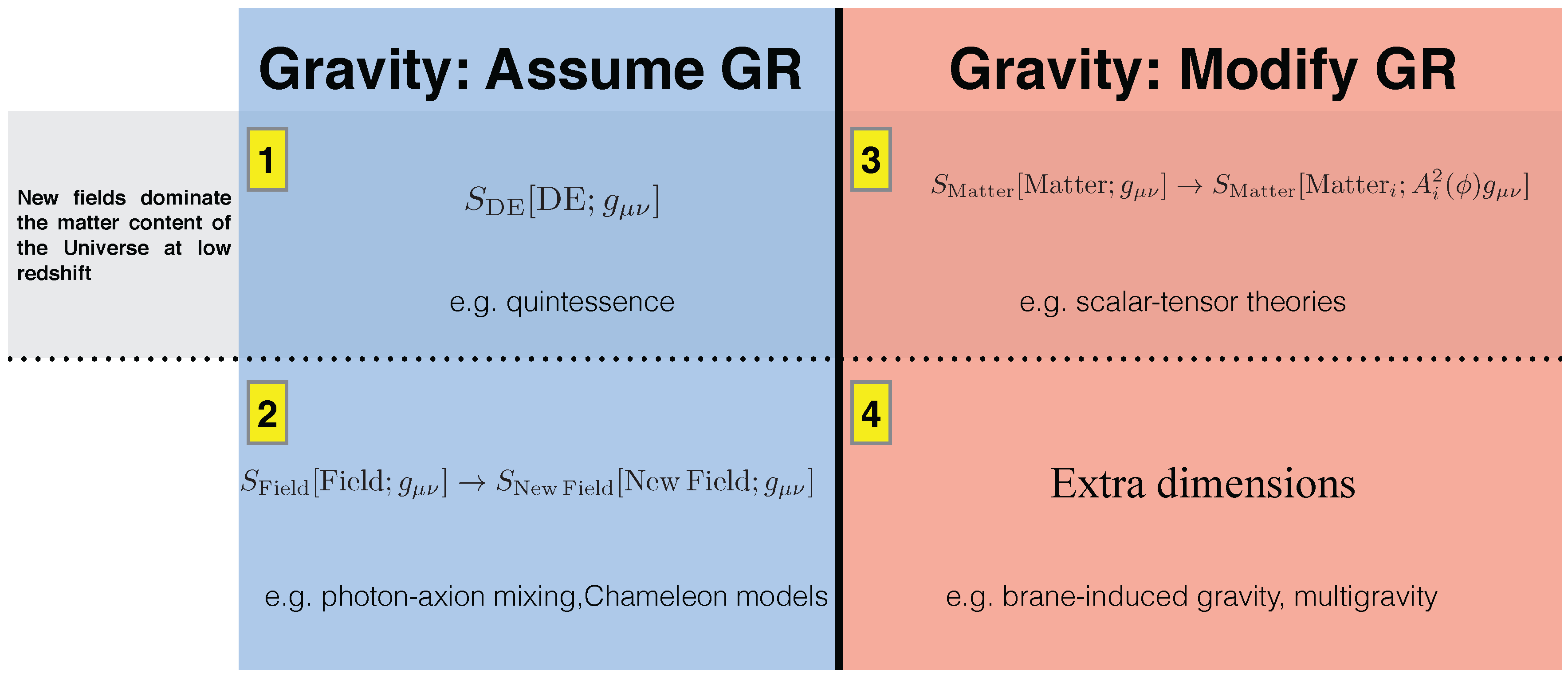
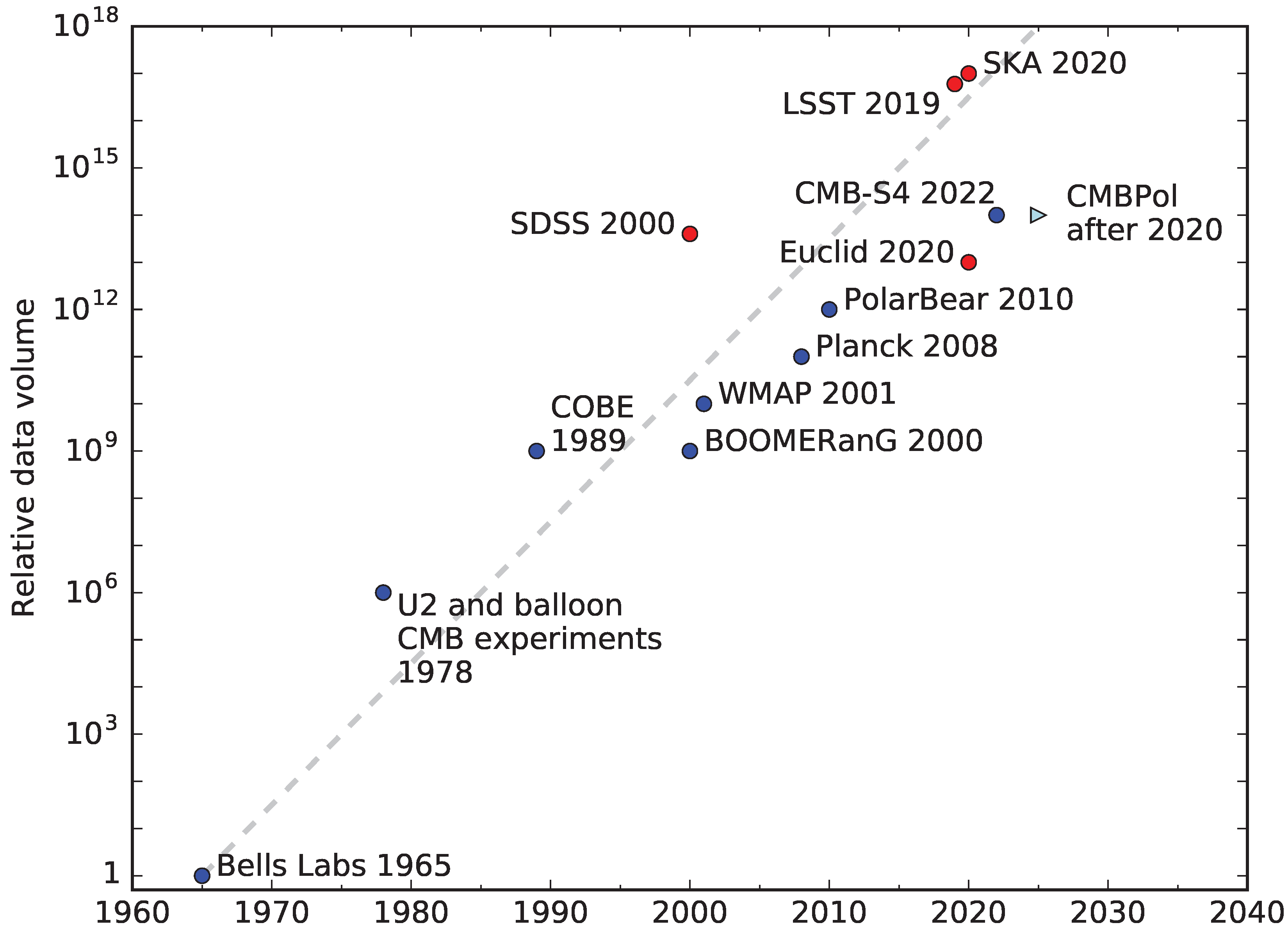
| Theory | Metric | Other Fields | Free Elements | Status |
|---|---|---|---|---|
| Newton 1687 [20] | Nonmetric | P | None | Nonrelativistic, implicit action at a distance |
| Poincaré 1890s–1900s [31,118] | Fails; does not mesh with electromagnetism | |||
| Nordstrøm 1913 [57] | Minkowski | S | None | Fails to predict observed light detection |
| General Relativity 1915 [46] | Dy | None | None | Viable |
| Whitehead 1922 [59] | Violates LLI; contradiction by everyday observation of tides | |||
| Cartan 1922–1925 [98] | ST | Still viable; introduces matter spin | ||
| Kaluza-Klein 1920s [119,120] | T | S | Extra dimensions | Violates Equivalence Principle |
| Birkhoff 1943 [61] | T | Fails Newtonian test; demands speed of sound equal to speed of light | ||
| Milne 1948 [121] | Machian background | Incomplete; no gravitational redshift prediction; contradicts cosmological observations. | ||
| Thiry 1948 [122] | ST | Unlikely; extremely constrained by results on | ||
| Belifante-Swihart 1957 [123] | Nonmetric | T | K param | Violates EEP; contradicted by Dicke–Braginsky experiments |
| Brans–Dicke 1961 [63] | Generic S | Dy | S | Viable for |
| Ni 1972 [48] | Minkowski | T, V, S | 1 param, 3 ftns | Violates LPI; predicts preferred-frame effects |
| Will-Nordtvedt 1972 [124] | Dy T | V | Viable but can only be significant at high energy regimes | |
| Barker 1978 [125] | ST | Unlikely; severely constrained. | ||
| Rosen 1973 [126,127] | Fixed | T | None | Contradicted by binary pulsar data |
| Rastall 1976 [128] | Minkowski | S, V | None | Contradicted by gravitational wave data |
| models 1970s [129,130] | ST | S | Free ftn | Consistent with Solar System tests; viable but severely constrained |
| MOND 1983 [131,132,133] | Nonmetric | P | Free ftn | Nonrelativistic theory |
| DGP 2000 [134] | ST/Quantum | Appears to be contradicted by BAOs, CMB and Supernovae Ia unless DE added | ||
| TeVeS 2004 [135] | T,V,S | Dy S | Free ftn | Highly unstable [136]; ruled out by SDSS data [137] |
| Component | w | ||
|---|---|---|---|
| Radiation (photons and relativistic neutrinos) | ∼ | ∼ | |
| Dust (includes CDM, baryons and non-relativistic neutrinos) | 0 | ∼ | ∼ |
| Curvature | ∼ | t | |
| Cosmic strings | ∼ | t | |
| Domain walls | ∼ | ||
| Inflation | ∼ | ||
| Vacuum energy | constant | ∼ |
| Method | Constraint | Experiment |
|---|---|---|
| Shift of perihelion of Mercury | Data to 1990 [333] | |
| Lunar laser ranging | Data to 2004 [334,335] | |
| Very long baseline interferometry | Data from 1979 to 1999 [336] | |
| Time-delay variation | Cassini spacecraft [67] | |
| Planetary perihelion precessions | Solar System ephemerides to 2013 [337] |
| Experiment | Assumption Tested |
|---|---|
| Solar System tests | Metric coupling |
| Quadrupolar shift of nuclear energy levels | Isotropy [340,341,342] |
| Lunar laser ranging and orbiting gyroscopes | Universality of freefall [343] and structure of metric |
| Space-borne clocks | Gravitational redshift [344] |
| Shift in perihelion of planets | Structure of metric [345] |
| Time invariance of physical constants | Metric coupling [346] |
| Detection of gravitational waves | Lorenz gauge condition and inhomogeneous wave equation |
| Test | Length Scale | Theories Probed | Current Status (and Future) |
|---|---|---|---|
| Growth vs. expansion history | GR with smooth dark energy | accuracy (–) | |
| Lensing vs. Dynamical mass | – | Test of GR | accuracy () |
| Astrophysical tests | – | MG screening mechanisms | ∼ (Up to 10 times improvement) |
| Laboratory and Solar System tests | – | PPN parameters in MG | Constraints are model dependent (Up to a tenfold improvement) |
| Effect | Milestones | Current, Future and Proposed Experiments | Status |
|---|---|---|---|
| Mass equivalence | Galileo [366,473] Eötvös [367] | Eöt-Wash Group [371] Lunar Laser Ranging [343] MICROSCOPE [474] STEP [475] Galileo Galilei satellite [476] | Confirmed |
| Gravitational time dilation [478] | Eddington solar eclipse [4] Pound-Rebka experiment [479] Space-borne hydrogen masers [481] | Quantum interference of atoms [477] ACES [480] Galileo 5 and 6 satellites [344] Einstein Gravity Explorer [482] | Confirmed |
| Precession of orbits | Orbit of Mercury (Einstein [3]) | Binary pulsar observations [483,484,485] Solar System and extrasolar planets [337,402] | Confirmed |
| De Sitter precession | Gravity Probe B [486] Lunar laser ranging [488,489,490] Binary pulsars [493,494] | Binary pulsars [487] Improved lunar laser ranging [491,492] | Confirmed |
| Lense-Thirring precession | Gravity Probe B [486] LARES [420,421,496] | LARASE [495] Laboratory tests [497] Solar System bodies [339] Binary pulsars [420,421] Black holes [478,496,498,499] | Confirmed |
| Gravitational waves | LIGO [80] | Advanced LIGO [500] eLISA https://www.elisascience.org | Recently confirmed in two events [80,501] |
| Strong field effects | PSR J0348 + 0432 [483] | Black holes [411,502] Binary pulsars [117] | Recently confirmed |
| Orbital precession due tooblateness of central body | Low-orbit satellites [503,504,505,506] Stars orbiting black holes [506] Juno spacecraft around Jupiter [507] | Not yet observed |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Debono, I.; Smoot, G.F. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe 2016, 2, 23. https://doi.org/10.3390/universe2040023
Debono I, Smoot GF. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe. 2016; 2(4):23. https://doi.org/10.3390/universe2040023
Chicago/Turabian StyleDebono, Ivan, and George F. Smoot. 2016. "General Relativity and Cosmology: Unsolved Questions and Future Directions" Universe 2, no. 4: 23. https://doi.org/10.3390/universe2040023
APA StyleDebono, I., & Smoot, G. F. (2016). General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe, 2(4), 23. https://doi.org/10.3390/universe2040023







