Predictions for Bottomonia Suppression in 5.023 TeV Pb-Pb Collisions
Abstract
:1. Introduction
2. 3 + 1d Anisotropic Hydrodynamics
3. Model Potential
4. Bottomonium Suppression
4.1. Survival Probability
4.2. Excited State Feed Down
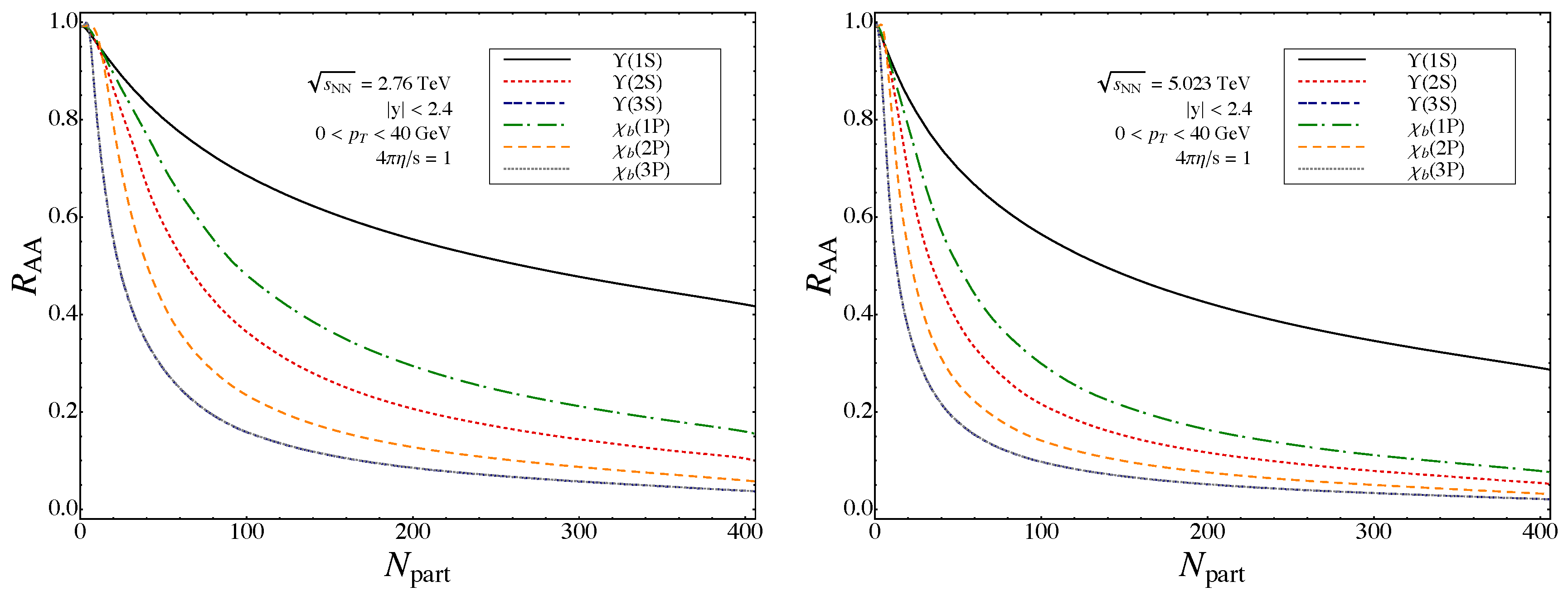
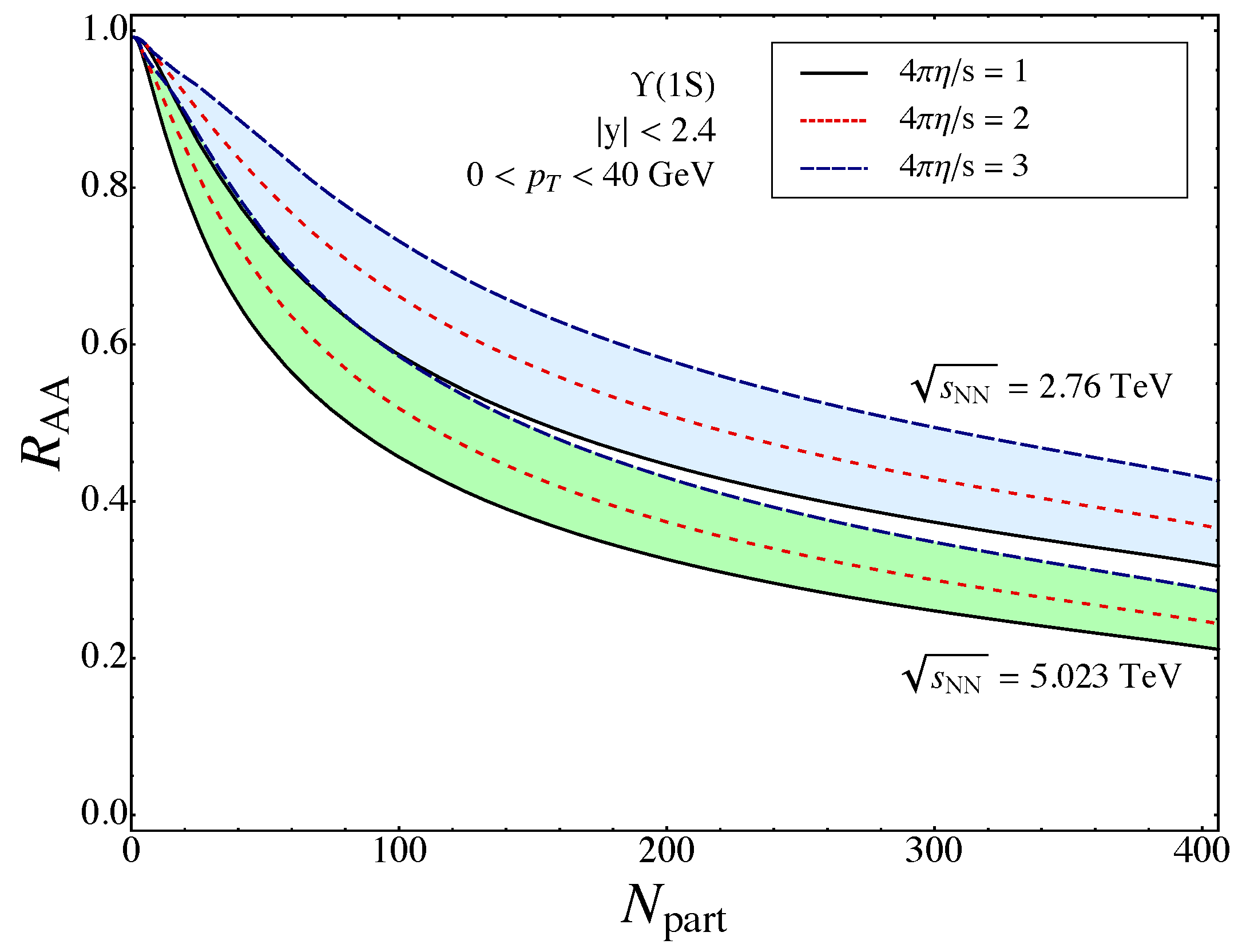
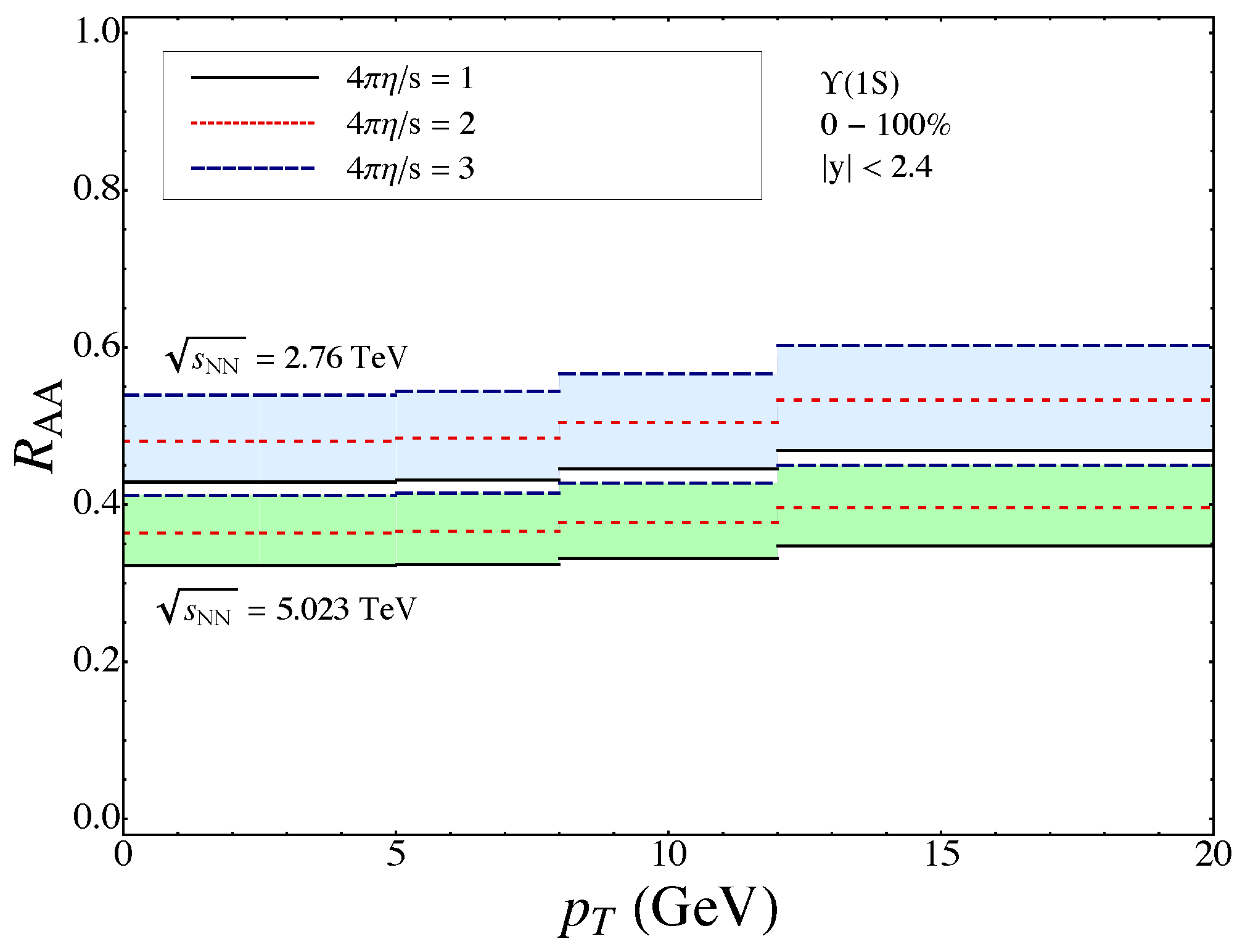
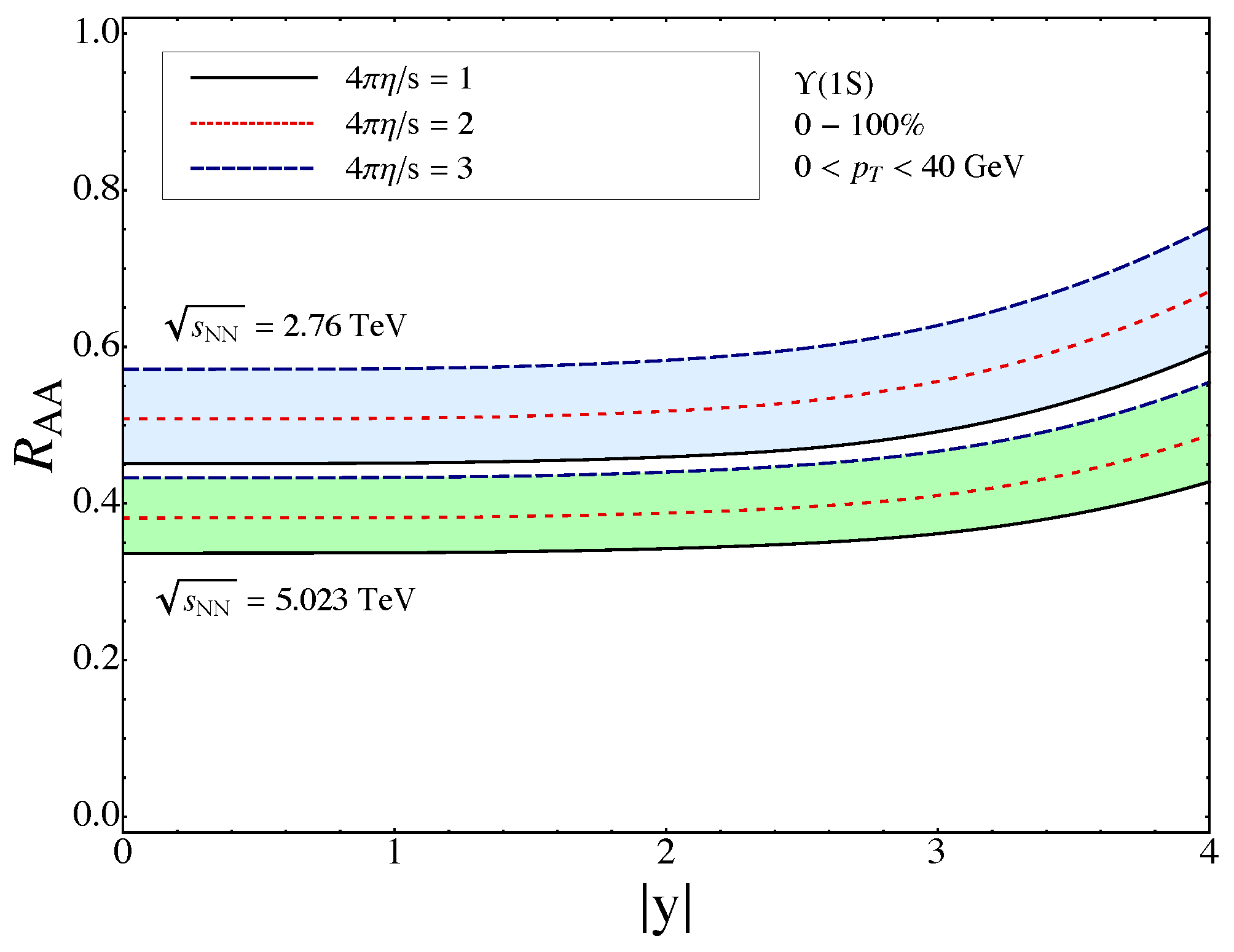
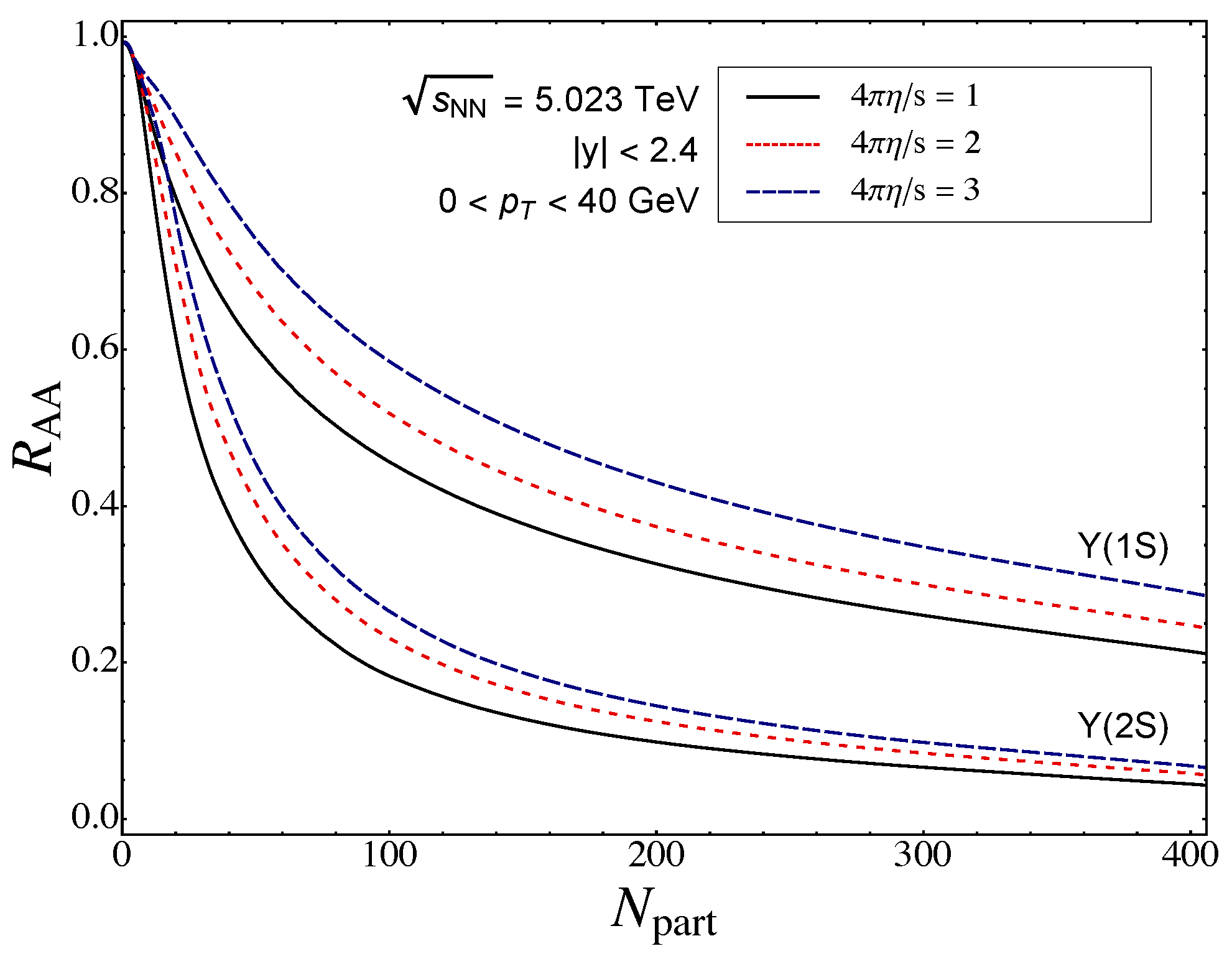
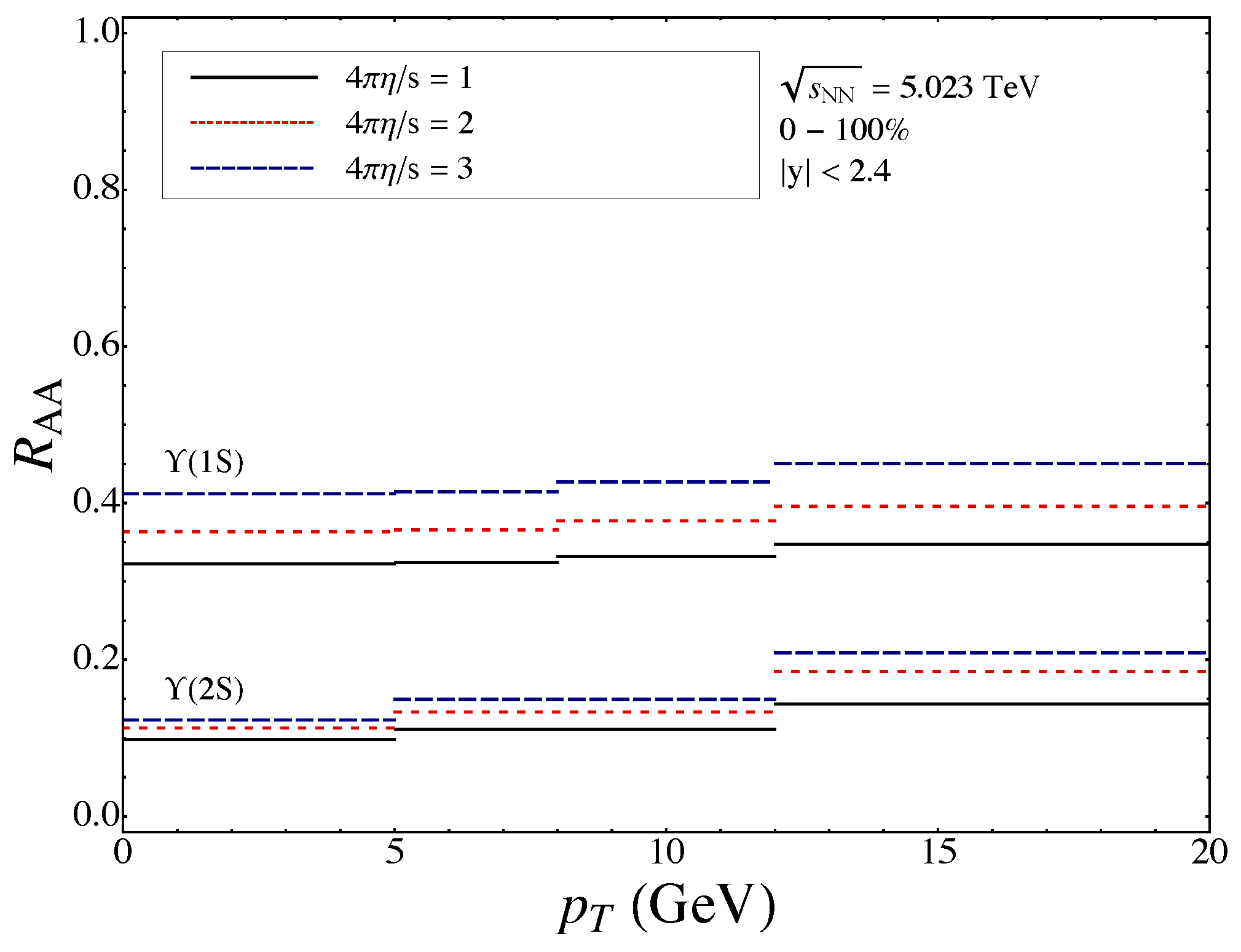
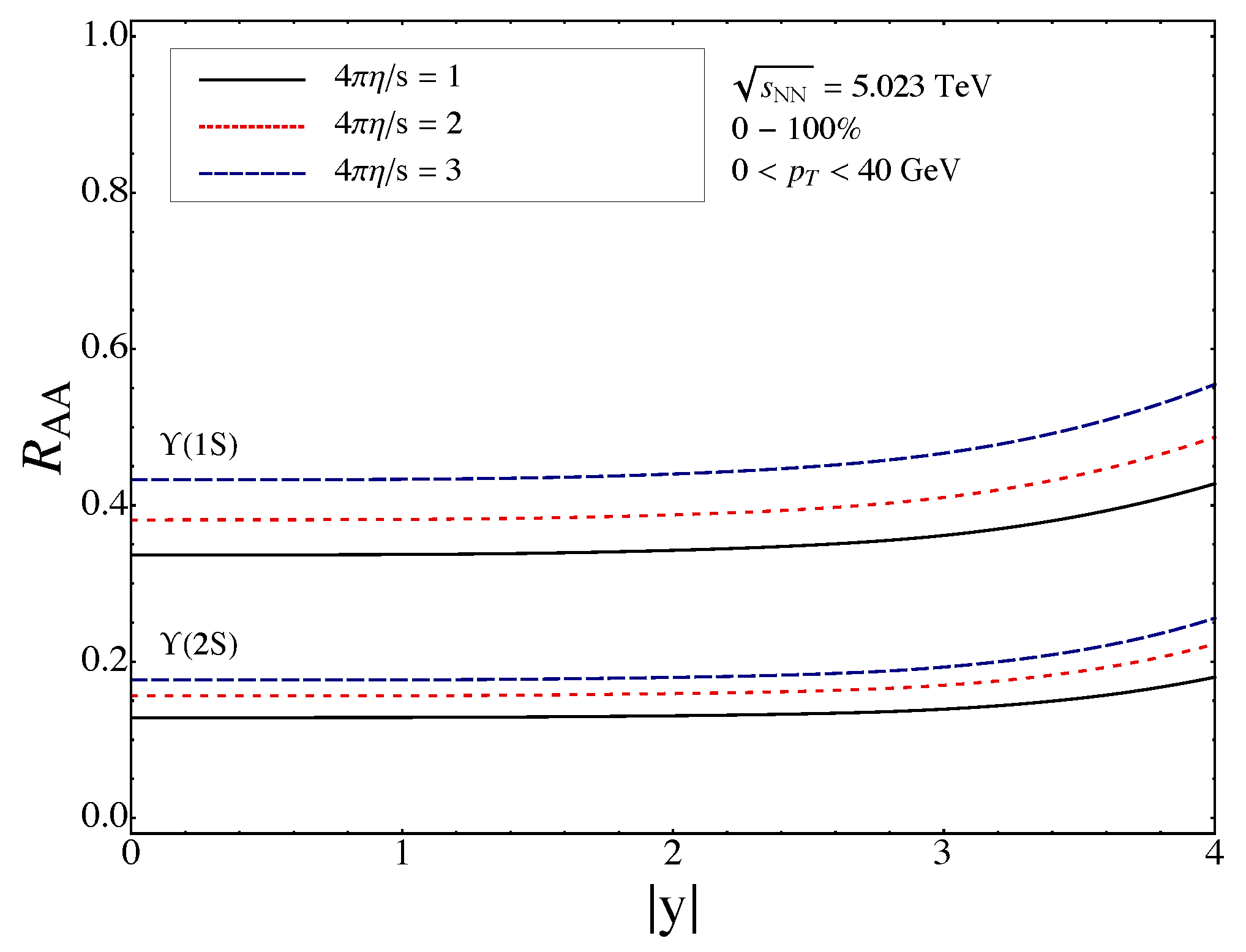
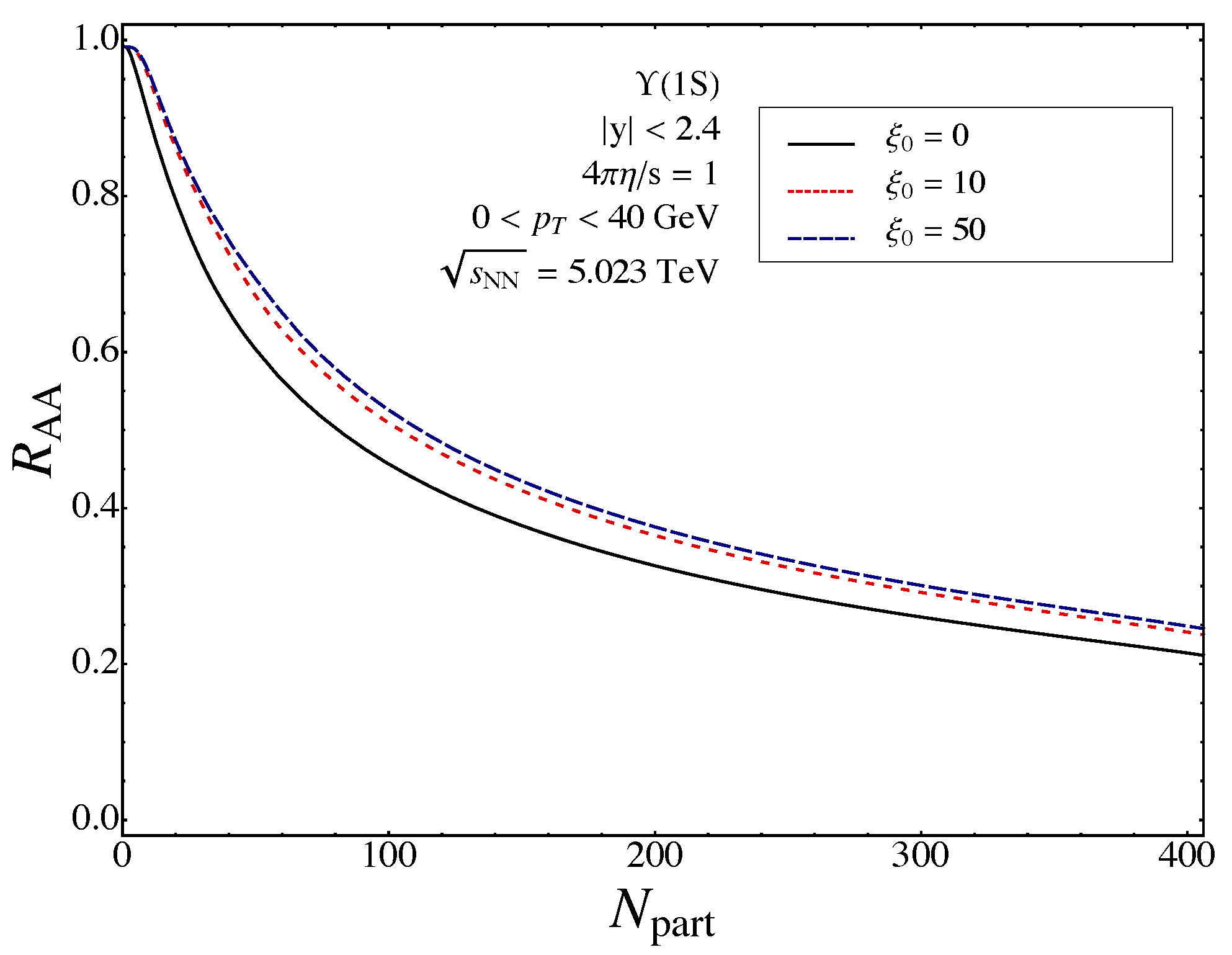
4.3. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Gale, C.; Jeon, S.; Schenke, B. Hydrodynamic modeling of heavy-ion Collisions. Int. J. Mod. Phys. A 2013, 28, 1340011. [Google Scholar] [CrossRef]
- Strickland, M. Anisotropic hydrodynamics: Three lectures. Acta Phys. Pol. B 2014, 45, 2355–2394. [Google Scholar] [CrossRef]
- Fukushima, K. Evolution to the Quark-Gluon Plasma. 2016; arXiv:1603.02340. [Google Scholar]
- Matsui, T.; Satz, H. J/ψ Suppression by quark-gluon plasma formation. Phys. Lett. B 1986, 178, 416–422. [Google Scholar] [CrossRef]
- Karsch, F.; Mehr, M.T.; Satz, H. Color screening and deconfinement for bound states of heavy quarks. Z. Phys. C 1988, 37, 617–622. [Google Scholar] [CrossRef]
- Emerick, A.; Zhao, X.; Rapp, R. Bottomonia in the quark-gluon plasma and their production at RHIC and LHC. Eur. Phys. J. A 2012, 48, 72. [Google Scholar] [CrossRef]
- Nendzig, F.; Wolschin, G. Y suppression in PbPb collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2013, 87, 024911. [Google Scholar] [CrossRef]
- Zhou, K.; Xu, N.; Xu, Z.; Zhuang, P. Medium effects on charmonium production at ultrarelativistic energies available at the CERN Large Hadron Collider. Phys. Rev. C 2014, 89, 054911. [Google Scholar] [CrossRef]
- Hoelck, J.; Nendzig, F.; Wolschin, G. In-Medium Y-Suppression and Feed-down in UU and PbPb Collisions. 2016; arXiv:1602.00019. [Google Scholar]
- Mocsy, A.; Petreczky, P.; Strickland, M. Quarkonia in the quark gluon plasma. Int. J. Mod. Phys. A 2013, 28, 1340012. [Google Scholar] [CrossRef]
- Karsch, F.; Kharzeev, D.; Satz, H. Sequential charmonium dissociation. Phys. Lett. B 2006, 637, 75–80. [Google Scholar] [CrossRef]
- Eichten, E.; Gottfried, K.; Kinoshita, T.; Lane, K.D.; Yan, T.M. Charmonium: Comparison with experiment. Phys. Rev. D 1980, 21, 203–233. [Google Scholar] [CrossRef]
- Lucha, W.; Schoberl, F.F.; Gromes, D. Bound states of quarks. Phys. Rep. 1991, 200, 127–240. [Google Scholar] [CrossRef]
- Brambilla, N.; Pineda, A.; Soto, J.; Vairo, A. Effective field theories for heavy quarkonium. Rev. Mod. Phys. 2005, 77, 1423–1496. [Google Scholar] [CrossRef]
- Brambilla, N.; Ghiglieri, J.; Vairo, A.; Petreczky, P. Static quark–antiquark pairs at finite temperature. Phys. Rev. D 2008, 78, 014017. [Google Scholar] [CrossRef]
- Brambilla, N.; Ghiglieri, J.; Petreczky, P.; Vairo, A. The Polyakov loop and correlator of Polyakov loops at next-to-next-to-leading order. Phys. Rev. D 2010, 82, 074019. [Google Scholar] [CrossRef]
- Laine, M.; Philipsen, O.; Romatschke, P.; Tassler, M. Real-time static potential in hot QCD. J. High Energy Phys. 2007, 3, 054. [Google Scholar] [CrossRef]
- Dumitru, A.; Guo, Y.; Strickland, M. The Heavy-quark potential in an anisotropic (viscous) plasma. Phys. Lett. B 2008, 662, 37–42. [Google Scholar] [CrossRef]
- Burnier, Y.; Laine, M.; Vepsalainen, M. Quarkonium dissociation in the presence of a small momentum space anisotropy. Phys. Lett. B 2009, 678, 86–89. [Google Scholar] [CrossRef]
- Dumitru, A.; Guo, Y.; Strickland, M. The imaginary part of the static gluon propagator in an anisotropic (viscous) QCD plasma. Phys. Rev. D 2009, 79, 114003. [Google Scholar] [CrossRef]
- Dumitru, A.; Guo, Y.; Mocsy, A.; Strickland, M. Quarkonium states in an anisotropic QCD plasma. Phys. Rev. D 2009, 79, 054019. [Google Scholar] [CrossRef]
- Margotta, M.; McCarty, K.; McGahan, C.; Strickland, M.; Yager-Elorriaga, D. Quarkonium states in a complex-valued potential. Phys. Rev. D 2011, 83, 105019. [Google Scholar] [CrossRef]
- Krouppa, B.; Ryblewski, R.; Strickland, M. Bottomonia suppression in 2.76 TeV Pb-Pb collisions. Phys. Rev. C 2015, 92, 061901. [Google Scholar] [CrossRef]
- Strickland, M.; Bazow, D. Thermal bottomonium suppression at RHIC and LHC. Nucl. Phys. A 2012, 879, 25–58. [Google Scholar] [CrossRef]
- Strickland, M. Thermal Upsilon(1s) and chi-b1 suppression in sqrt(s-NN) = 2.76 TeV Pb-Pb collisions at the LHC. Phys. Rev. Lett. 2011, 107, 132301. [Google Scholar] [CrossRef] [PubMed]
- Florkowski, W.; Ryblewski, R. Highly-anisotropic and strongly-dissipative hydrodynamics for early stages of relativistic heavy-ion collisions. Phys. Rev. C 2011, 83, 034907. [Google Scholar]
- Martinez, M.; Strickland, M. Dissipative dynamics of highly anisotropic systems. Nucl. Phys. A 2010, 848, 183–197. [Google Scholar] [CrossRef]
- Bazow, D.; Heinz, U.W.; Strickland, M. Second-order (2+1)-dimensional anisotropic hydrodynamics. Phys. Rev. C 2014, 90, 054910. [Google Scholar] [CrossRef]
- Nopoush, M.; Strickland, M.; Ryblewski, R.; Bazow, D.; Heinz, U.; Martinez, M. Leading-order anisotropic hydrodynamics for central collisions. Phys. Rev. C 2015, 92, 044912. [Google Scholar] [CrossRef]
- Bazow, D.; Heinz, U.W.; Martinez, M. Nonconformal viscous anisotropic hydrodynamics. Phys. Rev. C 2015, 91, 064903. [Google Scholar] [CrossRef]
- Romatschke, P.; Strickland, M. Collective modes of an anisotropic quark gluon plasma. Phys. Rev. D 2003, 68, 036004. [Google Scholar] [CrossRef]
- Martinez, M.; Ryblewski, R.; Strickland, M. Boost-Invariant (2 + 1)-dimensional Anisotropic Hydrodynamics. Phys. Rev. C 2012, 85, 064913. [Google Scholar] [CrossRef]
- Ryblewski, R.; Florkowski, W. Highly-anisotropic hydrodynamics in 3 + 1 space-time dimensions. Phys. Rev. C 2012, 85, 064901. [Google Scholar] [CrossRef]
- Miller, M.L.; Reygers, K.; Sanders, S.J.; Steinberg, P. Glauber modeling in high energy nuclear collisions. Ann. Rev. Nucl. Part. Sci. 2007, 57, 205–243. [Google Scholar] [CrossRef]
- Florkowski, W. Phenomenology of Ultra-Relativistic Heavy-Ion Collisions; World Scientific: Singapore, 2010. [Google Scholar]
- Bożek, P.; Wyskiel-Piekarska, I. Particle spectra in pb-pb collisions at tev. Phys. Rev. C 2012, 85, 064915. [Google Scholar] [CrossRef]
- Özönder, Ş.; Fries, R.J. Rapidity profile of the initial energy density in heavy-ion collisions. Phys. Rev. C 2014, 89, 034902. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. Anisotropic flow in sqrt(s) = 2.76 TeV Pb + Pb collisions at the LHC. Phys. Lett. B 2011, 702, 59–63. [Google Scholar] [CrossRef]
- Petreczky, P. Quarkonium in hot medium. J. Phys. G 2010, 37, 094009. [Google Scholar] [CrossRef]
- Bali, G.S.; Schilling, K.; Wachter, A. Complete O (v⌃2) corrections to the static interquark potential from SU(3) gauge theory. Phys. Rev. D 1997, 56, 2566–2589. [Google Scholar] [CrossRef]
- Strickland, M.; Yager-Elorriaga, D. A parallel algorithm for solving the 3d schrodinger equation. J. Comput. Phys. 2010, 229, 6015–6026. [Google Scholar] [CrossRef]
- Karsch, F.; Petronzio, R. Momentum Distribution of J/psi in the Presence of a Quark-Gluon Plasma. Phys. Lett. B 1987, 193, 105–109. [Google Scholar] [CrossRef]
- The CMS Collaboration; Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Fried, M.; et al. Suppression of non-prompt J/ψ, prompt J/ψ, and Y(1S) in PbPb collisions at = 2.76 TeV. J. High Energy Phys. 2012, 5, 063. [Google Scholar] [CrossRef]
- Wöeri, H. International Workshop on Heavy Quarkonium 2014. Available online: https://indico.cern.ch/event/278195/session/7/contribution/104/material/slides/0.pdf (accessed on 25 August 2016).
| ξ0 | 0 | 10 | 50 | |
|---|---|---|---|---|
| 4πη/s | ||||
| 1 | 0.552 | 0.765 | 0.925 | |
| 2 | 0.546 | 0.752 | 0.909 | |
| 3 | 0.544 | 0.748 | 0.906 | |
| ξ0 | 0 | 10 | 50 | |
|---|---|---|---|---|
| 4πη/s | ||||
| 1 | 0.641 | 0.888 | 1.076 | |
| 2 | 0.632 | 0.869 | 1.053 | |
| 3 | 0.629 | 0.863 | 1.046 | |
| Υ(1S) | Feed Down Fractions |
|---|---|
| Υ(1S) | 0.668 |
| Υ(2S) | 0.086 |
| Υ(3S) | 0.010 |
| χb(1P) | 0.170 |
| χb(2P) | 0.051 |
| χb(3P) | 0.015 |
| Υ(2S) | Feed Down Fractions |
|---|---|
| Υ(2S) | 0.604 |
| Υ(3S) | 0.043 |
| χb(2P) | 0.309 |
| χb(3P) | 0.044 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krouppa, B.; Strickland, M. Predictions for Bottomonia Suppression in 5.023 TeV Pb-Pb Collisions. Universe 2016, 2, 16. https://doi.org/10.3390/universe2030016
Krouppa B, Strickland M. Predictions for Bottomonia Suppression in 5.023 TeV Pb-Pb Collisions. Universe. 2016; 2(3):16. https://doi.org/10.3390/universe2030016
Chicago/Turabian StyleKrouppa, Brandon, and Michael Strickland. 2016. "Predictions for Bottomonia Suppression in 5.023 TeV Pb-Pb Collisions" Universe 2, no. 3: 16. https://doi.org/10.3390/universe2030016
APA StyleKrouppa, B., & Strickland, M. (2016). Predictions for Bottomonia Suppression in 5.023 TeV Pb-Pb Collisions. Universe, 2(3), 16. https://doi.org/10.3390/universe2030016





