Galaxy Clusters in Dark Matter Window: The Case of the Shapley Supercluster
Abstract
1. Introduction
- –
- Direct detection through collisions between DM and SM particles in terrestrial detectors;
- –
- Indirect detection via the observation of SM particles produced in DM annihilation or decay in space;
- –
- Production of DM particles in high-energy collisions using particle colliders.
2. GCs in SSC: Structure and DM Parameters
2.1. GCs: Structure and DM Distribution
2.2. -Ray and Neutrino Emission from DM Annihilation and Decay
2.3. CLUMPY and HDMSpectra Software for DM Annihilation/Decay Calculation
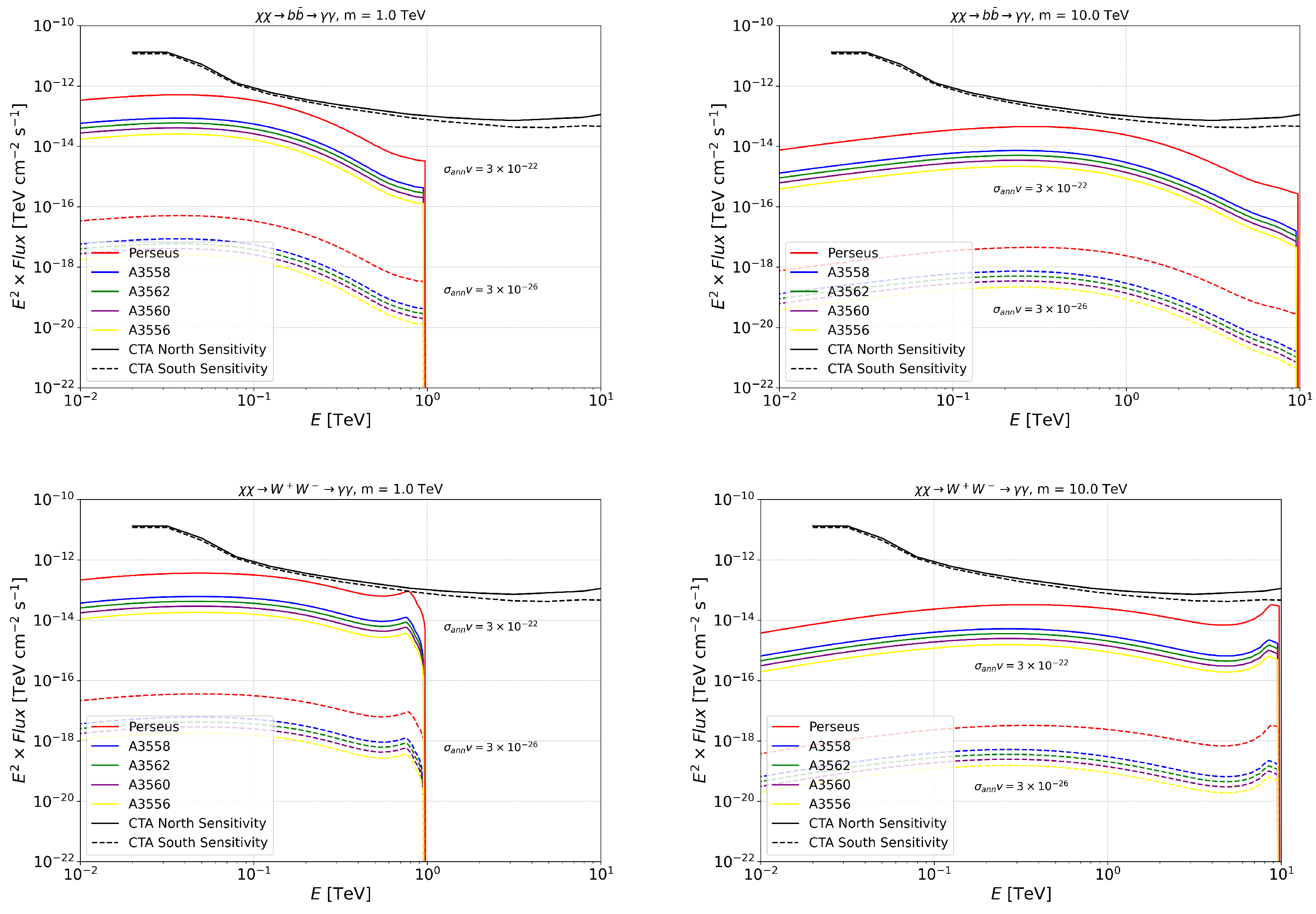
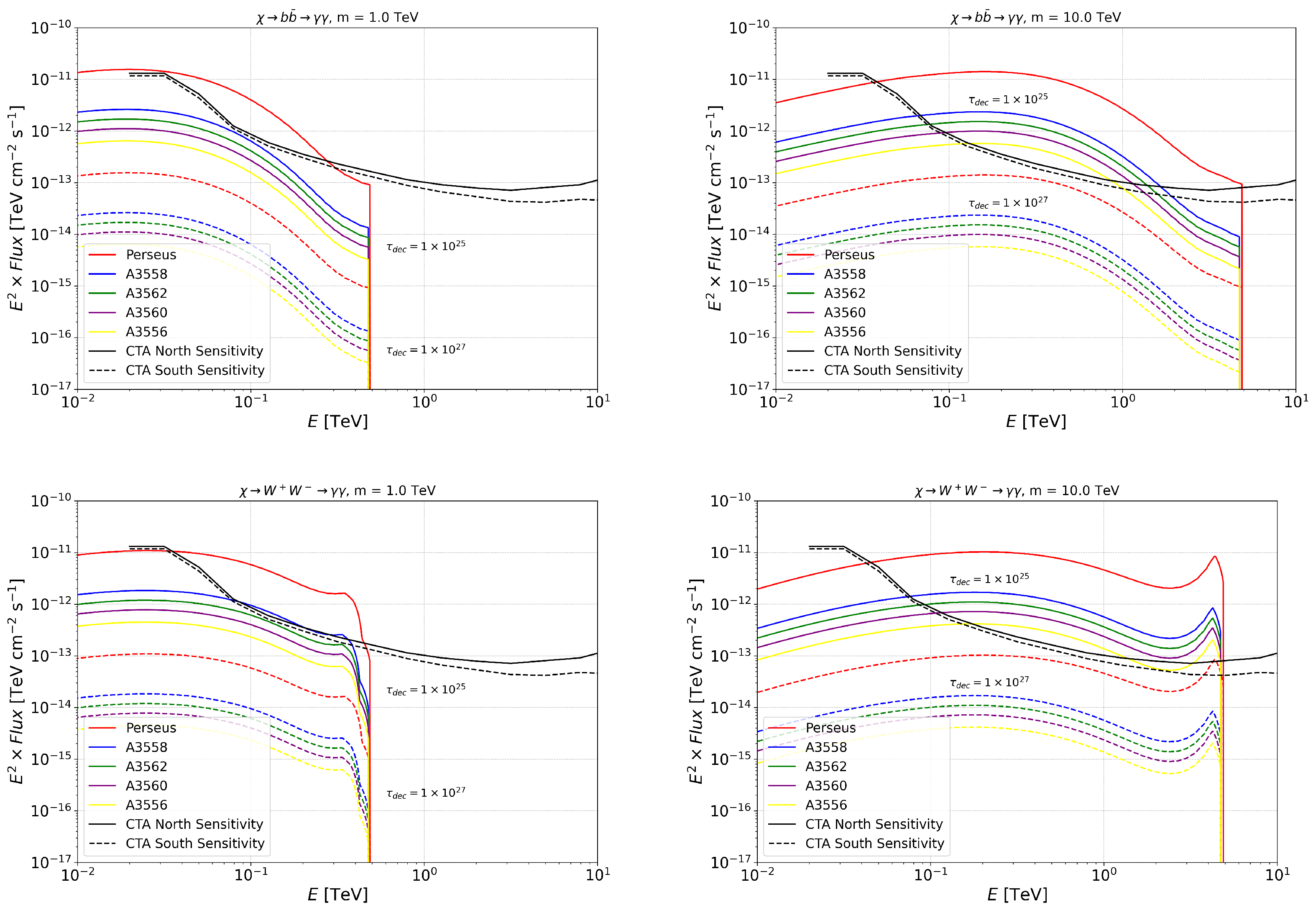
3. -Ray and Neutrino Spectral Fluxes from the Annihilation/Decay of WIMP DM in GCs
3.1. Expected -Ray Spectral Fluxes from the Annihilation/Decay of WIMP DM
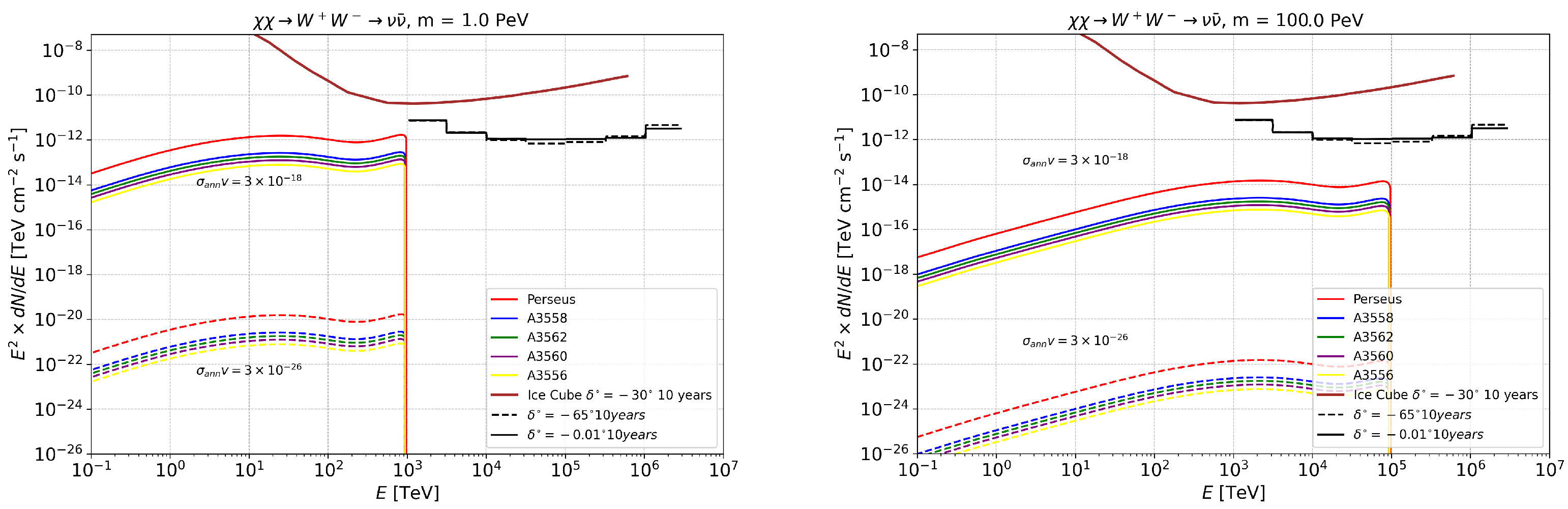
3.2. Expected Neutrino Fluxes and Detection Prospects with IceCube and KM3NeT
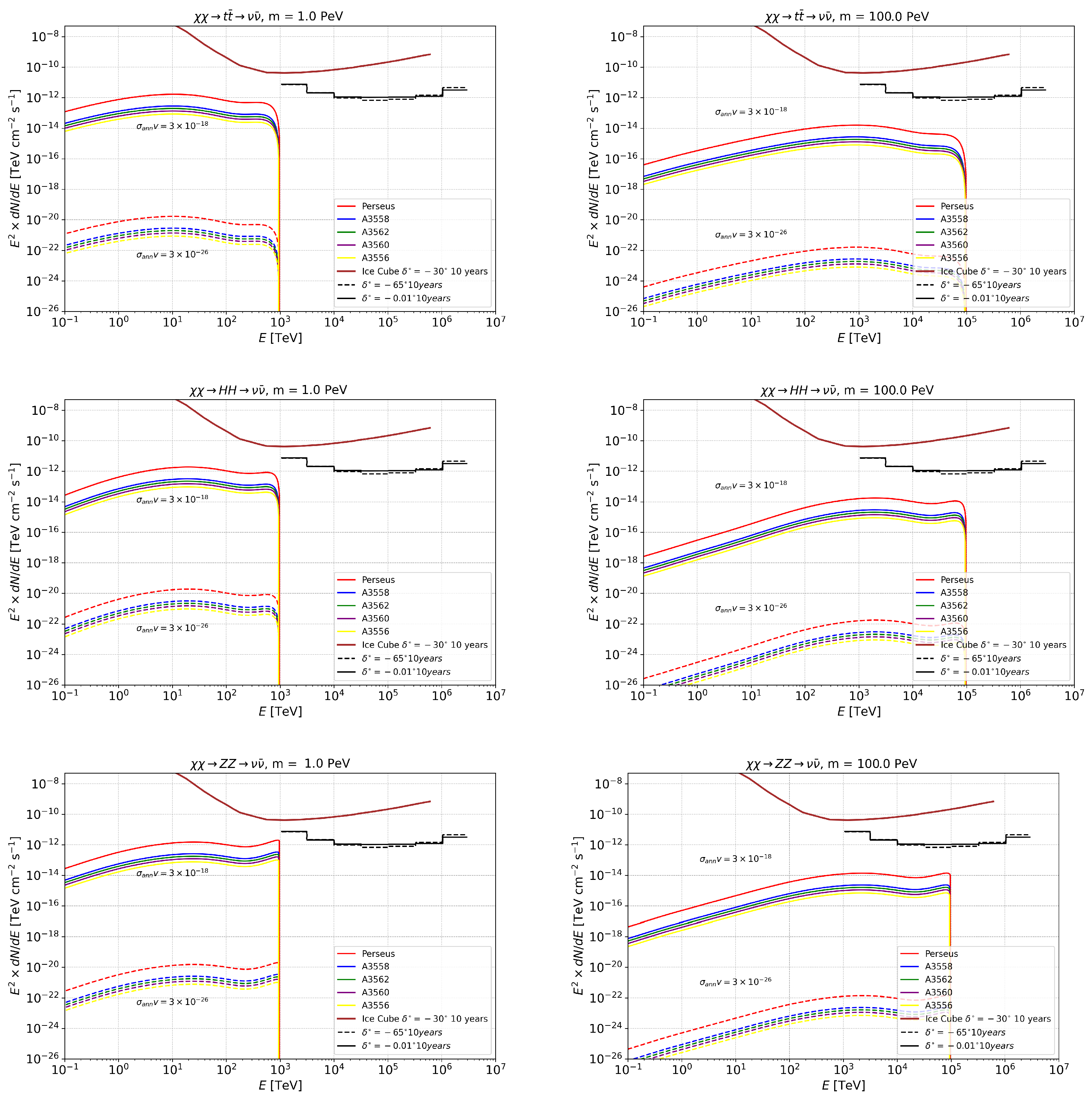
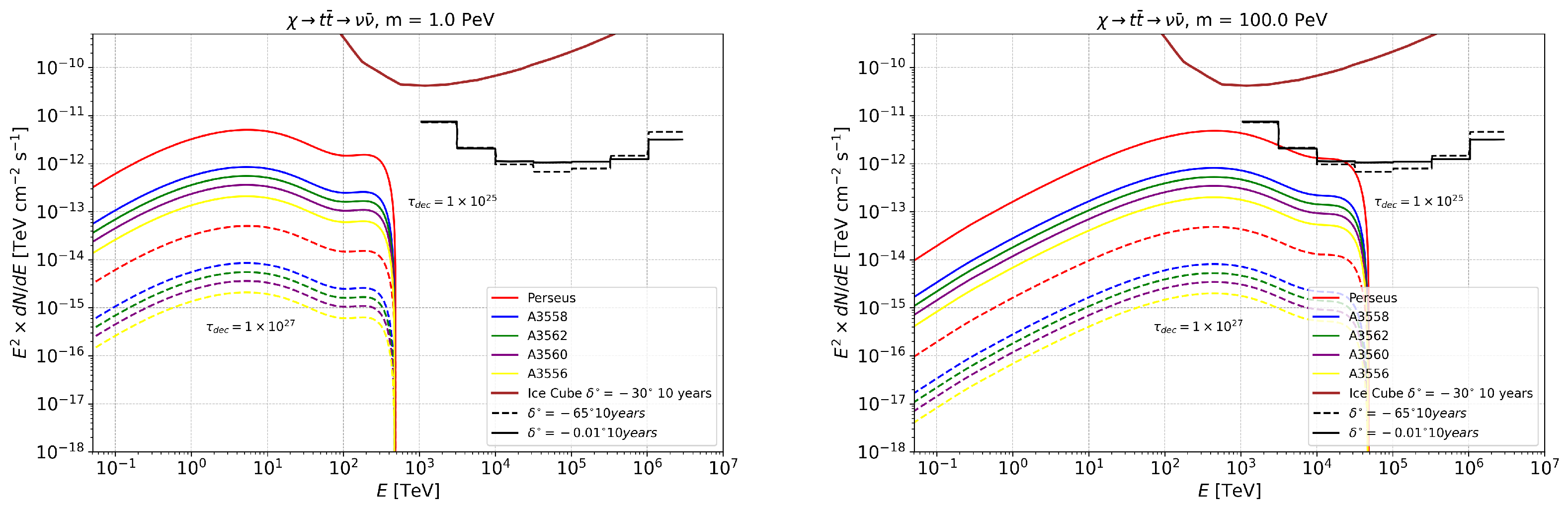
4. Annihilation and Decay Neutrino Spectral Fluxes for Superheavy (1–100 PeV) DM
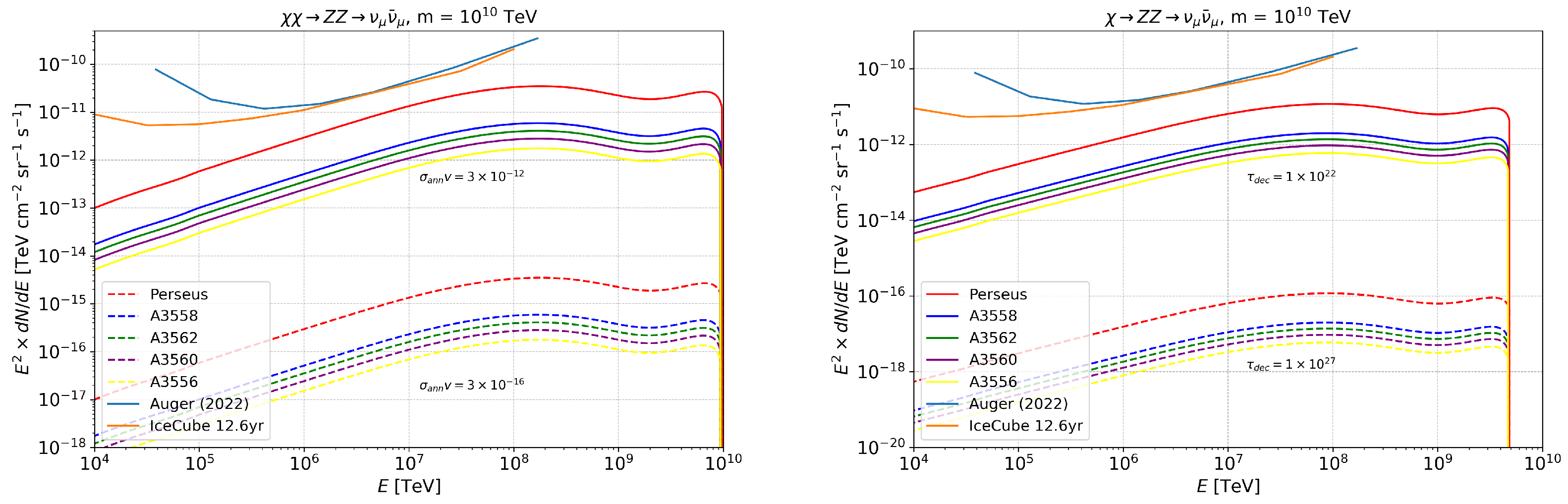
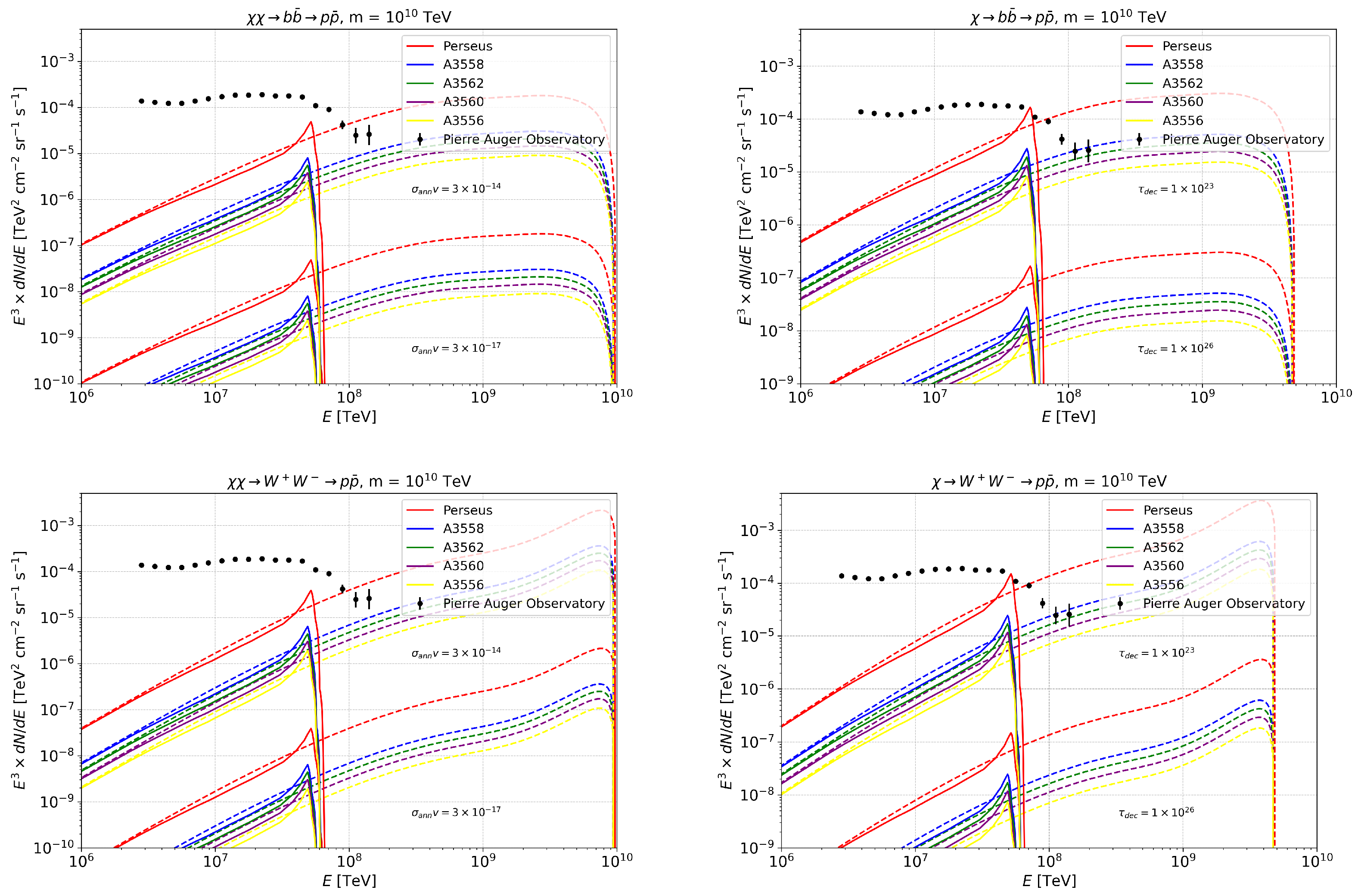
5. GC Neutrino and Cosmic Ray Proton Spectra for the Annihilation/Decay of 10 ZeV SHDM
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALP | axion-like particle |
| AMS-02 | Alpha Magnetic Spectrometer–02 |
| CLUMPY | CLUMPY code |
| CMB | Cosmic microwave background |
| CR | Cosmic ray |
| CTAO | Cherenkov Telescope Array Observatory |
| DAMPE | DArk Matter Particle Explorer |
| DM | Dark matter |
| EBL | Extragalactic background light |
| EECR | Extreme Energy Cosmic Ray |
| Fermi-LAT | Fermi Large-Area Telescope |
| GC | Galaxy cluster |
| GCOS | Global Cosmic-ray Observatory |
| GRAND | Giant Radio Array for Neutrino Detection |
| H.E.S.S. | High-Energy Stereoscopic System |
| HAWC | High-Altitude Water Cherenkov Observatory |
| HDMSpectra | HDMSpectra code |
| IACT | Imaging Atmospheric Cherenkov Telescope |
| IceCube | IceCube Neutrino Observatory |
| IceCube-Gen2 | Next-generation IceCube Neutrino Observatory |
| ICM | Intracluster medium |
| KM3NeT | Cubic Kilometer Neutrino Telescope |
| LHAASO | Large High-Altitude Air Shower Observatory |
| MAGIC | Major Atmospheric Gamma Imaging Cherenkov Telescopes |
| NFW | Navarro–Frenk–White profile |
| PAMELA | Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics |
| PAO | Pierre Auger Observatory |
| RHN | Right-handed neutrino |
| SHDM | Superheavy dark matter |
| SM | Standard Model |
| SSC | Shapley Supercluster |
| UHECR | Ultra-High-Energy Cosmic Ray |
| VERITAS | Very Energetic Radiation Imaging Telescope Array System |
| VHDM | Very Heavy Dark Matter |
| WIMP | Weakly Interacting Massive Particle |
Appendix A. γ-Ray and Neutrino Spectral Fluxes from the Annihilation/Decay of WIMP DM in GCs
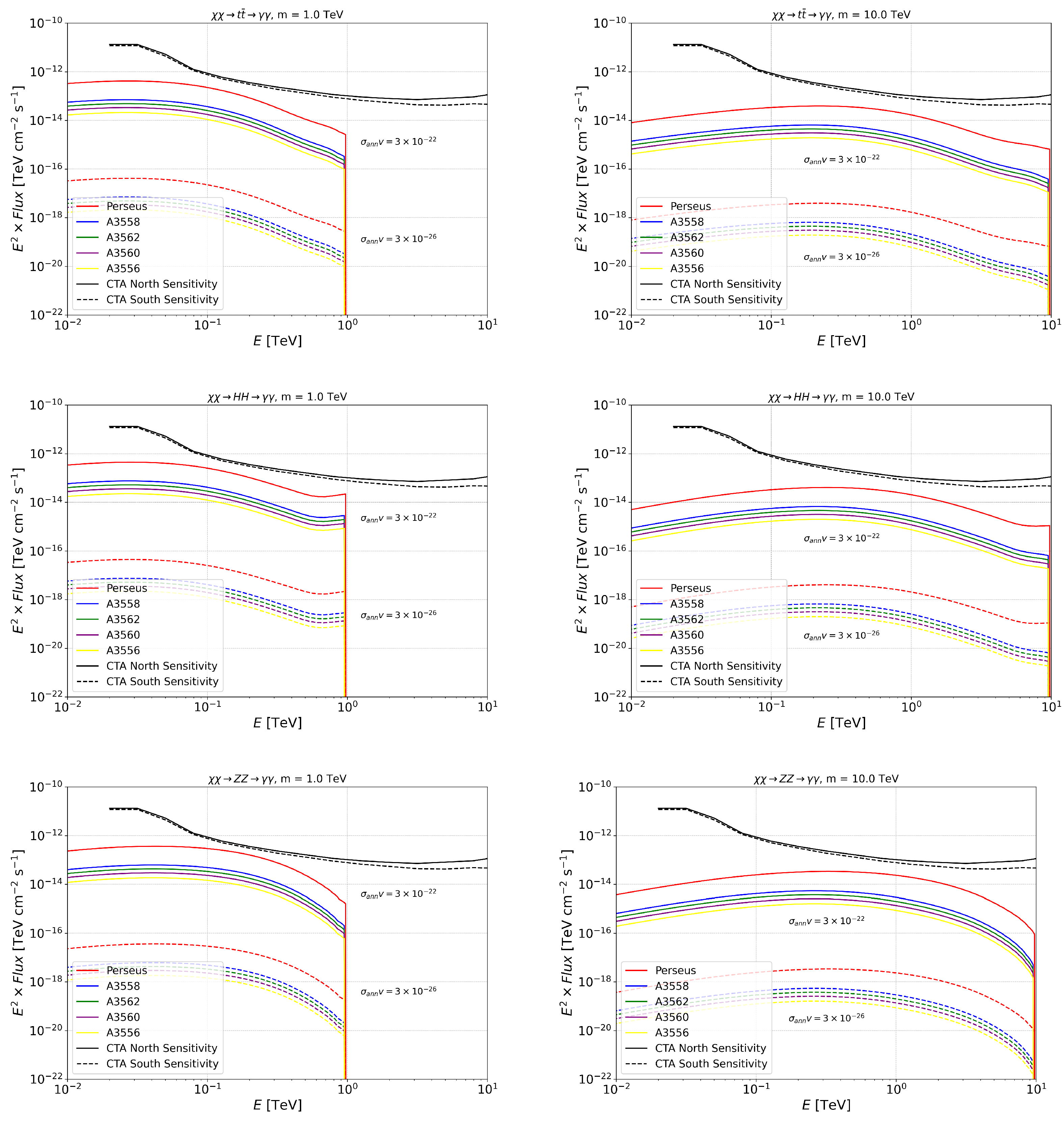
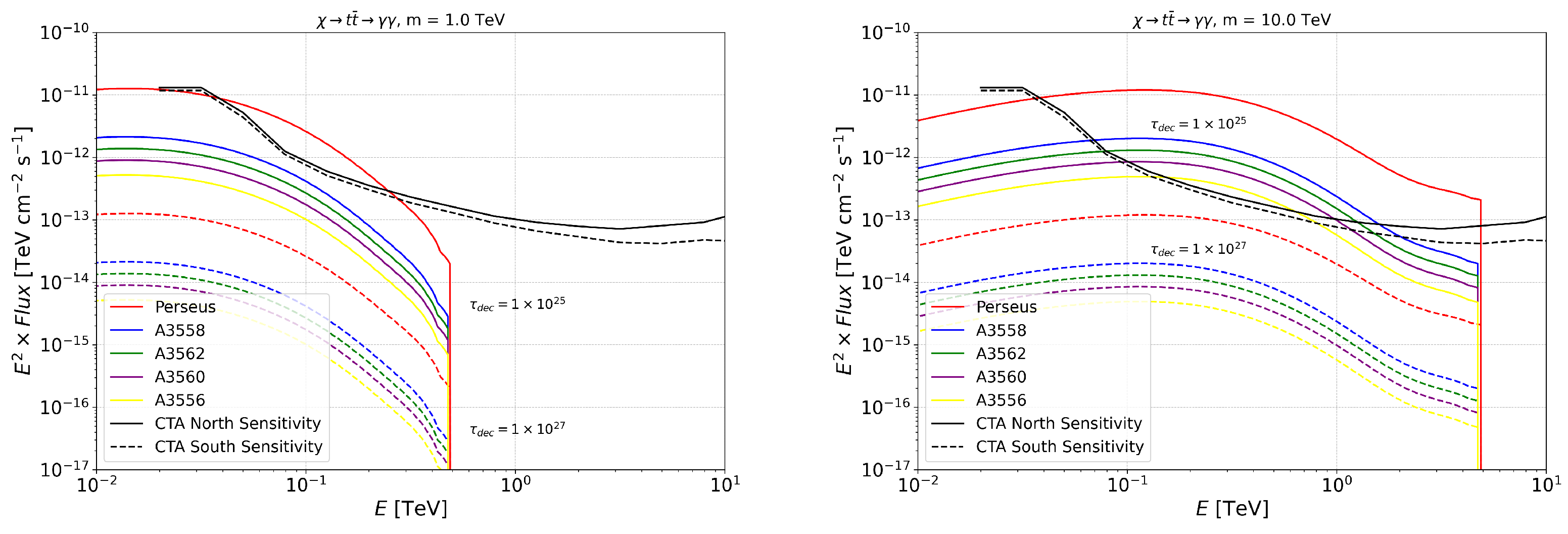
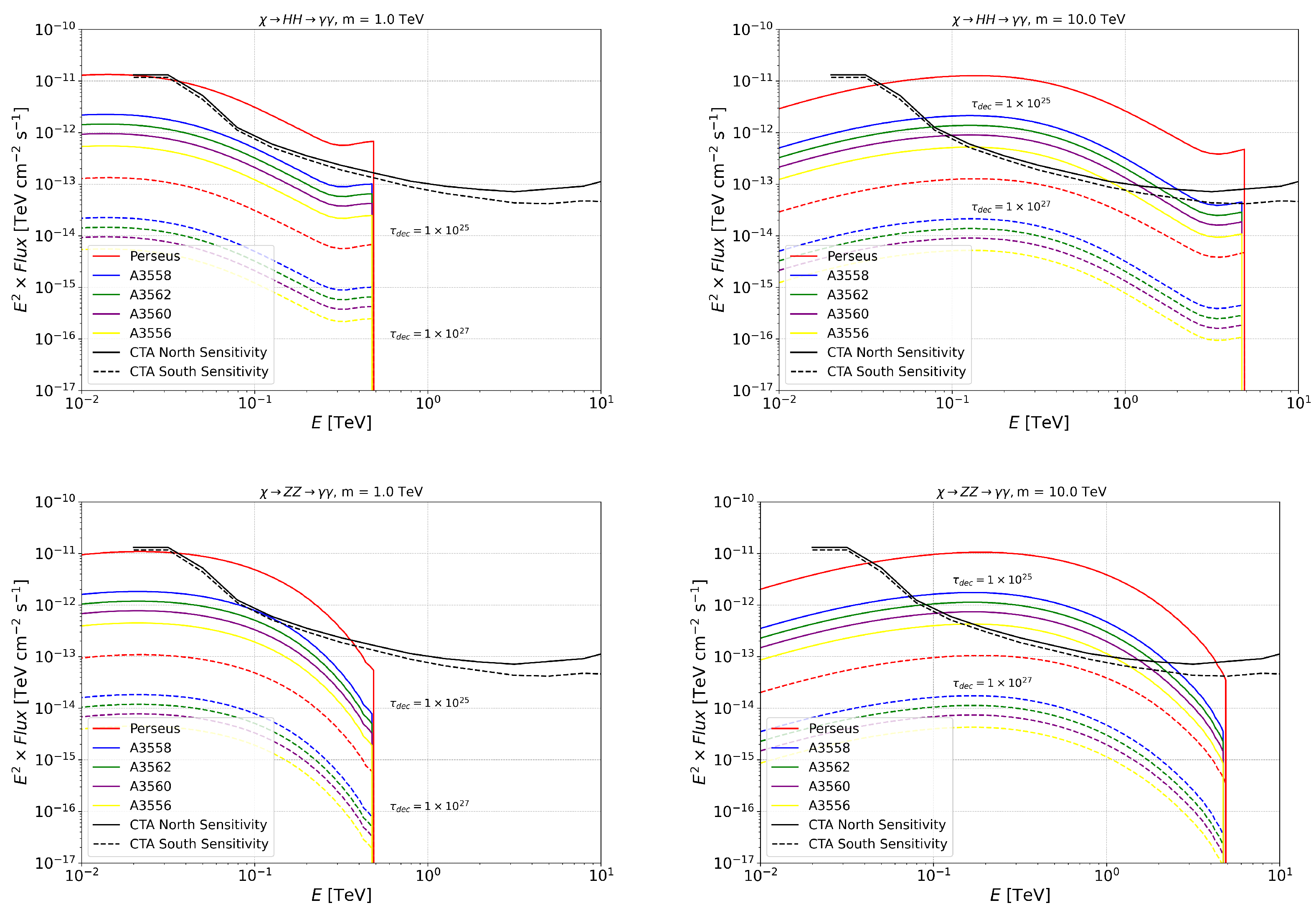
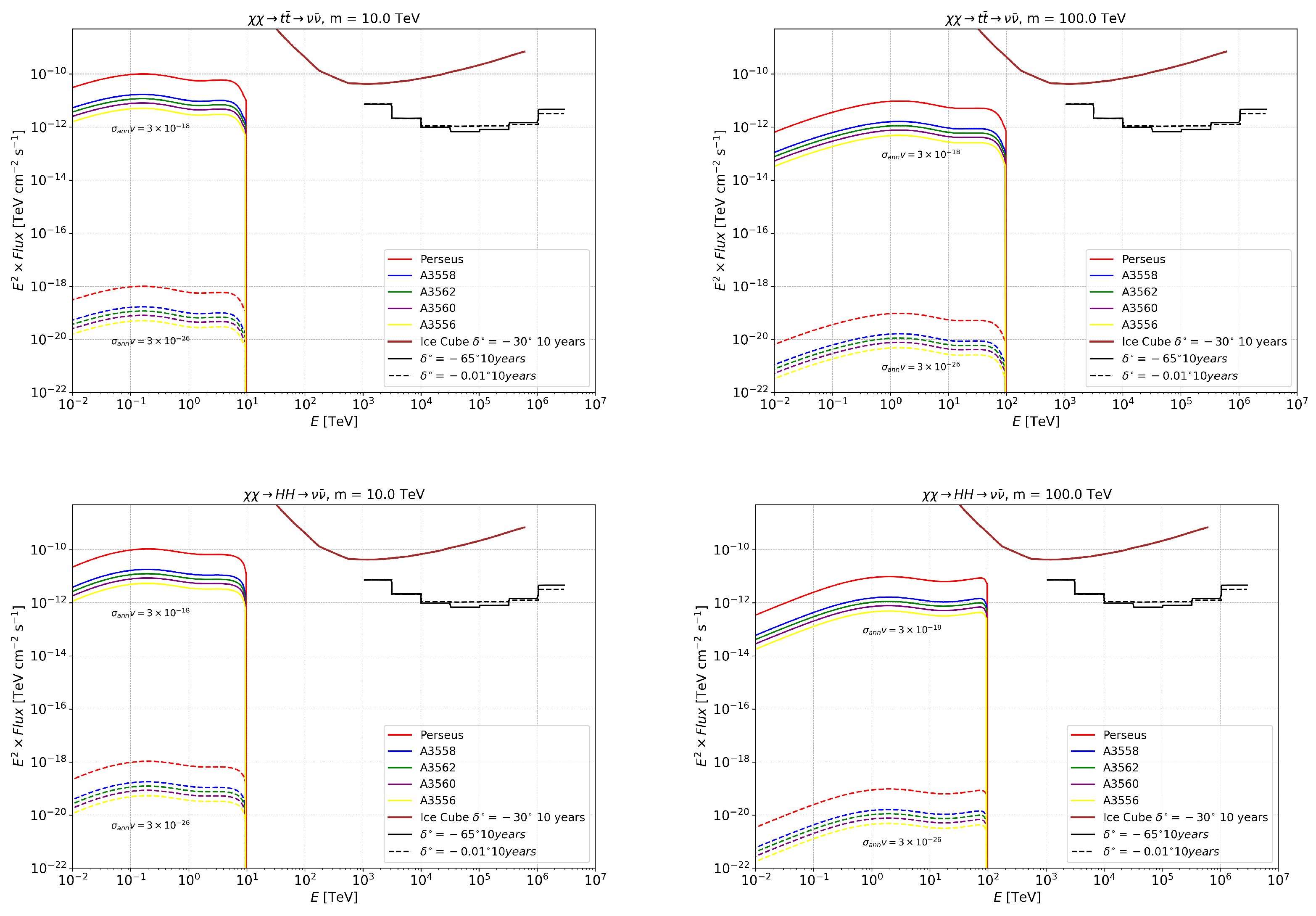


Appendix B. Annihilation and Decay Neutrino Spectral Fluxes for Superheavy (1–100 PeV) DM

Appendix C. GC Neutrino and Cosmic Ray Proton Spectra for Annihilation/Decay of 10 ZeV SHDM

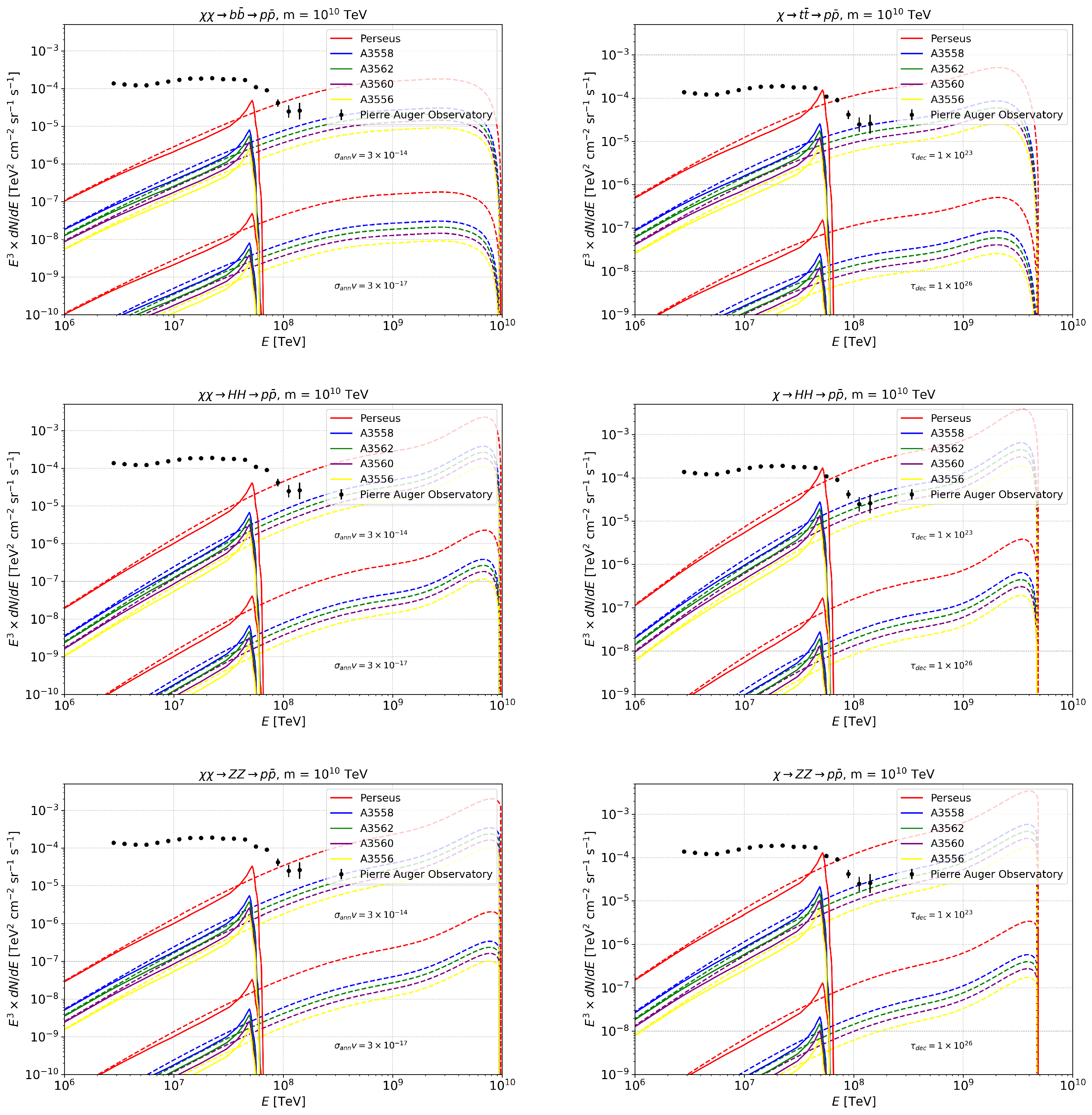
References
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Battaner, E.; et al. Planck intermediate results. XVI. Profile likelihoods for cosmological parameters. Astron. Astrophys. 2014, 566, A54. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Cushman, P.; Galbiati, C.; McKinsey, D.N.; Robertson, H.; Tait, T.M.P.; Bauer, D.; Borgland, A.; Cabrera, B.; Calaprice, F.; Cooley, J.; et al. Snowmass CF1 Summary: WIMP Dark Matter Direct Detection. arXiv 2013, arXiv:1310.8327. [Google Scholar] [CrossRef]
- Cirelli, M.; Corcella, G.; Hektor, A.; Hütsi, G.; Kadastik, M.; Panci, P.; Raidal, M.; Sala, F.; Strumia, A. PPPC 4 DM ID: A poor particle physicist cookbook for dark matter indirect detection. J. Cosmol. Astropart. Phys. 2011, 2011, 051. [Google Scholar] [CrossRef]
- Ciafaloni, P.; Comelli, D.; Riotto, A.; Sala, F.; Strumia, A.; Urbano, A. Weak corrections are relevant for dark matter indirect detection. J. Cosmol. Astropart. Phys. 2011, 2011, 019. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Williams, A.J. What next for the CMSSM and the NUHM: Improved prospects for superpartner and dark matter detection. J. High Energy Phys. 2014, 2014, 067. [Google Scholar] [CrossRef]
- Susskind, L. The Gauge Hierarchy Problem, Technicolor, Supersymmetry, and all that. Phys. Rep. 1984, 104, 181. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Williams, A.J. Prospects for dark matter searches in the pMSSM. J. High Energy Phys. 2015, 2015, 14. [Google Scholar] [CrossRef]
- Ackermann, M.; Albert, A.; Anderson, B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Bissaldi, E.; et al. Dark matter constraints from observations of 25 Milky Way satellite galaxies with the Fermi Large Area Telescope. Phys. Rev. D 2014, 89, 042001. [Google Scholar] [CrossRef]
- Abdalla, H.; Aharonian, F.; Benkhali, F.; Angüner, E.; Armand, C.; Ashkar, H.; Backes, M.; Baghmanyan, V.; Martins, V.B.; Batzofin, R.; et al. Search for dark matter annihilation signals in the H.E.S.S. inner galaxy survey. Phys. Rev. Lett. 2022, 129, 111101. [Google Scholar] [CrossRef] [PubMed]
- MAGIC Collaboration. Limits to dark matter annihilation cross-section from a combined analysis of MAGIC and Fermi-LAT observations of dwarf satellite galaxies. J. Cosmol. Astropart. Phys. 2016, 2016, 39. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Agarwalla, S.K.; Aguilar, J.A.; Ahlers, M.; Alameddine, J.M.; Amin, N.M.; Andeen, K.; Anton, G.; et al. Search for neutrino lines from dark matter annihilation and decay with IceCube. Phys. Rev. D 2023, 108, 102004. [Google Scholar] [CrossRef]
- Albert, A.; André, M.; Anghinolfi, M.; Ardid, M.; Aubert, J.J.; Aublin, J.; Baret, B.; Basa, S.; Belhorma, B.; Bertin, V.; et al. Combined search for neutrinos from dark matter self-annihilation in the Galactic Center with ANTARES and IceCube. Phys. Rev. D 2020, 102, 082002. [Google Scholar] [CrossRef]
- Kumar, J.; Sandick, P.; Teng, F.; Yamamoto, T. Gamma-ray Signals from Dark Matter Annihilation Via Charged Mediators. Phys. Rev. D 2016, 94, 015022. [Google Scholar] [CrossRef]
- Bergström, L.; Edsjö, J.; Ullio, P. Spectral gamma-ray signatures of cosmological dark matter annihilations. Phys. Rev. Lett. 2001, 87, 251301. [Google Scholar] [CrossRef]
- Bell, N.F.; Dent, J.B.; Jacques, T.D.; Weiler, T.J. Dark matter annihilation signatures from electroweak bremsstrahlung. Phys. Rev. D 2011, 84, 103517. [Google Scholar] [CrossRef]
- Domínguez, A.; Finke, J.D.; Prada, F.; Primack, J.R.; Kitaura, F.S.; Siana, B.; Paneque, D. Detection of the Cosmic γ-Ray Horizon from Multiwavelength Observations of Blazars. Astrophys. J. 2013, 770, 77. [Google Scholar] [CrossRef]
- Domínguez, A.; Østergaard Kirkeberg, P.; Wojtak, R.; Saldana-Lopez, A.; Desai, A.; Primack, J.R.; Finke, J.; Ajello, M.; Pérez-González, P.G.; Paliya, V.S.; et al. A new derivation of the Hubble constant from γ-ray attenuation using improved optical depths for the Fermi and CTA era. Mon. Not. R. Astron. Soc. 2024, 527, 4632–4642. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Constraining Dark Matter Models from a Combined Analysis of Milky Way Satellites with the Fermi Large Area Telescope. Phys. Rev. Lett. 2011, 107, 241302. [Google Scholar] [CrossRef] [PubMed]
- H.E.S.S. Collaboration; Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barnacka, A.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Becherini, Y.; et al. H.E.S.S. constraints on dark matter annihilations towards the sculptor and carina dwarf galaxies. Astropart. Phys. 2011, 34, 608–616. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; et al. Constraints on cosmological dark matter annihilation from the Fermi-LAT isotropic diffuse gamma-ray measurement. J. Cosmol. Astropart. Phys. 2010, 2010, 14. [Google Scholar] [CrossRef]
- Aleksić, J.; Alvarez, E.A.; Antonelli, L.A.; Antoranz, P.; Asensio, M.; Backes, M.; Barrio, J.A.; Bastieri, D.; Becerra González, J.; Bednarek, W.; et al. Searches for dark matter annihilation signatures in the Segue 1 satellite galaxy with the MAGIC-I telescope. J. Cosmol. Astropart. Phys. 2011, 2011, 35. [Google Scholar] [CrossRef]
- Beacom, J.F.; Bell, N.F.; Mack, G.D. Upper Bound on the Dark Matter Total Annihilation Cross Section. Phys. Rev. Lett. 2007, 99, 231301. [Google Scholar] [CrossRef] [PubMed]
- Yüksel, H.; Horiuchi, S.; Beacom, J.F.; Ando, S. Neutrino constraints on the dark matter total annihilation cross section. Phys. Rev. D 2007, 76, 123506. [Google Scholar] [CrossRef]
- Borah, D.; Das, N.; Okada, N.; Sarmah, P. Possible origin of the KM3-230213A neutrino event from dark matter decay. Phys. Rev. D 2025, 111, 123022. [Google Scholar] [CrossRef]
- Jho, Y.; Park, S.C.; Shin, C.S. Superheavy Supersymmetric Dark Matter for the origin of KM3NeT Ultra-High Energy signal. arXiv 2025, arXiv:2503.18737. [Google Scholar] [CrossRef]
- Murase, K.; Narita, Y.; Yin, W. Superheavy dark matter from the natural inflation in light of the highest-energy astroparticle events. arXiv 2025, arXiv:2504.15272. [Google Scholar] [CrossRef]
- Song, D.; Murase, K.; Kheirandish, A. Constraining decaying very heavy dark matter from galaxy clusters with 14 year Fermi-LAT data. J. Cosmol. Astropart. Phys. 2024, 2024, 24. [Google Scholar] [CrossRef]
- Lisanti, M.; Mishra-Sharma, S.; Rodd, N.L.; Safdi, B.R. Search for Dark Matter Annihilation in Galaxy Groups. Phys. Rev. Lett. 2018, 120, 101101. [Google Scholar] [CrossRef] [PubMed]
- Weng, Z.; Krasnopevtsev, D.; Kounine, A. Origins of cosmic positrons and electrons. Adv. Space Res. 2024, 74, 4333–4338. [Google Scholar] [CrossRef]
- Kachelrieß, M.; Ostapchenko, S.; Tjemsland, J. Revisiting cosmic ray antinuclei fluxes with a new coalescence model. J. Cosmol. Astropart. Phys. 2020, 2020, 48. [Google Scholar] [CrossRef]
- Abdul Halim, A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Allison, P.; Almeida Cheminant, K.; Almela, A.; Alvarez-Muñiz, J.; Ammerman Yebra, J.; Anastasi, G.A.; et al. A Catalog of the Highest-energy Cosmic Rays Recorded during Phase I of Operation of the Pierre Auger Observatory. Astrophys. J. Suppl. Ser. 2023, 264, 50. [Google Scholar] [CrossRef]
- Telescope Array Collaboration; Abbasi, R.U.; Allen, M.G.; Arimura, R.; Belz, J.W.; Bergman, D.R.; Blake, S.A.; Shin, B.K.; Buckland, I.J.; Cheon, B.G.; et al. An extremely energetic cosmic ray observed by a surface detector array. Science 2023, 382, 903–907. [Google Scholar] [CrossRef] [PubMed]
- Prechelt, R.; Wissel, S.A.; Romero-Wolf, A.; Burch, C.; Gorham, P.W.; Allison, P.; Alvarez-Muñiz, J.; Banerjee, O.; Batten, L.; Beatty, J.J.; et al. Analysis of a tau neutrino origin for the near-horizon air shower events observed by the fourth flight of the Antarctic Impulsive Transient Antenna. Phys. Rev. D 2022, 105, 042001. [Google Scholar] [CrossRef]
- Aloisio, R. Pierre Auger Observatory and Super Heavy Dark Matter. EPJ Web Conf. 2023, 280, 07001. [Google Scholar] [CrossRef]
- Creque-Sarbinowski, C.; Hyde, J.; Kamionkowski, M. High-energy astrophysical neutrinos from cosmic strings. Phys. Rev. D 2023, 107, 123019. [Google Scholar] [CrossRef]
- Das, S.; Murase, K.; Fujii, T. Revisiting ultrahigh-energy constraints on decaying superheavy dark matter. Phys. Rev. D 2023, 107, 103013. [Google Scholar] [CrossRef]
- Abreu, P.; Aglietta, M.; Albury, J.M.; Allekotte, I.; Almeida Cheminant, K.; Almela, A.; Aloisio, R.; Alvarez-Muñiz, J.; Alves Batista, R.; Ammerman Yebra, J.; et al. Cosmological implications of photon-flux upper limits at ultrahigh energies in scenarios of Planckian-interacting massive particles for dark matter. Phys. Rev. D 2023, 107, 042002. [Google Scholar] [CrossRef]
- Chianese, M.; Fiorillo, D.F.G.; Hajjar, R.; Miele, G.; Morisi, S.; Saviano, N. Heavy decaying dark matter at future neutrino radio telescopes. J. Cosmol. Astropart. Phys. 2021, 2021, 074. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Valera, V.B.; Bustamante, M.; Winter, W. Searches for dark matter decay with ultrahigh-energy neutrinos endure backgrounds. Phys. Rev. D 2023, 108, 103012. [Google Scholar] [CrossRef]
- Das, S.; Carpio, J.A.; Murase, K. Probing superheavy dark matter through lunar radio observations of ultrahigh-energy neutrinos and the impacts of neutrino cascades. Phys. Rev. D 2025, 111, 083007. [Google Scholar] [CrossRef]
- Sarmah, P.; Das, N.; Borah, D.; Chakraborty, S.; Mehta, P. Constraining the superheavy dark matter origin of ultrahigh-energy cosmic rays with the Amaterasu event. Phys. Rev. D 2025, 111, 083048. [Google Scholar] [CrossRef]
- Malyshev, D.; Zadorozhna, L.; Bidasyuk, Y.; Santangelo, A.; Ruchayskiy, O. Constraints on axion-like particles from active galactic nuclei seen through galaxy clusters. Nat. Astron. 2025. [CrossRef]
- Edwards, T.D.P.; Chianese, M.; Kavanagh, B.J.; Nissanke, S.M.; Weniger, C. Unique Multimessenger Signal of QCD Axion Dark Matter. Phys. Rev. Lett. 2020, 124, 161101. [Google Scholar] [CrossRef]
- Mastrototaro, L.; Carenza, P.; Chianese, M.; Fiorillo, D.F.G.; Miele, G.; Mirizzi, A.; Montanino, D. Constraining axion-like particles with the diffuse gamma-ray flux measured by the Large High Altitude Air Shower Observatory. Eur. Phys. J. C 2022, 82, 1012. [Google Scholar] [CrossRef]
- Quintana, H.; Ramirez, A.; Melnick, J.; Raychaudhury, S.; Slezak, E. The Shapley Supercluster. I. Spectroscopic Observations in the Central Region. Astron. J. 1995, 110, 463. [Google Scholar] [CrossRef]
- Proust, D.; Quintana, H.; Carrasco, E.R.; Reisenegger, A.; Slezak, E.; Muriel, H.; Dünner, R.; Sodré, L.; Drinkwater, M.J.; Parker, Q.A.; et al. Structure and dynamics of the Shapley Supercluster—Velocity catalogue, general morphology and mass. Astron. Astrophys. 2006, 447, 133–144. [Google Scholar] [CrossRef]
- Venturi, T.; Bardelli, S.; Morganti, R.; Hunstead, R.W. Radio properties of the Shapley Concentration—III. Merging clusters in the A3558 complex. Mon. Not. R. Astron. Soc. 2000, 314, 594–610. [Google Scholar] [CrossRef]
- Di Gennaro, G.; Venturi, T.; Giacintucci, S.; Brüggen, M.; Bulbul, E.; Sanders, J.; Liu, A.; Zhang, X.; Trehaeven, K.; Dallacasa, D.; et al. Cosmic dance in the Shapley Concentration Core: II. The uGMRT-MeerKAT view of filaments in the brightest cluster galaxies and tailed radio galaxies in the A3528 cluster complex. Astron. Astrophys. 2025, 694, A28. [Google Scholar] [CrossRef]
- Babur, V.; Gugnin, O.; Hnatyk, B. Prospects for Multimessenger Observations of the Shapley Supercluster. Universe 2025, 11, 239. [Google Scholar] [CrossRef]
- Charbonnier, A.; Combet, C.; Maurin, D. CLUMPY: A code for γ-ray signals from dark matter structures. Comput. Phys. Commun. 2012, 183, 656–668. [Google Scholar] [CrossRef]
- Bonnivard, V.; Hütten, M.; Nezri, E.; Charbonnier, A.; Combet, C.; Maurin, D. CLUMPY: Jeans analysis, γ-ray and ν fluxes from dark matter (sub-)structures. Comput. Phys. Commun. 2016, 200, 336–349. [Google Scholar] [CrossRef]
- Hütten, M.; Combet, C.; Maurin, D. CLUMPY v3: γ-ray and ν signals from dark matter at all scales. Comput. Phys. Commun. 2019, 235, 336–345. [Google Scholar] [CrossRef]
- Bauer, C.W.; Rodd, N.L.; Webber, B.R. Dark matter spectra from the electroweak to the Planck scale. J. High Energy Phys. 2021, 2021, 121. [Google Scholar] [CrossRef]
- Voit, G.M. Tracing cosmic evolution with clusters of galaxies. Rev. Mod. Phys. 2005, 77, 207–258. [Google Scholar] [CrossRef]
- Combet, C.; Maurin, D.; Nezri, E.; Pointecouteau, E.; Hinton, J.A.; White, R. Decaying dark matter: Stacking analysis of galaxy clusters to improve on current limits. Phys. Rev. D 2012, 85, 063517. [Google Scholar] [CrossRef][Green Version]
- Sánchez-Conde, M.A.; Prada, F. The flattening of the concentration–mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 2014, 442, 2271. [Google Scholar] [CrossRef]
- Pinzke, A.; Pfrommer, C.; Bergström, L. Gamma-rays from dark matter annihilations strongly constrain the substructure in halos. Phys. Rev. Lett. 2009, 103, 181302. [Google Scholar] [CrossRef]
- Pinzke, A.; Pfrommer, C.; Bergström, L. Prospects of detecting gamma-ray emission from galaxy clusters: Cosmic rays and dark matter annihilations. Phys. Rev. D 2011, 84, 123509. [Google Scholar] [CrossRef]
- Cirelli, M.; Moulin, E.; Panci, P.; Serpico, P.D.; Viana, A. Gamma ray constraints on Decaying Dark Matter. Phys. Rev. D 2012, 86, 083506. [Google Scholar] [CrossRef]
- Higuchi, Y.; Okabe, N.; Merluzzi, P.; Haines, C.P.; Busarello, G.; Grado, A.; Mercurio, A. Shapley supercluster survey: Mapping the dark matter distribution. Mon. Not. R. Astron. Soc. 2020, 497, 52–66. [Google Scholar] [CrossRef]
- Edge, A.; Stewart, G.; Fabian, A. Properties of cooling flows in a flux-limited sample of clusters of galaxies. Mon. Not. R. Astron. Soc. 1992, 258, 177. [Google Scholar] [CrossRef]
- Zhao, H. Analytical models for galactic nuclei. Mon. Not. R. Astron. Soc. 1996, 278, 488–496. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Ando, S.; Nagai, D. Fermi-LAT constraints on dark matter annihilation cross section from observations of the Fornax cluster. J. Cosmol. Astropart. Phys. 2012, 2012, 17. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Boddy, K.K.; Kumar, J.; Strigari, L.E. Effective J-factor of the Galactic Center for velocity-dependent dark matter annihilation. Phys. Rev. D 2018, 98, 063012. [Google Scholar] [CrossRef]
- Evans, N.W.; Sanders, J.L.; Geringer-Sameth, A. Simple J-factors and D-factors for indirect dark matter detection. Phys. Rev. D 2016, 93, 103512. [Google Scholar] [CrossRef]
- Cirelli, M. Indirect searches for dark matter. Pramana 2012, 79, 1021. [Google Scholar] [CrossRef]
- Acciari, V.A.; Ansoldi, S.; Antonelli, L.A.; Arbet Engels, A.; Arcaro, C.; Baack, D.; Babić, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; et al. Constraining dark matter lifetime with a deep gamma-ray survey of the Perseus galaxy cluster with MAGIC. Phys. Dark Universe 2018, 22, 38–47. [Google Scholar] [CrossRef]
- Abe, K.; Abe, S.; Acero, F.; Acharyya, A.; Adam, R.; Aguasca-Cabot, A.; Agudo, I.; Aguirre-Santaella, A.; Alfaro, J.; Alfaro, R.; et al. Prospects for γ-ray observations of the Perseus galaxy cluster with the Cherenkov Telescope Array. J. Cosmol. Astropart. Phys. 2024, 2024, 004. [Google Scholar] [CrossRef]
- Sommerfeld, A. Über die Beugung und Bremsung der Elektronen. Ann. Der Phys. 1931, 403, 257. [Google Scholar] [CrossRef]
- Finkbeiner, D.P.; Goodenough, L.; Slatyer, T.R.; Vogelsberger, M.; Weiner, N. Consistent scenarios for cosmic-ray excesses from Sommerfeld-enhanced dark matter annihilation. J. Cosmol. Astropart. Phys. 2011, 2011, 002. [Google Scholar] [CrossRef][Green Version]
- Facchinetti, G.; Stref, M.; Lacroix, T.; Lavalle, J.; Pérez-Romero, J.; Maurin, D.; Sánchez-Conde, M.A. Analytical insight into dark matter subhalo boost factors for Sommerfeld-enhanced s- and p-wave γ-ray signals. J. Cosmol. Astropart. Phys. 2023, 2023, 004. [Google Scholar] [CrossRef]
- Chan, M.H. Sommerfeld enhancement of invisible dark matter annihilation in galaxies and galaxy clusters. Astropart. Phys. 2016, 80, 1–7. [Google Scholar] [CrossRef]
- Slatyer, T.R.; Toro, N.; Weiner, N. Sommerfeld-enhanced annihilation in dark matter substructure: Consequences for constraints on cosmic-ray excesses. Phys. Rev. D 2012, 86, 083534. [Google Scholar] [CrossRef]
- Ando, S.; Ishiyama, T.; Hiroshima, N. Halo Substructure Boosts to the Signatures of Dark Matter Annihilation. Galaxies 2019, 7, 68. [Google Scholar] [CrossRef]
- Bovy, J. Substructure boosts to dark matter annihilation from Sommerfeld enhancement. Phys. Rev. D 2009, 79, 083539. [Google Scholar] [CrossRef][Green Version]
- Hiroshima, N.; Ando, S.; Ishiyama, T. Modeling evolution of dark matter substructure and annihilation boost. Phys. Rev. D 2018, 97, 123002. [Google Scholar] [CrossRef]
- Aiello, S.; Albert, A.; Alshamsi, M.; Garre, S.A.; Aly, Z.; Ambrosone, A.; Ameli, F.; Andre, M.; Androutsou, E.; Anguita, M.; et al. Differential Sensitivity of the KM3NeT/ARCA detector to a diffuse neutrino flux and to point-like source emission: Exploring the case of the Starburst Galaxies. Astropart. Phys. 2024, 162, 102990. [Google Scholar] [CrossRef]
- Berezinsky, V.; Gazizov, A.; Grigorieva, S. On astrophysical solution to ultrahigh energy cosmic rays. Phys. Rev. D 2006, 74, 043005. [Google Scholar] [CrossRef]
- Niechciol, M.; Pierre Auger Collaboration. Latest results from the searches for UHE photons and neutrinos at the Pierre Auger Observatory. PoS(ICRC2023) 2023, 1488. Available online: https://pos.sissa.it/444/1488/pdf (accessed on 30 July 2025).
- Roulet, E. Combined fit above 0.1 EeV to the cosmic-ray spectrum and composition measured with the Pierre Auger Observatory. arXiv 2025, arXiv:2507.10806. [Google Scholar] [CrossRef]
- Merloni, A.; Lamer, G.; Liu, T.; Ramos-Ceja, M.E.; Brunner, H.; Bulbul, E.; Dennerl, K.; Doroshenko, V.; Freyberg, M.J.; Friedrich, S.; et al. The SRG/eROSITA all-sky survey. First X-ray catalogues and data release of the western Galactic hemisphere. Astron. Astrophys. 2024, 682, A34. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Finkbeiner, D.P.; Slatyer, T.R.; Weiner, N. A theory of dark matter. Phys. Rev. D 2009, 79, 015014. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Albury, J.; Allekotte, I.; Almela, A.; Alvarez Castillo, J.; Alvarez-Muñiz, J.; Alves Batista, R.; Anastasi, G.; et al. Measurement of the cosmic-ray energy spectrum above 2.5 × 1018 eV using the Pierre Auger Observatory. Phys. Rev. D 2020, 102, 062005. [Google Scholar] [CrossRef]
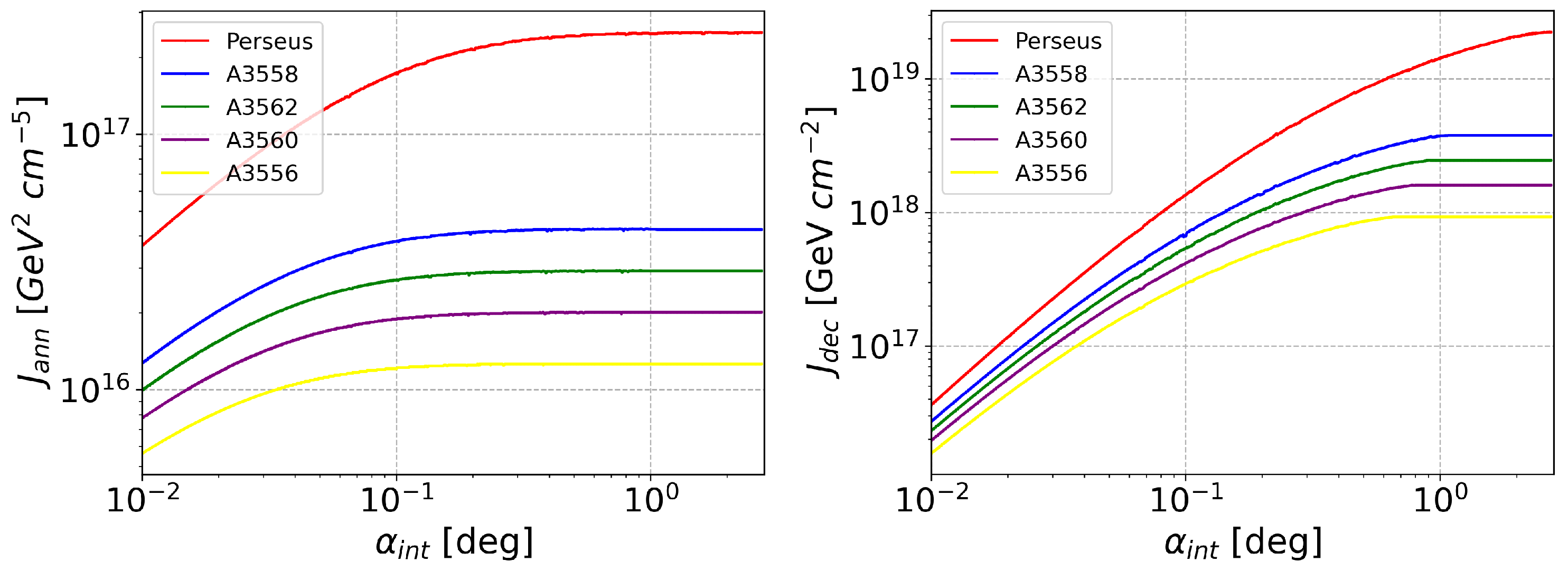
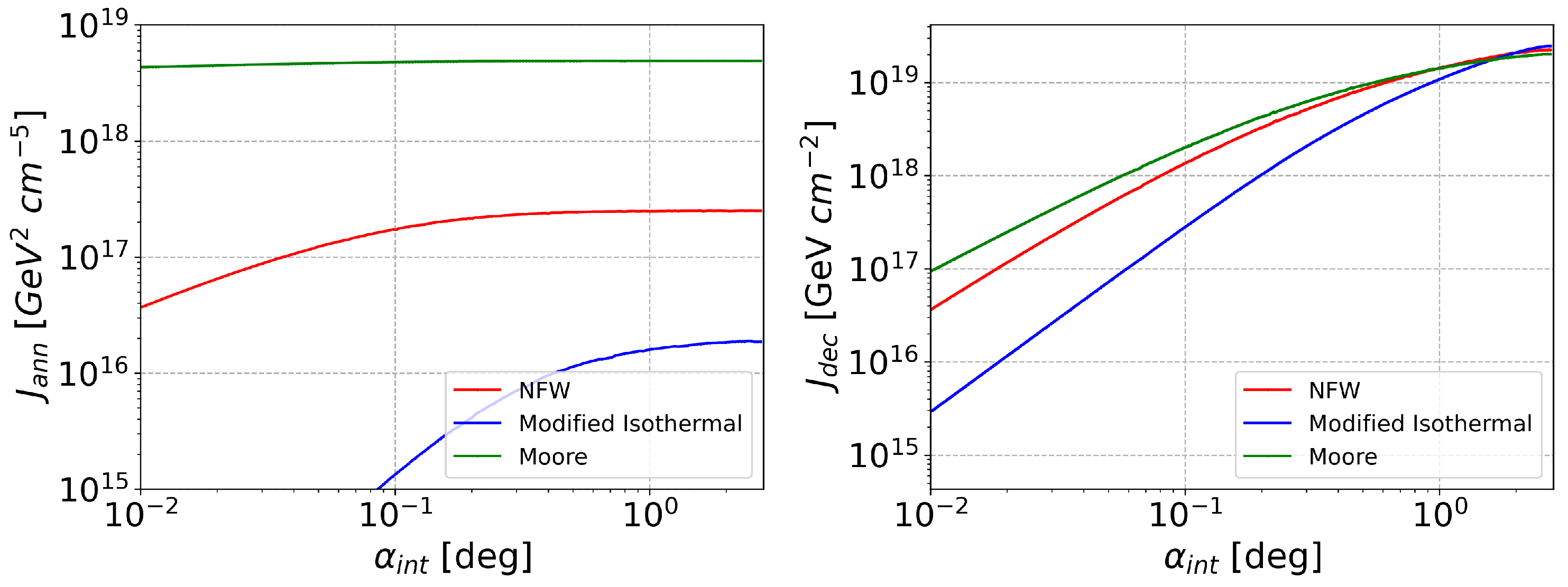
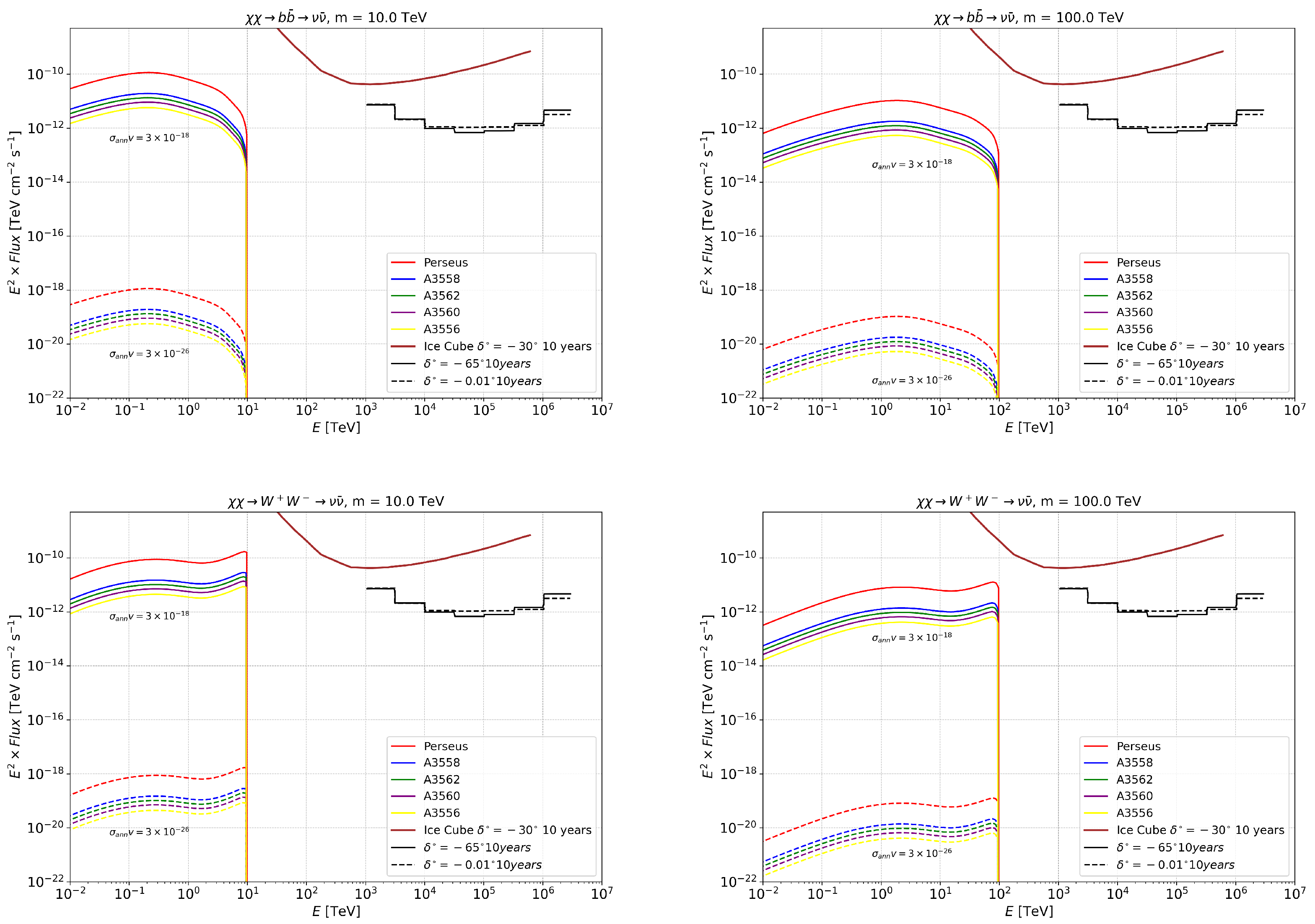
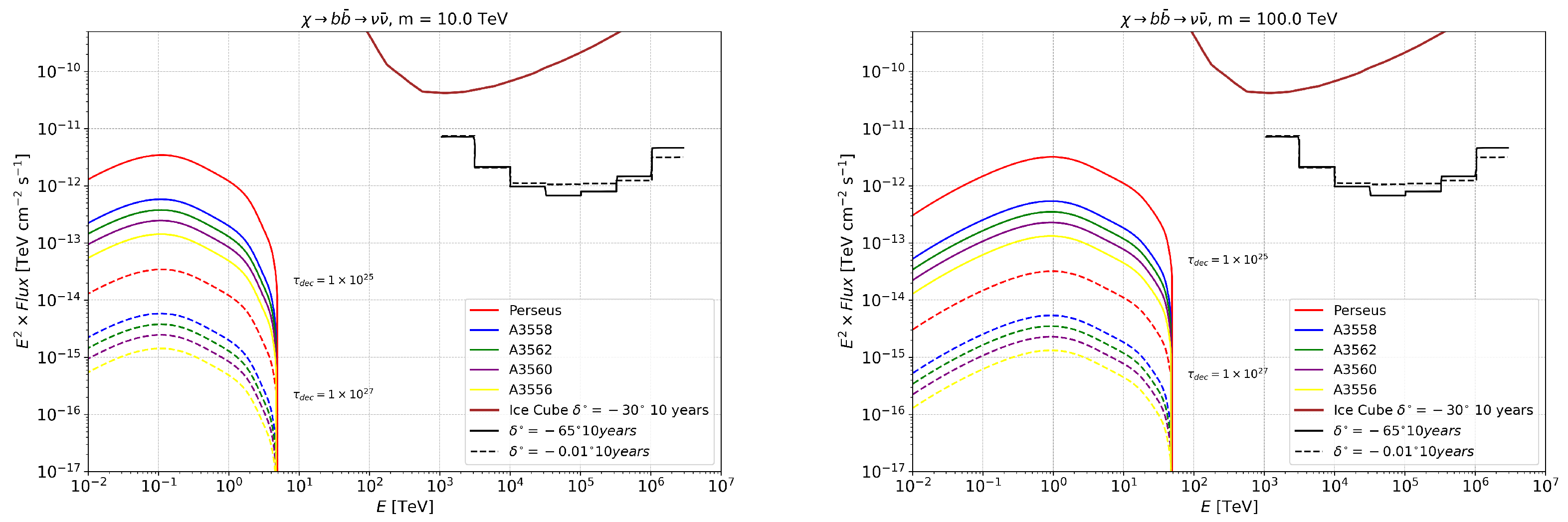
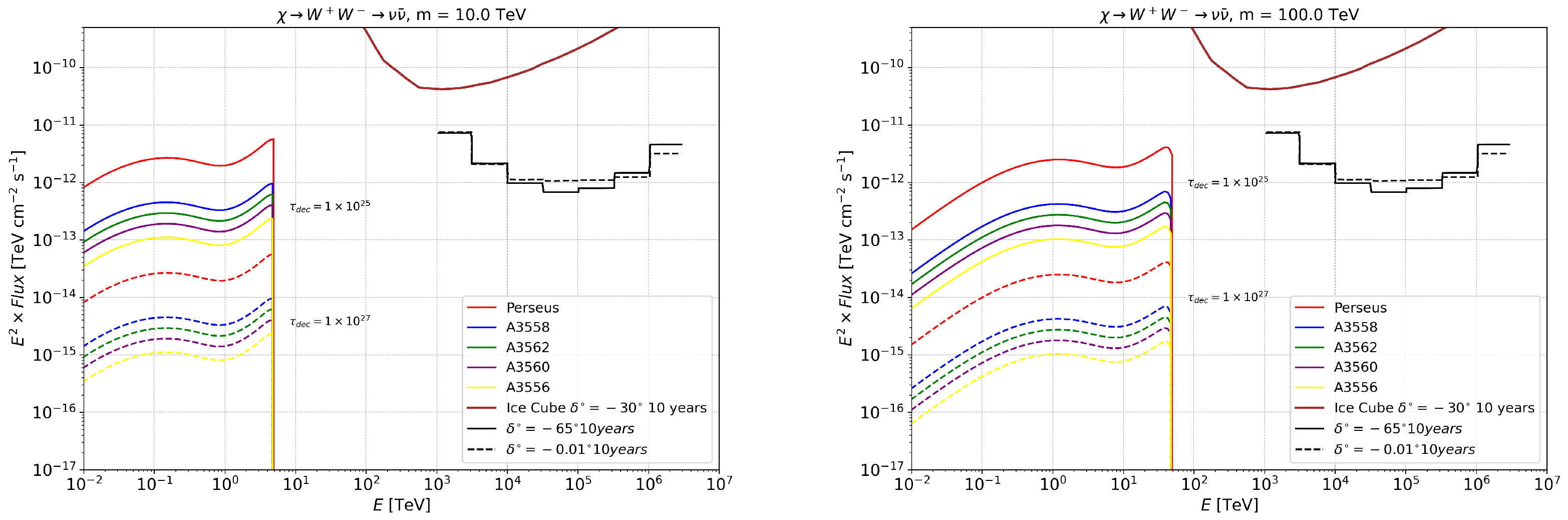
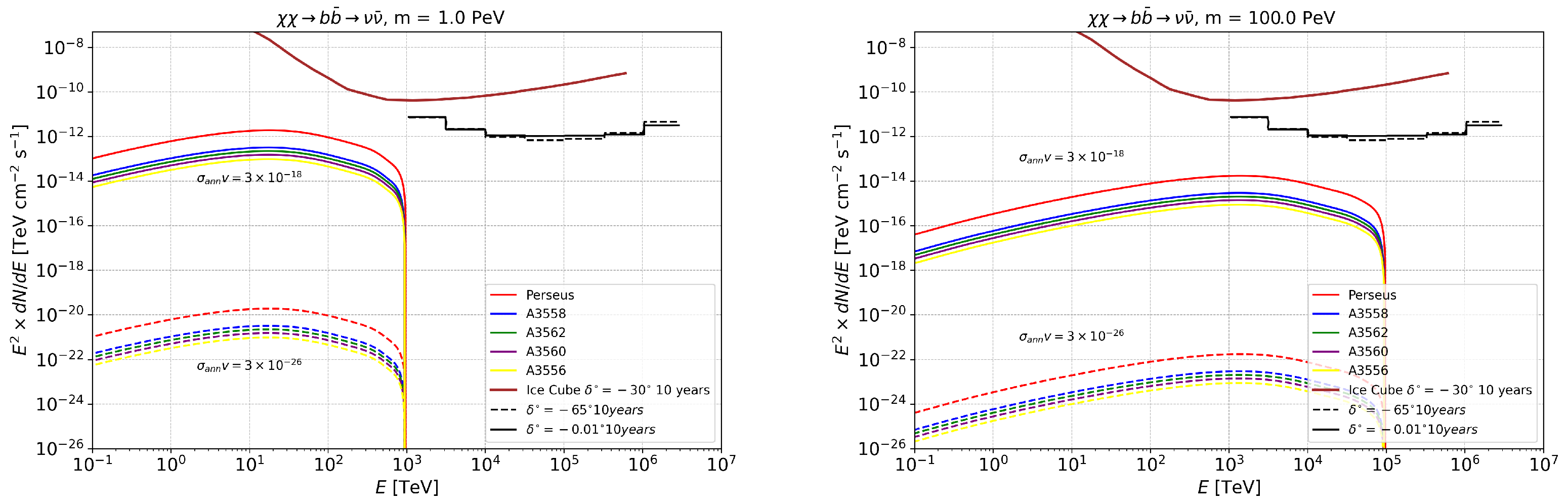


| Cluster | l | b | z | * | |||||
|---|---|---|---|---|---|---|---|---|---|
| Perseus | 150.57 | 0.0179 | 1870 | 3730 | 7.5 | 5.0 | 373.0 | 3.09 | |
| A3556 | 312.37 | 30.72 | 0.049 | 1258 | 2517 | 2.2 | 5.3 | 236.1 | 3.58 |
| A3558 | 311.98 | 31.31 | 0.048 | 1974 | 3948 | 8.6 | 4.8 | 412.9 | 2.79 |
| A3560 | 310.90 | 29.55 | 0.0495 | 1515 | 3031 | 3.9 | 5.1 | 297.6 | 3.22 |
| A3562 | 311.63 | 31.32 | 0.049 | 1732 | 3465 | 5.9 | 4.9 | 351.3 | 2.99 |
| Cluster | [deg] | [ Gec] | [ GeV c] |
|---|---|---|---|
| Perseus | 2.73 | 25.0 | 22.4 |
| A3556 | 0.66 | 1.26 | 0.93 |
| A3558 | 1.06 | 4.23 | 3.78 |
| A3560 | 0.78 | 2.01 | 1.60 |
| A3562 | 0.91 | 2.92 | 2.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stepanov, M.; Zadorozhna, L.; Babur, V.; Gugnin, O.; Hnatyk, B. Galaxy Clusters in Dark Matter Window: The Case of the Shapley Supercluster. Universe 2025, 11, 316. https://doi.org/10.3390/universe11090316
Stepanov M, Zadorozhna L, Babur V, Gugnin O, Hnatyk B. Galaxy Clusters in Dark Matter Window: The Case of the Shapley Supercluster. Universe. 2025; 11(9):316. https://doi.org/10.3390/universe11090316
Chicago/Turabian StyleStepanov, Maksym, Lidiia Zadorozhna, Valentyna Babur, Olexandr Gugnin, and Bohdan Hnatyk. 2025. "Galaxy Clusters in Dark Matter Window: The Case of the Shapley Supercluster" Universe 11, no. 9: 316. https://doi.org/10.3390/universe11090316
APA StyleStepanov, M., Zadorozhna, L., Babur, V., Gugnin, O., & Hnatyk, B. (2025). Galaxy Clusters in Dark Matter Window: The Case of the Shapley Supercluster. Universe, 11(9), 316. https://doi.org/10.3390/universe11090316






