Appendix A. Analytical TDI 2.0 Response Implemented in GBSIEVER
In this appendix, we present the analytical TDI 2.0 response to a GB signal as implemented in
GBSIEVER. All formulas are adapted, with only minor modifications, from [
58], and we follow similar notation and conventions.
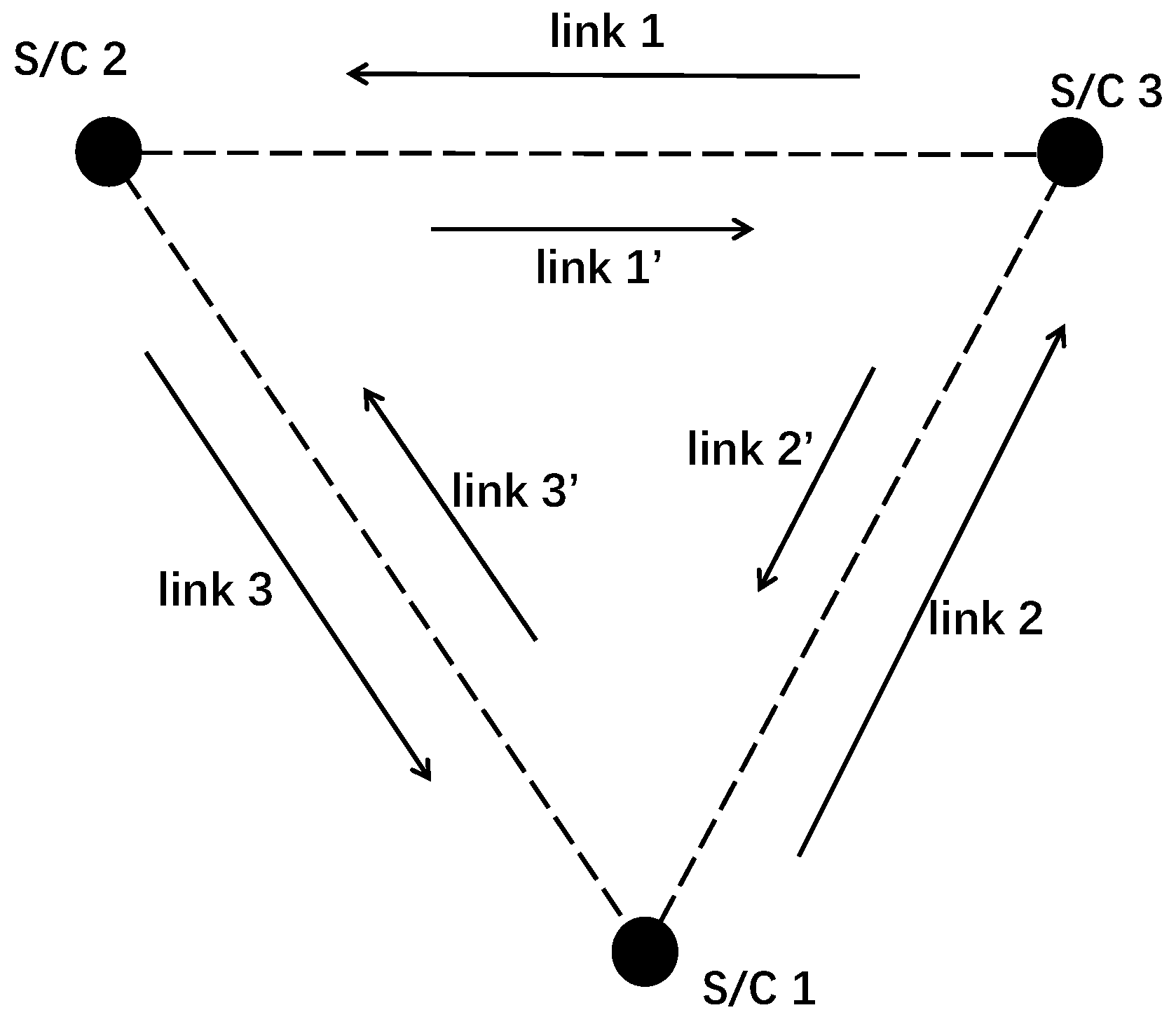
We model the three S/C orbits as an equilateral triangle whose centroid traces a circular orbit around the Sun. The position of S/C
i is
, where the orbital radius is fixed at
and the arm length
L is treated as constant under fixed arm length approximation. In the SSB frame,
Here
with
, and
for
. The constants
and
are, respectively, the initial ecliptic longitude of the guiding center and the initial rotation angle of the constellation. The arm-direction vectors are obtained by
,
,
. For TDC data,
.
The astrophysical parameters
,
,
,
map to the extrinsic parameters
,
,
,
through
with
and
.
For any Michelson-type TDI combination
(e.g.,
X,
Y,
Z, or their commonly used linear combinations
A,
E,
T), the response can be written as
where
with
. Here
and
are the angular frequency and its time derivative at
. The explicit
X-combination kernels are
Here
and
with
defined in
Section 2.2, and
i specifies the index of the link. We also set
and
for convenience, and the phase modulation function is
Responses for
Y and
Z combinations follow by cyclic permutation of the indices.
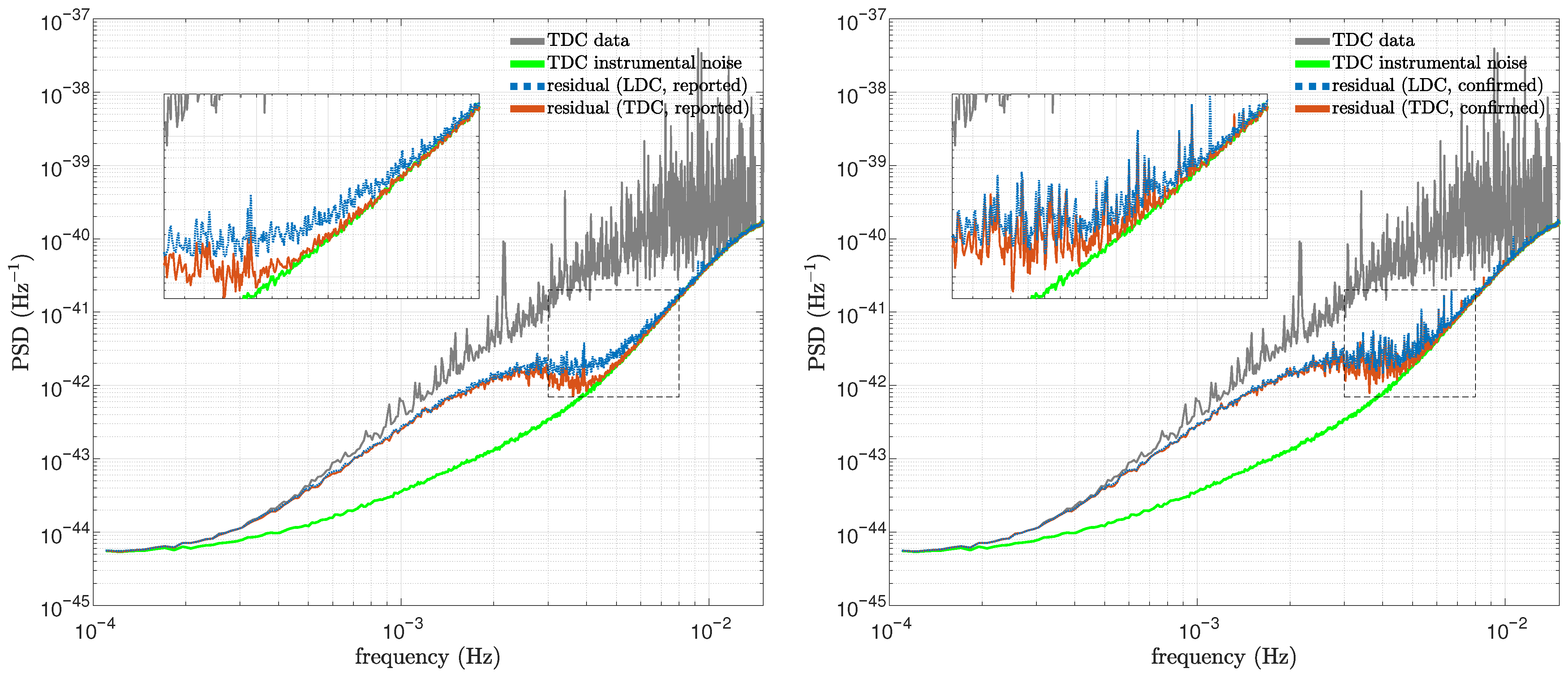
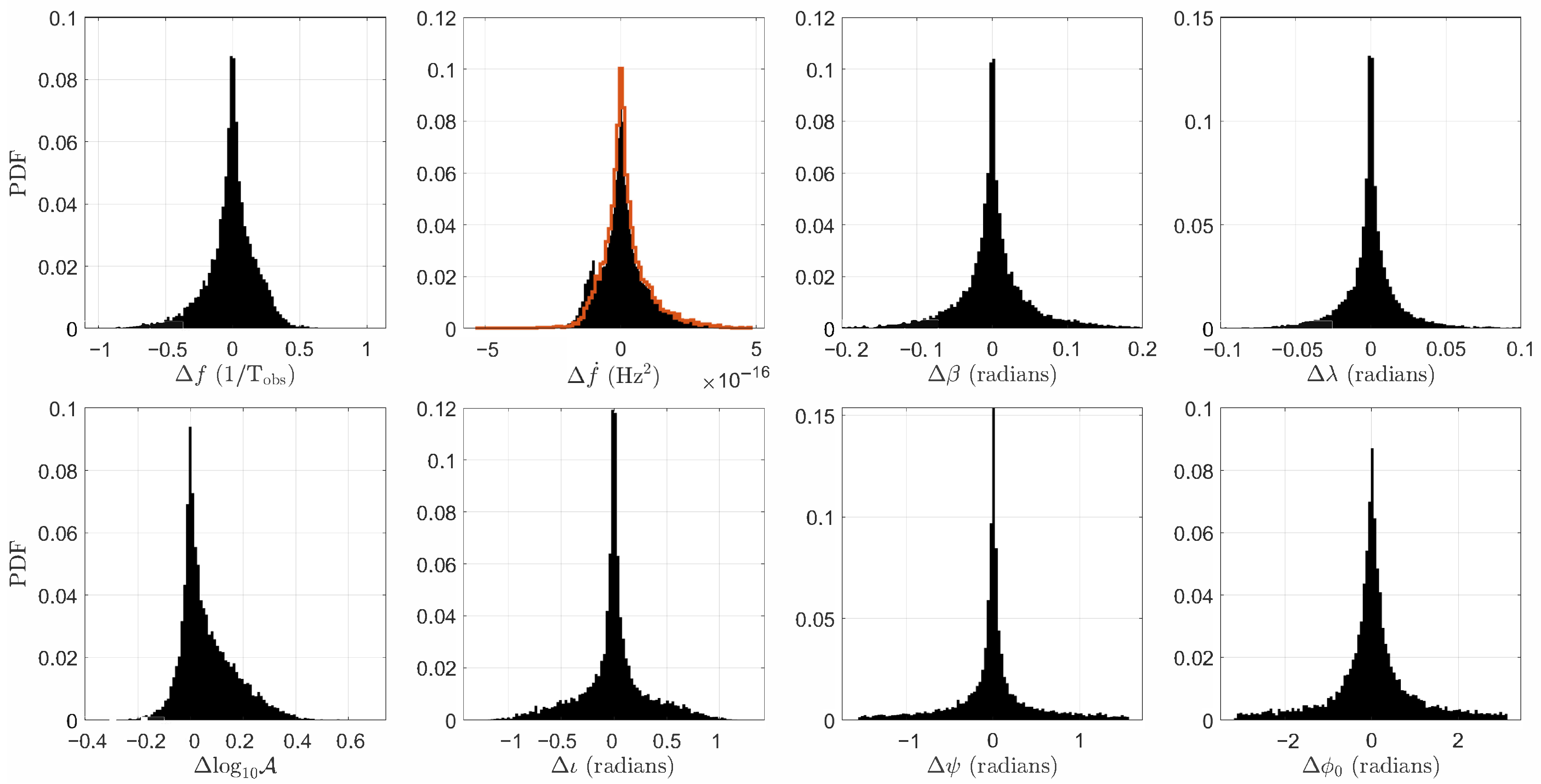
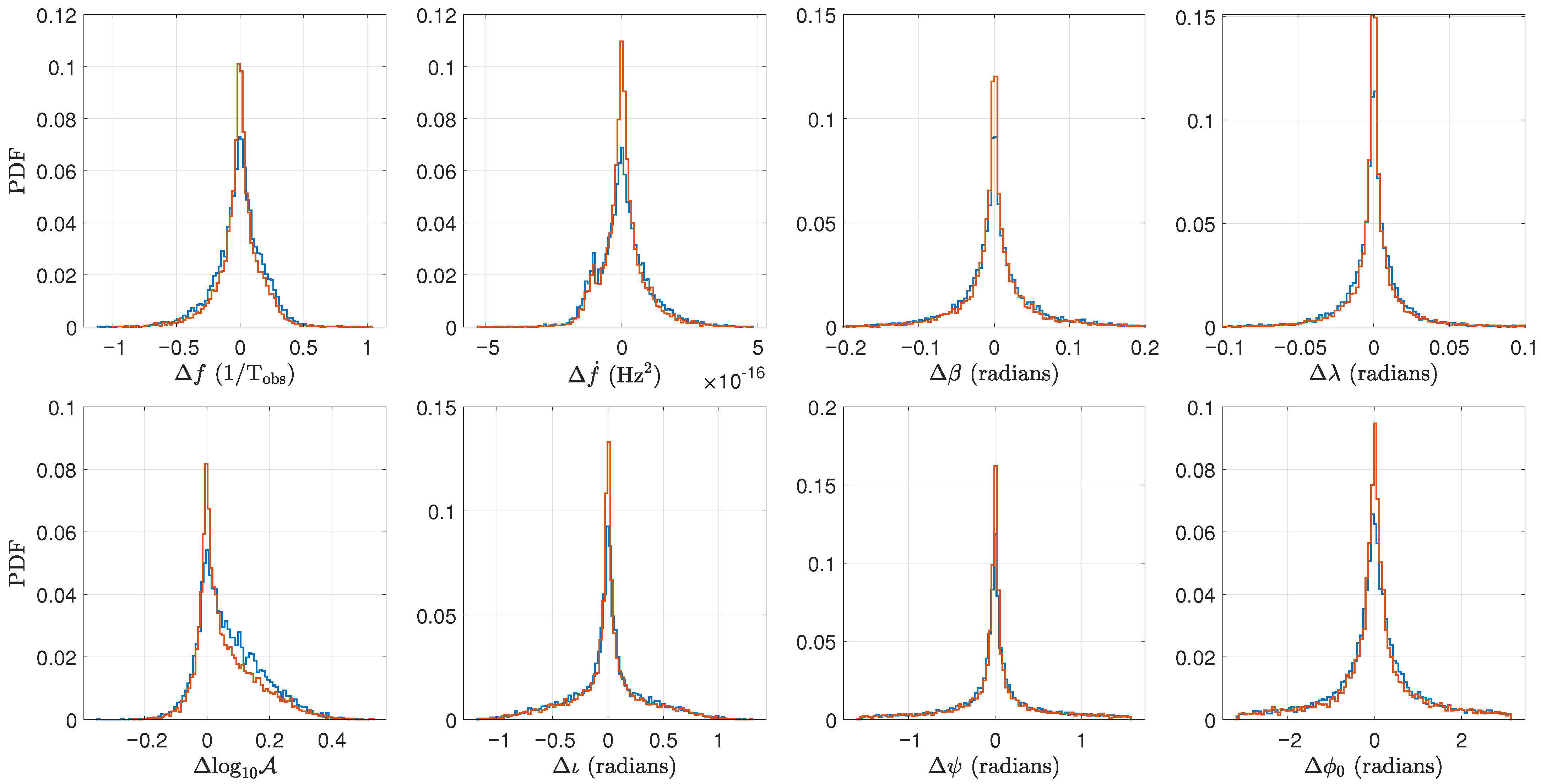
Appendix B. Block-Wise Source Statistics for All Pipeline Runs
This appendix collates the block-wise tables referenced throughout the paper. Each table lists the numbers of reported and confirmed sources, together with the corresponding detection rates, for every rerun discussed in
Section 5. The tables are grouped by dataset and computing platform as follows:
Together, these tables complement the overview statistics in
Table 3 and provide the detailed data underlying our discussion of algorithmic robustness, platform dependence, and stochastic variability.
Table A1.
Resolution performance of GBSIEVER-C on the TDC GB dataset under the Main selection settings. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
Table A1.
Resolution performance of GBSIEVER-C on the TDC GB dataset under the Main selection settings. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 24,813 | 3580 | 3733 | 2800 | 4995 |
| Reported | 2046 | 3402 | 1231 | 2726 | 4995 |
| Confirmed | 1244 | 2885 | 974 | 2420 | 4487 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 14,400 |
| Total confirmed | 12,010 |
| Detection rate | |
Table A2.
Resolution performance of GBSIEVER-C on the TDC GB dataset under the Main selection settings. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences b.
Table A2.
Resolution performance of GBSIEVER-C on the TDC GB dataset under the Main selection settings. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences b.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 24,841 | 3579 | 3740 | 2799 | 4990 |
| Reported | 2189 | 3421 | 1301 | 2740 | 4990 |
| Confirmed | 1316 | 2897 | 1029 | 2431 | 4523 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 14,641 |
| Total confirmed | 12,196 |
| Detection rate | |
Table A3.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
Table A3.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 22,953 | 2108 | 3701 | 1527 | 4244 |
| Reported | 2545 | 2083 | 1543 | 1505 | 4244 |
| Confirmed | 1608 | 1895 | 1249 | 1391 | 3972 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 11,920 |
| Total confirmed | 10,115 |
| Detection rate | |
Table A4.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences a.
Table A4.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences a.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 22,925 | 2108 | 3704 | 1527 | 4242 |
| Reported | 2545 | 2080 | 1510 | 1511 | 4242 |
| Confirmed | 1633 | 1892 | 1234 | 1398 | 3968 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 11,888 |
| Total confirmed | 10,125 |
| Detection rate | |
Table A5.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences b.
Table A5.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences b.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 22,880 | 2108 | 3683 | 1527 | 4275 |
| Reported | 2715 | 2080 | 1601 | 1514 | 4275 |
| Confirmed | 1723 | 1892 | 1301 | 1399 | 4016 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 12,185 |
| Total confirmed | 10,331 |
| Detection rate | |
Table A6.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences c.
Table A6.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P1. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences c.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 22,928 | 2107 | 3704 | 1528 | 4291 |
| Reported | 2738 | 2079 | 1601 | 1516 | 4291 |
| Confirmed | 1736 | 1891 | 1305 | 1401 | 4025 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 12,225 |
| Total confirmed | 10,358 |
| Detection rate | |
Table A7.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P2. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
Table A7.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P2. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the TACC cluster using random number sequences a.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 33,184 | 3935 | 3468 | 2527 | 4674 |
| Reported | 8095 | 3916 | 2367 | 2524 | 4674 |
| Confirmed | 5384 | 3601 | 2014 | 2411 | 4531 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 21,576 |
| Total confirmed | 17,941 |
| Detection rate | |
Table A8.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P2. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences a.
Table A8.
Resolution performance of GBSIEVER-C under the Main selection settings, based on a rerun of the analyses presented in P2. The data are divided into five contiguous frequency–SNR blocks, each with a potentially different threshold depending on the foreground noise level. For mHz, cross-validation is performed using two search ranges: for the primary search and for the secondary search. For mHz, only the primary search is performed with the same range of , and a value of in this block indicates that no threshold was applied. All identified sources shown are obtained from the CAS cluster using random number sequences a.
| | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR | mHz | SNR |
|---|
| | | | | | | | | | | |
|---|
| | | | | |
| Identified | 33,208 | 3935 | 3466 | 2527 | 4671 |
| Reported | 8035 | 3915 | 2379 | 2523 | 4671 |
| Confirmed | 5398 | 3600 | 2006 | 2410 | 4531 |
| Detection rate | | | | | |
| Lowest SNR (confirmed) | | | |
| Total reported | 21,523 |
| Total confirmed | 17,945 |
| Detection rate | |