The Lyra–Schwarzschild Spacetime

Abstract

In this paper, we provide a complete analysis of the most general spherical solution of the Lyra scalar-tensor (LyST) gravitational theory based on the proper definition of a Lyra manifold. Lyra’s geometry features the metric tensor and a scale function as fundamental fields, resulting in generalizations of geometrical quantities such as the affine connection, curvature, torsion, and non-metricity. A proper action is defined considering the correct invariant volume element and the scalar curvature, obeying the symmetry of Lyra’s reference frame transformations and resulting in a generalization of the Einstein–Hilbert action. The LyST gravity assumes zero torsion in a four-dimensional metric-compatible spacetime. In this work, geometrical quantities are presented and solved via Cartan’s technique for a spherically symmetric line element. Birkhoff’s theorem is demonstrated so that the solution is proven to be static, resulting in the Lyra–Schwarzschild metric, which depends on both the geometrical mass (through a modified version of the Schwarzschild radius $r_S$) and an integration constant dubbed the Lyra radius $r_L$. We study particle and light motion in Lyra–Schwarzschild spacetime using the Hamilton–Jacobi method. The motion of massive particles includes the determination of the $r_{\mathrm{ISCO}}$ and the periastron shift. The study of massless particle motion shows the last photon’s unstable orbit. Gravitational redshift in Lyra–Schwarzschild spacetime is also reviewed. We find a coordinate transformation that casts Lyra–Schwarzschild spacetime in the form of the standard Schwarzschild metric; the physical consequences of this fact are discussed.

1. Introduction

General Relativity (GR) is the current best theory for the gravitational interaction [1,2]. It passes all observational tests at the solar system scales (e.g., [3]), and provides the basis for technological applications, such as GPS [4]. GR predicts gravitational waves of coalescing massive stars that have been directly detected by the LVK Collaboration [5]. We should not forget about black holes, which were directly imaged twice by the EHT Collaboration [6,7]. The standard cosmological model stems from GR; it predicts the expansion and large-scale structure of the universe [8], along with the nucleosynthesis and relative abundances of light atomic nuclei (see [9] and references therein) and the existence of the cosmic microwave background radiation [10,11], all of which were measured with great precision [12,13,14,15,16,17].

For all its astonishing successes, GR still has a few shortcomings. The description of the present-day universe hinges on the existence of the dark sector, composed of dark matter and dark energy. The latter is responsible for the observed accelerated expansion of the recent cosmos [18]. On the other hand, dark matter is necessary to explain galaxy rotation curves [19], the cohesion of galaxy clusters [20], and even the large-scale structure of the universe [21], seeded by CMB anisotropies. On top of that, GR has to deal with singularities where its equations break down [22,23]. This happens (again) in cosmology when we consider the very early universe, where the Big Bang took place and the time-like geodesics terminate (according to the Penrose–Hawking theorem). The ultraviolet regime problem of GR also includes the interior singularities at the centers of black holes. In any case, a quantum version of GR is missing, which makes it difficult to hope for descriptions of spacetime points with extremely high curvature [24].

The limitations of GR motivate extensions (or modifications) of the theory [25,26,27]. One of the possible modifications is to explore the class of scalar-tensor theories of gravity [26,28], where a scalar degree of freedom is added to the already present metric field of GR. Two great examples of such theories may be found in the Kaluza–Klein model [29,30] and in the Jordan–Brans–Dicke theory [31].

Early in the 1950s, Lyra introduced a scalar field to Riemann spacetime based solely on geometrical motivations [32]. In effect, Lyra added a scale function $\varphi$ to the very definition of the reference frame. For this reason, the Lyra manifold generalizes the Riemannian manifold of GR in many ways. The transformations between spacetime points will involve both diffeomorphisms and scale transformations. This extends the notion of connection, curvature, and torsion, allowing the construction of a fresh gravitational theory with novel consequences.

Early works on Lyra gravity are those by Sen [33,34] and collaborators [35,36]; see also Ref. [37]. This first approach rendered a theory where a gauge potential $A_{\mu }:={\varphi }^{-1}{\partial }_{\mu }ln{\varphi }^2$ is introduced, resembling Weyl’s attempt to unify electromagnetism and gravity [38]. However, the resulting theory suffered from formal and physical inconsistencies. First, field equations are not covariant under Lyra’s transformations and do not come from a well-defined variational problem. Second, Weyl’s theory had to be abandoned due to the non-integrability of vector lengths [39], a feature that would produce modification of astrophysical spectral lines, an effect contrary to observations [40,41]. Sen tried to solve the problem using the gauge fixing condition $\varphi =1$. However, this would render $A_{\mu }$ null, and the resulting equations would become just Einstein field equations of GR [42]. After recognizing the second problem of the original model, Sen and Dunn [35] proposed a second model with field equations depending on the ordinary Einstein tensor $G_{\mu \nu }$ and the scalar field $\varphi$ as an additional degree of freedom, i.e., not only a gauge parameter. The drawback with the Sen–Dunn model goes beyond the lack of novelty (in effect, it was proven to be equal to Brans–Dicke theory for a specific value of the Brans–Dicke coupling $\omega$). The first problem was still an important issue.

In the face of these challenges, and inspired by Sen’s ideas, Ref. [42] proposes a new scalar-tensor theory on Lyra’s manifold. The remedy built upon the theory from the fundamental symmetries of the Lyra manifold: diffeomorphisms and scale transformations. The field equations do not present the problems of the previous models. Instead, they exhibit the suitable properties for a consistent gravity theory involving the metric tensor $g_{\mu \nu }$ and the scale $\varphi$ as the fundamental dynamical fields, including the correct Newtonian limit in the weak field regime and low-velocity motion of test particles.

In the same paper, the simplest solution for the LyST field equations is built. An ansatz was proposed for the line element $d{s}^2$, endowed with static and spherically symmetric character. Substitution in the field equations leads to differential equations involving the scale $\varphi$ and the function $\alpha \left(r\right)$, appearing as coefficients of the temporal and radial parts of $d{s}^2$. The solution to these differential equations gives the Lyra–Schwarzschild line element, a generalization of the Schwarzschild metric. A subsequent study [43] devoted attention to particle and light motion associated with the Lyra–Schwarzschild line element. To do so, the geodesic equations were built, and the study of possible trajectories was carried out.

The results described in the previous two paragraphs are reviewed by more fundamental methods in the present work. Section 2 brings an overview of the defining features of the Lyra manifold. It shows how the basis vectors depend on the scale $\varphi$; this propagates to the tensor transformation rules, the line element, and the volume element. The scale is also present in the expression of auto-parallel curves and geodesics (which are not automatically the same in the context of Lyra geometry). Connection, curvature, and torsion are also defined and compared to their Riemannian counterparts. The novelty of the procedure employed here rests on the use of the Cartan formalism [44]. Section 3 builds Lyra scalar-tensor gravity (LyST) from a properly defined action S towards the field equations. The Newtonian limit shows that these field equations recover the Poisson equation for a well-defined potential.

In Section 4, we build the Lyra–Schwarzschild spacetime by invoking spherical symmetry. However, as can be seen from Equation (50), the $d{t}^2$ coefficient and the $d{r}^2$ coefficient in $d{s}^2$ are not presumed to be inversely equal, in contrast with Ref. [43]. As we shall see, solving the geodesic equations demonstrates not only the once assumed line element, but also demonstrates the spherically symmetric solution to be static; this is equivalent to Birkhoff’s theorem [45]. Another difference between the approach of Ref. [43] and the one in the present paper concerns the technique employed to solve the field equations. Herein, we used tetrads fields $h^a$ instead of the standard technique. Cartan’s formalism is used to write the curvature in terms of the spin connection ${\Omega }_{\phantom{a}b}^a$. Imposing a metric-compatible torsion-free spacetime, ${\Omega }_{\phantom{a}b}^a$ values are uniquely related to $h^a$ by Cartan’s structure equation, which is then solved to provide the curvature 2-form and the curvature scalar.

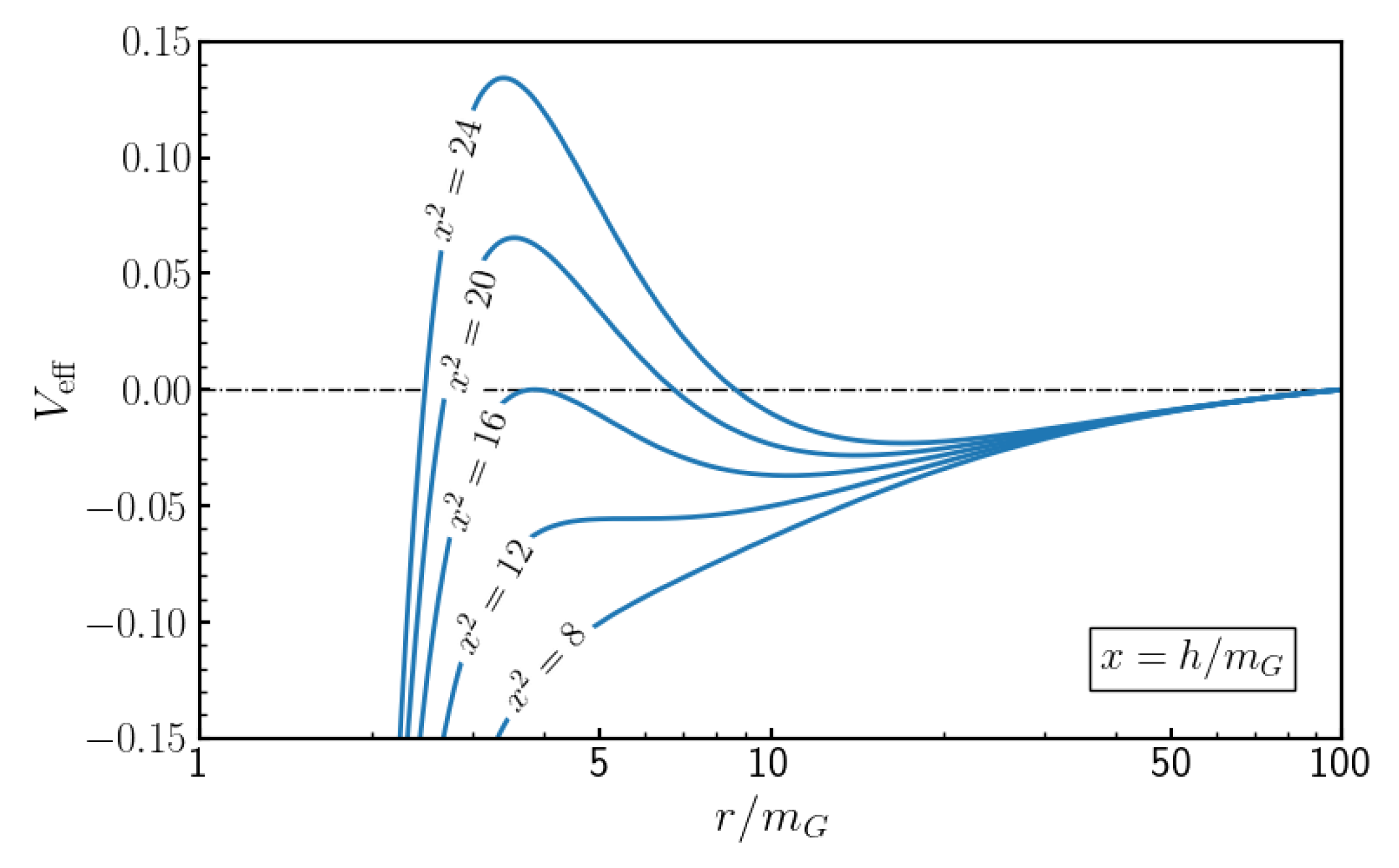
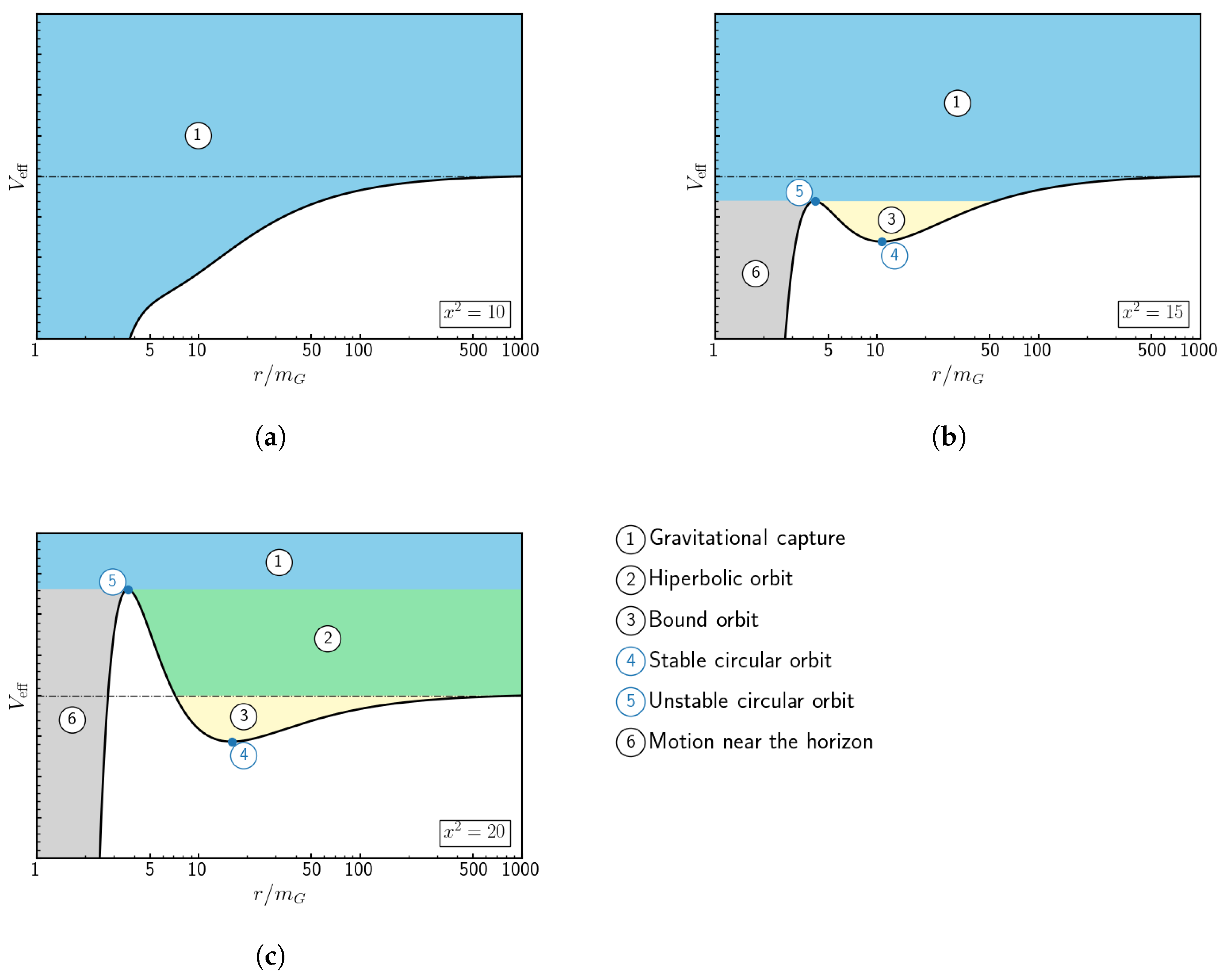
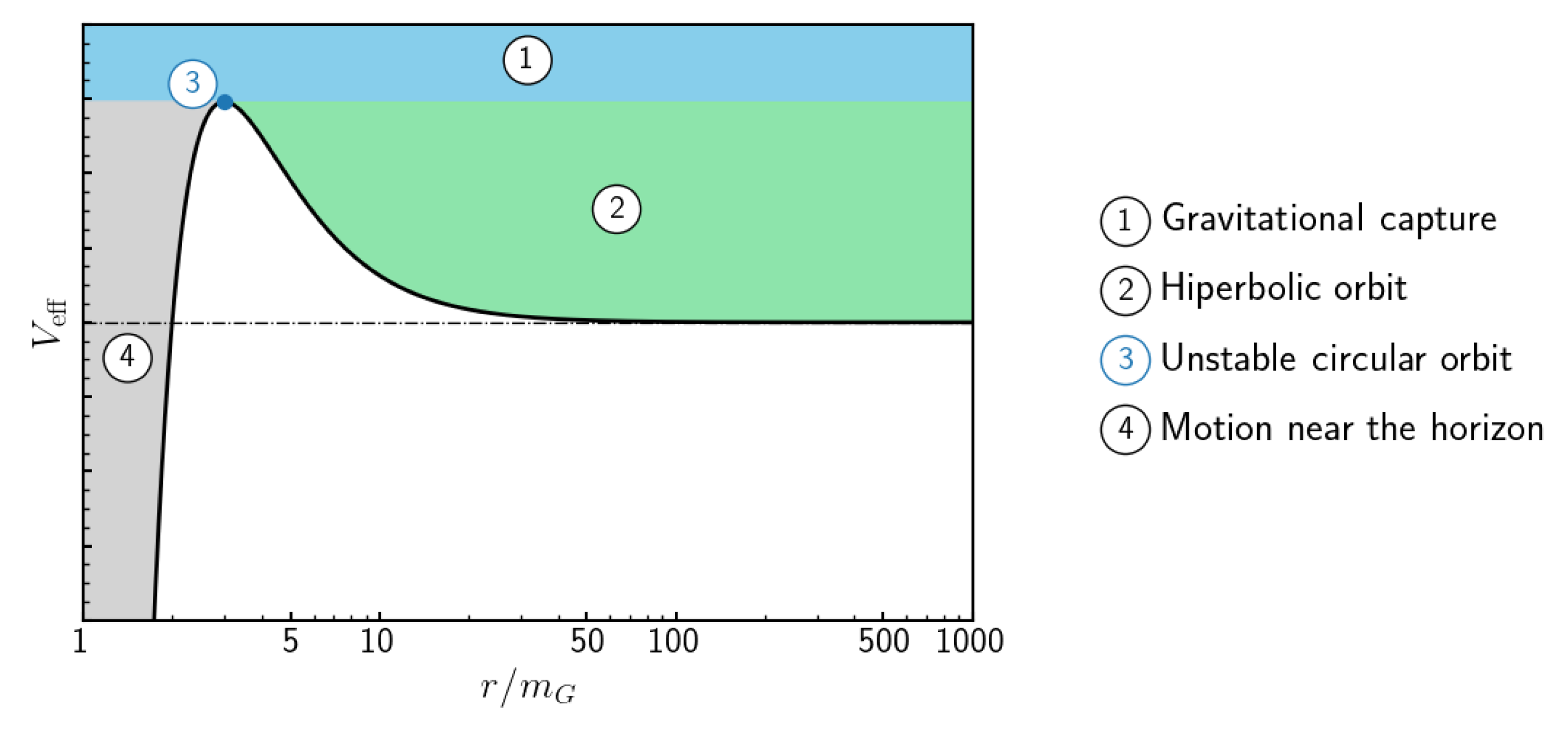
Massive and massless particle motion is discussed in Section 5. Here, as another distinct feature compared to previous approaches, we apply the Hamilton–Jacobi formalism in the spirit of Hagihara’s work [46]. The effective potential $V_{\mathrm{eff}}$ is defined for both massive and massless test particles. The different regions in the plots of $V_{\mathrm{eff}}$ correspond to different types of motion. We discuss the motion of massive particles, including the determination of the innermost stable circular orbit (ISCO) and the periastron shift. In the case of massless particle motion, the last photon’s stable orbit is discussed. Gravitational redshift and causal structure are also discussed. Section 6 brings our final remarks, physical interpretations, and perspectives.

2. The Lyra Spacetime

The Lyra spacetime is defined by a differential manifold M equipped with a pseudo-Riemannian metric g, a scale function $\varphi :M\to R^{*}$, and an affine connection $\Gamma$. Considering an open region $U\subset M$ and $\varphi \left(x\right)$ and the image of $\varphi$ in a point $P\in U$, the local coordinates $x_P:=\left\{x^{\mu }\right\}$ of P induce a basis $E_P:=\left\{e_{\mu }^P\right\}\subset T_{P}M$ in the tangent space $T_{P}M$ of the point P;

$$e_{\mu }^P:={\left.{\displaystyle \frac{1}{\varphi \left(x_P\right)}}{\displaystyle \frac{\partial }{\partial x^{\mu }}}\right|}_{x_P},$$

(1)

which will be written $e_{\mu }={\varphi }^{-1}\left(x\right){\partial }_{\mu }$ as a short notation. The basis $E_P$ is non-holonomic, since $\left[e_{\mu },e_{\nu }\right]={\gamma }_{\mu \nu }^{\lambda }{e}_{\lambda }$, with structure coefficients

$${\gamma }_{\mu \nu }^{\lambda }:={\varphi }^{-2}\left({\delta }_{\mu }^{\lambda }{\partial }_{\nu }\varphi -{\delta }_{\nu }^{\lambda }{\partial }_{\mu }\varphi \right).$$

$E_P$ defines a local Lyra reference frame.

The basis $E_P$ also induces a non-holonomic basis $E_P^{*}:=\left\{e_P^{\mu }\right\}\subset T_P^{*}M$ in the cotangent space $T_P^{*}M$. The 1-forms $e^{\mu }$ are related to the holonomic base $d{x}^{\mu }$ by $e^{\mu }=\varphi \left(x\right)d{x}^{\mu }$. In particular, the velocity field $v\in TM$ over a curve $\gamma :\left[{\lambda }_0,{\lambda }_f\right]\to U$ parameterized by a real variable $\lambda$ is defined by

$$v:={\displaystyle \frac{d}{d\lambda }}={\displaystyle \frac{d{x}^{\mu }}{d\lambda }}{\partial }_{\mu }=\varphi {\displaystyle \frac{d{x}^{\mu }}{d\lambda }}{e}_{\mu },$$

(2)

and the differential $df\in T^{*}M$ of a scalar function f becomes

$$df=d{x}^{\mu }{\partial }_{\mu }f={\varphi }^{-1}\left({\partial }_{\mu }f\right)e^{\mu },$$

(3)

where $TM$ and $T^{*}M$ are the tangent and cotangent bundles.

2.1. Lyra Tensors

With these elements, we can build $\left(r,s\right)$-type tensors,

$$T:\underset{r\mathrm{factors}}{\underbrace{T_p^{*}\mathcal{M}\times \cdots \times T_p^{*}\mathcal{M}}}\times \underset{s\mathrm{factors}}{\underbrace{T_p\mathcal{M}\times \cdots \times T_p\mathcal{M}}}\to \mathbb{R},$$

that are members of a tensor algebra with the usual tensor product ⊗. In a Lyra frame $E_P$, an $\left(r,s\right)$ tensor may be written by

$$T=T_{\phantom{{\mu }_1\cdots {\mu }_r}{\nu }_1\cdots {\nu }_s}^{{\mu }_1\cdots {\mu }_r}{e}_{{\mu }_1}\otimes \cdots \otimes e_{{\mu }_r}\otimes e^{{\nu }_1}\otimes \cdots \otimes e^{{\nu }_s}.$$

(4)

This structure also enables the rigorous definition of the exterior algebra, whose elements are skew-symmetric tensors of type $\left(0,n\right)$, known as n-forms, with operations given by the usual addition and the exterior product ∧. Furthermore, tensor fields over their corresponding bundle spaces are formally defined, enriching the framework of geometric objects with additional tools, such as the exterior derivative and the Lie derivative. We will also endow the tangent space with a bilinear symmetric inner product, denoted by $\left(•,•\right)$, which may be degenerate.

Considering two Lyra reference systems $E_P$ and ${\overline{E}}_P$, we define a smooth transformation

$$x^{\mu }\to {\overline{x}}^{\mu }={\overline{x}}^{\mu }\left(x\right),\varphi \left(x\right)\to \overline{\varphi }\left(\overline{x}\right).$$

(5)

The resulting geometry should be built to remain invariant under (5). For instance, the transformation rules for base vectors and co-vectors are given by

$$e_{\mu }\to {\overline{e}}_{\mu }={\displaystyle \frac{\varphi \left(x\right)}{\overline{\varphi }\left(\overline{x}\right)}}{\displaystyle \frac{\partial x^{\nu }}{\partial {\overline{x}}^{\mu }}}{e}_{\nu },e^{\mu }\to {\overline{e}}^{\mu }={\displaystyle \frac{\overline{\varphi }\left(\overline{x}\right)}{\varphi \left(x\right)}}{\displaystyle \frac{\partial {\overline{x}}^{\mu }}{\partial x^{\nu }}}{e}^{\nu }.$$

(6)

This implies the following transformation rules for $\left(r,s\right)$ tensor field components:

$$T_{\phantom{{\mu }_1\cdots {\mu }_r}{\nu }_1\cdots {\nu }_s}^{{\mu }_1\cdots {\mu }_r}\to {\overline{T}}_{\phantom{{\mu }_1\cdots {\mu }_r}{\nu }_1\cdots {\nu }_s}^{{\mu }_1\cdots {\mu }_r}={\left({\displaystyle \frac{\overline{\varphi }\left(\overline{x}\right)}{\varphi \left(x\right)}}\right)}^{r-s}\left({\displaystyle \frac{\partial {\overline{x}}^{{\mu }_1}}{\partial x^{{\alpha }_1}}}\cdots {\displaystyle \frac{\partial {\overline{x}}^{{\mu }_r}}{\partial x^{{\alpha }_r}}}\right)\left({\displaystyle \frac{\partial x^{{\beta }_1}}{\partial {\overline{x}}^{{\nu }_1}}}\cdots {\displaystyle \frac{\partial x^{{\beta }_s}}{\partial {\overline{x}}^{{\nu }_s}}}\right)T_{\phantom{{\alpha }_1\cdots {\alpha }_r}{\beta }_1\cdots {\beta }_s}^{{\alpha }_1\cdots {\alpha }_r}.$$

(7)

2.2. Metric, Geodesics, and Volume Element

In the tradition of Einstein’s equivalence principle, we relate each neighborhood $U\subset M$ with a Minkowski patch $U^{\prime }\in TM$, endowed with a set of orthonormal axes $\left\{h^a\right\}$ and metric ${\eta }_{\mu \nu }:=\mathrm{diag}\left(1,-1,-1,-1\right)$. Therefore, there is an invertible transformation

$$e^{\mu }\to h^a=h_{\mu }^a{e}^{\mu },h_a:=h_a^{\mu }{e}_{\mu },h_{\mu }^a{h}_b^{\mu }={\delta }_b^a.$$

(8)

The fields $h_{\mu }^a$ are the components of the well-known tetrad 1-forms $h^a=\varphi h_{\mu }^{a}d{x}^{\mu }$, which define a local Lorentz frame. The metric in $U^{\prime }$ induces the spacetime metric in the usual way:

$$d{s}^2={\eta }_{ab}{h}^a{h}^b=g_{\mu \nu }{e}^{\mu }{e}^{\nu },g_{\mu \nu }:={\eta }_{ab}{h}_{\mu }^a{h}_{\nu }^b=h_{\mu }^a{h}_{a\nu }.$$

(9)

The line element

$$d{s}^2={\varphi }^2{g}_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$$

(10)

is the Lyra-invariant line element in U.

Like in an ordinary Riemannian manifold, the tetrads also establish isomorphisms between the tensor algebras defined in M and those defined in the local Minkowski frame. For example, a vector $v:=v^a{\partial }_a$ in $T{U}^{\prime }$ is uniquely related to a vector $v:=v^{\mu }{e}_{\mu }$ provided $v^a=h_{\mu }^a{v}^{\mu }$. On the other hand, the components of a 1-form in $T_P^{*}M$, ${\alpha }_{\mu }$, are related to their counterpart in $T^{*}{U}^{\prime }$ by the expression ${\alpha }_{\mu }=h_{\mu }^a{\alpha }_a$. Moreover, given that ${\eta }_{ab}$ and its inverse provide an isomorphism between Lorentz vectors and Lorentz 1-forms, $g_{\mu \nu }$ defines an isomorphism between $T_{P}M$ and $T_P^{*}M$:

$$v^{\mu }=g^{\mu \nu }{v}_{\nu },v_{\mu }=g_{\mu \nu }{v}^{\nu }.$$

(11)

It is also straightforward to show that $g_{\mu \nu }$ coincides with the inner product $\left(e_{\mu },e_{\nu }\right)$.

Consider a curve $\gamma :I\to M$. If v is the corresponding tangent vector field, then the length of the curve, between two points $p_1=\gamma \left({\lambda }_1\right)$ and $p_2=\gamma \left({\lambda }_2\right)$, is

$$\mathsf{\ell }={\int }_{{\lambda }_1}^{{\lambda }_2}\sqrt{\left|\left(v,v\right)\right|}d\lambda ={\int }_{{\lambda }_1}^{{\lambda }_2}\sqrt{\left|{\varphi }^2{g}_{\mu \nu }\left(x\right){\displaystyle \frac{d{x}^{\mu }}{d\lambda }}{\displaystyle \frac{d{x}^{\nu }}{d\lambda }}\right|}d\lambda .$$

(12)

If the length of a curve is stationary under the condition of fixed end-points, the variation of (12) while considering $\lambda$ as an affine parameter yields the geodesic equation:

$${\displaystyle \frac{d^2{x}^{\mu }}{d{\lambda }^2}+\left\{\begin{array}{c}\mu \\ \alpha \beta \end{array}\right\}{\displaystyle \frac{d{x}^{\alpha }}{d\lambda }}{\displaystyle \frac{d{x}^{\beta }}{d\lambda }}+{\varphi }^{-1}\left({\delta }_{\alpha }^{\mu }{\partial }_{\beta }\varphi +{\delta }_{\beta }^{\mu }{\partial }_{\alpha }\varphi -g^{\mu \nu }{\partial }_{\nu }\varphi g_{\alpha \beta }\right){\displaystyle \frac{d{x}^{\alpha }}{d\lambda }}{\displaystyle \frac{d{x}^{\beta }}{d\lambda }}=0,}$$

(13)

where

$${\displaystyle \left\{\begin{array}{c}\mu \\ \alpha \beta \end{array}\right\}=\frac{1}{2}{g}^{\mu \nu }\left({\partial }_{\alpha }{g}_{\nu \beta }+{\partial }_{\beta }{g}_{\nu \alpha }-{\partial }_{\nu }{g}_{\alpha \beta }\right)}$$

(14)

denotes the well-known Christoffel symbols. The expression (13) contains additional terms that do not appear in the geodesic equation of the usual Riemannian geometry.

To conclude the discussion on the geometric structure, the concept of a volume element is introduced. In the Lorentz frame, the $\left(n+1\right)$-dimensional volume element is that of the Minkowski spacetime

$$dV:={\displaystyle \frac{1}{n!}}{ϵ}_{a_0{a}_1\cdots a_n}{h}^{a_0}\wedge h^{a_1}\wedge \cdots \wedge h^{a_n}.$$

(15)

With (8), this same volume density becomes

$$dV={ϵ}_{a_0\cdots a_n}{h}_0^{a_0}\cdots h_n^{a_n}{e}^0\cdots e^n={\varphi }^{n+1}h{d}^{n+1}x,$$

where $h:=det{h}_{\mu }^a$. Since $g:=det{g}_{\mu \nu }=-h^2$, the appropriate definition of the volume element in Lyra geometry is given by

$$dV={\varphi }^{n+1}\sqrt{\left|g\right|}{d}^{n+1}x,$$

(16)

and this expression remains invariant under Lyra reference systems transformations.

2.3. Affine Structure, Curvature, and Torsion

As usual, ordinary derivatives of tensor fields in a Minkowski patch are not covariant under local Lorentz transformations, which demands the introduction of a spin connection ${\Omega }_{\phantom{a}b}^a:={\Omega }_{cb}^a{h}^c$ and a corresponding covariant derivative for a $\left(r,s\right)$ tensor field

$$\begin{array}{cc}\hfill D_a{T}_{\phantom{b_1\cdots b_r}{c}_1\cdots c_s}^{b_1\cdots b_r}:=& h_a{T}_{\phantom{b_1\cdots b_r}{c}_1\cdots c_s}^{b_1\cdots b_r}+\hfill \\ \hfill & +{\Omega }_{ad}^{b_1}{T}_{\phantom{b_1\cdots b_r}{c}_1\cdots c_s}^{d\cdots b_r}+\cdots +{\Omega }_{ad}^{b_r}{T}_{\phantom{b_1\cdots b_r}{c}_1\cdots c_s}^{b_1\cdots d}+\hfill \\ \hfill & -{\Omega }_{a{c}_1}^d{T}_{\phantom{b_1\cdots b_r}d\cdots c_s}^{b_1\cdots b_r}-\cdots -{\Omega }_{a{c}_s}^d{T}_{\phantom{b_1\cdots b_r}{c}_1\cdots d}^{b_1\cdots b_r}.\hfill \end{array}$$

(17)

Following Cartan’s formalism [44], the torsion field is defined by

$$T^a:=D{h}^a=d{h}^a+{\Omega }_{\phantom{a}b}^a\wedge h^b,$$

(18)

and curvature is found by the expression

$$R_{\phantom{a}b}^a:=d{\Omega }_{\phantom{a}b}^a+{\Omega }_{\phantom{a}c}^a\wedge {\Omega }_{\phantom{a}b}^c,$$

(19)

where $D:=h^a{D}_a$ is the covariant differential.

From now on, we impose the same restrictions of General Relativity. The first restriction is the covariant conservation of the metric (metric compatibility), given by $D{\eta }_{ab}=0$, which implies ${\Omega }_{ab}=-{\Omega }_{ba}$. The second restriction is $T^a=0$. In a metric-compatible torsion-free theory, the spin connection is uniquely related to the tetrads by the first Cartan’s structure equation,

$$d{h}^a+{\Omega }_{\phantom{a}b}^a\wedge h^b=0,$$

(20)

whose solutions may be used to calculate the curvature 2-form from (19), which is the second structure equation. As usual, applying d in (18) and (19) yields the first and second Bianchi identities

$$D{T}^a=R_{\phantom{a}b}^a\wedge h^b,D{R}_{\phantom{a}b}^a=0,$$

so, in a torsion-free environment, $R_{\phantom{a}b}^a\wedge h^b=0$.

Defining ${\displaystyle {\nabla }_{\mu }:=h_{\mu }^a{D}_a}$, the covariant derivative in M,

$$\begin{array}{cc}\hfill {\displaystyle {\nabla }_{\mu }{T}_{\phantom{b_1\cdots b_r}{\gamma }_1\cdots {\gamma }_s}^{{\nu }_1\cdots {\nu }_r}:=}& e_{\mu }{T}_{\phantom{b_1\cdots b_r}{\gamma }_1\cdots {\gamma }_s}^{{\nu }_1\cdots {\nu }_r}+\hfill \\ \hfill & +{\Gamma }_{\mu \lambda }^{{\nu }_1}{T}_{\phantom{b_1\cdots b_r}{\gamma }_1\cdots {\gamma }_s}^{\lambda \cdots b_r}+\cdots +{\Gamma }_{\mu \lambda }^{{\nu }_r}{T}_{\phantom{b_1\cdots b_r}{\gamma }_1\cdots {\gamma }_s}^{{\nu }_1\cdots \lambda }+\hfill \\ \hfill & -{\Gamma }_{\mu {\gamma }_1}^{\lambda }{T}_{\phantom{b_1\cdots b_r}\lambda \cdots {\gamma }_s}^{{\nu }_1\cdots {\nu }_r}-\cdots -{\Gamma }_{\mu {\gamma }_s}^{\lambda }{T}_{\phantom{b_1\cdots b_r}{\gamma }_1\cdots \lambda }^{{\nu }_1\cdots {\nu }_r},\hfill \end{array}$$

(21)

implies the connection

$${\Gamma }_{\mu \nu }^{\lambda }=h_b^{\lambda }{e}_{\mu }\left(h_{\nu }^b\right)+h_b^{\lambda }{h}_{\mu }^a{h}_{\nu }^c{\Omega }_{ac}^b.$$

(22)

Direct calculation yields

$${\displaystyle {\Gamma }_{\mu \nu }^{\lambda }={\varphi }^{-1}\left\{\begin{array}{c}\lambda \\ \mu \nu \end{array}\right\}+{\varphi }^{-1}\left({\displaystyle {\delta }_{\mu }^{\lambda }{\nabla }_{\nu }\varphi -g_{\mu \nu }{\nabla }^{\lambda }\varphi }\right).}$$

(23)

The components of the curvature 2-form are given by

$$R_{\phantom{a}bcd}^a:=i_{h_c}{i}_{h_d}{R}_{\phantom{a}b}^a,$$

where $i_{e_{\nu }}$ denotes the interior product.1 The curvature components in M coordinates are $R_{\phantom{\alpha }\beta \mu \nu }^{\alpha }:=h_a^{\alpha }{h}_{\beta }^b{h}_{\mu }^c{h}_{\nu }^d{R}_{\phantom{a}bcd}^a$, resulting in

$${\displaystyle R_{\beta \mu \nu }^{\alpha }={\varphi }^{-1}{\partial }_{\mu }{\Gamma }_{\beta \nu }^{\alpha }-{\varphi }^{-1}{\partial }_{\nu }{\Gamma }_{\beta \mu }^{\alpha }+{\Gamma }_{\lambda \mu }^{\alpha }{\Gamma }_{\beta \nu }^{\lambda }-{\Gamma }_{\lambda \nu }^{\alpha }{\Gamma }_{\beta \mu }^{\lambda }-{\Gamma }_{\beta \lambda }^{\alpha }{\gamma }_{\mu \nu }^{\lambda }.}$$

(24)

The components of Ricci’s tensor in the Lorentz frame can be calculated from

$$\mathrm{R}\mathrm{i}{\mathrm{c}}_{ab}:=i_{h_b}{i}_{h_c}{R}_{\phantom{c}a}^c,$$

(25)

and Ricci’s scalar may be found by directly contracting (24) in the usual way, but a direct calculation results in the more appealing expression

$$R:=i_{h_b}{i}_{h_a}{R}^{ab}.$$

(26)

A generalization of the divergence theorem can be obtained in the M coordinates. While taking into account (15), let $X:=v^a{h}_a$ be a Lorentz vector. The following divergence theorem is valid:

$${\int }_{V}dV{D}_a{v}^a={\int }_{\partial V}{i}_{X}dV.$$

A direct calculation shows that

$${\displaystyle {\int }_V{d}^{n+1}x{\varphi }^{n+1}\sqrt{\left|g\right|}{\nabla }_{\mu }{v}^{\mu }={\int }_{\partial V}{d}^{n}x{\varphi }^n\sqrt{\left|g\right|}{n}_{\lambda }{v}^{\lambda },}$$

(27)

with $n_{\lambda }$ a vector locally orthogonal to $\partial V$.

We stress that these results are direct consequences of the metricity and torsion-free conditions. In a non-metric-compatible space with torsion, terms dependent on the non-metricity tensor and contortion will be present.

Finally, it is possible to relate the Lyra objects to the ones of ordinary pseudo-Riemannian geometry. Using the connection (23), referred to as the LyST connection from now on, we calculate the components of the curvature as

$$\begin{array}{cc}\hfill {\displaystyle R_{\beta \mu \nu }^{\alpha }}& {\displaystyle =\frac{1}{{\varphi }^2}{\mathcal{R}}_{\beta \mu \nu }^{\alpha }+\frac{1}{{\varphi }^2}(g_{\beta \nu }{\delta }_{\mu }^{\alpha }-g_{\beta \mu }{\delta }_{\nu }^{\alpha }){\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi }\hfill \\ \hfill & +{\displaystyle \frac{1}{\varphi }}\left({\delta }_{\nu }^{\alpha }{\nabla }_{\mu }{\nabla }_{\beta }\varphi -{\delta }_{\mu }^{\alpha }{\nabla }_{\nu }{\nabla }_{\beta }\varphi +g_{\beta \mu }{\nabla }_{\nu }{\nabla }^{\alpha }\varphi -g_{\beta \nu }{\nabla }_{\mu }{\nabla }^{\alpha }\varphi \right),\hfill \end{array}$$

(28)

where ${\mathcal{R}}_{\beta \mu \nu }^{\alpha }$ are the components of the usual Riemann curvature tensor. We also obtain the components of the Ricci tensor

$${\displaystyle R_{\beta \nu }=\frac{1}{{\varphi }^2}{\mathcal{R}}_{\beta \nu }+\frac{3}{{\varphi }^2}{g}_{\beta \nu }{\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi -\frac{2}{\varphi }{\nabla }_{\nu }{\nabla }_{\beta }\varphi -\frac{1}{\varphi }{g}_{\beta \nu }{\nabla }_{\lambda }{\nabla }^{\lambda }\varphi ,}$$

(29)

and the Ricci scalar

$${\displaystyle R=\frac{1}{{\varphi }^2}\mathcal{R}+\frac{12}{{\varphi }^2}{\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi -\frac{6}{\varphi }{\nabla }_{\lambda }{\nabla }^{\lambda }\varphi .}$$

(30)

The components ${\mathcal{R}}_{\beta \nu }$ and $\mathcal{R}$ refer to the corresponding Riemannian quantities.

3. Lyra Scalar-Tensor Gravity

According to the previous section, the general structure of a metric-compatible and torsion-free Lyra manifold depends on the scale functions $\varphi$, the metric tensor $g_{\mu \nu }$, and the connection 1-form (23). This setup ensures the invariance of physical quantities under Lyra’s reference transformation, meaning coordinate and scale transformations in M, but also under local Lorentz transformations. Therefore, diffeomorphism invariance and the equivalence principle are ensured.

Now, we establish a dynamical principle using the local action2

$$S:={\displaystyle \frac{1}{4\kappa }}{\int }_V{\epsilon }_{abcd}{h}^a\wedge h^b\wedge R^{cd}+S_m,$$

(31)

where $S_m$ is a minimally coupled matter action; partial derivatives ${\partial }_a$ are replaced by covariant derivatives $D_a$. In spacetime coordinates, the first functional reads

$$S_{\mathrm{LyST}}:={\displaystyle \frac{1}{2\kappa }}{\int }_V{d}^{4}x{\varphi }^4\sqrt{\left|g\right|}R,$$

(32)

which is an extension of the Einstein–Hilbert action. $\kappa$ is a constant to be determined later. The action functional for a non-gravitational matter field is obtained by writing $S_m$ in coordinates:

$$S_m={\int }_V{d}^{4}x{\varphi }^4\sqrt{\left|g\right|}{\mathcal{L}}_m.$$

(33)

3.1. Field Equations

As usual, the field equations are obtained from the variational principle of stationary action, i.e., $\delta S_{\mathrm{LyST}}=0$, with the following boundary conditions at $\partial V$: $\delta g_{\mu \nu }=0$, $\delta {\partial }_{\lambda }{g}_{\mu \nu }=0$, $\delta \varphi =0$, and $\delta {\partial }_{\lambda }\varphi =0$. Variation with respect to the metric components yields

$$G_{\mu \nu }=\kappa T_{\mu \nu },$$

(34)

where $G_{\mu \nu }:=R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }$ is the Einstein tensor in Lyra geometry and $T_{\mu \nu }$ is the energy-momentum tensor, defined as

$${\displaystyle T_{\mu \nu }:=-2{\displaystyle \frac{\partial {\mathcal{L}}_m}{\partial g^{\mu \nu }}}+g_{\mu \nu }{\mathcal{L}}_m.}$$

(35)

To clarify the difference between the field equations of Lyra spacetime and those of General Relativity, Equation (34) can be expanded as follows:

$${\displaystyle {\mathcal{R}}_{\mu \nu }-\frac{1}{2}\mathcal{R}{g}_{\mu \nu }-3g_{\mu \nu }{\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi -2\varphi {\nabla }_{\mu }{\nabla }_{\nu }\varphi +2\varphi g_{\mu \nu }{\nabla }_{\lambda }{\nabla }^{\lambda }\varphi =\kappa {\varphi }^2{T}_{\mu \nu }.}$$

(36)

The General Relativity field equations are recovered when $\varphi =1$.

On the other hand, variation with respect to the scale factor yields

$${\displaystyle \mathcal{R}+12{\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi -6\varphi {\nabla }^{\lambda }{\nabla }_{\lambda }\varphi =\kappa {\varphi }^{2}M,}$$

(37)

where

$${\displaystyle M:=-4{\mathcal{L}}_m+{\nabla }_{\mu }\varphi {\displaystyle \frac{\partial {\mathcal{L}}_m}{{\displaystyle \partial {\nabla }_{\mu }\varphi }}}-\varphi \left({\displaystyle {\displaystyle \frac{\partial {\mathcal{L}}_m}{\partial \varphi }}-{\nabla }_{\mu }{\displaystyle \frac{\partial {\mathcal{L}}_m}{{\displaystyle \partial {\nabla }_{\mu }\varphi }}}}\right).}$$

(38)

By comparing Equation (37) with the contraction of Equation (36), one obtains the following relation:

$$M=-T,$$

(39)

which implies that, in a non-empty space, the dependence of ${\mathcal{L}}_m$ on the metric tensor and the scale function is constrained. Furthermore, variation with respect to the matter field ${\psi }_i$ yields the covariant Euler–Lagrange equations:

$${\displaystyle {\displaystyle \frac{\partial {\mathcal{L}}_m}{\partial {\psi }_i}}-{\nabla }_{\mu }{\displaystyle \frac{\partial {\mathcal{L}}_m}{\partial \left({\nabla }_{\mu }{\psi }_i\right)}}=0,}$$

(40)

which, along with (36) and (37), form the complete set of equations governing the dynamics of all the fields in the system.

3.2. Energy-Momentum Conservation

It should be emphasized that, by performing the appropriate contractions of the second Bianchi identity and making use of the anti-symmetry property $R_{\alpha \beta \mu \nu }=-R_{\beta \alpha \mu \nu }$, one obtains the relation ${\nabla }_{\mu }{G}_{\nu }^{\mu }=0$, expressed here in terms of the Lyra connection. As a direct consequence, the field Equation (34) leads to the local conservation law of the energy-momentum tensor:

$${\nabla }_{\mu }{T}_{\nu }^{\mu }=0.$$

(41)

However, conservation with respect to the Riemannian connection is not, in general, guaranteed. In fact, the only quantity in (36) that remains conserved in this sense is the tensor ${\mathcal{G}}_{\mu \nu }={\mathcal{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}\mathcal{R}{g}_{\mu \nu }$. Nevertheless, the additional terms can be reorganized into a locally conserved effective energy-momentum tensor, defined as:

$$T_{\mu \nu }^{\left(eff\right)}={\varphi }^2{T}_{\mu \nu }+T_{\mu \nu }^{\left(\varphi \right)},$$

(42)

with

$$T_{\mu \nu }^{\left(\varphi \right)}={\kappa }^{-1}(2\varphi {\nabla }_{\mu }{\nabla }_{\nu }\varphi -2g_{\mu \nu }\varphi {\nabla }^{\lambda }{\nabla }_{\lambda }\varphi +3g_{\mu \nu }{\nabla }^{\lambda }\varphi {\nabla }_{\lambda }\varphi ).$$

(43)

Individual contributions to the effective energy–momentum tensor are not conserved separately in the Riemann sense, which indicates an exchange of energy–momentum between the matter sector and the scalar field associated with the scale factor. Such an exchange can, in certain frameworks, manifest itself as an effective fifth-force–like interaction, although this is not a necessary outcome and depends on the details of the coupling. A deeper analysis of these possible dynamical effects, however, lies beyond the scope of the present work.

3.3. Newtonian Limit

For LyST theory to be consistent with the predictions of Newtonian theory, the geodesic and field equations must reduce to their Newtonian form under the conditions of non-relativistic velocities:

$$\left|{\displaystyle {\displaystyle \frac{d{x}^i}{dt}}}\right|\ll 1,$$

(44)

static fields:

$${\partial }_0{g}_{\mu \nu }={\partial }_0\varphi =0,$$

(45)

and weak fields:

$$g_{\mu \nu }\approx {\eta }_{\mu \nu }+h_{\mu \nu }\mathrm{and}\varphi \approx 1+\delta \varphi ,$$

(46)

where $|h_{\mu \nu }|\ll 1$ and $\left|\delta \varphi \right|\ll 1$. Another consideration is that most classical matter distributions can be modeled as perfect fluids with density $\rho$ and pressure $p\ll \rho$:

$$T_{\mu \nu }\approx \rho u_{\mu }{u}_{\nu }.$$

(47)

By performing all the required calculations, the geodesic and field equations take the following form:

$${\displaystyle \frac{d^2\overrightarrow{\mathit{x}}}{d{t}^2}}=-\mathsf{\nabla }\mathcal{U}\mathrm{and}{\nabla }^2\mathcal{U}={\displaystyle \frac{\kappa }{2}}\rho ,$$

(48)

where the Newtonian potential $\mathcal{U}$ is defined as

$$\mathcal{U}={\displaystyle \frac{1}{2}}{h}_{00}+\delta \varphi .$$

(49)

The form of $\delta \varphi$ depends on the spacetime metric, as we shall see in Section 4.2.

Thus, it is evident that LyST theory aligns with Newtonian theory when $\kappa =8\pi G$, where G represents the Newtonian gravitational constant. However, it is important to note that the Newtonian potential is affected by both the metric tensor and the scale function.

4. Spherically Symmetric Solution

The task of finding spherically symmetric solutions of the field equations is usually carried out with Killing vector analysis. In rectangular coordinates, a spatial rotation is generated by the matrices ${{\left[L^{\left(i\right)}\right]}^{\mu }}_{\nu }:=-{\delta }_j^{\mu }{\delta }_{\nu }^k{ϵ}_{ijk}$, where $\left(i\right)$ denotes the i-th Cartesian spatial axis. The corresponding Killing vectors have the coefficients ${\xi }_{\left(i\right)}^{\mu }:={{\left[L^{\left(i\right)}\right]}^{\mu }}_{\nu }{x}^{\nu }=-{\delta }_j^{\mu }{ϵ}_{ijk}{x}^k$. In spherical coordinates $(t,r,\theta ,\phi )$, those vectors take the form

$$\begin{array}{cc}\hfill {\overline{\xi }}_{\left(1\right)}^{\mu }& =(0,0,-sin\phi ,-cot\theta cos\phi ),\hfill \\ \hfill {\overline{\xi }}_{\left(2\right)}^{\mu }& =(0,0,cos\phi ,-cot\theta sin\phi ),\hfill \\ \hfill {\overline{\xi }}_{\left(3\right)}^{\mu }& =(0,0,0,1).\hfill \end{array}$$

Rotational invariance constrains the scalar field $\varphi$ and the metric tensor $g_{\mu \nu }$. Applying the Lie derivative concerning the Killing vectors to the scalar field $\varphi$, we see that it must be independent of the angular coordinates, i.e., $\varphi =\varphi (t,r)$. In the case of the metric coefficients, we have

$${\xi }_{\left(i\right)}^{\alpha }{\partial }_{\alpha }{g}_{\mu \nu }+{\partial }_{\mu }{\xi }_{\left(i\right)}^{\alpha }{g}_{\alpha \nu }+{\partial }_{\nu }{\xi }_{\left(i\right)}^{\alpha }{g}_{\mu \alpha }=0,$$

that results in

$$d{s}^2={\varphi }^2(t,r)\left[g_{00}(t,r)d{t}^2+g_{11}(t,r)d{r}^2+2g_{01}(t,r)dtdr+g_{22}(t,r)(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right].$$

This expression can be simplified by suitable coordinate transformations. To this end, we introduce the quantities

$$\begin{array}{cccc}\hfill A(t,r)& ={\varphi }^2(t,r)g_{00}(t,r),\hfill & B(t,r)& =-{\varphi }^2(t,r)g_{11}(t,r),\hfill \\ \hfill C(t,r)& =-{\varphi }^2(t,r)g_{01}(t,r),\hfill & D^2(t,r)& =-{\varphi }^2(t,r)g_{22}(t,r).\hfill \end{array}$$

Next, we define a new radial coordinate through the relation $r^{\prime }{\varphi }^{\prime }\left(r^{\prime }\right)=D(t,r)$, where ${\varphi }^{\prime }\left(r^{\prime }\right)$ is an arbitrary function. With this change, the radial coordinate r can be expressed in terms of $(t,r^{\prime })$ through the relation

$$dr={\displaystyle \frac{{\partial }_{r^{\prime }}\left(r^{\prime }{\varphi }^{\prime }\right)}{{\partial }_{r}D}}d{r}^{\prime }-{\displaystyle \frac{{\partial }_{t}D}{{\partial }_{r}D}}dt,$$

thus preserving the general structure of the line element. We then enforce a rescaling by extracting an overall factor ${\varphi }^{\prime 2}\left(r^{\prime }\right)$, which yields

$$d{s}^2={\varphi }^{\prime 2}\left(r^{\prime }\right)\left[A^{\prime }(t,r^{\prime })d{t}^2-B^{\prime }(t,r^{\prime })d{r}^{\prime 2}-2C^{\prime }(t,r)dtd{r}^{\prime }+r^{\prime 2}(d{\theta }^2+{sin}^2\theta d{\varphi }^2)\right].$$

A further redefinition of the temporal coordinate $t^{\prime }$ allows the coefficient of the mixed term $d{t}^{\prime }d{r}^{\prime }$ to be eliminated, bringing the metric into a diagonal form. Locally, this is achieved through

$$d{t}^{\prime }={\displaystyle \frac{1}{E(t,r^{\prime })}}\left[A^{\prime }(t,r^{\prime })d{t}^{\prime }-C^{\prime }(t,r^{\prime })d{r}^{\prime }\right],$$

where $E(t,r^{\prime })$ is an appropriate integrating factor. The resulting expression, after suppressing the prime symbols for notational simplicity, can be written as

$$d{s}^2={\varphi }^2\left(r\right)\left[A(t,r)d{t}^2-B(t,r)d{r}^2-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right)\right],$$

(50)

where $\varphi$, A, and B are functions different from the former ones. In this case, the scalar field is independent of the transformed time coordinate, and $d{s}^2$ is diagonal in the transformed time and radial coordinates. Equation (50) is the most general form of a spherically symmetric line element.

Seeking to employ Cartan’s formalism, it is useful to define the orthonormal 1-form tetrad basis:

$$h^t:=e^{\gamma +\alpha }dt,h^r:=e^{\gamma +\beta }dr,h^{\theta }:=e^{\gamma }rd\theta ,h^{\phi }:=e^{\gamma }rsin\theta d\phi ,$$

(51)

where the undetermined functions have been written in exponential form:

$$\varphi (t,r)=e^{\gamma (t,r)},A(t,r)=e^{2\alpha (t,r)},B(t,r)=e^{2\beta (t,r)}.$$

(52)

By applying the first Cartan structure Equation (20) to the Lorentz frame (51), one can find the non-zero components of the connection 1-form:

$$\begin{array}{ccc}\hfill {\Omega }_r^t& =\hfill & e^{-\beta -\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)h^t+e^{-\alpha -\gamma }\left(\dot{\beta }+\dot{\gamma }\right)h^r,\hfill \\ \hfill {\Omega }_{\theta }^t& =\hfill & e^{-\alpha -\gamma }\dot{\gamma }{h}^{\theta },{\Omega }_{\phi }^t=e^{-\alpha -\gamma }\dot{\gamma }{h}^{\phi },\hfill \\ \hfill {\Omega }_{\theta }^r& =\hfill & -e^{-\beta -\gamma }\left(r^{-1}+{\gamma }^{\prime }\right)h^{\theta }.\hfill \\ \hfill {\Omega }_{\phi }^r& =\hfill & -e^{-\beta -\gamma }\left(r^{-1}+{\gamma }^{\prime }\right)h^{\phi }.\hfill \\ \hfill {\Omega }_{\phi }^{\theta }& =\hfill & -r^{-1}{e}^{-\gamma }cot\theta h^{\phi }.\hfill \end{array}$$

The second Cartan structure Equation (19) yields the following curvature coefficients:

$$\begin{array}{cc}\hfill R_{\phantom{a}r}^t=& -\left\{e^{-2\left(\beta +\gamma \right)}\left[{\alpha }^{″}+{\gamma }^{″}+\left({\alpha }^{\prime }-{\beta }^{\prime }\right)\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)\right]\right.\hfill \\ \hfill & \left.-e^{-2\left(\alpha +\gamma \right)}\left[\ddot{\beta }+\ddot{\gamma }+\left(\dot{\beta }-\dot{\alpha }\right)\left(\dot{\beta }+\dot{\gamma }\right)\right]\right\}{h}^t\wedge h^r,\hfill \\ \hfill R_{\phantom{a}\theta }^t=& \left[e^{-2\left(\alpha +\gamma \right)}\left(\ddot{\gamma }-\dot{\alpha }\dot{\gamma }\right)-e^{-2\left(\beta +\gamma \right)}\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^t\wedge h^{\theta }\hfill \\ \hfill & +e^{-\alpha -\beta -2\gamma }\left[{\dot{\gamma }}^{\prime }-\dot{\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-\dot{\beta }\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^r\wedge h^{\theta },\hfill \\ \hfill R_{\phantom{a}\phi }^t=& \left[e^{-2\left(\alpha +\gamma \right)}\left(\ddot{\gamma }-\dot{\alpha }\dot{\gamma }\right)-e^{-2\left(\beta +\gamma \right)}\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^t\wedge h^{\phi }\hfill \\ \hfill & +e^{-\alpha -\beta -2\gamma }\left[{\dot{\gamma }}^{\prime }-\dot{\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-\dot{\beta }\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^r\wedge h^{\phi },\hfill \\ \hfill R_{\phantom{a}\theta }^r=& -e^{-\alpha -\beta -2\gamma }\left[{\dot{\gamma }}^{\prime }-\dot{\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-\dot{\beta }\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^t\wedge h^{\theta }\hfill \\ \hfill & +\left\{e^{-2\left(\beta +\gamma \right)}\left[r^{-1}\left({\beta }^{\prime }-{\gamma }^{\prime }\right)+{\beta }^{\prime }{\gamma }^{\prime }-{\gamma }^{\prime \prime }\right]+e^{-2\left(\alpha +\gamma \right)}\left[\dot{\gamma }\left(\dot{\beta }+\dot{\gamma }\right)\right]\right\}{h}^r\wedge h^{\theta },\hfill \\ \hfill R_{\phantom{a}\phi }^r=& -e^{-\alpha -\beta -2\gamma }\left[{\dot{\gamma }}^{\prime }-\dot{\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-\dot{\beta }\left(r^{-1}+{\gamma }^{\prime }\right)\right]h^t\wedge h^{\phi }\hfill \\ \hfill & +\left\{e^{-2\left(\beta +\gamma \right)}\left[r^{-1}\left({\beta }^{\prime }-{\gamma }^{\prime }\right)+{\beta }^{\prime }{\gamma }^{\prime }-{\gamma }^{\prime \prime }\right]+e^{-2\left(\alpha +\gamma \right)}\left[\dot{\gamma }\left(\dot{\beta }+\dot{\gamma }\right)\right]\right\}{h}^r\wedge h^{\phi },\hfill \\ \hfill R_{\phantom{a}\phi }^{\theta }=& \left\{r^{-2}{e}^{-2\gamma }+e^{-2\left(\alpha +\gamma \right)}{\dot{\gamma }}^2-e^{-2\left(\beta +\gamma \right)}\left[{\gamma }^{\prime }\left({\gamma }^{\prime }+2r^{-1}\right)+r^{-2}\right]\right\}{h}^{\theta }\wedge h^{\phi }.\hfill \end{array}$$

The components of the Ricci tensor are calculated as

$$\begin{array}{cc}\hfill {\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{tt}=& -e^{-2\left(\alpha +\gamma \right)}\left[\ddot{\beta }+\ddot{\gamma }+2\left(\ddot{\gamma }-\dot{\alpha }\dot{\gamma }\right)+\left(\dot{\beta }-\dot{\alpha }\right)\left(\dot{\beta }+\dot{\gamma }\right)\right]\hfill \\ \hfill & +e^{-2\left(\beta +\gamma \right)}\left[{\alpha }^{″}+{\gamma }^{″}+\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)\left({\alpha }^{\prime }-{\beta }^{\prime }+2r^{-1}+2{\gamma }^{\prime }\right)\right],\hfill \\ \hfill {\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{rt}=& -2e^{-\alpha -\beta -2\gamma }\left[{\dot{\gamma }}^{\prime }-\dot{\gamma }\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-\dot{\beta }\left(r^{-1}+{\gamma }^{\prime }\right)\right]={\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{rt},\hfill \\ \hfill {\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{rr}=& -e^{-2\left(\beta +\gamma \right)}\left[{\alpha }^{″}+3{\gamma }^{″}+\left({\alpha }^{\prime }-{\beta }^{\prime }\right)\left({\alpha }^{\prime }+{\gamma }^{\prime }\right)-2{\beta }^{\prime }{\gamma }^{\prime }-2r^{-1}\left({\beta }^{\prime }-{\gamma }^{\prime }\right)\right]\hfill \\ \hfill & +e^{-2\left(\alpha +\gamma \right)}\left[\ddot{\beta }+\ddot{\gamma }+\left(\dot{\beta }+\dot{\gamma }\right)\left(\dot{\beta }-\dot{\alpha }+2\dot{\gamma }\right)\right],\hfill \\ \hfill {\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{\theta \theta }=& r^{-2}{e}^{-2\gamma }+e^{-2\left(\alpha +\gamma \right)}\left[\ddot{\gamma }+\dot{\gamma }\left(\dot{\beta }-\dot{\alpha }+2\dot{\gamma }\right)\right]\hfill \\ \hfill & -e^{-2\left(\beta +\gamma \right)}\left[{\gamma }^{″}+r^{-1}\left(r^{-1}+2{\gamma }^{\prime }\right)+\left(2{\gamma }^{\prime }-{\beta }^{\prime }+{\alpha }^{\prime }\right)\left(r^{-1}+{\gamma }^{\prime }\right)\right]={\left(\mathrm{R}\mathrm{i}\mathrm{c}\right)}_{\phi \phi }.\hfill \end{array}$$

Now, Ricci’s scalar is given by

$$\begin{array}{cc}\hfill R=& -2r^{-2}{e}^{-2\gamma }-2e^{-2\left(\alpha +\gamma \right)}\left[\ddot{\beta }+3\ddot{\gamma }+3\dot{\gamma }\left(\dot{\beta }-\dot{\alpha }+\dot{\gamma }\right)+\dot{\beta }\left(\dot{\beta }-\dot{\alpha }\right)\right]\hfill \\ \hfill & +2e^{-2\left(\beta +\gamma \right)}\left[{\alpha }^{″}+3{\gamma }^{″}+\left(r^{-1}+6{\gamma }^{\prime }-2{\beta }^{\prime }+2{\alpha }^{\prime }\right)\left(r^{-1}\right)\right]\hfill \\ \hfill & +2e^{-2\left(\beta +\gamma \right)}\left[\left(3{\gamma }^{\prime }+{\alpha }^{\prime }\right)\left({\gamma }^{\prime }-{\beta }^{\prime }\right)+\left(2{\gamma }^{\prime }+{\alpha }^{\prime }\right){\alpha }^{\prime }\right].\hfill \end{array}$$

Therefore, the non-zero components of the Einstein tensor in LyST theory are given by

$$\begin{array}{}\mathrm{(53a)}& \begin{array}{cc}{G}_{tt}=\hfill & {\displaystyle \frac{1}{r^2}}{e}^{-2\gamma }+\left(3{\dot{\gamma }}^2+2\dot{\gamma }\dot{\beta }\right)e^{-2\left(\alpha +\gamma \right)}\hfill \\ & -\left(2{\gamma }^{″}+{\gamma }^{\prime 2}-2{\gamma }^{\prime }{\beta }^{\prime }+{\displaystyle \frac{4{\gamma }^{\prime }}{r}}-{\displaystyle \frac{2{\beta }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}\right)e^{-2\left(\beta +\gamma \right)},\hfill \end{array}\mathrm{(53b)}& \begin{array}{cc}{G}_{tr}=\hfill & -2\left(\dot{{\gamma }^{\prime }}-\dot{\gamma }{\alpha }^{\prime }-{\gamma }^{\prime }\dot{\beta }-{\gamma }^{\prime }\dot{\gamma }-{\displaystyle \frac{\dot{\beta }}{r}}\right)e^{-\alpha -\beta -2\gamma },\hfill \end{array}\mathrm{(53c)}& \begin{array}{cc}{G}_{rr}=\hfill & {\displaystyle \frac{1}{r^2}}{e}^{-2\gamma }+\left(2\ddot{\gamma }+{\dot{\gamma }}^2-2\dot{\gamma }\dot{\alpha }\right)e^{-2\left(\alpha +\gamma \right)}\hfill \\ & -\left(3{\gamma }^{\prime 2}+2{\gamma }^{\prime }{\alpha }^{\prime }+{\displaystyle \frac{4{\gamma }^{\prime }}{r}}+{\displaystyle \frac{2{\alpha }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}\right)e^{-2\left(\beta +\gamma \right)},\hfill \end{array}\mathrm{(53d)}& \begin{array}{cc}{G}_{\theta \theta }=\hfill & G_{\phi \phi }=\left(\ddot{\beta }+2\ddot{\gamma }+{\dot{\beta }}^2+{\dot{\gamma }}^2+2\dot{\gamma }\dot{\beta }-2\dot{\gamma }\dot{\alpha }-\dot{\alpha }\dot{\beta }\right)e^{-2\left(\alpha +\gamma \right)}\hfill \\ & -\left({\alpha }^{″}+2{\gamma }^{″}+{\alpha }^{\prime 2}+{\gamma }^{\prime 2}+2{\gamma }^{\prime }{\alpha }^{\prime }-2{\gamma }^{\prime }{\beta }^{\prime }-{\alpha }^{\prime }{\beta }^{\prime }+{\displaystyle \frac{2{\gamma }^{\prime }}{r}}+{\displaystyle \frac{{\alpha }^{\prime }}{r}}-{\displaystyle \frac{{\beta }^{\prime }}{r}}\right)e^{-2\left(\beta +\gamma \right)}.\hfill \end{array}\end{array}$$

4.1. Vacuum Solution

Here, the energy-momentum tensor vanishes. If $\varphi$ is time independent, then $\dot{\gamma }=0$, and from Equation (53b), we have

$$\left({\gamma }^{\prime }+{\displaystyle \frac{1}{r}}\right)\dot{\beta }=0.$$

The solution ${\gamma }^{\prime }=-r^{-1}$ is incompatible with Equation (53c); therefore, we must have $\dot{\beta }=0$. In this case, Equation (53c) implies ${\alpha }^{\prime }={\alpha }^{\prime }\left(r\right)$, then $\alpha ={\alpha }_1\left(r\right)+{\alpha }_2\left(t\right)$. The only time-dependent coefficient in (50) is A, and we can absorb ${\alpha }_2$ into the time coordinate by redefining

$$e^{{\alpha }_2\left(t\right)}dt\to dt.$$

Since ${\alpha }_2$ is assumed to be smooth within our framework, it is also continuous and therefore integrable. This guarantees that the transformation above is well defined. This redefinition eliminates the explicit time dependence of the metric coefficients while preserving the general structure of the line element and introducing no mixed terms. Moreover, if we choose not to absorb ${\alpha }_2$, we will find that the field equations impose no restriction on it, so we may fix it arbitrarily, for instance by setting ${\alpha }_2=0$. Therefore, Birkhoff’s theorem3 holds when the scale function is time-independent.

Therefore, the nonzero components of the Einstein tensor can be written as follows:

$$\begin{array}{}\mathrm{(54a)}& \begin{array}{cc}{G}_{tt}\hfill & ={\varphi }^{-2}\left[{\displaystyle \frac{1}{r^2}}-\left(2{\gamma }^{″}+{\gamma }^{\prime 2}-2{\gamma }^{\prime }{\beta }^{\prime }+{\displaystyle \frac{4{\gamma }^{\prime }}{r}}-{\displaystyle \frac{2{\beta }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}\right)e^{-2\beta }\right],\hfill \end{array}\mathrm{(54b)}& \begin{array}{cc}{G}_{rr}\hfill & ={\varphi }^{-2}\left[{\displaystyle \frac{1}{r^2}}-\left(3{\gamma }^{\prime 2}+2{\gamma }^{\prime }{\alpha }^{\prime }+{\displaystyle \frac{4{\gamma }^{\prime }}{r}}+{\displaystyle \frac{2{\alpha }^{\prime }}{r}}+{\displaystyle \frac{1}{r^2}}\right)e^{-2\beta }\right],\hfill \end{array}\mathrm{(54c)}& \begin{array}{cc}{G}_{\theta \theta }& =G_{\phi \phi }=\hfill \\ & =-{\varphi }^{-2}\left({\alpha }^{″}+2{\gamma }^{″}+{\alpha }^{\prime 2}+{\gamma }^{\prime 2}+2{\gamma }^{\prime }{\alpha }^{\prime }-2{\gamma }^{\prime }{\beta }^{\prime }-{\alpha }^{\prime }{\beta }^{\prime }+{\displaystyle \frac{2{\gamma }^{\prime }}{r}}+{\displaystyle \frac{{\alpha }^{\prime }}{r}}-{\displaystyle \frac{{\beta }^{\prime }}{r}}\right)e^{-2\beta }.\hfill \end{array}\end{array}$$

The solution of the corresponding field equations is given by

$$d{s}^2={\varphi }^2\left[{\displaystyle \frac{1}{{\varphi }^2}}\left(1-{\displaystyle \frac{a}{r\varphi }}\right)d{t}^2-{\displaystyle \frac{{\left(r\varphi \right)}^{\prime 2}}{{\varphi }^2\left(1-{\displaystyle \frac{a}{r\varphi }}\right)}}d{r}^2-r^{2}d{\Omega }^2\right],$$

(55)

where $d{\Omega }^2=d{\theta }^2+{sin}^2\theta d{\phi }^2$, a is an integration constant, and $\varphi =\varphi \left(r\right)$ is still arbitrary.

By defining a new coordinate $\tilde{r}=r\varphi \left(r\right)$, one finds that the line element has the same functional form as the one in the Schwarzschild case, with $a={\tilde{r}}_s$ being the Schwarzschild radius:

$$d{s}^2=\left(1-{\displaystyle \frac{{\tilde{r}}_S}{\tilde{r}}}\right)d{t}^2-{\displaystyle \frac{d{\tilde{r}}^2}{\left(1-{\displaystyle \frac{{\tilde{r}}_S}{\tilde{r}}}\right)}}-{\tilde{r}}^{2}d{\Omega }^2.$$

(56)

This is an important result, as it shows that the Schwarzschild line element is not just a particular solution. In fact, it is the only solution, equivalent to any other solution with a non-trivial scale function, but expressed in a specific Lyra reference system. This solution can be expressed in another reference system with a non-trivial scale function, but keeping a Schwarzschild-type form with respect to the metric components

$$d{s}^2={\varphi }^2\left(r\right)\left[\mu \left(r\right)d{t}^2-{\displaystyle \frac{d{r}^2}{\mu \left(r\right)}}-r^{2}d{\Omega }^2\right].$$

(57)

Here, the scale function is

$$\varphi \left(r\right)={\left(1-{\displaystyle \frac{r}{r_L}}\right)}^{-1},$$

(58)

and

$$\mu \left(r\right)={\left(1-{\displaystyle \frac{r}{r_L}}\right)}^2\left(1-{\displaystyle \frac{a}{r}}+{\displaystyle \frac{a}{r_L}}\right)={\left(1-{\displaystyle \frac{r}{r_L}}\right)}^2\left({\displaystyle \frac{1-r_S/r}{1-r_S/r_L}}\right),$$

(59)

where

$$r_S={\displaystyle \frac{a}{1-{\displaystyle \frac{a}{r_L}}}},$$

(60)

is the Schwarzschild radius in the new Lyra reference system and $r_L$ is a positive integration constant called the Lyra radius.

If the line element (57) is interpreted as an exterior solution, the function $\mu \left(r\right)$ must remain positive, which holds only within the range $r_S<r<r_L$. This suggests the possibility of a spatially limited spacetime. However, cosmological observations indicate the existence of structures on extremely large scales, implying that spacetime is either infinite or bounded by a value of $r_L$ far beyond the currently observed scales of the universe. The latter scenario is also mathematically plausible, provided that cosmological observations occur within the range $r_S\ll r\ll r_L$, in a limit where the coordinates r and $\tilde{r}$ are practically indistinguishable. Given its significant implications, attention will be payed to the expression (57) of the line element, and it will be referred to as the Lyra–Schwarzschild solution.

4.2. Correction to Newtonian Gravity

In a spherically symmetric spacetime, the r equation of motion in the Newtonian limit, as given in Equation (48), simplifies to

$${\displaystyle \frac{d^{2}r}{d{t}^2}=-{\displaystyle \frac{d\mathcal{U}}{dr}},}$$

(61)

where $\mathcal{U}={\displaystyle \frac{1}{2}}{h}_{00}+\delta \varphi$. The weak field perturbations $\delta \varphi$ and $h_{00}$ are found by Taylor expanding the functions (58) and (59) within the range $r_S<r<r_L$:

$$\varphi \left(r\right)\approx 1+{\displaystyle \frac{r}{r_L}}+{\displaystyle \frac{r^2}{r_L^2}},$$

(62)

and

$$\mu \left(r\right)\approx 1+{\displaystyle \frac{3r_S}{r_L}}\left(1+{\displaystyle \frac{r_S}{r_L}}\right)-{\displaystyle \frac{r_S}{r}}\left(1+{\displaystyle \frac{r_S}{r_L}}\right)-{\displaystyle \frac{2r}{r_L}}\left(1+{\displaystyle \frac{3r_S}{2r_L}}\right)+{\displaystyle \frac{r^2}{r_L^2}}.$$

(63)

In (62) and (63), we made explicit the corrections to the Newtonian limit:

$$\delta \varphi :={\displaystyle \frac{r}{r_L}}+{\displaystyle \frac{r^2}{r_L^2}},h_{00}:=\left(1+{\displaystyle \frac{r_S}{r_L}}\right)\left({\displaystyle \frac{3}{r_L}}-{\displaystyle \frac{1}{r}}\right)r_S-{\displaystyle \frac{2r}{r_L}}\left(1+{\displaystyle \frac{3r_S}{2r_L}}\right)+{\displaystyle \frac{r^2}{r_L^2}}.$$

(64)

Thus, the r equation can be written as follows:

$${\displaystyle \frac{d^{2}r}{d{t}^2}}=-{\displaystyle \frac{m_G}{r^2}}+{\displaystyle \frac{3m_G}{r_L^2}}{\left(1+{\displaystyle \frac{2m_G}{r_L}}\right)}^{-1}-{\displaystyle \frac{3r}{r_L^2}},$$

(65)

where $m_G$ is the geometric mass defined by

$$m_G:={\displaystyle \frac{{\tilde{r}}_S}{2}}={\displaystyle \frac{r_S}{2\left(1-\frac{r_S}{r_L}\right)}}\approx {\displaystyle \frac{r_S}{2}}\left(1+{\displaystyle \frac{r_S}{r_L}}\right).$$

(66)

Equation (66) reveals that the geometric mass, which acts as the source of the gravitational field, depends not only on $r_S$ but also on $r_L$. Meanwhile, second-order effects in Equation (65) include a constant repulsive acceleration and a term linear in r analogous to an anti-de Sitter contribution.

The existence of a Newtonian limit allows the identification of the Newtonian mass, which is a real and positive quantity. Accordingly, solution (59) can be rewritten by expressing the constant $r_s$ in terms of $m_G$ and $r_L$:

$$r_s={\displaystyle \frac{1}{\frac{1}{2m_G}+\frac{1}{r_L}}}.$$

(67)

Substituting (67) into (59), one obtains

$$\mu \left(r\right)={\left(1-{\displaystyle \frac{r}{r_L}}\right)}^2\left(1-{\displaystyle \frac{2m_G}{r}}+{\displaystyle \frac{2m_G}{r_L}}\right),$$

(68)

while $\varphi$ retains the form (58). With this parametrization, the line element becomes

$$\begin{array}{cc}\hfill d{s}^2=& \left(1-{\displaystyle \frac{2m_G}{r}}+{\displaystyle \frac{2m_G}{r_L}}\right)d{t}^2+{\left(1-{\displaystyle \frac{r}{r_L}}\right)}^{-4}{\left(1-{\displaystyle \frac{2m_G}{r}}+{\displaystyle \frac{2m_G}{r_L}}\right)}^{-1}d{r}^2\hfill \\ & +{\left(1-{\displaystyle \frac{r}{r_L}}\right)}^{-2}{r}^{2}d{\Omega }^2.\hfill \end{array}$$

(69)

The limit $\varphi \to 1$, which is equivalent to $r_L\to \infty$, defines the Schwarzschild limit in GR. In this case,

$$\mu \left(r\right)\to 1-{\displaystyle \frac{2m_G}{r}}$$

in this limit. This confirms that the solution admits a Schwarzschild limit and, consequently, that the parameter $r_s$ may be regarded as the generalization, within Lyra geometry, of the Schwarzschild radius.

4.3. The Cosmological Constant

The gravitational field experienced by test particles at spatial infinity can be obtained by taking the limit $r\to \infty$ in (59). In this case, the dominant contribution is quadratic:

$$\mu \left(r\right)\simeq \left(1+{\displaystyle \frac{2m_G}{r_L}}\right){\displaystyle \frac{r^2}{r_L^2}}.$$

(70)

For comparison, the Schwarzschild–de Sitter solution at large distances reads

$$\mu \left(r\right)=1-{\displaystyle \frac{r_S}{r}}-{\displaystyle \frac{\Lambda }{3}}{r}^2\simeq -{\displaystyle \frac{\Lambda }{3}}{r}^2.$$

(71)

From this, it follows that the parameter $r_L$ is directly related to both the source mass and the cosmological constant:

$$\Lambda \simeq -{\displaystyle \frac{3}{r_L^2}}\left(1+{\displaystyle \frac{2m_G}{r_L}}\right).$$

(72)

The sign of $r_L$ determines whether $\Lambda$ is positive or negative. The solution is asymptotically de Sitter ($\Lambda >0$) when $-2m_G<r_L<0$. However, in this case, the function $\mu \left(r\right)$ is negative for all positive values of r. This also implies $g_{00}<0$ and $g_{11}>0$, leading to a metric with a signature of the form $(-+--)$. On the other hand, if $r_L<-2m_G$ or $r_L>0$, the spacetime at large distances from the gravitational source is of the AdS type. Therefore, the large distance behavior may be grouped into three distinct classes:

• Class 1: $r_L>0$, asymptotically AdS solutions with positive $r_L$;
• Class 2: $r_L<-2m_G$, asymptotically AdS solutions with negative $r_L$;
• Class 3: $-2m_G<r_L<0$, asymptotically de Sitter solutions.

In these, $\mu \left(r\right)$ exhibits two positive real roots, one at

$$r={\displaystyle \frac{1}{\frac{1}{2m_G}+\frac{1}{r_L}}},$$

(73)

and the other at $r=r_L$. The point $r=r_L$ corresponds to a minimum of $\mu$. In Class 2 solutions, $\mu$ increases monotonically with the radial coordinate, approaching an AdS regime as $r\to \infty$. Class 3 solutions, by contrast, approach the de Sitter regime for large r. Nevertheless, in this case, the function $\mu$ remains negative for all positive values of r. From this point onward, our analysis will focus on the Class 1 case, defined by $r_L>0$, since this case is manifestly the most physically relevant.

5. Free Particle Motion

5.1. The Hamilton–Jacobi Approach

This section is dedicated to the study of free particle motion in Lyra–Schwarzschild spacetime. The Hamilton–Jacobi approach is employed [46] as it directly provides the solution in integral form. A more detailed discussion can be found in Ref. [49]. In the first place, the Lagrangian and Hamiltonian of a free particle in LyST theory are given by

$$L(x,\dot{x},\lambda )={\displaystyle \frac{1}{2}}m{\varphi }^2{g}_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu },\mathrm{and}H(x,p,\lambda )={\displaystyle \frac{1}{2m{\varphi }^2}}{g}^{\mu \nu }{p}_{\mu }{p}_{\nu },$$

(74)

where m is the rest mass, ${\dot{x}}^{\mu }$ are the velocities with respect to $\lambda$, and $p_{\mu }=\partial L/\partial {\dot{x}}^{\mu }$ are the canonical conjugate momenta. If $\lambda$ is an affine parameter, the following constraint holds:

$${\varphi }^2{g}_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=\epsilon .$$

(75)

For massive particles, $\epsilon$ is set to 1 and $\lambda$ is interpreted as the proper time. In contrast, for massless particles, $\epsilon$ is set to 0.

The Hamilton principal function $S(x,P,\lambda )$ generates a canonical transformation from the coordinates $(x,p)$ to the new coordinates $(X,P)$, where $X^{\mu }$ and $P_{\mu }$ are constants. The canonical relations are given by

$${\displaystyle p_{\mu }={\displaystyle \frac{\partial S(x,P,\lambda )}{\partial x^{\mu }}}\mathrm{and}{X}^{\mu }={\displaystyle \frac{\partial S(x,P,\lambda )}{\partial P_{\mu }}}.}$$

(76)

The evolution of the system is governed by the Hamilton–Jacobi equation:

$${\displaystyle H\left({\displaystyle x,{\displaystyle \frac{\partial S}{\partial x}},\lambda }\right)+{\displaystyle \frac{\partial S}{\partial \lambda }}=0.}$$

(77)

In the case of Lyra–Schwarzschild spacetime, the metric is given by Equation (57). After some calculations, the general solution of Equation (77) is found:

$$S=-{\displaystyle \frac{\epsilon m\lambda }{2}}+Et-\mathsf{\ell }\phi \pm \int dr\sqrt{{\displaystyle \frac{E^2}{{\mu }^2}}-{\displaystyle \frac{\epsilon m^2{\varphi }^2}{\mu }}-{\displaystyle \frac{{\mathsf{\ell }}^2}{\mu r^2}}},$$

(78)

where the constants $P_t$, $P_r$, and $P_{\phi }$ can be chosen as $P_t=E$, $P_r=-\epsilon /2$, and $P_{\phi }=-\mathsf{\ell }$, and $\mu$ is defined in Equation (59). Here, the coordinate $\theta$ does not appear, as the motion is confined to a plane passing through the origin, which can be chosen such that $\theta ={\displaystyle \frac{\pi }{2}}$.

Now, by replacing S in the second relation of (76), one obtains the general solution for the motion of a free particle:

$$\begin{array}{cc}\hfill t& =\pm k\int {\displaystyle \frac{dr}{\mu \sqrt{k^2-\epsilon \mu {\varphi }^2-{\displaystyle \frac{h^2\mu }{r^2}}}}},\hfill \end{array}$$

(79a)

$$\begin{array}{cc}\hfill \lambda & =\pm \int {\displaystyle \frac{{\varphi }^{2}dr}{\sqrt{k^2-\epsilon \mu {\varphi }^2-{\displaystyle \frac{h^2\mu }{r^2}}}}},\hfill \end{array}$$

(79b)

$$\begin{array}{cc}\hfill \phi & =\pm h\int {\displaystyle \frac{dr}{r^2\sqrt{k^2-\epsilon \mu {\varphi }^2-{\displaystyle \frac{h^2\mu }{r^2}}}}},\hfill \end{array}$$

(79c)

where $k={\displaystyle \frac{E}{m}}$ is the specific energy and $h={\displaystyle \frac{\mathsf{\ell }}{m}}$ is the specific angular momentum.

Finally, by using the relation $\tilde{r}=r\varphi \left(r\right)$, the integrals take the form of the Schwarzschild case, as expected

$$\begin{array}{cc}\hfill t& =\pm k\int {\displaystyle \frac{d\tilde{r}}{\left(1-{\displaystyle \frac{2m_G}{\tilde{r}}}\right)\sqrt{k^2-\left(\epsilon +{\displaystyle \frac{h^2}{{\tilde{r}}^2}}\right)\left(1-{\displaystyle \frac{2m_G}{\tilde{r}}}\right)}}},\hfill \end{array}$$

(80a)

$$\begin{array}{cc}\hfill \lambda & =\pm \int {\displaystyle \frac{d\tilde{r}}{\sqrt{k^2-\left(\epsilon +{\displaystyle \frac{h^2}{{\tilde{r}}^2}}\right)\left(1-{\displaystyle \frac{2m_G}{\tilde{r}}}\right)}}},\hfill \end{array}$$

(80b)

$$\begin{array}{cc}\hfill \phi & =\pm h\int {\displaystyle \frac{d\tilde{r}}{{\tilde{r}}^2\sqrt{k^2-\left(\epsilon +{\displaystyle \frac{h^2}{{\tilde{r}}^2}}\right)\left(1-{\displaystyle \frac{2m_G}{\tilde{r}}}\right)}}}.\hfill \end{array}$$

(80c)

This shows that motion in Lyra–Schwarzschild spacetime can be directly obtained from the well-established results of the Schwarzschild case through the relation $\tilde{r}=r\varphi \left(r\right)$.

5.2. Massive Particles

For massive particles, we have $\epsilon =1$, and $\lambda =\tau$, the proper time. From Equation (80a), we obtain

$$\mathcal{E}={\displaystyle \frac{1}{2}}{\dot{\tilde{r}}}^2+V_{\mathrm{eff}}={\displaystyle \frac{1}{2}}{\varphi }^4{\dot{r}}^2+V_{\mathrm{eff}},$$

(81)

where $\mathcal{E}=(k^2-1)/2$. Here, the quantity $V_{\mathrm{eff}}$ is the effective potential

$$\begin{array}{cc}\hfill V_{\mathrm{eff}}& :=-{\displaystyle \frac{m_G}{\tilde{r}}}+{\displaystyle \frac{h^2}{2{\tilde{r}}^2}}-{\displaystyle \frac{m_G{h}^2}{{\tilde{r}}^3}}\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill & =-{\displaystyle \frac{m_G}{r}}\left(1-{\displaystyle \frac{r}{r_L}}\right)+{\displaystyle \frac{h^2}{2r^2}}{\left(1-{\displaystyle \frac{r}{r_L}}\right)}^2-{\displaystyle \frac{m_G{h}^2}{r^3}}{\left(1-{\displaystyle \frac{r}{r_L}}\right)}^3.\hfill \end{array}$$

(83)

Thus, deriving Equation (80c), one obtains

$${\left({\displaystyle {\displaystyle \frac{d\tilde{r}}{d\phi }}}\right)}^2={\displaystyle \frac{2{\tilde{r}}^4}{h^2}}(\mathcal{E}-V_{\mathrm{eff}})\Rightarrow {\left({\displaystyle {\displaystyle \frac{d\tilde{u}}{d\phi }}}\right)}^2={\displaystyle \frac{2}{h^2}}(\mathcal{E}-V_{\mathrm{eff}}),$$

(84)

where $\tilde{u}=1/\tilde{r}$. Moreover, differentiating the second expression in (84) with respect to $\phi$ gives

$${\displaystyle \frac{d^2\tilde{u}}{d{\phi }^2}=-\frac{1}{h^2}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{u}}}=\frac{m_G}{h^2}-\tilde{u}+3m_G{\tilde{u}}^2,}$$

(85)

whose solution for $\tilde{u}=1/\tilde{r}$ corresponds to the standard Schwarzschild result. Furthermore, the solution for $u=1/r$ follows from the relation $u=\tilde{u}+u_L$, with $u_L=1/r_L$.

The different types of motion can be determined by analyzing the behavior of the effective potential as a function of the parameters ℓ and $m_G$. To this end, it is necessary to examine the first and second derivatives of the effective potential:

$$\begin{array}{cc}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{dr}}\hfill & {\displaystyle ={\displaystyle \frac{d\tilde{r}}{dr}}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{r}}}={\varphi }^2{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{r}}},}\hfill \end{array}$$

(86)

$$\begin{array}{cc}{\displaystyle \frac{d^2{V}_{\mathrm{eff}}}{d{r}^2}}\hfill & {\displaystyle =\frac{d^2\tilde{r}}{d{r}^2}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{r}}}+{\left({\displaystyle {\displaystyle \frac{d\tilde{r}}{dr}}}\right)}^2\frac{d^2{V}_{\mathrm{eff}}}{d{\tilde{r}}^2}=\frac{2{\varphi }^3}{r_L}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{r}}}+{\varphi }^4\frac{d^2{V}_{\mathrm{eff}}}{d{\tilde{r}}^2}.}\hfill \end{array}$$

(87)

Since $\varphi \ne 0$, the number of critical points is the same in both coordinate systems,

$${\left({\displaystyle {\displaystyle \frac{d{V}_{\mathrm{eff}}}{dr}}}\right)}_{r_{crit}}={\left({\displaystyle {\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{r}}}}\right)}_{{\tilde{r}}_{crit}}=0,$$

(88)

as well as their stability,

$$\mathrm{sgn}{\left({\displaystyle \frac{d^2{V}_{\mathrm{eff}}}{d{r}^2}}\right)}_{r_{crit}}=\mathrm{sgn}{\left({\displaystyle \frac{d^2{V}_{\mathrm{eff}}}{d{\tilde{r}}^2}}\right)}_{{\tilde{r}}_{crit}}.$$

(89)

From Equation (88), the critical points are given by

$${\tilde{r}}_{\pm }={\displaystyle \frac{h^2}{2m_G}}\left(1\pm \sqrt{1-{\displaystyle \frac{12m_G^2}{h^2}}}\right)=6m_G{\left(1\mp \sqrt{1-{\displaystyle \frac{12m_G^2}{h^2}}}\right)}^{-1},$$

(90)

or, equivalently,

$$r_{\pm }=6m_G{\left[\left(1+{\displaystyle \frac{6m_G}{r_L}}\right)\mp \sqrt{1-{\displaystyle \frac{12m_G^2}{h^2}}}\right]}^{-1}.$$

(91)

From Equation (91), one obtains the following cases for the behavior of the effective potential:

• $h^2<12m_G^2$: No critical points.
• $h^2=12m_G^2$: One inflection point with zero slope at $r_{inf}\equiv 6m_G{\left(1+{\displaystyle \frac{6m_G}{r_L}}\right)}^{-1}$.
• $h^2>12m_G^2$: Two equilibrium points: $r_{+}$ (stable) and $r_{-}$ (unstable).

On the other hand, the roots of the effective potential are given by

$${\tilde{R}}_{\pm }={\displaystyle \frac{{\mathsf{\ell }}^2}{4m_G}}\left(1\pm \sqrt{1-{\displaystyle \frac{16m_G^2}{h^2}}}\right)=4m_G{\left(1\mp \sqrt{1-{\displaystyle \frac{16m_G^2}{h^2}}}\right)}^{-1},$$

(92)

or, equivalently

$$R_{\pm }=4m_G{\left[\left(1+{\displaystyle \frac{4m_G}{r_L}}\right)\mp \sqrt{1-{\displaystyle \frac{16m_G^2}{h^2}}}\right]}^{-1}.$$

(93)

Thus, one obtains the following cases:

• $h^2<16m_G^2$: No real roots.
• $h^2=16m_G^2$: One root, given by $r_{-}=R_0\equiv 4m_G{\left(1+{\displaystyle \frac{4m_G}{r_L}}\right)}^{-1}$.
• $h^2>16m_G^2$: Two roots, given by Equation (93).

In addition, the following asymptotic behavior is observed:

$$V_{\mathrm{eff}}(\tilde{r}\to \infty )\equiv V_{\mathrm{eff}}(r\to r_L)\to 0^{-},$$

(94)

$$V_{\mathrm{eff}}(\tilde{r}\to 0)\equiv V_{\mathrm{eff}}(r\to 0)\to -\infty .$$

(95)

All these results lead to Figure 1, which illustrates the general behavior of the effective potential as a function of the parameter $x^2=h^2/m_G^2$. Meanwhile, Figure 2 shows the different types of motion allowed for a massive particle, classified into three families of effective potential based on the value of $x^2$.

5.3. Bound Orbits and Perihelion Precession

The most interesting case for trajectories of massive particles corresponds to bound orbits, characterized by case 3 in Figure 2b,c. These are the familiar cyclic orbits of test particles around gravitational sources. It is useful to investigate the near-Newtonian regime to establish correspondences with observational data. In the Newtonian case, we remember that the orbital equation of motion has analytical solutions that describe closed elliptical orbits. In General Relativity, the geodesic acquires a cubic correction term with the form $m_G{u}^3$ for $u=1/r$, which prevents closed solutions but admits a perturbative treatment. The orbit resembles the Newtonian ellipse, but with an additional perihelion precession. For n revolutions, the angular shift in GR is given by

$$\Delta {\phi }_{\mathrm{GR}}={\displaystyle \frac{6\pi n{m}_G}{a(1-e^2)}},$$

(96)

where e is the eccentricity and a is the Newtonian major semi-axis. This result matches observations in the Solar System [50].

For LyST theory, the first-order approximation of the geodesic equation leads to

$${\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{du}{d\phi }}\right)}^2\approx {\displaystyle \frac{E}{h^2}}+{\displaystyle \frac{m_G}{h^2}}u-{\displaystyle \frac{1}{2}}{u}^2+m_G{u}^3+{\displaystyle \frac{u}{r_L}}.$$

(97)

Up to the second order in u, this has the same structure as the Newtonian equivalent, with an effective gravitational parameter

$${\tilde{m}}_G:=m_G+{\displaystyle \frac{h^2}{r_L}}.$$

(98)

At this order, the resulting orbit remains elliptical,

$$u={\displaystyle \frac{1}{r_{\mathrm{med}}}}\left({\displaystyle \frac{1+ecos\phi }{1-e^2}}\right),$$

(99)

with

$$e:=\sqrt{1+{\displaystyle \frac{2\mathcal{E}{h}^2}{{\tilde{m}}_G^2}}},\mathrm{and}{r}_{\mathrm{med}}:={\displaystyle \frac{h^2}{{\tilde{m}}_G}}{\displaystyle \frac{1}{1-e^2}}.$$

(100)

The orbit parameter $r_{\mathrm{med}}$ stands for the orbit’s medium radius.

Proceeding with perturbation theory, one finds that the precession becomes

$$\Delta \phi =6\pi n{\displaystyle \frac{m_G^2}{h^2}}\left[1+{\displaystyle \frac{h^2}{m_G{r}_L}}\right].$$

(101)

The first term in this equation is of first order, since the ratio $h^2/m_G$ must be of the same order of magnitude as the orbital radius. This term is precisely the expression for the perihelion precession of Mercury, as predicted by General Relativity. Equation (101) then results in

$$\Delta \phi =\Delta {\phi }_{\mathrm{GR}}\left[1+{\displaystyle \frac{r_{\mathrm{med}}}{r_L}}(1-e^2)\right].$$

(102)

On the other hand, the second term in (102) is of second order, due to the constraint $r_{\mathrm{med}}\ll r_L$ at the scales under consideration. In this sense, within the Solar System, where the most significant measurement of Mercury’s perihelion precession is given by ${(43.1\pm 0.5)}^{″}$ per century, ref. [51] the second term should not contribute by more than 1% of the General Relativity value. The only inference that can be drawn is that $r_L\gtrsim 100r^{\prime }$, where $r^{\prime }=0.4\mathrm{AU}$ is approximately Mercury’s orbital radius.

Thus, this result may be regarded as an indication that solar system phenomena are not suitable for constraining the values of $r_L$. On the other hand, we may conclude that, at least at the solar system level, LyST gravity cannot be ruled out.

5.4. Photons

In the case of photons, $\epsilon =0$. Then, from Equation (80b):

$${\displaystyle \frac{m_G^2}{b^2}}={\displaystyle \frac{m_G^2}{h^2}}{\varphi }^4{\dot{r}}^2+V_{\mathrm{eff}},$$

(103)

where $b=h/k$. Here, the effective potential is identified as

$$\begin{array}{cc}\hfill V_{\mathrm{eff}}& :={\displaystyle \frac{m_G^2}{{\tilde{r}}^2}}\left(1-{\displaystyle \frac{2m_G}{\tilde{r}}}\right)\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{m_G^2}{r^2}}{\left(1-{\displaystyle \frac{r}{r_L}}\right)}^2\left(1-{\displaystyle \frac{2m_G}{r}}+{\displaystyle \frac{2m_G}{r_L}}\right).\hfill \end{array}$$

(105)

Once again, from Equation (80c), one obtains

$${\displaystyle \frac{d^2\tilde{u}}{d{\phi }^2}=-\frac{1}{2m_G^2}{\displaystyle \frac{d{V}_{\mathrm{eff}}}{d\tilde{u}}}=-\tilde{u}+3m_G{\tilde{u}}^2,}$$

(106)

whose solution for $u=1/r$ follows from $u=\tilde{u}+u_L$, with $u_L=1/r_L$ and $\tilde{u}$ being the standard Schwarzschild solution.

The preservation of critical points and their stability follows from Equations (86) and (87). In this case, there is only one critical point:

$${\tilde{r}}_c=3m_G\mathrm{or}{r}_c={\displaystyle \frac{3m_G}{1+\frac{3m_G}{r_L}}},$$

(107)

which is a unstable equilibrium point, giving the maximum value for the potential:

$$V_{\mathrm{eff}}^{max}=V_{\mathrm{eff}}\left(r_c\right)={\displaystyle \frac{1}{27}}.$$

(108)

On the other hand, there is also only one root of the effective potential, which is precisely the Schwarzschild radius:

$${\tilde{r}}_S=2m_G\mathrm{or}{r}_S={\displaystyle \frac{2m_G}{1+\frac{2m_G}{r_L}}}.$$

(109)

Moreover, the following asymptotic behavior is observed:

$$V_{\mathrm{eff}}(\tilde{r}\to \infty )\equiv V_{\mathrm{eff}}(r\to r_L)\to 0^{+},$$

(110)

$$V_{\mathrm{eff}}(\tilde{r}\to 0)\equiv V_{\mathrm{eff}}(r\to 0)\to -\infty .$$

(111)

All these results lead to Figure 3, which illustrates the unique behavior of the potential, as it was chosen in such a way that it does not depend on the parameter h.

5.4.1. Hyperbolic Motion

The hyperbolic motion of photons describes a scattering process in which the light beam approaches the gravitational source with impact parameter $b>\sqrt{27}{m}_G$, reaches a radius of closest approach $r_a$, and is subsequently deflected outward. The point of closest approach $r_a$ is attained precisely when $\dot{r}=0$ in (103):

$${\displaystyle \frac{m_G^2}{b^2}}=V_{\mathrm{eff}}\left(r_a\right).$$

(112)

The final value of the azimuthal angular coordinate is $\pi +\alpha$, where $\alpha$ is the scattering angle. The trajectories of approach and departure, as usual in the case of spherically symmetric potentials, are symmetric, and the angular coordinate at the point of closest approach is $\phi =(\pi +\alpha )/2$.

The initial conditions for such a hyperbolic trajectory are imposed at a radial distance where $m_G\ll r\ll r_L$ (the Minkowski limit), with $y=b$ and $\phi ={\phi }_0$, where ${\phi }_0\ll 1$. Integrating (106), we obtain

$${\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{\alpha }{2}}-{\phi }_0=m_G{\int }_{r_0}^{r_a}{\displaystyle \frac{dr}{r^2\sqrt{\frac{m_G^2}{b^2}-V_{\mathrm{eff}}\left(r\right)}}}.$$

(113)

Two remarks are in order at this point. First, $r_a$ is determined by (112). Although this appears straightforward, its practical determination is not trivial. Expanding the effective potential in this relation, one finds:

$$\begin{array}{cc}\hfill {\displaystyle \frac{m_G^2}{b^2}}& ={\displaystyle \frac{m_G^2}{r_a^2}}\left(1-{\displaystyle \frac{2m_G}{r_a}}\right)+{\displaystyle \frac{2m_G^3}{r_L^3}}+{\displaystyle \frac{m_G^2}{r_L^2}}\left(1-{\displaystyle \frac{6m_G}{r_a}}\right)\hfill \\ \hfill & -{\displaystyle \frac{2m_G^2}{r_L{r}_a}}\left(1-{\displaystyle \frac{3m_G}{r_a}}\right),\hfill \end{array}$$

(114)

which is a third-order equation in $r_a$. In addition, the integral in (112) also requires expanding the expression of $V_{\mathrm{eff}}\left(r\right)$. When an accurate result is required, the most efficient approach is to solve the problem numerically.

5.4.2. Gravitational Redshift

Consider an observer and a light source, both fixed in space. The source emits a pulse at event A, with coordinates $(t_E,r_E,{\theta }_E,{\phi }_E)$, which is subsequently received by the observer at event B, with coordinates $(t_R,r_R,{\theta }_R,{\phi }_R)$. Another pulse is emitted by the source at event C, with coordinates $(t_E+\Delta t_E,r_E,{\theta }_E,{\phi }_E)$, and received by the observer at event D, with coordinates $(t_R+\Delta t_R,r_R,{\theta }_R,{\phi }_R)$. As is well known, the photons will follow null geodesics, where the line element is $d{s}^2=0$ at any point. Therefore,

$$\mu \left(r\right)d{t}^2={\mu }^{-1}\left(r\right)d{r}^2+r^{2}d{\Omega }^2=-g_{ij}d{x}^{i}d{x}^j.$$

(115)

By choosing a parameterization $\lambda$, one can write

$$t_R-t_E={\int }_{{\lambda }_E}^{{\lambda }_R}d\lambda {\mu }^{-1/2}{\left({\displaystyle -g_{ij}{\displaystyle \frac{d{x}^i}{d\lambda }}{\displaystyle \frac{d{x}^j}{d\lambda }}}\right)}^{1/2}.$$

(116)

It is important to note that the integral on the right-hand side of this equation does not strictly depend on the parameterization but only on the initial and final points. Then,

$$t_R-t_E=(t_R+\Delta t_R)-(t_E+\Delta t_E)\Rightarrow \Delta t_E=\Delta t_R.$$

(117)

Now, recall that the source and the observer have fixed spatial coordinates. So the curves described by them have a line element of the form $d{s}^2=d{\tau }^2={\varphi }^2{g}_{00}d{t}^2$, with $\tau$ being the corresponding proper time. Consequently,

$${\displaystyle \frac{\Delta {\tau }_E}{\Delta {\tau }_R}}={\displaystyle \frac{\sqrt{{\varphi }^2\left(r_E\right)\mu \left(r_E\right)}\Delta t_E}{\sqrt{{\varphi }^2\left(r_R\right)\mu \left(r_R\right)}\Delta t_R}}=\sqrt{{\displaystyle \frac{1-\frac{2m_G}{r_E}+\frac{2m_G}{r_L}}{1-\frac{2m_G}{r_R}+\frac{2m_G}{r_L}}}}.$$

(118)

The gravitational redshift is defined in terms of the emission and reception wavelengths:

$$z={\displaystyle \frac{{\lambda }_R-{\lambda }_E}{{\lambda }_E}}.$$

(119)

Here, $\lambda$ represents a wavelength instead of the parameter in Equation (116). In the current units, wavelengths and frequencies are related through $\lambda ={\nu }^{-1}=\Delta \tau$. The general form of the gravitational redshift in Lyra spacetime is obtained by replacing Equation (118) into Equation (119):

$$z=\sqrt{{\displaystyle \frac{1-\frac{2m_G}{r_R}+\frac{2m_G}{r_L}}{1-\frac{2m_G}{r_E}+\frac{2m_G}{r_L}}}}-1.$$

(120)

In particular, when the light source and the observer are far away from the gravitational source, such that $r_E,r_R\gg r_S$, expression (120) simplifies to

$$z\approx {\displaystyle \frac{m_G}{r_E}}\left(1-{\displaystyle \frac{r_E}{r_R}}\right).$$

(121)

The conclusion is that redshift occurs only for $r_E<r_R$, while the opposite case causes blueshift. This classification holds even for the general case in Equation (120).

It is well known that the surface redshift of a compact, spherically symmetric matter configuration in Riemannian geometry is bounded by $z<2$ as a direct consequence of Buchdahl’s theorem. This theorem, derived from the Tolman–Oppenheimer–Volkoff (TOV) equation, requires that mass $m_G$ and radius R satisfy

$${\displaystyle \frac{m_G}{R}}<{\displaystyle \frac{9}{4}},$$

(122)

under the standard assumptions of isotropic pressure, monotonically decreasing density, and regularity at the center. The substitution of Equation (122) into Equation (120), with $r_R,r_L\to \infty$, yields the aforementioned redshift bound. In the present work, however, we do not attempt to analyze the physical implications of the TOV equation when the Lyra scale function is introduced; this issue will be addressed in a subsequent study.

5.4.3. Causal Structure

The radial motion $(h^2=0)$ for photons $(\epsilon =0)$ can be determined from Equation (80a),

$$t=\pm {\displaystyle \frac{dr}{{\left(1-\frac{r}{r_L}\right)}^2\left(1-\frac{2m_G}{r}+\frac{2m_G}{r_L}\right)}},$$

(123)

whose solution is given by

$$t_{\pm }=\tau \pm \left[{\displaystyle \frac{r}{1-\frac{r}{r_L}}}+2m_{G}ln\left({\displaystyle \frac{r}{1-\frac{r}{r_L}}}-2m_G\right)\right],$$

(124)

where $\tau$ is an integration constant. Note that this expression diverges for $r=r_S$ and $r=r_L$. However, the only physical singularity is $r=0$, as one can verify from the expression of the Kretschmann scalar:

$$K={\displaystyle \frac{48m_G^2}{{\tilde{r}}^6}}={\displaystyle \frac{12r_S^2}{r^6}}{\displaystyle \frac{{\left(1-\frac{r}{r_L}\right)}^6}{{\left(1-\frac{r_S}{r_L}\right)}^2}}.$$

(125)

Therefore, $r=r_S$ and $r=r_L$ are just coordinate singularities, as shown in Figure 4. The singularity $r=r_S$ can be removed in a similar way to the Schwarzschild case. Meanwhile, the singularity $r=r_L$ is a consequence of the transformation $\tilde{r}=r\varphi \left(r\right)$. This makes sense when considering that $r=r_L$ corresponds to $\tilde{r}=\infty$, which is neither a physical singularity nor a physical place.

6. Final Remarks

Lyra scalar-tensor theory is formulated on a Lyra manifold with a torsion-free, metric-compatible connection. The fundamental fields of this theory are the metric tensor $g_{\mu \nu }$ and the scale function $\varphi$. The presence of the scalar field modifies the canonical basis of the tensor bundles, leading to a transformation law for Lyra reference systems that differs from that of General Relativity. The metric-compatible and torsion-free conditions are imposed to make LyST theory as similar to General Relativity as possible. In this sense, LyST theory can be viewed as an extension of General Relativity on a Lyra manifold with a nontrivial scale function.

Field equations in LyST theory are derived from the standard variational principle applied to a Lyra-invariant action. This action generalizes the Einstein–Hilbert action via the minimal coupling principle, incorporating a Lyra-invariant volume element. Equation (48) shows that LyST theory is compatible with Newtonian gravity in the linearized and static approximation. The resulting Newtonian gravitational potential is given by $\mathcal{U}={\displaystyle \frac{1}{2}}{h}_{00}+\delta \varphi$, where $\delta \varphi$ denotes the perturbation of the Lyra scale function. Thus, gravity in LyST theory is also governed by this perturbation, as it represents a quantity independent of the metric.

The most general spherically symmetric solution in LyST theory depends on a single parameter and a freely selectable scale function, as shown in Equation (55). This freedom suggests the existence of an infinite family of solutions satisfying the field equations. However, by defining a new radial coordinate $\tilde{r}=r\varphi \left(r\right)$, one obtains the exact expression of the standard Schwarzschild solution, where the aforementioned parameter is the Schwarzschild radius ${\tilde{r}}_S$. This leads us to the analogue of Birkhoff’s theorem in the case of Lyra gravity: the Schwarzschild solution is the only physical solution, and the general expression is simply a result of a coordinate transformation involving the scale function. Requiring that the general expression preserve the structure of the Schwarzschild metric leads to a specific choice of the scale function: $\varphi \left(r\right)={(1-r/r_L)}^{-1}$, where $r_L>0$ is a new parameter, known as the Lyra radius, with $r<r_L$. The resulting metric is referred to as the Lyra–Schwarzschild solution. It has a coordinate singularity at $r_S={(1/{\tilde{r}}_S+1/r_L)}^{-1}$ and $r=r_L$, yet it is equivalent to the Schwarzschild metric under the above transformation.

In the limit $r_L\to \infty$, one recovers the standard Schwarzschild metric, with the radial coordinates becoming identical, $\tilde{r}=r$. This suggests that the Lyra–Schwarzschild metric is merely an alternative representation of the Schwarzschild solution, adapted to the case of a spatially finite universe bounded by $r_L$. Could this apparent finiteness be an actual feature of the spatial extent of our universe, or is it merely a consequence of adopting a particular coordinate system? According to the standard ΛCDM model, the universe is generally considered spatially flat, which implies an infinite spatial extension. Thus, the finiteness in the Lyra–Schwarzschild expression seems to be just a matter of the coordinate system. However, the converse is also plausible: the universe might be spatially finite, characterized by an extremely large Lyra radius well beyond the bounds of any cosmological scale currently accessible to observation. In this case, the Lyra–Schwarzschild description would be nearly indistinguishable from that of the Schwarzschild solution, since the relevant scales satisfy $r⋘r_L$. This raises the possibility that we may be inadvertently confusing coordinate systems, interpreting physical results within an unintended frame.

In the Newtonian approximation of the spherically symmetric solution, the equation of motion for a massive particle, formulated in the Lyra–Schwarzschild description, is given by Equation (65). The geometric mass $m_G$, expressed in both coordinate systems, is provided by Equation (66). In the first order in $r_L^{-1}$ the equation of motion reduces to the standard expression in Newtonian gravity, with the geometric mass still influenced by the Lyra radius. Second-order effects introduce a constant repulsive acceleration and an additional term analogous to an anti-de Sitter contribution. It should be noted that particle motion remains affected by the Lyra radius even in the absence of matter distributions, since the anti-de Sitter term persists when $m_G=0$. The contribution of this term to the equation of motion increases as r approaches $r_L$. Therefore, while uncertainties in measurements at solar-system-size scales can be used to set lower bounds to $r_L$, Equation (65) could be employed to estimate its value by observing particle trajectories at large scales, where $r\sim r_L$.

The Hamilton–Jacobi method offers a formal and straightforward approach to derive the equations of motion for the spherically symmetric solution. More than merely serving as a consistency check with respect to the classical approach of integrating the equations of motion, this formalism provides a robust and effective framework for identifying the dynamical invariants that underlie the system’s integrability and its solutions. This is particularly valuable for more complex scenarios that may be addressed in future work, such as Lyra–Reissner–Nordstrom (charged black holes) and Lyra–Kerr–Newmann (rotating black hole) solutions. In the Lyra–Schwarzschild description, these equations are given by Equation (79). They are equivalent under the transformation $\tilde{r}=r\varphi \left(r\right)$ to those of the standard Schwarzschild case, as provided by Equation (80). An analysis of the effective potential in both coordinate systems suggests that $r_L$ appears as a new critical point introduced by the scale function. However, this value lies outside the physical domain, since $r>r_L$ is forbidden. As a result, the overall behavior of the effective potential, whether expressed in terms of r or $\tilde{r}$, remains nearly identical, i.e., yielding the same types of motion in both cases. Consequently, the particle trajectories in the Lyra–Schwarzschild description can be directly obtained from the well-known trajectories in the standard Schwarzschild case via the aforementioned coordinate transformation. In fact, the solutions expressed in terms of the inverse radial coordinate differ only by the constant $u_L=1/r_L$. In the case of photons, the redshift is given by Equation (120), which reduces to the standard Schwarzschild expression when both the source and the observer are located far from the event horizon at $r_S$ (for a fixed $r_L\gg r_S$).

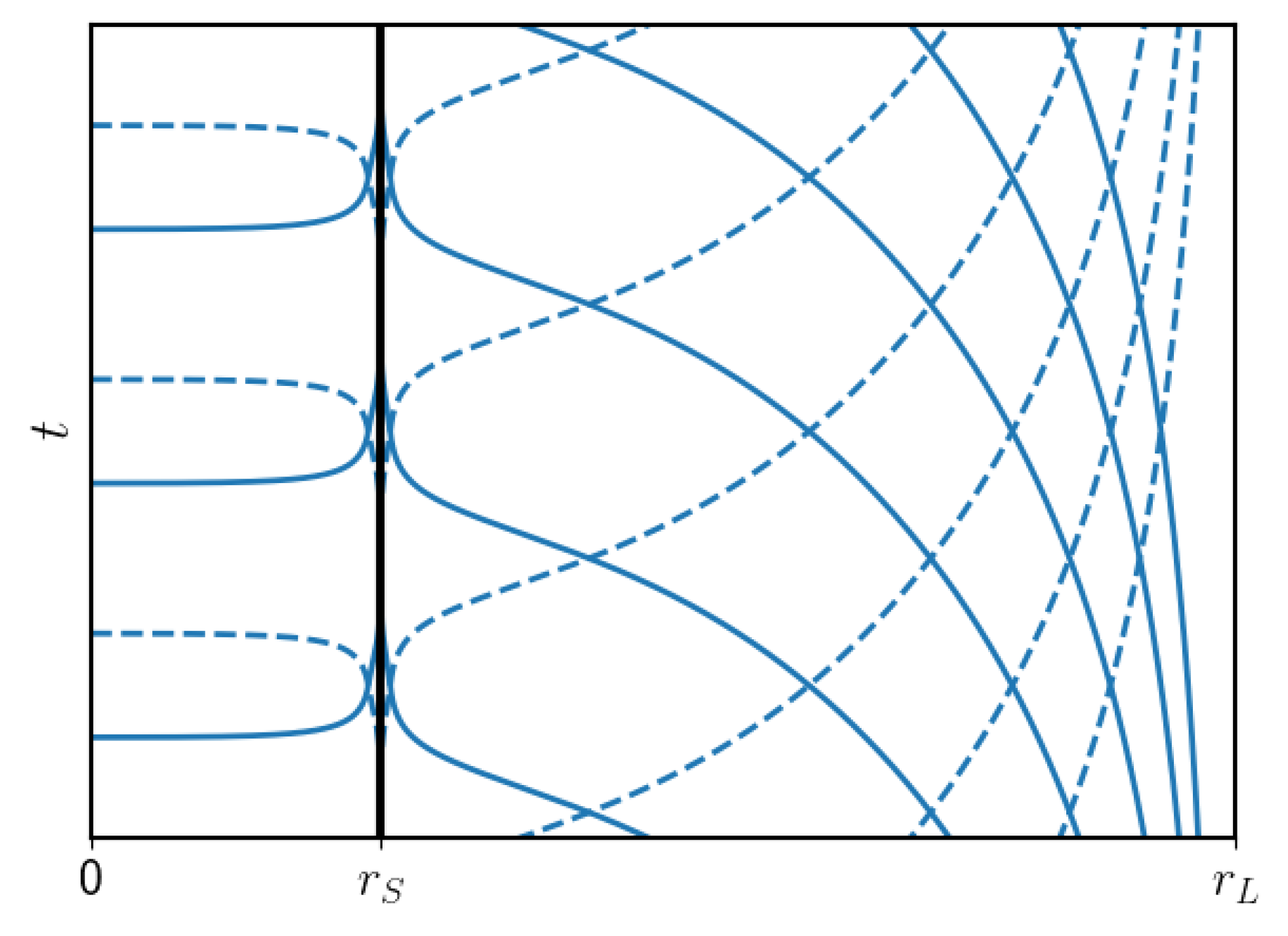
On the other hand, the causal structure presented by the Lyra–Schwarzschild description is very similar to that of the Schwarzschild case in the regime $r\ll r_L$. The only physical singularity remains at the coordinate origin $r=0$, as indicated by Equation (103). The main difference in the causal structure is that the lightcones become significantly narrower in the regime $r\gg r_S$, eventually collapsing at $r_L$. These results encourage the study of other spherically symmetric solutions, such as an analog of the Reissner–Nordstrom metric in GR, as well as other cases of LyST gravity applied to more general solutions with different symmetries, gravitational waves, and even more general constructions like the Einstein–Cartan theory.