Stability Analysis of Magnetized Quark Matter in Tsallis Statistics
Abstract
1. Introduction
2. Nonextensive NJL Model in the Strong Magnetic Field
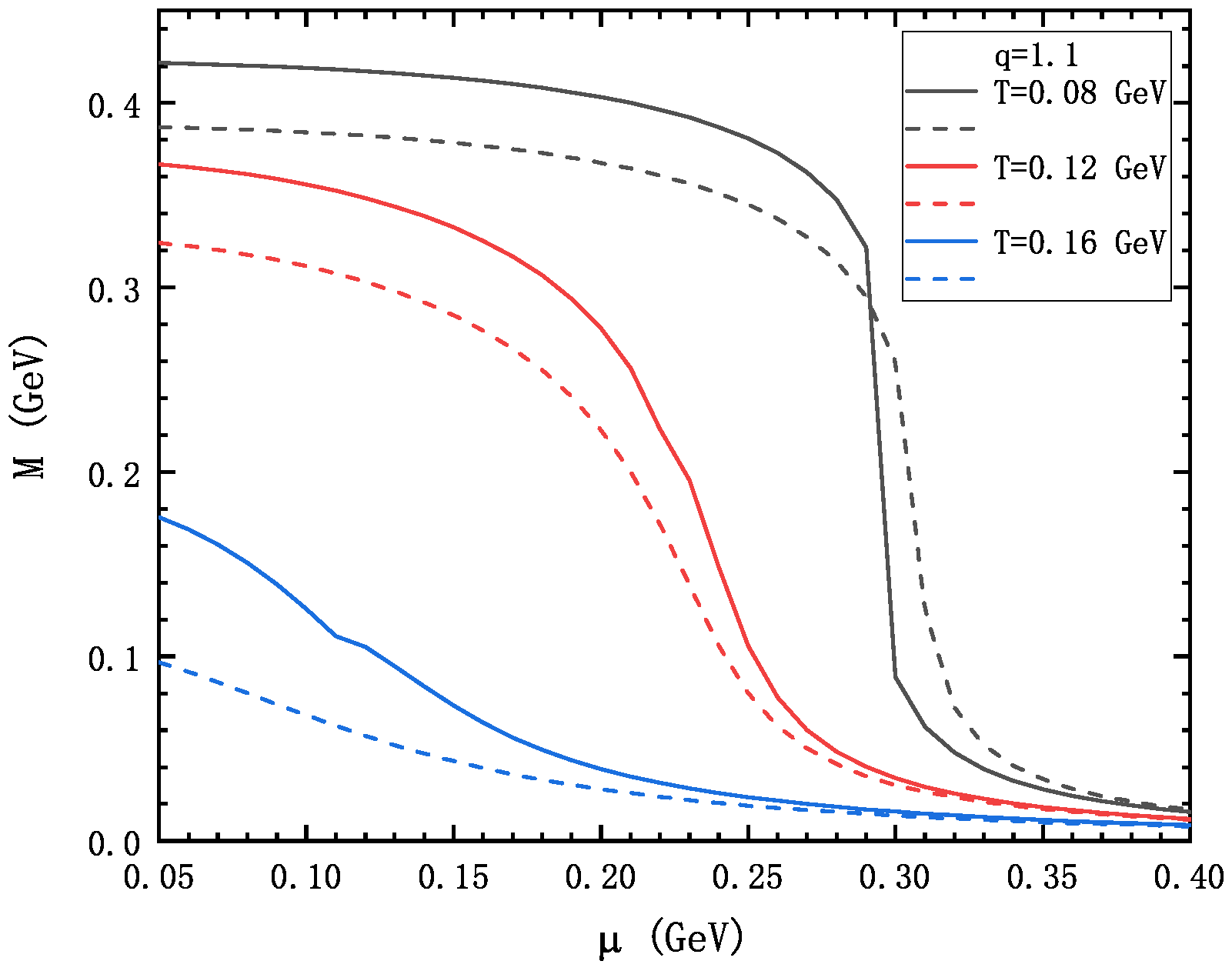
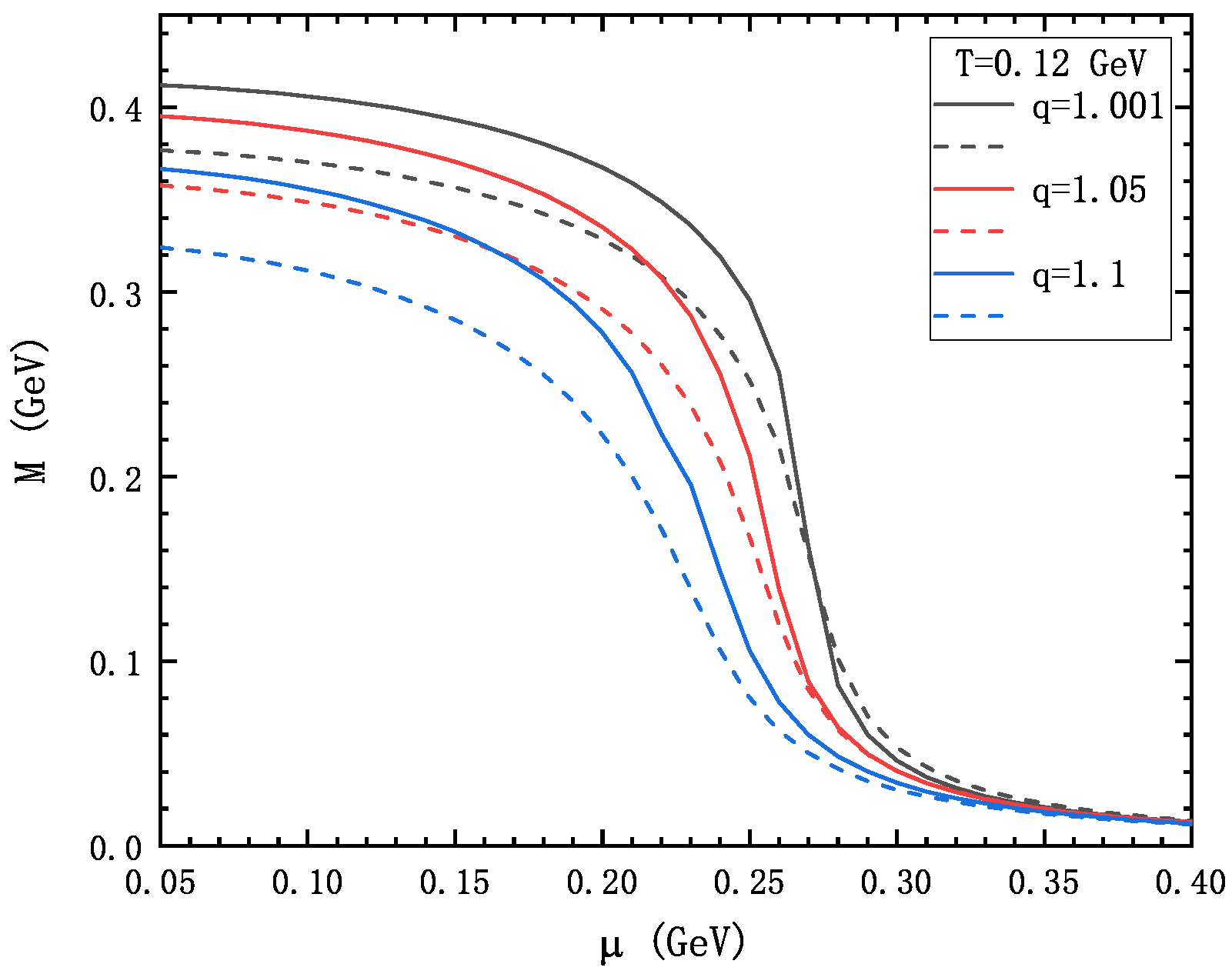
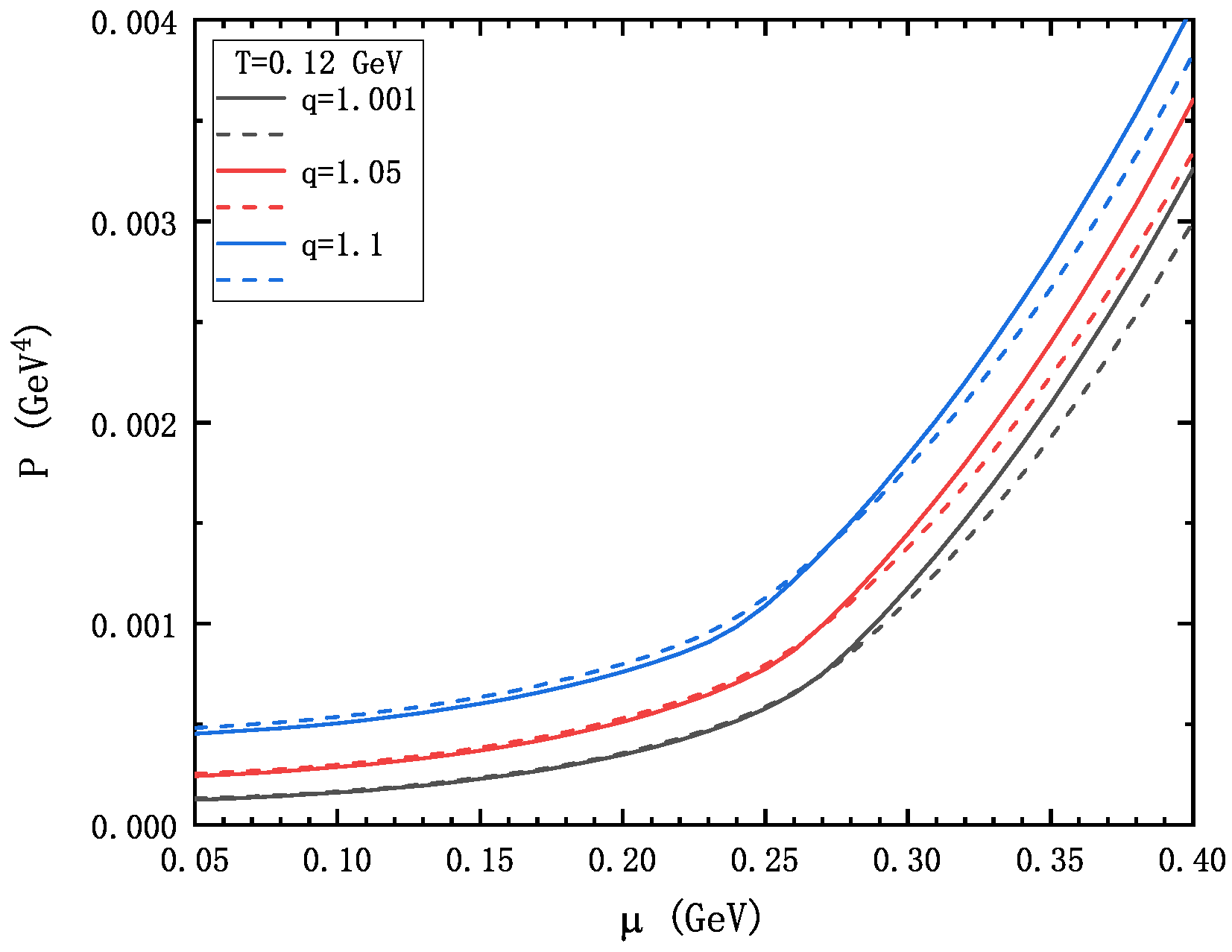
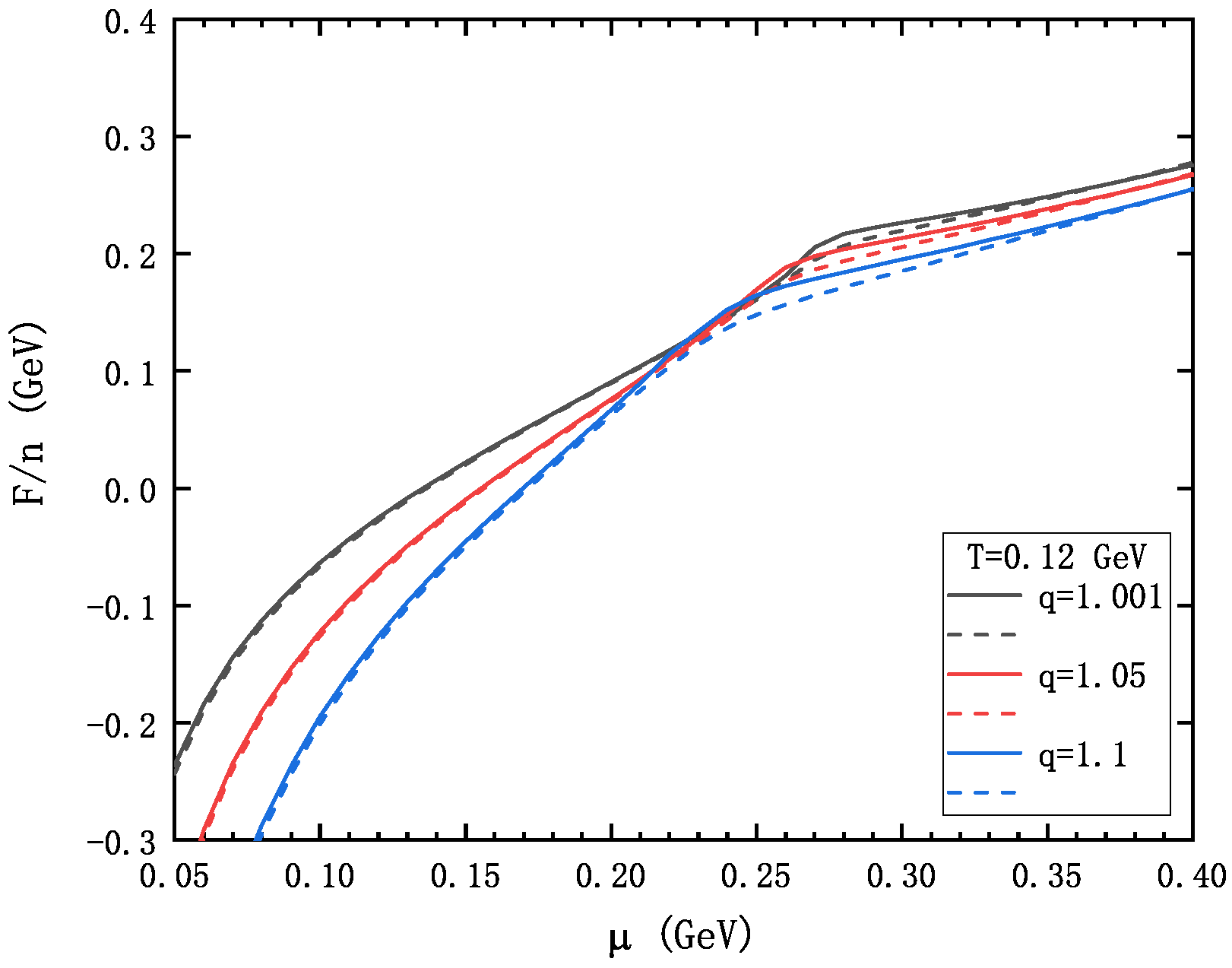
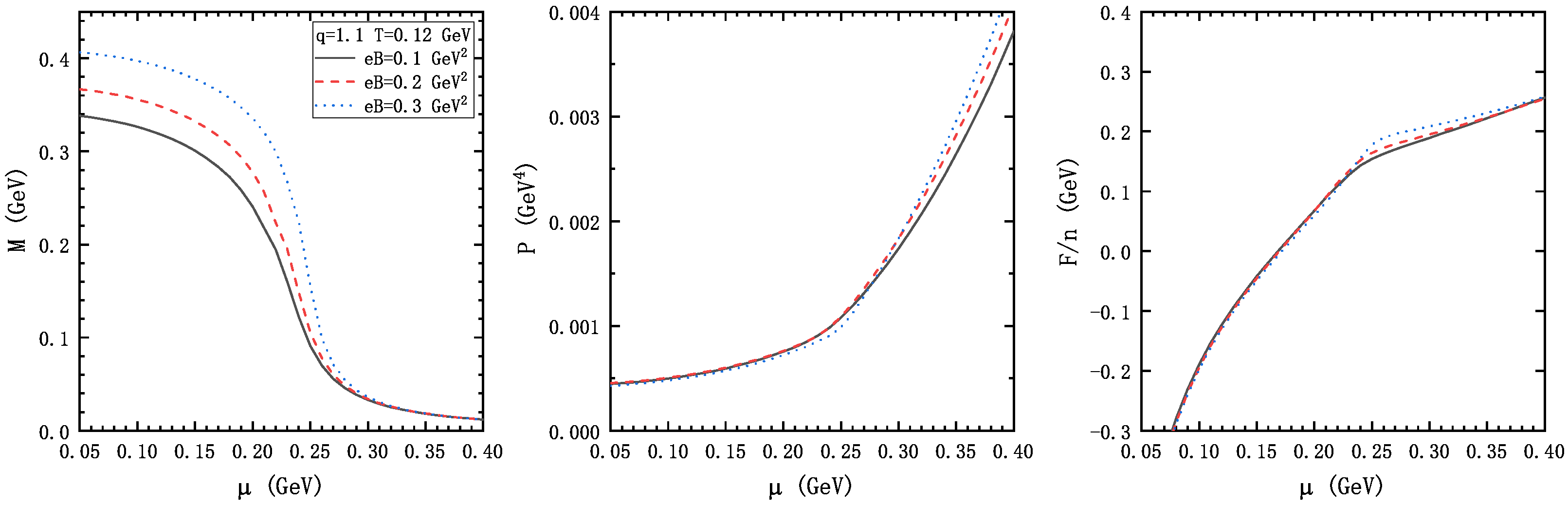
3. Numerical Result and Discussion
4. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuryak, E.V. Quantum Chromodynamics and the Theory of Superdense Matter. Phys. Rep. 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Abelev, B.I.; Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amoett, J.; Anderson, S.D.; Aderson, M.; Arkhipkin, D.; Averichev, G.S.; Averichev, G.S.; et al. [STAR] Strange particle production in p + p collisions at s**(1/2) = 200-GeV. Phys. Rev. C 2007, 75, 064901. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Quintana, A.A.; Abramyan, A.; Adamová, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Aguilar Salazar, S.; et al. [ALICE] Transverse momentum spectra of charged particles in proton-proton collisions at = 900 GeV with ALICE at the LHC. Phys. Lett. B 2010, 693, 53–68. [Google Scholar] [CrossRef]
- Tannenbaum, M.J. Recent results in relativistic heavy ion collisions: From ‘a new state of matter’ to ‘the perfect fluid’. Rep. Prog. Phys. 2006, 69, 2005–2060. [Google Scholar] [CrossRef]
- Wilson, K.G. Confinement of Quarks. Phys. Rev. D 1974, 10, 2445–2459. [Google Scholar] [CrossRef]
- Asakawa, M.; Yazaki, K. Chiral Restoration at Finite Density and Temperature. Nucl. Phys. A 1989, 504, 668–684. [Google Scholar] [CrossRef]
- Costa, P.; Ruivo, M.C.; de Sousa, C.A. Thermodynamics and critical behavior in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2008, 77, 096001. [Google Scholar] [CrossRef]
- Steinbrecher, P. [HotQCD] The QCD crossover at zero and non-zero baryon densities from Lattice QCD. Nucl. Phys. A 2019, 982, 847–850. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Karthik, N.; Laermann, E.; Lahiri, A.; Larsen, R.; Li, S.T.; et al. [HotQCD] Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 2019, 795, 15–21. [Google Scholar] [CrossRef]
- Satz, H. Color deconfinement in nuclear collisions. Rep. Prog. Phys. 2000, 63, 1511. [Google Scholar] [CrossRef]
- McLerran, L.; Pisarski, R.D. Phases of cold, dense quarks at large N(c). Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
- Kitazawa, M.; Koide, T.; Kunihiro, T.; Nemoto, Y. Chiral and color superconducting phase transitions with vector interaction in a simple model. Prog. Theor. Phys. 2002, 108, 929–951, Erratum in Prog. Theor. Phys. 2003, 110, 185–186. [Google Scholar] [CrossRef]
- Blaschke, D.; Volkov, M.K.; Yudichev, V.L. Coexistence of color superconductivity and chiral symmetry breaking within the NJL model. Eur. Phys. J. A 2003, 17, 103–110. [Google Scholar] [CrossRef]
- Hatsuda, T.; Tachibana, M.; Yamamoto, N.; Baym, G. New critical point induced by the axial anomaly in dense QCD. Phys. Rev. Lett. 2006, 97, 122001. [Google Scholar] [CrossRef] [PubMed]
- Carignano, S.; Nickel, D.; Buballa, M. Influence of vector interaction and Polyakov loop dynamics on inhomogeneous chiral symmetry breaking phases. Phys. Rev. D 2010, 82, 054009. [Google Scholar] [CrossRef]
- Bratovic, N.M.; Hatsuda, T.; Weise, W. Role of Vector Interaction and Axial Anomaly in the PNJL Modeling of the QCD Phase Diagram. Phys. Lett. B 2013, 719, 131–135. [Google Scholar] [CrossRef]
- Philipsen, O. The QCD equation of state from the lattice. Prog. Part. Nucl. Phys. 2013, 70, 55–107. [Google Scholar] [CrossRef]
- Ukawa, A. Kenneth Wilson and lattice QCD. J. Statist. Phys. 2015, 160, 1081. [Google Scholar] [CrossRef]
- Meyer, H.B. QCD at non-zero temperature from the lattice. In Proceedings of the 33rd International Symposium on Lattice Field Theory (LATTICE 2015), Kobe, Japan, 14–18 July 2015. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Hatsuda, T.; Kunihiro, T. QCD phenomenology based on a chiral effective Lagrangian. Phys. Rep. 1994, 247, 221–367. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Fukushima, K. Phase diagrams in the three-flavor Nambu-Jona-Lasinio model with the Polyakov loop. Phys. Rev. D 2008, 77, 114028, Erratum in Phys. Rev. D 2008, 78, 039902. [Google Scholar] [CrossRef]
- Lo, P.M. Polyakov loop susceptibilities in pure gauge system. J. Phys. Conf. Ser. 2014, 503, 012034. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Statist. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitanand, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Aoki, K.; Aphecetche, L.; Armendariz, R.; et al. [PHENIX] Identified charged hadron production in p + p collisions at = 200 and 62.4 GeV. Phys. Rev. C 2011, 83, 064903. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic Thermodynamics: Transverse Momentum Distributions in High-Energy Physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. On the interpretation of nonextensive parameter q in Tsallis statistics and Levy distributions. Phys. Rev. Lett. 2000, 84, 2770. [Google Scholar] [CrossRef]
- Wilk, G.; Wlodarczyk, Z. Power laws in elementary and heavy-ion collisions: A Story of fluctuations and nonextensivity? Eur. Phys. J. A 2009, 40, 299–312. [Google Scholar] [CrossRef]
- Marques, L.; Andrade-II, E.; Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 2013, 87, 114022. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and multiple hard scattering in pp collisions at the LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar] [CrossRef]
- Marques, L.; Cleymans, J.; Deppman, A. Description of High-Energy pp Collisions Using Tsallis Thermodynamics: Transverse Momentum and Rapidity Distributions. Phys. Rev. D 2015, 91, 054025. [Google Scholar] [CrossRef]
- Deppman, A. Thermodynamics with fractal structure, Tsallis statistics and hadrons. Phys. Rev. D 2016, 93, 054001. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy ion collisions: ‘Event by event P and CP violation’. Nucl. Phys. A 2008, 803, 227–253. [Google Scholar] [CrossRef]
- Kadam, G.; Pal, S.; Bhattacharyya, A. Interacting hadron resonance gas model in magnetic field and the fluctuations of conserved charges. J. Phys. G 2020, 47, 125106. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The Role of constraints within generalized nonextensive statistics. Physica A 1998, 261, 534. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009; ISBN 978-0-387-85358-1/978-0-387-85359-8. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis Distribution in Proton-Proton Collisions at = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. The Tsallis Distribution at Large Transverse Momenta. Eur. Phys. J. C 2015, 75, 430. [Google Scholar] [CrossRef]
- Endrödi, G. QCD equation of state at nonzero magnetic fields in the Hadron Resonance Gas model. J. High Energy Phys. 2013, 2013, 23. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrödi, G.; Katz, S.D.; Schäfer, A. The QCD equation of state in background magnetic fields. J. High Energy Phys. 2014, 2014, 177. [Google Scholar] [CrossRef]
- Menezes, D.P.; Benghi Pinto, M.; Avancini, S.S.; Perez Martinez, A.; Providencia, C. Quark matter under strong magnetic fields in the Nambu-Jona-Lasinio Model. Phys. Rev. C 2009, 79, 035807. [Google Scholar] [CrossRef]
- Boomsma, J.K.; Boer, D. The Influence of strong magnetic fields and instantons on the phase structure of the two-flavor NJL model. Phys. Rev. D 2010, 81, 074005. [Google Scholar] [CrossRef]
- Buballa, M.; Oertel, M. Strange quark matter with dynamically generated quark masses. Phys. Lett. B 1999, 457, 261–267. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Schafer, A. QCD quark condensate in external magnetic fields. Phys. Rev. D 2012, 86, 071502. [Google Scholar] [CrossRef]
- Avancini, S.S.; Menezes, D.P.; Providencia, C. Finite temperature quark matter under strong magnetic fields. Phys. Rev. C 2011, 83, 065805. [Google Scholar] [CrossRef]
- Rożynek, J.; Wilk, G. Nonextensive Nambu-Jona-Lasinio Model of QCD matter. Eur. Phys. J. A 2016, 52, 13, Erratum in Eur. Phys. J. A 2016, 52, 204. [Google Scholar] [CrossRef]
- Chakrabarty, S. Quark matter in strong magnetic field. Phys. Rev. D 1996, 54, 1306–1316. [Google Scholar] [CrossRef]
- Fraga, E.S.; Mizher, A.J. Chiral transition in a strong magnetic background. Phys. Rev. D 2008, 78, 025016. [Google Scholar] [CrossRef]
- Beck, C. Nonextensive statistical mechanics and particle spectra in elementary interactions. Physica A 2000, 286, 164–180. [Google Scholar] [CrossRef]
- Cleymans, J.; Hamar, G.; Levai, P.; Wheaton, S. Near-thermal equilibrium with Tsallis distributions in heavy ion collisions. J. Phys. G 2009, 36, 064018. [Google Scholar] [CrossRef]
- Beck, C. Superstatistics in high energy physics: Application to cosmic ray energy spectra and e+e− annihilation. Eur. Phys. J. A 2009, 40, 267–273. [Google Scholar] [CrossRef]
- Aamodt, K.; Abel, N.; Abeysekara, U.; Abrahantes, A.Q.; Abramyan, A.; Adamova, D.; Aggarwal, M.M.; Aglieri Rinella, G.; Agocs, A.G.; Aguilar Salazar, S.; et al. [ALICE] Production of pions, kaons and protons in pp collisions at = 900 GeV with ALICE at the LHC. Eur. Phys. J. C 2011, 71, 1655. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Diab, A.M. Chiral magnetic properties of QCD phase-diagram. Eur. Phys. J. A 2021, 57, 200. [Google Scholar] [CrossRef]
- Benvenuto, O.G. White dwarf stars as strange quark matter detectors. J. Phys. G 2005, 31, L13–L17. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ghosh, S.K.; Joardar, P.S.; Mallick, R.; Raha, S. The conversion of Neutron star to Strange star: A two step process. Phys. Rev. C 2006, 74, 065804. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wen, X.-J. Stability Analysis of Magnetized Quark Matter in Tsallis Statistics. Universe 2025, 11, 312. https://doi.org/10.3390/universe11090312
Zhang J, Wen X-J. Stability Analysis of Magnetized Quark Matter in Tsallis Statistics. Universe. 2025; 11(9):312. https://doi.org/10.3390/universe11090312
Chicago/Turabian StyleZhang, Jia, and Xin-Jian Wen. 2025. "Stability Analysis of Magnetized Quark Matter in Tsallis Statistics" Universe 11, no. 9: 312. https://doi.org/10.3390/universe11090312
APA StyleZhang, J., & Wen, X.-J. (2025). Stability Analysis of Magnetized Quark Matter in Tsallis Statistics. Universe, 11(9), 312. https://doi.org/10.3390/universe11090312






