Black Hole Solution Free of Ghosts in f(R) Gravity Coupled with Two Scalar Fields
Abstract
1. Introduction
2. Basis of Theory
3. Gravity with Two Scalar Fields
4. Spherically Symmetric Solution in Theory
4.1. Novel Solution
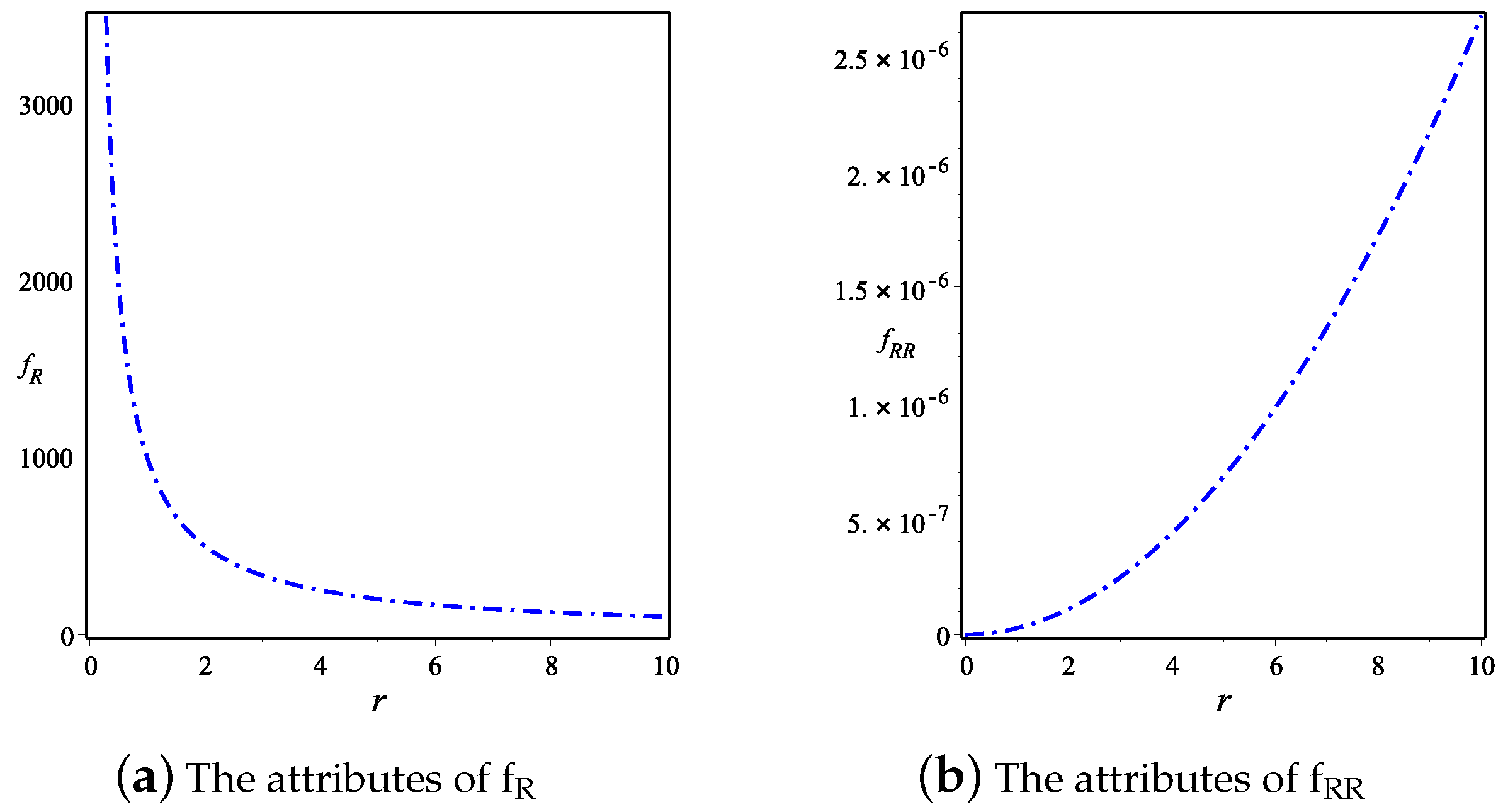
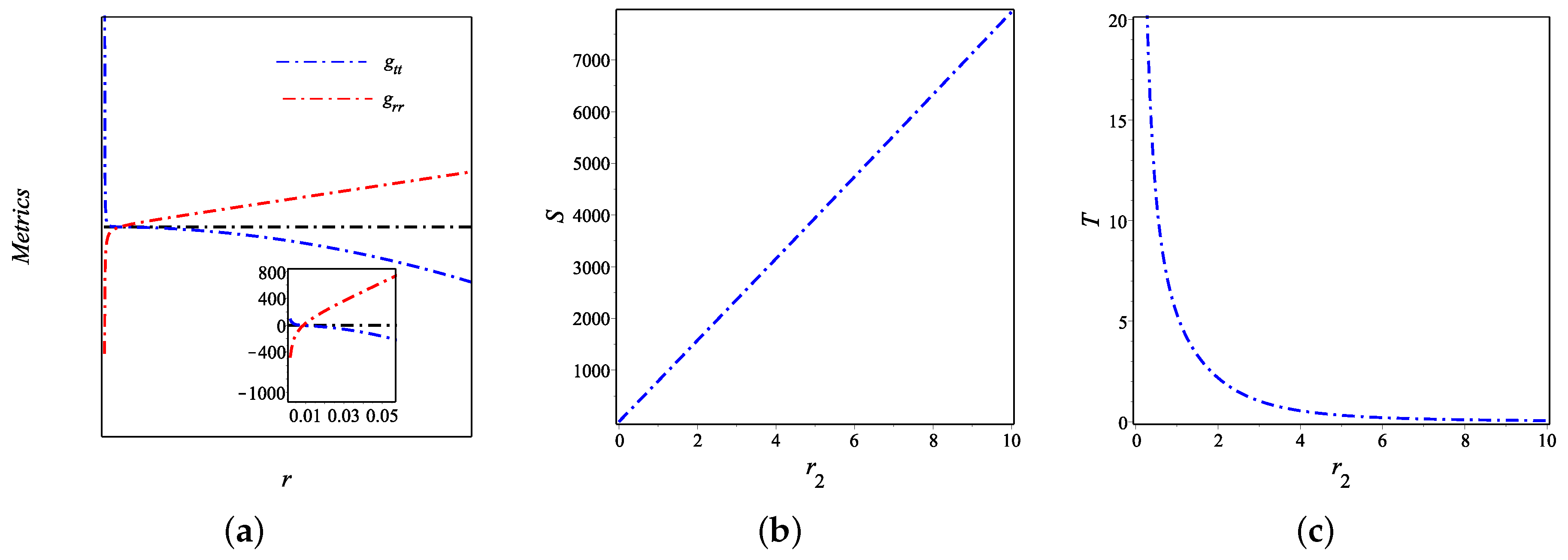
4.2. The Physical Characteristics of Solution (22)
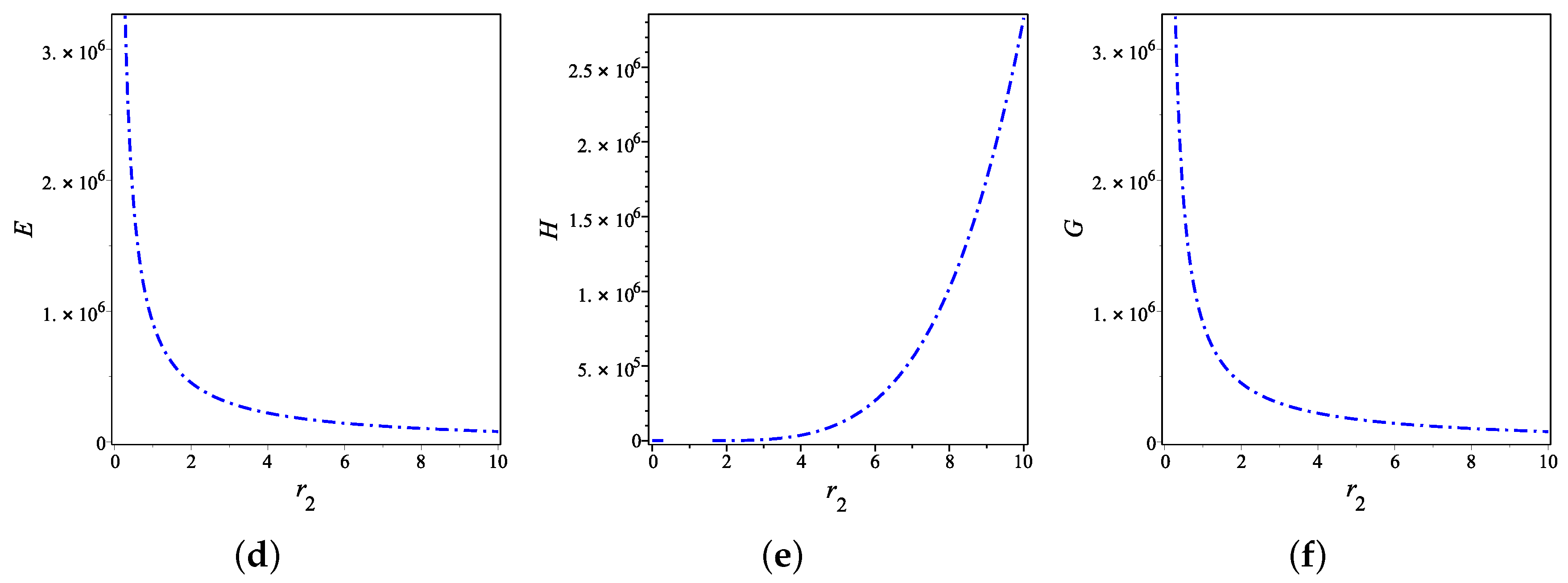
5. The Thermodynamic Characteristics of the Black Hole Solution
6. Solution of the Two Scalar Fields
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
| 1 | We verified all the computations in this work with the help of Maple 16 software. |
| 2 | Note that since we are dealing with spherical symmetry then . Therefore, . |
| 3 | |
| 4 | |
| 5 | Remember that the concept of entropy in linear non-metricity theory is not the same as in theory. By setting , we achieve a better understanding of the non-metricity theory. |
References
- Will, C.M. The confrontation between general relativity and experiment. Living Rev. Relativ. 2014, 17, 1–117. [Google Scholar] [CrossRef]
- Lalremruati, P.C.; Kalita, S. Periastron shift of compact stellar orbits from general relativistic and tidal distortion effects near Sgr A*. Mon. Not. R. Astron. Soc. 2021, 502, 3761–3768. [Google Scholar] [CrossRef]
- Abuter, R. et al. [GRAVITY Collaboration] Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Abuter, R. et al. [GRAVITY Collaboration] Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature quintessence. Int. J. Mod. Phys. D 2002, 11, 483–492. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Low surface brightness galaxies rotation curves in the low energy limit of Rn gravity: No need for dark matter? Mon. Not. R. Astron. Soc. 2007, 375, 1423–1440. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Disappearing cosmological constant in f(R) gravity. JETP Lett. 2007, 86, 157–163. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Large scale background temperature and mass fluctuations due to scale invariant primeval perturbations. Astrophys. J. Lett. 1982, 263, L1–L5. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Faber, S.M.; Primack, J.R.; Rees, M.J. Formation of Galaxies and Large Scale Structure with Cold Dark Matter. Nature 1984, 311, 517–525. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373–444. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Abercrombie, D.; Akchurin, N.; Akilli, E.; Maestre, J.A.; Allen, B.; Gonzalez, B.A.; Andrea, J.; Arbey, A.; Azuelos, G.; Azzi, P.; et al. Dark Matter benchmark models for early LHC Run-2 Searches: Report of the ATLAS/CMS Dark Matter Forum. Phys. Dark Universe 2020, 27, 100371. [Google Scholar] [CrossRef]
- Amole, C. et al. [PICO Collaboration] Improved dark matter search results from PICO-2L Run 2. Phys. Rev. D 2016, 93, 061101. [Google Scholar] [CrossRef]
- Aprile, E. et al. [XENON Collaboration] Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef]
- Ackermann, M. et al. [The Fermi-LAT Collaboration] Searching for Dark Matter Annihilation from Milky Way Dwarf Spheroidal Galaxies with Six Years of Fermi Large Area Telescope Data. Phys. Rev. Lett. 2015, 115, 231301. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.H.; Lee, C.M. Constraining the annihilating dark matter mass by the radio continuum spectral data of the NGC4214 galaxy. Phys. Rev. D 2020, 102, 063017. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. Constraining dark matter-nucleon scattering cross section by the background electron anti-neutrino flux data. Phys. Lett. B 2022, 825, 136887. [Google Scholar] [CrossRef]
- Chan, M.H.; Lee, C.M. Constraints on annihilating dark matter in the Omega Centauri cluster. Phys. Rev. D 2022, 105, 123006. [Google Scholar] [CrossRef]
- Riess, A.G. et al. [Supernova Search Team] Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S. et al. [Supernova Cosmology Project] Measurements of Ω and Λ from 42 High Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Stabile, A.; Capozziello, S. Galaxy rotation curves in f(R,ϕ) gravity. Phys. Rev. D 2013, 87, 064002. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Sharov, G.S. Early dark energy with power-law F(R) gravity. Phys. Lett. B 2023, 843, 137988. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Kalita, S. Gravitational Theories near the Galactic Center. Astrophys. J. 2018, 855, 70. [Google Scholar] [CrossRef]
- Hees, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Naoz, S.; Becklin, E.E.; Boehle, A.; Chappell, S.; Chu, D.; Dehghanfar, A.; et al. Testing General Relativity with stellar orbits around the supermassive black hole in our Galactic center. Phys. Rev. Lett. 2017, 118, 211101. [Google Scholar] [CrossRef] [PubMed]
- Kalita, S. The Galactic Center Black Hole, Sgr A*, as a Probe of New Gravitational Physics with the Scalaron Fifth Force. Astrophys. J. 2020, 893, 31. [Google Scholar] [CrossRef]
- Kalita, S. Scalaron Gravity near Sagittarius A*: Investigation of Spin of the Black Hole and Observing Requirements. Astrophys. J. 2021, 909, 189. [Google Scholar] [CrossRef]
- Lalremruati, P.C.; Kalita, S. Is It Possible to See the Breaking Point of General Relativity near the Galactic Center Black Hole? Consideration of Scalaron and Higher-dimensional Gravity. Astrophys. J. 2022, 925, 126. [Google Scholar] [CrossRef]
- Paul, D.; Kalita, S.; Talukdar, A. Unscreening of f(R) gravity near the galactic center black hole: Testability through pericenter shift below S0-2’s orbit. Int. J. Mod. Phys. D 2023, 32, 2350021. [Google Scholar] [CrossRef]
- Paul, D.; Bhattacharjee, P.; Kalita, S. Kerr-scalaron Metric and Astronomical Consequences near the Galactic Center Black Hole. Astrophys. J. 2024, 964, 127. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Lin, W.T.; Gu, J.A.; Chen, P. Cosmological and Solar-System Tests of f(R) Modified Gravity. Int. J. Mod. Phys. D 2011, 20, 1357–1362. [Google Scholar] [CrossRef]
- Xu, T.; Cao, S.; Qi, J.; Biesiada, M.; Zheng, X.; Zhu, Z.H. A new test of f(R) gravity with the cosmological standard rulers in radio quasars. J. Cosmol. Astropart. Phys. 2018, 2018, JCAP06(2018)042. [Google Scholar] [CrossRef]
- Wilson, C.; Bean, R. Testing f(R) gravity with scale dependent cosmic void velocity profiles. Phys. Rev. D 2021, 104, 023512. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Sheykhi, A. New black hole solutions in three-dimensional f(R) gravity. Phys. Dark Universe 2023, 40, 101174. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Specific neutral and charged black holes in f(R) gravitational theory. Phys. Rev. D 2021, 104, 124054. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Black Holes with Electric and Magnetic Charges in F(R)F(R) Gravity. Fortschr. Phys. 2023, 71, 2200091. [Google Scholar] [CrossRef]
- Hough, R.; Abebe, A.; Ferreira, S. Viability tests of f(R)-gravity models with Supernovae Type 1A data. Eur. Phys. J. C 2020, 80, 787. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Extension of the Schwarzschild black hole solution in f(R) gravitational theory and its physical properties. Eur. Phys. J. C 2024, 84, 5. [Google Scholar] [CrossRef]
- Bel, J.; Brax, P.; Marinoni, C.; Valageas, P. Cosmological tests of modified gravity: Constraints on F(R) theories from the galaxy clustering ratio. Phys. Rev. D 2015, 91, 103503. [Google Scholar] [CrossRef]
- de Martino, I.; della Monica, R.; de Laurentis, M. f(R) gravity after the detection of the orbital precession of the S2 star around the Galactic Center massive black hole. Phys. Rev. D 2021, 104, L101502. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Extension of Hayward black hole in f(R) gravity coupled with a scalar field. Phys. Dark Universe 2024, 44, 101462. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Wands, D. Metric perturbations in two field inflation. Phys. Rev. D 1996, 53, 5437–5445. [Google Scholar] [CrossRef]
- Coley, A.A.; van den Hoogen, R.J. The Dynamics of multiscalar field cosmological models and assisted inflation. Phys. Rev. D 2000, 62, 023517. [Google Scholar] [CrossRef]
- Wands, D.; Bartolo, N.; Matarrese, S.; Riotto, A. An Observational test of two-field inflation. Phys. Rev. D 2002, 66, 043520. [Google Scholar] [CrossRef]
- Do, T.Q.; Kao, W.F.; Lin, I.C. Anisotropic power-law inflation for a two scalar fields model. Phys. Rev. D 2011, 83, 123002. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Tretyakov, P.V. Inflation in a conformally-invariant two-scalar-field theory with an extra R2 term. Eur. Phys. J. C 2015, 75, 344. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D.; Faraoni, V. Reconstructing the universe history, from inflation to acceleration, with phantom and canonical scalar fields. Phys. Rev. D 2008, 77, 106005. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Zerbini, S. One-loop f(R) gravity in de Sitter universe. J. Cosmol. Astropart. Phys. 2005, 2005, JCAP02(2005)010. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Propagation of gravitational waves in Einstein-Gauss-Bonnet gravity for cosmological and spherically symmetric spacetimes. Phys. Rev. D 2024, 109, 044046. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B. Asymptotically flat vacuum solution in modified theory of Einstein’s gravity. Eur. Phys. J. C 2019, 79, 877. [Google Scholar] [CrossRef]
- Jaime, L.G.; Patino, L.; Salgado, M. Robust approach to f(R) gravity. Phys. Rev. D 2011, 83, 024039. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Nojiri, S. Slow-rotating charged black hole solution in dynamical Chern-Simons modified gravity. Phys. Rev. D 2023, 107, 064069. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H. Dirty black hole supported by a uniform electric field in Einstein-nonlinear electrodynamics-Dilaton theory. Eur. Phys. J. C 2023, 83, 406, Erratum in Eur. Phys. J. C 2023, 83, 597. [Google Scholar] [CrossRef]
- Sheykhi, A. Higher-dimensional charged f(R) black holes. Phys. Rev. D 2012, 86, 024013. [Google Scholar] [CrossRef]
- Sheykhi, A. Thermodynamics of apparent horizon and modified Friedmann equations. Eur. Phys. J. C 2010, 69, 265–269. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A.; Dehghani, M.H. Thermodynamics of higher dimensional topological charged AdS black branes in dilaton gravity. Eur. Phys. J. C 2010, 70, 703–712. [Google Scholar] [CrossRef]
- Sheykhi, A.; Dehghani, M.H.; Hendi, S.H. Thermodynamic instability of charged dilaton black holes in AdS spaces. Phys. Rev. D 2010, 81, 084040. [Google Scholar] [CrossRef]
- Cognola, G.; Gorbunova, O.; Sebastiani, L.; Zerbini, S. On the Energy Issue for a Class of Modified Higher Order Gravity Black Hole Solutions. Phys. Rev. D 2011, 84, 023515. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, R.J. Horizon thermodynamics in f(R) theory. Eur. Phys. J. C 2018, 78, 682. [Google Scholar] [CrossRef]
- Nouicer, K. Black holes thermodynamics to all order in the Planck length in extra dimensions. Class. Quantum Gravity 2007, 24, 5917–5934. [Google Scholar] [CrossRef]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Kim, W.; Kim, Y. Phase transition of quantum corrected Schwarzschild black hole. Phys. Lett. B 2012, 718, 687–691. [Google Scholar] [CrossRef]
- Chakraborty, S.; SenGupta, S. Strong gravitational lensing—A probe for extra dimensions and Kalb-Ramond field. J. Cosmol. Astropart. Phys. 2017, 2017, JCAP07(2017)045. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. D 2019, 99, 104018. [Google Scholar] [CrossRef]
- Elizalde, E.; Nashed, G.G.L.; Nojiri, S.; Odintsov, S.D. Spherically symmetric black holes with electric and magnetic charge in extended gravity: Physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames. Eur. Phys. J. C 2020, 80, 109. [Google Scholar] [CrossRef]
- Riegert, R.J. Birkhoff’s Theorem in Conformal Gravity. Phys. Rev. Lett. 1984, 53, 315–318. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. Black holes in scalar-tensor gravity. Phys. Rev. Lett. 2012, 108, 081103. [Google Scholar] [CrossRef]
- Sebastiani, L.; Zerbini, S. Static Spherically Symmetric Solutions in F(R) Gravity. Eur. Phys. J. C 2011, 71, 1591. [Google Scholar] [CrossRef]
- Perez Bergliaffa, S.E.; de Oliveira Nunes, Y.E.C. Static and spherically symmetric black holes in f(R) theories. Phys. Rev. D 2011, 84, 084006. [Google Scholar] [CrossRef]
- Gao, C.; Shen, Y.G. Exact solutions in f(R) theory of gravity. Gen. Relativ. Gravit. 2016, 48, 131. [Google Scholar] [CrossRef]
- Amirabi, Z.; Halilsoy, M.; Habib Mazharimousavi, S. Generation of spherically symmetric metrics in f(R) gravity. Eur. Phys. J. C 2016, 76, 338. [Google Scholar] [CrossRef]
- Calzà, M.; Rinaldi, M.; Sebastiani, L. A special class of solutions in F(R)-gravity. Eur. Phys. J. C 2018, 78, 178. [Google Scholar] [CrossRef]
- Oliva, J.; Ray, S. Birkhoff’s Theorem in Higher Derivative Theories of Gravity. Class. Quantum Gravity 2011, 28, 175007. [Google Scholar] [CrossRef]
- Capozziello, S.; Saez-Gomez, D. Scalar-tensor representation of f(R) gravity and Birkhoff’s theorem. Ann. Phys. 2012, 524, 279–285. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nashed, G.G.L.; Eid, A. Black Hole Solution Free of Ghosts in f(R) Gravity Coupled with Two Scalar Fields. Universe 2025, 11, 305. https://doi.org/10.3390/universe11090305
Nashed GGL, Eid A. Black Hole Solution Free of Ghosts in f(R) Gravity Coupled with Two Scalar Fields. Universe. 2025; 11(9):305. https://doi.org/10.3390/universe11090305
Chicago/Turabian StyleNashed, G. G. L., and A. Eid. 2025. "Black Hole Solution Free of Ghosts in f(R) Gravity Coupled with Two Scalar Fields" Universe 11, no. 9: 305. https://doi.org/10.3390/universe11090305
APA StyleNashed, G. G. L., & Eid, A. (2025). Black Hole Solution Free of Ghosts in f(R) Gravity Coupled with Two Scalar Fields. Universe, 11(9), 305. https://doi.org/10.3390/universe11090305





