A Proposed Test for the Gravitational Tunnel Effect

Abstract

This article addresses the problem of the tunnel effect with a gravitational potential. Specifically, the quasiclassical formulation is used here, and the Wentzel–Kramers–Brillouin approximation is applied to the potential. This allows the problem to be solved for different configurations with different values (masses, distances, etc.). The chosen values are intended to provide a clear comparison when varying the different parameters. Furthermore, feasible values are considered for practically replicating the experiment without resorting to astrophysical methods. Due to the low intensity of the gravitational force, these experiments will be difficult to replicate, but it is possible to improve some parameters at the expense of others.

1. Introduction

The quantum tunneling effect is a phenomenon that occurs when a particle moving with a certain kinetic energy E encounters an electromagnetic potential barrier of height V larger than its own kinetic energy E, and, even though $E<V$, the particle can still pass through the potential barrier, emerging on the other side. This well-known effect contradicts our classical expectation that a particle cannot pass through a potential barrier if its energy is lower than the barrier height [1,2] and has been leveraged in several applications, such as the scanning tunneling microscope, in flash memory for data storage, or in nuclear fusion, among others.

Having potential applications in the study of the quantum nature of gravity and black holes, the quantum tunneling effect has also been studied contemplating gravitational potentials without changing the theoretical nature of the problem [3,4], a phenomenon dubbed the gravitational tunneling effect. These previous works in this line establish the theoretical possibility of the phenomenon occurring with a gravitational potential.

The problem of the gravitational tunneling effect has been approached from the perspective of general relativity in several articles. In [5], it is established that Hawking (or Unruh) radiation arises as a semiclassical tunneling effect of particles through a potential barrier. In [6], it is shown that the difference between the semiclassical tunneling effect and that provided by general relativity is due to a difference in the temporal component. This is because, in general relativity, time is a dynamic coordinate (like spatial coordinates), whereas in quantum theory, time is a parameter distinct from the spatial coordinates.

Another consideration of the tunneling effect is made in [7], where it is considered a metric establishing a tunnel between a black hole and a white hole. Another interesting consideration of the tunneling effect is presented in [8]. The uncertainty principle is applied to the Klein–Gordon and Dirac equations to calculate the tunneling probability at the event horizon of a black hole. This method provides information on the type of particle that tunnels through the event horizon from the Hawking temperature associated with the black hole. In a recent article [9], it is established that the Wentzel–Kramers–Brillouin (WKB) approximation indicates that the tunneling probability from the interior towards the exterior of the event horizon of a black hole is proportional to the imaginary part of the action of the particles emitted through the horizon.

The problem of validating the gravitational tunneling effect on an astrophysical scale is that gravitational potentials have only one possible configuration and sign, in which the potential is inversely proportional to the distance from the mass generating it and is attractive. Another drawback is that, in the weak-field regime of gravity, the gravitational force is negligible compared to the electromagnetic force. So far, the gravitational tunneling effect has been studied for particles moving in the gravitational field of a black hole and astrophysical cases. In this work, we put forth an alternative configuration for the gravitational potential comprising that produced by a system of two spherical bodies separated by a constant distance. As we will see in this article, this configuration will not only allow for the experimental observation of the gravitational tunneling effect but also for its measurement in a laboratory setup. The objective of this article is thus to study the gravitational tunneling effect for moving particles in the gravitational system described above. Through a parametric study, we determine the experimental conditions for which electrons can experience a gravitational tunneling effect and the magnitude thereof. The results obtained in this research indicate that this phenomenon could be measured under various experimentally feasible conditions.

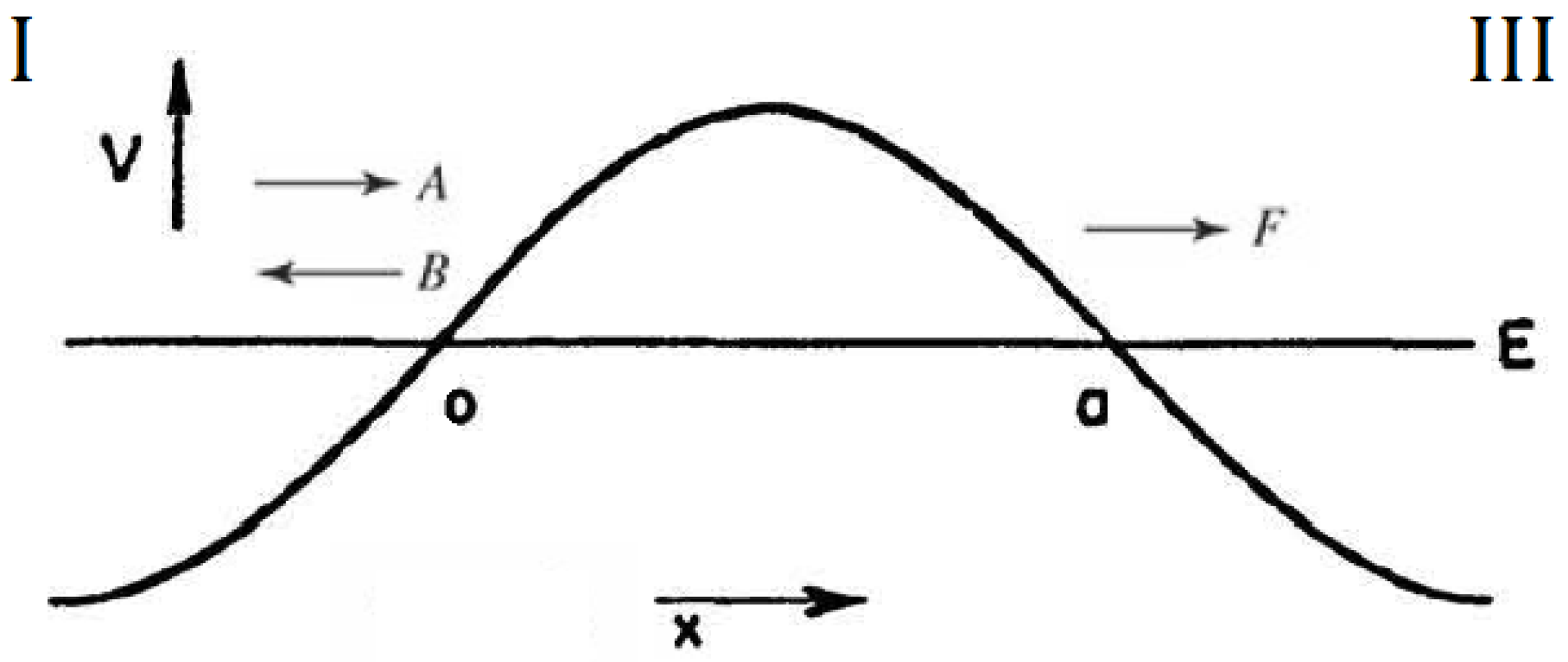
This article is organized as follows: In Section 2, a theoretical introduction to the quantum tunneling effect and the WKB approximation is provided. Section 3 addresses the gravitational tunneling effect and the methodology for the parametric study of the configuration proposed in this work, while Section 4 presents the results. Finally, the conclusions and future work are discussed in Section 5.

2. Theory

In Section 2.1, the theory of the tunneling effect produced by an ideal electromagnetic potential barrier is considered. In Section 2.2, the case in which this same potential does not have the shape of a perfect barrier is presented, with the WKB approximation being used for its solution.

2.1. Quantum Tunneling Effect

As illustrated in Figure 1, the quantum tunneling effect states that given a rectangular potential barrier

$$V\left(x\right)=\left\{\begin{array}{cc}\hfill 0& x<0\\ \hfill V& 0<x<a\\ \hfill 0& x>a\end{array}\right.$$

where a is the thickness of the potential barrier, a particle with energy E, given $E<V$, incident on the leftmost interface of the potential barrier at $x=0$, can pass through the potential barrier and emerge from its rightmost interface at $x=a$. This is a purely quantum phenomenon that does not occur in classical macroscopic physics [1,2].

If we study the problem of Figure 1, the wave functions of the particle in each region will be

$${\mathsf{\Psi }}_I\left(x\right)=A_I{e}^{{\displaystyle \frac{i{p}_{1}x}{\hslash }}}+B_I{e}^{-{\displaystyle \frac{i{p}_{1}x}{\hslash }}}$$

(1)

$${\mathsf{\Psi }}_{II}\left(x\right)=A_{II}{e}^{{\displaystyle \frac{i{p}_{2}x}{\hslash }}}+B_{II}{e}^{-{\displaystyle \frac{i{p}_{2}x}{\hslash }}}$$

(2)

$${\mathsf{\Psi }}_{III}\left(x\right)=A_{III}{e}^{{\displaystyle \frac{i{p}_{1}x}{\hslash }}}$$

(3)

where $p_1=\sqrt{2mE}$ and $p_2=\sqrt{2m(V-E)}$ are the momentum, with m being the mass of the particle and $A_i$ and $B_i$ unknown constants, where i runs as I, $II$, and $III$. These wave function configurations are chosen because in regions I and $II$ there are incident and reflected waves, whereas in region $III$, only traveling waves exist. The positive sign in the exponential function indicates that the particle moves to the right, while the negative sign means the particle moves to the left.

Considering the boundary conditions of the problem at the potential interfaces, where the wave functions must match on both sides of the potential boundary, we obtain the relation between the different undetermined constants A and B in each region. The probability that a particle incident at the left-side interface of the potential barrier, with energy $E<V$, tunnels through the potential barrier is given by the transmission coefficient T:

$$T={\displaystyle \frac{|A_{III}{|}^2}{|A_I{|}^2}}={\displaystyle \frac{16e^{-\frac{2p_{2}a}{\hslash }}}{[1+{(p_2/p_1)}^2][1+{(p_1/p_2)}^2]}}$$

(4)

For a better understanding of the derivation of Equation (4), the reader is referred to references [1,2,10].

2.2. WKB Approximation

In this section, we address the WKB method, which is a technique for obtaining approximate solutions to the time-independent Schrödinger equation in one dimension. Let the potential barrier $V\left(x\right)$ vary slowly compared to the wavelength associated with the particle $\lambda$, i.e., $\lambda \gg a$, so that the potential barrier can be discretized into a set of small potential barriers that can be integrated as illustrated in Figure 2. Assuming, in addition, that $E<V\left(x\right)$ in $0<x<a$, the wave function of the particles takes the form

$$\mathsf{\Psi }\left(x\right)=A{e}^{\pm kx}$$

(5)

with $k=\sqrt{2m(V-E)}/\hslash$ and $\lambda =2\pi /k$. As a result of the slow variation in the condition of the potential barrier, the constants A and the wave number k are also slowly varying functions of x.

Given a generic potential $V\left(x\right)$, as shown in Figure 2, which creates a potential barrier, it is possible to apply the WKB approximation to obtain the transmission coefficient T:

$${\mathsf{\Psi }}_I\left(x\right)=A{e}^{ikx}+B{e}^{-ikx}$$

(6)

$${\mathsf{\Psi }}_{III}\left(x\right)=F{e}^{ikx}$$

(7)

$$T={\displaystyle \frac{{\left|F\right|}^2}{{\left|A\right|}^2}}$$

(8)

Applying the WKB approximation to this potential $V\left(x\right)$ yields the following result for the transmission coefficient:

$$T\cong exp\left({\displaystyle \frac{-2}{\hslash }}{\int }_0^a\left|p\left(x\right)\right|dx)\right)$$

(9)

where $p\left(x\right)=\hslash k$. For a more detailed derivation of this transmission coefficient, see references [2,10].

The formal condition necessary for the application of the WKB approximation is that the barrier has sufficient thickness and height [2], determined by the following relation:

$${\displaystyle \frac{1}{\hslash }}{\int }_0^a\sqrt{2m\left(V\right(x)-E)}dx\gg 1$$

(10)

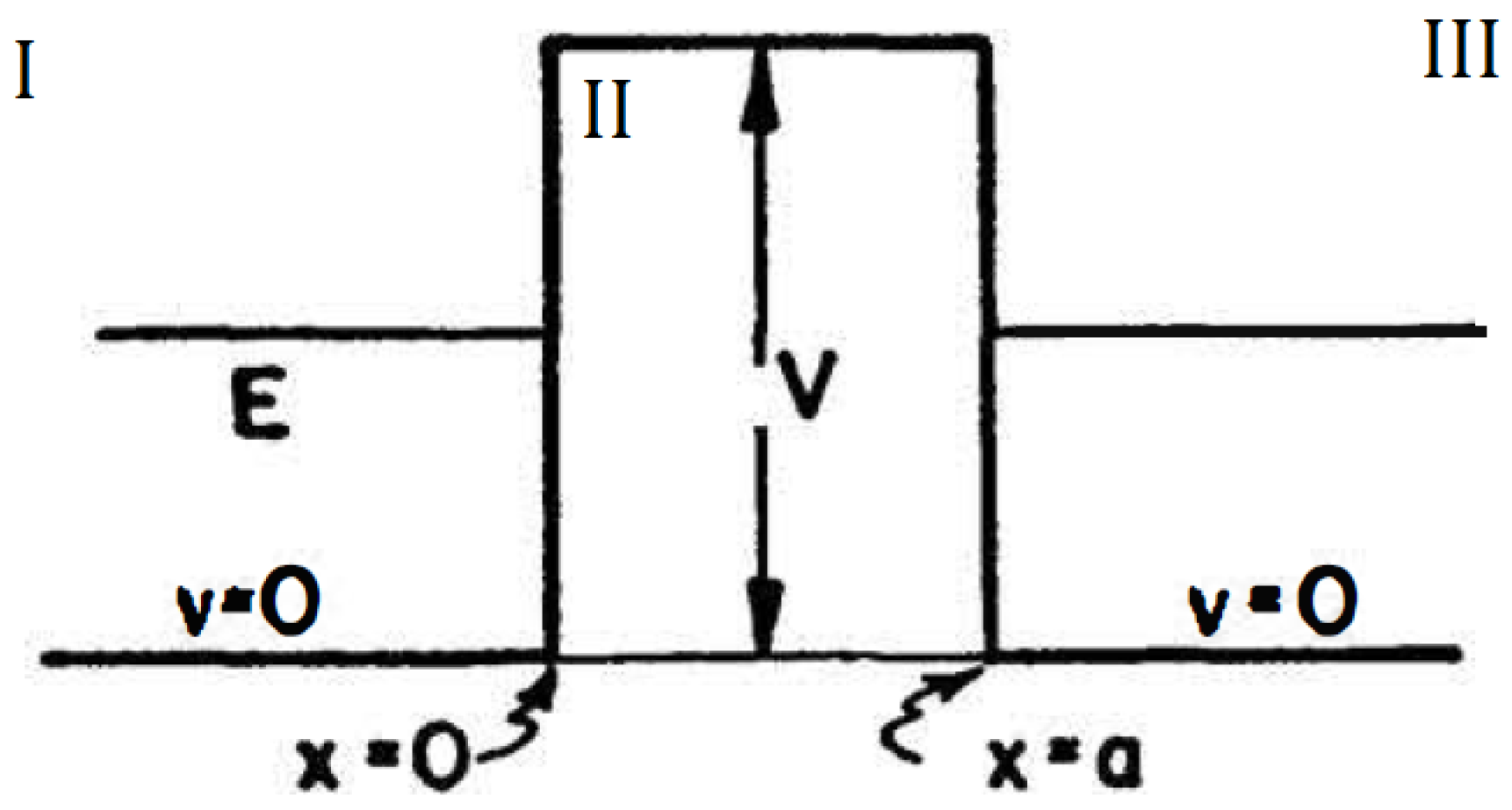
3. Method

This section explores the gravitational tunneling effect. In principle, there are no restrictions on the problem conditions that would prevent this phenomenon from occurring with a gravitational potential. The gravitational potential has the disadvantage compared to the electromagnetic one that it is more difficult to manipulate the sources to create it. While the electromagnetic potential can take both positive and negative values due to positive and negative charges, the gravitational potential can only have one sign (negative). Additionally, there is the further disadvantage that the gravitational force is much weaker than the electromagnetic force.

The gravitational potential produced by a spherically symmetric body of mass M, depending on the distance r, is given by the following expression:

$$V_s\left(r\right)=-{\displaystyle \frac{GM}{r}}$$

(11)

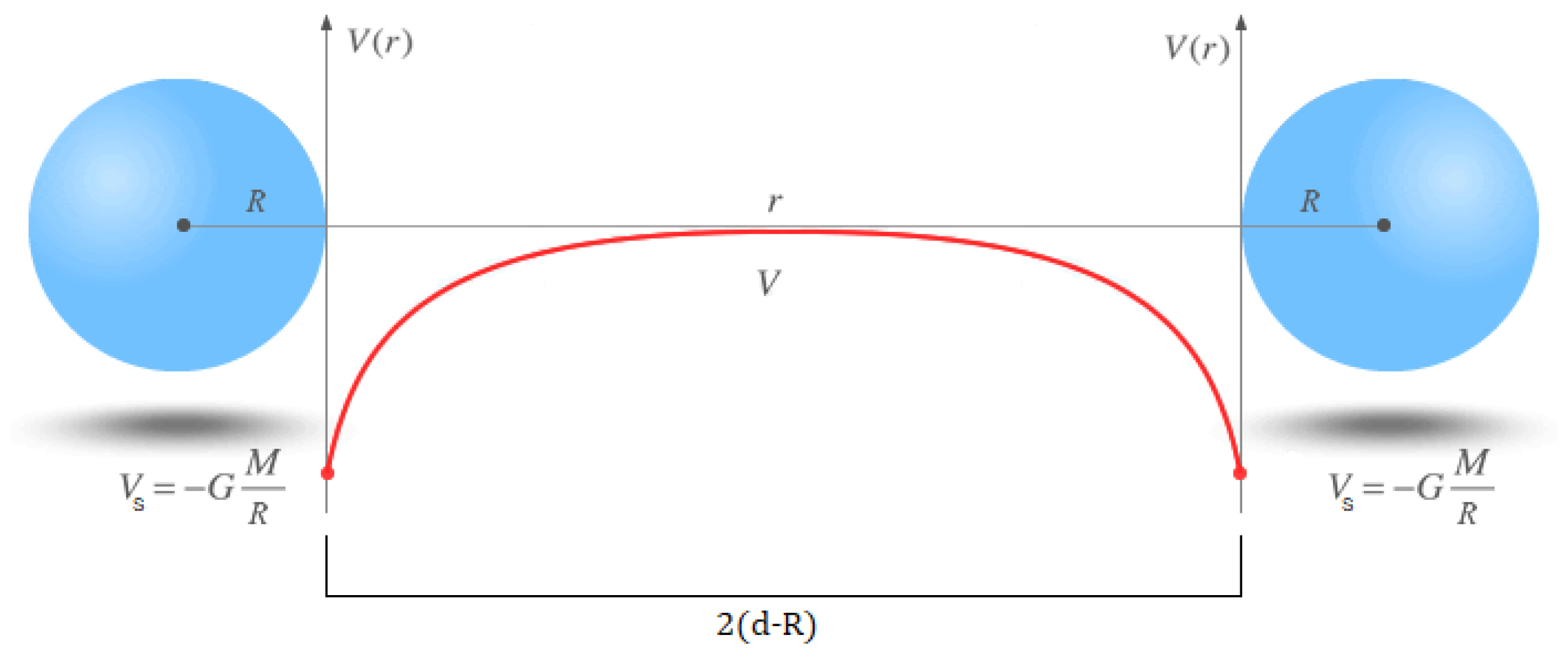
It is impossible to create a gravitational potential barrier classically with a single mass. However, it is possible to create a gravitational potential barrier by superposing the potentials created by two point masses close to each other (Figure 3) [11].

$$V\left(r\right)=-GM\left({\displaystyle \frac{1}{{[{(r-d)}^2]}^{1/2}}}+{\displaystyle \frac{1}{{[{(r+d)}^2]}^{1/2}}}\right)$$

(12)

where $2d$ is the separation between the two point masses that create the potential.

If instead of point masses, we consider that the potential is created by real masses with radius R, the potential shown in Figure 4 is obtained. There is a potential barrier between the two masses, with a finite value at the surface of each sphere. This gravitational potential barrier is usually too large in length, in quantum terms, for the tunneling effect to occur. We can reduce the distance $2d$ between the two spheres creating the potential so that the width of the potential barrier decreases, thus bringing this potential to values where the quantum tunneling effect occurs.

The particle launched, with mass m, used for the calculations was an electron, without taking electromagnetic interactions into account. A priori, the experiment could be replicated with another electromagnetally neutral massive particle, such as a neutron or hydrogen atom, without any theoretical inconvenience. It may be easier experimentally to use neutral particles than charged ones, as were used in [12] to demonstrate interference of neutrons in a gravitational field. We will use electrons, but this could be changed if necessary. The main reason an electron was used is that it is a less massive particle. The greater the mass of the particle, the lower its tunneling capacity, as indicated by Equation (5).

Due to the difference in nomenclature between electromagnetics and gravity, some terms of concordance must be included, since in the electromagnetic tunnel effect the potential is usually given in units of electron volts (eV) instead of (J/Kg) as in the gravitational case. Taking into account that 1 eV = 1.6·10⁻¹⁹ J and that the energy/potential conversion in the gravitational case will be $V_T=m$ V, a direct relationship is obtained with which to obtain the value of k in Equation (5) without dimensional problems.

Therefore, for the conditions of gravitational tunneling effect to be met with this potential (12), which allows the application of the WKB approximation, a particle with energy $E<V_T\left(r\right)$ must be launched from the surface of one of the spheres. This energy must be bounded between the minimum and maximum value of the potential (in the same way as in the case of electromagnetic quantum tunneling). There should then be a certain probability T that the particle tunnels through the potential barrier, given by (9).

The condition to apply the WKB approximation to the given potential, as mentioned in Section 2.2, is that relation (10) is fulfilled.

In our experiment, we will consider spherical masses with radii ranging from 0.02 m to 0.05 m and masses between 0.6 Kg and 10 Kg, which could be implemented with tungsten of density 19,250 Kg/m³. Additionally, the distance ranges will be limited between 0.6 m and 2.4 m. Under these conditions, the value of the condition (10) will be around ${10}^{14}\gg 1$. Therefore, it is completely valid to apply the WKB approximation to the gravitational potential in this situation.

In gravitational terms, for the case of two identical spheres (Figure 4), the problem can be seen as follows. If a particle is launched from the surface of one sphere with energy less than that required to reach exactly the midpoint between the two spheres and thus “escape” the potential, there is a probability that the particle tunnels through the potential. That is, with energy less than the particle’s escape energy, it could escape the potential and fall onto the surface of the other sphere at some point. This sounds quite strange, but in principle, nothing forbids it.

By imposing different values for the coefficient T in (9), we can adjust the other parameters of our problem. If we consider an electron, the mass would be fixed by the electron’s own mass. Thus, our problem would be limited to varying the integration distance of the barrier a, which is related to the difference between the potential and the energy.

The ideal potential barrier for tunneling to occur would be a step potential. Since this is impossible to create in the gravitational case, we will seek to create the steepest possible potential. This will be achieved by using the densest possible mass. For our problem simulations, two tungsten spherical masses will be used, which is one of the densest materials available. The greater the density of the material creating the gravitational potential, the larger and more abrupt the barrier produced will be, and this will increase the probability of tunneling. For this reason, we use a very dense material such as tungsten.

In this experimental setup, it is possible to calculate the velocity that must be imparted to the particle from the surface of one of the spheres so that it escapes the influence of that sphere and falls onto the other. This is what we will call the escape velocity for the joint potential $V_T$. This speed can be calculated in the same way as the escape velocity of a body with mass, using the conservation of energy. The difference in this case will be the potential used, which is the set $V_T$. Therefore, in this case, we will have

$$E_{k_0}+E_{p_0}=E_{p_f}$$

(13)

where $E_{k_0}$ is the initial kinetic energy of the particle with mass m at the surface of the initial sphere, $E_{p_0}$ is the gravitational potential energy of the particle at the surface of the initial sphere, and $E_{p_f}$ is the potential energy at the end point. To obtain the escape velocity, energy conservation (13) will be used, imposing the condition $E_{p_f}=m{V}_{T_{max}}$. To calculate the initial velocity when a lower energy E is provided for the tunnel effect to occur, the velocity that must be provided will be calculated by imposing $E_{p_f}=m{V}_{T_E}$, where $V_{T_E}$ is the potential value $V_T$ for the energy E.

Having fixed all these conditions in our problem, we can find the values of energy E needed for tunneling to occur, being able to play with the size of the spheres and the distance $2d$ between them.

4. Results

Having theoretically established the possibility of the gravitational tunneling effect, we can proceed to perform calculations for the ranges of values in which the effect may occur, attempting to choose appropriate values to replicate the process in a real experiment.

One example of a configuration that may be feasible for experimental replication is two identical tungsten spherical masses with radii of 0.02 m and a separation between them of 0.83686 m. The region of interest for our problem will be the straight line between the two masses, as this is the path where the potential barrier with the steepest potential change will occur. With this configuration, both masses create the potential observed in Figure 5. This can be clearly interpreted as a potential barrier to which the WKB approximation described above can be applied.

To calculate the different values in the table, condition (13) was used to calculate the velocities and Equation (9) was used to calculate the transmission coefficient with respect to the distance between the masses. This equation establishes a direct relationship between the transmission coefficient T, the potential created V, and the particle energy E. Distance values were sought that would yield transmission values similar to those obtained in the electromagnetic cases. In addition, an attempt was made to fix values. This was conducted deliberately in order to maintain the same values for certain parameters, such as the transmission coefficient in the latter cases, to see how the problem varies for this fixed value when changing the mass and/or the percentage of V by the value of E. All values in the table are theoretical considerations to clarify the phenomenon and obtain an idea of the values for which the phenomenon occurs and the trends it follows.

From this, different configurations of the problem can be established to obtain various results.

Table 1. Different configurations where the gravitational tunneling effect will be significant.

						Escape
	Mass of	Distance		Percentage		Velocity
Radius of	the	Between	Transmi	of V for	Velocity	for the
Spheres	Spheres	Spheres	-ssion	the Value	(m/s)	Joint
(m)	(Kg)	(m)	Coefficient	of E	$·{\mathbf{10}}^{-\mathbf{5}}$	Potential
						${\mathbf{V}}_{\mathbf{T}}$ (m/s)
						$·{\mathbf{10}}^{-\mathbf{5}}$
0.02	0.64507	0.83686	0.75	0.7	$5.66662$	$6.32396$
0.02	0.64507	0.60450	0.75	0.5	$5.01125$	$6.23133$
0.02	0.64507	1.52505	0.50	0.7	$5.58712$	$6.43178$
0.02	0.64507	1.13164	0.50	0.5	$4.84110$	$6.38632$
0.02	0.64507	2.37535	0.30	0.7	$5.55237$	$6.47840$
0.02	0.64507	1.78575	0.30	0.5	$4.76815$	$6.45082$
0.05	10.07928	1.67917	0.30	0.7	$14.27438$	$15.66195$
0.05	10.07928	1.19664	0.30	0.5	$12.76315$	$15.35735$
0.05	10.07928	0.96832	0.30	0.3	$11.13673$	$15.10500$

shows a wide range of problem configurations where the tunneling condition in the gravitational potential is met, with different probabilities and for different energies.

5. Conclusions

This article has provided a theoretical introduction to the tunneling effect and the WKB approximation, which is then applied to a gravitational-type potential in order to have an analog of the tunneling phenomenon with a gravitational potential.

In principle, theoretically, the process can occur, and it would be interesting to replicate it experimentally. This article has outlined the guidelines to replicate it experimentally, with the advantage of being able to change some parameters according to experimental limitations. The experimental setup would not be too complex to implement. The material, in our case tungsten, can be changed, as well as the size of the spheres creating the potential. For the particle (electron) to take a straight line between both masses, it is sufficient to open a hole through one of the spheres and launch the electron through it. The initial speed of the electron could be slowed down using electromagnetic methods. This is yet another parameter we can adjust in our problem.

The main drawback would be that this experiment should be performed in microgravity, in addition to taking into account the gravity of the surrounding setup. Even so, it may be feasible to replicate it experimentally without resorting to astrophysical cases.